知识点32 洛必达法则求极限
32洛必达法则共9页word资料
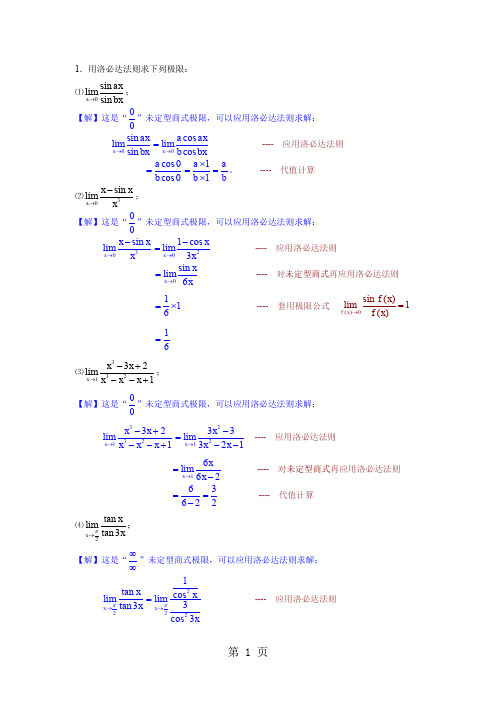
1．用洛必达法则求下列极限：⑴0sin limsin x axbx→；【解】这是“00”未定型商式极限，可以应用洛必达法则求解：0sin lim sin x ax bx →0cos limcos x a axb bx→= ---- 应用洛必达法则 cos 0cos 0a b =11a b ⨯=⨯ab=。
---- 代值计算 ⑵30sin lim x x x x→-； 【解】这是“00”未定型商式极限，可以应用洛必达法则求解：30sin lim x x x x →-201cos lim3x xx →-= ---- 应用洛必达法则 0sin lim6x xx→= ---- 对未定型商式再应用洛必达法则 116=⨯ ---- 套用极限公式 ()0sin ()lim1()f x f x f x →= 16=⑶332132lim 1x x x x x x →-+--+； 【解】这是“”未定型商式极限，可以应用洛必达法则求解： 332132lim 1x x x x x x →-+--+22133lim 321x x x x →-=-- ---- 应用洛必达法则 16lim62x xx →=- ---- 对未定型商式再应用洛必达法则63622==- ---- 代值计算 ⑷2tan limtan 3x xxπ→； 【解】这是“∞∞”未定型商式极限，可以应用洛必达法则求解： 2tan lim tan 3x xx π→2221cos lim 3cos 3x x xπ→= ---- 应用洛必达法则222cos 3lim3cos x xx π→= ---- 整理繁分式 22cos3(sin 3)3lim32cos (sin )x x x x x π→⋅-⋅=⋅⋅- ---- 对未定型商式再应用洛必达法则2sin 6limsin 2x xxπ→= ---- 化简复杂分式 26cos6lim2cos 2x xxπ→= ---- 对未定型商式再应用洛必达法则3cos3cos ππ=---- 代值计算3=⑸2(ln )lim x x x→+∞； 【解】这是“∞∞”未定型商式极限，可以应用洛必达法则求解： 2(ln )limx x x→+∞12ln lim 12x x x x→+∞⋅= ---- 应用洛必达法则 4ln limx xx→+∞= ---- 化简繁分式14lim 12x x x→+∞= ---- 对未定型商式再应用洛必达法则 8limx x→+∞= ---- 化简繁分式 0=⑹2ln()2lim tan x x x ππ+→-； 【解】这是“∞∞”未定型商式极限，可以应用洛必达法则求解：2ln()2lim tan x x x ππ+→-2212lim 1cos x x xππ+→-= ---- 应用洛必达法则 22cos lim 2x x x ππ+→=----- 化简繁分式22cos (sin )lim 1x x x π+→-= ---- 对未定型商式再应用洛必达法则2cossin22ππ=-0= ---- 代入计算⑺212lim x x x e →；【解】这是“0⨯∞”未定型极限，应化为商式极限后应用洛必达法则求解：212lim xx x e →2102lim 1x x e x →= ---- 化为商式后，成为“∞∞”未定型商式极限 212021()'lim1()'x x e x x→= ---- 应用洛必达法则 2211lim x x e →+∞= ---- 化简繁分式 =+∞ ---- 代入计算⑻0lim cot x x x →；【解】这是“0⨯∞”未定型极限，应化为商式极限后应用洛必达法则求解：lim cot x x x →0limtan x xx →= ---- 化为商式后，成为“∞∞”未定型商式极限021lim 1cos x x →= ---- 应用洛必达法则 20limcos x x →= ---- 化简繁分式2cos 01== ---- 代入计算⑼2lim(sec tan )x x x π→-；【解】这是“∞-∞”未定型极限，应化为商式极限后应用洛必达法则求解：2lim(sec tan )x x x π→-21sin lim()cos cos x x x xπ→=- ---- 为通分化为商式作准备 21sin limcos x xx π→-= ---- 成为“00”未定型商式极限2cos limsin x xxπ→-=- ---- 应用洛必达法则cos 20sin2ππ== ---- 代入计算⑽11lim()1ln x x x x→--； 【解】这是“∞-∞”未定型极限，应化为商式极限后应用洛必达法则求解：11lim()1ln x x x x→--1ln (1)lim(1)ln x x x x x x →--=- ---- 通分化为商式，成为“00”未定型 1ln 11lim1ln x x x x x→+-=-+---- 应用洛必达法则1ln limln 1x x xx x x →=+- ---- 化简繁分式，成为“00”未定型 1ln 1limln 11x x x →+=++ ---- 应用洛必达法则 011022+==+ ---- 代入计算 ⑾tan 0lim xx x +→；【解】这是“00”幂指函数未定型极限，应化为商式极限后应用洛必达法则求解： 【解法一】应用对数法，令tan xy x=，则tan ln ln ln tan ln cot xxy xx x x===， 于是，00ln lim ln lim cot x x xy x ++→→= ---- 成为“∞∞”未定型021lim 1sin x x x+→=- ---- 应用洛必达法则20sin lim x x x +→= ---- 化简繁分式，成为“00”未定型 02sin cos lim 1x x x+→= ---- 应用洛必达法则2sin0cos00== ---- 代入计算得到 0l i m l n 0x y +→=，亦即0ln lim 0x y +→=， 从而有 0l i m 1x y e +→==，亦即tan 0lim 1xx x +→=。
3.2 洛必达法则
f '( x ) 存在 及 g' ( x ) 都存在且 g' ( x ) ≠ 0; (3) lim x→a g ' ( x ) →
(或为无穷大 , 那么 或为无穷大), 或为无穷大
f ( x) f '( x ) lim . = lim x →a g ( x ) x →a g' ( x )
证 因函数在某点的极限是否存在 与函数在该点 取何值无关, 取何值无关, 故可补充定义 f (a ) = g (a ) = 0. 根据定理的条件, 根据定理的条件, 知函数 f ( x ) 与 g ( x ) 在以 a 与 x
f ( x ) f ( x ) − f (a ) f ' (ξ ) = = (ξ 在 x 与 a 之间 之间), g ( x ) g ( x ) − g (a ) g' (ξ )
又当 x → a 时, 有 ξ → a , 所以
f ( x) f ' (ξ ) lim = A. 证毕. = lim 证毕. x →a g ( x ) ξ → a g' (ξ )
e x − e−x − 2 x . 例3 求 lim x →0 x − sin x
解
e x − e − x − 2 x = lim e x + e − x − 2 lim x →0 x →0 1 − cos x x − sin x
e x − e−x = lim x → 0 sin x e x + e−x = lim x → 0 cos x
故洛必达法则失效, 不能使用. 但原极限是存在的, 使用. 洛必达法则失效, 不能使用 但原极限是存在的, 可用下法求得 求得: 可用下法求得:
1 x sin lim x sin 1 x = lim( x ⋅ x sin 1 ) = x→0 x lim x → 0 sin x x → 0 sin x x lim sin x x →0 x 0 = 0. = 1
最新32洛必达法则汇总
32洛必达法则1．用洛必达法则求下列极限：⑴«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...»«Skip Record If...»«Skip Record If...»。
---- 代值计算⑵«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 套用极限公式«Skip Record If...»«Skip Record If...»⑶«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 代值计算⑷«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 整理繁分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 化简复杂分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 代值计算«Skip Record If...»⑸«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...»⑹«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...»«Skip Record If...» ---- 代入计算⑺«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 化为商式后，成为“«Skip Record If...»”未定型商式极限«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 代入计算⑻«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 化为商式后，成为“«Skip Record If...»”未定型商式极限«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 代入计算⑼«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 为通分化为商式作准备«Skip Record If...» ---- 成为“«Skip Record If...»”未定型商式极限«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 代入计算⑽«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 通分化为商式，成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式，成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 代入计算⑾«Skip Record If...»；【解】这是“«Skip Record If...»”幂指函数未定型极限，应化为商式极限后应用洛必达法则求解：【解法一】应用对数法，令«Skip Record If...»，则«Skip Record If...»，于是，«Skip Record If...»---- 成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式，成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 代入计算得到 «Skip Record If...»，亦即«Skip Record If...»，从而有 «Skip Record If...»，亦即«Skip Record If...»。
洛必达法则
6 cos 6 x 3. = = lim π x → 2 cos 2 x
2
注意:洛必达法则是求未定式的一种有效方法, 注意:洛必达法则是求未定式的一种有效方法, 但与其它求极限方法结合使用,效果更好. 但与其它求极限方法结合使用,效果更好. 例6 解
tan x x . 求 lim 2 x → 0 x tan x
0 ( ) 0
(tan x )′ sec2 x = 1. 原式 = lim = lim x →0 x→0 → ( x )′ 1
x3 3 x + 2 . 例2 求 lim 3 2 x →1 x x x + 1
0 ( ) 0
3 x2 3 6x 3 解 原式 = lim 2 = lim = . x →1 3 x 2 x 1 x →1 6 x 2 2
2
1 ln(1 + ) x ; 2, 2, lim x → +∞ arctan x
3,lim x cot 2 x ;
x →0
2 1 ); 4, 4,lim( 2 x →1 x 1 x 1
1 tan x 6, 6, lim ( ) ; x → +0 x
5, lim x
x → +0
sin x
;
2 7, lim ( arctan x) x . x → +∞ π
sec 2 x 1 tan x x = lim 原式 = lim 2 3 x →0 x →0 3x x tan x 1 2 sec 2 x tan x 1 = lim = lim = . x →0 6x 3 x →0 x 3
0 二, ∞ , ∞ ∞ ,0 ,1 , ∞ 型未定式解法
0 0
∞
关键:将其它类型未定式化为洛必达法则可解决 关键: 的类型 ( 0 ), ( ∞ ) .
会用洛必达法则求不定式的极限`f
说明： 1 把定理中的“ xa ”换成“ x ” 把条件 (2)换成“当|x|>N时f(x)和g(x)都可导且g(x)0” 结论仍然成立
2
f ( x) 0 如果 仍属 型，且 f ( x), F ( x) 满足 g ( x) 0
f ( x) f ( x) f ( x) lim lim lim . x a g ( x ) x a g ( x) x a g ( x)
2
0 ( ) 0
3x 3 6 x 3 解 原式 lim 2 lim . x 1 3 x 2 x 1 x 1 6 x 2 2
注意: 不是未定式不能用洛必达法则 !
6 lim 1 x1 6
“零比零”型不定式的定值法
x sin x 例 3 例 3 求 lim 3 x0 x x sin x lim 1 cos x lim sin x 1 解 解 lim 3 2 x0 x0 3x x0 6x x 6
ln a1 ln a2 n ln(a1a2 an )
1 n
ln an
故 a a a l i m( ) x0 n
x 1 x 2 x n 1 x
n a1a 2 a n
•应注意的问题 5. 本节定理给出的是求不定式的一种方法 当定理条 件满足时 所求的极限当然存在(或为) 但定理条件不 满足时 所求极限却不一定不存在 x sin x 例 10 例 11 求 lim x x (x sin x) lim 1 cos x 不存在 解 解 因为极限 lim x 1 x (x) 所以不能用洛必达法则 但其极限是存在的 sin sin sin x x x x x sin sin sin x x x lim lim lim x lim lim lim(1 (1 (1 )) ) 1 1 1 xx x xx x x x x x x x
洛必达法则的内容
洛必达法则
一、洛必达法则的基本形式
洛必达法则是微积分中的一个重要定理，用于解决0/0或无穷/无穷的极限问题。
其基本形式为：如果函数f(x)和g(x)满足以下条件：
1. f(x)和g(x)在某点a的某个邻域内可导；
2. g'(x)不等于0；
3. 存在一个实数点b，使得f(b)=0；
4. 存在一个实数点c，使得g(c)=0。
那么，当x趋近于a时，f'(x)/g'(x)的极限等于f(a)/g(a)。
二、洛必达法则的推导过程
洛必达法则的推导过程涉及到极限、导数和微分的知识。
其证明过程为：根据泰勒公式，f(x)和g(x)都可以展开为泰勒级数，然后通过比较系数，可以证明f'(x)/g'(x)的极限等于f(a)/g(a)。
三、洛必达法则的应用范围
洛必达法则可以应用于解决0/0或无穷/无穷的极限问题。
具体来说，当分母或分子为无穷大时，可以通过求导数的方法来解决极限问题。
此外，洛必达法则还可以应用于一些其他类型的极限问题，例如求定积分、不定积分等。
四、洛必达法则的局限性
虽然洛必达法则是微积分中的一个重要定理，但是它也存在一些局限性。
首先，洛必达法则只适用于0/0或无穷/无穷的极限问题，对于其他类型的极限问题无法应用。
其次，在使用洛必达法则时需要注意满足其前提条件，否则可能导致错误的结果。
此外，洛必达法则也无法应用于一些复杂的极限问题，例如涉及到多个变量或多个函数的极限问题。
因此，在使用洛必达法则时需要结合其他方法来解决复杂的极限问题。
极限的计算方法洛必达法则和泰勒展开
极限的计算方法洛必达法则和泰勒展开洛必达法则和泰勒展开是数学中极限的计算方法，它们在求解复杂函数的极限问题时非常有用。
本文将详细介绍这两种计算方法的原理和应用。
一、洛必达法则洛必达法则是一种计算不定型极限的方法，它是由17世纪法国数学家洛必达提出的。
当我们计算一个函数的极限时，如果得到的是0/0或无穷大/无穷大的形式，就可以运用洛必达法则来求解。
洛必达法则的思想是利用两个函数的导数之商来逼近函数的极限，具体步骤如下：1. 若极限形式为0/0或无穷大/无穷大，先对分子函数和分母函数分别求导；2. 如果导数的极限存在，即可得到原极限的结果。
如果导数的极限不存在，或者求导后的函数仍然为0/0或无穷大/无穷大的形式，就可以继续使用洛必达法则。
以下是一个应用洛必达法则求解极限的示例：设函数f(x) = (sinx - x)/x^3，求lim(x→0) f(x)的极限。
解：首先对函数f(x)分子分母求导，得到f'(x) = (cosx - 1)/x^3 - 3sinx/x^4。
然后计算极限lim(x→0) f'(x)，仍然得到0/0的形式。
再次对f'(x)进行求导，得到f''(x) = (-2sinx - 9cosx)/x^4 +12sinx/x^5。
继续计算极限lim(x→0) f''(x)，仍然得到0/0的形式。
最后再对f''(x)求导，得到f'''(x) = (-16sinx - 4cosx)/x^5 -60cosx/x^6。
继续计算极限lim(x→0) f'''(x)，得到极限值为-4/3。
因此，lim(x→0) f(x)的极限为-4/3。
二、泰勒展开泰勒展开是一种将函数在某点附近进行多项式逼近的方法。
根据泰勒定理，如果一个函数在某点处存在各阶导数，则可以用一个多项式逼近该函数。
泰勒展开的公式如下：f(x) = f(a) + f'(a)(x - a)/1! + f''(a)(x - a)^2/2! + ... + f^n(a)(x - a)^n/n! + R_n(x)其中，f(a)表示函数在点a处的函数值，f^(n)(a)表示函数在点a 处的n阶导数，R_n(x)为余项。
用洛必达法则求下列极限(学习资料)
x0 x
x0 1
x0 1 x
(2) lim e x ex lim e x ex 2 x0 sin x x0 cos x
(3) lim sin x sin a lim cos x cos a
xa x a
xa 1
(4) lim sin 3x lim 3cos 3x 3 x tan 5x x 5sec2 5x 5
习题 32 1 用洛必达法则求下列极限 (1) lim ln(1 x) x0 x (2) lim e x ex x0 sin x (3) lim sin x sin a xa x a (4) lim sin 3x x tan5x
(5) lim ln sin x x ( 2x)2
2
x x0
x0
2 验证极限 lim x sin x 存在 但不能用洛必达法则得出 x x
知识类+
3
解 lim x sin x lim (1 sin x) 1 极限 lim x sin x 是存在的
x x
x
x
x x
但 lim (x sin x) lim 1 cos x lim (1 cos x) 不存在不能用洛必达法则
x
x x 1
x
1
x x a x 1
x
x2
所以
lim (1
a)x
lim
x ln(1 a )
ex
ea
x
x
x
(15)因为 lim xsin x lim esin xln x
x0
x0
1
而
lim sin x ln x lim ln x lim
x
lim sin 2 x 0
x0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 0 0
由此可见 lim(
x 0
1 a 2bx) 1 a 0 ，故 a 1 ； 1 x
1 1 1 2b a 2bx a 1 1 2bx 0 0 1 2b (1 x) 2 1 x 1 x lim 又 2 lim ，则 lim x 0 x 0 x 0 2 2 2x 2x 5 b . 2
+
ln( e x 1)
e
x 0+ ln( e
lim
ln x
x
x 0 +
lim
1)
e
e
x 0 +
lim
e x 1 xe x
e x0+ xe e x0+ e e .
x x
lim
x
lim
0
解：(C). 例32.9(难度系数0.4) 设 lim
ln(1 x) (ax bx 2 ) 2 ，则( ). x 0 x2
5 2 5 (C) a 0, b 2
(A) a 1, b
(B) a 0, b 2 (D) a 1, b 2
解析：对已知极限利用洛必达法则求解可得
解析：本题属于“ 00 ”型极限，通过 u v ev ln u 变换，化为“ 穷小代换和洛必达法则求解即可.
解： lim x ( x
x 0
x
1)
lim e( x
x 0
x
1) ln x
.
x 0
lim ( x x 1) ln x lim (e x ln x
x 0
x
1)
e0 1 .
1
例32.12(难度系数0.2) 求 lim x
x 0+
ln( e x 1)
.
”型极限利用等价无
解析：本题属于“ 00 ”型极限，通过 u v ev ln u 换底，化为“ 穷小代换和洛必达法则求解即可.
1 x ex e x 1
1
解： lim x
x 0
学科：高等数学
第三章 微分中值定理与导数的应用
知识点32
相关概念、公式定理或结论
● ● ●
洛必达法则求极限
定义 ** 定理 ** 结论 **
考频：5
知识点32 配套习题
例32.1(难度系数0.4) 下列极限中能用洛必达法则的有( ).
x 2 sin sin x 1 x
(A) lim
x 0
(B) lim x( arctan x)
1 2 3 2ln 3 ln 9 ， ln 3 lim x x 1 1 3
x
所以 lim (3 9 ) = lim e
x x x
1 x x
1 ln(3x 9c ) x
=e
x
lim
ln(3x 9 x ) x
x
2
(C) lim
x sin x x x sin x
(D) lim
x sin x x x2
1 1 1 ( x 2 sin ) ' 2 x sin cos x lim x x ， lim cos 1 不存在，因此对(A)中 解析：(A)由于 lim x 0 x 0 (sin x ) ' x 0 x cos x
0 0
4
arctan 1 x
1 1
1 1 arctan x lim 4 1 t t 0 t
lim
t 0
1 1 1 1 2 (1 t ) 2 2 1 ( ) 1 t
x
例32.11(难度系数0.4) 求极限 lim x ( x
x 0
1)
.
”型极限利用等价无
x x 1 1 ln(3x 9c )
”型极限后利用洛必
=e
x
lim
ln(3x 9 x ) x
，
ln(3x 9 x ) 3x ln 3 9 x ln 9 3x 2 9 x lim lim ln 3 x x x x 3x 9 x 3x 9 x lim
极限不能用洛必达法则.
(B)由于 lim x( arctan x) lim 2
x
arctan x 1 x
2
x
lim
x
1 1 x 2 1 ，极限可用洛必达 1 2 x
法则求出. (C)由于 lim
1 cos x ( x sin x) ' 1 cos x ，而 lim 不存在，因此(C)中极限不 lim x x 1 cos x ( x sin x) ' 1 cos x
解：(B). 温馨提示:对于洛必达法则,需要注意“瞻前顾后”，“瞻前”指在用前确认是“ ”或“
”未定式,不是以上未定式不能用, 0 0
“顾后”指的是用后极限存在或为 ,否则失效.
1 cos 2 x ). 2 sin x x2
例32.2(难度系数0.2，2004年数学二真题) 求 lim(
lim
sin 2 x cos 2 x 2 1 1 x lim 2 x 0 sin x 2 2 1 x2
例32.4(难度系数0.2) 求 lim (3x 9 x ) x .
x
1
解析：本题属于“ 0 ”型极限，通过 u v ev ln u 换底，化为“ 达法则求解即可. 解： lim (3x 9 x ) x = lim e x
= eln 9 9 .
1 ln 1 x 例32.5(难度系数0.2) 求极限 lim . x arc cot x 0 解析：本题属于“ ”型极限，通过等价无穷小代换和洛必达法则求解即可. 0
1 1 2 2 x x lim 1 x 1 . 解：原式 lim lim x arc cot x x x 1 x2 2 1 x
0 0
例32.3(难度系数0.4) 求极限 lim
x 0
arcsin x sin x . arctan x tan x
解析：本题属于“ ”型极限，先利用洛必达法则求解，整理后再利用分式有理 化即可.
cos x 2 arcsin x sin x 1 x 解： lim lim x 0 arctan x tan x x 0 1 1 2 1+x cos 2 x 1
sec2 t 1 3t 2
e
tan 2 t lim 2 t 0 3 t
e 3 ， （洛必达法则）
n2
1
1 1 根据函数极限与数列极限的关系,得 lim n tan e 3 . n n
例32.7(难度系数0.2) 求极限 lim
0 0
Байду номын сангаас
e x esin x . x 0 x sin x
x 0
解析：本题属于求“ ”型极限，先通分化为“ ”型极限，再利用等价无穷 小代换与洛必达法则求解即可.
1 cos 2 x x 2 sin 2 x cos 2 x lim 解： lim( 2 2 ) lim x 0 sin x x 0 x 0 x x 2 sin 2 x 1 2 x sin 4 x 1 cos 4 x 2 lim lim 3 x 0 x 0 4x 6x2 1 (4 x) 2 4 lim 2 2 . x 0 6x 3 1 x 2 sin 2 2 x 4 x4
x
能用洛必达法则求出. (D)由于 lim x 2 ，而 lim x sin x 不存在，因此(D)中极限也不能用洛必达法
x
x
则求出.故应选(B).
注：不能用洛必达法则求出的极限未必就不存在，本例的三个不能用洛必达 法则计算的极限可用其他方法计算：
1 x lim x lim x sin 1 1 0 0 . (A) lim x 0 sin x x 0 sin x x 0 x x 2 sin sin x x sin x x 1 .(D) lim x sin x lim sin x lim 1 sin x 0 . (C) lim lim x x x x x x sin x x sin x x2 x 1 x 1
0 0
lim
1 1 x 2 cos x (1 x 2 ) cos 2 x 1 1 x 2 cos x lim lim x 0 cos 2 x 1 x 2 x 0 x 0 sin 2 x x 2 1 x2
1 (1 x 2 ) cos 2 x 1 1 sin 2 x x 2 cos 2 x . lim lim x 0 x 0 sin 2 x x 2 2 x 0 sin 2 x x 2 1 1 x 2 cos x
tan t t t3
1 x
t tan t t tan t t tan t t lim tlim 1 t 0 0 t t
2
（第二个重要极限）
e
t 0
lim
tan t t t3
e
t 0
lim
0 0
例32.8(难度系数0.4) 若 lim
x 0
(A)0
(B)6
sin 6 x xf ( x) 6 f ( x) 0 ，则 lim 的值为( ). 3 x 0 x x2 (C)36 (D)
解析：将所求极限通过添加变量使其出现已知极限，然后再利用洛必达法则 ，求解过程如下：