法兰克系统椭圆球面宏程序
椭圆宏程序在数控车床加工的方法

椭圆宏程序在数控车床加工的方法椭圆宏程序的基本原理是利用圆的特性来实现椭圆形的加工。
椭圆是一种圆的特殊形式,其变形是通过改变加工过程中的切削刀具的移动轨迹来实现的。
椭圆宏程序通过数学计算和编程实现刀具的移动轨迹变化,从而实现椭圆形的加工。
1.定义椭圆的参数:椭圆的形状可以通过两个半径参数来定义,分别为长半径和短半径。
这些参数可以根据零件的要求进行调整。
2.计算椭圆的切削路径:通过数学计算,可以确定刀具在加工过程中的移动轨迹。
这个轨迹是一个连续而光滑的曲线,可以通过数学公式或计算机模拟来得到。
3.编写椭圆宏程序:根据计算所得的切削路径,编写相应的宏程序。
宏程序是一种特殊的程序,可以在数控机床上执行。
它包含了一系列指令,用于控制刀具的移动、切削深度等参数。
4.设定加工参数:在执行宏程序之前,需要将一些重要的加工参数进行设定。
这些参数包括切削速度、进给速度、切削深度等。
它们的选择需要根据材料的性质和要求进行调整。
5.执行宏程序:当所有参数设置完成后,就可以执行宏程序了。
数控机床会按照宏程序中定义的指令和轨迹来进行切削,从而实现椭圆形的加工。
椭圆宏程序的优点是可以高效地制造复杂形状的椭圆零件。
相比于传统的手工加工或其他编程方法,椭圆宏程序的精度更高,生产效率更高。
此外,它还具有良好的可编程性和易于调整的特点,可以适应不同类型的椭圆加工需求。
总结起来,椭圆宏程序是一种用于数控车床加工的方法,通过定义椭圆参数、计算切削路径、编写宏程序以及设定加工参数等步骤来实现椭圆形的加工。
它能够提高零件的精度和质量,提高生产效率,适用于制造复杂形状的椭圆零件。
FANUC数控系统用户宏程序应用——椭圆凸台数控铣削加工

这些在手工编程时可以很好应用 。
三、 圆凸台宏程序编程应用 椭
如图 1 所示为椭圆凸台。加工椭 圆凸台, #0 14:刀尖在工件坐标系 中 x坐标 值变 具有变量运算 、 判断 和条件转移等功能 , 因此 不仅 加工椭 圆需要变量编程 ,凸台方向也需 量; 可以编制出更简单 、 通用性更强的程序。 要变量编程 。如 图 2所 示 , 加工椭 圆时 , 以角 # 0 :刀尖在工件坐标系中 Y坐标值变 15 编写宏程序 时,可 根据工件加工要求先 度 n 为 自变 量 , 则在 x 面内 , 圆上 各点 y平 椭 量。 用宏 指令列 出加T点 坐标值 的计 算过程 , 计 坐标分别是 (8o?s ? , 1cs, n )坐标值 随角度的变 i 加工程序 如下 : 算过程 中的数据可 以用 变量暂代 ,在加工时 化而变化。对于椭 圆的锥度加工 , Z 当 向每抬 根据工件 的具体尺寸要求 ,由加工主程序输 高 d时 ,长 轴 及 短 轴 的 半 径 将 减 小 d×
漏洞 。笔者知识粗浅 , 只能举 出以上应用 , 其 中或错或对恳请大家批评指正。
蕾I I l
表2
如完成记数 6 0次后 才 向下 执行 ,编程
为:
N1 #1 1 0 =;
设定 #1 初始值
图 2 宏程 序 变 照运算
N 0 #1 # + ; 2 : 11 #1 值累加 图 1 宏 程 序 编 程 实 例 N 0 F #1L 0 G T 0; 判 别次 图 2宏程序变量运算 3 I【 E6 ] O O 1 数, 转移执行顺序 编程时 , 用以下变量进行运算。 使
关键 词 : 户宏 程 序 变量 编 程 曲 面 用
一
、
宏程序编程概念
N4 0 ・ ・ N5 ・ 0
宏程序椭圆曲面体的加工

宏程序椭圆曲面体的加工摘要在手工编程中,宏程序是其精髓,对小容量数控宏程序的应用,可以使普通数控机床的效率最大限度的提高,也能弥补自动编程软件存在的不足。
在实际应用中,处于某些原因,相关专业的教学中过分的以来CAM/CAD软件,对于手工编程只是简单的介绍,置于宏程序,往往忽视掉。
手工编程作为自动编程的基础,应该牢固的掌握,对于宏程序而言是基础中的基础,更应该掌握。
本文主要针对宏程序在数控编程技术及椭圆曲面体加工中的应用进行介绍,并对在编制椭圆曲面零件时的思路和方法进行详细的介绍。
关键词宏程序;数控编程;变量;编程原点;对刀点随着科学技术的不断发展,现在所应用的数控机床已经不是仅仅依靠挡块、凸轮模拟及挡块开关等传统的控制手段就可以实现数控加工的。
在第一台电子计算机出现以后,如何将电子计算机运用到机床的实际操作中成为人们的一大设想,对于复杂零件加工的问题如何很好的去解决成为研究的重点。
经过多年来的不断研究,尤其是在近20年的发展中,工业体系趋向于完善,大量的数控设备逐步的运用到电子、模具、机床等行业中,其信息化和智能化的程度在某些方面已经超过了人工的精雕细刻,随着数控设备的大量应用,对于制造业和加工也而言,是一次革命性的变革。
随着我国工业化社会的不断发展,很多复杂零件的加工越来越多,越来越复杂,例如抛物线形、椭圆形及非圆形零件等,如果采用常规的编程方法,肯定是行不通的,为了使数控机床的功能得到最大程度的发挥,在编程方法方面就应该考虑宏程序,这也是对难点问题进行解决的有效手段。
1宏程序简介2椭圆曲面零件分析加工该零件的时候,要求表面形状呈椭圆形镜面。
如果采用传统的加工方法和加工工艺的话,根本无法达到椭圆形状、镜面的要求;如果是采用一般数控机床加工方法进行零件的加工的话,因为数控机床软件中只有圆弧插补G20、G03,直线插补G01等,并没有针对椭圆形的指令,如果一定要采用此法完成椭圆的加工,就只能采用“等效法”。
宏程序加工球面椭圆在数控铣床上的应用

宏程序加工球面椭圆在数控铣床上的应用【摘要】宏程序是手工编程的高级形式,合理的运用宏程序会使程序变得简单、而且加工精度很高、相对于CAD/CAM自动编程软件的数控程序、加工时间也会大大缩短。
文章通过实际的加工实例、从椭圆程序结构上探索了宏程序在数控加工上的运用。
【关键词】数控宏程序椭圆变量运用1 导言随着科学技术的发展,数控机床在机械制造业中的应用越来越广泛,而在对数控机床的应用中,机床系统所提供的宏程序、参数编程的功能,并没有得到广泛的运用。
在程序中大量使用变量,通过对变量进行赋值及处理的方法达到程序功能,实现加工,这种有变量的数控程序称之为宏程序。
宏程序与普通的程序的区别在于:普通程序只可指定常量、常量之间不可以运算,程序只能按顺序执行,不能跳转、功能是固定的。
宏程序可以使用变量、可以给变量赋值、变量之间可以进行运算、程序运行可以跳转。
实际的教学和生产中,普通的数控指令、程序都是针对平面、直线和简单的圆弧等轮廓。
当遇到诸如球面、椭圆等非圆曲线零件的加工,除非运用CAD/CAM 软件进行自动编程,否则将无法加工零件。
尽管现在使用各种CAD/CAM软件编程已成为数控加工的潮流,但手工编程毕竟还是基础,各种疑难杂症的解决,往往还是要运用到宏程序。
宏程序具有灵活性、通用性、和智能性等特点。
宏程序在生产实践中应用广泛,尤其是在各种曲面的编程中最为常用。
掌握宏程序在数控编程和加工中的运用。
是学好数控技术的基础。
2 平面椭圆宏程序在加工中的运用椭圆是数控加工中常遇到的曲面之一,也是现有数控系统中须用宏程序来进行编程和加工的曲面。
编制椭圆加工程序和加工方法也就是利用了椭圆的方程和参数,运用椭圆变量之间的关系构成加工程序,形成刀具加工轨迹。
2.1 椭圆标准方程。
X=acosθy=bsinθ2.2 平面椭圆零件加工图例。
零件的加工使用TK7650型FANUC系统数控铣床,采用手动换刀方式加工。
设椭圆的中心为坐标原点、运用椭圆的参数方程通过选择椭圆极角θ的增量将椭圆分成若干线段或圆弧,每次增加角度变量为2,从极角θ=90开始,切削到极角θ=460终点结束。
FANUC用户宏程序(椭圆篇)
用户宏程序宏程序是指含有变量的子程序,在程序中调用用户宏程序的那条指令叫做用户宏指令(这里用G65)1、变量用一个可赋值的代号代替具体的坐标值,这个代号称为变量。
变量分为系统变量、全局变量和局部变量三类,它们的性质和用途个不相同。
(1)系统变量是固定用途的变量,它的值决定了系统的状态。
FANUC 中的系统变量为#1000~#1005、#1032、#3000等。
(2)全局变量是指在主程序内和由主程序调用的各用户宏程序内公用的变量。
FANUC中的全局变量有60个,它们分两组,一组是#100~#149;另一组是#500~#509。
(3)局部变量是仅局限于在用户宏程序内使用的变量。
同一个局部变量在不同的宏程序内的值是不通用的。
FANUC中的局部变量有33个,分别为#1~#33。
(1)加减型运算加减型运算包括加、减、逻辑加和排它的逻辑加。
分别用以下四个形式表达:#i = #j +#k#i = #j -#k#i = #j OR #k#i = #j XOR #k式中,i、j、k为变量;+、-、OR、XOR称为为演算子。
(2)乘除型运算乘除型运算包括乘、除和逻辑乘。
分别用以下形式表达:#i = #j * #k#i = #j / #k#i = #j AND #k4.变量的赋值由于系统变量的赋值情况比较复杂,这里只介绍公共变量和局部变量的赋值。
变量的赋值方式可分为直接和间接两种。
(1)直接赋值例:#1=115(表示将变量115赋值于#1变量)#100=#2(表示将变量#2的即时值赋于变量#100)(2)间接赋值间接赋值就是用演算式赋值,即把演算式内演算的结果赋给某个变量。
在演算式中有自变量代号,自变量每得到一个即时值,相应就得到一个演算结果,该结果就赋值给变量,该变量也叫应变量。
5.转向语句转向语句分为无条件转向语句和条件转向语句两种。
(1)无条件转向语句程序段格式:GOTO N ;其中N后面的数值为程序段号。
例如:GOTO 55;表示无条件转向执行N55程序段,而不论N55程序段在转向语句之前还是之后。
FANUC系统宏程序铣削椭圆方法研究

工业设计2020年第21期0引言椭圆轮廓的加工,是宏程序在实际加工应用中一个很典型的例子,在各类数控技能鉴定和数控技能大赛中也会经常出现。
因目前大多数的数控系统只提供直线插补、圆弧插补和螺旋插补三种插补类型。
更高档的数控系统(如FANUC16i)也仅提供双曲线、正弦曲线和样条曲线插补功能,一般都没有椭圆插补的功能。
这时就需要采用宏程序语句套用椭圆参数方程来实现椭圆轮廓的加工。
本文归纳总结了Fanuc0i系统编制椭圆轮廓宏程序几种编程思路和方法。
1椭圆轮廓宏程序编程方法加工如图1所示椭圆工件,将工件坐标系建立在工件上表面中心处,采用刀具直径为φ10mm立铣刀。
利用椭圆参数方程配合条件转移语句来编制宏程序,目前常用的几种编程方法如下:图1 椭圆工件1.1不加刀补型关于椭圆轮廓宏程序编制,人们往往有一种错误的认识,以为只要刀具中心轨迹走出的形状是椭圆,那加工出的轮廓就是椭圆,许多常见的椭圆轮廓宏程序就是在这个错误认识基础上编写的,既在整个椭圆的加工过程中不采用刀具半径补偿G41(G42),而是直接利用椭圆的长、短半轴值减去刀具的半径值来进行编程。
程序如下:O0001;(程序名)……#1=0;(椭圆起始角度)WHILE [#1LE360] DO1;(当#1小于等于360°时执行循环1)G1 X[35*COS[#1]] Y-[25*SIN[#1]] F1000;(椭圆插补)#1=#1+1;(#1角度每次递增1°)END1;(循环1结束)……M30;(程序结束)需要说明的是这种编程方法看上去非常简单易懂,而且也不会因为刀具补偿的错误应用而引起椭圆轮廓的过切。
很多编程人员也早已习惯了这种编程方法,但是这样加工出来的形状绝对不是真正意义上的椭圆,而是与椭圆轮廓等距一个刀具半径的等距曲线,如图2所示。
如果要加工一个真正意义上的椭圆是不能采用这种方法的,需要采用后两种方法。
数字1代表基准椭圆a=30mm,b=20mm;数字2代表铣刀直径;数字3代表大椭圆a=35mm,b=25mm;数字4代表正确的刀具中心运行轨迹;图2椭圆轮廓轨迹加工示意图1.2刀补加在循环外型如果第一种方法不可行,必须加上刀具半径补偿才能编制出正确的椭圆程序,那么按照常规的编程思路会将刀具半径补偿加在循环外面来进行编程,程序如下:O0002;(程序名)……G1 G41 X30 Y0 D1 F1000;(加入刀具半径补偿)#1=0;(椭圆起始角度)WHILE [#1LE360] DO1;(当#1小于等于360°时执行循环1)G1 X[30*COS[#1]] Y-[20*SIN[#1]];(椭圆插补)#1=#1+1;(#1角度每次递增1°)END1;(循环1结束)FANUC系统宏程序铣削椭圆方法研究陈行行(中国工程物理研究院机械制造工艺研究所 四川 绵阳 621999)摘 要:对于椭圆轮廓的加工,数控系统中是没有能够直接实现椭圆插补的G代码指令,这时就需要采用宏程序语句套用椭圆参数方程来实现椭圆轮廓的加工。
运用FANUC的B类宏程序参数化车削椭圆
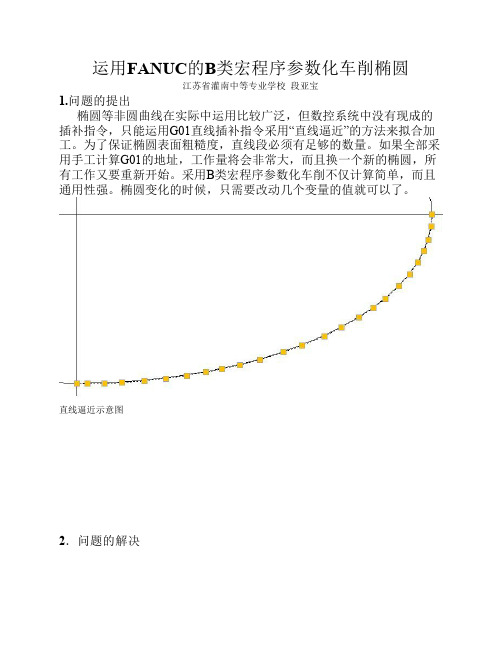
运用FANUC的B类宏程序参数化车削椭圆江苏省灌南中等专业学校段亚宝1.问题的提出椭圆等非圆曲线在实际中运用比较广泛,但数控系统中没有现成的插补指令,只能运用G01直线插补指令采用“直线逼近”的方法来拟合加工。
为了保证椭圆表面粗糙度,直线段必须有足够的数量。
如果全部采用手工计算G01的地址,工作量将会非常大,而且换一个新的椭圆,所有工作又要重新开始。
采用B类宏程序参数化车削不仅计算简单,而且通用性强。
椭圆变化的时候,只需要改动几个变量的值就可以了。
直线逼近示意图2.问题的解决2.1认识椭圆方程图1如右图1所示的椭圆有两个方程,x2/b2+z2/a2=1一个是标准方程由标准方程可得:x=bsinβz=acosβ一个是参数方程2.2去除余量的粗车2.2.1粗车思路由椭圆的标准方程可知,z=f(x),即每一个具体x 值都有一个对应的Z值。
所以粗车的思路就是把每次X向的起刀点设为一个变量,并与精车余量进行比较。
如果小于,粗车结束。
如果大于等于,则根据这个变量计算出对应的Z值(由于通常的编程习惯是把工件的右端面的中心设为编程原点,所以这个求得的Z值必须进行相应的转换)。
车完这个Z值之后,X变量减小一个切深,继续进行比较。
这个过程如下图2所示。
小于大于等于X向起刀点判断与精车余量的关系粗车结束根据Z=f(x),去除余量X值减小图2 粗车流程2.2.2 实例车削一个长轴半径40短轴半径15如图1右半边的椭圆,毛坯直径32。
最终效果如图3粗车程序如下:O0056图3 粗车效果图T0101;1号粗车刀M03S600;G00X100.Z100.;#1=32;毛坯直径#2=40;椭圆长轴半径a#3=15;椭圆短轴半径b#4=0.5;精车余量#5=2;切深#6=#3*2-#5;X向起刀点WHILE[#6GE#4]DO1;判断X值是否大于等于精车余量G00X[#6]Z[#4];定点#7=#2*SQRT[1-#6*#6/[#3*#3*4]];考虑屏幕输入宽度#8=#7-#2+#4;Z向粗车长度G01Z[#8]F0.1;余量去除G00X[#1]Z[#4];退刀#6=#6-#5;每次进给#5的切深END1;G00X100.Z100.;2.3 保证粗糙度的精车精车椭圆是利用椭圆的参数方程,采用直线逼近方法,利用角度的微小变化来拟合最终的椭圆表面。
发那科椭圆圆周打孔宏程序

发那科椭圆圆周打孔宏程序
使用格式:多余的就不说了就直接从打孔开始固定循环开始了
G98G81Z_R_F_K0;(K0必须要加哦,不然圆中心会打个孔哦
G65P0001X_Y_A_B_C_H_Q_R_;
G80
----------------
O0001(宏子程序)
G52X#24Y#25 ;
G68X0Y0R#18;
#7=0;
WHILE[#7LT#11]DO1;
G90X[#1*COS[#3+#7*#17]]Y[#2*SIN[#3+#7*#17]];
#7=#7+1;
END1;
G69;
G52X0Y0;
M99;
%
------------------------------------
G65P0001X_Y_A_B_C_H_Q_R_;变量解释
X:X轴圆心坐标(绝对值哦)
Y:Y轴圆心坐标(绝对值哦)
A:长轴半径
B:短轴半径
C:第一个孔与长轴X正方向的夹角(顺负逆正,与G68里的R值使用方法相同)H:孔的个数
Q:孔之间的间隔角
R:椭圆长轴与X轴正方向的夹角,(顺负逆正,和平时使用G68时一样)
你是30°一个孔,就是Q30 H12了
像上面一样把你需要的数据填入X_Y_A_B_C_H_Q_R_这些变量里面就可以了。
就是这么简单。
---------------------------------
授人以鱼不如授人以渔
---------------------------------。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
法兰克系统椭圆球面宏程序
Summary: This text synopsis introduced the set up of concept, the plait distance priniple and mathematics pattern of the great procedure a method. Also take processing oval sphere as solid instance, introduced draw up of great procedure process in detail. Finally give adoption Siemens 802 D the system draw up of procedure and procedure annotation
of the process of oval sphere.
Key words:Great procedure;Oval sphere;The parameter square distance;
Great variable;R parameter)
一、导言
对于具有曲面或复杂轮廓的零件,特别是包含三维曲面的零件,采用一般手工编程困难很大,且容易出现错误,有的甚至无法编制程序。
而采用宏程序,就
能很好的解决这一问题。
二、宏程序
宏程序就是使用了宏变量的程序。
在一般的程序编制中,程序字中地址字符后为一常量,一个程序只能描述一个几何形状,所以缺乏灵活性和适用性。
宏程序中的地址字符后则为一变量(也称宏变量),可以根据需要通过赋值语句加以改变,使程序具用通用性。
配合循环语句、分支语句和子程序调用语句,可以编制各种复杂零件的加工程序。
三、宏程序的编制
编制宏程序时必须建立被加工零件的数学模型。
也就是通过数学处理找出能
够描述加工零件的数学公式。
数学处理一般有以下两个环节:一是选择插补方式;二是求出插补节点的坐
标计算通式。
1.所谓插补方式,就是根据被加工零件的特点所做的拟合处理。
一般常用直线拟合和圆弧拟合两种。
在相同加工精度要求下,直线拟合虽比圆弧拟合插补节点多、运算数据量大,但数学处理较为简单,因而较为常用。
2.求出插补节点的坐标计算通式,就是根据曲面特点及所给条件,列出曲面上任意节点的坐标计算通式。
根据选取参变量方式,一般可分等间距法和等节距
法。
(1)等间距法
所谓等间距法,就是在一个坐标轴上进行等增量,然后,根据曲线公式计算出另一个坐标轴的相应坐标值。
这样,在实际编程时,将相邻的两节点连成直线,用这一系列直线段组成的折线近似理论轮廓曲线。
如图1所示,在X轴上进行等增量△X,根据曲线公式z=f(x)计算出一系列z轴坐标值,得到在XOZ坐标平面
的节点坐标。
其特点是计算简单,坐标增量△X的大小决定着曲面的加工精度,越小加工
精度越高,同时计算数据增多。
图1 等间距法
等间距法在实际加工中有一定的局限性。
例如,在加工球面等“坡度”变化较大的零件时,层高不均匀,造成加工质量不高。
如图1所示,同样的Δx,得到的δz却有很大的变化,球面的上下部分残留高度不相等。
加工此类零件时,比较理想的方法是采用等节距法。
(2)等节距法
所谓等节距法,如图2所示,就是把被加工曲面在某一截面内的轮廓线,按固定的长度分割成若干个小线段,实现轮廓线的拟合。
图2 等节距法图3等角度法这种方法加工精度较高,但计算复杂。
为此,可经过适当转化,采用等角度法,如图3所示。
每增加一个转角α,通过曲线方程就能计算一个节点坐标。
因为采用了等角度增量,所以曲面各加工部位保持加工精度一致。
本例中加工椭圆凹槽就是采用了等角度法。
四、加工实例
1.零件图纸及要求
加工如图4所示的椭圆球面,采用西门子802D系统编程,使用R5球头立
铣刀加工。
图4 零件图
2.建立工件坐标系
建立工件坐标系如图5所示。
椭圆球的球心O点设为坐标系原点,椭圆长轴
设为X轴,椭圆短轴设为Y轴。
图5 建立工件坐标系
3.零件的数学分析
椭圆球面是一个空间曲面,用YOZ坐标平面可截得一个半径为R15的圆,如图5中左视图所示;用平行于XOY坐标平面的平面可截得一族同心椭圆,其长短轴对应成比例。
利用这一特点,进行尺寸计算,确定各轴的宏变量计算公式。
考虑到加工的方便性,这里以“刀心”编程。
4. 计算宏变量方程通式
(1) XOY平面内椭圆的宏变量方程,参见图6。
图6 XOY平面内椭圆宏变量设置
根据椭圆的参数方程: x=a×cost; y=b×sint
这里:a为椭圆短半轴长度,设为参数R1;
b为椭圆长半轴长度,设为参数R2;
t 为角度增量,设为参数R0。
可得到XOY平面内椭圆的宏变量方程通式:
x = R1*cos(R0); y = R2*sin(R0)。
……式1 (2)任意椭圆短半轴(R2)及Z轴坐标的计算公式,如图7所示
根据圆的参数方程:x=r×sint;y=r×cost
得:R2=(15-5)*sin(R3)=10*sin(R3);……式2 Z =(15-5)*cos(R3)=10*cos(R3);……式3 其中:R3为ZOY平面内的角度增量;
“(15-5)”为“刀心”在YOZ平面内的轨迹半径;
“15”为最大椭圆的短半轴,在YOZ平面内为截面圆半径;
“5”是刀具半径。
图7 任意椭圆短半轴(R2)及Z轴坐标的计算
(3)任意椭圆长半轴的计算公式:
因为沿Z轴方向一系列椭圆长短半轴对应成比例,
即:R1/R2=(20-5)/(15-5)=15/10
因此得到:R1=R2*15/10
将式2代入得:R1=15*sin(R3) ……式4
5.根据以上分析计算,编制宏程序如下表所示(西门子802D系统)
6.说明
(1)因为采用的是“刀心”编程,对刀时注意Z轴坐标原点的设定。
(2)程序中有两个循环,主程序段AA至N110为一个循环,主程序段BB 至N140为另一个循环。
前者用于加工一系列平行于XOY平面的椭圆,后者用于
确定各椭圆的大小及Z轴位置。
(3)N120 X=IC(-0.2)采用增量退刀,为下一次循环中Z轴的进刀做准备。
