正余弦函数的图像
合集下载
正余弦函数的图象

-4 -3
-2
(0,11)
3
( 2 ,1)
-
(-o12 ,0)
( 2 ,0)
2
( ,-1)
3
线
4
5 6 x
正弦、余弦函数的图象
练习:在同一坐标系内,用五点法分别画出函数
y= sinx,x[0, 2] 和 y= cosx,x[ , 3 ]的简图:
22
x
02
20
csionsx
10
01
向左平y 移 个单位长度 22
2 ,0) x
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象
y
余弦曲
1.列表 2.描点 3.连线
3
2
x
2
2 y=sinx,x[0, 2]
正弦、余弦函数的图象
例2 画出函数y= - cosx,x[0, 2]的简图:
x
0
2
3
2
2
cosx
1
0
-1
0
1
- cosx -1
0
1
0
-1
y 1
o
2
2
-1
y=cosx,x[0, 2]
3
2
2
x
y= - cosx,x[0, 2]
正余弦函数的图像及性质

1 类似 : cos x ≥ x ∈ ____________________ 2
了解单调性
5.若α , β 为锐角, 且 sin α < cos β , 则α , β 满足( A.α > β B .α < β C .α + β < )
π
2
D.α + β >
π
2
提高
π 设 x ∈ 0, , f ( x ) = sin(cos x ), g ( x ) = cos(sin x ), 2 求 f ( x )和 g ( x )的最大值和最小值 , 并将它们按 大小顺序排列起来
记忆y=cosx图像 图像 记忆
y=1 y = 1
图 (1)图像是一条无限延伸的 波浪线 像 ( 2 )夹在 y = 1和 y = 1两条直线间 特 ( 3 )图像上有特殊的五个点 点 π 3π ( 0,1), ( ,0 ), (π , 1), ( ,0 ), ( 2π ,1) 2 2
正余弦函数图像的作图方法 五点法 正余弦函数的性质 记图像来记性质
4.函数y = 2 sin x 1的定义域为( B ) π 5π 点拨 A. , 6 6 用好一个周期图像 5π π B . + 2 kπ , + 2kπ , k ∈ Z 6 6 找一带全 5π π C .( + 2kπ , + 2kπ ), k ∈ Z 6 6 5π π D . + kπ , + kπ , k ∈ Z 6 6
问y = sin 2 x是奇函数还是偶函数 ? y = cos 2 x呢 ?
了解图像对称性
3.已知函数 y = 2 cos x ( 0 ≤ x ≤ 2π )的图像和直 线 y = 2围成一个封闭的平面图 形 , 那么这个 ) 封闭的图形的面积是 ( A .4 B .2π C .8 D .4π
正弦函数、余弦函数的图像(完整)

(
3 2
,1)
(1) 列表(列出对图象形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连y线(用光滑的曲线顺次连结五个点)
图象的最高点
1-
-
(0,1) (2 ,1)
与x轴的交点
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 5
2
3
11 6
2
x
(
2
,0)
(
3 2
,0)
-1 -
图象的最低点 ( ,1)
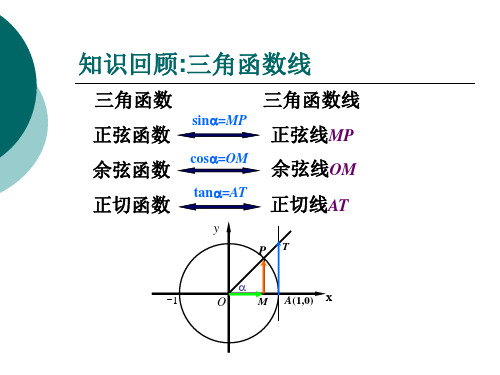
三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦函数的图象
问题:如何作出正弦函数的图象?
途径:利用单位圆中正弦线来解决。
描图:用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
4
5 6 x
正弦、余弦函数的图象
如何由正弦函数图像得y 到余弦函数图像?
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象
y=cosx=sin(x+ ), xR
2
余弦函数的图象
y
1
正弦曲 线
形状完全一样 只是位置不同
余弦曲 线
-4 -3
-2
- o
-1
正弦和余弦的图像和性质
其定义域为R,值域为[-1,1],周期为2
y sin x, x [0, 2 ]的图象 作法: (1) 等分
(2) 作正弦线
问题:如何作出比较精确的正弦函数图象? (3) 平移
途径:利用单位圆中正弦线来解决。
(4) 连线
y
B
1
用光滑曲线将这些正弦线 的终点连结起来!
A
O1
O 2 5 7 4 3 5 11 22
2
(
,1)
(
2 ,1)
(
2
,1)
(
2
,1)
( 2( ,21),1) ( 2 ,1)
,0) 3
(
2
( ,0) 2
(
((((((,,0,00),)0,),(003)2))(32,(-312,(1)32),1(33,)(212(3(323)2,21-,1,-),-1)-11)))
2 ,0) x
2 ,0)
解: x
3
0
2
2
2
sinx
0
1
0
-1
0
1+sinx
1
2
1
0
1
y
2
y=1+sinx,x[0, 2]
1
o
2
-1
2
3
2
x
2
典型例题:
例1(2) 画出函数y= -cosx,x[0, 2]的简图:
x
0
2
3
2
2
cosx
1
0
-1 0
1
-cosx
-1
0
1
0
-1
y
1
y=-cosx,x[0, 2]
y sin x, x [0, 2 ]的图象 作法: (1) 等分
(2) 作正弦线
问题:如何作出比较精确的正弦函数图象? (3) 平移
途径:利用单位圆中正弦线来解决。
(4) 连线
y
B
1
用光滑曲线将这些正弦线 的终点连结起来!
A
O1
O 2 5 7 4 3 5 11 22
2
(
,1)
(
2 ,1)
(
2
,1)
(
2
,1)
( 2( ,21),1) ( 2 ,1)
,0) 3
(
2
( ,0) 2
(
((((((,,0,00),)0,),(003)2))(32,(-312,(1)32),1(33,)(212(3(323)2,21-,1,-),-1)-11)))
2 ,0) x
2 ,0)
解: x
3
0
2
2
2
sinx
0
1
0
-1
0
1+sinx
1
2
1
0
1
y
2
y=1+sinx,x[0, 2]
1
o
2
-1
2
3
2
x
2
典型例题:
例1(2) 画出函数y= -cosx,x[0, 2]的简图:
x
0
2
3
2
2
cosx
1
0
-1 0
1
-cosx
-1
0
1
0
-1
y
1
y=-cosx,x[0, 2]
正弦余弦函数的图象

陈经纶中学
高一备课组
复习
y r=1 α O M P(x,y)
y=sinα= MP (正弦线 正弦线) 正弦线
x
y=cosα=OM (余弦线 余弦线) 余弦线
正弦函数、 正弦函数、余弦函数
y=sinα y=sin x
一般地,我们用x表示自变量,即x表示角的大小, 表示自变量, 表示角的大小, 一般地,我们用 表示自变量 表示角的大小 表示函数值, 用y表示函数值,这样,我们就定义了任意角的 表示函数值 这样, 正弦函数y=sinx,其定义域为 正弦函数 ,其定义域为R.
上移1 上移1个单位
横坐标不变, 横坐标不变, 纵坐标伸长 为原来的2 为原来的2倍
沿x轴翻折
四、小结 小结
正弦、 正弦、余弦函数的图象
几何法 五点作图法(作图常用此法) 五点作图法(作图常用此法)
1. 正弦曲线、余弦曲线 正弦曲线、
2.注意与诱导公式、三角函数线等知识的联系 注意与诱导公式、 注意与诱导公式
●
-1 -2
3π 2
●
●
2π
x
练习( ) 练习(2) 画y=-cosx,x∈[0, 2π]的简图 , ∈ π 的简图 解:按五个关键点列表 π 3π π 2π x 0 2 2 cosx -cosx
y 1
1 -1
0 0
-1 1
0 0
1 -1
y=-cosx x∈ 2 ] [0, π
●
o
-1
●
π
●
2
π
y=cosx x∈ [0, 2π ]
y 1
π
2
y=cosx,x∈[0, 2π] , ∈ π
π
2
−
o -1
高一备课组
复习
y r=1 α O M P(x,y)
y=sinα= MP (正弦线 正弦线) 正弦线
x
y=cosα=OM (余弦线 余弦线) 余弦线
正弦函数、 正弦函数、余弦函数
y=sinα y=sin x
一般地,我们用x表示自变量,即x表示角的大小, 表示自变量, 表示角的大小, 一般地,我们用 表示自变量 表示角的大小 表示函数值, 用y表示函数值,这样,我们就定义了任意角的 表示函数值 这样, 正弦函数y=sinx,其定义域为 正弦函数 ,其定义域为R.
上移1 上移1个单位
横坐标不变, 横坐标不变, 纵坐标伸长 为原来的2 为原来的2倍
沿x轴翻折
四、小结 小结
正弦、 正弦、余弦函数的图象
几何法 五点作图法(作图常用此法) 五点作图法(作图常用此法)
1. 正弦曲线、余弦曲线 正弦曲线、
2.注意与诱导公式、三角函数线等知识的联系 注意与诱导公式、 注意与诱导公式
●
-1 -2
3π 2
●
●
2π
x
练习( ) 练习(2) 画y=-cosx,x∈[0, 2π]的简图 , ∈ π 的简图 解:按五个关键点列表 π 3π π 2π x 0 2 2 cosx -cosx
y 1
1 -1
0 0
-1 1
0 0
1 -1
y=-cosx x∈ 2 ] [0, π
●
o
-1
●
π
●
2
π
y=cosx x∈ [0, 2π ]
y 1
π
2
y=cosx,x∈[0, 2π] , ∈ π
π
2
−
o -1
正弦函数、余弦函数的图像 课件

探究点一
五点法作图
当(0,0),π2,1,(π,0),32π,-1,(2π,0)这五点 描出后,正弦函数 y=sinx,x∈[0,2π]的图像的形状就基本 上确定了.
当(0,1),π2,0,(π,-1),32π,0,(2π,1)这五点 描出后,余弦函数 y=cosx,x∈[0,2π]的图像的形状就基 本上确定了. 在精确度要求不高的情况下,画正弦函数和余弦函数的图 像常用“五点法”作图.
[错因] 在 y=tanx·cosx 中,定义域为 x|x≠kπ+π2,因此 在[0,2π]中 ,x≠π2,32π,图像中应挖去两个点(π2,1),(32 π,-1),错解的原因是没有考虑定义域.
[正解] 如图所示
法二:(利用单位圆中三角函数线): 如图(2),在 0≤x<2π 中满足 sinx≥12的角 x 的集合为 {x|π6≤x≤56π};因此当 x∈R 时, 集合为{x|2kπ+π6≤x≤2kπ+56π,k∈Z}.
求满足 sin(x+π4)≤12的 x 的范围.
解:令 z=x+π4,sinz≤12,在同一坐标系中作出 y=sinz 与直线 y=12的图像,如图,然后观察在区间长度为 2π 上的情况,在[-32π,π2]内适合 sinz≤12的 z∈[-76π,π6], 根据诱导公式(一),知当 z∈[-76π+2kπ,π6+2kπ](k∈Z),
=sinx 的图像向 左平移π2 单位长度便可. (2)用“五点法”画出余弦曲线 y=cosx 在[0,2π]上的图像时
所取的五个关键点分别为: (0,1) ,π2,0 (π,-1) , 32π,0 ,(2π,1)
正弦曲线和余弦曲线有什么区别与联系? 提示:正弦曲线和余弦曲线形状相同,只是位置不同.
即-76π+2kπ≤x+π4≤π6+2kπ,k∈Z. ∴-1172π+2kπ≤x≤-1π2+2kπ,k∈Z. 即适合 sinx+π4≤12的 x 的范围为: x∈[-1172π+2kπ,-1π2+2kπ](k∈Z).
正弦函数余弦函数的图像(公开课)
o
A
M
1
x
正切线AT tan=AT
既然作与单位圆有关的三角函数线可得相应的角的 三角函数值,那么通过描点( x, sin x) ,连线即可得到函数 y sin x, x 0,2 的图象
问题:如何作出正弦、余弦函数的图象?
途径:利用单位圆中正弦、余弦线来解决。
B
y
1
描图:用光滑曲线 将这些正弦线的 终点连结起来
余弦函数的图象
y
(0,1) 1
3 ( 2 ,0)
( 2 ,1) 2 3 4
余弦曲 线
5 6
8
-4
-3
-2
-
(o ,0) 2 -1
( ,-1)
x
像作二次函数图象那样为了快速用描点法 作出正弦曲线与余弦曲线。下面我们通过观察 函数图象寻找图象上起关键作用的点:
y sin x, x 0,2
2 ]的简图 例1:(1)画出y=1+sinx , x∈[0,
x
sinx
1s i n x
0 0 1
2
π
0 1
3π 2
2π
0 1
1
-1 0
2 y
1. o -1
.
π 2
2
y 1 sinx, x [0,2 π ]
.
.
3π 2
.
2
x
y sinx, x [0,2π]
(2)画出y=-cosx , x∈[0,2]的简图
解:按关键点列表
x sinx 0 0
y sin x , x R 的简图
2
0 0
-1 1
正余弦函数的图像及性质.
定义域,值域,单调性,奇偶性,最值 对称性 对称轴及对称中心 周期性 最小正周期
<金榜>P136.2表格
正余弦函数性质的简单使用 认识图像
1.方程sin x lg x的解有几个?
了解奇偶性
2.已知f ( x) ax bsin x 1,若f (5) 7,求f (5)的值
问y sin2x是奇函数还是偶函数? y cos 2x呢?
了解图像对称性
3.已 知函 数y 2cos x(0 x 2 )的 图像 和直
线y 2围 成一 个封 闭 的平 面 图形, 那 么这 个
封 闭的 图形 的 面积 是( )
A.4
B.2
C.8 D.4
了解图像周期性
4.函数y 2sin x 1的定义 域为( B )
A.
6
,
5
6
点拨
B.
6
2k , 5
6
2k , k Z
C.(
2k ,
5
2k ),k
Z
用好一个周期图像 找一带全
6
6
D.6
k , 5
6
k __________________ 2
了解单调性
5.若 , 为锐角,且sin cos ,则 , 满足( )
A.
B.
C. D.
正余弦函数的图像及性质
请记好笔记,用好笔记
记忆y=sinx图像
y1
y 1
图 (1)图 像 是 一 条 无 限 延 伸 的波 浪 线
像 (2)夹 在y 1和y 1两 条 直 线 间
特 点
(3)图 像 上 有 特 殊 的 五 个 点
(0,0),( ,1),( ,0),( 3 ,1),(2 ,0)
<金榜>P136.2表格
正余弦函数性质的简单使用 认识图像
1.方程sin x lg x的解有几个?
了解奇偶性
2.已知f ( x) ax bsin x 1,若f (5) 7,求f (5)的值
问y sin2x是奇函数还是偶函数? y cos 2x呢?
了解图像对称性
3.已 知函 数y 2cos x(0 x 2 )的 图像 和直
线y 2围 成一 个封 闭 的平 面 图形, 那 么这 个
封 闭的 图形 的 面积 是( )
A.4
B.2
C.8 D.4
了解图像周期性
4.函数y 2sin x 1的定义 域为( B )
A.
6
,
5
6
点拨
B.
6
2k , 5
6
2k , k Z
C.(
2k ,
5
2k ),k
Z
用好一个周期图像 找一带全
6
6
D.6
k , 5
6
k __________________ 2
了解单调性
5.若 , 为锐角,且sin cos ,则 , 满足( )
A.
B.
C. D.
正余弦函数的图像及性质
请记好笔记,用好笔记
记忆y=sinx图像
y1
y 1
图 (1)图 像 是 一 条 无 限 延 伸 的波 浪 线
像 (2)夹 在y 1和y 1两 条 直 线 间
特 点
(3)图 像 上 有 特 殊 的 五 个 点
(0,0),( ,1),( ,0),( 3 ,1),(2 ,0)
正弦函数、余弦函数的图像课件
2.余弦函数的图像 (1)余弦曲线:余弦函数y=cos x,x∈R的图像叫做余弦 曲线.
(2)余弦函数图像的画法:
①要得到 y=cos x 的图像,只须把 y=sin x 的图像 向左平移 π2个单位长度 便可,这是由于 cos x= sin(x+π2).
②用“五点法”画余弦曲线 y=cos x 在[0,2π]上的图像时,所取
()
A.y=sin x
B.y=sin |x|
C.y=-sin |x|
D.y=-|sin x| 解析:由 y=sin x 的图像知 A 不正确,D 中图像都在 x 轴下方
不正确,当 x=π2时,由图像知 y<0,故排除 B. 答案:C
[研一题]
[例 3] 在[0,2π]内,使 sin x>cos x 成立的 x 值的取值范围
[悟一法] 1.把y=sin x的图像在x轴上方的部分保留,x轴下方的 图像沿x轴翻折到x轴上方,就可得y=|sin x|的图像. 2.把y=sin x图像在y轴右侧的部分保留,去掉y轴左侧 的图像,再把y轴右侧的图像沿y轴翻折到y轴左侧,就可得y =sin |x|的图像.
[通一类]
2.与图中曲线对应的函数是
是
()
A.(π4,π2)∪(π,54π)
B.(π4,π)
C.(π4,54π)
D.(π4,π)∪(54π,32π)
[自主解答] 用“五点法”作出y=sin x,y=cos x(0≤x≤2π)的简图.
由图像可知(1)当 x=π4或 x=54π时,sin x=cos x. (2)当π4<x<54π时,sin x>cos x. (3)当 0≤x<π4或54π<x≤2π 时,sin x<cos x.
正余弦函数的图象
将函数图像沿y轴方向折叠,得到关于 x轴对称的新函数图像。
水平翻折
将函数图像沿x轴方向折叠,得到关于 y轴对称的新函数图像。
05
三角函数图象的应用
在物理学中的应用
01
描述周期性运动
正余弦函数可以用来描述许多周 期性运动,如简谐振动、交流电 等。
02
03
电磁波传播
波动现象
电磁波的传播可以用正余弦函数 来描述,例如在研究无线电波、 光波等传播规律时。
正余弦函数的图象
目录
• 正弦函数的图象 • 余弦函数的图象 • 正余弦函数图象的对比 • 正余弦函数图象的变换 • 三角函数图象的应用
01
正弦函数的图象
正弦函数的定义
总结词
正弦函数是三角函数的一种,它描述 了直角三角形中锐角对应的对边与斜 边的比值。
详细描述
正弦函数定义为 $sin x = frac{y}{r}$, 其中 $x$ 是角度,$y$ 是直角三角形中 锐角的对边长度,$r$ 是斜边长度。
正弦函数的周期性
总结词
正弦函数具有周期性,这意味着函数 值会重复出现。
详细描述
正弦函数的周期为 $360^circ$ 或 $2pi$ 弧度。这意味着在角度增加 $360^circ$ 或 $2pi$ 的过程中,函 数值会重复。
正弦函数的奇偶性
总结词
正弦函数是奇函数,因为对于任何角度 $x$,都有 $sin(-x) = sin x$。
VS
形状
正弦函数的图像在y轴两侧是对称的,而 余弦函数的图像在y轴两侧是不对称的。
正余弦函数在实际问题中的应用
01
02
03
振动与波动
正余弦函数在描述振动和 波动现象中有着广泛的应 用,如机械振动、电磁波 等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教材34页练习
六、作业
教材46页第1题
谢谢观赏 再见
向左平移a个单位.
思考2:设想由正弦函数的图象作出余弦 函数的图象,那么先要将余弦函数 y=cosx转化为正弦函数,你可以根据哪 个公式完成这个转化?
思考3:由诱导公式可知,y=cosx与
y
sin( 2
x) 是同一个函数,如何作函
数 y sin( 2 x)在[0,2π]内的图象?
y
1
y=sinx
2
请同学们点下面的图标,看如何用几何方法在直角坐标
系中做出点(
3
,
sin
3
)。
我们就借助上面做点方法在直角坐标系中作出正
弦函数y=sinx,x R的图像。
二、新课 1、用几何方法作y=sinx,x[0,2 ]的图像
请同学们点下面的图标,观察如何用几何方
法作函数y=sinx,x[0,2 ]的图象。
作函数y=sinx,x R在[0,2 ]上的图像,具体分为如下五个
(5)连线:用平滑的曲线将12个点依次从左至右连接起来,
即得y=sinx,x [0,2 ]的图像。
2、作正弦函数y=sinx,x R的图像
因为终边相同的角的三角函数值相等,所以 函数y=sinx,x[2k ,2(k 1) ],k Z 的图像与函数 y=sinx,x[0,2 ] 的图像的形状完全一样,只是位置 不同,于是我们只要将函数y=sinx,x[0,2 ] 的图
点及最高点和最低点这五个点,它们的坐标是(0,0),
(关键2 ,点用1)光,滑(曲线,连0)结,起(来32, ,就-得1)到,(函2数,的0)简。图将,这这五种个方
法称为“五点法”作图。
知识探究(二):余弦函数的图象
思 考 1 : 一 般 地 , 函 数 y=f(x + a)(a>0) 的图象是由函数y=f(x)的图象经过怎样 的变换而得到的?
像向左、右平移(每次 2 个单位长度),就可以
得到正弦函数y=sinx, x R 的图像。请同学们点下 面的图标,看演示过程。
思考:在函数y=sinx,x∈[0,2π]的图象上,起关键作 用的点有哪几个?
3.五点法作函数y=sinx,x[0,2 ]的简图
在作正弦函数y=sinx,x[0,2 ]的图象时,我们描了12 个点,其中起关键作用的是函数y=sinx,x[0,2 ]与x轴的交
y 用五点法做出简图
3
2
2
0
-1
0
1
0
1
y=1+sinx,x[0,2 ]
0
2
3
2 x
2
y=sinx,x[0,2 ]
函数 y=1+sinx,x[0,2]与函数 y=sinx,x[0,2 ]
的图象之间有何联系?请点击图标:
(2)按五个关键点列表
x
0
2
cosx 1
0
-cosx -
(1)作直角坐标系,并在直角坐标系中y轴左侧画单位圆
(2)把单位圆分成12等分(等分越多,画出的图像越精确),
可分别在单位圆中作出对应于x的0,
函数线。
6
,
3
,
2
,
,2
的正弦
(3)找横坐标:把x轴上从0到2 ( 2 ≈6.28)这一段分成12等
分。
(4)找纵坐标:将正弦线对应平移,即可指出相应12个点。
O -1
2
π
2π x
4、余弦函数y=cosx,x R 图像 因为y=cosx=cos(-x)=sin[2 -(-x)]=sin(x+2 )。 由此可以看出:余弦函数y=cosx, x R与函数y=sin(x+2 ),
x左平R 移是同2 个一单个位函长数度;而余得弦到函。数请的点图下像面可的以图通标过:将正弦曲线向
思考2:用描点法作正弦函数y=sinx在[0, 2π]内的图象,可取哪些点?
思考3:如何在直角坐标系中比较精确地 描出这些点,并画出y=sinx在[0,2π] 内的图象?
在直角坐标系中如何作点 (,sin)
由单位圆中的正弦线知识,我们只要知道一个角α的
大小,就能用几何方法做出对应的正弦值sinα的大小。
思考:函数y=cosx,x∈[0,2π]的图象 如何?其中起关键作用的点有哪几个?
y 1
O
π
2π x
-1
2
2
三、例题 例1画出下列函数的简图: (1)y=1+sinx, x[0,2 ] ; (2)y=-cosx, x[0,2 ]
解:(1)按五个关键点列表
x
0
2
sinx 0
1
1+sinx 1
2
1
0 -1
3
2
2
-1
0
1
1
0
-1
y=-cosx,x [0,2]
3 2 x
2
2
y=cosx,x[0,2]
函数 y=-cosx,x [0,2]与函数 y=cosx,x[0,2]的图象有
何联系?请点击图标:
四、本节小结
本节课我们学习了用单位圆中的正弦线做出 正弦函数的图像,用五点法作正弦函数余弦函数 的简图及用变换法做出余弦函数的图像。要熟练 掌握五点法作函数的简图,它是我们后面学习的 基础。 五、课堂练习
三 三角函数的图像和性质
4.8 正弦函数、余弦函数的图像和性质
第一课时 正弦函数、余弦函数的图像
问题提出
t
p
1 2
5730
1.在单位圆中,角α的正弦线、余弦线
分别是什么?
y
sinα=MP
P(x,y)
cosα=OM
OM x
2.任意给定一个实数x,对应的正弦值 (sinx)、余弦值(cosx)是否存在?惟一?
3.设实数x对应的角的正弦值为y,则对 应关系y=sinx就是一个函数,称为正弦 函数;同样y= cosx也是一个函数,称为 余弦函数,这两个函数的定义域是什么?
4.一个函数总具有许多基本性质,要直 观、全面了解正、余弦函数的基本特性, 我们应从哪个方面人手?
知识探究(一):正弦函数的图象 思考1:作函数图象最原始的方法是什么?
六、作业
教材46页第1题
谢谢观赏 再见
向左平移a个单位.
思考2:设想由正弦函数的图象作出余弦 函数的图象,那么先要将余弦函数 y=cosx转化为正弦函数,你可以根据哪 个公式完成这个转化?
思考3:由诱导公式可知,y=cosx与
y
sin( 2
x) 是同一个函数,如何作函
数 y sin( 2 x)在[0,2π]内的图象?
y
1
y=sinx
2
请同学们点下面的图标,看如何用几何方法在直角坐标
系中做出点(
3
,
sin
3
)。
我们就借助上面做点方法在直角坐标系中作出正
弦函数y=sinx,x R的图像。
二、新课 1、用几何方法作y=sinx,x[0,2 ]的图像
请同学们点下面的图标,观察如何用几何方
法作函数y=sinx,x[0,2 ]的图象。
作函数y=sinx,x R在[0,2 ]上的图像,具体分为如下五个
(5)连线:用平滑的曲线将12个点依次从左至右连接起来,
即得y=sinx,x [0,2 ]的图像。
2、作正弦函数y=sinx,x R的图像
因为终边相同的角的三角函数值相等,所以 函数y=sinx,x[2k ,2(k 1) ],k Z 的图像与函数 y=sinx,x[0,2 ] 的图像的形状完全一样,只是位置 不同,于是我们只要将函数y=sinx,x[0,2 ] 的图
点及最高点和最低点这五个点,它们的坐标是(0,0),
(关键2 ,点用1)光,滑(曲线,连0)结,起(来32, ,就-得1)到,(函2数,的0)简。图将,这这五种个方
法称为“五点法”作图。
知识探究(二):余弦函数的图象
思 考 1 : 一 般 地 , 函 数 y=f(x + a)(a>0) 的图象是由函数y=f(x)的图象经过怎样 的变换而得到的?
像向左、右平移(每次 2 个单位长度),就可以
得到正弦函数y=sinx, x R 的图像。请同学们点下 面的图标,看演示过程。
思考:在函数y=sinx,x∈[0,2π]的图象上,起关键作 用的点有哪几个?
3.五点法作函数y=sinx,x[0,2 ]的简图
在作正弦函数y=sinx,x[0,2 ]的图象时,我们描了12 个点,其中起关键作用的是函数y=sinx,x[0,2 ]与x轴的交
y 用五点法做出简图
3
2
2
0
-1
0
1
0
1
y=1+sinx,x[0,2 ]
0
2
3
2 x
2
y=sinx,x[0,2 ]
函数 y=1+sinx,x[0,2]与函数 y=sinx,x[0,2 ]
的图象之间有何联系?请点击图标:
(2)按五个关键点列表
x
0
2
cosx 1
0
-cosx -
(1)作直角坐标系,并在直角坐标系中y轴左侧画单位圆
(2)把单位圆分成12等分(等分越多,画出的图像越精确),
可分别在单位圆中作出对应于x的0,
函数线。
6
,
3
,
2
,
,2
的正弦
(3)找横坐标:把x轴上从0到2 ( 2 ≈6.28)这一段分成12等
分。
(4)找纵坐标:将正弦线对应平移,即可指出相应12个点。
O -1
2
π
2π x
4、余弦函数y=cosx,x R 图像 因为y=cosx=cos(-x)=sin[2 -(-x)]=sin(x+2 )。 由此可以看出:余弦函数y=cosx, x R与函数y=sin(x+2 ),
x左平R 移是同2 个一单个位函长数度;而余得弦到函。数请的点图下像面可的以图通标过:将正弦曲线向
思考2:用描点法作正弦函数y=sinx在[0, 2π]内的图象,可取哪些点?
思考3:如何在直角坐标系中比较精确地 描出这些点,并画出y=sinx在[0,2π] 内的图象?
在直角坐标系中如何作点 (,sin)
由单位圆中的正弦线知识,我们只要知道一个角α的
大小,就能用几何方法做出对应的正弦值sinα的大小。
思考:函数y=cosx,x∈[0,2π]的图象 如何?其中起关键作用的点有哪几个?
y 1
O
π
2π x
-1
2
2
三、例题 例1画出下列函数的简图: (1)y=1+sinx, x[0,2 ] ; (2)y=-cosx, x[0,2 ]
解:(1)按五个关键点列表
x
0
2
sinx 0
1
1+sinx 1
2
1
0 -1
3
2
2
-1
0
1
1
0
-1
y=-cosx,x [0,2]
3 2 x
2
2
y=cosx,x[0,2]
函数 y=-cosx,x [0,2]与函数 y=cosx,x[0,2]的图象有
何联系?请点击图标:
四、本节小结
本节课我们学习了用单位圆中的正弦线做出 正弦函数的图像,用五点法作正弦函数余弦函数 的简图及用变换法做出余弦函数的图像。要熟练 掌握五点法作函数的简图,它是我们后面学习的 基础。 五、课堂练习
三 三角函数的图像和性质
4.8 正弦函数、余弦函数的图像和性质
第一课时 正弦函数、余弦函数的图像
问题提出
t
p
1 2
5730
1.在单位圆中,角α的正弦线、余弦线
分别是什么?
y
sinα=MP
P(x,y)
cosα=OM
OM x
2.任意给定一个实数x,对应的正弦值 (sinx)、余弦值(cosx)是否存在?惟一?
3.设实数x对应的角的正弦值为y,则对 应关系y=sinx就是一个函数,称为正弦 函数;同样y= cosx也是一个函数,称为 余弦函数,这两个函数的定义域是什么?
4.一个函数总具有许多基本性质,要直 观、全面了解正、余弦函数的基本特性, 我们应从哪个方面人手?
知识探究(一):正弦函数的图象 思考1:作函数图象最原始的方法是什么?
