七年级数学上册第四章基本平面图形4角的比较典型例题素材新版北师大版
七年级数学上册第四章基本平面图形第4节角的比较同步练习含解析新版北师大版word格式

第四章 基本平面图形4 角的比较1.根据图所示,回答下列问题:( 1 ) 试 比 较 ∠AOB ,∠AOD ,∠AOE ,∠AOC 的大小,并找出其中的锐角、直角、钝角、平角;(2)在图中找出三对大小相等的角.解:(1)由图可知,∠AOB 是平角,∠AOC 是钝角,∠AOD 是直角,∠AOE 是锐角, 所以∠AOB >∠AOC >∠AOD >∠AOE .(2)∠BOD =∠AOD =∠EOC ,∠AOE =∠COD ,∠DOE =∠CO B .2. 如图,OC 是∠AOD 的平分线,OE 是∠BOD 的平分线.(1)如果∠AOB =140°,求∠COE 的度数;(2)在(1)的条件下,∠COD =20°,求∠BOE 的度数.解:(1)∠COE =∠COD +∠DOE =12∠AOD +12∠DOB =12(∠AOD +∠DOB )=12∠AOB =70°. (2)由(1)知∠COE =70°,又因为∠COD =20°,所以∠DOE =50°,所以∠BOE =∠DOE =50°.3.已知O 是直线上AB 上一点,OC 是一条射线,则∠AOC 与∠BOC 的关系是( D )A .∠AOC 一定大于∠BOCB .∠AOC 一定小于∠BOCC .∠AOC 一定等于∠BOCD .∠AOC 可能大于、等于或小于∠BOC4.下列结论正确的个数有( A )①从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;②∠AOB +∠BOC =180°时,射线OA ,OC 在一条直线上;③延长射线OP ;④有共同顶点的两个直角组成一个平角.A .1个B .2个C .3个D .以上结论都不对5.已知OC 平分∠AOB ,∠AOB =64°,则∠AOC 的度数是( B )A .64°B .32°C .128°D .不能计算6.已知OC 是∠AOB 的平分线,下列结论不正确的是( A )A .∠AOB =12∠BOC B .∠AOC =12∠AOB C .∠AOC =∠BOCD .∠AOB =2∠AOC7.如图,∠AOB =90°,若∠1=35°,则∠2的度数是( C )A .35°B .45°C .55°D .70°第7题图)第8题图)8.如图,直线AB ,CD 相交于点O ,射线OM 平分∠AOC ,∠MON =90°.若∠AOM =25°,则∠CON 的度数为( C )A .45°B .55°C .65°D .75°9.如图,AB 和CD 都是直线,∠EOB 是直角,OF 平分∠AOD ,∠1=27°20′,求∠2,∠3的度数.解:∵∠EOB 是直角,∴∠EOA =180°-90°=90°.∵∠1=27°20′,∴∠2=90°-∠1=62°40′,∠AOD =180°-∠1=152°40′.∵OF 平分∠AOD ,∴∠3=12∠AOD =76°20′. 10.如图,将一副三角板叠放在一起,使直角的顶点重合于点O ,并能绕O 点自由旋转.若∠DOB =65°,则∠AOC 的度数为__115°__.【解析】 ∵∠DOB =65°,∴∠BOC =90°-65°=25°,∴∠AOC =∠AOB +∠BOC =90°+25°=115°.,第10题图) ,第11题图)11.如图,已知OB 的方向是南偏东60°,OA ,OC 分别平分∠NOB 和∠NOE .(1)请直接写出OA ,OC 的方向;(2)求∠AOC 的度数.解:(1)OA 的方向是北偏东60°,OC 的方向是北偏东45°.(2)∵OB 的方向是南偏东60°,∴∠BOE =30°,∴∠NOB =30°+90°=120°.∵OA 平分∠NOB ,∴∠NOA =12∠NOB =60°. ∵OC 平分∠NOE ,∴∠NOC =12∠NOE =45°,∴∠AOC =∠NOA -∠NOC =60°-45°=15°. 12.如图,OB 是∠AOC 的平分线,OD 是∠COE 的平分线.(1)如果∠AOB =40°,∠DOE =30°,那么∠BOD 是多少度?(2)如果∠AOE =140°,∠COD =30°,那么∠AOB 是多少度?解:(1)∵OB 是∠AOC 的平分线,∴∠BOC =∠AOB =40°.∵OD 是∠COE 的平分线,∴∠COD =∠DOE =30°,∴∠BOD =∠BOC +∠COD =40°+30°=70°.(2)∵OD 是∠COE 的平分线,∴∠COE =2∠COD =2×30°=60°,∴∠AOC =∠AOE -∠COE =140°-60°=80°.∵OB 是∠AOC 的平分线,1 2∠AOC=12×80°=40°.∴∠AOB=。
北师大版七年级数学上册第四章基本平面图形角的比较课件

3. (1)角的分类:0°<( 锐角 )<90°;( 直角 )=90°;90°<( 钝角 )< 180°;平角=( 180°);
周角=( 360° ); (2)1度=( 60 )分;1分=( 60 )秒. 4. 如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=144°, OE为∠BOC的平分线,则∠BOE的度数为是 18°.
∠BOD =
.
1. 如图,已知∠AOB=∠COD=90°,且∠AOD=150°, 则∠BOC的度数为( A )
A. 30° B. 60° C. 45° D. 70° 2. 如图,将一副三角板叠在一起使直角顶点重合于点O, (两块三角板可以在同一平面内自由转动,且∠BOD,∠AOC均 小于180°),下列结论一定成立的是( C ) A. ∠BOD>∠AOC B. ∠BOD-∠AOC=90° C. ∠BOD+∠AOC=180° D. ∠BOD≠∠AOC
(1)∠MON的度数为45°. (2)∠MON的度数为. (3)∠MON的度数为45°. (4)根据题意可知不论∠AOB和∠BOC为多少 度,∠MON的度数是∠AOB度数的一半.
6. 已知∠AOB=3∠BOC,且∠BOC=30°,则∠AOC= 120°或60 .
7. 如图,已知∠AOF=∠BOC=110°,∠BOF=80°,OE是∠AOC的平分线,求
∠COE的度数.
∵∠AOF=∠BOC,
∴∠AOF-∠BOF,∠BOC=110°,
∴∠COF=∠BOC-∠BOF=30°,
∴∠AOB=30°,
∴∠AOC=∠BOC+∠AOB=140°,
∵OE是∠AOC的平分线,
∴∠COE=∠AOC=70°.
【拓展训练】 8. (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC, 求∠MON的度数; (2)在(1)中,∠AOB=m°,其他条件不变,求∠MON的度数; (3)在(1)中,∠BOC=n°(∠BOC为锐角),其他条件不变,求∠MON的度数; (4)从(1)(2)(3)的结果中能得出什么结论?
七年级数学上册 4.4角的比较例题与讲解(北师大七年级上)

4 角的比较1.角的大小比较(1)度量法:先用量角器测量出各角的度数,再按照角的度数比较大小,从而确定两个角的大小关系.(2)叠合法:两个角比较大小时,把两个角的顶点和一条边分别重合,另一条边放在重合边的同侧,根据另一条边的位置确定角的大小.如比较∠ABC 和∠DEF 的大小,可把∠DEF 移到∠ABC 上,使它的顶点E 和∠ABC 的顶点B 重合,一边ED 和BA 重合,另一边EF 和BC 落在BA 的同一侧.①如果EF 和BC 重合(如图1),那么∠DEF 等于∠ABC ,记作∠DEF =∠ABC ; ②如果EF 落在∠ABC 的外部(如图2),那么∠DEF 大于∠ABC ,记作∠DEF >∠ABC ; ③如果EF 落在∠ABC 的内部(如图3),那么∠DEF 小于∠ABC ,记作∠DEF <∠ABC .【例1】 如图,求解下列问题:(1)比较∠COD 和∠COE 的大小;(2)借助三角尺,比较∠EOD 和∠COD 的大小;(3)用量角器度量,比较∠BOC 和∠COD 的大小.分析:(1)可用叠合法比较.∠COD 和∠COE 有一条公共边OC ,而OD 在∠COE 的内部,故∠COD 小;(2)我们要选择三角尺的一个角来估算这两个角的度数,就可以达到比较的目的;(3)通过度量容易得出结论.解:(1)由图可以看出,∠COD <∠COE .(2)用三角尺中30°的角分别和这两个角比较,可以发现∠EOD <30°,∠COD >30°,所以∠EOD <∠COD .(3)通过度量可知:∠BOC =46°,∠COD =44°,所以,∠BOC >∠COD .2.角的平分线(1)定义:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线. ①角平分线是以角的顶点为端点的特殊射线,它在角的内部;②角平分线把角分成两个相等的角.(2)角平分线的表示:①OC 是∠AOB 的平分线;②∠AOC =∠COB =12∠AOB ,∠AOB =2∠AOC =2∠COB .(3)作角平分线的方法:①利用量角器量出角的度数,取角的度数的一半并画出射线;②折叠:把已知角的两边重合后再折叠,可得已知角的平分线.【例2】 如图,已知∠AOC =80°,∠BOC =50°,OD 平分∠BOC ,求∠AOD .分析:由图可知∠AOD =∠AOC +∠DOC ,所以只要求出∠DOC 即可.解:因为OD 平分∠BOC ,所以∠DOC =12∠BOC . 又因为∠BOC =50°,所以∠DOC =12×50°=25°. 所以∠AOD =∠AOC +∠DOC =80°+25°=105°.3.角平分线及角的和、差计算(1)角的和、差的意义如图,①和:∠AOB =∠1+∠2;②差:∠1=∠AOB -∠2,∠2=∠AOB -∠1.(2)角平分线及角的和、差计算与角有关的计算,是本节的重点,也是易错点. 解决这类问题,关键是根据角平分线得到相等的角,或求出一个较大的角,借助于某一个中间的角,把未知量转化为已知量.(3)三角板中角的和与差一副三角板有两块,一块含30°角,60°角,90°角;一块含45°角,45°角,90°角. 借助于三角板,即可以画出上面的角. 利用三角板和角的和、差,还可以得到以下度数的角:15°,75°,105°,120°,135°,150°,165°.________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________【例3-1】 已知∠AOB =30°,∠BOC =20°,则∠AOC 的角度是__________. 错解:50°错解分析:误以为∠AOC 只是∠AOB 与∠BOC 的和,即∠AOC =∠AOB +∠BOC =30°+20°=50°.正解:10°或50°正解思路:如图,①∠AOC =∠AOB +∠BOC =30°+20°=50°;②∠AOC =∠AOB -∠BOC =30°-20°=10°. 【例3-2】 如图,AOC 为一直线,OD 是∠AOB 的平分线,∠BOE =12∠EOC ,∠DOE=72°,求∠EOC 的度数.分析:本题中角之间的关系较复杂,直接求解有困难,可以通过设未知数、列方程的方法求解.设∠AOB =x °,因为OD 是∠AOB 的平分线,所以∠BOD =⎝⎛⎭⎫x 2°;观察图形知,∠AOB 和∠BOC 互为补角,所以∠BOC =(180-x )°;又因为∠BOE =12∠EOC ,所以∠BOE =13∠BOC =⎝⎛⎭⎫180-x 3°;然后根据∠DOE =∠BOD +∠BOE =72°可列出方程x 2+180-x 3=72,解方程求出x 的值后,再根据∠EOC =23(180-x )°求出∠EOC 的度数. 解:设∠AOB =x °,则∠BOD =⎝⎛⎭⎫x 2°,∠BOC =(180-x )°,∠BOE =⎝⎛⎭⎫180-x 3°,由∠DOE =72°可得x 2+180-x 3=72. 解这个方程,得x =72.∴∠EOC =23(180-x )°=72°.4.角的分类(1)角的分类:根据角的度数,常常把大于0°而小于180°的角分为锐角、直角、钝角三类.(2)各种角的规定:锐角:大于0°且小于90°的角.直角:等于90°的角.钝角:大于90°且小于180°的角.平角:等于180°的角.周角:等于360°的角.(3)角之间的关系:锐角<直角<钝角<平角<周角.1平角=2直角=180°;1周角=2平角=4直角=360°.若没有特别说明,我们平常所说的角是指小于平角的角.【例4】 如图,解答下列问题:(1)比较图中∠AOB ,∠AOC ,∠AOD 的大小;(2)找出图中的直角、锐角和钝角.分析:(1)角的大小可以观察得出;(2)根据各类角的特征观察得出.解:(1)∠AOD >∠AOC >∠AOB ;(2)直角有∠AOC ,锐角有∠AOB ,∠BOC ,∠COD ,钝角有∠AOD ,∠BOD .。
七年级数学上册第四章大体平面图形4角的比较典型例题素材新版北师大版
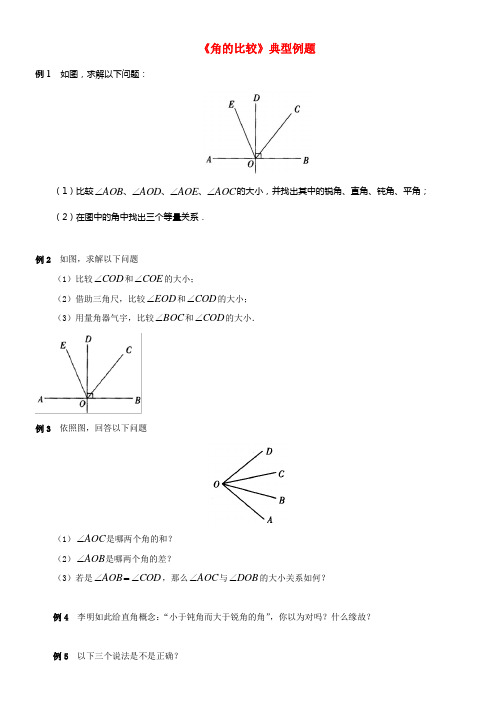
《角的比较》典型例题例1 如图,求解以下问题:(1)比较AOC AOE AOD AOB ∠∠∠∠、、、的大小,并找出其中的锐角、直角、钝角、平角;(2)在图中的角中找出三个等量关系.例2 如图,求解以下问题(1)比较COD ∠和COE ∠的大小;(2)借助三角尺,比较EOD ∠和COD ∠的大小;(3)用量角器气宇,比较BOC ∠和COD ∠的大小.例3 依照图,回答以下问题(1)AOC ∠是哪两个角的和?(2)AOB ∠是哪两个角的差?(3)若是COD AOB ∠=∠,那么AOC ∠与DOB ∠的大小关系如何?例4 李明如此给直角概念:“小于钝角而大于锐角的角”,你以为对吗?什么缘故?例5 以下三个说法是不是正确?(l)两条射线组成的图形叫做角;(2)平角是一条直线;(3)周角是一条射线。
参考答案例1 分析 AOB ∠是平角,AOC ∠是钝角,AOD ∠是直角,AOE ∠是锐角这就找到了这几个角的大小关系;相等关系通过观看图也容易找到,如:.DOC EOD COE ∠+∠=∠解 (1)由图能够看出,AOE AOD AOC AOB ∠>∠>∠>∠;(2)等量关系有:EOD AOE AOD BOD AOD AOB DOC EOD COE ∠+∠=∠∠=∠=∠∠+∠=∠,22,,….说明:(1)若是已知角是锐角、直角、周角、平角,咱们就以直接由它们之间的关系比较出它们的大小;(2)若是两个直角有一条公共边,而且另一边都在公共边的同侧,依照图形也能观看出两个角的大小.例 2 分析 (1)是显然的;(2)通过气宇也容易患出结论;(3)咱们要选择三角尺的一个角来估算这两个角大的度数,就能够够达到比较的目的.解 (1)由图能够看出,COE COD ∠<∠;(2)用三角尺中30°的角别离和这两个角比较,能够发觉︒>∠︒<∠30,30COD EOD ,因此COD BOD ∠<∠;(3)通过气宇可知:︒=∠︒=∠44,46COD BOC ,因此,COD BOC ∠>∠.说明:当借助三角尺比较两个角的大小时咱们选择的三角尺的角要适当;当两个角的大小超级接近时,咱们能够借助量角器来比较这两个角的大小.例3 解:(1)AOC ∠是AOB ∠与BOC ∠的和.(2)AOB ∠是AOC ∠与BOC ∠的差,或AOB ∠是AOD ∠与BOD ∠的差.(3)因为COD AOB ∠=∠,因此BOC COD BOC AOB ∠+∠=∠+∠,即DOB AOC ∠=∠.说明:等式的性质也适用于几何中的量,如长度、角度等等.例4 解:不对!因为咱们是按如此的顺序来概念角的概念的:由角→平角与周角→直角→锐角与钝角. 几何里咱们是用前面已学的概念来讲明后面未学的概念,一环扣一环,形成按角的大小分类的各个概念的结构. 锐角、钝角已经用直角的概念来讲明它们的特点了,故再用锐角、钝角的概念来描述直角,就犯了循环概念的错误. 例5 分析:(1)两条射线若是没有公共端点就不组成角。
七年级数学上册第四章基本平面图形4角的比较典型例题素材北师大版解析

七年级数学上册第四章基本平面图形4角的比较典型例题素材北师大版解析-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN《角的比较》典型例题例1 如图,求解下列问题:(1)比较AOC∠、∠、、的大小,并找出其中的锐角、AOB∠∠AOEAOD直角、钝角、平角;(2)在图中的角中找出三个等量关系.例2 如图,求解下列问题(1)比较COD∠的大小;∠和COE(2)借助三角尺,比较EOD∠的大小;∠和COD(3)用量角器度量,比较BOC∠和COD∠的大小.例3 根据图,回答下列问题(1)AOC∠是哪两个角的和?(2)AOB∠是哪两个角的差?(3)如果COD∠,那么AOC∠的大小关系如何?∠与DOB=AOB∠例4 李明这样给直角定义:“小于钝角而大于锐角的角”,你认为对吗为什么例5 下列三个说法是否正确?(l)两条射线组成的图形叫做角;(2)平角是一条直线;(3)周角是一条射线。
参考答案例1 分析AOB∠是直角,AOE∠是锐角这∠是钝角,AOD∠是平角,AOC就找到了这几个角的大小关系;相等关系通过观察图也容易找到,如:∠=∠+EODDOC.COE∠解(1)由图可以看出,AOE∠>∠;>AOB∠∠AOCAOD>(2)等量关系有:∠∠∠+==∠,∠22=∠,BODAODAODAOEEODAOBDOC∠=+ COE∠EOD∠,….说明:(1)如果已知角是锐角、直角、周角、平角,我们就以直接由它们之间的关系比较出它们的大小;(2)如果两个直角有一条公共边,并且另一边都在公共边的同侧,根据图形也能观察出两个角的大小.例2 分析(1)是显然的;(2)通过度量也容易得出结论;(3)我们要选择三角尺的一个角来估算这两个角大的度数,就可以达到比较的目的.解(1)由图可以看出,COE∠;COD∠<(2)用三角尺中30°的角分别和这两个角比较,可以发现︒,30COD∠30EOD,所以COD<>∠︒∠;<BOD∠(3)通过度量可知:︒,46CODBOC,所以,COD∠44=∠︒=∠.>BOC∠说明:当借助三角尺比较两个角的大小时我们选择的三角尺的角要适当;当两个角的大小非常接近时,我们可以借助量角器来比较这两个角的大小.例3 解:(1)AOC∠的和.∠与BOC∠是AOB(2)AOB∠与BOD∠是AOD∠的差.∠是AOC∠与BOC∠的差,或AOB(3)因为COD∠,=AOB∠所以BOC COD BOC AOB ∠+∠=∠+∠,即DOB AOC ∠=∠.说明:等式的性质也适用于几何中的量,如长度、角度等等.例4 解:不对!因为我们是按这样的顺序来定义角的概念的:由角→平角与周角→直角→锐角与钝角. 几何里我们是用前面已学的概念来说明后面未学的概念,一环扣一环,形成按角的大小分类的各个概念的结构. 锐角、钝角已经用直角的概念来说明它们的特征了,故再用锐角、钝角的概念来描述直角,就犯了循环定义的错误.例5 分析:(1)两条射线如果没有公共端点就不构成角。
2022七年级数学上册 第四章 基本平面图形4.4角的比较习题课件(新版)北师大版

9、 人的价值,在招收诱惑的一瞬间被决定 。22.5.822.5.8Sunday, ay 08, 2022 10、低头要有勇气,抬头要有低气。17:11:4817:11:4817:115/8/2022 5:11:48 PM
11、人总是珍惜为得到。22.5.817:11:4817:11May-228-May-22 12、人乱于心,不宽余请。17:11:4817:11:4817:11Sunday, May 08, 2022 13、生气是拿别人做错的事来惩罚自 己。22.5.822.5.817:11:4817:11:48May 8, 2022 14、抱最大的希望,作最大的努力。2022年5月8日 星期日 下午5时 11分48秒17:11:4822.5.8 15、一个人炫耀什么,说明他内心缺 少什么 。。2022年5月 下午5时11分22.5.817:11May 8, 2022 16、业余生活要有意义,不要越轨。2022年5月8日 星期日5时11分 48秒17:11:488 May 2022 17、一个人即使已登上顶峰,也仍要 自强不 息。下 午5时11分48秒 下午5时11分17:11:4822.5.8
9、 人的价值,在招收诱惑的一瞬间被决定 。22.5.822.5.8Sunday, May 08, 2022 10、低头要有勇气,抬头要有低气。17:11:4817:11:4817:115/8/2022 5:11:48 PM
11、人总是珍惜为得到。22.5.817:11:4817:11May-228-May-22 12、人乱于心,不宽余请。17:11:4817:11:4817:11Sunday, May 08, 2022 13、生气是拿别人做错的事来惩罚自 己。22.5.822.5.817:11:4817:11:48May 8, 2022 14、抱最大的希望,作最大的努力。2022年5月8日 星期日 下午5时 11分48秒17:11:4822.5.8 15、一个人炫耀什么,说明他内心缺 少什么 。。2022年5月 下午5时11分22.5.817:11May 8, 2022 16、业余生活要有意义,不要越轨。2022年5月8日 星期日5时11分 48秒17:11:488 May 2022 17、一个人即使已登上顶峰,也仍要 自强不 息。下 午5时11分48秒 下午5时11分17:11:4822.5.8
北师大版七年级数学上册第四章基本平面图形4.4 角的比较
探究新知
讨论探究
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,
∠BOC.
O
它们的关系:
C B
A
∠AOC 是∠AOB 与∠BOC的和,记作∠AOC = ∠AOB
+∠BOC; ∠AOB 是∠AOC与∠BOC的差,记作∠AOB = ∠AOC-
∠BOC; 类似地,∠AOC-∠AOB=∠BOC .
巩固练习
变式训练 计算下列角的度数.
(1) 如图①,若∠AOC=35°,∠BOC=40°,则
∠AOB= 75 °.
A
A
C
C
O
B
图①
O
B
图②
(2) 如图②,若∠AOB= 60°,∠BOC=40°, 则 ∠AOC=20°.
巩固练习
(3) 若∠AOB =60°,∠AOC =30°,则 ∠BOC= 90或30 °. 提示:无图条件下要分情况讨论.
所以∠COD=∠DOE = 30°, O
A
所以∠BOD =∠BOC+∠COD = 40°+30°= 70°.
探究新知
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB
是多少度?
DC
解:因为 ∠COD=30°, E
OD 平分∠COE,
B
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
C
成两个相等的角,这条射
线叫做这个角的平分线.
O
A
应用格式:
因为OC 是∠AOB 的角平分线,
所以
∠AOC
=∠BOC
=
1 2
∠AOB,
∠AOB =2∠BOC =2∠AOC.
北师版七年级上册数学 第4章 基本平面图形 角的比较
9.【中考•滨州】如图,OB是∠AOC的平分线,OD是
∠COEቤተ መጻሕፍቲ ባይዱ平分线,若∠AOB=40°,∠COE=60°,
则∠BOD的度数为( )
A.50°
D
B.60°
C.65°
D.70°
*10.【2019•烟台】小明将一张正方形纸片按如图所示顺
序折叠成纸飞机,当机翼展开在同一平面时(机翼间无
缝隙),∠AOB的度数是________. 45°
A.∠AOB=110° B.∠AOB=∠AOC C.∠AOB+∠AOC=90° D.∠AOB+∠AOC=180°
*5.借助一副三角尺,你能画出的角的度数是( B ) A.65°B.75°C.85°D.95°
【点拨】利用一副三角尺的角度特点求解.
6.【中考·百色】如图,AM 为∠BAC 的平分线,下列等式 中,错误的是( C ) A.12∠BAC=∠BAM B.∠BAM=∠CAM C.∠BAM=2∠CAM D.2∠CAM=∠BAC
(2)如果∠AOM=51°17′,求∠BON的度数.
解:∠BON=∠AOB-∠AOM-∠MON=180°- 51°17′-90°=38°43′.
13.如图,已知∠AOE=130°,∠AOB∶∠BOC=2∶1, 且3∠COE=2∠AOB,求∠AOB的度数.
【点拨】在解决数学问题时,有一种从未知转化为 已知的手段是通过设元,寻找已知与未知之间的等 量关系,构造方程,然后求解方程完成未知向已知 的转化,这种解决问题的思想称为方程思想.
15.如图,已知∠AOB=90°,且∠BOC=30°,OM平 分∠AOC,ON平分∠BOC.
(1)求∠MON的度数;
解:因为 OM 平分∠AOC, 所以∠MOC=12∠AOC, 因为 ON 平分∠BOC, 所以∠NOC=12∠BOC.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《角的比较》典型例题
例1 如图,求解下列问题:
(1)比较AOC AOE AOD AOB ∠∠∠∠、、、的大小,并找出其中的锐角、直角、钝角、平角;
(2)在图中的角中找出三个等量关系.
例2 如图,求解下列问题
(1)比较COD ∠和COE ∠的大小;
(2)借助三角尺,比较EOD ∠和COD ∠的大小;
(3)用量角器度量,比较BOC ∠和COD ∠的大小.
例3 根据图,回答下列问题
(1)AOC ∠是哪两个角的和?
(2)AOB ∠是哪两个角的差?
(3)如果COD AOB ∠=∠,那么AOC ∠与DOB ∠的大小关系如何?
例4 李明这样给直角定义:“小于钝角而大于锐角的角”,你认为对吗?为什么?
例5 下列三个说法是否正确?
(l)两条射线组成的图形叫做角;
(2)平角是一条直线;
(3)周角是一条射线。
参考答案
例1 分析 AOB ∠是平角,AOC ∠是钝角,AOD ∠是直角,AOE ∠是锐角这就找到了这几个角的大小关系;相等关系通过观察图也容易找到,如:.DOC EOD COE ∠+∠=∠
解 (1)由图可以看出,AOE AOD AOC AOB ∠>∠>∠>∠;
(2)等量关系有:
EOD AOE AOD BOD AOD AOB DOC EOD COE ∠+∠=∠∠=∠=∠∠+∠=∠,22,,….
说明:(1)如果已知角是锐角、直角、周角、平角,我们就以直接由它们之间的关系比较出它们的大小;(2)如果两个直角有一条公共边,并且另一边都在公共边的同侧,根据图形也能观察出两个角的大小.
例2 分析 (1)是显然的;(2)通过度量也容易得出结论;(3)我们要选择三角尺的一个角来估算这两个角大的度数,就可以达到比较的目的.
解 (1)由图可以看出,COE COD ∠<∠;
(2)用三角尺中30°的角分别和这两个角比较,
可以发现︒>∠︒<∠30,30COD EOD ,所以COD BOD ∠<∠;
(3)通过度量可知:︒=∠︒=∠44,46COD BOC ,所以,COD BOC ∠>∠.
说明:当借助三角尺比较两个角的大小时我们选择的三角尺的角要适当;当两个角的大小非常接近时,我们可以借助量角器来比较这两个角的大小.
例3 解:(1)AOC ∠是AOB ∠与BOC ∠的和.
(2)AOB ∠是AOC ∠与BOC ∠的差,或AOB ∠是AOD ∠与BOD ∠的差.
(3)因为COD AOB ∠=∠,
所以BOC COD BOC AOB ∠+∠=∠+∠,即DOB AOC ∠=∠.
说明:等式的性质也适用于几何中的量,如长度、角度等等.
例4 解:不对!因为我们是按这样的顺序来定义角的概念的:由角→平角与周角→直角→锐角与钝角. 几何里我们是用前面已学的概念来说明后面未学的概念,一环扣一环,形成按角的大小分类的各个概念的结构. 锐角、钝角已经用直角的概念来说明它们的特征了,故再用锐角、钝角的概念来描述直角,就犯了循环定义的错误.
例5 分析:(1)两条射线如果没有公共端点就不构成角。
(2)平角是两边成特殊位置的角,平角也有顶点和两边并可以确定角的内部;平角的
两边成一直线。
两边的顶点分直线成两条射线。
(3)周角是两边重合成一条射线的角,不是一条射线。
解:以上三种说法都不正确。
