第三章直流电阻电路的分析与计算

合集下载

直流电阻原理

直流电阻原理
直流电阻是指在直流电路中阻碍电流通过的元件，它是电路中的基本元件之一。

直流电阻的原理主要涉及电阻的定义、电阻的特性以及电阻的计算方法。

首先，电阻是指电路中阻碍电流通过的元件，其单位是欧姆（Ω）。

电阻的大
小与电路中材料的导电性质有关，通常用ρ表示。

电阻的大小与电路中的长度、横截面积以及材料的电阻率有关，可以用以下公式表示：
R = ρ l / A。

其中，R表示电阻的大小，ρ表示材料的电阻率，l表示电路中的长度，A表
示电路的横截面积。

由此可见，电阻的大小与电路中的材料和尺寸有直接关系。

其次，电阻的特性主要包括电阻的电压-电流特性和电阻的功率特性。

在直流
电路中，电阻的电压-电流特性呈线性关系，即电阻的电压与电流成正比。

而电阻
的功率特性则是指电阻消耗的功率与电流和电压的关系。

根据功率公式P=VI，可
以得出电阻消耗的功率与电流的平方成正比，与电压的平方成正比。

最后，电阻的计算方法主要涉及串联电阻和并联电阻的计算。

在串联电路中，
电阻的总和等于各个电阻的和，即Rt = R1 + R2 + ... + Rn。

而在并联电路中，电阻
的倒数之和等于各个电阻的倒数之和的倒数，即1/Rt = 1/R1 + 1/R2 + ... + 1/Rn。

总之，直流电阻的原理涉及电阻的定义、特性和计算方法。

了解电阻的原理对
于理解电路的工作原理和进行电路设计都具有重要意义。

希望本文对直流电阻的原理有所帮助。

直流电路分析与定理总结

直流电路分析与定理总结直流电路是指电流方向固定的电路，其内部的电压和电流均为直流。

在电路分析中，我们常常需要使用一些电路定理来帮助我们推导和解决问题。

本文将对直流电路分析中常用的几个定理进行总结，包括欧姆定律、基尔霍夫定律、电阻的串并联、电压分压和电流分流定律等。

1. 欧姆定律欧姆定律是直流电路分析的基础，它描述了电流、电压和电阻之间的关系。

根据欧姆定律，电流等于电压与电阻之比，即I=U/R，其中I为电流，U为电压，R为电阻。

欧姆定律适用于电阻为常数的线性电阻元件。

2. 基尔霍夫定律基尔霍夫定律是直流电路分析中常用的定理，它包括基尔霍夫第一定律和基尔霍夫第二定律。

（1）基尔霍夫第一定律（电流定律）：在任意一个电路节点，电流的代数和为零。

这意味着电流在节点处的分配与汇总相等。

（2）基尔霍夫第二定律（电压定律）：沿着闭合回路的电压代数和为零。

这意味着电压在闭合回路中的升降和消耗相等。

3. 电阻的串并联在直流电路中，电阻可以串联或并联连接。

我们可以利用串并联电阻的等效性来简化电路分析。

（1）电阻的串联：当多个电阻依次连接在电路中时，它们的等效电阻等于各电阻之和，即R=R1+R2+...+Rn。

（2）电阻的并联：当多个电阻并联连接在电路中时，它们的等效电阻等于各电阻倒数之和的倒数，即1/R=1/R1+1/R2+...+1/Rn。

4. 电压分压定律电压分压定律描述了在电路中，电压在串联电阻上按比例分布的关系。

根据电压分压定律，电压分布与电阻值成正比，即U=U1+U2+...+Un。

当电阻值相同时，电压分布均匀；当电阻值不同时，电压分布不均匀，较大电阻上的电压较高。

5. 电流分流定律电流分流定律描述了在电路中，电流在并联电阻上按比例分流的关系。

根据电流分流定律，电流分流与电阻值成反比，即I=I1+I2+...+In。

当电阻值相同时，电流分布均匀；当电阻值不同时，电流分布不均匀，较小电阻上的电流较高。

通过应用欧姆定律、基尔霍夫定律、电阻的串并联、电压分压和电流分流定律，我们可以对直流电路进行准确的分析和计算。

直流电路中的电阻分析

直流电路中的电阻分析引言直流电路作为电子学的基础，广泛应用于各个领域。

其中一个重要的元件就是电阻。

电阻作为电路中的重要成分，对电流的流动起着限制和调节作用。

本文将围绕直流电路中的电阻进行探讨，并分析电阻对电流和电压的影响。

电阻的基本概念电阻是电路中的一种基本元件，用来阻碍电流的流动。

它可以通过材料的导电性来决定，导电性强的材料通常会产生低阻的电阻器。

电阻的单位是欧姆（Ω），其一般表示为R。

电阻与电流和电压的关系由欧姆定律来描述。

欧姆定律欧姆定律是描述直流电路中电压、电流和电阻之间关系的基本定律。

根据欧姆定律，电阻R上的电流I与通过它的电压V之间的关系可以表示为：I = V / R这个式子指出，电流的大小与电压成正比，与电阻成反比。

当电压不变时，电阻越大，电流越小；反之亦然。

这个定律在电路的设计和分析中具有重要的作用。

串联电阻串联电阻是指将多个电阻依次连接在电路中，形成一个电路的分支。

在串联电路中，电流依次通过每个电阻，并且电流大小一致。

由于电阻阻碍电流的流动，串联电阻会增加电路中的总阻力，降低电流的大小。

根据欧姆定律，串联电阻的总阻力可以通过所有电阻的阻力之和来计算。

并联电阻并联电阻是指将多个电阻同时连接到电路的不同分支上。

在并联电路中，每个电阻上的电压相同，而电流可以在分支之间分流。

由于分流，电流在电路中的总阻力会减小，增加电流的大小。

根据欧姆定律，并联电阻的总阻力可以通过所有电阻的阻力之和的倒数来计算。

电阻和功率除了对电流和电压的影响外，电阻还对电路中的功率起着重要的影响。

根据功率定律，电路中所消耗的功率（P）可以通过电流（I）和电压（V）的乘积来计算。

P = IV由于电流和电压与电阻有关，因此电阻对功率的影响十分明显。

当电流固定时，阻值越大，功率越小；当电压固定时，阻值越大，功率也越小。

因此，在电路设计中，需要根据需求合理选择电阻值以达到所需的功率输出。

总结直流电路中的电阻分析是电子学中的重要内容。

直流电阻电路的分析与计算

3
1
1
I 4A
2
4
I 1
2A
1A
1A
举例解： 2
2 4A 1A 4 I
2
1
+ 8V -
4 1A 2
I 1
I 2A
I
1A 4
1 4
3A
2 1
2 I 3A 2A 21
{end}
{end}
2.2 电阻的串联与并联 2.2.1 电阻的串联
1. 电路特点: R1 i + Rk Rn + u1 _ _
+ u1 _ + uk _ u
(a) 各电阻顺序连接，流过同一电流 (KCL)； (b) 总电压等于各串联电阻的电压之和 (KVL)。
2.2 电阻的串联与并联
2. 等效电阻Req R1 i + Rk Rn Req 等效 i + u _
R12
–
i2 + 2 R23 u23 3 –
i2Y i3 + –
i3Y +
若 u12 u12 , u23 u23 , u31 u31 而
i1 i1 , i2 i2 ,
i3 i3
则Δ形连接与Y形连接等效
2.3 电阻星形连接与三角形连接之间的等效变换
2.2 电阻的串联与并联
2.2.2 电阻的并联
i
+ i1 i2 ik in
u _
R1
R2
Rk
Rn
1. 电路特点:
(a) 各电阻两端分别接在一起，两端为同一电压 (KVL)；
(b) 总电流等于流过各并联电阻的电流之和 (KCL)。
2.2 电阻的串联与并联

直流电路电的电阻计算公式

直流电路电的电阻计算公式在直流电路中，电阻是一个非常重要的参数，它决定了电流的大小和电压的变化。

在电路中，电阻可以是一个电阻器、导线、电池等元件，它们都对电流的流动产生一定的阻碍。

因此，了解电阻的计算公式对于设计和分析电路非常重要。

电阻的定义。

电阻是指电流在通过电路时所遇到的阻力，它的大小与电路中的材料、长度、截面积等因素有关。

通常用符号R表示，单位是欧姆（Ω）。

电阻的计算公式。

在直流电路中，电阻的计算公式是：R = ρ L / A。

其中，R表示电阻的大小，ρ表示电阻率，L表示电阻的长度，A表示电阻的截面积。

电阻率ρ是一个材料固有的属性，它与材料的导电性有关，不同的材料具有不同的电阻率。

通常情况下，金属的电阻率比较小，而绝缘体的电阻率比较大。

电阻的长度L是指电阻器或导线的实际长度，单位是米。

电阻的截面积A是指电阻器或导线横截面的面积，单位是平方米。

根据这个公式，我们可以看到电阻的大小与电阻率成正比，与电阻的长度成正比，与电阻的截面积成反比。

这也就是说，电阻的大小取决于材料的导电性、长度和截面积。

电阻的串联和并联。

在电路中，电阻可以串联连接或并联连接。

串联连接是指多个电阻依次连接在一起，形成一个电阻链，电流依次通过每个电阻。

并联连接是指多个电阻同时连接在一起，电流可以选择不同的路径通过每个电阻。

对于串联连接的电阻，总电阻的计算公式是：R = R1 + R2 + R3 + ...对于并联连接的电阻，总电阻的计算公式是：1/R = 1/R1 + 1/R2 + 1/R3 + ...这两个公式可以帮助我们计算出串联和并联电阻的大小，从而分析电路中的电流和电压变化。

电阻的应用。

电阻在电路中有着广泛的应用，它可以用来限制电流、调节电压、分压、分流等。

在实际电路设计中，我们经常需要根据电路的要求来选择合适的电阻值，以达到所需的电流和电压变化。

此外，电阻还可以用来测量电流和电压。

通过欧姆定律，我们可以利用电阻来测量电路中的电流和电压，从而对电路进行分析和测试。

直流电阻电路的分析

直流电阻电路的分析2.1 电路的等效2.1.1 电路等效的一般概念在电路分析中，可以把由多个元器件组成的电路作为一个整体看待。

若这个整体只有两个端钮与外电路相连，则称为二端网络（two terminal network）或单端口网络。

二端网络的一般符号如图2-3所示。

二端网络的端钮电流称为端口电流，两个端钮之间的电压称为端口电压。

图2-3中标出的端口电流i和端口电压u为关联参考方向。

一个二端网络的特性由网络端口电压u与端口电流i的关系（即伏安关系）来表征。

若两个二端网络内部结构完全不同，但端钮具有相同的伏安关系，则称这两个二端网络对同一负载（或外电路）而言是等效的，即互为等效网络（equivalent network）。

相互等效的电路对外电路的影响是完全相同的，也就是说“等效”是指“对外等效”。

利用电路的等效变换分析电路，可以把结构较复杂的电路用一个较为简单的等效电路代替，简化电路分析和计算，它是电路分析中常用的分析方法。

但要注意的是，若要求被代替的复杂电路中的电压和电流时，必须回到原电路中去计算。

图2-3 二端网络2.1.2 电阻的串联、并联与混联1.电阻的串联两个或两个以上电阻首尾相连，中间没有分支，各电阻流过同一电流的连接方式，称为电阻的串联（series connection）。

图2-4（a）为三个电阻串联电路，a、b两端外加电压U，各电阻流过电流I，参考方向如图所示。

由图2-4（a）所示，根据KVL和欧姆定律，可得图2-4 电阻的串联由图2-4（b）所示，根据欧姆定律，可得两个电路等效的条件是具有完全相同的伏安特性，即式（2.1）与式（2.2）完全一致，由此可得式（2.3）中R称为串联等效电阻，式（2.3）表明串联电阻的等效电阻等于各电阻之和。

推广到一般情况：n个电阻串联等效电阻等于各个电阻之和。

即电阻串联时电流相等，各电阻上的电压为写成一般形式式（2.6）为串联电阻的分压公式。

由此可见，电阻串联时，各个电阻上的电压与电阻值成正比，即电阻值越大，分得的电压越大。

第三章复杂直流电路计算部分

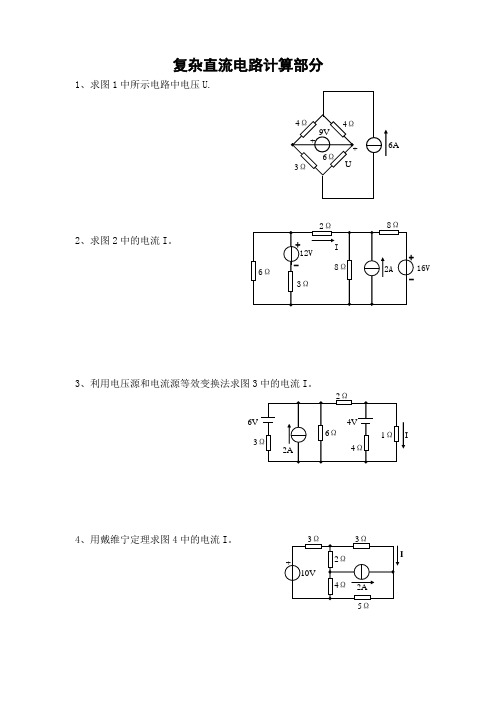
复杂直流电路计算部分1、求图1中所示电路中电压U.2、求图2中的电流I 。

3、利用电压源和电流源等效变换法求图3中的电流I 。

4、用戴维宁定理求图4中的电流I 。

16V6A3I5、计算图5所示电路中5Ω电阻中的电流I 。

6、用戴维宁定理求图6所示的电流I.7、试用叠加原理求图7中的电压U 。

8、图8所示电路,负载电阻R L 可以改变，求（1）R L =2Ω时的电流I ab ; （2）R L =3Ω时的电流I ab 。

46ΩI U-9、试用叠加原理求图9电路中的电压U.10、图10中已知R 1=R=12Ω,R 2=4Ω，R 3=R 4=6Ω,E 1=21V ,E 2=5V ,E 3=9V ，E 4=6V ，I S =2A 。

求（1）打开开关K 时，I 、U AB ；（2）开关K 闭合时,I 和U 。

11、试用戴维宁定理求图11所示电路中电流12R 4 E ΩI 10Ω13、如图13所示，N A 为线性有源二端网络，电流表、电压表均为理想的，已知当开关S 置“1"位置时，电流表读数为2A ；当S 置“2”位置时，电压表读数为4V .求当S 置于“3"位置时，图中的电压U 。

14、图14所示电路为计算机加法原理电路,已知V a =12V ，V d =6V ，R 1=9K Ω,R 2=3K Ω,R 3=2K Ω，R 4=4K Ω,求ab 两端的开路电压Uab 。

15、求图15中各支路电流。

1Ad6A16、求图16所示电路中R L17、图17所示，已知电源电动势E=12V ,电源内阻不计,电阻R 1=9Ω, R 2=6Ω，R 3=18Ω，R 4=2Ω,用戴维宁定理求R 4中的电流I 。

18、利用叠加原理求如图18所示的电路中当开关K 由1改向2时，电容器C 上电荷的变化。

已知C=20μF 。

19、如图19所示电路中,N 为有源二端网络,当开关K 断开时，电流表的读数为1。

8A,当开关K 闭合时，电流表的读数为1A ，试求有源二端网络N 的等值电压源参数.LR 41A20、用叠加原理计算图20所示电路的电流I.21、计算图21所示电路中的电压U ab 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
在图3.5 中根据KVL定理可知，并联的各个电阻的电压定理可知，在图 (a)中，根据定理可知相等，均等于U，则由KCL定理可得相等，均等于，则由定理可得 I=I1+I2+...In 即电阻的并联网络的端电流等于各电阻电流之和。即电阻的并联网络的端电流等于各电阻电流之和。又由欧姆定律可得 I1=U/R1,I2=U/R2,...In=U/Rn于是 I=I1+I2+...In=U/R1+U/R2+...+U/Rn=(1/R1+1/R2+...+1/Rn)U
即电阻的并联网络的每个电阻的电流与端电流的比等于该电导与等效电导之比，这个比值称为“分流比” 导与等效电导之比，这个比值称为“分流比”。在端电流一定时，适当选择并联电阻，可使每个电阻得到所需要的电流，定时，适当选择并联电阻，可使每个电阻得到所需要的电流，因此并联电阻有“分流”作用。因此并联电阻有“分流”作用。
下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
3.1.1电阻的串联电阻的串联
电压表的表头所能测量的最大电压就是其量程，电压表的表头所能测量的最大电压就是其量程，通常它都较小。在测量时，通过表头的电流是不能超过其量程的，较小。在测量时，通过表头的电流是不能超过其量程的，否则将损坏电流表。而实际用于测量电压的多量程的电压表(如则将损坏电流表。而实际用于测量电压的多量程的电压表如 C30-v型磁电系电压表是由表头与电阻串联的电路组成，如型磁电系电压表)是由表头与电阻串联的电路组成型磁电系电压表是由表头与电阻串联的电路组成，所示。图3.2所示。其中，Rg为表头的内阻，Ig为流过表头的电流，所示其中，为表头的内阻，为流过表头的电流， Ug为表头两端的电压，R1, R2, R3,R4为电压表各挡的分压电为表头两端的电压，对应一个电阻挡位，电压表有一个量程。阻。对应一个电阻挡位，电压表有一个量程。
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
以上就是利用了串联电阻的“分压” 以上就是利用了串联电阻的“分压”作用来扩大电压表的量程。各电阻元件顺次联接起来，各电阻元件顺次联接起来，所构成的一端网络称为电阻的串联网络，所示。串联网络，如图3.3 (a)所示。所示在图3.3 中根据KCL定理可知，串联的各个电阻的电定理可知，在图 (a)中，根据定理可知流相等，均等于I，则由KVL定理可得流相等，均等于，则由定理可得 U=U1+U2+...+Un 即电阻的串联网络的端口电压等于各电阻电压之和。即电阻的串联网络的端口电压等于各电阻电压之和。又由欧姆定律可得 U1=R1I，U2=R2I，...，Un=RnI，，，，，于是U=R1I+R2I+...RnI=(R1+R2+...Rn)I 于是
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
同理，并联的每个电阻的功率也与它们的电导成正比，同理，并联的每个电阻的功率也与它们的电导成正比，与它们的电阻成反比。们的电阻成反比。即 1 1 1 P : P2 : ... : Pn = : : L : = G1 : G2 : LGn 1 R1 R2 Rn 若只有R1, R2两个电阻并联，如图3.6所示，两个电阻并联，所示，若只有所示 1 1 1 R1 + R2 = + = Ri R1 R2 R1 R2 可得等效电阻R 可得等效电阻 i为
上一页下一页返回
பைடு நூலகம்
3.1电路的串、并联等效变换电路的串、电路的串
联接的电阻等效变换为△ 将Y联接的电阻等效变换为△联接的电阻，己知 a、Rb、Rc 联接的电阻等效变换为联接的电阻，己知R 电阻，则等效的电阻R 电阻，则等效的电阻 ab、Rbc、Rca为
Ra Rb Rab = Ra + Rb + Rc Rb Rc Rbc = Rb + Rc + Ra RR Rca = Rc + Ra + c a Rb
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
3.1.3电阻星形联接与三角形联接的等效变电阻星形联接与三角形联接的等效变换
3个电阻的一端联接在一起构成一个节点，另一端分别为个电阻的一端联接在一起构成一个节点O，个电阻的一端联接在一起构成一个节点网络的3个端钮个端钮a, 网络的个端钮 b, c，它们分别与外电路相连，这种三端网，它们分别与外电路相连，络叫电阻的星形联接，又叫电阻的Y联接联接，所示。络叫电阻的星形联接，又叫电阻的联接，如图3.7 (a)所示。所示 3个电阻串联起来构成一个回路，而3个联接点为网络的个个电阻串联起来构成一个回路，个联接点为网络的个联接点为网络的3个个电阻串联起来构成一个回路端钮a, 端钮 b, c，它们分别与外电路相连，这种三端网络叫电阻，它们分别与外电路相连，的三角形联接，又叫电阻的△联接，如图3.7 所示所示。的三角形联接，又叫电阻的△联接，如图 (b)所示。
Ri = R1 R2 R1 + R2
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
两个电阻的电流分别为 U Ri I R2 I1 = = = I R1 R1 R1 + R2
U Ri I R1 = = I R2 R2 R1 + R2 如果R 如果 1=R2=R，则有， R I Ri = , I1 = I 2 = 2 2 I2 =
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
I1 G1U G1 G1 = = = 1 G1U G1 G1 + G2 + ... + Gn I 2 G2U G2 G2 = = = 1 G1U G1 G1 + G2 + ... + Gn M I n GnU Gn Gn = = = 1 G1U G1 G1 + G2 + ... + Gn
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
3.1.2电阻的并联电阻的并联
实际用于测量电流的多量程的电流表(如实际用于测量电流的多量程的电流表如C41-uA磁电系电流磁电系电流由表头与电阻串、所示。表)由表头与电阻串、并联的电路组成，如图3.4所示。其中，由表头与电阻串并联的电路组成，所示其中， Rg为表头的内阻，Ig为流过表头的电流，Ug为表头两端的电为表头的内阻，为流过表头的电流，压，R1、R2、R3、R4为电流表各挡的分流电阻。对应一个电为电流表各挡的分流电阻。阻挡位，电流表有一个量程。阻挡位，电流表有一个量程。以上就是利用了并联电阻的“分流” 以上就是利用了并联电阻的“分流”作用来扩大电流表的量程。量程。各电阻元件的两端钮分别联接起来所构成的一端网络称为电阻的并联网络，所示。电阻的并联网络，如图3.5 (a)所示。所示
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
即电阻的串联网络的每个电阻的电压与端口电压之比等于该电阻与等效电阻的比，这个比值称为“分压比” 电阻与等效电阻的比，这个比值称为“分压比”。在端口电压一定时，适当选择串联电阻，压一定时，适当选择串联电阻，可使每个电阻得到所需要的电压，因此串联电阻有“分压”作用。电压，因此串联电阻有“分压”作用。同理，串联的每个电阻的功率也与它们的电阻成正比，同理，串联的每个电阻的功率也与它们的电阻成正比，即 P1:P2:...:Pn=R1:R2:...:Rn
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
是图3.3 所示的等效电路根据等效的概念，所示的等效电路，图3.3 (b)是图 (a)所示的等效电路，根据等效的概念，在是图中有:U=RiI 图3.3 ( b)中有中有因此，因此，Ri=R1+R2+...+Rn，即电阻的串联网络的等效电阻等于各电阻之和。即电阻的串联网络的等效电阻等于各电阻之和。串联电阻的等效电阻比每个电阻都大，在端口电压一定时，串联电阻的等效电阻比每个电阻都大，在端口电压一定时，串联电阻越多，电流则越小，因此串联电阻有“限流”作用。串联电阻越多，电流则越小，因此串联电阻有“限流”作用。
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
在图小参考方向下，定理可知: 在图小参考方向下，由KCL, KVL定理可知定理可知 Ia+Ib+Ic=0 Uab+Ubc+Uca=0 可以证明，联接的电阻等效变换为Y联接的电阻联接的电阻，可以证明，将△联接的电阻等效变换为联接的电阻，己知电阻R 则等效的电阻R 电阻 ab、Rbc、Rca，则等效的电阻 a、Rb、Rc为 Rab Rca Ra = Rab + Rbc + Rca Rbc Rca Rb = Rab + Rbc + Rca Rca Rbc Rc = Rab + Rbc + Rca
上一页下一页返回
3.1电路的串、并联等效变换电路的串、电路的串
是图3.5 所示电路的等效电路根据等效的概念，所示电路的等效电路，图3.5 (b)是图 (a)所示电路的等效电路，根据等效的概念，是图在图3.5 中有中有I=U/R1 在图 (b)中有因此，因此，1/R1=1/R1+1/R2+...+1/Rn或G1=G1+G2+...+Gn 即电阻的并联网络的等效电阻的倒数等于各电阻倒数之和，即电阻的并联网络的等效电阻的倒数等于各电阻倒数之和，或电阻的并联网络的等效电导等于各电阻的电导之和，或电阻的并联网络的等效电导等于各电阻的电导之和，目并联电阻的等效电阻比每个电阻都小。联电阻的等效电阻比每个电阻都小。并联电阻的电压相等，并联电阻的电压相等，则各电阻的电流与它们的电导成正与它们的电阻成反比，比，与它们的电阻成反比，即 I1:I2:...In=1/R1:1/R2:...:1/Rn=G1:G2:...:Gn,各电阻的电流与端电各电阻的电流与端电的关系为。流I的关系为。的关系为