雨量预报的评价

合集下载

数学建模历年试题及论文

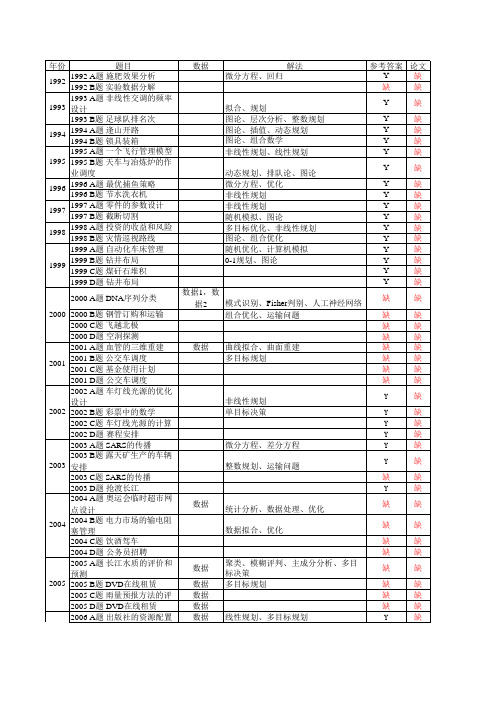
拟合、规划图论、层次分析、整数队论、图论微分方程、优化非线性规划非线性规划随机模拟、图论多目标优化、非线性规划图论、组合优化随机优化、计算机模拟 0-1规划、图论
2000 2000 B题钢管订购和运输缺 2000 C题飞越北极缺 2000 D题空洞探测缺 2001 A题血管的三维重建数据曲线拟合、曲面重建缺多目标规划 2001 B题公交车调度缺 2001 2001 C题基金使用计划缺 2001 D题公交车调度缺 2002 A题车灯线光源的优化设计非线性规划 Y 2002 B题彩票中的数学单目标决策 Y 2002 2002 C题车灯线光源的计算 Y 2002 D题赛程安排 Y 2003 A题 SARS的传播微分方程、差分方程 Y 2003 B题露天矿生产的车辆安排整数规划、运输问题 Y 2003 2003 C题 SARS的传播缺 2003 D题抢渡长江 Y 2004 A题奥运会临时超市网点设计数据统计分析、数据处理、优化缺 2004 B题电力市场的输电阻塞管理数据拟合、优化缺 2004 2004 C题饮酒驾车缺 2004 D题公务员招聘缺 2005 A题长江水质的评价和预测数据聚类、模糊评判、主成分分析、多目标决策缺 2005 B题 DVD在线租赁数据多目标规划缺 2005 2005 C题雨量预报方法的评价数据缺 2005 D题 DVD在线租赁数据缺 2006 A题出版社的资源配置数据线性规划、多目标规划 Y 2006 B题艾滋病疗法的评价及疗效的预测回归、线性规划数据 Y 2006 2006 C题易拉罐形状和尺寸的最优设计缺 2006 D题煤矿瓦斯和煤尘的监测与控制数据缺 2007 A题中国人口增长预测数据微分、差分方程 Y 2007 B题乘公交，看奥运数据图论、0-1 规划、动态规划 Y 2007 2007 C题手机“套餐”优惠几何数据 Y

珠江骨干水库调度水情成情特点及预报评价

维普资讯
２００７年第６期・ＥＲＩＥＰＡＬＲＶＲ人民珠江
珠江骨干水库调度水情成情特点及预报评价
姚章民，刘智森，强吴伟
（江水利委员会水文局，珠广东摘广州５０１）１６１要：水情和成情预报是珠江骨干水库调度工作的重要组成部分，开展骨干水库调度工作的基础和决策依据。是
用。但枯季的水情和成情预报是水文预报领域的难点，预报方法仍不完善，可借鉴的经验不多，需深入开展研究的课题很多。支撑预报的水文基础工作仍相当薄弱，需加大力度加强。关键词：骨干水库调度；水情；成潮；水文预报；江珠中图分类号：Ｖ２２；３８Ｔ６．Ｐ３
左江及右江卜偏少５成以上，北盘江、水河、江、游南红柳桂
江面积３％，全部集中在中上游地区。西江其余６％６且４（２７万ｋ面积的下游地区无大型控制性水利工程。骨２．ｍ）
关注的热点问题，并引起中央和国务院的高度重视。
根据长期气象、水文预测，江流域２０２０珠０６— ０７年冬春季来水仍然偏枯，江ｊ角洲地区仍将面临严峻的供水局珠面，０６年又恰遇两江红水河上的龙滩水电站下闸蓄水，２０下
０前言
文献标识码：Ｂ
文章编号：０１９３（０７０－０－１０．２５２０）６０７００４
量为１３以来历史第二枯，次于１９，Ｐ：７９６年仅９２年属９％年型。１０月１日主力骨干水库蓄水量偏少，天生桥一级水库蓄水量仅为６．９亿ｍ，２０同期少５９７１比０５年．１亿ｍ。汛末，西江流域降雨量与同期相比偏少，来水偏枯，主力骨干水库天生桥一级蓄水量严重偏小，使可调度水量不足。１２调度期总体来水偏枯，．降水区域分布极不均匀

数学建模C题论文

191])()([),(20200y y x x r z y x z -+--=c y b x a y x y x z +⋅+⋅++=22),(4753⨯41i D i D 20.000160.001162021421339915152112032534791410.1 6660.1 2.5 2.666.11212.12525.16060.1/mcm05/probX 53⨯47Y 53⨯47k n m Z ⨯53⨯47 k n m Z ⨯~53⨯47i n m k H ⨯m m n k n 21n +120i n m k S ⨯i D126 18319719141164512X Y⎪⎪⎪⎭⎫ ⎝⎛=⨯⨯⨯⨯⨯⨯47532531534712111..................x x x x x x X ⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111..................y y y y y y),(y x Z =mnk ⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯),(...),,(),,(............),(...),,(),,(4753475325325315315347147121211111y x f y x f y x f y x f y x f y x f ⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111..................Z Z Z Z Z Z 1=imnk Z ~⎪⎪⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111~...~~............~...~~Z Z Z Z Z Z i imnkH ∆mnk Z i mnk Z ~⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯ii i i i i h h h h h h 47532531534712111............... (2)i mnkS∆∑∑=⨯=⨯4712531)(47531j i ji i hi D ∆∑=16411641i mnk S 4i i imnk H 5347imnk S mnk H i D 41 2),(y x Z = ),(y x Z =i D nk m ⨯ i mnk H mnk Z i mnk Z ~1~mnk Z 2~mnk Z 1mnk H 2mnk H imnkS∆∑∑=⨯=⨯4712531)(47531j ij i i h1mnk S 2mnk S⑤ 用i D ∆∑=16411641i mnk S 计算出1D 与2D ，则1D 和2D 的值较小者为最优方案.3 主要程序及结论通过数据处理与分析我们认为预测方法一比预测方法二好.所得计算结果值分别为：（1）不同时段的两种方法的实测与预测值的均方差：1mnkS =[0.9247218269e-1, .165797962696, 0.9247218269e-1,0.9247218269e-1, .2586806182, .2586806182, .2586806182, 2.791713932, .2474029514, .2539943168, .2715902174, .2715902174182, .2586806182, 2.791713932, .2474029514, .2539943168, .2715902174]2mnkS := [0.921412432e-1, .1098068392, 0.2234955063e-1,0.1592933205e-1, .2851304286, .2851304286, .2851304286, 2.792910527, .2612701098, .2381007694, .2613774987, 0.5183032655e-1,.2851304286,2.792810527, .2612701098, .2381007694, .2613774987] （2）方法一的均方差为：1D := .8311398371方案二的均方差： 2D = .8417760978得1D <2D .主要程序与运行结果为：（1）局域曲面拟合程序> solve({0.3=0.6-r*(0.045^2+0.042^2)},{r});> z1:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> z2:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> z3:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> z4:=0.6-79.17656374*[(x-120.2500)^2+(y-33.7667)^2];> solve({0.15=0.3-r*(0.045^2+0.042^2)},{r});> z4:=0.3-39.58828187*[(x-118.1833)^2+(y-31.0833)^2];> solve({5.1=10.2-r*(0.045^2+0.042^2)},{r});> z1:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> z2:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> z3:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> z4:=10.2-1346.001584*[(x-120.3167)^2+(y-31.5833)^2];> solve({0.1=0.2-r*(0.045^2+0.042^2)},{r});> z4:=0.2-26.39218791*[(x-118.4000)^2+(y-30.6833)^2];>z4:=solve({118.9833^2+30.6167^2+a*118.9833+b*30.6167+c=0.7000,118.5833^ 2+30.0833^2+a*118.5833+b*30.0833+c=1.8000,119.4167^2+30.8833^2+a*119.41 67+b*30.8833+c=0.5});> solve({0.05=0.1-r*(0.045^2+0.042^2)},{r});> z1:=0.1-13.19609396*[(x-119.4167)^2+(y-30.8833)^2];>> solve({2.9=5.8-r*(0.045^2+0.042^2)},{r});> z4:=0.1-765.3734495*[(x-118.2833)^2+(y-29.7167)^2];（2）均方差求值程序：>sq1:=[0.09247218269,0.165797962696,0.09247218269,0.09247218269,0.258680 6182,0.2586806182,0.2586806182,2.791713932,0.2474029514,0.2539943168,0. 2715902174,0.2715902174182,0.2586806182,2.791713932,0.2474029514,0.2539 943168,0.2715902174];> sum1:=add(i,i=sq1);> ave1:=sum1/17;>ve1:=[.5222900020,.5222900020,.5222900020,.5222900020,.5222900020,.5222 900020,.5222900020,.5222900020,.5222900020,.5222900020,.5222900020,.522 2900020,.5222900020,.5222900020,.5222900020,.5222900020,.5222900020,.52 22900020];>sq2:=[0.0921412432,0.1098068392,0.022********,0.01592933205,0.285130428 6,0.2851304286,0.2851304286,2.792910527,0.2612701098,0.2381007694,0.261 3774987,0.0518*******,0.2851304286,2.792810527,0.2612701098,0.238100769 4,0.2613774987];（2）数据模拟图程序：> with(linalg):> l:=matrix(91,7,[58138,32.9833,118.5167, 0.0000, 5.0000, 0.2000, 0.0000, 58139, 33.3000,118.8500, 0.0000, 3.9000, 0.0000, 0.0000,58141, 33.6667,119.2667, 0.0000, 0.0000, 0.0000, 0.0000,58143, 33.8000,119.8000, 0.0000, 0.0000, 0.0000, 0.0000,58146, 33.4833,119.8167, 0.0000, 0.0000, 0.0000, 0.0000,58147, 33.0333,119.0333, 0.0000, 6.0000, 1.4000, 0.0000,58148, 33.2333,119.3000, 0.0000, 1.1000, 0.3000, 0.0000,58150, 33.7667,120.2500, 0.0000, 0.0000, 0.0000, 0.1000,58154, 33.3833,120.1500, 0.0000, 0.0000, 0.0000, 0.0000,58158, 33.2000,120.4833, 0.0000, 0.0000, 0.0000, 0.0000,58230, 32.1000,118.2667, 3.3000,20.7000, 6.6000, 0.0000,58236, 32.3000,118.3000, 0.0000, 8.2000, 3.6000, 1.4000,58238, 32.0000,118.8000, 0.0000, 0.0000, 0.0000, 0.0000,58240, 32.6833,119.0167, 0.0000, 3.0000, 1.4000, 0.0000,58241, 32.8000,119.4500, 0.1000, 1.4000, 1.5000, 0.1000,58243, 32.9333,119.8333, 0.0000, 0.7000, 0.4000, 0.0000,58245, 32.4167,119.4167, 0.3000, 2.7000, 3.8000, 0.0000,58246, 32.3333,119.9333, 7.9000, 2.7000, 0.1000, 0.0000,58249, 32.2000,120.0000,12.3000, 2.4000, 5.6000, 0.0000,58251, 32.8667,120.3167, 5.2000, 0.1000, 0.0000, 0.0000, 58252, 32.1833,119.4667, 0.4000, 3.2000, 4.8000, 0.0000, 58254, 32.5333,120.4500, 0.0000, 0.0000, 0.0000, 0.0000, 58255, 32.3833,120.5667, 1.1000,18.5000, 0.5000, 0.0000, 58264, 32.3333,121.1833,35.4000, 0.1000, 0.2000, 0.0000, 58265, 32.0667,121.6000, 0.0000, 0.0000, 0.0000, 0.0000, 58269, 31.8000,121.6667,31.3000, 0.7000, 2.8000, 0.1000, 58333, 31.9500,118.8500, 8.2000, 8.5000,16.9000, 0.1000, 58334, 31.3333,118.3833, 4.9000,58.1000, 9.0000, 0.1000, 58335, 31.5667,118.5000, 5.4000,26.0000,11.0000, 0.8000, 58336, 31.7000,118.5167, 3.6000,27.8000,15.3000, 0.6000, 58337, 31.0833,118.1833, 7.0000, 6.4000,15.3000, 0.2000, 58341, 31.9833,119.5833,11.5000, 5.4000,16.1000, 0.0000, 58342, 31.7500,119.5500,32.6000,37.9000, 5.8000, 0.0000, 58343, 31.7667,119.9333,20.7000,24.3000, 5.3000, 0.0000, 58344, 31.9500,119.1667,12.4000, 5.9000,16.3000, 0.0000, 58345, 31.4333,119.4833,21.8000,18.1000, 9.8000, 0.1000, 58346, 31.3667,119.8167, 0.1000,12.7000, 5.1000, 0.2000, 58349, 31.2667,120.6333, 1.1000, 5.1000, 0.0000, 0.0000, 58351, 31.8833,120.2667,22.9000,15.5000, 6.2000, 0.0000, 58352, 31.6500,120.7333,15.1000, 5.4000, 2.4000, 0.0000, 58354, 31.5833,120.3167, 0.1000,12.5000, 2.4000, 0.0000, 58356, 31.4167,120.9500, 5.1000, 4.9000, 0.4000, 0.0000, 58358, 31.0667,120.4333, 2.4000, 3.4000, 0.0000, 0.8000, 58359, 31.1500,120.6333, 1.5000, 3.8000, 0.5000, 0.1000, 58360, 31.9000,121.2000, 5.6000, 3.2000, 2.9000, 0.1000, 58361, 31.1000,121.3667, 3.5000, 0.6000, 0.2000, 0.7000, 58362, 31.4000,121.4833,33.0000, 4.1000, 0.9000, 0.0000, 58365, 31.3667,121.2500,17.7000, 2.2000, 0.1000, 0.0000, 58366, 31.6167,121.4500,75.2000, 0.4000, 1.5000, 0.0000, 58367, 31.2000,121.4333, 7.2000, 2.8000, 0.2000, 0.2000, 58369, 31.0500,121.7833, 3.2000, 0.3000, 0.0000, 0.3000, 58370, 31.2333,121.5333, 7.0000, 3.4000, 0.2000, 0.2000, 58377, 31.4667,121.1000, 7.8000, 7.2000, 0.3000, 0.0000, 58426, 30.3000,118.1333, 0.0000, 0.0000,17.6000, 6.2000, 58431, 30.8500,118.3167, 5.1000, 2.3000,16.5000, 0.1000, 58432, 30.6833,118.4000, 3.6000, 1.4000,20.5000, 0.2000, 58433, 30.9333,118.7500, 2.1000, 3.4000, 8.5000, 0.2000, 58435, 30.3000,118.5333, 0.0000, 0.0000,13.6000, 8.5000, 58436, 30.6167,118.9833, 0.0000, 0.0000, 5.3000, 0.5000, 58438, 30.0833,118.5833, 0.0000, 0.0000,27.6000,21.8000, 58441, 30.8833,119.4167, 0.1000, 1.6000, 1.6000, 1.0000, 58442, 31.1333,119.1833, 3.0000, 8.8000, 5.4000, 0.2000, 58443, 30.9833,119.8833, 0.1000, 2.7000, 0.1000, 0.9000,58446, 30.9667,119.6833, 0.0000, 0.1000, 5.1000, 2.5000, 58448, 30.2333,119.7000, 0.0000, 0.0000,15.1000, 6.9000, 58449, 30.0500,119.9500, 0.0000, 0.0000,23.5000, 8.2000, 58450, 30.8500,120.0833, 0.0000, 0.7000, 0.0000, 4.1000, 58451, 30.8500,120.9000, 0.5000, 0.1000, 0.0000, 3.8000, 58452, 30.7833,120.7333, 0.3000, 0.0000, 0.0000, 3.0000, 58453, 30.0000,120.6333, 0.0000, 0.0000, 0.0000,18.2000, 58454, 30.5333,120.0667, 0.0000, 0.0000, 0.5000, 4.9000, 58455, 30.5167,120.6833, 0.0000, 0.0000, 0.0000, 4.6000, 58456, 30.6333,120.5333, 0.0000, 0.0000, 0.0000, 4.2000, 58457, 30.2333,120.1667, 0.0000, 0.0000, 2.0000,12.6000, 58459, 30.2000,120.3167, 0.0000, 0.0000, 0.0000,15.0000, 58460, 30.8833,121.1667, 1.2000, 0.1000, 0.0000, 2.3000, 58461, 31.1333,121.1167, 4.0000, 1.4000, 0.4000, 0.2000, 58462, 31.0000,121.2500, 2.7000, 0.3000, 0.4000, 1.7000, 58463, 30.9333,121.4833, 1.7000, 0.1000, 0.0000, 0.8000, 58464, 30.6167,121.0833, 0.0000, 0.0000, 0.0000, 3.6000, 58467, 30.2667,121.2167, 0.0000, 0.0000, 0.0000, 1.8000, 58468, 30.0667,121.1500, 0.0000, 0.1000, 5.1000, 2.5000, 58472, 30.7333,122.4500, 0.3000, 0.6000, 0.0000, 4.9000, 58477, 30.0333,122.1000, 0.0000, 0.0000, 0.0000, 0.0000, 58484, 30.2500,122.1833, 0.0000, 0.0000, 0.0000, 0.0000, 58530, 29.8667,118.4333, 0.0000, 0.0000,27.5000,23.6000, 58531, 29.7167,118.2833, 0.0000, 0.0000, 3.7000,11.5000, 58534, 29.7833,118.1833, 0.0000, 0.0000, 9.3000, 6.5000, 58542, 29.8167,119.6833, 0.0000, 0.0000, 0.0000,27.6000, 58550, 29.7000,120.2500, 0.0000, 0.0000, 0.0000, 4.9000, 58562, 29.9667,121.7500, 0.0000, 0.0000, 0.0000, 0.9000]);> lat:=col(l,2);> lon:=col(l,3); > sd1:=col(l,4);> sd2:=col(l,5); > sd3:=col(l,6); > sd4:=col(l,7);> abc1:=seq([lat[i],lon[i],sd1[i]],i=1..91);> abc2:=seq([lat[i],lon[i],sd2[i]],i=1..91);> abc3:=seq([lat[i],lon[i],sd3[i]],i=1..91);> abc4:=seq([lat[i],lon[i],sd4[i]],i=1..91);> with(plots):> pointplot3d([abc1],color=green,axes=boxed);> surfdata([abc1],labels=["x","y","z"],axes=boxed);> with(stats):> with(fit):> with(plots):fx1:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc1]);> plot3d(fx1,x=25..35,y=119..135);> pointplot3d([abc2],color=blue,axes=boxed);> surfdata([abc2],labels=["x","y","z"],axes=boxed);>fx2:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc2]);> plot3d(fx2,x=25..35,y=119..135);> pointplot3d([abc3],color=red,axes=boxed)> surfdata([abc3],labels=["x","y","z"],axes=boxed);>fx3:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc3]);> surfdata([abc4],labels=["x","y","z"],axes=boxed);>fx4:=leastsquare[[x,y,z],z=x^3+y^3+a*x^2+b*y^2+c*x*y+d*x+e*y+f,{a,b,c,d ,e,f}]([abc4]);五.如何在评价方法中考虑公众感受的数学模型建立.1660.1 2.5 2.666.11212.12525.16060.1z } 1.00 {0≤≤=z z R } 5.21.0 {1≤≤=z z R } 66.2 {2≤≤=z z R } 121.6 {3≤≤=z z R } 251.12 {4≤≤=z z R } 601.25 {5≤≤=z z R } 1.60 {6≥=z z R 0ˆR 1ˆR 2ˆR 3ˆR 4ˆR 5ˆR 6ˆR } 1)( {ˆ000R z z z R ∈≤=，μ} 1)( {ˆ111R z z z R ∈≤=，μ} 1)( {ˆ222R z z z R ∈≤=，μ } 1)( {ˆ333R z z z R ∈≤=，μ} 1)( {ˆ444R z z z R ∈≤=，μ} 1)( {ˆ555R z z z R ∈≤=，μ } 1)( {ˆ666R z z z R ∈≤=，μ)(z i μ i 1z ∈i R i R )(z i μ i 16i R ˆ i 1 2)(z i μ i 1⎩⎨⎧≤<+-≤≤=1.006.0 , 5.22506.00, 1)(0z z z z μ)(1z μ] 2369277587.0e [2369277587.0112)3.1(----z 5.21.0≤≤z )(2z μ] 20555762126.0e [20555762126.0112)3.4(----z 66.2≤≤z)(3z μ] 2287787270.0e [2287787270.0119.5)05.9(2----z 121.6≤≤z )(4z μ] 70397557815.0e[70397557815.0119.12)55.18(2----z 251.12≤≤z)(5z μ] 00475951221.0e[00475951221.011100)55.42(2----z 601.25≤≤z)(6z μ2)]5.60(5 [11--+z 1.60≥z 74)(z i μ及iR ˆ i =0，1，…,6合并可得} 0 {≥=z z R 上的模糊集合} , 1)( {ˆR z z z R∈≤=μ.其中R 是论域,)(z μ是模糊集合R ˆ的隶属函数，由)(z i μ分段合)(z μ小雨的隶属函数图特大暴雨隶属函数图大暴雨隶属函数图暴雨隶属函数图⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧>≤<≤<≤<≤<≤<≤≤=60)(6025)(2512)(126)(65.2)(5.21.0)(1.00)()(6543210z z z z z z z z z z z z z z t μμμμμμμμ 5 353⨯47imnkZ ~)(z μ53⨯47=M mnk⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111..................μμμμμμ=M imnk~⎪⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯⨯47532531534712111~...~~............~...~~μμμμμμi ),(y x Z =i mnk ∏∆mnk M =M i mnk~⎪⎪⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯⨯i i i i i i 47532531534712111..................λλλλλλ 6imnkΓ∆∑∑=⨯=⨯4712531)(47531j i j i i λ i Ω∆∑=16411641i imnkΓ 8 i 2i i i mnk ∏5347imnk Γi mnk ∏i Ω411Ω2Ω 1Ω2Ω1D 2D19811999。

全国大学生数学建模竞赛历年赛题

全国大学生数学建模竞赛历年赛题1992：A?施肥效果分析 B?实验数据分解1993：A?非线性交调的频率设计 B?足球队排名次1994：A?逢山开路 B?锁具装箱1995：A?一个飞行管理问题 B?天车与冶炼炉的作业调度1996：A?最优捕鱼策略 B?节水洗衣机1997：A?零件参数 B?截断切割1998：A?投资的收益和风险 B?灾情巡视路线1999：A?自动化车床管理 B?钻井布局 C?煤矸石堆积 D?钻井布局2000：A?DNA序列分类 B?钢管购运 C?飞越北极 D?空洞探测2001：A?血管三维重建 B?公交车调度 C?基金使用2002：A?车灯线光源 B?彩票中数学 D?赛程安排2003：A?SARS的传播 B?露天矿生产 D?抢渡长江2004：A?奥运会临时超市网点设计 B?电力市场的输电阻塞管理C?饮酒驾车 D?公务员招聘2005：A 长江水质的评价和预测 B?DVD在线租赁C?雨量预报方法的评价 D?DVD在线租赁?2006：A出版社的资源配置 B 艾滋病疗法的评价及疗效的预测C易拉罐形状和尺寸的最优设计D 煤矿瓦斯和煤尘的监测与控制2007：A 中国人口增长预测 B 乘公交，看奥运C 手机“套餐”优惠几何D 体能测试时间安排2008：A 数码相机定位 B 高等教育学费标准探讨C 地面搜索D NBA赛程的分析与评价2009：A 制动器试验台的控制方法分析 B 眼科病床的合理安排C 卫星和飞船的跟踪测控 D会议筹备2010：A储油罐的变位识别与罐容表标定B 2010年上海世博会影响力的定量评估C输油管的布置D对学生宿舍设计方案的评价2011: A 城市表层土壤重金属污染分析B 交巡警服务平台的设置与调度C 企业退休职工养老金制度的改革D 天然肠衣搭配问题2012: A 葡萄酒的评价B 太阳能小屋的设计C 脑卒中发病环境因素分析及干预D 机器人避障问题2013: A 车道被占用对城市道路通行能力的影响B 碎纸片的拼接复原C 古塔的变形D 公共自行车服务系统2014: A 嫦娥三号软着陆轨道设计与控制策略B 创意平板折叠桌C 生猪养殖场的经营管理D 储药柜的设计2015: A ?太阳影子定位B?“互联网+”时代的出租车资源配置C? 月上柳梢头D? 众筹筑屋规划方案设计。

1996年全国大学生数学建模竞赛题目A题最优捕鱼策略B题节水

1996年全国大学生数学建模竞赛题目...................................................................... 错误！未定义书签。

A题最优捕鱼策略.............................................................................................. 错误！未定义书签。

B题节水洗衣机................................................................................................ 错误！未定义书签。

1997年全国大学生数学建模竞赛题目...................................................................... 错误！未定义书签。

A题零件的参数设计........................................................................................ 错误！未定义书签。

B题截断切割.................................................................................................... 错误！未定义书签。

1998年全国大学生数学建模竞赛题目...................................................................... 错误！未定义书签。

A题投资的收益和风险...................................................................................... 错误！未定义书签。

历年数学建模试题

1998年
(A) 投资的收益和风险问题（浙江大学：陈淑平） (B) 灾情巡视路线问题（上海海运学院：丁颂康）

1999年
(A) 自动化车床管理问题（北京大学：孙山泽） (B) 钻井布局问题（郑州大学：林诒勋） (C) 煤矸石堆积问题（太原理工大学：贾晓峰） (D) 钻井布局问题（郑州大学：林诒勋）

2004年
(A) 奥运会临时超市网点设计问题(北京工业大学：孟大志) (B) 电力市场的输电阻塞管理问题(浙江大学:刘康生) (C) 酒后开车问题（清华大学：姜启源） (D) 招聘公务员问题（解放军信息工程大学：韩中庚）

2005年
(A) 长江水质的评价和预测问题（解放军信息工程大学：韩中庚） (B) DVD在线租赁问题(清华大学: 谢金星等) (C) 雨量预报方法的评价问题(复旦大学:谭永基) (D) DVD在线租赁问题(清华大学: 谢金星等)

2008年
（A）数码相机定位，（B）高等教育学费标准探讨，（C）地面搜索，（D）NBA赛程的分析与评价

2009年
（A）制动器试验台的控制方法分析（B）眼科病床的合理安排（C）卫星和飞船的跟踪测控（D）会议筹备

2010年
（A）储油罐的变位识别与罐容表标定（B）2010年上海世博会影响力的定量评估（C）输油管的布置（D）对学生宿舍设计方案的评价

2002年
(A) 车灯线光源的优化设计问题（复旦大学:谭永基，华东理工大学:俞文此） (B) 彩票中的数学问题（解放军信息工程大学：韩中庚） (C) 车灯线光源的优化设计问题（复旦大学:谭永基，华东理工大学:俞文此） (D) 赛程安排问题（清华大学：姜启源）

淮河流域面雨量多模式预报效果比较及典型过程检验分析

式中，第一项是有雨预报正确的基
行集成应用，是提高流域面雨量预报２Ｏ时为日界，下同）采用淮河流域１７２本文基于ＥＣＭＷＦ全球模式、资料来源于国家气象信息中心。
规定为６０分；第二项为强度预报个国家级地面气象观测站整编资料，础分，
雨洪水的汇流特点，结合流域防汛抗旱Ｒｆ为有雨且预报正确时的面雨量预
２．资料
２０１１年６～８月四种模式对淮河流
Ｒｏ为有雨预报正确时的面雨量域不同时效（２４～７２ｈ）面雨量预报的模服务需求，将流域划分为１５个子单元。报值，
２４７２ｈ）面雨量预报的平均绝对Ｅａ）、模糊评分（简称ＭＰ）以及Ｔｒｅａｔ５．９ｒａｍ）、中雨（６．０～１４．９ｍｍ）、大雨流域（
Ｅ）（图１）可看出，随预报时效延１５．０２９．９ｍｍ）、暴雨（ ≥３Ｏ．０ｍｍ）四误差（Ｓｃｏｒｅ（简称ＴＳ）等统计评价指标，对（均呈增大四个模式的淮河流域面雨量短期预报个等级。采用平均绝对误差（Ｅａ）、模糊长，四种模式面雨量预报的Ｅ
淮河流域面雨量预报中最具有参考意义，其次为ＪＭＡ。
２．模糊评分（ＭＰ）检验
年内分配也极为不均，夏季（６～８月）实况值的平均绝对误差，其计算式为：
●
ｎ
Ｅａ： ÷∑Ｉ — ＲＦＲ。ｌ

全国雷达分钟降水方法在面雨量预报上应用的检验

全国雷达分钟降水方法在面雨量预报上应用的检验作者：丁劲张国平高金兵王曙东王阔音薛冰章芳杨静来源：《安徽农业科学》2021年第17期摘要为了解基于全国雷达分钟降水方法在面雨量上的短期预报效果，利用2020年7月25日08：00—28日08：00安徽巢湖及其子流域的实况面雨量数据，依据平均绝对误差、均方根误差、TS评分、漏报率和空报率几项检验指标，对安徽巢湖及其子流域研究时段内逐小时和累计2 h面雨量预报结果进行检验评估。

结果表明，全国雷达分钟降水方法对巢湖北部平原区子流域的预报效果好于南部丘陵地区子流域;累积2 h产品的预报效果好于逐小时产品的预报效果;对小雨量的预报结果优于大雨量的预报结果。

关键词全国雷达分钟降水方法;流域;面雨量;短期预报;检验中图分类号 S165 文献标识码 A文章编号 0517-6611（2021）17-0221-05doi：10.3969/j.issn.0517-6611.2021.17.056Abstract In order to understand the short-term forecasting effect on the surface rainfall based on the minute quantitative precipitation forecast （MQPF），the actual surface rainfall data of Anhui Chaohu Lake and its sub-catchments from 08：00 July 25 to 08：00 July 28， 2020 were used to relyon the average absolute error，root mean square error，TS score，omission rate and false prediction ratio were several test indicators to test and evaluate the hourly and cumulative 2-h area rainfall forecast results during the study period of Chaohu Lake and its sub-catchments in Anhui.The results showed that the MQPF forecast had a better forecasting effect on the sub-basins in the northern plain area of Chaohu Lake than those in the southern hilly area.More accurate forecast could be seen in cumulative two-hour products than hourly products.The low rainfall level showed better results than the forecast for high rainfall level.Key words Minute quantitative precipitation forecast （MQPF）;Basins;Area rainfall;Short-term forecast;Verification面雨量是水文预报中的一个重要参量，面雨量预报的精度直接关系到洪水预报精度和洪水调度决策的科学性[1]。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第2段
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 4.0000 1.1000 0.0000 0.0000
第3段
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 7.6000 3.5000 0.0000 0.2000
第4段
2.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 1.1000 0.9000 0.0000 1.0000
NCU MCM 暑期培训
雨量用毫米做单位，小于0.1毫米视为无雨。 (1) 请建立数学模型来评价两种6小时雨量预报方法的准确性； (2) 气象部门将6小时降雨量分为6等： 0.1—2.5毫米为小雨， 2.6—6毫米为中雨， 6.1—12毫米为大雨， 12.1—25毫米为暴雨， 25.1—60毫米为大暴雨，大于 60.1毫米为特大暴雨。若按此分级向公众预报，如何在评价方法中考虑公众的感受？
要求cx取行向量，cy取为列向量。
所用指令有一维的interp1、二维的interp2、三维的interp3。这些指令分别有不同的方法（method），设计者可以根据需要选择适当的方法，以满足系统属性的要求。Help polyfun可以得到更详细的内容。
NCU MCM 暑期培训
在有限样本点向量xs与ys中，插值产生向量 x和y，所用方法定义在method中，有4种选择： nearest：执行速度最快，输出结果为直角转折 linear：默认值，在样本点上斜率变化很大 spline：最花时间，但输出结果也最平滑 cubic：最占内存，输出结果与spline差不多
散乱点数据的插值计算
插值函数griddata格式为:
NCU MCM 暑期培训
cz =griddata（x，y，z，cx，cy，‘method’）
被插值点的函数值
插值节点
被插值点
插值方法
‘nearest’ 最邻近插值 ‘linear’ 双线性插值 ‘cubic’ 双三次插值 'v4'- Matlab提供的插值方法缺省时, 双线性插值
NCU MCM 暑期培训
2. 评价准则由预报误差可以采取各种合理的定义给出评价准则函数，如对离散点（误差计算方法的A, B）可用相对预报误差平方和、绝对预报误差平方和、误差绝对值之和（相对或绝对）等, 对连续函数（误差计算方法的C）可将求和改为积分。 3. 插值方法如用误差计算方法A，注意到91个观测站的分布是散乱的, 可采用散乱数据的曲面拟合方法，如径向基插值、Shepard插值等. 如用误差计算方法B，网格点是规则的，可用线性、样条等多种方法. 插值可在直角坐标或球面坐标下进行, 但在直角坐标下要将观测站经纬度数据转换为直角坐标。
最后将两种雨量预报方法的等级差频率进行比较，从中找出较优的雨量预报方法
NCU MCM 暑期培训
三、模型假设
NCU MCM 暑期培训
1.观测站所测得的值准确可靠,各预测数据不受人为等因素的影响. 2.地球可以近似地看作一个球体. 3.两种预报方法是相互独立的.
三、误差分析问题 1: 评价两种 6 小时雨量预报准确性的数学模型和方法 . 1:评价方法 . A. 计算5347个网格点上的预报误差：将91个观测点上的实测数据进行插值, 得到5347个网格点的实测值，与已给出的网格点上的雨量预报值比较； B. 计算91个观测点上的预报误差: 将5347个网格点的预报数据进行插值 , 得到 91 个观测点上的预报值与已给出的观测点上的雨量实测值比较； C. 计算连续雨量分布函数（在数据区域内）的预报误差：分别用91个观测点上的实测数据和5347个网格点的预报数据进行插值, 得到区域内的实测和预报两个雨量分布函数，进行比较。
NCU MCM 暑期培训
1、关键词；
2、相关理论；
3、数学模型； 4、软件编程。
NCU MCM 暑期培训
二、问题分析
1.相关背景资料本题中的2491个网格点,从东经117度到125度，北纬27.6度到35度.跨越8个经度和7.4个纬度.覆盖了江苏整个省及其相临省的部分地区,且大约有1/2 以上的网格点位于海洋中.通过描点法将2491个网格点与91个气象站的位置描于同一张图中,发现气象站全部位于图形的中部,且分布不均匀. 下面是根据已知的lon.dat 和 lat.dat两个文件中的数据并通过Matlab软件编程画出的53*47个网格点与91个观测站的位置图。
纬度
32.9833 33.3000 33.6667 33.8000 33.4833 33.0333 33.2333 33.7667 33.3833 33.2000 32.1000 32.3000 32.0000 32.6833
020618.SIX 经度第1段
118.5167 118.8500 119.2667 119.8000 119.8167 119.0333 119.3000 120.2500 120.1500 120.4833 118.2667 118.3000 118.8000 119.0167 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
2. 用写字板方式打开MEASURING中的文件, 将文件中的字符导入Excel文件表格中(数据-导入外部数据导入数据),将字符转化为数值,再利用Matlab文件中的 Importdate将数据导入到Matlab中. 3. 从MEASURING中的某一文件内取出表示91个观测站经纬度的数据. 根据已知的FORECAST中的lon.dat 和 lat.dat两个文件得到表示53 47网格点的经纬度的数据. 用球坐标公式 :
NCU MCM 暑期培训
2. 将5347个网格点的预报数据进行插值,得到91个观测点上的预报值.
NCU MCM 暑期培训
在问题二中,由于公众抱怨直接取决于预报的结果与实际观测结果的偏差, 例如： 1.气象部门预报为无雨，而实际是有雨， 2.气象部门预报为有雨，而实际是无雨或预报为小雨. 3.气象部门预报为无雨实际是中雨、大雨、或暴雨. 这时公众就会产生抱怨情绪。而且预报的雨量等级与实际测量的雨量等级相差越大，则公众抱怨的程度就越大。因此，应建立两者之间的等级偏差与公众抱怨程度的函数关系。
为了比较2491个网格点的预报数据和实测数据之间雨量等级上的差别,分别将降雨量的预报值与实测值按大小划分成7个级别, 然后把两种雨量预报方法对应的预测降雨量矩阵 (由问题一可得)与实测降雨量矩阵转化为对应的等级矩阵,将两种雨量预报方法对应的预测等级矩阵分别与实测等级矩阵进行比较,分别统计预报数据和实测数据处在同一级别、相差一级、相差二级、相差三级、相差四级、相差五级、相差六级的频数,并计算出对应频率.
注意：所有的插值方法都要求x是单调的，并且xi不能够超过x的范围。
NCU MCM 暑期培训
网格节点数据的插值
z=interp2(x0,y0,z0,x,y,’method’)
被插值点的函数值
插值节点
被插值点
插值方法
‘nearest’ 最邻近插值 ‘linear’ 双线性插值 ‘cubic’ 双三次插值缺省时, 双线性插值要求x0,y0单调；x，y可取为矩阵，或x取行向量， y取为列向量，x,y的值分别不能超出x0,y0的范围。
NCU MCM 暑期培训 MEASURING 中包含了41个名为<日期 >.SIX的文
件，如020618.SIX表示2002年6月18日晚上21点开始的连续 4 个时段各站点的实测数据（雨量），这些文件的数据格式是：
站号
58138 58139 58141 58143 58146 58147 58148 58150 58154 58158 58230 58236 58238 58240
NCU MCM 暑期培训
用MATLAB作插值计算一维插值函数：
NCU MCM 暑期培训
yi=interp1(x，y，xi，'method')
xi处的插值结果插值节点被插值点插值方法
‘nearest’ ：最邻近插值 ‘linear’ ：线性插值； ‘spline’ ：三次样条插值； ‘cubic’ ：立方插值。缺省时：分段线性插值。
NCU MCM 暑期培训
4. 两种预报方法的比较对提供的41组包含164个时段的数据, 可求出评价准则函数的平均值和标准差, 对两种预报方法进行评价。例如，如果采用计算方法A计算误差、相对预报误差平方和为准则、径向基插值，结论是第一种预报方法较优。注1 对实测无雨的情形计算时可能会出现分母为零的问题，应注意预报错误（误报有雨）的处理方法。注2 若在评价预报方法时不仅考虑降雨量大小, 还考虑雨区的形态等, 可视为有创造性。
NCU MCM 暑期培训
气象部门希望建立一种科学评价预报方法好坏的数学模型与方法。气象部门提供了41天的用两种不同方法的预报数据和相应的实测数据。预报数据在文件夹FORECAST中，实测数据在文件夹MEASURING中，其中的文件都可以用Windows系统的“写字板”程序打开阅读。 FORECAST中的文件lon.dat和lat.dat分别包含网格点的经纬度，其余文件名为<f日期i>_dis1和<f日期 i>_dis2，例如f6181_dis1中包含2002年6月18日晚上20 点采用第一种方法预报的第一时段数据（其2491个数据为该时段各网格点的雨量），而f6183_dis2中包含 2002年6月18日晚上20点采用第二种方法预报的第三时段数据。