电磁场与电磁波课件第5章 静态场的边值问题
合集下载
电磁场与电磁波6静态场边值问题的求解

n 1
( An ' cos K n x Bn ' sin K n x)(Cn ' chKn y Dn ' shKn y )
n 1
4)利用给定边界条件确定积分常数,最终得到电位函数的解。 a ) y轴 x 0 0 y a 0
b ) x轴 y 0 0 x a 0 0 C0 0 Cn 0 Cn c) x a 0 y a 0 B0 0 Bn 0
400
1 n n sin xsh y n1 nshn a a
接地金属槽内的等位线分布
(n 1, 3, 5 )
三、分离变量法:柱坐标系中
电位微分方程在圆柱坐标系中的展开式为
1 1 2 2 2 0 r 2 2 r r r r z
( ) A sin m B cosm
考虑到 k m,以及变量 的方程式,则前述方程可表示为
1 d dR m 2 1 d 2 Z 0 r 2 2 Rr dr dr r Z dz
三、分离变量法:柱坐标系中
上式左边第一项仅为变量 r 的函数,第二项仅为变量 z 的函数,因
(6 )
(7 )
1 d 21 2 K n 1 dx2
1 d 2 2 2 K n 2 dy2
Kn 2 0
(8)
3)解常微分方程,将各特解线性叠加得通解。
1 ( x) 2 ( y) ( A0 B0 x)(C0 D0 y)
( An chKn x Bn shKn x)(Cn cos K n y Dn sin K n y )
1 d 2 2 k d 2
( An ' cos K n x Bn ' sin K n x)(Cn ' chKn y Dn ' shKn y )
n 1
4)利用给定边界条件确定积分常数,最终得到电位函数的解。 a ) y轴 x 0 0 y a 0
b ) x轴 y 0 0 x a 0 0 C0 0 Cn 0 Cn c) x a 0 y a 0 B0 0 Bn 0
400
1 n n sin xsh y n1 nshn a a
接地金属槽内的等位线分布
(n 1, 3, 5 )
三、分离变量法:柱坐标系中
电位微分方程在圆柱坐标系中的展开式为
1 1 2 2 2 0 r 2 2 r r r r z
( ) A sin m B cosm
考虑到 k m,以及变量 的方程式,则前述方程可表示为
1 d dR m 2 1 d 2 Z 0 r 2 2 Rr dr dr r Z dz
三、分离变量法:柱坐标系中
上式左边第一项仅为变量 r 的函数,第二项仅为变量 z 的函数,因
(6 )
(7 )
1 d 21 2 K n 1 dx2
1 d 2 2 2 K n 2 dy2
Kn 2 0
(8)
3)解常微分方程,将各特解线性叠加得通解。
1 ( x) 2 ( y) ( A0 B0 x)(C0 D0 y)
( An chKn x Bn shKn x)(Cn cos K n y Dn sin K n y )
1 d 2 2 k d 2
静态场及其边值问题的解PPT教案

并 选 择 有 限 远处为 电位参 考点。 例如, 选择ρ= a 的 点 为电位 参 考点,则有
(r ) l0 ln 2L C 20
C l0 ln 2L 20 a
(r ) l0 ln a 20
第13页/共152页
14
5. 电 位 的 微 分 方程
在 均 匀 介 质 中,有
D
E
grr
(o) 0
x
P
r
o
z E0
在 球 坐 标 系 中, 取极轴 与 的方 向一致 ,即 , 则 有
E0
E0
ez E0
(P)
r E0
grr
r ez
grr
E0
E0r
cos
在 圆 柱 面 坐标 系中, 取 与 x轴方向 一致, 即 ,故
,而
r e ez z
(P)
ErE0 g0rr
r ex
z
(,, z)
L
R
z ' dl dz
y
x
-L
13
在 上 式 中 若令
, 则可 得到无 限长直 线电荷 的电位 。当
时 , 上 式 可 写为
L R
L
(r ) l0 ln
2 L2 L
l 0
ln
2 L2 L
l 0
ln 2L
40 2 L2 L 20
20
L
当
时 , 上 式 变 为无 穷大, 这是因 为电荷 不是分 布在有 限区域 内,而 将电位 参考点 选在无 穷远点 之故。 这时可 在上式 中加上 一个任 意常数 ,则有
2 (x) C2 x D2
第16页/共152页
17
静态电磁场边值问题精品PPT课件

φ=0 h r2
场源、边界条件不变
-q
19
待求电位:
点电荷q与-q各自产生电位的叠加:
q q
qq
4r1 4r2
20
待求区域电场强度:
Ex
4qx
1 r13
1 r23
Ey
4qy
1 r13
1 r23
Ez 4qzr13hzr23h
21
导体平面上的感应电荷:
s DnEz
qh
2 x2y2h2 3
qs sdS
n Si gi
i 1,2,, n
gi:边界Si上的位函数外法向偏导数值
10
第三类边值问题
边界条件:求解区域边界分为两部分,一部分边 界上给定位函数值,另一部分边界上 给定位函数沿边界外法向的偏导数值
2
F 0
Si
fi
i 1,2, , k
n Si gi
i k 1, k 2, , n
电磁场与电磁波
静态电磁场边值问题
内容
边值问题 唯一性定理 镜像法 分离变量法
2
作业
1. P137:4.1、4.2、4.3 2. 矩形槽沿直角坐标y方向无限延伸,槽两侧电位为 零,当y→∞时,电位φ→0,底部电位为φ(x, 0) =U0 , 求槽内电位分布。
3
边值问题
概述
静态场问题
分布型问题:已知场源(电荷、电流),直接计 算空间各点的场强或位函数 边值型问题:已知⑴.位函数方程;⑵.空间某一 确定区域内的场源分布;⑶.该区域的边界条件 (边界面上的位函数或位函数的法向导数),求 区域内位函数的分布
分析:待求电位由q与导体平面感应电荷共同产生;
导体平面感应电荷未知,其
场源、边界条件不变
-q
19
待求电位:
点电荷q与-q各自产生电位的叠加:
q q
4r1 4r2
20
待求区域电场强度:
Ex
4qx
1 r13
1 r23
Ey
4qy
1 r13
1 r23
Ez 4qzr13hzr23h
21
导体平面上的感应电荷:
s DnEz
qh
2 x2y2h2 3
qs sdS
n Si gi
i 1,2,, n
gi:边界Si上的位函数外法向偏导数值
10
第三类边值问题
边界条件:求解区域边界分为两部分,一部分边 界上给定位函数值,另一部分边界上 给定位函数沿边界外法向的偏导数值
2
F 0
Si
fi
i 1,2, , k
n Si gi
i k 1, k 2, , n
电磁场与电磁波
静态电磁场边值问题
内容
边值问题 唯一性定理 镜像法 分离变量法
2
作业
1. P137:4.1、4.2、4.3 2. 矩形槽沿直角坐标y方向无限延伸,槽两侧电位为 零,当y→∞时,电位φ→0,底部电位为φ(x, 0) =U0 , 求槽内电位分布。
3
边值问题
概述
静态场问题
分布型问题:已知场源(电荷、电流),直接计 算空间各点的场强或位函数 边值型问题:已知⑴.位函数方程;⑵.空间某一 确定区域内的场源分布;⑶.该区域的边界条件 (边界面上的位函数或位函数的法向导数),求 区域内位函数的分布
分析:待求电位由q与导体平面感应电荷共同产生;
导体平面感应电荷未知,其
电磁场与电磁波 静态场边值问题

代入上式, 代入上式,得
1 d 2 f ( x ) 1 d 2 g ( y ) 1 d 2 h( z ) ⋅ + ⋅ + ⋅ =0 2 2 2 g h dz f dx dy
上式中每项都只是一个变量的函数, 上式中每项都只是一个变量的函数,其成立的唯一条件是 三项中每项都是一个常数, 三项中每项都是一个常数,故有
d 2 f ( x) = −k 2 x f ( x) dx 2
d 2 g ( y) = −k 2 y f ( y ) dy 2
d 2 h( z ) = −k 2 z f ( z ) dz 2
分离常数, 其中 k x,k y,k z 为分离常数,且 ※ 分析 与 讨论 ① 当 kx2 = 0 时
2010-12-8
边值问题 是指存在边界面的电磁问题。 是指存在边界面的电磁问题。 根据给定边界条件对边值问题分类: 根据给定边界条件对边值问题分类: 第一类边值问题: 第一类边值问题: 已知位函数在全部边界面上的分布值 边值问题
φ
∂φ ∂n
S
= f
= f
S
狄里赫利问题( 狄里赫利问题(Dirichlet) )
第二类边值问题:已知位函数在全部边界面上的法向导数值 第二类边值问题: 边值问题 诺埃曼问题 (Neumann) )
解: 选择直角坐标系
在区域 0<x<a、0<y<b内 、 内
y y
∇ φ =0
2
b b
φ φ = 0(x) =U φ =0
0 0
∂φ ∂φ + 2 =0 2 ∂x ∂y
2 2
∂φ =0 ∂x
φ =0 φ =U φ =0 φ =0
a a
x x
1 d 2 f ( x ) 1 d 2 g ( y ) 1 d 2 h( z ) ⋅ + ⋅ + ⋅ =0 2 2 2 g h dz f dx dy
上式中每项都只是一个变量的函数, 上式中每项都只是一个变量的函数,其成立的唯一条件是 三项中每项都是一个常数, 三项中每项都是一个常数,故有
d 2 f ( x) = −k 2 x f ( x) dx 2
d 2 g ( y) = −k 2 y f ( y ) dy 2
d 2 h( z ) = −k 2 z f ( z ) dz 2
分离常数, 其中 k x,k y,k z 为分离常数,且 ※ 分析 与 讨论 ① 当 kx2 = 0 时
2010-12-8
边值问题 是指存在边界面的电磁问题。 是指存在边界面的电磁问题。 根据给定边界条件对边值问题分类: 根据给定边界条件对边值问题分类: 第一类边值问题: 第一类边值问题: 已知位函数在全部边界面上的分布值 边值问题
φ
∂φ ∂n
S
= f
= f
S
狄里赫利问题( 狄里赫利问题(Dirichlet) )
第二类边值问题:已知位函数在全部边界面上的法向导数值 第二类边值问题: 边值问题 诺埃曼问题 (Neumann) )
解: 选择直角坐标系
在区域 0<x<a、0<y<b内 、 内
y y
∇ φ =0
2
b b
φ φ = 0(x) =U φ =0
0 0
∂φ ∂φ + 2 =0 2 ∂x ∂y
2 2
∂φ =0 ∂x
φ =0 φ =U φ =0 φ =0
a a
x x
第5章 边值问题
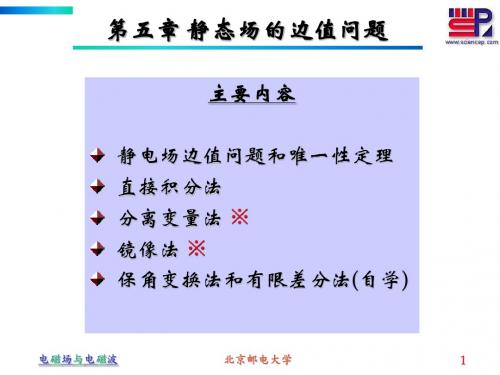
有源——Poission’s 有源——Poission’s Equation ∇ 2ψ = − ρ ε Poission’s Equation+边界条件 Equation+边界条件 Laplace’s Equation +边界条件 +边界条件
边值问题:在给定边界条件下求解偏微分方程 边值问题:在给定边界条件下求解偏微分方程
2
∴ψ = C1 ln r + C 2
代入边界条件: r=a时 代入边界条件: r=a时ψ=U,r=b时ψ=0,C1=?, C2=? r=b时 =0,
电磁场与电磁波 北京邮电大学
4
例2
已知:导体球,半径a,球体电位U 基准?) 已知:导体球,半径a,球体电位U (基准?) 求:球外的电位? 分析:
[
]
[
]
18
上题中边界处的 电位分布
v( x,0) = ∑ ( An + Bn ) sin(nπx / a )
n =1
∞
探讨一下边界处分布函数的形状:
电磁场与电磁波
北京邮电大学
19
例2. 书124页的例5.3 124页的例 页的例5.3
…… 简化的步骤(2 简化的步骤(2)
判断解的形式 求特征值,写出通解形式 代入边界,求待定系数 写出问题的解
第五章 静态场的边值问题
主要内容 静电场边值问题和唯一性定理 直接积分法 分离变量法 ※ 镜像法 ※ 保角变换法和有限差分法(自学) 保角变换法和有限差分法(自学)
电 磁 场 与 电 磁波
北京邮电大学
1
静电场的边值问题
一般情况下电位或场强满足两个方程 一般情况下电位或场强满足两个方程 无源——Laplace’s 无源——Laplace’s Equation ∇ 2ψ = 0
《静态场的边值问题》PPT课件

nπ a
b
a nπ
sin
0
a
x sin mπ a
xdx
(x,
y)
n1
4U 0 nsh n
b
sin
nπ a
x sh nπ y a
a
(n 1,3,5,)
(2)U
(
x)
U
0
s
in
π a
x
π
U0 sin a
x
n1
Dn
sin
nπ a
x sh nπ b a
D1=U 0
sh b
a
Dn=0 (n 0)
双曲函数
例5-1
一长直金属槽的长度方向上平行于Z轴,其横截面如图5-1所示。其侧壁与
底面电位均为0,而顶盖电位 x, b U x。
分别以(1)U
(2)U x U0
sixnxU,求0,槽内电位
a
的解。
解 本例是一个矩形域的二维场问题。在直角坐标系下,位函数
x,
y
的边值问题为
y
2
x
2
2
y 2
(1) (2) (3) (4)
(5)
2) 分离变量 (x, y) 1 (x)2 ( y)
代入式(1)有
1
1
d 21
dx2
1
2
d 22
dy2
设
1
1
d 21
dx2
,
1
2
d 22
dy2
称为分离常数,可以取值 0, 0和 0
根据 可能的取值,可有6个常微分方程:
1
1
d 21
dx2
0
1 2
静态场及其边值问题的解
3.1.2 电位函数 1. 电位函数旳定义
E 0
E
即静电场能够用一种标量函数旳梯度来表达,标量函数 称
为静电场旳标量电位或简称电位。
2. 电位旳体现式
对于连续旳体分布电荷,由
R r r
E(r )
1
4
V
(r ) R3
RdV
1
4
V
(r)( 1 )dV
R
[ 1
4
V
(r)( 1 )dV ]
3.
电位差
将
E
两端点乘 dl,则有
E
dl
dl
(
dx
dy
dy)
d
x y y
上式两边从点P到点Q沿任意途径进行积分,得
电场力对单 位正电荷做
旳功
Q
Q
P E dl P d (P) (Q)
有关电位差旳阐明:
P、Q 两点间旳电位差
P、Q 两点间旳电位差等于电场力将单位正电荷从P点移至Q 点 所做旳功,电场力使单位正电荷由高电位处移到低电位处; 电位差也称为电压,可用U 表达; 电位差有拟定值,只与首尾两点位置有关,与积分途径无关。
U
2
ln(b / a)
F/m
21
电磁场与电磁波 第3章 静态电磁场及其边值问题的解
3.1.4 静电场旳能量 静电场对电荷有作用力,这表白静电场具有能量。静电场能
量起源于建立电荷系统旳过程中外电源提供旳能量。
1. 静电场旳能量 体分布电荷旳电场能量为
We
1 2
dV
V
对于面分布电荷,电场能量为
We
电磁场与电磁波 第3章 静态电磁场及其边值问题的解
1
静态场及其边值问题的解
R r r
3. 电位差 将 E 两端点乘 dl ,则有 E dl dl ( dx dy dy) d x y y 上式两边从点P到点Q沿任意路径进行积分,得
电场力做 的功
Q
P
Q E dl d ( P) (Q)
P
关于电位差的说明
P、Q 两点间的电位差
P、Q 两点间的电位差等于电场力将单位正电荷从P点移至Q 点 所做的功,电场力使单位正电荷由高电位处移到低电位处。
电位差也称为电压,可用U 表示。
电位差有确定值,只与首尾两点位臵有关,与积分路径无关。
4. 电位参考点 静电位不惟一,可以相差一个常数,即
C ( C )
•
• •
静态电磁场:场量不随时间变化,包括:
静电场、恒定电场和恒定磁场 时变情况下,电场和磁场相互关联,构成统一的电磁场 静态情况下,电场和磁场由各自的源激发,且相互独立
本章内容
3.1 静电场分析 3.2 导电媒质中的恒定电场分析 3.3 恒定磁场分析 3.4 静态场的边值问题及解的惟一性定理 3.5 镜像法
如果选择参考点在rQ=∞,得P=∞,显然不合理。 l 1 ln ,显然这种形式最简单。 如果选择rQ=1,得 P 2 0 rP l 1 由此得到线电荷电位的一般表达式 ln 2 0 r l l 1 1 对于位于r 的线电荷,电位表达式为 ln ln 2 0 r r 2 0 R
线电荷:设线电荷 l 在原点,参考点 Q ,场点 ( 电位考察 点)P,沿如前路径进行积分,有 M Q l Q r P E d l E d l d r 2 P M M 2 0 r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2 ,
然后进行 证明.同样可得出结论,其解唯一.
设φ1φ2是同一有源区域的边值问题
2 的解。 | f1 ( S )
即在区域V内,φ1和φ2满泊松方程,即
1 2 2
2
在V的边界S上,φ1和φ2满足同样的边界条件, 即
5.3.1 导体平面镜像
设在无限大导体平面(z=0)附近有一点电荷与平面距离为z=h 。 若导体平面接地,则导体平面电位为零,如图所示。求上半 空间中的电场。 分析:上半空间任一点 P处的电位,应等于点 电荷q和无限大导体平 板上感应的负电荷产生 的的电位总和。因此, 上半空间的电位问题可 表示为 :
2
C (常数)
0
1 2
C 0
5.3 镜像法
实质:是以一个或几个等效电荷代替边界的影响,将原来具有边
界的非均匀空间变成无限大的均匀自由空间,从而使计算过程 大为简化。
依据:惟一性定理。等效电荷的引入必须维持原来的边界 条件不变。这些等效电荷通常处于镜像位置,因此称为镜 像电荷,而这种方法称为镜像法。
2 A ( A) A J
人为规定
A 0
这个规定被称为库仑规范
于是有
2 A J
此式即为矢量磁位的泊松方程。
在没有电流的区域有J 0
2 A0
此式即为矢量磁位的拉普拉斯方程。 (2) 磁场的标量位函数 在没有电流分布的区域内,恒定磁场的基本方程变为 H 0 B 0 这样,在无源区域内,磁场也成了无旋场,具有位场的性 质,因此,象静电场一样,我们可以引入一个标量函数, 即标量磁位函数
即φ1φ2是同一无源区域的边值问题
即有
2 0 | f1 ( S )的解。
1 0
2
2 0
2
1 | f1 ( S )
2 | f1 ( S )
由格林第一定理知:对任意标量函数
2
( )dV ds n V s
1 n
2 n
0
S曲面上
S曲面内 S曲面上
0 n
0 C
当 1 和 2 选择相同的参考点时, C 0
1 2 解唯一.
3.
1
三类边界问题
f1 ( s )
n
f 2 (s)
2
将格林第一恒等式的积分曲面写成
1 | f1 ( S ) 2 | f1 ( S )
令φ* =φ1-φ2,则在V内,▽2φ*=0,在边界面S上,φ*|S=0。 代入 格林第一恒等式有:
V
* * dV * dS S n
2
在S上φ* =0,因而上式右边为零,因而有
体积V内 S曲面上
V
* dV 0
重点:
1.静电场、恒定电场 、恒定磁场的基本方程。 2.静态场的位函数方程。 3.理论依据:唯一性定理、叠加原理。 4.镜像法 、分离变量法。
静态场的基本方程
静态场与时变场最基本的区别在于静态场的电场和磁场是 彼此独立存在的,即电场只由电荷产生,磁场只由电流产 生。没有变化的磁场,也没有变化的电场。
S n
因此,表面电荷给定等于给定了电位的法向导数值。
唯一性定理:满足三类给定边值之一的泊 松方程或拉普拉斯方程的解是唯一的。
换句话说,如果一个函数即满足泊松方程(或拉 普拉斯方程)又满足给定的边界条件,则该函数 是唯一的。
唯一性定理的证明: 1.设在体积V内,其满足边值 f1 ( s) 的拉普 1 拉斯方程的解不是唯一的,有 和2 两个解。
满足
上式即为在有电荷分布的区域内,或者说在有“源”的区
域内,静电场的电位函数所满足的方程,我们将这种形式 的方程称为 泊松方程。
如果场中某处有ρ=0,即在无源区域,则上式变为
0
我们将这种形式的方程称为 拉普拉斯方程。它 是在不存在电荷的区域内,电位函数 应满足的方程。
2 在不同的坐标系中有不同的表达形式: 拉普拉斯算符
2 2 2 2则源自 V 2 dV ds n S
又 ∵ ∴ 故
由边界条件有
1 2
在曲面边界上,
1 2
0
V
2
dV ds 0 n S
体积V内
即
0
C (常数)
S曲面上
C 0 0 1 2 故其解是唯一的。
f ( s ) 的拉普拉斯 2.设在体积V内,其满足边值 方程的解不是唯一的,有 和 两个解。
2
n
仍然采用反证法证明.设有两个解满足拉氏方程.
则 即 则
1 n
2 n
n
n
( )dV ds 0 n V S
1、静电场的基本方程 静电场是静止电荷或静止带电体产生的场,其基本方程为
s D d s q E dl 0
c
D E 0
上式表明:静电场中的旋度为0,即静电场中的电场不可 能由旋涡源产生;电荷是产生电场的通量源。 电介质的本构方程为
静电场可以用一个标量函数 即
的梯度来表示它:
E
式中的标量函数 电位函数。
称为
对于均匀、线性、各向同性的介质,ε为常数, 0 所以有 D ( E ) E
( )
即
2
静电场的位函数 的方程。
第5章 静态场的边值问题
5.1 引言
数学物理方程是描述物理量随空间和时间的变化规律。
对于某一特定的区域和时刻,方程的解取决于物理量的初始 值与边界值,这些初始值和边界值分别称为初始条件和边界 条件,两者又统称为该方程的定解条件。 静态场是指场量不随时间变化的场,静态场包括:静电场、 恒定电场及恒定磁场。静电场的场量与时间无关,位函数所 满足的泊松方程及拉普拉斯方程的解仅决定于边界条件。 静电场的边值问题:给定边界条件下,求泊松方程或拉普拉 斯方程解的问题。
则有
=0
2
这说明,在无电源区域,恒定电场的位函数满足拉普拉 斯方程。
3、恒定磁场的位函数分布
(1) 磁场的矢量位函数
恒定磁场是有旋场,即 B J ,但它却是无散场, 即 B 0 引入一个矢量磁位 A 后,由于 B= A ,可得
2 0 z 0 z0 0
P r
q
r1
P
介质
导体
q h
h
r2
边值问题的分类:
边值问题根据边界条件给出的形式不同可分为以下三 种类型。 第一类边值问题:给定整个边界上的位函数求区域中位 函数的分布,这类问题又称为狄里赫利问题。
第二类边值问题:给定整个边界上位函数的法向导数 求区域中位函数的分布,这类问题又称为纽曼问题。
第三类边值问题:给定一部分边界上的位函数和其余部 分边界上的法向导数,求区域中位函数的分布,这类问 题混合问题。
完全用数学方法求解。在介绍具体的求解方法之前,我们 要先介绍几个重要的基本原理,这些原理将成为以后求解 方程的理论依据。
5.2.1 唯一性定理
在求解静态场问题时,我们希望其 解是唯一的,那么,在什么条件下, 其解才是唯一?
三类边值条件:
1. 给定边界上的位函数,即已知
S为边界
f1 ( s ) ,
c
ò E ?dl
c
eE
恒定电场在无电源区的基本方程的积分形式和微分形式分别为
s J ds 0 E dl 0
c
J 0 E 0
导体中的本构方程为
J E
3、恒定磁场的基本方程 恒定电流的导体周围或内部不仅存在电场,而且存在 磁场,但这个磁场不随时间变化,是恒定磁场。假设导体 中的传导电流为I,电流密度为 J ,则有
在无电源区域,恒定电场是一个位场,即有 E 0 这时同样可以引入一个标量位函数 使得 E
根据电流连续性方程 J 0 及物态方程 J E 并设电导率 为一常数(对应于均匀导电媒质),则有
2、恒定电场的位函数分布
2 J ( E ) ( ) 0
关键:确定镜像电荷的大小及其位置。 局限性:仅仅对于某些特殊的边界以及特殊分布的电荷才有可
能确定其镜像电荷。
注意: 1、镜象电荷不能放在要讨论的区域中,放在被讨 论的区域中时将会改变所放置区域的电位分布,所 得出的位函数将不满足原来的拉普拉斯方程或泊松 方程。 2、所得位函数必须满足原来的边界条件。 3、镜像电荷周围的介质应该是与被讨论的区间一 致的。
s B ds 0 H dl I
c
B 0 H J
这是恒定磁场的基本方程。
磁介质中的本构方程为
B H
从以上方程可知,恒定磁场是一个旋涡场,电流是这个旋 涡场的源,电流线是闭合的。
静态场的位函数
1、静电场的位函数分布
令
则有
( )dV ds n V S
2
令
1 2
2
