梅森公式例子 PPT
合集下载
自动控制原理第二章梅森公式-信号流图课件
ABCD
然后，通过分析梅森公式 的各项系数，确定系统的 极点和零点。
最后，将梅森公式的分析 结果转换为信号流图，进 一步明确系统各变量之间 的传递关系。
梅森公式在信号流图中的应用实例
假设一个控制系统的传递函数为 (G(s) = frac{s^2 + 2s + 5}{s^2 + 3s + 2})
在信号流图中，将极点和零点表示为相 应的节点，并根据梅森公式的各项系数 确定各节点之间的传递关系。
02
信号流图基础
信号流图定义与构成
信号流图定义
信号流图是一种用于描述线性动 态系统数学模型的图形表示方法 ，通过节点和支路表示系统中的 信号传递和转换过程。
信号流图构成
信号流图由节点和支路组成，节 点表示系统的动态方程，支路表 示输入输出之间的关系。
信号流图的绘制方法
确定系统动态方程
根据系统描述，列出系统的动态方程。
2
梅森公式与信号流图在描述和分析线性时不变系 统时具有互补性，二者可以相互转换。
3
信号流图能够直观地表示系统各变量之间的传递 关系，而梅森公式则提供了对系统频率特性的分 析手段。
如何使用梅森公式进行信号流图分析
首先，将系统的传递函数 转换为梅森公式的形式。
根据极点和零点的位置， 判断系统的稳定性、频率 响应特性等。
在未来研究中的可能发展方向
随着科技的不断进步和应用需求的不断变化，控制系统面临着越来越多的 挑战和机遇。
在未来研究中，可以利用梅森公式和信号流图进一步探索复杂系统的分析 和设计方法，提高系统的性能和稳定性。
同时，随着人工智能和大数据技术的应用，可以结合这些技术对控制系统 进行智能化分析和优化设计，提高系统的自适应和学习能力。
信号与系统7_梅森公式的证明及应用PPT共22页
信号与系统7_梅森公式的证明及应用
21、没有人陪你走一辈子，所以你要 适应孤 独，没 有人会 帮你一 辈子， 所以你 要奋斗 一生。 22、当眼泪流尽的时候，留下的应该 是坚强 。 23、要改变命运，首先改变自己。
24、勇气很有理由被当作人类德性之 首，因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿． 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ，它只 是让人 们的脚 放上一 段时间 ，以便 让别一 只脚能 够再往 上登。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 5、内外相应，言行相称。——韩非
最新梅森公式例子
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2 第三条回路增益 L3= - G2 G3 G4 G5 G6 H3 第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3 第六条回路增益 L6= - GG7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2 第三条回路增益 L3= - G2 G3 G4 G5 G6 H3 第四条回路增益 L4= - G2 G3 G4 G9 G6 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
R(s) G1 G2 G3 G4 G5
G6
1
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
第二条前向通路增益 P2=G1 G2 G8
第三条前向通路增益 P3=G1 G7 G4 G5 G6 第四条前向通路增益 P4=G1 G2 G3 G4 G9 G6
1 第九章 梅森公式 状态方程
1
系统的信号流图表示法
X s H s
H s
Y s
方框图 流图
X s
Y s
实际上是用一些点和支路来描述系统：
X s 、 Y s
称为结点
线段表示信号传输的路径，称为支路。
信号的传输方向用箭头表示，转移函数标在箭头附近， 相当于乘法器。
2
术语定义
X 1 X1
e (t )
vC t
R 1 1 d d t i L t L i L t L v C t L e t d v t 1 i t L dt C C
33
写为矩阵形式：
d R d t i L t L d v t 1 dt C C
L LL
d e d ,e , f
f
6
1 H
g
k
k
k
——表示由源点到阱点之间第k条前向通路的标号。 k
gk——表示由源点到阱点之间的第k 条前向通路的增益。
它是除去与 k 条前向通路相接触的环路外，余下的特征 行列式。
条前向通路特征行列式的余因子。 k ——称为对于第 k
7
例
4
方框图 to 信号流图
信号流图的梅森增益公式 1 H gk k k 式中： △——称为流图的特征行列式。 1 (所有不同环路增益之和）
（每两个互不接触环路增益乘积之和） （每三个互不接触环路增益乘积之和） 1 La Lb Lc
a b ,c
X
2
X3
H3 G3
X
4
H5
Y
它只有一对两两互不接触的回路 X 3 X X1 X 2 X1
系统的信号流图表示法
X s H s
H s
Y s
方框图 流图
X s
Y s
实际上是用一些点和支路来描述系统：
X s 、 Y s
称为结点
线段表示信号传输的路径，称为支路。
信号的传输方向用箭头表示，转移函数标在箭头附近， 相当于乘法器。
2
术语定义
X 1 X1
e (t )
vC t
R 1 1 d d t i L t L i L t L v C t L e t d v t 1 i t L dt C C
33
写为矩阵形式：
d R d t i L t L d v t 1 dt C C
L LL
d e d ,e , f
f
6
1 H
g
k
k
k
——表示由源点到阱点之间第k条前向通路的标号。 k
gk——表示由源点到阱点之间的第k 条前向通路的增益。
它是除去与 k 条前向通路相接触的环路外，余下的特征 行列式。
条前向通路特征行列式的余因子。 k ——称为对于第 k
7
例
4
方框图 to 信号流图
信号流图的梅森增益公式 1 H gk k k 式中： △——称为流图的特征行列式。 1 (所有不同环路增益之和）
（每两个互不接触环路增益乘积之和） （每三个互不接触环路增益乘积之和） 1 La Lb Lc
a b ,c
X
2
X3
H3 G3
X
4
H5
Y
它只有一对两两互不接触的回路 X 3 X X1 X 2 X1
信号与系统7_梅森公式的证明及应用
W=[wij]，wij={ wij，i=j，wij是支路i的权，即支路传输 }
0，
i j
• 上述B，S，W三个矩阵完全描叙了信号流图。
梅森公式的推导
• 下面介绍一些定理和性质。
对于下列方程组： AX=Y ………………（1）
式中
A=
1
a a a a 21
...
12
1 ...
，Y=
y
回路传输乘积之和；
k 第k个前向通道的特征式的余子式；其值为 中除去与
第k个前向通道接触的回路后的剩余部分；
梅森公式的推导
梅森公式的推导（先 用一个一般性的图来证明）
如右图已知信号流图如图所 示，所对应的代数方程为
V1 mV1 lV3 bR
f
m
h
R1
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
Ⅳ
C
V1 d Ⅴ e V2 1
• 由定理6和7很容易推出梅森公式。
梅森公式
• 梅森公式不仅能求输入输出函数的比值的 （传输函数），对与流图中的任意一个节 点的信号与输入结点信号的比值也同样是 成立的。这个很好理解，因为输出节点并 没有什么特殊的地方，也仅仅是流图中的 一般点，只是我们赋予了它特殊的含义罢 了。下面就就举一例说明梅森公式对流图 中任一点与输入点的信号的比值的作用。
二、分别用梅森公式求取输出节点及该节点对输入节点的传递 函数，然后把它们的结果相比，即可得到输出对该混合节点的 传递函数。
mk e
于是传递函数为
(s) C(s) 2
bde f (1 m dl) bg
R(s) R 1 (m dl ke h gkl) mh dlh mke
梅森公式,求零状态响应
梅森公式，求零状态响应梅森公式（Mason's formula）是控制工程中用于求解线性时不变系统传递函数的一种方法，它基于信号流图的分析。
然而，梅森公式本身并不直接用于求解零状态响应，而是用于确定系统的整体传递函数。
零状态响应是指系统在初始状态为零时，对输入信号的响应。
要求零状态响应，通常需要通过以下步骤：1.确定系统的微分方程或差分方程，这通常基于系统的物理特性或电路元件的关系。
2.对微分方程或差分方程进行拉普拉斯变换或Z变换，将时域方程转换为复频域或Z域的代数方程。
3.利用代数方法求解变换后的方程，得到系统的传递函数H(s)或H(z)。
4.对传递函数进行反拉普拉斯变换或反Z变换，将其转换回时域，得到系统的单位冲激响应h(t)或单位样本响应h[n]。
5.最后，通过卷积积分（连续时间系统）或卷积和（离散时间系统）将输入信号f(t)或f[n]与单位冲激响应h(t)或单位样本响应h[n]结合起来，得到零状态响应y(t)或y[n]。
在实际应用中，可能会使用各种工具和软件（如MATLAB）来辅助完成这些计算。
如果你有一个具体的系统描述或信号流图，并且想要使用梅森公式来求解传递函数，进而找到零状态响应，你需要首先根据梅森公式计算出传递函数，然后按照上述步骤找到零状态响应。
请注意，以上步骤是一般性的指导，具体问题可能需要特定的处理方法和技巧。
如果你有具体的系统或问题，请提供更多信息以便给出更准确的指导。
以下是一个实际例子：假设我们有一个简单的RC电路，其微分方程为：(\frac{d}{dt}V(t)+\frac{1}{RC}V(t)=0)其中(V(t))是电压，(R)是电阻，(C)是电容。
1.首先，我们对微分方程进行拉普拉斯变换，得到传递函数(H(s)=\frac{1}{RCs+1})。
2.然后，对传递函数进行反拉普拉斯变换，得到单位冲激响应(h(t)=e^{-\frac{t}{RC}})。
3.假设输入信号是(f(t)=\sin(t))，我们将输入信号和单位冲激响应进行卷积积分，得到零状态响应(y(t)=\int_{0}^{t}e^{-\frac{(t-u)}{RC}}\sin(u)du)。
02-求梅森素数(PPT)
专题6 程序设计综合举例 6.1 求π的近似值 6.2 求定积分的近似值 6.3 求一元方程的根 6.4 求勾股数 6.5 求梅森素数 6.6 程序调试
6.5 求梅森素数 判断整数性质的基本思路 判断素数 判断梅森素数
1 判断整数性质的基本思路 （1）处理方法。
m能否被n整除
m%n的值为0 m-m/n*n的值为0
分离m各位数字
个位数字：m%10 十位数字：m/10%10
1 判断整数的性质的基本思路 （2）求某一范围内符合某种条件的整数。 考虑判断单个整数是否满足条件的算法。 在指定范围内重复执行“判断单个数”的程序段。
2 判断素数的程序实现 素数（Prime Number）是大于1，且除了1和它本身以外，不能被其他任何整数所整除的整数。
m/2或 m
3 判断梅森素数的程序实现
所谓梅森数（Mersenne Number），是指形如2p-1的一类正整数，其中指数p是素数，记为Mp。如果一个梅森数是素数， 则称其为梅森素数（Mersenne Prime）。试求p<20的所有梅森素数和梅森素数的个数。
2p-1是素数
P一定是素数
3 判断梅森素数的程序实现
if (f==1)
{
ห้องสมุดไป่ตู้
printf("M(%d)=%d\n",p,mp);
n++;
}
}
printf("The number of Mersenne Prime less than 20 is %d.\n",n);
return 0;
}
判断单个的整数是否符合条件。 利用穷举法求某个范围内符合条件的整数。
#include <stdio.h>
6.5 求梅森素数 判断整数性质的基本思路 判断素数 判断梅森素数
1 判断整数性质的基本思路 （1）处理方法。
m能否被n整除
m%n的值为0 m-m/n*n的值为0
分离m各位数字
个位数字：m%10 十位数字：m/10%10
1 判断整数的性质的基本思路 （2）求某一范围内符合某种条件的整数。 考虑判断单个整数是否满足条件的算法。 在指定范围内重复执行“判断单个数”的程序段。
2 判断素数的程序实现 素数（Prime Number）是大于1，且除了1和它本身以外，不能被其他任何整数所整除的整数。
m/2或 m
3 判断梅森素数的程序实现
所谓梅森数（Mersenne Number），是指形如2p-1的一类正整数，其中指数p是素数，记为Mp。如果一个梅森数是素数， 则称其为梅森素数（Mersenne Prime）。试求p<20的所有梅森素数和梅森素数的个数。
2p-1是素数
P一定是素数
3 判断梅森素数的程序实现
if (f==1)
{
ห้องสมุดไป่ตู้
printf("M(%d)=%d\n",p,mp);
n++;
}
}
printf("The number of Mersenne Prime less than 20 is %d.\n",n);
return 0;
}
判断单个的整数是否符合条件。 利用穷举法求某个范围内符合条件的整数。
#include <stdio.h>
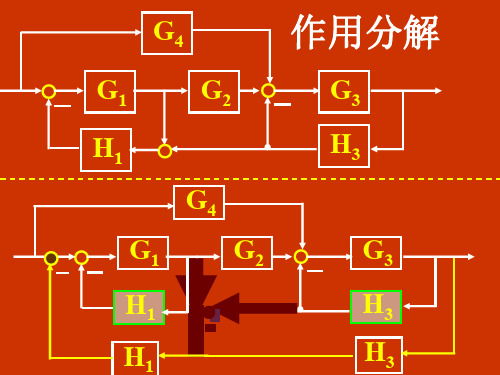
梅森公式-信号流图
L4 a23a34a45a52
x5 L5 a23a35a52
P
a12 a23a34 a45 (1 a44 )a12 a23a35
1 (a23a32 a23a34a42 a44 a23a34a52 a23a35a52 ) a23a32 a44 a23a35a52a44
G3(s)
梅逊公式求E(s)
R(s)
E(SG)GG3(33s(()ss))
RRR(s(()ss)) EEE(S((S)S))
P2= - G3G2H3
GGG1(11s(()ss))
△2= 1 P2△2=?
HHH1(11s(()ss))
G1(s)
NNN((s(ss)))
G2(s)
GGG2(22s(()ss))
CCC(s(()ss))
HHH2(22s(()ss)) H3(s)
HHH3(33s(()ss))
C(s)
R(s)
E(S) P1=H–P1G(s1)2=H13 △△1=11=+G1 2HH2 2(s)P1△1= ?
E(s)= R(s)[ (1+G2H2) +(- G3G2H3)] +(–G2H3)N(s)
1 G1H1 G2G7 H 2 G6G4G5 H 2 G2G3G4G5 H 2 G4G5G7 H1H 2
x1
x2
x3
x7 I(s) x4
x5
o在源节点上，只有信号输出 支路而没有信号输入的支路，
1/R1 1+R1C1s R2
它一般代表系统的输入变量。
-1
•阱节点（输出节点）：
在阱节点上，只有信号输入的支路而没有信号输出的支路，它
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3
1 1 C(s)
G8
1 1 C(s)
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6 第二条前向通路增益 P2=G1 G2 G8 第三条前向通路增益 P3=G1 G7 G4 G5 G6
1 1 C(s)
G8
G7 G9
R(s) G1 G2 G3 G4 G5
三．（15分）系统的方框图如图所示，用Mason公式求系统的传递函数
C(s)
C (s)
E (s)
R(s)
N (s)
R (s)
（要求有主要过程，只给出结果的要扣分）
R(s) G1
R(s) G1
G7 G2 G3
H3 G7 G2 G3 G4
G9
G4
G5
H1 G8
G8
G9
G5 G6
1
-H1
-H2
-H3
C(s) G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2 第三条回路增益 L3= - G2 G3 G4 G5 G6 H3 第四条回路增益 L4= - G2 G3 G4 G9 G6 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3 第六条回路增益 L6= - G7 G4 G9 G6 H3
+ G7 G4 G5 G6 H3 + G7 G4 G9 G6 H3 +G2 G8 H3 + G4 G6 H1 H2 + G2 G4 G8 H1 H3 + G2 G6 G8 H2 H3 + G2 G4 G6 G8H1 H2 H3
G5 G6
1
1 1 C(s)
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
第二条前向通路增益 P2=G1 G2 G8
还有没有前向通路啦？
第三条前向通路增益 P3=G1 G7 G4 G5 G6
第四条前向通路增益 P4=G1 G2 G3 G4 G9 G6 第五条前向通路增益 P5=G1 G7 G4 G9 G6
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1 -H3
第一条回路增益 L1= - G4 H1
-H2 注意：要考虑负号！
大家有疑问的，可以询问和交流
可以互相讨论下，但要小声点
9
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1
-H2
-H3
三三互不接触回路增益乘积
L1 L2 L7= - G2 G4 G6 G8H1 H2 H3 =1-(L1+ L2 + L3+ L4 + L5+ L6 + L7)+ L1 L2+ L1 L7+ L2 L7- L1 L2 L7 =1+ G4 H1 + G6 H2 + G2 G3 G4 G5 G6 H3 + G2 G3 G4 G9 G6 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2 第三条回路增益 L3= - G2 G3 G4 G5 G6 H3 第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3 第六条回路增益 L6= - G7 G4 G9 G6 H3
H2
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
1C(s)
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6 第二条前向通路增益 P1=G1 G2 G8
G6
1
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6 第二条前向通路增益 P2=G1 G2 G8 第三条前向通路增益 P3=G1 G7 G4 G5 G6 第四条前向通路增益 P4=G1 G2 G3 G4 G9 G6
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
第七条回路增益 L7= - G2 G8 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4G5 G61 Nhomakorabea1
C(s) 1
-H1
-H2
-H3
两两互不接触(没有公共的节点）回路增益乘积 L1 L2= G4 G6 H1 H2
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1
-H2
-H3
两两互不接触(没有公共的节点）回路增益乘积 L1 L2= G4 G6 H1 H2 L1 L7= G2 G4 G8 H1 H3
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1
-H2
-H3
两两互不接触(没有公共的节点）回路增益乘积 L1 L2= G4 G6 H1 H2 L1 L7= G2 G4 G8 H1 H3 L2 L7= G2 G6 G8 H2 H3