(河北专版)2017中考数学第三编综合专题闯关篇题型一选择题、填空题重热点突破专题二图形的折叠与计算试题
(河北专版)2017中考数学 第三编 综合专题闯关篇 题型二 解答题重难点突破 专题三 动态变化问题试题

专题三动态变化问题专题命题规律1.动态问题为河北中考的常考点,近8年共考查8次,对动点问题的考查都会结合几何图形的综合考查,且都是以解答题形式出现,分值为9~12分.2.考查类型:(1)几何图形中的动点问题(2012年25题,2010年25题,2009年26题);(2)一次函数中的动点问题(2013年23题);(3)二次函数中的动点问题(2011年26题).2017预测预计2017年河北中考对动态变化问题仍会考查,且图形中的动点问题为重点考查对象,注意解决此类问题常会用到分类讨论思想和数形结合思想,并且一次函数中的动点问题难度会有所降低.,中考重难点突破)一次函数中的动点问题【经典导例】【例1】(2013河北中考)如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.(1)当t=3时,求l的解析式;(2)若点M,N位于l的异侧,确定t的取值范围;(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.【解析】(1),(2)求出直线与y轴的交点,以及P点坐标与t之间的关系,用对应的点的坐标代入解析式,即可求出答案;(3)过点M作l的垂线,求出直线与坐标轴的交点,然后再来计算即可.【学生解答】(1)直线y=-x+b交y轴于点P(0,b),由题意,得b>0,t≥0,b=1+t,当t=3时,b=4.∴y=-x+4;(2)当直线y=-x+b过M(3,2)时,2=-3+b,解得b=5,∵5=1+t,∴t=4.当直线y=-x+b过N(4,4)时,4=-4+b,解得b=8.∵8=1+t,∴t=7.∴当点M,N位于l的异侧时,4<t<7;(3)t=1时,落在y轴上;t=2时,落在x轴上.【方法指导】k、b对一次函数图象y=kx+b的影响:①当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小;②k决定着一次函数图象的倾斜程度,|k|越大,其图象与x轴的夹角就越大;③b决定着直线与y轴的交点,当b大于0时,交点在y轴正半轴;当b小于0时,交点在y轴负半轴;④直线y=kx+b可以看作由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移);⑤直线y=k1x+b1、y =k2x+b2的几种位置关系:平行:k1=k2,b1≠b2;重合:k1=k2,b1=b2;关于y轴对称:k1+k2=0,b1=b2;关于x轴对称:k1+k2=0,b1+b2=0;垂直:k1k2=-1.1.(2016邯郸二十五中一模)如图,在平面直角坐标系中,矩形ABCD的顶点A,B,C的坐标分别为(0,5), (0,2),(4,2),直线l的解析式为y = kx+5-4k(k> 0).(1)当直线l经过点B时,求一次函数的解析式;(2)通过计算说明:不论k为何值,直线l总经过点D;(3)直线l与y轴交于点M,点N是线段DM上的一点,且△NBD为等腰三角形,试探究:①当函数y = kx +5-4k 为正比例函数时,点N 的个数有________个;②点M 在不同位置时,k 的取值会相应变化,点N 的个数情况可能会改变,请直接写出点N 所有不同的个数情况以及相应的k 的取值范围.解:(1)将点B(0,2)代入y =kx +5-4k ,得k =34.∴直线l 的解析式为y =34x +2;(2)由题意可得,点D 坐标为(4,5),把x =4代入y =kx +5-4k ,得y =5,∴不论k 为何值,直线l 总经过点D ;(3)①2;②当k≥2时,有3个点;当34<k<2时,有2个点;当k =34时,有0个点;当 0<x<34时,有1个点.2.(2016承德二中二模)如图,直线y =kx -4与x 轴、y 轴分别交于B ,C 两点,且tan ∠OBC =43.(1)求点B 的坐标及k 的值;(2)若点A 是第一象限内直线y =kx -4上一动点,则当△AOB 的面积为6时,求点A 的坐标; (3)在(2)成立的条件下,在坐标轴上找一点P ,使得∠APC=90°,直接写出P 点坐标.解:(1)当x =0时,y =kx -4=-4,∴C(0,-4),则OC =4.又∵tan ∠OBC =OC OB =43,∴OB =3,∴B 点坐标为(3.0).将x =3,y =0代入y =kx -4,得0=3k -4,解得k =43;(2)已知点A 在第一象限,过点A 作AH⊥x 轴,垂足为H ,由题意得S △AOB =12OB ·AH =12×3×AH =6,∴AH =4,即点A 的纵坐标为4.将y =4代入y =43x -4,解得x =6,∴当△AOB 的面积为6时,点A 的坐标为(6,4);(3)P 点的坐标为(0,4)或(-2,0)或(8,0).3.(2016长沙中考)如图,直线l :y =-x +1与x 轴,y 轴分别交于A ,B 两点,点P ,Q 是直线l 上的两个动点,且点P 在第二象限,Q 在第四象限,∠POQ =135°.(1)求△AOB 的周长;(2)设AQ =t >0,试用含t 的代数式表示点P 的坐标;(3)当动点P ,Q 在直线l 上运动到使得△AOQ 与△BPO 的周长相等时,记tan ∠AOQ =m ,若过点A 的二次函数y =ax 2+bx +c 同时满足以下两个条件:①6a +3b +2c =0;②当m≤x≤m+2,函数y 的最大值等于2m,求二次项系数a 的值.解:(1)对函数y =-x +1,令x =0,则y =1,∴B(0,1),令y =0,则x =1,∴A(1,0),则OA =1,OB =1,AB =2,△AOB 周长为1+1+2=2+2;(2)∵OA=OB ,故∠ABO=∠BAO=45°,∴∠PBO =∠QAO=135°,设∠POB=x ,则∠OPB=∠AOQ=180°-135°-x =45°-x ,∴△PBO ∽△OAQ ,故PB OA =OB AQ ,∴PB =OA ×OB AQ =1t,过点P 作PH⊥OB 于H 点,则△PHB 为等腰直角三角形.∵PB=1t ,则PH =HB =22t ,∴点P 的坐标为⎝ ⎛⎭⎪⎫-22t,1+22t ;(3)由(2)知△PBO∽△OAQ,若它们周长相等,则相似比为1,即△AOQ≌△BPO,则AQ =OB =1,∴t =1,同(2)中做法,得Q ⎝ ⎛⎭⎪⎫1+22,-22,∴m =221+22=2-1.∵m≤x≤m+2,∴2-1≤x≤2+1,∵抛物线过A 点,∴a +b +c =0,而6a +3b +2c =0,∴b =-4a ,c =3a ,故二次函数为y =ax 2-4ax +3a ,∴对称轴为x =2,取值范围是2-1≤x≤2+1.Ⅰ.若a>0,则开口向上,在x =2-1取最大值y max =a(2-1)2-4a(2-1)+3a =(10-62)a ,又∵y max =2m =22-1=22+2,∴(10-62)a =22+2.解得a =11+827.Ⅱ若a<0,则开口向下,在x =2取最大值22+2,即4a +2b +c =22+2,解得a =-22-2.综上,所求a 的值为11+827或-22-2.二次函数中的动点问题【经典导例】【例2】(2011河北中考)如图,在平面直角坐标系中,点P 从原点O 出发,沿x 轴向右以每秒1个单位长度的速度运动t(t >0)秒,抛物线y =x 2+bx +c 经过点O 和点P ,已知矩形ABCD 的三个顶点为A(1,0),B(1,-5),D(4,0).(1)求c 、b ;(用含t 的代数式表示)(2)当4<t <5时,设抛物线分别与线段AB 、CD 交于点M ,N.①在点P 的运动过程中,你认为∠AMP 的大小是否会变化?若变化,说明理由;若不变,求出∠AMP 的值;②求△MPN 的面积S 与t 的函数关系式,并求t 为何值时,S =218;(3)在矩形ABCD 的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接写出t 的取值范围.【解析】(1)由抛物线y =x 2+bx +c 经过点O 和点P ,将点O 与点P 的坐标代入方程即可求得c ,b ;(2)①当x =1时,y =1-t ,求得点M 的坐标,则可求得∠AMP 的度数;②由S =S 四边形AMNP -S △PAM =S △DPN +S 梯形NDAM -S △PAM ,即可求得关于t 的二次函数,列方程即可求得t 的值;(3)根据图形,即可直接求得答案,分别分析左边有4,3,2,1,0个好点时,t 的取值范围.【学生解答】(1)把x =0,y =0代入y =x 2+bx +c ,得c =0,再把x =t ,y =0代入y =x 2+bx ,得t 2+bt =0,∵t >0,∴b =-t ;(2)①不变,∵抛物线的解析式为:y =x 2-tx ,且点M 的横坐标为1,∴当x =1时,y =1-t ,M(1,1-t),∴AM =|1-t|=t -1,∵OP =t ,∴AP =t -1,∴AM =AP ,∵∠PAM =90°,∴∠AMP =45°;②S=S 四边形AMNP -S △PAM =S △DPN +S 梯形DNMA -S △PAM =12(t -4)(4t -16)+12[(4t -16)+(t -1)]×3-12(t -1)(t -1)=32t2-152t +6.解32t 2-152t +6=218,得t 1=12,t 2=92,∵4<t <5,∴t 1=12(舍去),∴t =92;(3)①左边4个好点在抛物线上方,右边4个好点在抛物线下方:无解;②左边3个好点在抛物线上方,右边3个好点在抛物线下方,则有-4<y 2<-3,-2<y 3<-1,即-4<4-2t <-3,-2<9-3t <-1,72<t <4且103<t <113,解得72<t <113;③左边2个好点在抛物线上方,右边2个好点在抛物线下方:无解;④左边1个好点在抛物线上方,右边1个好点在抛物线下方:无解;⑤左边0个好点在抛物线上方,右边0个好点在抛物线下方:无解;综上所述,t的取值范围是72<t <113.4.(2016保定八中三模)已知在平面直角坐标系xOy 中,O 为坐标原点,线段AB 的两个端点A(0,2),B(1,0)分别在y 轴和x 轴的正半轴上,点C 为线段AB 的中点,现将线段BA 绕点B 按顺时针方向旋转90°得到线段BD ,抛物线y =ax 2+bx +c(a≠0)经过点D.(1) 如图①,若该抛物线经过原点O ,且a =-13.①求点D 的坐标及该抛物线的解析式;②连接CD ,在抛物线上是否存在点P ,使得∠POB 与∠BCD 互余?若存在,请求出所有满足条件的点P 的坐标,若不存在,请说明理由;(2)如图②,若该抛物线y =ax 2+bx +c(a≠0)经过点E(1,1),点Q 在抛物线上,且满足∠QOB 与∠BCD 互余,若符合条件的Q 点的个数是4个,请直接写出a 的取值范围.解:(1)①过点D 作DF⊥x 轴于点F, ∵∠DBF +∠ABO=90°,∠BAO +∠ABO=90°,∴∠DBF =∠BAO.又∵∠AOB=∠BFD=90°, AB =BD ,∴△AOB ≌△BFD(AAS ),∴DF =BO =1,BF =AO =2,∴点D 的坐标为(3,1).根据题意得a =-13,c =0,且a·32+b·3+c =1, 解得b =43, ∴抛物线的解析式y =-13x 2+43x. ②∵点C ,D的纵坐标都为1, ∴CD ∥x 轴.∴∠BCD=∠ABO,∴∠BAO 与∠BCD 互余. 若要使得∠POB 和∠BCD 互余,则只要满足∠POB=∠BAO. 设点P 的坐标为(x ,-13x 2+43x), i .当点P 1在x 轴上方时,如答图,过点P 1作P 1G ⊥x 轴于点G,则tan ∠P 1OB =tan ∠BAO ,即P 1G OG =BD AO .∴-13x 2+43x x =12,解得x 1=52,x 2=0(舍去). ∴将x =52代入得-13x 2+43x =54.∴点P 1的坐标为(52,54). ii.当点P 2在x 轴下方时,如答图,过点P 2作BH⊥x 轴于点H,则tan ∠P 2OB =tan ∠BAO ,即P 2H OH =BO AO . ∴-(-13x 2+43x )x =12,解得x 1=0(舍去).x 2=112.将 x =112代入抛物线解析式得-13x 2+43x =-114. ∴点P 2的坐标为(112,-114). 综上所述,在抛物线上存在点P ,使得∠POB 与∠BCD互余,点P 的坐标为(52,54)或(112,-114);(2)∵该抛物线y =ax 2+bx +c(a≠0)经过点E(1,1),D(3,1),∴抛物线的解析式为ax 2-4ax +3a +1.若要使得∠QOB 和∠BCD 互余,则只要满足∠QOB=∠BAO,据此分a<0和a>0两种情况讨论.a 的取值范围为a<-13或a>4+154.5.(2016河北中考)如图,抛物线L :y =-12(x -t)(x -t +4)(常数t>0)与x 轴从左到右的交点为B ,A, 过线段OA 的中点M 作MP⊥x 轴,交双曲线y =kx(k>0,x>0)于点P ,且OA·MP=12.(1)求k 值;(2)当t =1时,求AB 长,并求直线MP 与L 对称轴之间的距离;(3)把L 在直线MP 左侧部分的图象(含与直线MP 的交点)记为G ,用t 表示图象G 最高点的坐标;(4)设L 与双曲线有个交点的横坐标为x 0,且满足4≤x 0≤6,通过L 位置随t 变化的过程,直接写出t 的取值范围.解:(1)设点P(x ,y),则MP =y ,由OA 的中点为M 知OA =2x ,代入OA·MP=12,得2x·y=12,即xy =6,∴k =xy =6;(2)当t =1时,令y =0,0=-12(x -1)(x +3),∴x 1=1,x 2=-3,∴由B 在A 左边,得B(-3,0),A(1,0),∴AB =4.∵L 的对称轴为x =-1,而M 为(12,0),∴MP 与L 对称轴的距离为32;(3)∵A(t,0),B(t -4,0),∴L 的对称轴为x =t -2,又MP 为x =t 2.当t -2≤t2,即t≤4时,顶点(t -2,2)就是G 的最高点;当t -2>t 2即t>4时,L 与MP 的交点(t 2,-18t 2+t)就是G 的最高点;(4)5≤t≤8-2或7≤t≤8+ 2.与图形中的动态问题【经典导例】【例3】(2016河北中考)如图,A(-5,0),B(-3,0).点C 在y 轴的正半轴上,∠CBO =45°,CD ∥AB ,∠CDA =90°.点P 从点Q(4,0)出发,沿x 轴向左以每秒1个单位长的速度运动,运动时间为t 秒.(1)求点C 的坐标;(2)当∠BCP=15°时,求t 的值;(3)以点P 为圆心,PC 为半径的⊙P 随点P 的运动而变化,当⊙P 与四边形ABCD 的边(或边所在的直线)相切时,求t 的值.【学生解答】(1)∵∠BCO=∠CBO=45°,∴OC =OB =3.又∵点C 在y 轴的正半轴上,∴点C 的坐标为(0,3);(2)当点P 在点B 右侧时,如答图①.若∠BCP=15°,得∠PCO=30°. ∴OP =OC·tan 30°=3,此时t =4+ 3.当点P 在点B 左侧时,如答图②,由∠BCP=15°,得∠PCO=60°,∴t 的值为4+3或4+33;(3)由题意知,若⊙P 与四边形ABCD 的边相切,有以下三种情况:①当⊙P 与BC 相切于点C 时,有∠BCP=90°,从而∠OCP=45°,得到OP =3,此时t =1.②当⊙P 与CD 相切于点C 时,有PC⊥CD,即点P 与点O 重合,此时t =4.③当⊙P 与AD 相切时,由题意,∠DAO =90°,∴点A 为切点.PC 2=PA 2=(9-t)2,PO 2=(t -4)2,于是(9-t)2=(t -4)2+32,解得t =5.6,∴t 的值为1或4或5.6.【方法指导】本题涉及到的知识有矩形的性质、锐角三角函数、圆的切线的相关知识,需要学生根据题目的条件进行分类讨论,从而确定问题的完整答案.6.(2016石家庄四十一中二模)如图,已知∠MON=90°,A 是∠MON 内部的一点,过点A 作AB⊥ON,垂足为点B ,AB =3 cm ,OB =4 cm ,动点E ,F 同时从O 点出发,点E 以1.5 cm /s 的速度沿ON 方向运动,点F 以2 cm /s 的速度沿OM 方向运动,EF 与OA 交于点C ,连接AE ,当点E 到达点B 时,点F 随之停止运动.设运动时间为t s (t >0).(1)当t =1 s 时,△EOF 与△ABO 是否相似?请说明理由; (2)在运动过程中,不论t 取何值时,总有EF⊥OA.为什么?(3)连接AF ,在运动过程中,是否存在某一时刻t ,使得S △AEF =12S 四边形AEOF ?若存在,请求出此时t 的值;若不存在,请说明理由.解:(1)相似.理由如下:当t =1,OE =1.5 cm ,OF =2 cm ,则OE∶OF=3∶4.∵AB∶OB=3∶4,∴OE ∶OF =AB∶OB.∵∠FOE=∠ABO=90°,∴△EOF ∽△ABO ;(2)无论t 为何值,在运动过程中,△EOF ∽△ABO ,则∠FEO=∠OAB.∵∠AOB+∠OAB=90°,则∠AOB+∠FEO=90°,∴∠OCE =90°,即EF⊥OA;(3)存在.∵S 四边形AEOF =S △AEF +S △EOF ,∴S △AEF =S △EOF .∵EF ⊥OA ,∴S △EOF =12EF ·OC ,S △AEF =12EF ·AC ,∴OC =AC ,∴EF 垂直平分OA ,∴OE =AE.∵OE=32t ,BE =4-32t ,在Rt △ABE 中,∵AB 2+BE 2=AE 2,∴32+(4-32t)2=94t 2,解得t =2512,∴当t =2512时,S △AEF =12S 四边形AEOF .7.(2016广东中考)如图,在同一平面上,两块斜边相等的直角三角板Rt △ABC 与Rt △ADC 拼在一起,使斜边AC 完全重合,且顶点B ,D 分别在AC 的两旁,∠ABC =∠ADC=90°,∠CAD =30°, AB =BC =4 cm .(1) 填空:AD =________cm ,DC =________cm ;(2) 点M ,N 分别从A 点,C 点同时以每秒1 cm 的速度等速出发,且分别在AD ,CB 上沿A→D, C →B 的方向运动,当N 点运动到B 点时,M ,N 两点同时停止运动,连接MN ,求当M ,N 点运动了x 秒时,点N 到AD 的距离;(用含x 的式子表示)(3) 在(2)的条件下,取DC 中点P ,连接MP ,NP ,设△PMN 的面积为y(cm 2),在整个运动过程中,△PMN 的面积y 存在最大值,请求出这个最大值. (参考数据:sin 75°=6+24,sin 15°=6-24)解:(1)26;2 2.(2)过点N 作NE⊥AD 于点E ,作NF⊥DC 的延长线于点F ,则NE =DF.∵∠ACD=60°,∠ACB =45°,∴∠NCF=75°,∠CNF =15°,∴FC =6-24x ,∴NE =DF =6-24x +22,∴点N 到AD 的距离为(6-24x +22)cm ;(3)∵sin 75°=FN NC ,FN =6+24x ,∵PD =CP =2,PF =6-24x +2,S △PMN =S 梯形FNMD-S △MPD -S △NPF ,∴y=12(6+24x +26-x)(6-24x +22)-12(26-x)×2-12(6-24x +2)·(6+24x).即y =2-68x 2+7-3-224x +23,即y 是x 的二次函数:∵2-68<0,∴当x =-7-3-2242×2-68=7-3-226-2时,y 最大值=66+73-102-3042-46.二次函数与几何图形【经典导例】【例4】(2016益阳中考)如图,顶点为A(3,1)的抛物线经过坐标原点O ,与x 轴交于点B. (1)求抛物线对应的二次函数的解析式;(2)过B 作OA 的平行线交y 轴于点C ,交抛物线于点D ,求证:△OCD≌△OAB; (3)在x 轴上找一点P ,使得△PCD 的周长最小,求出P 点的坐标.【解析】(1)可设顶点求解析式;(2)可先利用函数分别求出C ,D 坐标,从而利用SSS 来证明两三角形全等;(3)可利用轴对称求出C 点关于x 轴的对称点,再利用相似或直线C′D 与x 轴交点,求出P 点坐标.【学生解答】解:(1)∵抛物线顶点为A(3,1),设抛物线对应的二次函数的解析式为y =a(x -3)2+1,将原点坐标(0,0)代入解析式,得a =-13,∴抛物线对应的二次函数的解析式为:y =-13x 2+233x ;(2)将y =0代入y =-13x 2+233x 中,得B 点坐标为(23,0),设直线OA 对应的一次函数的解析式为y =kx ,将A(3,1)代入解析式y =kx 中,得k =33,∴直线OA 对应的一次函数的解析式为y =33x.∵BD ∥AO ,设直线BD 对应的一次函数的解析式为y =33x +b ,将B(23,0)代入y =33x +b 中,得b =-2,∴直线BD 对应的一次函数的解析式为y =33x -2.由⎩⎪⎨⎪⎧y =33x -2,y =-13x 2+233x ,得交点D 的坐标为(-3,-3),将x =0代入y =33x -2中,得C 点的坐标为(0,-2),由勾股定理,得:OA =2=OC ,AB =2=CD ,OB =23=OD.在△OAB 与△OCD 中,⎩⎪⎨⎪⎧OA =OC ,AB =CD ,OB =OD ,∴△OAB ≌△OCD ;(3)点C 关于x 轴的对称点C′的坐标为(0,2),则C′D 与x 轴的交点即为点P ,它使得△PCD 的周长最小.过点D 作DQ⊥y 轴,垂足为点Q ,则PO∥DQ,∴△C ′PO ∽△C ′DQ ,∴PO DQ =C ′O C ′Q ,即PO 3=25,∴PO =235,∴点P 的坐标为(-235,0).8.(2016张家口九中二模)如图,已知抛物线y =x 2+bx +c 与x 轴交于点A ,B ,AB =2,与y 轴交于点C ,对称轴为直线x =2.(1)求抛物线的函数解析式;(2)设P 为对称轴上一动点,求△APC 周长的最值.解:(1)∵AB=2,对称轴为直线x =2,∴A(1,0),B(3,0).∵抛物线y =x 2+bx +c 与x 轴交于点A ,B ,∴1,3是方程x 2+bx +c =0的两个根.由根与系数的关系,得1+3=-b ,1×3=c ,∴b =-4,c =3,∴抛物数的函数解析式为y =x 2-4x +3;(2)连接AC ,BC ,BC 交对称轴于点P ,连接PA.由(1)知抛物线的函数解析式为y =x 2-4x +3,点A ,B 的坐标分别为(1,0),(3,0),∴点C 的坐标为(0,3),∴BC =32+32=32,AC =32+12=10.∵点A ,B 关于对称轴x =2对称,∴PA =PB ,∴PA +PC =PB +PC ,此时,PB +PC =BC ,当P 点在对称轴上运动时,PA +PC 的最小值等于BC ,∴△APC 周长的最小值为AC +AP +PC =AC +BC =32+10.直角三角形、等腰三角形、特殊四边形性质问题【经典导例】【例5】(2016漳州中考)如图,抛物线y =x 2+bx +c 与x 轴交于点A 和点B(3,0),与 y 轴交于点C(0,3).(1)求抛物线的解析式;(2)若点M 是抛物线在x 轴下方上的动点,过点M 作MN//y 轴交直线BC 于点N ,求线MN 的最大值;(3)在(2)的条件下,当MN 取最大值时,在抛物线的对称轴l 上是否存在点P ,使△PBN 是等腰三角形?若存在,请直接写出所有点P 的坐标;若不存在,请说明理由.【解析】(1)可利用待定系数法求二次函数解析式;(2)要先求出MN 关于x 的函数解析式,利用函数性质求出MN 的最大值;(3)注意要分类讨论各种情况.【学生解答】(1)∵点B(3,0),C(0,3),在抛物线y =x 2+bx +c 上,∴抛物线的解析式y =x 2-4x +3;(2)令x 2-4x +3=0,则x 1=1,x 2=3,设直线BC 的解析式y =kx +b.∵点B(3,0),C(0,3)在直线BC 上,∴直线BC 的解析式y =-x +3,设N(x ,-x +3),则M(x ,x 2-4x +3)(1<x<3),∴MN =-x +3-(x 2-4x +3)=⎝ ⎛⎭⎪⎫x -322+94,∴当x =32时,MN 的最大值为94;(3)存在.所有点P 的坐标分别是:P 1⎝⎛⎭⎪⎫2,3+172,P 2⎝ ⎛⎭⎪⎫2,3-172,P 3⎝ ⎛⎭⎪⎫2,142,P 4⎝⎛⎭⎪⎫2,-142,P 5⎝ ⎛⎭⎪⎫2,12.9.(2016石家庄四十二中模拟)如图,已知二次函数的图象过点A(0,-3),B(3,3),对称轴为直线x =-12,点P 是抛物线上的一动点,过点P 分别作PM⊥x 轴于点M ,PN ⊥y 轴于点N ,在四边形PMON 上分别截取PC =13MP ,MD =13OM ,OE =13ON ,NF =13NP. (1)求此二次函数的解析式;(2)求证:以C ,D ,E ,F 为顶点的四边形CDEF 是平行四边形;(3)在抛物线上是否存在这样的点P ,使四边形CDEF 为矩形?若存在,请求出所有符合条件的P 点坐标;若不存在,请说明理由.解:(1)∵二次函数图象的对称轴为直线y =-12,∴设二次函数的解析式为y =a(x +12)2+k.∵点A(0,-3),B(3,3)在抛物线上,∴⎩⎪⎨⎪⎧14a +k =-3,a (3+12)2+k =3,解得⎩⎪⎨⎪⎧a =1,k =-134.∴抛物线的解解析式为y =(x +12)2-134,即y =x 2+x -3; (2)连接CD ,DE ,EF ,FC.∵PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,∴四边形PMON 为矩形,∴PM =ON ,PN =OM.∵PC=13MP ,OE =13ON ,∴PC =OE.∵MD=13OM ,NF =13NP ,∴MD =NF ,∴PF =OD.在△PCF 与△OED 中,⎩⎪⎨⎪⎧PC =OE ,∠FPC =∠DOE=90°,PF =OD.∴△PCF ≌△OED(SAS ),∴CF =DE ,同理可证:△CDM≌△EFN,∴CD =EF.∵CF=DE ,CD =EF ,∴四边形CDEF 是平行四边形;(3)假设存在这样的点P ,使四边形CDEF 为矩形,设矩形PMON 的边长PM =ON=m ,PN =OM =n ,则PC =13m ,MC =23m ,MD =13n ,PF =23n.若四边形CDEF 为矩形,则∠DCF=90°,易证△PCF∽△MDC,∴PC MD =PF MC ,即13m 13n =23n 23m ,化简得m 2=n 2,∴m =n ,即矩形PMON 为正方形,∴点P 为抛物线y =x 2+x-3与坐标象限角平分线y =x 或y =-x 的交点.将y =x 代入y =x 2+x -3,解得x 1=3,x 2=-3,∴P 1(3,3),P 2(-3,-3).将y =-x 代入y =x 2+x -3,解得x 1=-3,x 2=1,∴P 3(-3,3),P 4(1,-1),∴抛物线上存在点P ,使四边形CDEF 为矩形,这样的点有四个,在四个坐标象限内各一个,其坐标分别为:P 1(3,3),P 2(-3,-3),P 3(-3,3),P 4(1,-1).10.(2016唐山模拟)如图,边长为1的正方形ABCD 一边AD 在x 负半轴上,直线l :y =12x +2经过点B(x ,1)与x 轴,y 轴分别交于点H ,F ,抛物线y =-x 2+bx +c 的顶点E 在直线l 上.(1)求A ,D 两点的坐标及抛物线经过A ,D 两点时的解析式;(2)当抛物线的顶点E(m ,n)在直线l 上运动时,连接EA ,ED ,试求△EAD 的面积S 与m 之间的函数解析式,并写出m 的取值范围;(3)设抛物线与y 轴交于Q 点,当抛物线顶点E 在直线l 上运动时,以A ,C ,E ,Q 为顶点的四边形能否成为平行四边形?若能,求出E 点坐标;若不能,请说明理由.解:(1)∵直线l :y =12x +2经过点B(x ,1),∴1=12x +2,解得x =-2,∴B(-2,1),∴A(-2,0),D(-3,0).∵抛物线经过A ,D 两点,∴⎩⎪⎨⎪⎧-4-2b +c =0,-9-3b +c =0,解得,∴⎩⎪⎨⎪⎧b =-5,c =-6,∴抛物线经过A ,D 两点时的解析式为y =-x 2-5x -6;(2)连接EA ,ED ,∵顶点E(m ,n)在直线l 上,∴n =12m +2,∴S =12×1×(12m +2)=14m +1,即S=14m +1(m≠4);(3)如图,若以A ,C ,E ,Q 为顶点的四边形能成为平行四边形,则AC =EQ ,AC ∥EQ ,作EM∥y 轴交过Q 点平行于x 轴的直线于点M ,则EM⊥QM,△EMQ ≌△CDA ,∴QM =AD =1,∴点E 的横坐标为±1.∵顶点E在直线l 上,∴y =12×(-1)+2=32,或y =12×1+2=52,∴E(-1,32)或(1,52).又∵当点E 坐标为(1,52)时,以A ,C ,E ,Q 为顶点的四边形不能成为平行四边形,∴E 点坐标为(-1,32).11.(2016潍坊中考)如图,已知抛物线y =13x 2+bx +c 经过△ABC 的三个顶点,其中点A(0,1),点B(-9,10),AC ∥x 轴,点P 是直线AC 下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P 且与y 轴平行的直线l 与直线AB ,AC 分别交于点E ,F ,当四边形AECP 的面积最大时,求点P 的坐标;(3)当点P 为抛物线的顶点时,在直线AC 上是否存在点Q ,使得以C ,P ,Q 为顶点的三角形与△ABC 相似,若存在,求出点Q 的坐标;若不存在,请说明理由.解:(1)把点A(0,1),B(-9,10)的坐标代入y =13x 2+bx +c ,得⎩⎪⎨⎪⎧1=c ,10=13×(-9)2-9b +c.解得⎩⎪⎨⎪⎧b =2,c =1.所以,抛物线的解析式是y =13x 2+2x +1;(2)∵AC∥x 轴,A(0,1),由13x 2+2x +1=1,解得x 1=-6,x 2=0,∴C(-6,1),设直线AB 的解析式是y =kx +b(k≠0),由⎩⎪⎨⎪⎧1=b ,10=-9k +b.解得⎩⎪⎨⎪⎧k =-1,b =1.则直线AB 的解析式是y =-x +1.设点P 的坐标为(m ,13m 2+2m +1),则点E 为坐标为(m ,-m +1).则EP =-m +1-(13m 2+2m +1)=-13m 2-3m.∵AC⊥EP,AC =6,∴S 四边形AECP =S △AEC +S △APC =12AC ·EF +12AC ·PF =12AC ·(EF +PF)=12AC ·EP =12×6×(-13m 2-3m)=-m 2-9m =-(m +92)2+814.又∵-6<m<0,则当m =-94时,四边形AECP 面积的最大值是814,此时点P 的坐标是(-92,-54);(3)由y =13x 2+2x +1=13(x +3)2-2,得顶点P 的坐标是(-3,-2),此时PF =y F -y P =3,CF =x F-x C =3,则在Rt △CFP 中,PF =CF ,∴∠PCF =45°,同理可求∠EAF=45°,∴∠PCF =∠EAF,∴在直线AC 上存在满足条件的点Q ,使△CPQ 1∽△ABC 或△CQ 2P ∽△ABC.可求AB =92,AC =6,CP =32,①当△CPQ 1∽△ABC时,设Q 1(t 1,1),由CQ 1AC =CP AB ,得t 1+66=3292,解得t 1=-4.②当△CQ 2P ∽△ABC 时,设Q 2(t 2,1),由CQ 2AB =CPAC ,得t 2+692=326,解得t 2=3.综上,满足条件的点Q 有两个,坐标分别是Q 1(-4,1)或Q 2(3,1).。
2017年河北省中考数学试卷含答案

数学试卷 第1页(共20页) 数学试卷 第2页(共20页)绝密★启用前河北省2017年初中毕业生升学文化课考试数 学(本试卷满分120分,考试时间120分钟)第Ⅰ卷(选择题 共42分)一、选择题(本大题共16小题,1~10小题,每小题3分,11~16小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下列运算结果为正数的是( ) A .2(3)-B .32-÷C .0( 2 017)⨯-D .23- 2.把0.0813写成10n a ⨯(110a ≤<,n 为整数)的形式,则a 为( ) A .1B .2-C .0.813D .8.13 3.用量角器测量MON ∠的度数,下列操作正确的是( )ABCD4.23222333m n ⨯⨯⨯=+++个个……( )A .23n mB .23m nC .32m nD .23m n5.图1和图2中所有的小正方形都全等.将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( )A .①B .②C .③D .④ 6.如图为张小亮的答卷,他的得分应是( )A .100分B .80分C .60分D .40分7.若ABC △的每条边长增加各自的10%得'''A B C △,则'B ∠的度数与其对应角B ∠的度数相比 ( ) A .增加了10%B .减少了10%C .增加了(110)+%D .没有改变8.如图是由相同的小正方体木块粘在一起的几何体,它的主视图是()ABCD9.求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD 是菱形,对角线AC ,BD 交于点O . 求证:AC BD ⊥.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共20页) 数学试卷 第4页(共20页)以下是排乱的证明过程: ①又BO DO ⊥,②AO BD ∴⊥即AC BD ⊥. ③四边形ABCD 是菱形, ④=AB AD ∴. 证明步骤正确的顺序是( )A .③→②→①→④B .③→④→①→②C .①→②→④→③D .①→④→③→②10.如图,码头A 在码头B 的正西方向,甲、乙两船分别从A 、B 同时出发,并以等速驶向某海域.甲的航向是北偏东35,为避免行进中甲、乙相撞,则乙的航向不能是 ( )A .北偏东55 B .北偏西55 C .北偏东35D .北偏西3511.如图是边长为10 cm 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm )不正确的是( )ABCD12.如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是 ( )A.446+ B .04446++= C.46=D.1446-= 13.若321x x -=-( )11x +-,则( )中的数是 ( ) A .1-B .2-C .3-D 任意实数.14.甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图.比较5月份两组家庭用水量的中位数,下列说法正确的是( ) A .甲组比乙组大B .甲、乙两组相同C .乙组比甲组大D .无法判断15.如图,若抛物线23y x =-+与x 轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k ,则反比例函数ky x=(0)x >的图象是( )ABC D16.已知正方形MNOK 和正六边形ABCDEF 边长均为1,把正方形放在正六边形中,使OK 边与AB 边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C 顺时针旋转,使MN边与CD 边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B ,M 间的距离可能是( )A .1.4B .1.1C .0.8D .0.5甲组12户家庭用水量统计表数学试卷 第5页(共20页) 数学试卷 第6页(共20页)第Ⅱ卷(非选择题 共78分)二、填空题(本大题共3小题,共10分.17,18小题,每小题3分;共19小题共4分.请把答案填写在题中的横线上)17.如图,,A B 两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C ,连接,CA CB ,分别延长到点,M N ,使AM AC =,BN BC =,测得200 m MN =,则,A B 间的距离为 m .18.如图,依据尺规作图的痕迹,计算=α∠ . 19.对于实数p ,q ,我们用符号}{min ,p q 表示p ,q 两数中较小的数,如}{min 1 ,21=. 因此,{min = ; 若}{22min (1),1x x -=,则x = .三、解答题(本大题共7个小题,共68分.解答应写出文字说明、证明过程或演算步骤) 20.(本小题满分8分)在一条不完整的数轴上从左到右有点,,A B C 其中2AB =,1BC =,如图所示.设点,,A B C 所对应数的和是p .(1)若以B 为原点,写出点,A C 所对应的数,并计算p 的值;若以C 为原点,p 又是多少?(2)若原点O 在图中数轴上点C 的右边,且28CO =,求p .21.(本小题满分9分)编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分.如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;(3)最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.22.(本小题满分9分)发现 任意五个连续整数的平方和是5的倍数. 验证 (1)22222(1)0123-++++的结果是5的几倍?(2)设五个连续整数的中间一个为n ,写出它们的平方和,并说明是5的倍数. 延伸 任意三个连续整数的平方和被3除的余数是几呢?请写出理由.23.(本小题满分9分)如图,16AB =,O 为AB 中点,点C 在线段OB 上(不与点,O B 重合),将OC 绕点O 逆时针旋转270后得到扇形COD ,,AP BQ 分别切优弧CD 于点,P Q ,且点,P Q 在AB 异侧,连接OP .(1)求证:AP BQ =;(2)当BQ =时,求QD 的长(结果保留π);毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页(共20页) 数学试卷 第8页(共20页)(3)若APO △的外心在扇形COD 的内部,求OC 的取值范围.24.(本小题满分10分)如图,直角坐标系xOy 中,(0,5)A ,直线5x =-与x 轴交于点D ,直线33988y x =--与x 轴及直线5x =-分别交于点,C E .点,B E 关于x 轴对称,连接AB .(1)求点,C E 的坐标及直线AB 的解析式;(2)设面积的和CDE ABDO S S S ∆=+四边形,求S 的值;(3)在求(2)中S 时,嘉琪有个想法:“将CDE △沿x 轴翻折到CDB △的位置,而CDB △与四边形ABDO 拼接后可看成AOC △,这样求S 便转化为直接求AOC △的面积不更快捷吗?”但大家经反复验算,发现AOC S S ≠△,请通过计算解释他的想法错在哪里.25.(本小题满分11分)平面内,如图,在□ABCD 中,10AB =,15AD =,4tan 3A =.点P 为AD 边上任意一点,连接PB ,将PB 绕点P 逆时针旋转90得到线段PQ .(1)当10DPQ =∠时,求APB ∠的大小;(2)当tan :tan 3:2ABP A =∠时,求点Q 与点B 间的距离(结果保留根号); (3)若点Q 恰好落在□ABCD 的边所在的直线上,直接写出PB 旋转到PQ 所扫过的面积(结果保留π).26.(本小题满分12分)某厂按用户的月需求量x (件)完成一种产品的生产,其中0x >.每件的售价为18万元,每件的成本y (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x (件)成反比.经市场调研发现,月需求量x 与月份n (n 为整数,112n ≤≤)符合关系式2229(3)x n kn k =-++(k 为常数),且得到了表中的数据.(1)求y 与x 满足的关系式,请说明一件产品的利润能否是12万元; (2)求k ,并推断是否存在某个月既无盈利也不亏损;(3)在这一年12个月中,若第m 个月和第(1)m +个月的利润相差最大,求m .数学试卷 第9页(共20页) 数学试卷 第10页(共20页)河北省2017年初中毕业生升学文化课考试数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】239=(-);3322-÷=-;020170⨯=(-);231-=-,所以运算结果为正数的是2(3)-,故选A 。
2017年河北省中考数学试卷Word版含问题详解下载
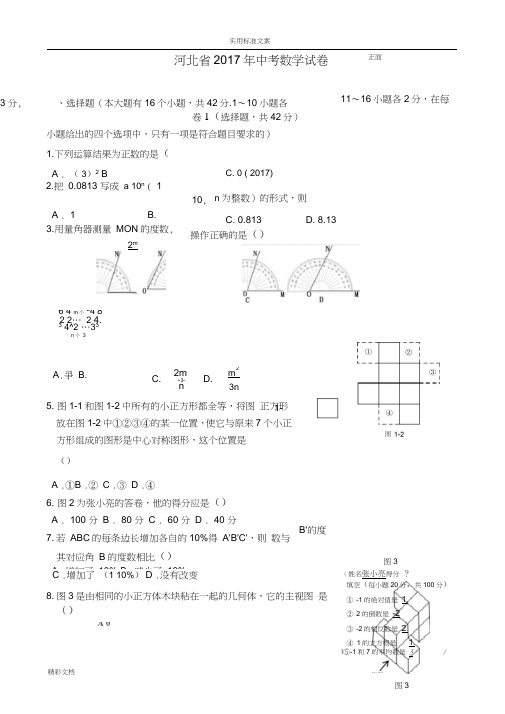
河北省2017年中考数学试卷卷1(选择题,共42分)小题给出的四个选项中,只有一项是符合题目要求的) 1.下列运算结果为正数的是( A . ( 3)2 BC .增加了 (1 10%)D .没有改变8. 图3是由相同的小正方体木块粘在一起的几何体,它的主视图 是()、选择题(本大题有16个小题,共42分.1〜10小题各3 分,11〜16小题各2分,在每C. 0 ( 2017)2.把 0.0813 写成 a 10n ( 1 10, n 为整数)的形式,则A . 1 B.3.用量角器测量 MON 的度数,C. 0.813操作正确的是()D. 8.136 4 m 个 24 8 2 2… 2 4. 34^2 (33)n 个 3A .爭 B.2m 3nC.2m ~3- nD.2m3n5. 图1-1和图1-2中所有的小正方形都全等,将图 正方形放在图1-2中①②③④的某一位置,使它与原来 7个小正方形组成的图形是中心对称图形,这个位置是 ()A .①B .②C .③D .④6. 图2为张小亮的答卷,他的得分应是() A . 100 分 B . 80 分 C . 60 分 D . 40 分7. 若 ABC 的每条边长增加各自的10%得 A'B'C',则 数与其对应角 B 的度数相比()A .增加了 10%B .减少了 10% 1-1 B'的度A 0(姓名张小亮得分 ?填空(每小题20分,共100分)① -1的绝对值是 1. ② 2的倒数是 -2③ -2的相反数是 2. ④ 1的立方根是 1.I ⑤-1和7的平均数是 3/图3正面9. 求证:菱形的两条对角线互相垂直.已知:如图4,四边形ABCD 是菱形,对角线AC , 求证:AC BD .以下是排乱的证明过程:①又BO DO ,② ••• AO BD ,即 AC BD . ③ •••四边形ABCD 是菱形, ④ 二 AB AD .证明步骤正确的顺序是()A .③-②-①-④ BC .①-②-④-③ D10. 如图5,码头A 在码头B 的正西方向,甲、乙两船分别从A 、B 同时出发,并以等速驶向某海域,甲的航向是北偏东 35 ,为避免行 进中甲、乙相撞,则乙的航向不能是()A.北偏东55B.北偏西55C.北偏东35D.北偏西3511. 图6是边长为10cm 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪 线长度所标的数据(单位:cm )不正确的()12. 图7是国际数学日当天淇淇和嘉嘉的微信对话,根据对话 内容,下列选项错误.的是()ABCDC淇淇嘉嘉,咱俩玩一个数学 ,游戏,好吗?好啊!玩什么游戏? 淇淇了 --------------在44 4=6等号的左边添加合适的数学运算J 符号,使等式成立..③-④-①-② .①-④-③-② BD 交于点0 . B . 4 40 406434 4 6 D . 4 1 4 413.若()—,则(x 1x 1A . 1B. 2)中的数是()C. 3D.任意实数{图4A . 4 4.46实用标准文案14.甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图 8, 乙组12户家庭用水量统计图比较5月份两组家庭用水量的中位数,下列说法正确的是用水量(吨)4 5 6 9 户数4521D •无法判断甲组12户家庭用水量统计图8实用标准文案A •甲组比乙组大 B.甲、乙两组相同 C •乙组比甲组大15.如图9,若抛物线yx 2 3与x 轴围成封闭区域(边界除外) 内整点(点的横、纵坐标都是整数)的个数为k ,则反比例函数y k ( x 0)x的图象是()16.已知正方形MNOK 和正六边形ABCDEF 边长均为1,把正方形放在正六边形中,使 0K 边与AB 边重合,如图10所示•按下列步骤操作: 将正方形在正六边形中绕点 B 顺时针旋转,使KM 边与BC 边重 合,完成第一次旋转;再绕点C 顺时针旋转,使MN 边与CD 边重 合,完成第二次旋转;……在这样连续 6次旋转的过程中,点B , M 间的距离可能是()A . 1.4B . 1.1C . 0.8D . 0.5第U 卷(共78分)、填空题(本大题有3个小题,共10分.17〜18小题各3分;19小题有2个空,每空2分. 把答案写在题中横线上)17.如图11, A ,B 两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点 C,连接 CA CB 分别延长到点M, N,使AM=ACBN=BC 测得MN=200m 则A , B 间的距离为 m E DA(Q) B(K)图10实用标准文案19. 对于实数p , q ,我们用符号min p, q 表示p , q 两数中较小的数,如min 1, 2 1.因此,min . 2,.3 _______________若 min (x 1)2, x 2 1,则 x三、解答题(本大题有7个小题,共68分.解答应写出文字说明、证明过程或演算步骤) 20. (本小题满分8分)在一条不完整的数轴上从左到右有点 A, B, C,其中AB=2 BC=1如图13所示.设点A , B, C 所对应数的和是p.(1)若以B 为原点,写出点A, C 所对应的数,并计算p 的值;(2) 若原点0在图13中数轴上点C 的右边,且CO=28求p.21. (本小题满分9分)编号为1〜5号的5名学生进行定点投篮,规定每人投 5次,每命中1次记1分,没有命 中记0分.图14是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样 记分规定投了 5次,其命中率为40%.精彩文档(1) 求第6号学生的积分,并将图14增补为这6名学生积分的条形统计图;(2) 在这6名学生中,随机选一名学生,求选上命中率高于 50%勺学生的概率;18.如图12,依据尺规作图的痕迹,计算/a =若以C 为原点,p 又是多少?a68°rCB图12AB C 图13(3) 最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.22. (本小题满分9分)发现任意五个连续整数的平方和是5的倍数.验证⑴ 1 2 02 12 22 32的结果是5的几倍?(2) 设五个连续整数的中间一个为n,写出它们的平方和,并说明是5的倍数.延伸任意三个连续整数的平方和被3除的余数是几呢?请写出理由.23. (本小题满分9分)如图15, AB=16,0为AB中点,点C在线段OB上(不与点O, B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,B①别切优弧Cb于点P,Q,且点P,Q在AB异侧,连接OP.(1) 求证:AP=BQ(2) 当BQ斗3时,求&D的长(结果保留町;(3) 若厶APO勺外心在扇形COD勺内部,求OC的取值范围.24. (本小题满分10分)如图16,直角坐标系xOy中,A(0, 5),直线x=-5与x轴交于点D,直线y |x 39与8 8x轴及直线x=-5分别交于点C, E.点B,E关于x轴对称,连接AB.(1) 求点C, E的坐标及直线AB的解析式;(2) 设面积的和S S CDE S四边形ABDO,求S的值;(3) 在求⑵ 中S时,嘉琪有个想法:“将厶CDE沿x轴翻折到厶CDB的位置,而△ CDB与四边形ABDO拼接后可看成△ AOC这样求S便转化为直接求厶AOC勺面积不更快捷吗?”但大家经反复验算,发现S^OC S,请通过计算解释他的想法错在哪里.25. (本小题满分11分)平面内,如图17,在口ABCDK AB 10 , AD 15 , ta nA 4•点P为AD边上任意一3点,连接PB,将PB绕点P逆时针旋转90得到线段PQ .(1)当DPQ 10时,求APB的大小;(2)当tan ABP:tanA 3: 2时,求点Q与点B间的距离(结果保留根号);(3)若点Q恰好落在口ABCD勺边所在的直线上,直接写出PB旋转到PQ所扫过的面积(结果保留B图17备用图26. (本小题满分12分)某厂按用户的月需求量x (件)完成一种产品的生产,其中x 0 •每件的售价为18万元,每件的成本y (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x (件)成反比•经市场调研发现,月需求量x与月份n (n为整数,1 n 12 )符合关系式x 2n2 2kn 9(k 3)(k 为常数),且得到了表中的数据.(2)求k,并推断是否存在某个月既无盈利也不亏损;(3)在这一年12个月中,若第m个月和第(m 1)个月的利润相差大,求m .2017年泗北省初屮毕业主升学文化课考试数学试题参考答案说孙「在阅卷过程中*如考生还畜其它正确解法.可参照评廿参考按步秫酌博蛤分-2”坚持每JS 评阅到底的原则.肖考生的解答在猱一步出现镐谓.影响TJ&ffiSS 分时, 如集该步以后的解答未改蛮谴F 的内容和XA.同视总响的程度决定后面那分的 给分*但不掲超过后堆部分应给分数的一半;如果谡一步馬而的解書有綾严重的措 «<就不给分.3・廉善右端所注分戳n 護示皿确做到这一步应得的累加弁散一只给整数分St 一“ fiBE < +大题好16个小題.*42分-】小理各』分.1)-16小JS 各2分)二 填空HH 本大題召3个小施‘儿10分.17-18^58^3^: 19小嗨打2亍空.侮空2分】17, tOO1& 5619. 』=.解菩題(水大題有7个小1S.共6S5I )<3) p = (-2g7・2)*J2&-D + (-鱗:(!) &兮的秋分为5«40%x1 = 2龙分).・5——【劲丁这6名学生朝 有4名学生的命中华1号2号3号46号京临览号 ・・丹命中率ifii 于50瞄的学牛} =4-…&分图I<1)以B 为原点・点孰匚分别对应-2. I.4 + DU21.;Jn U&分4分(3)T S出现的次数眾务•二这个金数是3 .................. ......■/ 7豁学工积分的众散址乩化7环询中3空或没有命中./- 1的积分是3分或。
河北省2017年中考数学试题含答案

河北省2017年中考数学试题及答案
一、选择题:本大题共16个小题,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列运算结果为正数的是()
5.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()
A.①B.②C.③D.④6.如图为张小亮的答卷,他的得分应是()
A.100分B.80分C.60分D.40分
&
11.如图是边长为10的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:)不正确的()
12.如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是()
14.甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,比较5月份两组家庭用水量的中位数,下列说法正确的是()
A.甲组比乙组大B.甲、乙两组相同C.乙组比甲组大 D.无法判断
A.1.4 B.1.1 C.0.8 D.0.5
二、填空题(本题共有3个小题,满分10分,将答案填在答题纸上)
]
答案:一、选择题
一、填空题
17.100 18. 560 19. ;2或-1 .
三、解答题。
(完整版)17-2017年河北省中考数学试卷

2017年河北省中考数学试卷一、选择题(本大题共16小题,共42分。
1~10小题各3分,11~16小题各2分,小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)下列运算结果为正数的是()A.(﹣3)2 B.﹣3÷2 C.0×(﹣2017)D.2﹣32.(3分)把0.0813写成a×10n(1≤a<10,n为整数)的形式,则a为()A.1 B.﹣2 C.0.813 D.8.133.(3分)用量角器测得∠MON的度数,下列操作正确的是()A.B.C.D.4.(3分)=()A.B.C.D.5.(3分)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()A.①B.②C.③D.④6.(3分)如图为张小亮的答卷,他的得分应是()A.100分B.80分C.60分D.40分7.(3分)若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比()A.增加了10% B.减少了10% C.增加了(1+10%)D.没有改变8.(3分)如图是由相同的小正方体木块粘在一起的几何体,它的主视图是()A.B.C.D.9.(3分)求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.求证:AC⊥BD.以下是排乱的证明过程:①又BO=DO;②∴AO⊥BD,即AC⊥BD;③∵四边形ABCD是菱形;④∴AB=AD.证明步骤正确的顺序是()A.③→②→①→④B.③→④→①→②C.①→②→④→③D.①→④→③→②10.(3分)如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能..是()A.北偏东55°B.北偏西55°C.北偏东35°D.北偏西35°11.(2分)如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确...的是()A. B. C.D.12.(2分)如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误..的是()A.4+4﹣=6 B.4+40+40=6 C.4+=6 D.4﹣1÷+4=613.(2分)若= +,则中的数是()A.﹣1 B.﹣2 C.﹣3 D.任意实数14.(2分)甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,甲组12户家庭用水量统计表用水量(吨)4569户数4521比较5月份两组家庭用水量的中位数,下列说法正确的是()A.甲组比乙组大B.甲、乙两组相同C.乙组比甲组大D.无法判断15.(2分)如图,若抛物线y=﹣x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=(x>0)的图象是()A.B.C.D.16.(2分)已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是()A.1.4 B.1.1 C.0.8 D.0.5二、填空题(本大题共3小题,共10分。
河北省2017年中考数学真题试题(精品解析)

河北省2017年中考数学真题试题第Ⅰ卷(共42分)一、选择题:本大题共16个小题,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.下列运算结果为正数的是( ) A .2(3)- B .32-÷ C .0(2017)⨯- D .23-【答案】A. 【解析】试题分析:因为负数的偶数次方是正数,异号两数相除商为负,零乘以任何数都等于0,较小的数减去较大的数差为负数,故答案选A.考点:乘方,有理数的除法,有理数的乘法,有理数的减法.2.把0.0813写成10na ⨯(110a ≤<,n 为整数)的形式,则a 为( ) A .1 B .2-C .0.813D .8.13【答案】D. 【解析】试题分析:科学记数法中,a 的整数位数是一位,故答案选D. 考点:科学记数法.3.用量角器测量MON ∠的度数,操作正确的是( )【答案】C.考点:角的比较.4.23222333m n ⨯⨯⨯=+++个个……( )A .23n mB .23m nC .32m nD .23m n【答案】B. 【解析】试题分析:m 个2相乘表示为2m ,n 个3相加表示为3n ,故答案选B. 考点:有理数的乘方.5.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( )A .①B .②C .③D .④【答案】C.考点:中心对称图形.6.如图为张小亮的答卷,他的得分应是( )A .100分B .80分C .60分D .40分【答案】B.考点:绝对值,倒数,相反数,立方根,平均数.7.若ABC ∆的每条边长增加各自的10%得'''A B C ∆,则'B ∠的度数与其对应角B ∠的度数相比( ) A .增加了10% B .减少了10%C .增加了(110%)+D .没有改变【答案】D. 【解析】试题分析:角的度数与角的边的大小没有关系,故答案选D. 考点:角的比较.8.如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( )【答案】A.【解析】试题分析:主视图从图形的正面观察得到的图形,注意后排左上角的那个小正方体,故答案选A. 考点:三视图.9.求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD 是菱形,对角线AC ,BD 交于点O . 求证:AC BD ⊥.以下是排乱的证明过程:①又BO DO =, ②∴AO BD ⊥,即AC BD ⊥. ③∵四边形ABCD 是菱形,④∴AB AD =.证明步骤正确的顺序是( )A .③→②→①→④B .③→④→①→②C .①→②→④→③D .①→④→③→②【答案】D.考点:菱形的性质,等腰三角形的性质.10.如图,码头A 在码头B 的正西方向,甲、乙两船分别从A 、B 同时出发,并以等速驶向某海域,甲的航向是北偏东35︒,为避免行进中甲、乙相撞,则乙的航向不能是( ) A .北偏东55︒B .北偏西55︒C .北偏东35︒D .北偏西35︒【答案】D.考点:方向角.11.如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的( )【答案】A.【解析】试题分析:正方形的对角线的长是14.14,所以正方形内部的每一个点,到正方形的顶点的距离都有小于14.14,故答案选A.考点:正方形的性质,勾股定理.12.如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )A .446+=B .04446++= C .46=D .1446-=【答案】D.考点:算术平方根,立方根,0指数幂,负数指数幂. 13.若321x x -=-( )11x +-,则( )中的数是( ) A .1- B .2-C .3-D .任意实数【答案】B. 【解析】 试题分析:因为321222111x xx x x ---==----,故答案选B. 考点:分式的加减.14.甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,比较5月份两组家庭用水量的中位数,下列说法正确的是( )A .甲组比乙组大B .甲、乙两组相同C .乙组比甲组大D .无法判断【答案】B.考点:中位数,扇形统计图.15.如图,若抛物线23y x =-+与x 轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k ,则反比例函数ky x=(0x >)的图象是( )【答案】D. 【解析】试题分析:因为在封闭区域内的整数点的个数是4,所以k =4,故答案选D. 考点:二次函数的图象,反比例函数的图象.16.已知正方形MNOK 和正六边形ABCDEF 边长均为1,把正方形放在正六边形中,使OK 边与AB 边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B 顺时针旋转,使KM 边与BC 边重合,完成第一次旋转;再绕点C 顺时针旋转,使MN 边与CD 边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B ,M 间的距离可能是( )A .1.4B .1.1C .0.8D .0.5第Ⅱ卷(共78分)【答案】C.考点:正多边形的有关计算.二、填空题(本题共有3个小题,满分10分,将答案填在答题纸上)17.如图,A ,B 两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C ,连接CA ,CB ,分别延长到点M ,N ,使AM AC =,BN BC =,测得200MN m =,则A ,B 间的距离为m .【答案】100.考点:三角形的中位线定理.18.如图,依据尺规作图的痕迹,计算α∠=°.【答案】56.【解析】试题分析:如图,根据作图痕迹可知,GH垂直平分AC,AG平分∠CAD. ∵四边形ABCD是矩形,∴AD∥BC,∴∠CAD=∠ABC=68°。
河北中考数学试题及答案
河北中考数学试题及答案2017年河北中考数学试题及答案导语:数学题是透过抽象化和逻辑推理的使用,由计数、计算、量度和对物体形状及运动的观察中产生的。
下面为大家带来了2017年河北中考数学试题及答案,欢迎大家参考阅读!2017年河北中考数学试题及答案本试卷分卷I和卷II两部分;卷I为选择题,卷II为非选择题本试卷总分120分,考试时间120分钟、卷I(选择题,共42分)一、选择题(本大题有16个小题,共42分、1~10小题各3分,11~16小题各2分、在每小题给出的四个选项中,只有一项是符合题目要求的)1、计算:―(―1)=()A、±1B、―2C、―1D、1答案:D解析:利用“负负得正”的口诀,就可以解题。
知识点:有理数的运算2、计算正确的是()A、(―5)0=0B、x2+x3=x5C、(ab2)3=a2b5D、2a2a―1=2a答案:D解析:除0以外的任何数的0次幂都等于1,故A项错误;x2+x3的结果不是指数相加,故B项错误;(ab2)3的结果是括号里的指数和外面的指数都相乘,结果是a3b6,故C项错误;2a2a―1的结果是2不变,指数相加,正好是2a。
知识点:x0=0(x≠0);(ambn)p=ampbnp;aman=am+n3、下列图形中,既是轴对称图形,又是中心对称图形的是()ABCD答案:A解析:先根据轴对称图形,排除C、D两项,再根据中心对称,排除B项。
知识点:轴对称,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形;中心对称,如果把一个图形绕某一点旋转180度后能与自身重合,这个图形就是中心对称图形。
4、下列运算结果为x―1的是()A、B、C、D、答案:B解析:挨个算就可以了,A项结果为――,B项的结果为x―1,C项的结果为――D项的结果为x+1。
知识点:(x+1)(x―1)=x2―1;(x+1)2=x2+2x+1,(x―1)2=x2―2x+1。
5、若k≠0,b<0,则y=kx+b的图象可能是()答案:B解析:一次函数,k≠0,不可能与x轴平行,排除D选项;b<0,说明过3、4象限,排除A、C选项。
2017年河北省中考数学试卷(Word编辑版)
2017年河北省中考数学试卷一、选择题(本大题共16小题,共42分。
1~10小题各3分,11~16小题各2分,小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)下列运算结果为正数的是()A.(﹣3)2B.﹣3÷2 C.0×(﹣2017)D.2﹣32.(3分)把0.0813写成a×10n(1≤a<10,n为整数)的形式,则a为()A.1 B.﹣2 C.0.813 D.8.133.(3分)用量角器测得∠MON的度数,下列操作正确的是()A.B.C.D.4.(3分)=()A.B.C.D.5.(3分)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()A.①B.②C.③D.④6.(3分)如图为张小亮的答卷,他的得分应是()A.100分B.80分C.60分D.40分7.(3分)若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比()A.增加了10% B.减少了10% C.增加了(1+10%)D.没有改变8.(3分)如图是由相同的小正方体木块粘在一起的几何体,它的主视图是()A.B.C.D.9.(3分)求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.求证:AC⊥BD.以下是排乱的证明过程:①又BO=DO;②∴AO⊥BD,即AC⊥BD;③∵四边形ABCD是菱形;④∴AB=AD.证明步骤正确的顺序是()A.③→②→①→④B.③→④→①→②C.①→②→④→③D.①→④→③→②10.(3分)如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能..是()A.北偏东55°B.北偏西55°C.北偏东35°D.北偏西35°11.(2分)如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确...的是()A. B. C.D.12.(2分)如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误..的是()A.4+4﹣=6 B.4+40+40=6 C.4+=6 D.4﹣1÷+4=613.(2分)若= +,则中的数是()A.﹣1 B.﹣2 C.﹣3 D.任意实数14.(2分)甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,甲组12户家庭用水量统计表比较5月份两组家庭用水量的中位数,下列说法正确的是()A.甲组比乙组大B.甲、乙两组相同C.乙组比甲组大D.无法判断15.(2分)如图,若抛物线y=﹣x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=(x>0)的图象是()A.B.C.D.16.(2分)已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是()A.1.4 B.1.1 C.0.8 D.0.5二、填空题(本大题共3小题,共10分。
考数学第三编综合专题闯关篇题型二解答题重难点突破专题一猜想证明与探究试题
(河北专版)2017中考数学第三编综合专题闯关篇题型二解答题重难点突破专题一猜想证明与探究试题题型二解答题重难点突破专题一猜想证明与探究1 •猜想与证明问题河北中考近8年共考查8次,为每年必考内容,都是以解答题的形式出现,分值为9—14分.2•考查类型:(1)与图形的位似有关,探究两条边之间的关系,此类题在2012年考查过一次,主要是利用三角形的性质来解决,分值为9分;(2)与尺规作图有关,利用正方形的性质探究边与边之间的关系,其中有一问会涉及到如何作图,此题在2011年考查过一次,分值为9分;(3)与旋转有关,主要是利用旋转前后的性质,分别涉及到直线和正方形,在2010年和2009年考查过,分值为10分,在2013年考查过,分值为11分;(4)折叠问题主要是折叠过程中对图形变化具体情况的分析,此题在2014年考查过,分值为11分;与图形的折叠、平移有关,2015年考查,分值14分,平移问题主要是用到了平移前后的性质和三角形的性质,探究边与边之间的关系,在2008年考查过,分值为10分.2016年在此题型上来考查.预计2017年河北中考很有可能考查此内容,在训练时多做涉及利用三角形全等、三角形相似等有关的知识的综合题.,中考重难点突破)与图形旋转有关的证明【经典导例】【例1】(2010河北中考)在图①至图③中,直线MN与线段AB相交于点O, / 1 = 7 2= 45(1) 如图①,若Ad OB请写出AC与BD的数量关系和位置关系;⑵将图①中的MN绕点O顺时针旋转得到图②,其中AO OB.求证:AC= BD AC丄BD(3)将图②中的BDOB拉长为AO的k倍得到图③,求AC的值.【学生解答】(1)AO = BD, AOL BD (2)如图②,过点 B 作BE// CA 交DO 于点E ,「./ ACO=Z BEO 又•/ AO= OB / AOC=Z BOE 二△ AOC^A BOE 二 AC= BE.又••律 1= 45°, A / ACO=Z BEO= 135° . /-Z DEB= 45°, v/ 2= 45°, /• BE = BD Z EBD= 90° . /• AC = BD.延长 AC 交 DB 的延长线于点 F , •/ BE / AC /•/ AFD= 90° , /• AC 丄 BD【方法指导】(1)在探索两线段的数量关系时常以三角形全等或者相似为工具,由对应角的关系得到两线段相 等或者对应成比例•有时需先进行等量代换,将两线段放到相似三角形或全等三角形中,若出现直角三角形,则 利用直角三角形的性质求解.(2) 两线段的位置关系通常为平行或垂直•先观察图形,根据图形先推测两线段的位置关系是平行或垂直•若 平行,则常通过以下方法进行证解:①平行线的判定定理;②平行四边形对边平行;③三角形中位线性质等•若 垂直,则可考虑以下途径:①证明两线段所在直线夹角为 90°;②两线段是矩形的邻边;③两线段是菱形的对角线;④勾股定理的逆定理;⑤利用等腰三角形三线合一的性质等方式证明.1. (2015重庆中考)在厶ABC 中,AB= AC / A = 60°,点 D 是线段 BC 的中点,/ EDM 120°, DE 与线段 AB 相交于点E , DF 与线段AC(或AC 的延长线)相交于点F.(1) 如图1,若DF 丄AC 垂足为点 F , AB= 4,求BE 的长;1(2) 如图2,将(1)中的/ EDF 绕点D 顺时针旋 转一定的角度,DF 仍与线段 AC 相交于点F.求证:BE + CF =- AB;(3) 如图3,将(2)中的/ EDF 继续绕点 D 顺时针旋转一定的角度,使 DF 与线段AC 的延长线交与点 F ,作DN 丄AC 于点 N,若 DN = FN,求证:BE + CF = :3(BE — CF).解:⑴ 由四边形AEDF 的内角和为360 °,可知DEL AB 故BE = 1; (2)取AB 的中点G,连接DG.易证:DG 为 △ ABC 的中位线,故 DG = DC , / BGD = ZC = 60 ° ,又四边形 AEDF 的对角互补,故/ GED =1Z DFC /.^ DEG2A DFC 故 EG^ CF.A BE + CF = BE + EG^ BG^ gAB; (3)取 AB 的中点 G,连接 DG 同(2),易证 1⑶如图③,过点 B 作 BE// CA 交 DO 于点 E , /Z BEO=Z ACO 又 vZ BO =Z AOC /•△ BE BO Bo® AOC /AAC = A O 又v OB= kAO,由(2)的方法易得BDBE= BD 二 AC= «△DEG2A DFC 故E* CF,故BE- CF= BE— EG^ Bd ^AB.设CN= x,在Rt^ DCN中 , CD= 2x , DN= 3x ,在Rt△DFN 中,NF= DN= 3x ,故EG^ CF= ( 3 —1)x.BE = BG+ EG^ DC+ CF= 2x+ ( 3 —1)x = ( 3 + 1)x.故BE+ CF= (3+ 1)x + ( 3—1)x = 2 3x. 3(BE —CF)= 3[( - 3+ 1)x —( 3 —1)x] = 2 3x.故BE+ CF= 3(BE —CF).2. (2016河北中考)如图,△ OAB中,OA= OB= 10 , Z AOB= 80°,以点O为圆心,6为半径的优弧M分别交OA OB 于点M N.(1) 点P在右半弧上(Z BOP是锐角),将OP绕点O逆时针旋转80°得OP .求证:AP= BP ;(2) 点T在左半弧上,若AT与弧相切,求点T到OA的距离;(3) 设点Q在优弧MNk ,当厶AOQ的面积最大时,直接写出Z BOQ的度数.解:(1) •••/ AOP=Z AOBH Z BOP= 80° +Z BOP / BOP =Z POP +Z BOP= 80° +Z BOP /-Z AOP= OA= OB,Z BOP,又T OA= OB OP= OP,在△ AOP 和厶BOP 中,Z AOP=Z BOP , /.△ AOP^A BOP (SAS,•/ AP=OP= OP .BP ;(2)如图1,连接OT,过点T 作TF U OA 于点H, •/ AT 与M N相切,/•/ ATO= 90°,/ AT= OA—OT =2 2 1 1 1 1 8X 6 2410 —6 = 8 ,•••—X OA^ TH=-X AT X OT,即一X 10X TH=-X 8X 6,即卩TH= ,•/ T= ,即为所求的距离;¥ 2 2 2 210 5(3) 如图2,当OQLOA时,△ AOQ的面积最大.理由::OQL0A, /• QO是厶AOQ中最长的高,则△ AOQ的面积最大,•••/ BOQ=Z AOQ-Z AOB= 90°+ 80°= 170°, 当Q 点在优弧M f N右侧上,T OQL OA, /• QO是厶AOQ 中最长的高,则△ AOQ的面积最大,BOQ=Z AOQ-Z AO= 90°—80°= 10°,综上所述:当/ BOQ的度数为10°或170°时,△ AOQ的面积最大.3. (2016廊坊二模)如图①,已知△ ABC是等腰直角三角形,Z BAC= 90°,点D是BC的中点.作正方形DEFG使点A, C分别在DG和DE上,连接AE, BG.(1) 试猜想线段BG和AE的数量关系是________ ;(2) 将正方形DEFG绕点D逆时针方向旋转a (0 ° <a< 360° ).①判断(1)中的结论是否仍然成立?请利用图②证明你的结论;②若BC= DE= 4,当AE取最大值时,求AF的值.解:图①(1) AE = BG (2)①成立,BG= AE.如图①,连接AD「.•在Rt A BAC中,AB= AC, D为斜边BC的中点,二AD= BD, AD丄BCADG-Z BDG= 90° . :•四边形EFGD为正方形,二DE= DQ 且/ GDE= 90°,二/ ADG-Z ADE=BD= AD,90°,「.Z BDG=Z ADE在厶BDG和厶ADE中,Z BDG=Z ADE BDG^A ADE(SA$,二GD= AEGD= ED.图②②••• BG= AE,「.当BG取得最大值时AE取得最大值,如图②,当旋转面为270°时,BG= AE.v BC= DE= 4, D1为BC 的中点,四边形DEFG为正方形,••• BD= CD= 2BC= 2, EF= DG= DE= 4,「. BG= BD- GD= 2+ 4 = 6, A AE=BG =6,A AF= ,62+ 42= 2 . 13.4. (2016沧州八中模拟)如图①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中Z C= 90°, ZB=Z E= 30°.(1)操作发现如图②,固定△ ABC使厶DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是 ________;②设△ BDC的面积为$,△ AEC的面积为S2,贝U S与S2的数量关系是 _________ .(2)猜想论证当厶DEC绕点C旋转到图③所示的位置时,小明猜想(1)中S与S的数量关系仍然成立,并尝试分别作出了△ BDC和△ AEC中BC CE边上的高,请你证明小明的猜想.(3)拓展探究已知/ ABC= 60°,点 D 是其角平分线上一点, BD - CD= 4, DE// AB 交BC 于点E (如图④).若在射线 BA 上存在点F ,使DCF - BDE,请直接写出相应的 BF 的长.解:⑴①DE// AC ②S 1-S;⑵ 如图:•••△ DEC 是由△ ABC 绕点 C 旋转得到,••• BC -CE AC -CD.:/ACN bZ BCN - 90°,/ DCW /BCN -/ ACN -/ DCM180°— 90°- 90°, •/ ACN -/。
2017年河北省中考数学试卷(含详细答案)
数学试卷 第1页(共28页) 数学试卷 第2页(共28页)绝密★启用前河北省2017年初中毕业生升学文化课考试数 学(本试卷满分120分,考试时间120分钟)第Ⅰ卷(选择题 共42分)一、选择题(本大题共16小题,1~10小题,每小题3分,11~16小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下列运算结果为正数的是( ) A .2(3)-B .32-÷C .0( 2 017)⨯-D .23- 2.把0.0813写成10n a ⨯(110a ≤<,n 为整数)的形式,则a 为( ) A .1B .2-C .0.813D .8.13 3.用量角器测量MON ∠的度数,下列操作正确的是( )ABCD4.23222333m n ⨯⨯⨯=+++个个……( )A .23n mB .23m nC .32m nD .23m n5.图1和图2中所有的小正方形都全等.将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( )A .①B .②C .③D .④ 6.如图为张小亮的答卷,他的得分应是( )A .100分B .80分C .60分D .40分7.若ABC △的每条边长增加各自的10%得'''A B C △,则'B ∠的度数与其对应角B ∠的度数相比 ( ) A .增加了10%B .减少了10%C .增加了(110)+%D .没有改变8.如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( )ABCD9.求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD 是菱形,对角线AC ,BD 交于点O . 求证:AC BD ⊥.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共28页) 数学试卷 第4页(共28页)以下是排乱的证明过程: ①又BO DO ⊥,②AO BD ∴⊥即AC BD ⊥. ③四边形ABCD 是菱形, ④=AB AD ∴. 证明步骤正确的顺序是( )A .③→②→①→④B .③→④→①→②C .①→②→④→③D .①→④→③→②10.如图,码头A 在码头B 的正西方向,甲、乙两船分别从A 、B 同时出发,并以等速驶向某海域.甲的航向是北偏东35,为避免行进中甲、乙相撞,则乙的航向不能是 ( )A .北偏东55 B .北偏西55 C .北偏东35D .北偏西3511.如图是边长为10 cm 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm )不正确的是( )ABCD12.如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是 ( )A.446+ B .04446++= C.46 D.1446-=13.若321x x -=-( )11x +-,则( )中的数是 ( ) A .1-B .2-C .3-D 任意实数.14.甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图.比较5月份两组家庭用水量的中位数,下列说法正确的是( ) A .甲组比乙组大B .甲、乙两组相同C .乙组比甲组大D .无法判断15.如图,若抛物线23y x =-+与x 轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k ,则反比例函数ky x=(0)x >的图象是( )ABC D16.已知正方形MNOK 和正六边形ABCDEF 边长均为1,把正方形放在正六边形中,使OK 边与AB 边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C 顺时针旋转,使MN边与CD 边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B ,M 间的距离可能是( )A .1.4B .1.1C .0.8D .0.5甲组12户家庭用水量统计表数学试卷 第5页(共28页) 数学试卷 第6页(共28页)第Ⅱ卷(非选择题 共78分)二、填空题(本大题共3小题,共10分.17,18小题,每小题3分;共19小题共4分.请把答案填写在题中的横线上)17.如图,,A B 两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C ,连接,CA CB ,分别延长到点,M N ,使AM AC =,BN BC =,测得200 m MN =,则,A B 间的距离为 m .18.如图,依据尺规作图的痕迹,计算=α∠ . 19.对于实数p ,q ,我们用符号}{min ,p q 表示p ,q 两数中较小的数,如}{min 1 ,21=. 因此,{min = ; 若}{22min (1),1x x -=,则x = .三、解答题(本大题共7个小题,共68分.解答应写出文字说明、证明过程或演算步骤) 20.(本小题满分8分)在一条不完整的数轴上从左到右有点,,A B C 其中2AB =,1BC =,如图所示.设点,,A B C 所对应数的和是p .(1)若以B 为原点,写出点,A C 所对应的数,并计算p 的值;若以C 为原点,p 又是多少?(2)若原点O 在图中数轴上点C 的右边,且28CO =,求p .21.(本小题满分9分)编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分.如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;(3)最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.22.(本小题满分9分)发现 任意五个连续整数的平方和是5的倍数. 验证 (1)22222(1)0123-++++的结果是5的几倍?(2)设五个连续整数的中间一个为n ,写出它们的平方和,并说明是5的倍数. 延伸 任意三个连续整数的平方和被3除的余数是几呢?请写出理由.23.(本小题满分9分)如图,16AB =,O 为AB 中点,点C 在线段OB 上(不与点,O B 重合),将OC 绕点O 逆时针旋转270后得到扇形COD ,,AP BQ 分别切优弧CD 于点,P Q ,且点,P Q 在AB 异侧,连接OP .(1)求证:AP BQ =;(2)当BQ =时,求QD 的长(结果保留π);毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页(共28页) 数学试卷 第8页(共28页)(3)若APO △的外心在扇形COD 的内部,求OC 的取值范围.24.(本小题满分10分)如图,直角坐标系xOy 中,(0,5)A ,直线5x =-与x 轴交于点D ,直线33988y x =--与x 轴及直线5x =-分别交于点,C E .点,B E 关于x 轴对称,连接AB .(1)求点,C E 的坐标及直线AB 的解析式;(2)设面积的和CDE ABDO S S S ∆=+四边形,求S 的值;(3)在求(2)中S 时,嘉琪有个想法:“将CDE △沿x 轴翻折到CDB △的位置,而CDB △与四边形ABDO 拼接后可看成AOC △,这样求S 便转化为直接求AOC △的面积不更快捷吗?”但大家经反复验算,发现AOC S S ≠△,请通过计算解释他的想法错在哪里.25.(本小题满分11分)平面内,如图,在□ABCD 中,10AB =,15AD =,4tan 3A =.点P 为AD 边上任意一点,连接PB ,将PB 绕点P 逆时针旋转90得到线段PQ .(1)当10DPQ =∠时,求APB ∠的大小;(2)当tan :tan 3:2ABP A =∠时,求点Q 与点B 间的距离(结果保留根号);(3)若点Q 恰好落在□ABCD 的边所在的直线上,直接写出PB 旋转到PQ 所扫过的面积(结果保留π).26.(本小题满分12分)某厂按用户的月需求量x (件)完成一种产品的生产,其中0x >.每件的售价为18万元,每件的成本y (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x (件)成反比.经市场调研发现,月需求量x 与月份n (n 为整数,112n ≤≤)符合关系式2229(3)x n kn k =-++(k 为常数),且得到了表中的数据.(1)求y 与x 满足的关系式,请说明一件产品的利润能否是12万元; (2)求k ,并推断是否存在某个月既无盈利也不亏损;(3)在这一年12个月中,若第m 个月和第(1)m +个月的利润相差最大,求m .5 / 14河北省2017年初中毕业生升学文化课考试数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】239=(-);3322-÷=-;020170⨯=(-);231-=-,所以运算结果为正数的是2(3)-,故选A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题二图形的折叠与计算
专题命题规律
纵观河北8年中考,有4年都汲及图形的折叠与计算问题,主要以选择、填空形式考查,3分左右难度中等,类型有以圆形折叠为背景求角和,2012年9题、2013年19题、2016年13题,以图形折叠求线段长和2011年第9题.
解题策略
抓住折叠前后图形全等,从而产生相等的角或相等的线段.
2017预测
预计2017年河北中考还会以类似方式和方法、复习时应突出训练,总结规律.
,中考重难点突破)
以图形折叠为背景(针对2016年13题,2012年9题,2013年19题)
【经典导例】
【例1】(2013河北中考)如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=__95°__.
【思路分析】∵MF∥AD,FN∥DC,∴∠BMF=∠A=100°,∠BNF=∠C=70°,∵∠BMF+∠B+∠BNF+
∠F=360°.又∵△FMN 是△BMN 沿MN 翻折得到的,∴∠F =∠B=12(360°-∠BNF-∠BMF)=1
2
(360°-70°-
100°)=95°.
【方法指导】抓住折叠前后图形全等再运用多边形内角和和平行线求进行推理.
1.(2016天津中考)如图,已知在▱ABCD 中, AE ⊥BC 于点E ,以点B 为中心,取旋转角等于∠ABC,把△BAE 顺时针旋转,得到△BA′E′,连接DA′. 若∠ADC=60°,∠ADA ′=50°,则∠DA′E′的大小为( C )
A .130°
B .150°
C .160°
D .170°
,(第1题图))
,(第2题图))
2.(2016沧州中考)已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM 沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( A)
A.30°B.40°C.50°D.60°
3.(2016唐山九中模拟)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB 中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为__75°__.
,(第3题图))
,(第4题图))
4.如图,在Rt△ABC中,AC=BC.将Rt△AB C沿过点B的直线折叠,使点C落在AB边上的点F处,折痕为BE,这样可求出22.5°的正切值是__2-1__.
5.(2016保定调研试题)如图,点D,E为△ABC两边AB,AC的中点,将△ABC沿线段DE折叠后使点A落在点F处,若∠B=55°,则∠BDF=__70°__.
6.(2016邯郸二模)如图,等腰△ABC的纸片(AB=AC)按图中所示方法,恰好能折成一个四边形,首先使点A 与点B重合,然后使点C与点D重合,则等腰△ABC中∠B的度数是__72°__.
以图形折叠为背景,求线段长(针对2011年9题) 【经典导例】
【例2】(2011河北中考)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( B)
A.1
2
B.2 C.3 D.4
【思路分析】∵A′是CE的中点,又AE=A′E,∴E是AC的三等分点,又∠DEA=∠DEA′,∴∠DEA=∠C=
90°,∴△ADE∽△ABC,∴AE
AC =
DE
BC
,∴DE=
1
3
BC=2.故选B.
【方法指导】图形折叠类问题主要以四边形和三角形的折叠为背景,构造出平行线和三角形,解题的关键是抓住折叠前后图形全等的性质,根据对应角(或边)相等,将所求角度(或边长)转化到相应的三角形(或四边形)中,再根据三角形内角和定理、三角形相似等知识求解.
7.(2016唐山路南区一模)如图,△ABC的周长为21 m,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC于点D,交AC边于点E,连接AD,若AE=3 cm,则△ABD的周长是( A)
A.15 cm B.18 cm C.21 cm D.24 cm
,(第7题图))
,(第8题图))
8.(2016无锡中考)如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB 上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为 ( B)
A.3
5
B.
4
5
C.
2
3
D.
3
2
9.(2016石家庄质量检测)如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( B)
A.1
3
B.
4
9
C.
2
3
D.
5
9
,(第9题图))
,(第10题图))
10.(2016吉林中考)如图,在矩形ABCD中,AB=6 cm,点E,F分别是边BC,AD上一点,将矩形ABCD沿EF折叠,使点C,D分别落在点C′,D′处.若C′E⊥AD,则EF的长为 __62__cm.
11.(2016梅州中考) 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,或AB=4,BC=2,那么线段EF的长为__5__.
,(第11题图))
,(第12题图))
12.(2016河南中考)如图,正方形ABCD的边长是16,点E在边AB上,AE=3, 点F是边BC上不与点B、C重合的一个动点,把△EBF沿 EF折叠,点B落在B′处,若△CDB′恰为等腰三角形,则DB′的长为 __16或45
__.。
