配电网潮流计算
含分布式电源的配电网潮流计算

含分布式电源的配电网潮流计算一、本文概述随着可再生能源的快速发展和广泛应用,分布式电源(Distributed Generation,DG)在配电网中的渗透率逐年提高。
分布式电源包括风力发电、光伏发电、微型燃气轮机等,它们具有位置灵活、规模适中、与环境兼容性强等特点,是智能电网的重要组成部分。
然而,分布式电源的接入对配电网的潮流分布、电压质量、系统稳定性等方面都产生了显著影响。
因此,准确进行含分布式电源的配电网潮流计算,对于保障配电网安全、经济运行具有重要意义。
本文旨在探讨含分布式电源的配电网潮流计算方法。
本文将对分布式电源的类型、特性及其在配电网中的应用进行简要介绍。
将重点分析分布式电源接入对配电网潮流计算的影响,包括电源位置、容量、出力特性等因素。
在此基础上,本文将提出一种适用于含分布式电源的配电网潮流计算模型和方法,并对其准确性、有效性进行验证。
本文还将对含分布式电源的配电网潮流计算在实际工程中的应用前景进行讨论。
通过本文的研究,旨在为配电网规划、运行和管理人员提供一套有效的潮流计算工具和方法,以应对分布式电源大量接入带来的挑战。
本文的研究成果也有助于推动智能电网、可再生能源等领域的技术进步和应用发展。
二、分布式电源建模在配电网潮流计算中,分布式电源(Distributed Generation,DG)的建模是至关重要的一步。
分布式电源通常包括风能、太阳能、小水电、生物质能等多种类型,它们的接入位置和容量对配电网的潮流分布、电压质量、系统稳定性等方面都有显著影响。
建模过程中,首先需要明确分布式电源的类型和特性。
例如,对于光伏电源,其输出功率受到光照强度、温度等自然条件的影响,具有随机性和波动性;而对于风力发电,其输出功率则受到风速、风向、湍流强度等因素的影响,同样具有不确定性。
因此,在建模时需要考虑这些不确定性因素,以更准确地描述分布式电源的实际运行状况。
需要根据分布式电源的具体接入方式和位置,建立相应的数学模型。
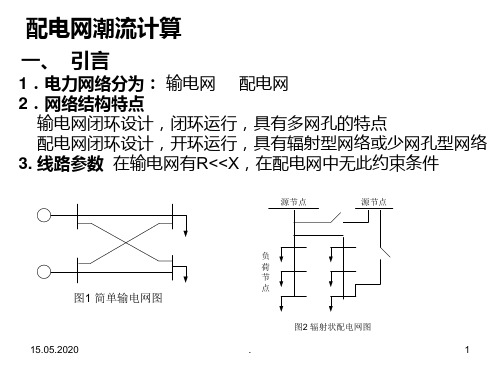
配电网潮流计算

配电网潮流计算的数学模型可以描述为,对于N 个节点的配电网,已知配电网的电源点电压,各节点的有功负荷和无功负荷值,配电网的拓扑结构信息以及各个支路的阻抗。
求得各节点的节点电压以及流经各支路的功率、各支路的电流,系统的有功损耗以及其他电力系统分析量。
配电网潮流算法实质上可以看做初始条件为根节点(电源节点电压)和节点负荷功率已知的情况下,根据前代更新和回退更新确定配电网的功率分布和电压分布。
因为配电网为辐射状,电能流动具有单向性,所以从电源点出发,上游支路向下游各个支路提供电能。
以支路功率表示的前推回代法的基本计算步骤如下:
(1)初始化迭代的有关参数,设置根节点电压,并为其他节点电压赋值,置迭代次数k 为零
(2)从数据文件读取各个节点注入的有功负荷功率以及其无功负荷功率;(3)从整个树状配电网结构的叶子节点往根节点计算,先子支路后父支路,利用式(2-1)、式(2-2)计算配电网的功率分布;
(4)从根节点出发,先父节点后子节点,利用式(3)计算配电网的电压分布;(5)判断相邻两次迭代电压差幅值的电流最大值max|ΔVi|是否小于给定的收敛数值ε。
如果满足收敛条件,则停止计算;反之则置k=k+1,返回步骤(3)重新执行。
含分布式电源的配电网潮流计算

含分布式电源的配电网潮流计算一、概述随着智能电网的建设和电力市场的逐步推行,传统的集中式大电网供电模式已无法满足当今社会对电力的需求。
分布式发电技术具有环保、高效、灵活的特点,已成为未来电网发展的重要方向。
由于分布式电源的引入,配电网中将出现许多新的节点类型,传统的潮流算法在处理这些节点时往往难以达到预期的效果。
潮流计算是开展配电网其他研究工作的基础,因此研究含分布式电源的配电网潮流计算显得尤为重要。
本文将针对含分布式电源的配电网潮流计算方法进行论述,包括分布式电源配电网潮流计算的必要性、分布式电源的类型和特性、传统潮流计算方法的局限性以及改进和优化的潮流计算算法等内容。
通过研究和分析,旨在为含分布式电源的配电网潮流计算提供有效的方法和思路,以促进智能电网的可持续发展。
1. 分布式电源的发展背景与现状分布式电源的兴起是地球环境可持续发展政策与技术进步的产物。
在21世纪初,随着高效绿色的小型独立电源的发展,分布式电源的概念应运而生。
分布式电源主要指传统的分散独立小型电源,以及采用分布式技术联网上网的一“群”或成组的小型分散电源。
这些电源包括自然能源(如水电、风电、太阳能发电等)、化石燃料发电(如内燃发电机组、燃气轮机发电机组、燃料电池等)、废弃物发电(如垃圾发电等)和贮能电源(如抽水蓄能发电、蓄电池组等)。
分布式电源的发展受到世界能源、电力界的关注,并在工业发达国家中得到热议。
其发展的原因主要有三个方面:各种小型分散型绿色环保电源的迅速发展,对电力系统的影响越来越大大电网的发展受到环保和需求的限制,为分布式电源的发展提供了机遇分布式电源可以充分利用用户附近各种分散的能源,提高能源利用率,减少因远距离输送电力产生的线路损耗,具有经济和环保意义。
近年来,分布式电源在能源系统中的比例不断提高,正在给能源工业带来革命性的变化。
特别是在全球倡导节能减排、调整能源结构的大背景下,分布式电源项目得到大力推广。
例如,我国在2013年以后,国家电网公司积极为分布式电源项目接入电网提供便利,并在项目的前期受理及工程建设等方面开辟绿色通道。
第四章 配电网潮流计算

第四章 配电网潮流计算4.1 配电网负荷模型4.1.1 概述配电网潮流计算的模型可描述为:对一个有n 个节点的的配电系统,已知量为根节点的电压0∙U 。
各节点的负荷值)1-n 21(,,,⋯⋯=+i jQ P i i 及配电系统拓扑结构和各支路的阻抗。
待求量为各节点的节点电压)1n 21(-⋯⋯=∙,,,i U i ,各支路的潮流功率)121(,,-⋯⋯=+n i jQ P j L j L ,,,及各支路的电流和系统的有功网损。
在辐射状的配电子系统中,对于支路j b 有:)(j j j i j jX R I U U +-=∙式(1)如果支路j b 的末点j v 为网损点,则该支路的电流j I ∙等于流过末梢点的电流j ,L I ∙。
即等于该末梢点的负荷电流为j L jI I,∙∙= 式(2)节点j v 的负荷电流j L I ,∙可表示为∙∙-=*,,,jjL j L j L U jQ P I 式(3)式中j L j L jQ P ,,-为节点j v 的负荷功率的共轭,*j U ∙为节点j v 的电压共轭。
如果支路j b 的末点j v 不是末梢点,则支路电流j I ∙应为该支路末点j v 的电流和其所有子支路的电流之和,即∑∈∙∙∙+=dk kj L j II I , 式(4)式中,d 为以节点j v 为父节点的支路的集合。
显然,根据式(2)-(4)由末梢点的电源点递推,就可以得到支路的电流,然后根据(1)式从电源向末梢点回推,就可以求得各节点电压。
4.1.2 负荷模型一般可将与节点电压有关的负荷模型描述为:βα⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛=ffU U jQ U UP S Re Re 式(5)式中,U 为节点实际电压,f U Re 为节点参考电压。
如果式(5)中0==βα,S 为恒功率负荷,如果1==βα,S 为恒电流负荷,如果2==βα,S 为恒阻抗负荷。
为讨论方便,假定S 为恒阻抗负荷,则有:22U jG U G S I R += 式(6)因此,可以将节点j v 的恒阻抗表示为22,2,,,i i I i i R i L i L U jG U G jQ P +=+ 式(7)式中,i U 为节点j v 的电压。
配电网潮流计算PPT课件
点有多个馈出支路)
负荷功率 -- 任意节点流出到用户中
的功率
15.05.2020
.
4
2.3 配电网的描述 —— (辐射表)
辐射表反映配电网支路与节点的关系
在配电网中,每一个负荷节点只有
源节点(根节点)
0
对应于变电站母
一个馈入支路,其馈入支路编号与
1
6
7
负荷节点编号相一致。馈入支路与
1
6
负荷节点是一对一的。
或已计算得出,计算各支路的功率
对末端节点的馈入电流有
i
I j I Lj
IL j — 负荷电流
ILj
Sˆ Lj Vˆ j
SOjVk Iˆj
Ik
SˆLk Vˆk
Sˆoj
(j末端节点) k
k j
j
这样的计算一直进行到源节点的馈出支路,
末端节点
从而全部节点的各馈出复功率都求解出来。
15.05.2020
.
11
V kV i cosk (i)(PIiRiQIiXi)V i2
V kV i sink(i)(PIiXiQIiRi)
上面两式作平方和,有
V i4 2 ( P I iR i Q I iX i) V k 2 V i2 ( P I i2 Q I i2 )R i 2 ( X i 2 ) 0
5
5 末端节点
图 辐射表的例
Ik
SO k Vˆi
7
由基尔霍夫电流定律,对于节点i,有
I i I Li I ok
Iok 节点i馈出支路的电流
IL i 负荷电流
IL i
Sˆ L i Vˆi
对于源节点的馈出支路电流,有
I1 SˆLi
第四章配电网潮流计算

第四章配电网潮流计算第四章配电网潮流计算4.1 配电网负荷模型4.1.1 概述配电网潮流计算的模型可描述为:对一个有n 个节点的的配电系统,已知量为根节点的电压0?U 。
各节点的负荷值)1-n 21(,,,??=+i jQ P i i 及配电系统拓扑结构和各支路的阻抗。
待求量为各节点的节点电压)1n 21(-??=?,,,i U i ,各支路的潮流功率)121(,,-??=+n i jQ P j L j L ,,,及各支路的电流和系统的有功网损。
在辐射状的配电子系统中,对于支路j b 有:)(j j j i j jX R I U U +-=?式(1)如果支路j b 的末点j v 为网损点,则该支路的电流j I ?等于流过末梢点的电流j ,L I ?。
即等于该末梢点的负荷电流为j L jI I,?= 式(2)节点j v 的负荷电流j L I ,?可表示为-=*,,,jjL j L j L U jQ P I 式(3)式中j L j L jQ P ,,-为节点j v 的负荷功率的共轭,*j U ?为节点j v 的电压共轭。
如果支路j b 的末点j v 不是末梢点,则支路电流j I ?应为该支路末点j v 的电流和其所有子支路的电流之和,即∑∈??+=dk kj L j II I , 式(4)式中,d 为以节点j v 为父节点的支路的集合。
显然,根据式(2)-(4)由末梢点的电源点递推,就可以得到支路的电流,然后根据(1)式从电源向末梢点回推,就可以求得各节点电压。
4.1.2 负荷模型一般可将与节点电压有关的负荷模型描述为:βα+???? ??=ffU U jQ U UP S Re Re 式(5)式中,U 为节点实际电压,f U Re 为节点参考电压。
如果式(5)中0==βα,S 为恒功率负荷,如果1==βα,S 为恒电流负荷,如果2==βα,S 为恒阻抗负荷。
为讨论方便,假定S 为恒阻抗负荷,则有:22U jG U G S I R += 式(6)因此,可以将节点j v 的恒阻抗表示为22,2,,,i i I i i R i L i L U jG U G jQ P +=+ 式(7)式中,i U 为节点j v 的电压。
含分布式电源配电网潮流计算方法

含分布式电源配电网潮流计算方法摘要:传统单馈线辐射状配电网将无法满足分布式电源的接入和用户对供电高可靠性的要求。
越来越多的分布式能源接入配电网,改变了配电网的潮流流向,因此需要单独研究含分布式电源配电网的潮流计算方法。
关键词:分布式电源配电网;前推回代法;潮流计算中图分类号:TM7111 含DG配电网潮流计算1 基本前推回推法前推回推潮流由于编程简单、收敛速度快的特点,广泛地应用于配电网的潮流计算。
这种算法先假定各节点电压为根节点电压,从末端节点开始,根据已知的各负荷功率、节点电压,向辐射网络始端推算各支路的电流或始端功率。
然后根据根节点的电压和求得的各支路的电流或始端功率,向末端推算各节点电压,重复以上过程直至迭代收敛。
计算过程为:a)为除始端外的所有节点电压赋初值;b)从末梢点开始,逐步前推各支路电流,第次迭代,流经支路的电流向量:(2.18)表示负荷电流和电容电流流过节点的节点集合;为第个节点处的负荷功率,c)从始端出发,由支路电流,逐段回推各节点电压:(2.19)d)直到满足下式的收敛准则,完成潮流计算:(2.20)2 含DG配电网潮流计算流程DG并入配电网后的潮流计算过程增加了新的节点类型,即PI和PV节点,基于前推回推法,含DG配电网潮流计算流程为:1)读入系统数据,进行配电网拓扑分析,确定每个节点的属层;2)初始化所有节点电压为根节点电压;3)求取每个节点的等效注入电流:PQ节点由2.18式求取;PV节点由2.2.1的方法转换为PQ节点;PI节点通过下式转换为PQ节点。
(2.21)4)由节点的属层和连接关系,前推支路电流;5)由已知的根节点电压,由式2.19回推各节点电压;6)对PV节点计算节点电压幅值不匹配量,由式2.16修正其无功出力,并检验其无功出力是否越限,越限则转化为PQ节点。
7)检验迭代收敛条件:所有节点,无功不越限PV节点,无功越限PV节点无功出力为或。
满足收敛条件则进入第8)步;否则转入第3)步。
配电网三相潮流计算方法研究

配电网三相潮流计算方法研究摘要:随着用户对供电可靠性及电能质量要求的提高,作为电力系统相对薄弱的配电网日益得到重视。
配网环网结构、辐射状运行,联络开关经常切换,运行方式多变,潮流计算作为电力系统分析最基本的计算,不仅可以计算网损、校验各种运行方式的合理性等,也可以为暂态计算提供初值,配电网基本潮流计算的重要性不言而喻。
关键词:配电网;三相潮流;计算方法1 配电网潮流计算的三相数学模型1.1 三相变压器模型基于相分量的适合配电网实际情况的变压器三相模型。
由于铁损与负载电流无关,基本上是一个恒定值,因此可以将铁损作为额外功率,并联在变压器等值电路的二次侧各相上。
变压器的节点电流向量和节点电压向量之间关系的变压器节点导纳矩阵YT,仍然可由变压器的原始导纳矩阵Y和变压器的节点-支路关联矩阵A共同表示为YT=AT×Y×A。
此时YT为6×6的矩阵。
但接线方式为Dyn11、Yyn0的变压器导纳矩阵中Y12和Y21是奇异的,而这对于前推回代算法来说,将不能进行正常的迭代。
将导纳矩阵用线分量和相分量混合表述,则可以解决这个问题。
1.2 单相变压器模型在实际生活中,配电网中的居民用户普遍采用的单相供电模式,是将单相变压器的高压侧连接在配电网的线电压上,然后从低压侧引出相线和零线对用户进行供电。
由此可建立单相变压器模型。
三相变压器的三相模型共考虑了两侧的六个节点,而单相变压器只有四个节点,故无法将求解三相变压器导纳矩阵的方法应用到单相变压器中。
对于单相变压器,本文采用了传统的T型等值电路。
实际上,对于基于电流的前推回代算法,进行反复迭代的主要根据是注入各个节点的电流和由其衍生的各支路电流。
而实践证明,采用双绕组变压器的传统型等值电路模型,完全可以得到准确有效的电流。
2 配电网潮流算法2.1 前推回代法前推回代法是配电网潮流计算中比较常用的方法,其基本思想是:首先将各节点电压设为额定电压值,并计算各节点的注入电流,然后从末端向首端前推求出配电网各支路电流;再依据各支路电流,从首端向末端回代求出各节点电压;反复进行前推回代计算,直至各节点的电压偏差满足迭代收敛条件为止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要配电网潮流计算是配电管理系统应用软件功能组成之一。
本设计在分析配电网元件模型的基础上,建立了配电网潮流计算的数学模型。
由于配电网的结构参数与输电网有很大的区别,因此配电网的潮流计算采用相适应的算法。
配电网的结构特点呈辐射状,在正常运行时是开环的;配电网的另一个特点是配电线路的总长度较输电线路要长并且分支较多,配电线路的线径比输电网的细以至于配电网的R/X较大,且线路的充电电容可以忽略。
配电网的潮流计算采用的方法是前推回代法,文中对前推回代法的基本原理,收敛性及计算速度等进行了理论分析比较仿真和算例表明,前推回代法具有编程简单、计算速度快、收敛性好的特点,这个方法是配电网潮流计算的有效算法,具有很强的实用性。
关键词配电网,潮流计算,前推回代法AbstractFlow solution of distribution networks is one of software in DMS. Because of the different structures between transmission networks and distribution networks, the corresponding methods in flow solution of distribution networks must be applied. Distributions network is radial shape and in the condition of regular is annular. Another characteristic of distribution networks is cabinet minister of distribution long than transmission networks. The line diameter of distribution networks is thin than transmission networks, it cause R/X is large of distribution networks and the line’s capacitance can neglect. Load flow calculation of distributions network use back/ forward sweep. It has some peculiarities such as simple procedures and good restrain and so on. This method of distribution network is an effective method of calculating the trend, with some practicality.Key words :distribution network,load flow calculation,back/ forward sweep一.电力系统潮流概述1.1 配电网的分类在电力网中起重要分配电能作用的网络称为配电网。
配电网按电压等级进行分类,可以分为高压配电网(35—110KV),中压配电网(6—10KV),低压配电网(220-380V)。
按供电区的功能分类,可以分为城市配电网,农村配电网和工厂配电网等。
在城市电网系统中,主网是指110KV及其以上电压等级的电网,主要起连接区域高压(220KV及以上)电网的作用。
配电网是指35KV及其以下电压等级的电网,作用是给城市里各个配电站和各类用电负荷的供给电源。
从投资的角度看,我国与外国先进国家的发电、输电、配电投资比率差异很大,外国基本上是电网投资大于电厂投资,输电投资小于配电投资。
我国从重视发电轻视供电状态中转变过来,但是在供电投资中,输电投资大于配电投资。
从我国城网改造之后,将逐渐从输电投资转入配电建设为主。
本设计是基于前推回代法的配电网潮流分析计算的研究,研究是是以根节点为10kV的电压等级的配电网。
1.2配电网潮流计算的目的和意义电力系统的潮流计算是研究电力系统稳态运行情况的一种基本计算,是电力系统规划和运行中不可缺少的一个重要组成部分。
也可以说,潮流计算是电力系统分析中最基本、最重要的计算,是电力系统安全、经济分析和实时控制的基础。
潮流计算的任务是根据给定的运行条件和网络结构确定整个系统的运行状态,如母线上的电压(幅值及相角)、网络中的功率分布及功率损耗等。
即潮流计算是对电力系统的功率分布和电压分布的计算, 其具体任务就是编制系统的调度计划和电气设备检修计划, 确定电力系统中变压器分接头位置和系统中枢点与电压控制点的电压曲线,进行事故运行方式的分析, 为电力系统短路和稳定的计算提供数据, 为继电保护及自动装置的整定与电力系统设计规划提供依据等。
潮流计算的目的是对现有电力系统的正常运行状态进行分析,提示必要的改进措施, 同时为新建系统或扩建系统的有关分析和计算打下了基础。
配电网潮流计算是配电网的经济运行、系统分析等重要基础,但由于配电网与输电网有着明显的差异:配电网具有环形结构, 而通常以开环方式运行。
通常呈辐射状,支路比值较大,分支线较多;配电线路中的R/X 比值偏大使输电网中常用的潮流计算算法如传统的牛顿法和快速分解法在应用于配电网潮流计算时容易形成病态而无法收敛,因此,研究适用配电网的潮流算法也是至关重要的。
目前,输电系统潮流计算方法已经较为成熟,并且获得了广泛的实际应用。
但随着电力系统规模的不断扩大,潮流计算方程阶数越来越高,对这种规模的方程不是采用任何数学方法都能保证给出正确答案的,因此,这也成为促使电力系统研究人员不断寻求新的、更可靠的潮流计算方法的动力。
随着现代电力系统大系统、强非线性与多元件的特点日益突出, 其计算量和计算复杂度急剧增加。
旧的计算机软件在处理潮流计算时, 其速度已无法满足大电网模拟与实时控制的仿真要求, 而高效的潮流问题的相关软件的研究已成为大规模电力系统仿真计算的关键。
1.3配电网运行的特点和要求配电系统相对于输电系统来说,由于电压等级低、供电范围小,但是配电网与用户直接相连,是供电部门对用户服务的窗口,因而决定了配电网运行有如下特点和基本要求:(1)10kV中压配电网在运行中,负荷节点数多,一般没有表计实时记录负荷,无法应用现在传统潮流程序进行配电网的计算分析,所以要求建立新的数学模型和计算方法。
(2)随着铁道电气化和用户电子设备的大量使用,配电网运行中有大量的谐波源、三相电压不平衡、电压闪变等污染,要求准确测量和计算配电网中的谐波分布,从而采取有效的措施抑制配电网运行中的谐波危害。
(3)由于环保条件日趋严格的制约,要求配电网运行能制定不影响城市绿化、防火、防爆、防噪音等技术和组织措施,以便减少配电网运行对环境的污染。
(4)随着用户对供电可靠性和电压质量指标的提高,靠人工操作已无法适应,要求现代的配电网运行不断提高自动化、智能水平。
1.4 MATLAB运用简介1.4.1MATLAB简介目前电子计算机已经应用于电力系统的分析计算,潮流计算是其基本应用软件之一。
现在有很多潮流计算方法。
对潮流计算方法有五方面的要求:(1)计算的速度快,(2)内存需要少,(3)计算结果有良好的可靠性,(4)适应性好,也能处理变压器变比调整、系统元件的不同描述和与其它程序配合的能力强,(5)简单。
MATLAB是一种交互式、面向对象的程序设计语言,广泛应用于工业界和学术界,主要用于矩阵运算,同时在数值分析、自动控制模拟、数字信号处理、动态分析、绘图等方面具有强大的功能。
MATLAB程序设计结构完整,并且具有优良的移植性,它的基本数据是不需要定义的数组。
它可以高效率地解决工业计算问题,特别是关于矩阵和矢量的计算。
MATLAB与C语言相比更容易被掌握。
通过运用MATLAB语言,可以用类似数学公式的方式来编写算法,大大降低了程序所需要的难度并且节省了时间,从而可以把主要的精力集中在算法的构思上。
另外,MATLAB提供了一种特殊的工具:工具箱(TOOLBOXES).这些工具箱主要包括:信号处理(SIGNAL PROCESSING)、控制系统(CONTROL SYSTEMS)、神经网络(NEURAL NETWORKS)、模糊逻辑(FUZZY LOGIC)和模拟(SIMULATION)等。
不同领域、不同层次的用户通过相应工具的学习和应用,可以更方便地进行计算、分析及设计工作。
MATLAB设计中,原始数据的格式是关键的一个环节,它与程序使用的方便性和灵活性有直接的关系。
原始数据输入格式的设计,主要应从使用者的角度出发,原则是简单明了,便于修改。
1.4.2 MATLAB矩阵运算矩阵是MATLAB数据存储的基本单元,而矩阵的运算是MATLAB语言的核心,在MATLAB 语言系统中几乎所有的运算都是以对矩阵的操作为基础的。
矩阵的基本数学运算包括矩阵的四则运算、与常数的运算、逆运算、行列式运算、特征值运算等基本函数运算,这里进行简单介绍。
(1)四则运算矩阵的加、减、乘运算符分别为“+,—,*”,用法与数字运算几乎相同,但计算时要满足其数学要求在MATLAB中矩阵的除法有两种形式:左除,右除。
在传统的MATLAB算法中,右除先计算矩阵的逆再相乘,而左除则不需要计算逆矩阵直接进行除运算。
通常情况下,右除速度快一点,但是左除可避免被除矩阵的奇异性所带来的麻烦。
在MATLAB中两者的区别不太大。
(2)与常数的运算常数与矩阵的运算即是同该矩阵的每一元素进行运算。
但需注意进行数除时,常数通常只能做除数。
(3)基本函数运算矩阵的函数运算是矩阵运算中最实用的部分,常用的主要有以下几个:det(a) 求矩阵a的行列式eig(a) 求矩阵a的特征值inv(a)或a ^ (-1) 求矩阵a的逆矩阵rank(a) 求矩阵a的秩trace(a) 求矩阵a的迹(对角线元素之和)我们在进行工程计算时遇到矩阵对应元素之间的运算。
这种运算不同于前面讲的数学运算,为有所区别,我们称之为数组运算。
(4)基本数学运算数组的加、减和矩阵的加、减运算完全相同。
而乘除法运算有区别,数组的乘除法是指两同维数组对应元素之间的乘除法,它们的运算符为“.*”和“./”或“.\”。
前面讲过常数与矩阵的除法运算中常数只能做除数。
在数组运算中有了“对应关系”的规定,数组与常数之间的除法运算没有任何限制。
另外,矩阵的数组运算中还有幂运算(运算符为.^ )、指数运算(exp)、对数运算(log)、和开方运算(sqrt)等。
有了“对应元素”的规定,数组的运算就是针对数组内部的每个元素进行的。
