平均值的精密度和置信区间
分析化学误差和分析数据处理2

15
(三)准确度与精密度的关系
1. 准确度高,要求精密度一定高,精密度高 是准确度高的前提,但精密度好,准确度不一 定高。 2. 准确度反映了测量结果的正确性,精密度 反映了测量结果的重现性。
12
例: 两人分析同一试样中Cu的含量,其结果ω如下: 甲 0.3610 0.3612 0.3608 乙 0.3641 0.3642 0.3643 已知其含Cu的量的真实值为0.3606,试问何人结果的准 确度高? 解:
x RE % 100% 100%
甲: X =0.3610
16
四、提高分析准确度的方法
1.选择恰当的分析方法 例:测全Fe含量 K2Cr2O7法 40.20% ±0.2%×40.20% 比色法 40.20% ±2.0%×40.20% (常量组分的分析,常采用化学分析,而微量和痕量分 析常采用灵敏度较高的仪器分析方法) 2.减小测量误差 1)称量 例:天平一次的称量误差为 0.0001g,两次的称量误差为 0.0002g,RE%≤ 0.1%,计算最少称样量?
n x
100%
10
滴定分析中时, R d 一般要求<0.2﹪
3. 标准偏差(standard deviation)与相对标准偏差 (1).标准偏差S
S
( xi x)
i 1
n
2
n 1
n
di
i 1
n
2
n-1=f
自由度
n 1
当n→∞,标准偏差用б表示
( xi ) 2 μ 为无限多次测定的平均值(总体平均值) 若无系统误差存在,µ 就是真实值 i 1 n
平均值的置信区间

平均值的置信区间什么是置信区间?统计学家经常必须从样本数据推断总体数据的特征。
在这个过程中,一个单独的样本本身代表的是总体的一部分,因此不能仅仅依靠简单地描述样本来了解总体。
这就是置信区间的意义所在。
置信区间是总体平均值的一个估计值,因此是样本平均值的范围。
平均值的置信区间是一种用来估计某个总体参数范围的工具。
换句话说,它是一个实数区间,可能包含某个待估计参数的真实值。
例如,如果我们根据样本数据计算出来的平均值是12,那么我们可能会使用置信区间来推断总体平均值的真实值(假设总体符合正态分布)。
这个置信区间告诉我们,在一定置信度下,总体平均值可能位于某个范围内,例如11至13之间。
在置信区间的范围内,我们可以以某一个概率推测待估计参数的真实值。
但是,由于我们只能够进行样本数据的抽样,因此我们无法知道总体的真实情况,也无法肯定某个置信区间是否覆盖了总体真实值。
因此,置信区间只是一个通过样本数据估计总体数据的工具,不能对总体答案的正确性做出绝对保证。
置信区间的理论基础置信区间的关键是$t$分布。
$t$分布是概率论和统计学中的一个重要分布。
在统计推断中,为计算总体平均值的置信区间而被广泛使用。
$t$分布是由William S. Gossett发明的,是在样本量较小、总体标准差未知的情況下针对总体平均值的推断所采用的一种概率分布。
当样本容量较少时,总体标准差通常被视为不知道。
此时,如果使用普通的$z$分布进行推断,则推断的误差非常大。
而当样本容量较大时,通常可以将总体标准差视为已知。
这时,我们可以使用$z$分布进行推断。
但是,如果我们无法确认总体标准差,却需要进行总体平均值的推断,那么我们就可以使用$t$分布。
$t$分布与正态分布不同,它没有一个固定的标准差。
相反,它的标准差是根据样本数据中的方差估计得出的。
与正态分布相比,$t$分布的曲线更高、更平,它的尾部比正态分布更粗、更长。
在样本容量较小(小于30)时,$t$分布对总体平均值的估计要比正态分布更准确。
统计学(置信度)

统计学基础----置信度与置信区间[原创2006-08-06 21:27:49]置信度与置信区间如何确定测定数据的可靠程度?数据的可信程度与偶然误差的存在及出现的几率有着直接关系。
对于不含系统误差的无数个测定数据,其误差分布可用正态分布曲线(高斯曲线)来表征。
以(x-μ)为横坐标,误差出现的频率y为纵坐标,误差正态分布曲线如图所示。
曲线的形状受总体标准偏差σ控制,越小,曲线又高又窄,表明数据精密度好。
σ 的数值等于曲线上的拐点到对称轴的距离,曲线的峰高等于1/[σ(2π)1/2]。
正态分布曲线与横轴所包围的面积代表了大小误差出现的概率(可由高斯方程积分获得)。
由数据可见,偶然误差出现在m ±3σ范围内的几率高达99.7%。
置信度是指人们所做判断的可靠性,所测数据的可信程度,在数值上与几率相等。
对于分析化学来讲:置信度:以测量值为中心,在一定范围内,真值出现在该范围内的几率。
置信区间:在某一置信度下,以测量值为中心,真值出现的范围。
t =(X - m )/s平均值的置信区间可表示为:s 有限次测定的标准偏差;t 值表一、平均偏差平均偏差又称算术平均偏差,用来表示一组数据的精密度。
平均偏差:优点:简单;缺点:大偏差得不到应有反映。
二、标准偏差S=标准偏差又称均方根偏差。
标准偏差的计算分两种情况:1.当测定次数趋于无穷大时标准偏差:μ 为无限多次测定的平均值(总体平均值);即:当消除系统误差时,μ即为真值。
2.当有限测定次数时标准偏差:相对标准偏差(变异系数):用标准偏差比用平均偏差更科学更准确.例: 两组数据1.X-X:0.11, -0.73, 0.24, 0.51,-0.14, 0.00, 0.30, -0.21,n=8 d1=0.28 S1=0.382.X-X:0.18,0.26,-0.25,-0.37,0.32 ,-0.28,0.31,-0.27n=8 d2=0.28 S2=0.29可见:d1=d2,而:S1>S2三、平均值的标准偏差m 个n 次平行测定的平均值:由统计学可得上列m 个数据的标准偏差(平均值的标准偏差)SX与n 次平行测定的标准偏差S 之间的关系:由SX/S — n 关系曲线:当n 大于5以后,曲线变化趋缓;当n 大于10以后,曲线变化不大。
化学分析 第二章 误差(第五版)

R E % =20.01100% 0.1% V
V20mL
h
22
[例]以K2Cr2O7标定0.02mol/L 的Na2S2O3要使VNa2S2O3 = 25 mL,称 mK2Cr2O7=?
[解] (1) Cr2O72++6I -+14H+=2Cr3++3I2+7H2O
I2+2S2O32-=2I -+S4O62 -
S = i=1 n -1
h
35
正态分布与 t 分布区别
1.正态分布——描述无限次测量数据 t 分布——描述有限次测量数据
2.正态分布——横坐标为 u ,t 分布——横坐标为 t
u = x-m s
m为总体均值 s为总体标准差
t= x-m s
s为有限次测量值的标准 差
3.两者所包含面积均是一定范围内测量值出现的概率P
2. 哪些操作影响准确度?
3. 哪些操作影响精密度?
h
25
实验四 明矾的含量测定
操作步骤:
精密称取明矾样品约1.4 g于50 ml烧杯中,用适量蒸馏水溶解后 转移至100 ml容量瓶中,稀释至刻线,摇匀。用移液管吸取 25.00 ml上述溶液于250 ml锥形瓶中,加蒸馏水25 ml,然后精密 加入EDTA标准液(0.05 mol/L)25.00 ml,在沸水浴中加热10分 钟,冷至室温,再加蒸馏水10 ml及HAc – NaAc缓冲液5 ml,二 甲酚橙指示剂4 ~ 5滴,用ZnSO4标准液滴定至溶液由黄色变为橙 色,即为终点。 1. 为什么用容量瓶配制样品溶液?
(5) 为使 RE<0.1%,加大称样,扩大10倍,配置
250mL(取25mL即为0.024g的量)
误差和数据处理

三、有效数字的运算法则
根据误差传递规律
加减法中 按小数点后位数最少的(绝对误差传递) 0.5362 + 0.001 + 0.25 = 0.79
0.5362 0.001 0.25
绝对误差 0.0001 0.001
0.01
29
有效数字的运算法则
根据误差传递规律
乘除法中 按有效数字位数最少的(相对误差传递) 0.0121 25.64 1.0578 = 0.328
例2-5:用8-羟基喹啉测定Al含量,9次测定的标准偏差为0.042%,
平均值为10.79%。估计真值在95%和99%置信水平时应是多大?
95%置信度时:
P =0.95 a =1-P =0.05 f=9-1=8
查表 t0.05,8=2.306
代入公式 =x tS/n =10.79 0.032%
测量步骤的准确度应与分析方 法的准确度相当
增加平行测定的次数
(四)消除测量中的系统误差
19
提高分析结果准确度的方法
(一)选择恰当的分析方法 (二)减小测量误差 (三)减小偶然误差的影响
(四)消除测量中的系统误差
经典方法比较 校准仪器 对照实验 回收实验 空白实验
试样中组分含量
标样中组分含量
=
试样中组分测得量
26
有效数字的修约规则
在修约标准偏差等时 修约的结果应使准确度 降低 例如:标准偏差(S)=0.213
取两位时,修约为 0.22 取一位时,修约为 0.3
27
有效数字的修约规则
与标准限度值比较时不应修约
例如:
某标准试样中镍含量≤0.03%为合格
获得的测量值为
0.033%
修约为
无机化学第三章误差小结
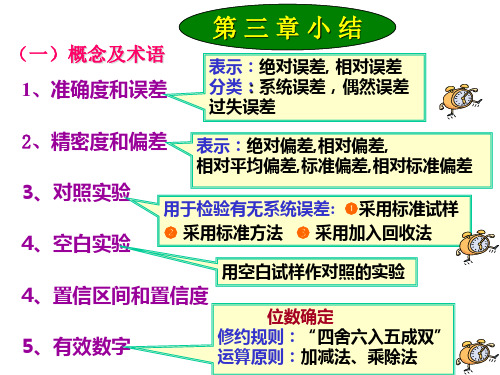
4、置信区间和置信度
位数确定
5、有效数字
修约规则:“四舍六入五成双” 运算原则:加减法、乘除法
绝对误差
(二)公式
E = x – xT
Q检验法--- 取舍可疑值
排列各数:小大;
相对误差
RE= E 1000‰ xT
Q计=
x疑 xmax
x邻 xmin
个别测定值的绝对偏差 个别测定值的相对偏差
di xi x
A.增加平行测定次数 B. 对照实验 C.空白实验 D. 加入回收法 3、按有效数字运算规则(0.85×lg 2.13)÷(2.314 + 6.5)的结 果保留的有效数字位数是( )
A. 1位 B. 2位 C. 3位 D. 4位
判断题
1、对某项测定来说,它的系统误差大小是可以测量的。 2、偶然误差的分布有一定的规律,因此可以通过校正消除。 3、滴定分析的相对误差一般要求为0.1%,滴定时耗用标准溶液的 体积应控制在15-20mL。 4、多次分析结果的重现性越好,则分析的准确度越好。 填空题
(±0.01/25.56) ×1000‰
“四舍六入五成双”
当尾数≤4时则舍,尾数≥6时则入。 当尾数=5而“5”后面还有不全部是零的任何数时,皆入。 尾数=5而“5”后面的数字全部为0时,若“5”前面的数字 为偶数则舍,如为奇数则入。
有效数字运算原则
加减法
按照小数点后位数最少的那个数(绝对误差最大)来 保留计算结果的小数点后位数
可减小
随着测定次数的增加,偶然误差的算 多次测量求平均值 术平均值逐渐趋近于0。
有 有效数字一般包括全部准确数 + 最末一位可疑数
效 可疑数:通常有±1单位的误差。 例如:25.56mL
第二章 实验数据误差分析和数据处理
第二章误差和分析数据处理•2.1 测量值的准确度和精密度•2.2 提高分析结果准确度的方法(自学)•2.3 有效数字及其运算规则•2.4 有限量测量数据的统计处理•2.5 相关分析和回归分析(自学)§2.1 测量值的准确度和精密度误差(Error) : 测量值与真值之差。
➢真值T (True value)某一物理量本身具有的客观存在的真实值。
真值是未知的、客观存在的量。
在特定情况下认为是已知的:1、理论真值(如化合物的理论组成)(如,NaCl中Cl的含量)2、计量学约定真值(如国际计量大会确定的长度、质量、物质的量单位等等)3、相对真值(如高一级精度的测量值相对于低一级精度的测量值)(例如,标准样品的标准值)误差分类•系统误差(Systematic error)—某种固定的因素造成的误差方法误差、仪器误差、试剂误差、操作误差•随机误差(Random error)—不定的因素造成的误差仪器误差、操作误差系统误差与随机误差的比较项目系统误差随机误差产生原因固定因素,有时不存在不定因素,总是存在分类方法误差、仪器与试剂误差、主观误差环境的变化因素、主观的变化因素等性质重现性、单向性(或周期性)、可测性服从概率统计规律、不可测性影响准确度精密度消除或减小的方法校正增加测定的次数系统误差的校正•方法系统误差——方法校正•主观系统误差——对照实验校正(外检)•仪器系统误差——对照实验校正•试剂系统误差——空白实验校正如何判断是否存在系统误差?E a = x –x T 相对误差x <x T 为负误差,说明测定结果偏低x >x T 为正误差,说明测定结果偏高误差越小,分析结果越接近真实值,准确度也越高x -x T x T x T E r = ——= ————常用%表示Ea 绝对误差 误差的表示:对一B 物质客观存在量为T 的分析对象进行分析,得到n 个个别测定值x 1、x 2、x 3、••• x n ,对n 个测定值进行平均,得到测定结果的平均值,那么:个别测定的误差为:T x i -测定结果的绝对误差为:T x E a -=测定结果的相对误差为:%100⨯=TE E a r 平均值偏差(deviation): 单次测量值与测量平均值之差。
误差和分析数据处理(2)
Analytical chemistryErrors and data treatment(2)二、有效数字及运算法则2非测量所得的自然数测量次数、样品份数 计算中的倍数反应中的化学计量关系 各类常数测量所得的数字测量值数据计算的结果3数字位数应与分析方法的准确度及仪器测量的精度相适应4有效数字: 分析工作中实际能测得的数字1. 有效数字(significant figure)☐在记录测量数据时,只保留一位可疑数(欠准数)☐只有数据的末尾数欠准,误差是末位数的±1个单位☐有效数字位数反映了测量和结果的准确程度,决不能随意增加或减少5m ◇分析天平(称至0.1mg):12.8228g (6),0.2348g (4) , 0.0600g (3)◇千分之一天平(称至0.001g): 0.235g (3)◇1%天平(称至0.01g): 4.03g (3), 0.23g (2)◇台秤(称至0.1g): 4.0g (2), 0.2g (1)V ☆滴定管(量至0.01mL):26.32mL (4), 3.97mL (3)☆容量瓶:100.0mL (4),250.0mL (4)☆移液管:25.00mL (4);☆量筒(量至1mL或0.1mL):25mL (2), 4.0mL (2)重量分析和滴定分析允许的误差一般在±0.2%之内,各测量数据应保留四位有效数字,注意计算结果的有效数字位数6☐数字1~9均为有效数字☐数字前0不是有效数字,其他数字之间的0计入有效数字: 0.0304(3)☐数字后的0,在小数中,计入有效数字位数:0.03400(4)☐数字后的0,在整数中,含义不清楚时, 最好用指数形式表示: 1000 (1.0×103, 1.00×103, 1.000 ×103)☐很小的数字,也可以用指数形式表示,但有效数字位数需保持不变:0.000018 → 1.8 ×10-5☐变换单位时,有效数字位数需保持不变:0.0038g→3.8mg ☐数据的第一位数≥8的,可多计一位有效数字,如9.35×104(4), 95.2%(4), 8.65(4)☐对数的有效数字位数按小数部分数字的位数计,其整数部分的数字只代表原值的幂次,如pH=10.28(2), 则[H +]=5.2×10-11有效数字位数72. 有效数字运算中的修约规则尾数≤4时舍; 尾数≥6时入尾数=5时, 若后面无数,或后面数为0, 舍5成双;若5后面还有不是0的任何数皆入四舍六入五成双例下列值修约为四位有效数字0.3247 40.3247 6 0.3247 50.3248 50.3248 500.3248 510.32470.32480.32480.32480.32480.32498禁止分次修约0.57490.570.5750.58×9运算时可多保留一位有效数字进行5.3527+2.3+0.054+3.355.35+2.3+0.05+3.35=11.0511.010标准限度值0.03%测定值0.033%修约标准偏差对标准偏差的修约,应使准确度降低统计检验时,标准偏差可多保留1-2位数参与运算表示标准偏差和RSD时,一般取两位有效数字与标准限度值比较时不修约×不合格0.03%0.2130.2211加减法:结果的绝对误差应不小于各项中绝对误差最大的数。
第二章 误差和分析数据处理-分析化学
第二章 误差和分析数据处理
第一节 概述
xie 分 析 化 学
产生测定误差的原因:
抽样的代表性; 测定方法的可靠性; 仪器的准确性; 测定方法的复杂性;
测定者的主观性;
操作者的熟练性
xie 分 析 化 学 一、绝对误差和相对误差
第二节 测量误差
绝对误差(absolute error)
减小测量误差
取样量大于0.2g;
滴定液消耗的体积大于20ml;
紫外吸收度在0.2~0.7之间。
xie 分 析 化 学
相对误差=δw/W<1‰
W>δw/1‰=0.0002/1‰=0.2g 相对误差=δv/V<1‰ V>δv/1‰=0.02/1‰=20 ml
增加平行测定次数
xie 分 析 化 学
2 i
n
相对标准偏差(relative standarddeviation;RSD) 或称变异系数(coefficient of variation;CV)
2 ( x x ) i n i 1
S RSD 100% x
n 1 x
100%
例题 :四次标定某溶液的浓度,结果为0.2041、
标准偏差法:
R=x+y-z
R=xy/z
2 2 2 2 SR Sx Sy Sz
Sy 2 Sx 2 SR 2 Sz 2 ( ) ( ) ( ) ( ) R x y z
五、提高分析准确度的方法
xie 分 析 化 学
选择恰当的分析方法
被测组分的含量; 被测组分共存的其它物质的干扰。
0.00022 0.00062 0.00042 0.00002 标准偏差 S 0.0004 (mol/ L) 4 1
平均值的精密度和置信区间
偏差-Deviation 表示个别测量值与平均值之间的差值; 一组分析结果的精密度可以用平均偏差和标准偏 差两种方法来表示。 1、偏差—Absolute deviation
d xi x
2、平均偏差— average deviation
x1 x2 x3 .... xn 1 n x xi n n i 1
第二章 误差和分析数据的处理
目的与要求: 1.熟悉误差的概念、误差分类; 2.掌握准确度与精密度; 3.掌握系统误差、偶然误差产生原因、 特点、分类及其克服方法; 4.掌握平均值、偏差、相对平均偏 差和标准偏差、相对标准偏差的计算; 5.掌握数据的处理原则。
第一节 测量的准确度和精密度
一、准确度与精密度 (一)、准确度与误差 真值( µ )-True value 某一物理量本身具有的客观存在的真实数值,即 为该量的真值。
x x d
i
3 、 相 对 平 均 偏 差 ( Rd% ) —relative average deviation
n
d Rd % 100% x
4、标准偏差—standard deviation S
n 1 2 2 2 xi ( xi ) ( xi x ) i 1 i 1 n i 1 S 或S n 1 n 1 n n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、提高分析结果准确度的方法
(一)选择合适的分析方法 例:测全Fe含量 K2Cr2O7法 40.20% ±0.2%×40.20% 比色法 40.20% ±2.0%×40.20% (二)减小测量误差 1)称量 例: 天平一次的称量误差为 0.0001g,两次的 称量误差为 0.0002g,Rd% 0.1%,计算最少称 样量?
问题1: a:下列那项属于系统误差? (1)滴定管第四位读数不准; (2)基准物质中含有杂质; (3)称量时天平有微小波动; (4)试样洒落。 b:下列那项属于偶然误差? (1)基准物质含有杂质; (2)滴定管读数不准; (3)仪器未校正; (4)指示剂选择不当。
c:系统误差的特点是: (1)不可校正; (2)大小不确定; (3)可以消除; (4)与分析方法无关。 d:偶然误差的特点是: (1)重复出现; (2)大小不确定; (3)无法消除; (4)可以消除。
平均值 甲 50.29%
(一)50.40% (二) 50.30% (三) 50.25% (四) 50.23%
乙 50.30%
(一)50.36% (二) 50.35% (三) 50.34% (四) 50.33%
丙 50.33%
二、系统误差和偶然误差 (一)系统误差
解:
C NaOH
2 sC 2 C NaOH
CHCL VHCL 0.1000 30.00 0.1200mol / L VNaOH 25.00
2 s1
V12
2
2 s2
V22
2 2
sC C NaOH
0.02 0.01 4 4 2 0.12 9.2 10 1.110 25 30
标准差法
R ax by cz
SR a 2 S x b2 S y c 2 S z
2 2 2 2
2.乘除法计算
R x y z
SR / R2 Sx x2 S y
2
2
2
y2 Sz z2
2
例:设天平称量时的标准偏差 s = 0.10mg,求称量试样 时的标准偏差sm 。
第三节 有限量测量数据的统计处理 一、 偶然误差的正态分布 正态分布的概率密度函数式
1 y f ( x) e 2 ( x )2 2 2
1.x 表示测量值,y 为测量值出现的概率密度 2.正态分布的两个重要参数 (1)μ为无限次测量的总体均值,表示无限个 数据的集中趋势(无系统误差时即为真值) (2)σ是总体标准差,表示数据的离散程度 3.x -μ为偶然误差
(三)减小偶然误差 在消除系统误差的前提下,平行测定次数多, 平均值愈接近真实值。因此,增加测定次数,可 以提高平均值精密度。在化学分析中,对于同一 试样,通常要求平行测定2~4次。 (四)消除测量过程中的系统误差
1)校准仪器:消除仪器的误差
2)空白试验:消除试剂误差
3)对照实验:消除方法误差
4)回收实验:加样回收以检验是否存在方法误差
第二节
有效数字及其运算规则
一、有效数字:实际可以测得的数字
1. 有效数字位数包括所有准确数字和一位欠准数字 例:滴定读数20.30mL,最多可以读准三位 第四位欠准(估计读数)±1% 2. 在0~9中,只有0既是有效数字,又是无效数字 例: 0.06050 四位有效数字 定位 有效位数 例:3600 → 3.6×103 两位 → 3.60×103 三位 3.单位变换不影响有效数字位数 例:10.00[mL]→0.001000[L] 均为四位
正态分布曲线—— x ~ N(μ ,σ2 ) 曲线 以x-μ~y作图
x =μ时,y 最大→大部分测量值集中 在算术平均值附近 曲线以x =μ的直线为对称→正负误差 出现的概率相等 当x →﹣∞或﹢∞时,曲线渐进x 轴, 小误差出现的几率大,大误差出现的 几率小,极大误差出现的几率极小 σ↑,y↓, 数据分散,曲线平坦 σ↓,y↑, 数据集中,曲线尖锐 测量值都落在-∞~+∞,总概率为1
ห้องสมุดไป่ตู้
m m1 m2 , s m
2 s1
2 s2
2s 0.14 mg
2
例:用移液管移取NaOH溶液25.00mL,以0.1000mol/L的 HCl溶液滴定之,用去30.00mL,已知用移液管移 取溶液的标准差s1=0.02mL,每次读取滴定管读数的 标准差s2=0.01mL,假设HCl溶液的浓度是准确的, 计算标定NaOH溶液的标准偏差?
3、真值与标准参考物质
(1)约定真值 (2)相对真值与标准参考物质
(二)精密度与偏差 精密度-Precision
用相同的方法对同一个试样平行测定多次,得到 结果的相互接近程度。
以偏差来衡量其好坏 重复性—Repeatability 同一分析人员在同一条件下所得分析结果的精 密度。 再现性-Reproducibility 不同分析人员或不同实验室之间各自的条件下 所得分析结果得精密度。
1、绝对误差(Absolute error) 表示测量值与真值( µ )的差。 =X- µ
注:绝对误差有正、有负
2、相对误差(relative error) 表示误差在真值中所占的百分率
相对误差% 100或相对误差 % 100 x
用分析天平称量两个试样,一个是0.0021g,另 一个是0.5432g 。两个的绝对误差都是0.0001g , 但相对误差?
中位数(XM) 一组测量数据按大小顺序排列,中 间一个数据即为中位数XM,当测 量值的个数位偶数时,中位数为中 间相临两个测量值的平均值。它的 优点是能简单直观说明一组测量数 据的结果,且不受两端具有过大误 差数据的影响;缺点是不能充分利 用数据,因而不如平均值准确。
准确度 指测量值与真值之间接近的程度,其好坏 用误差来衡量。 误差 测量值(X)与真值( µ )之间的差值 ()。
(三)准确度与精密度的关系 精密度是保证准确度的先决条件。精密度 差,所测结果不可靠,就失去了衡量准确度 的前提。 高的精密度不一定能保证高的准确度。在 消除系统误差的前提下,精密度高,准确度 也会高。
(一)50.36% (二) 50.30% (三) 50.28% (四) 50.27%
三、误差的传递 (一)系统误差的传递
1.加减法计算
R ax by cz R ax b y cz
R x y z R / R x x y y z z
2.乘除法计算
(二)偶然误差的传递
R f ( x, y, z)
1.加减法计算
Sx , Sy , Sz
4.pH,pM,pK,lgC,lgK等对数值,其有效 数字的位数取决于小数部分(尾数)数字的 位数,整数部分只代表该数的方次 例: pH = 11.20 → [H+]= 6.3×10-12[mol/L] 两位 5.结果首位为8和9时,有效数字可以多计一位 例:90.0% ,可示为四位有效数字 例:99.87% →99.9% 进位
三、有效数字的运算法则 1 .加减法:以小数点后位数最少的数为准 (即以绝对误差最大的数为准) 例: 50.1 + 1.45 + 0.5812 = ? 52.1
δ ±0.1 ±0.01 ±0.0001
保留三位有效数字
2 .乘除法:以有效数字位数最少的数为准 (即以 相对误差最大的数为准)
例:0.0121 × 25.64 × 1.05782 = 0.328 ? δ ±0.0001 ±0.01 ±0.00001 Rd ±0.8% ±0.4% ±0.009% 保留三位有效数字
二、有效数字的修约规则 1.四舍六入五留双
例:0.37456 , 0.3745 均修约至三位有效数字 0.374 0.375
2.只能对数字进行一次性修约
例:6.549, 2.451
6.5
一次修约至两位有效数字
2.5
3.当对标准偏差修约时,修约后会使标准偏差 结果变差,从而提高可信度 例:s = 0.134 → 修约至0.14,可信度↑ 4.可多保留一位有效数字进行计算,最后进行修 约
x x d
i
3 、 相 对 平 均 偏 差 ( Rd% ) —relative average deviation
n
d Rd % 100% x
4、标准偏差—standard deviation S
n 1 2 2 2 xi ( xi ) ( xi x ) i 1 i 1 n i 1 S 或S n 1 n 1 n n
systematic error
determination error
由固定的原因造成的,使测定结果系统偏高或偏 低,重复出现,其大小可测,具有“单向性”,可用 校正法消除的误差。 根据其产生的原因分为以下4种
1.方法误差(method error):分析方法本身 不完善而引起的。
2.仪器和试剂误差(instrument and reagent error):仪器本身不够精确,试剂不纯引起 误差。
3.操作误差(operational error):分析人员操 作与正确操作差别引起的。 4.主观误差(Personal error):分析人员本身 主观因素引起的。
(二)偶然误差 random error accidental error
indeterminate error
由一些随机偶然原因造成的、可变的、无法避免, 符合“正态分布”。由不确定因素造成。
理论真值:如某化合物的理论组成等。
计量学约定真值: 国际计量大会上确定的长度、 质量、物质的量单位等。 相对真值: 认定精度高一个数量级的测定值作为 低一级的测量值的真值。例如科研中 使用的标准样品及管理样品中组分的 含量等。
平均值:n 次测量值的算术平均值。虽不是真值, 但比单次测量结果更接近真值,它表 示一组测定数据的集中趋势。
