限时训练1集合与简易逻辑
2021第1练 集合、简易逻辑、不等式
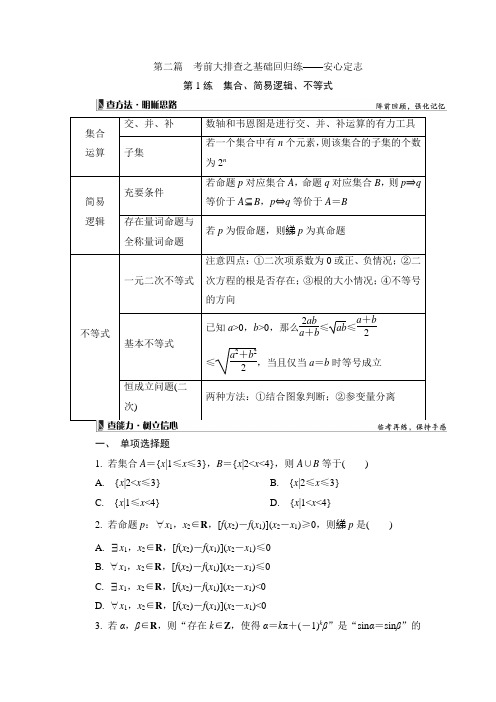
第二篇 考前大排查之基础回归练——安心定志第1练 集合、简易逻辑、不等式一、 单项选择题1. 若集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B 等于( ) A. {x |2<x ≤3} B. {x |2≤x ≤3} C. {x |1≤x <4}D. {x |1<x <4}2. 若命题p :∀x 1,x 2∈R ,[f (x 2)-f (x 1)](x 2-x 1)≥0,则綈p 是( ) A. ∃x 1,x 2∈R ,[f (x 2)-f (x 1)](x 2-x 1)≤0 B. ∀x 1,x 2∈R ,[f (x 2)-f (x 1)](x 2-x 1)≤0 C. ∃x 1,x 2∈R ,[f (x 2)-f (x 1)](x 2-x 1)<0D. ∀x 1,x 2∈R ,[f (x 2)-f (x 1)](x 2-x 1)<03. 若α,β∈R ,则“存在k ∈Z ,使得α=k π+(-1)k β”是“sin α=sin β”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 若函数f (x )=2x -x -1,则不等式f (x )>0的解集是( ) A. (-1,1) B. (-∞,-1)∪(1,+∞) C. (0,1) D. (-∞,0)∪(1,+∞)二、 多项选择题5. 若a ,b ,c ,m ∈R ,则下列推证中不正确的是( ) A. a >b ⇒am 2>bm 2 B. a c >bc ⇒a >b C. ac 2>bc 2⇒a >bD. a 2>b 2,ab >0⇒1a <1b6. 若a >0,b >0,且a +b =1,则( ) A. a 2+b 2≥12 B. 2a -b >12 C. log 2a +log 2b ≥-2 D. a +b ≤ 2三、 填空题7. 已知p :x 3-4x2x ≤0,q :x 2-(2m +1)x +m 2+m ≤0,若p 是q 的必要不充分条件,则实数m 的取值范围为______________.8. 若直线ax -2by =2(a >0,b >0)过圆x 2+y 2-4x +2y +1=0的圆心,则4a +2+1b +1的最小值为________. 四、 解答题9. 某单位拟建一个扇环面形状的花坛,如图所示,该扇环面是由以点O 为圆心的两个同心圆弧和延长后通过点O 的两条直线段围成.按设计要求扇环面的周长为30 m ,其中大圆弧所在圆的半径为10 m .设小圆弧所在圆的半径为x (单位:m),圆心角为θ(单位:rad).(1) 求θ关于x 的函数关系式;(2) 已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/m ,弧线部分的装饰费用为9元/m.设花坛的面积与装饰总费用的比为y ,求y关于x的函数关系式,并求出当x为何值时,y取得最大值.(第9题)10. 已知函数f(x)=ax2-|x-1|+2a(a∈R).(1) 当a=12时,解不等式f(x)≥0;(2) 若f(x)≥0恒成立,求a的取值范围.。
专题1.1 集合与简易逻辑(测试卷)(原卷版)

专题一 集合与简易逻辑测试卷一.填空题(14*5=70分)1.【温州二外2016届上学期高三10月阶段性测试1】已知}22{≤≤-=x x M ,}1{x y x N -==,那么=N M .2.【江苏省泰州中学2015--2016学年度第一学期高三第二次月考】命题“02016,10200>-+->∃x x x ”的否定是 .3.【哈尔滨市第六中学2016届上学期期中考试】已知集合}1,1{-=M ,},4221|{1Z ∈<<=+x x N x ,则=⋂N M __________.4.【山东师范大学附属中学2016届高三上学期第二次模拟】已知集合{}cos0,sin 270A =,{}20B x x x =+=,则A B ⋂为 .5.【重庆市巴蜀中学2016级高三学期期中考试】已知命题1p :函数22x x y -=-在R 上为增函数,2p :函数22x x y -=+在R 上为减函数,在下列四个命题112:q p p ∨;212:q p p ∧;()312:q p p ⌝∨和()412:q p p ∧⌝中,真命题是 .6.【江苏省泰州中学2015--2016学年度第一学期高三第二次月考】已知命题1211:≤+-x p ,命题)0(012:22><-+-m m x x q ,若p 是q 的充分不必要条件,则实数m 的范围是 .7.【河北省衡水中学2016届高三二调】设全集{}1,3,5,6,8U =,集合{}1,6A =,集合{}5,6,8B =,则()U A B ⋂= .8.【江苏省清江中学2016届高三上学期周练】若函数()f x 是定义在R 上的函数,则“()00f =”是“函数()f x 为奇函数”的 条件(“充分不必要” “必要不充分” “充要” “既不充分也不必要”中选一个).9.【哈尔滨市第六中学2016届上学期期中】定义在R 上的函数)(x f y =满足5522f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭,5()02x f x ⎛⎫'-> ⎪⎝⎭,则对任意的21x x <,都有)()(21x f x f >是521<+x x 的 条件.10.【泰州市2015届高三第三次调研测试】给出下列三个命题:①“a >b ”是“3a >3b”的充分不必要条件; ②“α>β”是“cos α<co s β”的必要不充分条件;③“0a =”是“函数()()32f x x ax x =+∈R 为奇函数”的充要条件.其中正确命题的序号为 .11.【黑龙江省牡丹江市一高2016届高三10月】已知, a b 是两个非零向量,给定命题:p ⋅=a b a b ,命题:q t ∃∈R ,使得t =a b ,则p 是q 的________条件.12.【吉林省长春外国语学校2016届上学期高三第一次质量检测】设集合}log ,3{2a P =,{}b a Q ,=,若}0{=Q P ,则=Q P ________.13.【2016届河北省邯郸市馆陶县一中高三7月调研考试】下列说法中,正确的是________.①任取x >0,均有3x >2x ;②当a >0,且a ≠1时,有a 3>a 2; ③y =(3)-x 是增函数;④y =2|x |的最小值为1; ⑤在同一坐标系中,y =2x 与y =2-x的图象关于y 轴对称. 14.【2016届湖北省部分重点中学高三上学期起点考试】以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数()x ϕ组成的集合:对于函数()x ϕ,存在一个正数M ,使得函数()x ϕ的值域包含于区间[,]MM -.例如,当31()x x ϕ=,2()s i n x x ϕ=时,1()x A ϕ∈,2()x B ϕ∈.现有如下命题: ①设函数()f x 的定义域为D ,则“()f x A ∈”的充要条件是“b ∀∈R ,a D ∃∈,()f a b =”;②函数()f x B∈的充要条件是()f x 有最大值和最小值; ③若函数()f x ,()g x 的定义域相同,且()f x A ∈,()g x B ∈,则()()f x g x B+∉; ④若函数2()ln(2)1x f x a x x =+++(2x >-,a ∈R )有最大值,则()f x B ∈. 其中的真命题有__________________.(写出所有真命题的序号)二.解答题(6*12=72分)15.【湖北宜昌一中、龙泉中学2016届高三十月联考】已知函数()(2)()f x x x m =-+-(其中2m >-),()22x g x =-﹒(1)若命题“2log ()1g x ≤”是真命题,求x 的取值范围;(2)设命题p :(1,)x ∀∈+∞,()0f x <或()0g x <,若p ⌝是假命题,求m 的取值范围﹒16.【江西临川一中2016届上学期高三期中】已知集合{}015A x ax =∈<+≤R ,()1202B x x a ⎧⎫=∈-<≤≠⎨⎬⎩⎭R . ⑴若B A =,求出实数a 的值;⑵若命题,:A x p ∈命题B x q ∈:且p 是q 的充分不必要条件,求实数a 的取值范围.17.【山东省潍坊第一中学2016届高三10月月考16】已知集合{}2log 8A x x =<,204x B x x ⎧⎫+=<⎨⎬-⎩⎭,{}|1C x a x a =<<+.(1)求集合A B ⋂; (2)若B C B ⋃=,求实数a 的取值范围.18.【山东省潍坊第一中学2016届高三10月月考】设命题p :函数1y kx =+在R 上是增函数,命题q :x ∃∈R ,2(23)10x k x +-+=,如果p q ∧是假命题,p q ∨是真命题,求k 的取值范围.19.【辽宁省葫芦岛市一高2016届上学期期中考试】已知命题p :函数()log 21a y x =+在定义域上单调递增;命题q :不等式2(2)2(2)40a x a x -+--<对任意实数x 恒成立,若p 且q ⌝为真命题,求实数a 的取值范围.20.【江苏省阜宁中学2016届高三年级第一次调研考试】已知命题p :指数函数()()26xf x a =-在R 上是单调减函数;命题q :关于x 的方程223210x ax a -++=的两根均大于3,若p 或q 为真,p 且q 为假,求实数a 的范围.。
第一章《集合与简易逻辑》练习题.docx

第一章《集合与简易逻辑》练习题一. 选择题1.若关于 x 的不等式 ax 2bx c 0 (a 0) 的解集是空集 , 则( )( A ) a0且 b 2 4ac(B)a0且 b 2 4ac( C ) a 0且 b 2 4ac 0 (D)a 0且b 24ac2.如果命题“ p 或 q ”与命题“非p ”都是真命题,那么()( A )命题 p 不一定是假命题 ( B )不一定是真命题( C )命题 q 一定是真命题( D )命题 p 与命题 q 真值相同3.设全集 U=R ,集合22UM={ x ︱ x -2x - 3>0}, N={ x ︱ 3+2x - x >0}。
则 M ( C N )等于( )( A ) M( B ) N( C ) C U M(D ) C U N4.下列说法准确的是( )( A ) x ≥ 3 是 x>5 的充分不必要条件 ( B ) x ≠± 1 是 x ≠1 的充要条件 ( C )若﹁ p ﹁ q ,则 p 是 q 的充分条件( D )一个四边形是矩形的充分条件是它是平行四边形5.若 A ∩ B={ a , b }, A ∪ B={ a , b , c , d },则符合条件的不同的集合A 、B 有()( A ) 16 对 ( B )8 对 ( C ) 4 对 ( D )3 对6.已知集合 M{ x | x 1} , P { x | x t} ,若 M P,则实数t 应该满足的φ条件是 ( )( A ) t 1 ( B ) t 1( C ) t 1(D ) t 17.方程 mx 2 2x 1 0 至少有一个负根,则()( A ) 0 m 1 或 m 0( B ) 0m 1 ( C ) m 1( D ) m 18.当 a0 时,关于 x 的不等式 x 2 4ax 5a 2 0的解集是 ( )( A ) { x | x 5a 或 x a } ( B ) { x | x 5a 或 x a }( C ) { x | a x 5a }( D ){ x | 5a x a }9. 抛 物 线 yax 2 bx c 与 X 轴 的 两 个 交 点 为2, 0 , 2, 0 则 不 等 式ax 2 bxc0 的解集为()(A)x 2 x 2(B) x x 2或 x 2( C ) x x2(D)不确定 , 与 a 值相关 . 10.“ x 2+2x-8=0 ”是“ x-2=2 x ”的 ()(A) 充分不必要条件 (B)必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件11.已知集合 A={y|y=-x2∈R}, B={y|y=-x+3,x ∈ R}, 则 A ∩ B=()+3,x (A){(0,3),(1,2)} (B){0,1}(C){3,2}(D){y|y ≤ 3}12.已知集合 A={x|x1 0 },B={x|x ≤ a} ,若 A ∩ B=B,则 a 的取值范围是( )x2(A)a ≥ 1 (B)a ≥2(C)a ≤ -2 (D) a<-213.设全集为 S,对任意子集合 A, B 若 A B , 则下列集合为空集的是 ( )(A) A C S B(B)C S AC S B(C)C S AB(D)AB14.“ a 2 b 20 ”的含义是 ( )(A)a, b 全不为 0(B) a, b不全为 0(C) a, b至少有一个为 0 (D) a, b至少有一个不为 015.已知 P :∣ 2x -3∣>1; q :10 ;则﹁ p 是﹁ q 的()条件x2x 6( A )充分不必要条件 ( B )必要不充分条件( C )充分必要条件( D )既非充分条件又非必要条件16.如果命题“ P 或 Q ”是真命题,命题“ P 且 Q ”是假命题,那么()(A)命题 P 和命题 Q 都是假命题(B)命题 P 和命题 Q 都是真命题 ( C )命题 P 和命题“非 Q ”真值不同(D) 命题 Q 和命题“非 P ”真值相同17.满足关系 {1}B{11 , 2,3, 4} 的集合 B 有( )( A ) 5 个( B ) 7 个( C ) 8 个( D ) 6 个18. a 、 b ∈R +是 a+b > 2 ab 的()( A )充分条件但不是必要条件 ( B ) 必要条件但不是充分条件( C )充分必要条件( D ) 既不充分也不必要条件29.已知 I=R , M={x ︱( x-2 )( 3-x )> 0} , N={x ︱x1> 2} ,则 C U M ∩N 是()x 1( A ) { x | x 3 }( B ) { x | 2 x1 }( C ) { x | 3 x 2 }( D )ф20.如果集合 Mx | xk 1, Nk 1 , k Z ,那么()2 , k Zy | y2( ) M N44(B) MN (C)MN (D)MNA21.下列命题中假命题 是()...( A )“正三角形边长与高的比是2︰ 3 ”的逆否命题( B )“若 x,y 不全为0,则 x 2y 2 0 ”的否命题 ( C )“ p 或 q 是假命题”是“非 p 为真命题”的充分条件( D )若 A B A C ,则 B C22.已知集合( A )φA 是全集 S 的任一子集,下列关系中准确的是() C S A ( B ) C S A S( C )( A ∩ C S A ) =φ ( D )( A ∪ C S A )S23.设全集 U={(x,y)|x∈R,y ∈ R},集合 M={(x,y)|y22( A )( C U M )∩( C U N ) (B )( C U M ≠ x})∪ N,N={(x,y)|y≠ -x},则集合( C )( C U M )∪( C U N )(D ) M ∪( C U N )24.下列说法:①若一个命题的否命题是真命题,则这个命题不一定是真命题;②若一个命题的逆否命题是真命题,则这个命题是真命题;③若一个命题的逆命题是真命题,则这个命题不一定是真命题;④若一个命题的逆命题和否命题都是真命题,则这个命题一定是真命题;其中准确的说法是( )( A )①②( B )①③④ ( C )②③④( D )①②③25.若二次不等式 ax 2+bx+c>0 的解集是x | 1 x1,那么不等式 2cx 2-2bx-a<0 的解54集是( )( A ) x | x 10或 x 1 ( B ) ( C ) x | 4x 5( D )1x1x |5 4 x | 5 x426.集合 {x-1 , x 2-1, 2} 中的 x 不能取值个数是()( A ) 2( B ) 3( C )4( D ) 527.设 M={2,a 2-3a+5,5},N={1,a2-6a+10,3},且 M ∩ N={2,3} 则 a 的值是 ( ) ( A ) 1 或 2 ( B ) 2 或 4( C ) 2( D ) 1二.填空题28. x>y 是x >1 成立的 _________________________________________ 条件 .y29.若集合 A 1,3, x , B1, x 2 ,且 AB 1,3, x ,则 x30.使x 2 x 2成立的充要条件是 _______________________________.x 2 3xx 23x31.写出命题“个位数是5 的自然数能被 5 整除”的逆命题、否命题及逆否命题,并判定其真假。
新高考2021届高考数学小题必练1集合与简易逻辑(含答案)

高考数学小题必练1.集合的概念与表示①通过实例,了解集合的含义,理解元素与集合的“属于”关系.②针对具体问题,能够在自然语言和图形语言的基础上,用符号语言刻画集合.③在具体情境中,了解全集与空集的含义.2.集合的基本关系理解集合之间包含与相等的含义,能识别给定集合的子集.3.集合的基本运算①理解两个集合的并集与交集的含义,能求两个集合的并集与交集.②理解在给定集合中一个子集的补集的含义,能求给定子集的补集.③能使用Venn 图表达集合的基本关系与基本运算,体会图形对理解抽象概念的作用.4.必要条件、充分条件、充要条件①通过对典型数学命题的梳理,理解必要条件的意义,理解性质定理与必要条件的关系.②通过对典型数学命题的梳理,理解充分条件的意义,理解判定定理与充分条件的关系.③通过对典型数学命题的梳理,理解充要条件的意义,理解数学定义与充要条件的关系.5.全称量词与存在量词通过已知的数学实例,理解全称量词与存在量词的意义.6.全称量词命题与存在量词命题的否定①能正确使用存在量词对全称量词命题进行否定.②能正确使用全称量词对存在量词命题进行否定.1.【2020全国I 卷理科】设集合2{|40}A x x =-≤,{|20}B x x a =+≤,且{|21}A B x x =-≤≤,则a =()A .4-B .2-C .2D .4【答案】B【解析】由题意知{|22}A x x =-≤≤,{|}2aB x x =≤-, 又因为{|21}A B x x =-≤≤,所以12a -=,解得2a =-. 【点睛】含参的交集运算,是高考的常规考查.2.【2020北京卷】已知,αβ∈R ,则“存在k ∈Z ,使得π(1)kk αβ=+-”是“βαsin sin =”的() A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【解析】sin sin 2πk αβαβ=⇔-=或π2π()π(1)()k k k k k αβαβ+=+∈⇔=+-∈Z Z .【点睛】考查三角函数和充分条件与必要条件,利用诱导公式即可得,属于常规考查.一、单选题.1.已知集合{|24}A x x =<<,2{|430}B x x x =-+≤,则A B =()A .{|14}x x -<≤B .{|14}x x -≤≤C .{|23}x x <≤D .{|23}x x ≤≤【答案】C【解析】由2430x x -+≤,解得13x ≤≤,故{|23}A B x x =<≤.2.“2a ”是“复数(2i)(1i)()z a a R 为纯虚数”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C【解析】当2a 时,(22i)(1i)4i z ,则z 为纯虚数,可知“2a ”是“复数(2i)(1i)()z a a R 为纯虚数”的充分条件;当(2i)(1i)(2)(2)i z a a a 为纯虚数时,2020a a ,解得2a ,可知“2a ”是“复数(2i)(1i)()z a a R 为纯虚数”的必要条件,综上所述,“2a ”是“复数(2i)(1i)()z a a R 为纯虚数”的充要条件.3.命题“0x ∃>,21x x =-”的否定是()A .0x ∃>,21x x ≠-B .0x ∀≤,21x x =-C .0x ∃≤,21x x =-D .0x ∀>,21x x ≠-【答案】D【解析】因为存在量词命题的否定是全称量词命题,注意到要否定结论,所以:命题“0x ∃>,21x x =-”的否定是:0x ∀>,21x x ≠-.4.设m ,n 是两条不同的直线,,αβ是两个不同的平面,则命题p :m n ⊥的一个充分条件是()A .q :αβ∥,m α⊂,n β⊥B .q :αβ∥,m α⊥,n β⊥C .q :αβ⊥,m α⊥,n β∥D .q :αβ⊥,m α⊂,n β∥【答案】A【解析】若p 的充分条件是q ,则需要满足q p ⇒.对于选项A ,αβ∥,m α⊂,n β⊥,故m n ⊥,所以满足q p ⇒,故选项A 正确;对于选项B ,由命题q 可得m n ∥,q p ,故选项B 错误;对于选项C ,由命题q 可得m ,n 的位置关系是平行或相交或异面,q p ,故选项C 错误;对于选项D ,由命题q 可得m ,n 的位置关系是平行或相交或异面,q p ,故选项D 错误,故选A .5.若命题:p “0x ∃∈R ,20010x ax +≤+”是真命题,则实数a 的取值范围是()A .[2,2]-B .(,2][2,)-∞-+∞C .(2,2)-D .(,2)(2,)-∞-+∞【答案】B【解析】命题:p “0x ∃∈R ,20010x ax +≤+”是真命题,则需满足240Δa =-≥,解得2a ≥或2a ≤-.6.下列命题中,真命题是()A .若||||=a b ,则=a bB .命题“x ∀∈R ,20x ≥”的否定是“x ∀∈R ,20x <”C .“1x >”是“21x >”的充分不必要条件D .对任意x ∈R ,1sin 2sin x x +≥【答案】C【解析】A .若||||=a b ,则=a b 不成立,故A 错误;B .命题“x ∀∈R ,20x ≥”的否定是“x ∃∈R ,20x <”故B 错误;C .由21x >,得1x >或1x <-,即“1x >”是“21x >”的充分不必要条件,故C 正确;D .当sin 0x <时,1sin 2sin x x +≥不成立,故D 错误.7.已知等差数列{}n a 的公差为d ,前n 项和为n S ,则“10a >,0d >”是“5762S S S +>”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】由题意得576762S S S a a d +-=-=,因此当10a >,0d >时,57620S S S d +-=>,则5762S S S +>;当5762S S S +>时,57620S S S d +-=>,此时1a ∈R 都可以,∴“10a >,0d >”是“5762S S S +>”的充分不必要条件.8.设x ∈R ,若“13x ≤≤”是“||2x a -<”的充分而不必要条件,则实数a 的取值范围是()A .(1,3)B .[1,3)C .(1,3]D .[1,3]【答案】A【解析】由||2x a -<,解得22a x a -<<+,∵“13x ≤≤”是“||2x a -<”的充分而不必要条件,∴[1,3](2,2)a a -+,∴2123a a -<⎧⎨+>⎩,解得13a <<,∴实数a 的取值范围是(1,3).二、多选题.9.下面命题正确的是()A .“1a >”是“11a <”的充分不必要条件B .命题“任意x ∈R ,则210x x ++<”的否定是“存在x ∈R ,则210x x ++≥”C .设,x y ∈R ,则“2x ≥且2y ≥”是“224x y +≥”的必要而不充分条件D .设,a b ∈R ,则“0a ≠”是“0ab ≠”的必要不充分条件【答案】ABD【解析】对于A ,1110(1)00a a a a a a-<⇔>⇔->⇔<或1a >, 则“1a >”是“11a <”的充分不必要条件,故A 对; 对于B ,全称量词命题的否定是存在量词命题,“任意x ∈R ,则210x x ++<”的否定是“存在x ∈R ,则210x x ++≥”,故B 对; 对于C ,“2x ≥且2y ≥”⇒“224x y +≥”,“2x ≥且2y ≥”是“224x y +≥”的充分条件,故C 错;对于D ,00ab a ≠⇔≠且0b ≠,则“0a ≠”是“0ab ≠”的必要不充分条件,故D 对,故选ABD .10.下列结论正确的是()A .x ∀∈R ,12x x+≥ B .“0x ∃∈R ,2000x x -≤”的否定是“x ∀∈R ,20x x ->”C .直线1:210l ax y ++=,2:220x ay l ++=,12l l //的充要条件是12a =D .在ABC △中,若sin sin A B >,则A B >【答案】BD【解析】对于A ,当0x <,10x x +<,故A 不正确; 对于B ,“0x ∃∈R ,2000x x -≤”的否定是“x ∀∈R ,20x x ->”,故B 正确;对于C ,12//l l 等价于241a =,即12a =±,得12//l l 的充要条件是12a =±,故C 不正确; 对于D ,若sin sin A B >,由正弦定理可得ab >,由于大边对大角,故A B >,故D 正确,故选BD .11.下列四种说法中正确的有()A .命题“x ∀∈R ,231x x >+”的否定是“x ∃∈R ,231x x <+”;B .若不等式210ax bx ++>的解集为{}13x x -<<,则不等式23650ax bx ++<的解集为(,1)(5,)-∞-+∞C .复数z 满足2i 1z -=,z 在复平面对应的点为(),x y ,则22(2)1x y +-=D .已知1:32p x ≤≤,21:()10(0)q x a x a a-++≤>,若p 是q 的充分不必要条件,则实数a 的取值范围是1(0,][3,)3+∞ 【答案】BCD【解析】选项A :命题“x ∀∈R ,231x x >+”的否定应该是“0x ∃∈R ,02031x x ≤+”,故选项A 错误; 选项B :因为不等式210ax bx ++>的解集为{}13x x -<<,所以方程210ax bx ++=的两个根为1-和3,且0a <. 由213b a a ⎧-=⎪⎪⎨⎪=-⎪⎩,解出1323a b ⎧=-⎪⎪⎨⎪=⎪⎩,所以不等式23650ax bx ++<可化为2450x x -++<,即2450x x -->,解得1x <-或5x >.所以不等式23650ax bx ++<的解集为(,1)(5,)-∞-+∞,故选项B 正确;选项C :设i z a b =+,()2i 2i 1z a b -=+-==,所以满足22(2)1x y +-=,故选项C 正确;由21()10(0)x a x a a -++≤>,得到1()()0x a x a --≤.当1a ≥时,1a a >,所以有1:q x a a ≤≤,由题意可得1123a a ⎧≤⎪⎨⎪≥⎩,解得3a ≥;当01a <<时,1a a <,所以有1:q a x a ≤≤,由题意可得1213a a ⎧≤⎪⎪⎨⎪≥⎪⎩,解得103a <≤,因此,实数a 的取值范围是1(0,][3,)3+∞,故选项D 正确,故选BCD .12.下列选项中说法正确的是()A .若非零向量a ,b 满足0⋅>a b ,则a 与b 的夹角为锐角B .若命题p :存在0x ∈R ,使得20010x x -+<,则p 的否定是:对任意x ∈R ,都有210x x -+>C .已知()y f x =是R 上的可导函数,则“0()0f x '=”是“0x 是函数()y f x =的极值点”的必要不充分条件D .在ABC △中,cos cos B A >是A B >的充要条件【答案】CD【解析】对于A ,a ,b 同向时,a 与b 的夹角为0度,不是锐角,故A 不正确;对于B ,存在0x ∈R ,使得20010x x -+<的否定为:对任意x ∈R ,都有210x x -+≥,故B 不正确; 对于C ,已知()y f x =是R 上的可导函数,则“0()0f x '=”时,函数不一定有极值,若“0x 是函数()y f x =的极值点”,则一定有“0()0f x '=”,所以已知()y f x =是R 上的可导函数,则“()0'0f x =”是“0x 是函数()y f x =的极值点”的必要不充分条件,故C 正确;对于D ,,(0,π)A B ∈,cos y x =,(0,π)x ∈时单调递减,∴cos cos B A B A >⇔<,故D 正确, 故选CD .三、填空题.13.已知集合{,,}{0,1,2}a b c =,且若下列三个关系:①2a ≠;②2b =;③0c ≠,有且只有一个正确,则10010a b c ++=.【答案】201【解析】由{,,}{0,1,2}a b c =,得,,a b c 的取值情况如下:当0a =时,1b =,2c =或2b =,1c =,此时不满足条件;当1a =时,0b =,2c =或2b =,0c =此时不满足条件;当2a =时,1b =,0c =此时不满足条件;当2a =时,0b =,1c =此时满足条件;综上得2a =,0b =,1c =代入100102001201a b c ++=+=.14.已知:13p x -<<,:11q x m -<<+,若q 是p 的必要不充分条件,则实数m 的取值范围是.【答案】(2,)+∞【解析】由题意,命题:13p x -<<,:11q x m -<<+,因为q 是p 的必要不充分条件,即pq ,则13m +>,解得2m >,则实数m 的取值范围是(2,)+∞.15.设有两个命题:(1)不等式|||1|x x m ++>的解集为R ;(2)函数()(73)x f x m =-在R 上是增函数;如果这两个命题中有且只有一个是真命题,则m 的取值范围是.【答案】12m ≤<【解析】①∵不等式|||1|x x m ++>的解集为R ,而|||1|x x ++表示数轴上的x 到0和1-的距离之和,最小值等于1,∴1m <,②∵函数()(73)x f x m =-在R 上是增函数,∴731m ->,2m <, ∴当12m ≤<时,①不正确,而②正确,两个命题有且只有一个正确,实数m 的取值范围为12m ≤<.16.用列举法表示集合**(,)|5,,{}A x y x y x y =+=∈∈N N 是;用描述法表示“所有被4除余1的整数组成的集合”是.【答案】{(1,4),(2,3),(3,2),(4,1)},{|41,}x x k k ∈=+∈Z Z【解析】由题意{(1,4),(2,3),(3,2),(4,1)}A =,所有被4除余1的整数组成的集合为{|41,}x x k k ∈=+∈Z Z .。
高考数学考前必做训练一 集合与简易逻辑 函数

高三数学训练题(一) 集合与简易逻辑、函数(时间:100分钟 满分100分)一、选择题:本大题共12小题,每小题4分,共48分.在每个小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案填入下面的表格内.(1)若集合==-==+=B A y x y x B y x y x A 则},1|),{(},3|),{( Φ)()}1,2){((}1,2){()}2,1{(D C B A )((2)条件p :|x |>1,条件q :x <-2,则p 是q 的)(A 必要不充分条件 )(B 充分不必要条件 )(C 充要条件 )(D 非充分非必要条件(3)已知f (x )=⎩⎨⎧<≥)0()0(2x x x x ,⎩⎨⎧<-≥=)0()0()(2x x x x x g ,则=-)]2([g f)(A -4 )(B 4 )(C -2 )(D 2(4)定义集合A 、B 的一种运算:A *B ={x |x =x 1+x 2,x 1∈A ,x 2∈B },若A ={1,2,3}, B={1,2},则A *B 中的所有元素之和为(A )21 (B )18 (C )14 (D )9 (5)已知函数y =tan (2x +φ)的图象过点(12π,0),则φ可以是 ( ) (A )6π (B )-6π (C)-12π (D)12π (6)函数221+=x y 的反函数是22()og 2(2)()og (2)(3)A y l x xB y l x x =-->=-->()22()og (2)(3)()og 2(2)C y l x xD y l x x =->=-->(7)设全集为R ,A=}|5||{},065|{2a x x B x x x <-=>--(a 为常数),且11∈B ,则 ()()R A A B R=ð )(B ()R A B R=ð)(C ()()R R A B R =痧 )(D R B A =(8)函数322+-=x x y 在区间],0[m 上有最大值3,最小值2,则m 的取值范围是()[1,)()[0,2]()(,2]()[1,2]A B C D +∞-∞ (9)函数)0(|1|ln ≠-=a ax y 图象的对称轴方程是2=x ,那么a 等于11()()()2()222A B C D --(10)下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间),(∞+0上是减函数;(3)是偶函数.这样的函数是3||||211log ||222x x A y x B y x C y D y =+=+==()()()()()()(11)设)(x f 是定义在),(∞+∞-上的函数,对于任意,)()()(,x f x f x f R x +-=+∈111且当10≤<x 时,(),f x x =则=)5.5(f11()1()1()()23A B C D -(12)右图所示的某池塘中的浮萍蔓延的面积)(2m y 与时间t (月)的关系为:ta y =.有以下判断:①这个指数函数的底数为2;②第5个月后,浮萍面积就会超过302m ;③浮萍每月增加的面积都相等;④若浮萍蔓延到22m ,226,3m m 所经过的时间分别为,,,321t t t 则321t t t =+.其中判断正确的个数是()1()2()A B C 4)(3D二、填空题:本大题共4小题,每小题3分,共12分。
广西南宁市东盟中学2020届高考考前专项突破训练系列 之1《集合与简易逻辑》

(时间40分钟,满分80分)一、选择题1.设集合M ={0,1,2},N ={}2|320x x x -+≤,则M N =A .{1}B .{2}C .{0,1}D .{1,2}2.已知集合{}R x x x M ∈<-=),4)1(|2,{}3,2,1,0,1-=N ,则M N =A .{0,1,2}B .{-1,0,1,2}C .{-1,0,2,3}D .{0,1,2,3}3.下面是关于复数21z i=-+的四个命题:其中的真命题为1:2p z =22:2p z i =3:p z 的共轭复数为1i+4:p z 的虚部为-1A .23,p p B .12,p p C .,p p 24D .,p p 344.已知集合{||2,}A x x x R =≤∈,{4,}B x x Z =≤∈,则A B = A .(0,2)B .[0,2]C .{0,2]D .{0,1,2}5.设集合{}{}(x 2)(x 3)0,T 0S x x x =--≥=>,则S I T =A .[2,3]B .(-∞,2]∪[3,+∞)C .[3,+∞)D .(0,2]∪[3,+∞)6.设集合2{|430}A x x x =-+<,{|230}B x x =->,则A B =A .3(3,2--B .3(3,)2-C .3(1,2D .3(,3)27.已知集合{}022>-=x x x A ,{55B <<-=x x ,则A .AB =ΦI B .A B =R UC .AB ⊆D .B A ⊆8.已知集合{}|1{|31}x A x x B x =<=<,,则A .{}0AB x x =< B .A B R =C .{}1A B x x =>D .A B φ= 9.已知集合()(){}120,,A x x x x Z =+-<∈{}123B =,,,则=B A A .{}1B .{}2,1C .{}3,2,10,D .{}3,2,101,,-10.已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;则B 中所含元素的个数为A .3B .6C .8D .1011.已知命题1p :函数22x x y -=-在R 为增函数,2p :函数22x xy -=+在R 为减函数,则在命题1q :12p p ∨,2q :12p p ∧,3q :()12p p -∨和4q :()12p p ∧-中,真命题是A .1q ,3qB .2q ,3qC .1q ,4qD .2q ,4q 12.已知a 与b 均为单位向量,其夹角为θ,有下列四个命题1:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭22:1,3P a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是A.14,P P B .13,P P C .23,P P D .24,P P 请将选择题的答案填入下表:题号123456789101112答案二、填空题13.已知集合A ={-2,-1,0,1,2},B ={x |(x -1)(x +2)<0},则A ∩B =_______.14.设集合{}240A x x x m =-+=,{}1,2,4B =,.若{1}A B = ,则m =______.15.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:①:(,),22x y D x y ∀∈+≥-,②:(,),22x y D x y ∃∈+≥,③:(,),23x y D x y ∀∈+≤,④:(,),21x y D x y ∃∈+≤-.其中真命题是__________.(填写编号)16.α、β是两个平面,m 、n 是两条直线,有下列四个命题:①如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β.②如果m ⊥α,n ∥α,那么m ⊥n .③如果α∥β,α⊂m ,那么m ∥β.④如果m ∥n ,α∥β,那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有____________.(填写编号)参考答案:DACD BDBA CCCB {1,0}3①②②③④。
全品高考数学考前专题限时训练含答案(基础+提升)作业手册
全品高考数学考前专题限时训练含答案(基础+提升)作业手册-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN专题限时集训(一)[第1讲 集合与常用逻辑用语](时间:5分钟+30分钟)基础演练1.已知全集U ={x ∈Z |1≤x ≤5},集合A ={1,2,3},∁U B ={1,2},则A ∩B =( ) A .{1,2} B .{1,3} C .{3} D .{1,2,3}2.命题“对任意x ∈R ,都有x 3>x 2”的否定是( )A .存在x 0∈R ,使得x 30>x 2B .不存在x 0∈R ,使得x 30>x 2C .存在x 0∈R ,使得x 30≤x 20 D .对任意x ∈R ,都有x 3≤x 23.若p :(x -3)(x -4)=0,q :x -3=0,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.已知集合M ={x |x ≥x 2},N ={y |y =2x ,x ∈R },则M ∩N =( ) A .(0,1) B .[0,1] C .[0,1) D .(0,1]5.已知集合A ={0,1,2,3},B ={x |x 2-x =0},则集合A ∩B 的子集个数是________.提升训练6.已知全集I ={1,2,3,4,5,6},集合M ={3,4,5},N ={1,2,3,4},则图1-1中阴影部分表示的集合为( )图1-1A .{1,2}B .{1,2,6}C .{1,2,3,4,5}D .{1,2,3,4,6}7.已知集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪x -1x =0,x ∈R ,则满足A ∪B ={-1,0,1}的集合B 的个数是( )A .2B .3C .4D .98.命题“若a ,b ,c 成等比数列,则b 2=ac ”的逆否命题是( ) A .若a ,b ,c 成等比数列,则b 2≠ac B .若a ,b ,c 不成等比数列,则b 2≠ac C .若b 2=ac ,则a ,b ,c 成等比数列D .若b 2≠ac ,则a ,b ,c 不成等比数列9.已知集合M ={y |y =lg(x 2+1)},N ={x |4x <4},则M ∩N 等于( ) A .[0,+∞) B .[0,1) C .(1,+∞) D .(0,1]10.已知集合M ={x |x 2-3x =0},集合N ={x |x =2n -1,n ∈Z },则M ∩N =( ) A .{3} B .{0} C .{0,3} D .{-3}11.若a ,b 为实数,则“ab <1”是“0<a <1b ”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件 12.给出如下四个判断: ①∃x 0∈R ,e x 0≤0; ②∀x ∈R +,2x >x 2;③设集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x -1x +1<0,B ={x |x 2-2x +1-a 2<0,a ≥0},则“a =1”是“A ∩B ≠∅”的必要不充分条件;④a ,b 为单位向量,其夹角为θ,若|a -b |>1,则π3<θ≤π. 其中正确判断的个数是( ) A .1 B .2 C .3 D .413.命题“若f (x )是奇函数,则f (-x )是奇函数”的否命题是________________________________________________________________________.14.若集合P ={0,1,2},Q =(x ,y )⎩⎪⎨⎪⎧x -y +1>0,x -y -2<0,x ,y ∈P ,则集合Q 中元素的个数是__________.15.命题“存在实数x ,使得不等式(m +1)x 2-mx +m -1≤0”是假命题,则实数m 的取值范围是________.专题限时集训(二)[第2讲 平面向量与复数](时间:5分钟+30分钟)基础演练1.复数5i1+2i的虚部是( )A .1B .-1C .iD .-i2.若复数z 满足(z -3)(2-i)=5(i 为虚数单位),则在复平面内z 对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.在△ABC 中,“AB →·BC →>0”是“△ABC 是钝角三角形”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.向量a =(3,-4),向量|b|=2,若a·b =-5,则向量a 与b 的夹角为( )A .π3B .π6C .2π3D .3π45.已知平面向量a ,b ,若|a |=3,|a -b |=13,a ·b =6,则|b |=________,向量a ,b 夹角的大小为________.提升训练6.复数5i -2的共轭复数是( )A .-2+iB .2+iC .-2-iD .2-i7.在复平面内,复数z =(1+2i)2对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限8.已知复数z 1=(2-i)i ,复数z 2=a +3i(a ∈R ).若复数z 2=kz 1(k ∈R ),则a =( )A .32B .1C .2D .139.如果复数2-b i1+2i (b ∈R ,i 为虚数单位)的实部和虚部互为相反数,那么b 等于( )A . 2B .23C .-23D .210.已知△ABC 的三边长AC =3,BC =4,AB =5,P 为AB 边上任意一点,则CP →·(BA→-BC )的最大值为( )A .8B .9C .12D .15 11.已知向量a ·(a +2b )=0,|a |=|b |=1,且|c -a -2b|=1,则|c |的最大值为( ) A .2 B .4C .5+1D .3+112.已知a ,b ∈R ,i 是虚数单位.若(1+a i )(1-i )b +i=2-i ,则a +b i =________.13.在△ABC 中,AB =2,D 为BC 的中点.若AD →·BC →=-32,则AC =________.14.已知四边形ABCD 是边长为3的正方形,若DE →=2EC →,CF →=2FB →,则AE →·AF →的值为________.15.在平面直角坐标系xOy 中,已知点A 的坐标为(3,a ),a ∈R ,点P 满足OP →=λOA →,λ∈R ,|OA →|·|OP →|=72,则线段OP 在x 轴上的投影长度的最大值为________.专题限时集训(三)[第3讲 不等式与线性规划](时间:5分钟+30分钟)基础演练1.已知集合A ={x |0<x <2},B ={x |(x -1)(x +1)>0},则A ∩B = ( ) A .(0,1) B .(1,2)C .(-∞,-1)∪(0,+∞)D .(-∞,-1)∪(1,+∞)2.已知全集U =R ,集合M =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x -1x +1<0,N ={x |x 2-x <0},则集合M ,N 的关系用图示法可以表示为( )图3-13.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥1,x -y ≥0,2x -y -2≤0,则目标函数z =x -2y 的最大值为( )A .32 B .1C .-12D .-24.若a <b <0,则下列不等式不成立的是( )A .1a -b >1aB .1a >1bC .|a |>|b |D .a 2>b 25.若x >0,y >0,则x +yx +y的最小值为( )A . 2B .1C .22D .12提升训练6.已知集合A ={x |x 2-2x -3<0},集合B ={x |2x +1>1},则∁B A =( ) A .(3,+∞) B .[3,+∞)C .(-∞,-1]∪[3,+∞)D .(-∞,-1)∪(3,+∞)7.已知集合A ={x |x 2-6x +5≤0},B ={y |y =2x +2},则A ∩B =( ) A .∅ B .[1,2) C .[1,5] D .(2,5]8.已知向量a =(m ,1-n ),b =(1,2),其中m >0,n >0.若a ∥b ,则1m +1n的最小值是( )A .2 2B .3+2 2C .4 2D .3+ 29.已知M (x ,y )是不等式组⎩⎪⎨⎪⎧x ≥0,y ≥0,x -y +1≥0,2x +y -4≤0表示的平面区域内的动点,则(x +1)2+(y +1)2的最大值是( )A .10B .495C .13D .1310.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .若a 2+b 2=3c 2,则cos C 的最小值为( )A .12B .14C .32D .2311.设x ,y 满足约束条件⎩⎪⎨⎪⎧y ≥0,y ≤x ,x +2y -a ≤0,若目标函数z =3x +y 的最大值为6,则a =________.12.已知x ,y 均为正实数,且xy =x +y +3,则xy 的最小值为________.13.已知x ,y 满足⎩⎪⎨⎪⎧y -2≤0,x +3≥0,x -y -1≤0,则x +2y -6x -4的最大值是________.14.已知函数f (x )=x (x -a )(x -b )的导函数为f ′(x ),且f ′(0)=4,则a 2+2b 2的最小值为________.15.设x ,y 满足约束条件⎩⎪⎨⎪⎧2x -y +2≥0,8x -y -4≤0,x ≥0,y ≥0,若目标函数z =ax +by (a >0,b >0)的最大值为8,则ab 的最大值为________.专题限时集训(四)[第4讲 算法、推理证明、排列、组合与二项式定理](时间:5分钟+30分钟)基础演练1.给出下面类比推理的命题(其中Q 为有理数集,R 为实数集,C 为复数集):①“若a ,b ∈R ,则a -b =0⇒a =b ”,类比推出“若a ,b ∈C ,则a -b =0⇒a =b ”;②“若a ,b ,c ,d ∈R ,则复数a +b i =c +d i ⇒a =c ,b =d ”,类比推出“若a ,b ,c ,d ∈Q ,则a +b 2=c +d 2⇒a =c ,b =d ”;③“若a ,b ∈R ,则a -b >0⇒a >b ”,类比推出“若a ,b ∈C ,则a -b >0⇒a >b ”; ④“若x ∈R ,则|x |<1⇒-1<x <1”,类比推出“若z ∈C ,则|z |<1⇒-1<z <1”. 其中类比正确的为( ) A .①② B .①④ C .①②③ D .②③④2.二项式⎝⎛⎭⎫2x +1x 展开式中的常数项是( )A .15B .60C .120D .2403.执行如图4-1所示的程序框图,其输出结果是( )A .-54B .12C .54D .-124.现有3位男生和3位女生排成一行,若要求任何两位女生和任何两位男生均不能相邻,且男生甲和女生乙必须相邻,则这样的排法总数是( )A .20B .40C .60D .805.观察下列等式:13=12,13+23=32,13+23+33=62,13+23+33+43=102,….根据上述规律,第n 个等式为____________.提升训练6.阅读如图4-2所示的程序框图,若输入n 的值为1,则输出的S 的值为( )A .176B .160C .145D .1177.已知a n=3n +2,n ∈N *,如果执行如图4-3所示的程序框图,那么输出的S 等于( )A .18.5B .37C .185 D8.阅读如图4-4所示的程序框图,则输出s 的值为( )A .12B .32C .- 3D . 39.6个人站成一排,其中甲、乙必须站在两端,且丙、丁相邻,则不同站法的种数为( )A .12B .18C .24D .3610.⎝⎛⎭⎪⎫3x -13x 的展开式中各项系数之和为A ,所有偶数项的二项式系数和为B .若A +B =96,则展开式中含有x 2的项的系数为 ( )A .-540B .-180C .540D .18011.对任意实数x ,都有x 3=a 0+a 1(x -2)+a 2(x -2)2+a 3(x -2)3,则a 2=________. 12.航天员拟在太空授课,准备进行标号为0,1,2,3,4,5的六项实验,向全世界人民普及太空知识,其中0号实验不能放在第一项,且最后一项的标号小于它前面相邻一项的标号,则实验顺序的编排方法种数为________.(用数字作答)13.观察下列等式:121=1,12+221+2=53,12+22+321+2+3=73,12+22+32+421+2+3+4=93,则第n 个等式为__________________.14.阅读如图4-5所示的程序框图,若输入i =5,则输出的k 的值为________.图4-515.有n个球(n≥2,n∈N*),任意将它们分成两堆,求出两堆球数的乘积,再将其中一堆任意分成两堆,求出这两堆球数的乘积,如此下去,每次任意将其中一堆分成两堆,求出这两堆球数的乘积,直到不能分为止,记所有乘积之和为S n.例如,对于4个球有如下两种分法:(4)→(1,3)→(1,1,2)→(1,1,1,1),此时S4=1×3+1×2+1×1=6;(4)→(2,2)→(1,1,2)→(1,1,1,1),此时S4=2×2+1×1+1×1=6.于是发现S4为定值6,则S5的值为________.专题限时集训(五)A[第5讲 函数、基本初等函数Ⅰ的图像与性质](时间:5分钟+30分钟)基础演练1.已知定义在复数集C 上的函数f (x )满足f (x )=⎩⎪⎨⎪⎧1+x ,x ∈R ,(1-i )x ,x ∉R ,则f (1+i)=( )A .-2B .0C .2D .2+i2.下列函数中,在定义域内既是奇函数又是增函数的是( )A .y =⎝⎛⎭⎫12 B .y =sin xC .y =x 3D .y =log 12x3.已知a =21.2,b =0.50.8,c =log 23则( ) A .a >b >c B .c >b >a C .c >a >b D .a >c >b4.已知函数y =f (2x )+x 是偶函数,且f (2)=1,则f (-2)=( ) A .2 B .3 C .4 D .55.已知函数f (x )=⎩⎪⎨⎪⎧log 4 x ,x >0,3x ,x ≤0,则f ⎣⎡⎦⎤f ⎝⎛⎭⎫14=________. 提升训练6.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=2x ,则f (-3)=( )A .18B .-18C .8D .-87.设函数f (x )=⎩⎪⎨⎪⎧2-x -1,x ≤0,x 12,x >0,若f (x )>1,则x 的取值范围是( )A .(-1,1)B .(-1,+∞)C .(-∞,-1)∪(1,+∞)D .(-∞,-2)∪(0,+∞)8.下列函数中,在区间(0,+∞)上单调递减,且是偶函数的是( ) A .y =x 2 B .y =-x 3 C .y =-lg|x | D .y =2x9.设a =log 32,b =log 23,c =log 125,则( )A .c <b <aB .a <c <bC .c <a <bD .b <c <a10.定义区间[x 1,x 2]的长度为x 2-x 1.若函数y =|log 2x |的定义域为[a ,b ],值域为[0,2],则区间[a ,b ]的长度的最大值为( )A .152B .154C .3D .3411.设函数f (x )=x 2AC 图5-112.已知函数f (x )对定义域内的任意x ,都有f (x +2)+f (x )<2f (x +1),则函数f (x )可以是( )A .f (x )=2x +1B .f (x )=e xC .f (x )=ln xD .f (x )=x sin x13.函数f (x )=16-x -x 2的定义域是________.14.已知y =f (x )是定义在R 上的偶函数,且在区间[0,+∞)上单调递增,则满足f (m )<f (1) 的实数m 的取值范围是________.15.设函数f (x )=a ln x +b lg x +1,则f (1)+f (2)+…+f (2014)+f ⎝⎛⎭⎫12+f ⎝⎛⎭⎫13+…+f ⎝⎛⎭⎫12014=________.专题限时集训(五)B[第5讲 函数、基本初等函数Ⅰ的图像与性质](时间:5分钟+30分钟)基础演练1.对于函数y =f (x ),x ∈R ,“函数y =|f (x )|的图像关于y 轴对称”是“y =f (x )为奇函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.下列函数中,既是偶函数又在区间(1,2)上单调递增的是( ) A .y =log 2|x | B .y =cos 2xC .y =2x -2-x 2 D .y =log 22-x2+x3.f (x )=tan x +sin x +1,若f (b )=2,则f (-b )=( ) A .0 B .3 C .-1 D .-24.已知函数f (x )=⎩⎪⎨⎪⎧2x +1,x <1,x 2+ax ,x ≥1,若f [f (0)]=4a ,则实数a =( )A .12B .45C .2D .95.已知y =f (x )是定义在R 上的奇函数,且当x ≥0时,f (x )=-14x +12x ,则此函数的值域为________.提升训练6.函数y =1x -sin x的大致图像是( )AC 图5-27.已知定义在R 上的函数f (x )满足f (4)=2-3,且对任意的x 都有f (x +2)=1-f (x ),则f (2014)=( )A .-2- 3B .-2+ 3C .2- 3D .2+ 38.设a =14,b =log 985,c =log 83,则a ,b ,c 的大小关系是( )A .a >b >cB .a >c >bC .c >a >bD .c >b >a9.已知定义在R 上的函数f (x )满足f (x )+2f ⎝ ⎛⎭⎪⎫x +2012x -1=3x ,则f (2014)=( )A .0B .2010C .-2010D .201410.已知函数y =f (x ),若对于任意的正数a ,函数g (x )=f (x +a )-f (x )都是其定义域上的增函数,则函数y =f (x )可能是( )A .y =2xB .y =log 3(x +3)C .y =x 3D .y =-x 2+4x -611.若a >2,b >2,且12log 2(a +b )+log 22a =12log 21a +b +log 2b2,则log 2(a -2)+log 2(b-2)=( )A .2B .1C .12D .012.已知定义在R 上的函数y =f (x )在区间(-∞,a )上是增函数,且函数y =f (x +a )是偶函数,当x 1<a ,x 2>a ,且|x 1-a |<|x 2-a |时,有( )A .f (x 1)>f (x 2)B .f (x 1)≥f (x 2)C .f (x 1)<f (x 2)D .f (x 1)≤f (x 2)13.若x ,y ∈R ,设M =x 2-2xy +3y 2-x +y ,则M 的最小值为________.14.设函数f (x )的定义域为D ,若存在非零实数l ,使得对于任意x ∈M (M ⊆D ),有x +l ∈D ,且f (x +l )≥f (x ),则称f (x )为M 上的“l 高调函数”.如果定义域是[0,+∞)的函数f (x )=(x -1)2为[0,+∞)上的“m 高调函数”,那么实数m 的取值范围是________. 15.函数f (x )=2sin πx 与函数g (x )=3x -1的图像的所有交点的橫坐标之和为________.专题限时集训(六)[第6讲 函数与方程、函数模型及其应用](时间:5分钟+40分钟)基础演练1.“m <0”是“函数f (x )=m +log 2x (x ≥1)存在零点”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件2.函数f (x )=2x +4x -3的零点所在的区间是( )A .⎝⎛⎭⎫14,12B .⎝⎛⎭⎫-14,0 C .⎝⎛⎭⎫0,14 D .⎝⎛⎭⎫12,343.函数f (x )=tan x -1x 在区间⎝⎛⎭⎫0,π2内零点的个数是( )A .0B .1C .2D .34.已知函数f (x )与g (x )的图像在R 上连续,由下表知方程f (x )=g (x )的实数解所在的区间是( )A .(-1C .(1,2) D .(2,3)5.若函数f (x )=ax +b 的零点为x =2,则函数g (x )=bx 2-ax 的零点是x =0和x =________.提升训练6.已知函数f (x )=⎩⎪⎨⎪⎧0,x ≤0,e x ,x >0,则使函数g (x )=f (x )+x -m 有零点的实数m 的取值范围是( )A .[0,1)B .(-∞,1)C .(-∞,0]∪(1,+∞)D .(-∞,1]∪(2,+∞)7.已知函数f (x )是定义域为R 的奇函数,且当x ≤0时,f (x )=2x -12x +a ,则函数f (x )的零点的个数是( )A .1B .2C .3D .48.已知函数f (x )=4-a x ,g (x )=4-log b x ,h (x )=4-x c 的图像都经过点P ⎝⎛⎭⎫12,2,若函数f (x ),g (x ),h (x )的零点分别为x 1,x 2,x 3,则x 1+x 2+x 3=( )A .76B .65C .54D .329.若直角坐标平面内的两个不同的点P ,Q 满足条件:①P ,Q 都在函数y =f (x )的图像上;②P ,Q 关于原点对称.则称点对[P ,Q ]是函数y =f (x )的一对“友好点对”(注:点对[P ,Q ]与[Q ,P ]看作同一对“友好点对”).已知函数f (x )=⎩⎪⎨⎪⎧⎝⎛⎭⎫12,x >0,-x 2-4x ,x ≤0,则此函数的“友好点对”有( )A .0对B .1对C .2对D .3对10.若关于x 的方程⎪⎪⎪⎪x +1x -⎪⎪⎪⎪x -1x -kx -1=0有五个互不相等的实根,则k 的取值范围是( )A .⎝⎛⎭⎫-14,14 B .⎝⎛⎭⎫-∞,-14∪⎝⎛⎭⎫14,+∞ C .⎝⎛⎭⎫-∞,-18∪⎝⎛⎭⎫18,+∞ D .⎝⎛⎭⎫-18,0∪⎝⎛⎭⎫0,18 11.已知函数f (x )=1x +2-m |x |有三个零点,则实数m 的取值范围为________.12.已知定义在R 上的函数f (x )为增函数,且对任意x ∈(0,+∞),有f [f (x )-log 2x ]=1恒成立,则函数f (x )的零点为________.13.已知函数g (x )=⎩⎪⎨⎪⎧1,x >0,0,x =0,-1,x <0,若函数f (x )=2x ·g (ln x )+1-x 2,则函数f (x )的零点个数为________.14.已知函数f (x )=2x ,x ∈R .(1)当m 取何值时,方程|f (x )-2|=m 分别有一个解、两个解?(2)若不等式f 2(x )+f (x )-m >0在R 上恒成立,求m 的取值范围.15.某单位拟建一个扇环面形状的花坛(如图6-1所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米,设小圆弧所在圆的半径为x米,圆心角为θ(弧度).(1)求θ关于x的函数关系式.(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比值为y,求y关于x的函数关系式,并求出x为何值时,y取得最大值?16.如图6-2所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径r=310 mm,滴管内液体忽略不计.(1)如果瓶内的药液恰好156 min滴完,问每分钟滴下多少滴?(2)在条件(1)下,设开始输液x min后,瓶内液面与进气管的距离为h cm,已知当x=0时,h=13,试将h表示为x的函数.(注:1 cm3=1000 mm3)专题限时集训(七)[第7讲 导数及其应用](时间:5分钟+40分钟)基础演练1.已知f (x )=x 2+2xf ′(1),则f ′(0)等于( ) A .0 B .-4 C .-2 D .22.曲线f (x )=x 3+x -2在点P 0处的切线平行于直线y =4x -1,则P 0点的坐标为( ) A .(1,0) B .(2,8)C .(2,8)或(-1,-4)D .(1,0)或(-1,-4) 3.如图7-1所示,阴影区域是由函数y =cos x 的一段图像与x 轴围成的封闭图形,那么这个阴影区域的面积是( )A .1B .2C .π2 D .π4.函数f (x )=12x 2-ln x 的最小值为( )A .12B .1C .-2D .35.曲线y =ln x -1在x =1处的切线方程为____________.提升训练6.若曲线y =ax 2-ln x 在点(1,a )处的切线平行于x 轴,则a =( )A .1B .12C .0D .-17.函数f (x )=x cos x ( )AC 图7-28.如图7-3所示,长方形的四个顶点为O (0,0),A (4,0),B (4,2),C (0,2),曲线y=x 经过点B .现将一质点随机投入长方形OABC 中,则质点落在图中阴影区域的概率是( )A .512B .12C .23D .349.已知a ≥0,函数f (x )=(x 2-2ax )e x,若f (x )在区间[-1,1]上是减函数,则a 的取值范围是( )A .0<a <34B .12<a <34C .a ≥34D .0<a <1210.方程f (x )=f ′(x )的实数根x 0叫作函数f (x )的“新驻点”.如果函数g (x )=x ,h (x )=ln(x +1),φ(x )=cos x ⎝⎛⎭⎫x ∈⎝⎛⎭⎫π2,π的“新驻点”分别为α,β,γ,那么α,β,γ的大小关系是( )A .α<β<γB .α<γ<βC .γ<α<βD .β<α<γ11.已知定义在区间⎝⎛⎭⎫0,π2上的函数f (x ),f ′(x )是它的导函数,且恒有f (x )<f ′(x )·tan x成立,则( )A .3f ⎝⎛⎭⎫π4>2f ⎝⎛⎭⎫π3B .f (1)<2f ⎝⎛⎭⎫π6sin 1C .2f ⎝⎛⎭⎫π6>f ⎝⎛⎭⎫π4D .3f ⎝⎛⎭⎫π6<f ⎝⎛⎭⎫π312.函数f (x )=2ln x +x 2在点x =1处的切线方程是________.13.由曲线y =2x 2,直线y =-4x -2,x =1围成的封闭图形的面积为________. 14.已知函数f (x )=x 2+2x ,g (x )=x e x . (1)求f (x )-g (x )的极值;(2)当x ∈(-2,0)时,f (x )+1≥ag (x )恒成立,求实数a 的取值范围.15.已知函数f (x )=x ln x . (1)求f (x )的单调区间和极值;(2)设A (x 1,f (x 1)),B (x 2,f (x 2)),且x 1≠x 2,证明:f (x 2)-f (x 1)x 2-x 1<f ′⎝⎛⎭⎫x 1+x 22.16.设函数f (x )=e x -ax -2. (1)求f (x )的单调区间;(2)若a =1,k 为整数,且当x >0时,(x -k )f ′(x )+x +1>0恒成立,求k 的最大值.专题限时集训(八)[第8讲 三角函数的图像与性质](时间:5分钟+40分钟)基础演练1.函数y =sin x sin ⎝⎛⎭⎫π2+x 的最小正周期是( )A .π2B .2πC .πD .4π2.将函数y =sin ⎝⎛⎭⎫x +π6(x ∈R )的图像上所有的点向左平移π4个单位长度,再把所得图像上各点的横坐标扩大到原来的2倍,所得的函数图像的解析式为( )A .y =sin ⎝⎛⎭⎫2x +5π12(x ∈R )B .y =sin ⎝⎛⎭⎫x 2+5π12(x ∈R )C .y =sin ⎝⎛⎭⎫x 2-π12(x ∈R )D .y =sin ⎝⎛⎭⎫x 2+5π24(x ∈R )3.为了得到函数y =cos ⎝⎛⎭⎫2x +π3的图像,可将函数y =sin 2x 的图像( )A .向左平移5π6B .向右平移 5π6C .向左平移 5π12D .向右平移5π124.已知向量a =(sin θ,cos θ),b =(2,-3),且a ∥b ,则tan θ=________.5.若点P (cos α,sin α) 在直线y =-2x 上,则tan ⎝⎛⎭⎫α+π4=________.提升训练6.函数f (x )=2sin(ωx +φ)(ω>0,0≤φ≤π)的部分图像如图8-1所示,其 中A ,B 两点之间的距离为5,则f (x )的单调递增区间是( )A .[6k -1,6k +2](k ∈Z )B .[6k -4,6k -1](k ∈Z )C .[3k -1,3k +2](k ∈Z )D .[3k -4,3k -1](k ∈Z )7. 已知P 是圆(x -1)2+y 2=1上异于坐标原点O 的任意一点,直线OP 的倾斜角为θ.若|OP |=d ,则函数d =f (θ)的大致图像是( )AC 图8-28.函数f (x )=sin(2x +φ)⎝⎛⎭⎫|φ|<π2的图像向左平移π6个单位后关于原点对称,则函数f (x )在区间⎣⎡⎦⎤0,π2上的最小值为( )A .-32B .-12C .12D .329.已知f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2,满足f (x )=-f (x +π),f (0)=12,则g (x )=2cos(ωx +φ)在区间⎣⎡⎦⎤0,π2上的最大值与最小值之和为( )A .3-1B .3-2C .23-1D .210.将函数f (x )=3sin 2x -cos 2x 的图像向左平移m 个单位⎝⎛⎭⎫m >-π2,若所得的图像关于直线x =π6对称,则m 的最小值为( )A .-π6B .-π3C .0D .π1211.如图8-3所示,直角三角形POB 中,∠PBO =90°,以O 为圆心、OB 为半径作圆弧交OP 于A 点,若AB 等分△OPB 的面积,且∠AOB =α,则αtan α=________.12.将函数f (x )=sin ⎝⎛⎭⎫3x +π4的图像向右平移π3个单位长度,得到函数y =g (x )的图像,则函数y =g (x )在区间⎣⎡⎦⎤π3,2π3上的最小值为 ________ .13.已知α∈R ,sin α+3cos α=5,则tan 2α=________.14.已知函数f (x )=4sin 2⎝⎛⎭⎫π4+x -23cos 2x -1,且π4≤x ≤π2.(1)求f (x )的最大值及最小值;(2)求f (x )在定义域上的单调递减区间.15.已知函数f (x )=23cos x sin x +2cos 2 x .(1)求f ⎝⎛⎭⎫4π3的值;(2)当x ∈⎣⎡⎦⎤0,π2时,求函数f (x )的值域.16.在平面直角坐标系xOy 中,点A (cos θ,2sin θ),B (sin θ,0),其中θ∈R .(1)当θ=2π3时,求向量AB →的坐标;(2)当θ∈⎣⎡⎦⎤0,π2时,求|AB →|的最大值.专题限时集训(九)[第9讲 三角恒等变换与解三角形](时间:5分钟+40分钟)基础演练1.在钝角三角形ABC 中,AB =3,AC =1,B =30°,则△ABC 的面积为( ) A .14 B .32C .34D .122.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若a =2,A =45°,B =105°,则c = ( )A .32B .1C . 3D .6+223.函数f (x )=sin 2x -sin ⎝⎛⎭⎫2x +π3的最小值为( )A .0B .-1C .- 2D .-24.若cos 2θ=13,则sin 4θ+cos 4θ的值为( )A .1318B .1118C .59D .15.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .若sin 2 A +sin 2C -sin 2B =3sin A sin C ,则B =________.提升训练6.已知sin 2α=13,则cos 2 ⎝⎛⎭⎫α-π4=( )A .13B .-13C .23D .-237.已知△ABC 的外接圆O 的半径为1,且OA →·OB →=-12,C =π3.从圆O 内随机取一点M ,若点M 在△ABC 内的概率恰为334π,则△ABC 为( )A .直角三角形B .等边三角形C .钝角三角形D .等腰直角三角形8.已知A ,B ,C 是△ABC 的三个内角,其对边分别为a ,b ,c .若(sin A +sin B )(sin A -sin B )=sin C (2sin A -sin C ),则B =( )A .π4B .π3C .π2D .2π39.在△ABC 中,若AB →·AC →=7,||AB →-AC →=6,则△ABC 的面积的最大值为( ) A .24 B .16 C .12 D .810.已知△ABC 的重心为G ,内角A ,B ,C 的对边分别为a ,b ,c .若aGA →+bGB →+33cGC →=0,则A 等于( ) A . π6 B .π4C . π3D .π211.已知α∈⎝⎛⎭⎫-π2,0,cos(π-α)=-45,则tan 2α=______ .12.在△ABC 中,C =60°,AB =3,AB 边上的高为43,则AC +BC =________.13.已知∠MON =60°,由此角内一点A 向角的两边引垂线,垂足分别为B ,C ,AB =a ,AC =b ,若a +b =2,则△ABC 外接圆的直径的最小值是________.14.已知△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2cos 2B2=3sin B ,b =1.(1)若A =5π12,求c ;(2)若a =2c ,求△ABC 的面积.15.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若a cos 2C 2+c cos 2A 2=32b .(1)求证:a ,b ,c 成等差数列;(2)若B =60°,b =4,求△ABC 的面积.16.如图9-1所示,已知OPQ 是半径为3,圆心角为π3的扇形,C 是扇形弧上的动点(不与P ,Q 重合),ABCD 是扇形的内接矩形,记∠COP =x ,矩形ABCD 的面积为f (x ).(1)求函数f (x )的解析式,并写出其定义域;(2)求函数y =f (x )+f ⎝⎛⎭⎫x +π4的最大值及相应的x 值.专题限时集训(十)[第10讲数列、等差数列、等比数列](时间:5分钟+40分钟)基础演练1.若等差数列{a n}的前n项和为S n,已知a5=8,S3=6,则a9=() A.8 B.12C.16 D.242.等比数列{a n}中,a2=1,a8=64,则a5=()A.8 B.12C.8或-8 D.12或-123.已知等差数列{a n}中,a3+a4-a5+a6=8,则S7=()A.8 B.21C.28 D.354.已知数列{a n}为等差数列,且a1+a7+a13=π,则tan(a2+a12)的值为()A. 3 B.- 3C.33 D.-335.等比数列{a n}满足对任意n∈N*,2(a n+2-a n)=3a n+1,a n+1>a n,则数列{a n}的公比q=________.提升训练6.设等差数列{a n}的前n项和为S n,若a2+a4+a9=24,则S9= ()A.36 B.72C.144 D.707.设S n为等差数列{a n}的前n项和,若a1=1,公差d=2,S n+2-S n=36,则n=() A.5 B.6C.7 D.88.已知数列{a n}是各项均为正数的等比数列,若a2=2,2a3+a4=16,则a5=() A.4 B.8C.16 D.329.在数列{a n}中,“a n=2a n-1(n=2,3,4,…)”是“{a n}是公比为2的等比数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10.在各项均为正数的等比数列{a n}中,a m+1a m-1=2a m(m≥2),数列{a n}的前n项积为T n,若T2k-1=512(k∈N*),则k的值为()A.4 B.5C.6 D.711.设等差数列{a n}的前n项和为S n,若S9=11,S11=9,则S20=________.12.已知等比数列{a n}的前n项积为T n,若a3a4a8=8,则T9=________.13.已知等比数列{a n}中,a4+a8=⎠⎛24-x2dx,则a6(a2+2a6+a10)=________.14.已知数列{a n}的首项为1,其前n项和为S n,且对任意正整数n,有n,a n,S n成等差数列.(1)求证:数列{S n+n+2}为等比数列;(2)求数列{a n}的通项公式.15.已知数列{a n}的前n项和为S n,a1=1且3a n+1+2S n=3(n为正整数).(1)求数列{a n}的通项公式;(2)若∀n∈N*,32k≤S n恒成立,求实数k的最大值.16.已知数列{a n}是公差不为零的等差数列,a1=2且a2,a4,a8成等比数列.(1)求数列{a n}的通项公式;(2)若{b n-(-1)n a n}是等比数列,且b2=7,b5=71,求数列{b n}的前2n项和.专题限时集训(十一)[第11讲 数列求和及数列的简单应用](时间:5分钟+40分钟)基础演练1.等差数列{a n }的通项公式为a n =2n +1,其前n 项和为S n ,则数列⎩⎨⎧⎭⎬⎫S n n 的前10项和为( )A .70B .75C .100D .1202.已知等比数列{a n }的各项均为正数,且a 5a 6+a 4a 7=18,则log 3a 1+log 3a 2+…+log 3a 10=( )A .12B .10C . 8D .2+log 3 53.等差数列{a n }的前n 项和为S n (n =1,2,3,…),若当首项a 1和公差d 变化时, a 5+a 8+a 11是一个定值,则下列选项中为定值的是( )A .S 17B .S 16C .S 15D .S 144.数列{a n }的前n 项和为S n ,若a n =1n (n +2),则S 10等于( )A .1112B .1124C .175132D .1752645.设等比数列{a n }的各项均为正数,其前n 项和为S n .若a 1=1,a 3=4,S k =63,则k =________.提升训练6.等差数列{a n }的前n 项和为S n ,且满足S 35=S 3992 ,a =(1,a n ),b =(2014,a 2014),则a ·b 的值为( )A . 2014B . -2014C . 1D .07.已知一次函数f (x )=kx +b 的图像经过点P (1,2)和Q (-2,-4),令a n =f (n )f (n +1),n ∈N *,记数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为S n ,当S n =625时,n 的值为( )A .24B .25C .23D .268.已知幂函数y =f (x )的图像过点(4,2),令a n =f (n +1)+f (n ),n ∈N *,记数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为S n ,则当S n =10时,n 的值是( )A . 110B . 120C . 130D . 1409.已知a n =⎠⎛0n (2x +1)d x(n ∈N *),数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为S n ,数列{b n }的通项公式为b n=n -8,则b n S n 的最小值为( )A .-3B .-4C .3D .410.设数列{a n }满足a 1=2,a n +1=4a n -3n +1,n ∈N *,则数列{a n }的前n 项和可以表示为( )A .B .C .D .11.设直线nx +(n +1)y =2(n ∈N *)与两坐标轴围成的三角形的面积为S n ,则S 1+S 2+…+S 2014=________ .12.在数列{a n }中,a 1=1,a 2=2,且a n +2-a n =1+(-1)n (n ∈N *),则S 100=________.13.已知函数 f (x )=⎩⎨⎧(-1)n sin πx2+2n ,x ∈[2n ,2n +1),(-1)n +1 sin πx 2+2n +2,x ∈[2n +1,2n +2)(n ∈N ),若数列{a m }满足a m =f ⎝⎛⎭⎫m 2(m ∈N *),且{a m }的前m 项和为S m ,则S 2014-S 2006=________. 14.已知数列{a n }与{b n },若a 1=3,且对任意正整数n 满足a n +1-a n =2, 数列{b n }的前n 项和S n =n 2+a n .(1)求数列{a n },{b n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫1b n b n +1的前n 项和T n .15. 已知函数f (x )=4x ,数列{a n }中,2a n +1-2a n +a n +1a n =0,a 1=1,且a n ≠0, 数列{b n }中, b 1=2,b n =f ⎝⎛⎭⎫1a n -1(n ≥2,n ∈N *).(1)求证:数列⎩⎨⎧⎭⎬⎫1a n 是等差数列,并求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫b n a n 的前n 项和T n .16. 中国人口已经出现老龄化与少子化并存的结构特征,测算显示中国是世界上人口老龄化速度最快的国家之一,再不实施“放开二胎”新政策,整个社会将会出现一系列的问题.若某地区2012年人口总数为45万,专家估计实施 “放开二胎” 新政策后人口总数将发生如下变化:从2013年开始到2022年每年人口比上年增加0.5万,从2023年开始到2032年每年人口为上一年的99%.(1)求实施新政策后第n 年的人口总数a n 的表达式(注:2013年为第一年).(2)若新政策实施后2013年到2032年的人口平均值超过49万,则需调整政策,否则继续实施.问2032年后是否需要调整政策?(0.9910=(1-0.01)10≈0.9)专题限时集训(十二)A[第12讲 空间几何体的三视图、表面积及体积](时间:5分钟+30分钟)基础演练1.某几何体的三视图如图12-1所示,根据图中标出的尺寸(单位:cm)可得这个几何体的体积是( )A .13 cm 3B .23 cm 3C .4 cm 3D .8cm 3图 图2.图12-2是一个封闭几何体的三视图,则该几何体的表面积为( )A .7πB .8πC .9πD .11π3. 一只蚂蚁从正方体 ABCD -A 1B 1C 1D 1的顶点A 处出发,经正方体的表面,按最短路线爬行到达顶点 C 1的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )图12-A .①② B .①③ C .②④ D .③④4. 某四棱锥的三视图如图12-5( )图12-5A .2∈A ,且4∈AB .2∈A ,且4∈AC . 2∈A ,且25∈AD .2∈A ,且17∈A提升训练5.如图12-6所示,三棱柱ABC -A 1B 1C 1的侧棱长和底边长均为2,且侧棱 AA 1⊥底面A 1B 1C 1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为( )A .3B .23C .4图12-6 图6.某几何体的三视图如图12-7所示,则它的体积是( )A .8+433B .8+423C .8+233D .3237.若某棱锥的三视图(单位:cm)如图12-8所示,则该棱锥的体积等于( )A .10 cm 3B .33 D .40 cm 3图 8.一个简单组合体的三视图及尺寸如图12-9所示,则该组合体的体积为( )A .42B .48C .56D .449. 某由圆柱切割获得的几何体的三视图如图12-10所示,其中俯视图是中心角为60°的扇形, 则该几何体的侧面积为( )A .12+103πB .6+103π C . 12+2π D .6+4π图12-10 图12-1110. 如图12-11所示,边长为2的正方形ABCD 中,点E ,F 分别是边AB ,BC 的中点,△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′.若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为()A.2 B.62 C.112 D.5211.边长是22的正三角形ABC内接于体积为43π的球O,则球面上的点到平面ABC的最大距离为________.专题限时集训(十二)B[第12讲 空间几何体的三视图、表面积及体积](时间:5分钟+30分钟)基础演练1.某空间几何体的三视图如图12-12所示,则该几何体的体积为( )A .83B .8C .323D .16图 2.一个几何体的三视图如图12-13所示,则该几何体的体积为( )A .13B .23 C .2 D .13. 图12-14 ( )A .3+π6B . 3+43πC .33+43πD .33+π64. 一个四面体的四个顶点在空间直角坐标系O -xyz 中的坐标分别是(0,0,0),(1,2,0),(0,2,2),(3,0,1),则该四面体以yOz 平面为投影面的正视图的面积为( )A .3B .52C . 2D .72提升训练5.一个几何体的三视图如图12-15所示,其中正视图是边长为2的正三角形,俯视图为正六边形,则该几何体的侧视图的面积为( )A .32B .1C .52D .126.一个几何体的三视图如图12-16所示,则它的体积为( )A .203B .403C .20D .407. 已知某几何体的三视图如图12-17所示,其中俯视图是圆,则该几何体的体积为( )A .π3B .2π3C . 23D .13图 8.图12-18是一个几何体的三视图,则该几何体的体积是( )A .54B .27C .18D .99. 用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图12-19所示),则鸡蛋中心(球心)与蛋托底面的距离为___________.图10. 直三棱柱ABC -A 1B 1C 1的各顶点都在同一个球面上.若AB =AC =AA 1=2,∠BAC=120°,则此球的表面积为________.11. 如图12-20所示,已知球O 是棱长为1的正方体ABCD -A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为________.专题限时集训(十三)[第13讲空间中的平行与垂直](时间:5分钟+40分钟)基础演练1.能够得出平面α与平面β一定重合的条件是:它们的公共部分有() A.两个公共点B.三个公共点C.无数个公共点D.共圆的四个公共点2.直线a⊥平面α,b∥α,则a与b的关系为()A.a⊥b,且a与b相交 B.a⊥b,且a与b不相交C.a⊥b D.a与b不一定垂直3.a,b,c表示不同直线,M表示平面,给出四个命题:①若a∥M,b∥M,则a∥b或a,b相交或a,b异面;②若b⊂M,a∥b,则a∥M;③a⊥c,b⊥c,则a∥b;④a⊥M,b⊥M,则a∥b.其中为真命题的是()A.①② B.②③ C.③④ D.①④4.设α,β,γ为平面,m,n为直线,则m⊥β的一个充分条件是() A.α⊥β,α∩β=n,m⊥nB.α∩γ=m,α⊥γ,β⊥γC.α⊥β,m⊥αD.n⊥α,n⊥β,m⊥α5.已知m,n,l是不同的直线,α,β,γ是不同的平面,给出下列命题:①若m∥n,n⊂α,则m∥α;②若m⊥l,n⊥l,则m∥n;③若m⊥n,m∥α,n∥β,则α⊥β;④若α⊥γ,β⊥γ,则α∥β.其中真命题有()A.0个 B.1个C.2个 D.3个提升训练6.已知α,β是两个不同的平面,则α∥β的一个充分条件是()A.存在一条直线l,l⊂α,l∥βB.存在一个平面γ,γ⊥α,γ⊥βC.存在一条直线l,l⊥α,l⊥βD.存在一个平面γ,γ⊥α,γ∥β7.设l为直线,α,β是两个不同的平面,下列命题中为真的是()A.若l∥α,l∥β,则α∥β B.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥β D.若α⊥β,l∥α,则l⊥β8.在正方体中,二面角A1BDA的正切值是()A. 2 B.22 C. 2 D.129.已知α,β是两个不同的平面,m,n是两条不同的直线,给出下列命题:①若m⊥α,m⊂β,则α⊥β;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β;③如果m⊂α,n ⊄α,m ,n 是异面直线,那么n 与α相交;④若α∩β=m ,n ∥m ,且n ⊄α,n ⊄β,则n ∥α,且n ∥β.其中为真命题的是 ( )A .①②B .②③C . ③④D .①④ 10.如图13-1所示,正方体ABCD -A 1B 1C 1D 1的棱长为1,线段B 1D 1上有两个动点E ,F ,且EF =12,则下列结论中错误的是( )A .AC ⊥BEB .EF ∥平面ABCDC .三棱锥A -BEF 的体积为定值D .△AEF 的面积与△BEF 的面积相等图 图13-211.如图13-2所示,已知三个平面α,β,γ互相平行,a ,b 是异面直线,a 与α,β,γ分别交于A ,B ,C 三点,b 与α,β,γ分别交于D ,E ,F 三点,连接AF 交平面β于点G ,连接CD 交平面β于点H ,则四边形BGEH 必为________.12. 在三棱锥C -ABD 中(如图13-3所示),△ABD 与△CBD 是全等的等腰直角三角形,O 为斜边BD 的中点,AB =4,二面角A -BD -C 的大小为60°,并给出下面结论:①AC ⊥BD ;②AD ⊥CO ;③△AOC 为正三角形;④ cos ∠ADC =34;⑤四面体ABCD 的外接球的表面积为 32π.其中正确的是________.13. 已知四棱锥P -ABCD 的底面ABCD 是边长为2的正方形,且俯视图如图13-4所示.关于该四棱锥的下列说法中:①该四棱锥中至少有两组侧面互相垂直;②该四棱锥的侧面中可能存在三个直角三角形;③该四棱锥中不可能存在四组互相垂直的侧面;④该四棱锥的四个侧面不可能都是等腰三角形.其中,所有正确说法的序号是________________.14.如图13-5所示,正方形ABCD和四边形ACEF所在的平面互相垂直,EF∥AC,AB=2,CE=EF=1.(1)求证:AF∥平面BDE;(2)求证:CF⊥平面BD F.15.如图13-6所示,平行四边形ABCD中,BD⊥CD,正方形ADEF所在的平面和平面ABCD垂直,H是BE的中点,G是AE,DF的交点.(1)求证:GH∥平面CDE;(2)求证:BD⊥平面CDE.16.已知在梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,CD=3,点E 是线段AB的中点,G为CD的中点,现沿ED将△AED折起到△PED位置,使PE⊥EB.(1)求证:平面PEG⊥平面PCD;(2)求点A到平面PDC的距离.专题限时集训(十四)[第14讲 空间向量与立体几何](时间:5分钟+40分钟)基础演练1. 直线l 1的方向向量s 1=(1,0,-2),直线l 2的方向向量s 2=(-1,2,2),则直线l 1,l 2所成角的余弦值是( )A .53B .-53C . 23D .-232.平面α,β的法向量分别是 n 1=(1,1,1),n 2=(-1,0,-1),则平面α,β所成锐二面角的余弦值是( )A .33B .-33C . 63D .-633.已知A (1,0,0),B (0,1,0),C (0,0,1),则平面ABC 的单位法向量是( )A .±(1,1,1)B .±⎝⎛⎭⎫22,22,22C .±⎝⎛⎭⎫33,33,33D .±⎝⎛⎭⎫33,-33,334.已知a ,b 是两个非零的向量,α,β是两个平面,下列命题中正确的是( ) A .a ∥b 的必要条件是a ,b 是共面向量 B .a ,b 是共面向量,则a ∥b C .a ∥α,b ∥β,则α∥βD .a ∥α,b ∥β,则a ,b 不是共面向量5.若a ⊥b ,a ⊥c ,l =αb +β c (α,β∈R ),m ∥a ,则m 与l 一定( ) A .共线 B .相交 C . 垂直 D .不共面提升训练6. 如图14-1所示,三棱锥A -BCD 的棱长全相等,E 为AD 的中点,则直线CE 与BD所成角的余弦值为( )1A .36 B .32 C . 336 D .12 7. 在正方体ABCD -A 1B 1C 1D 1中,E 是C 1D 1的中点,则异面直线DE 与AC 所成角的余弦值为( )A .120B .1010C . -1010D .-1208. 对于空间任意一点O 和不共线的三点A ,B ,C ,有OP →=xOA →+yOB →+zOC →(x ,y ,z ∈R ),则x =2,y =-3,z =2是P ,A ,B ,C 四点共面的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分又不必要条件9.已知O 点为空间直角坐标系的原点,向量OA →=(1,2,3),OB →=(2,1,2),OP →=(1,1,2),且点Q 在直线OP 上运动,当QA →·QB →取得最小值时,OQ →=________.10.在底面是直角梯形的四棱锥S -ABCD 中,∠ABC =90°,SA ⊥平面ABCD ,SA =AB =BC =1,AD =12,则平面SCD 与平面SBA 夹角的余弦值是_________.11.平行四边形ABCD 中,AB =1,AD =2,且∠BAD =45°,以BD 为折线,把△ABD 折起到△A 1BD 的位置,使平面A 1BD ⊥平面BCD ,连接A 1C .(1)求证:A 1B ⊥DC ; (2)求二面角B -A 1C D 的大小.图12.如图14-3所示,四棱锥P -ABCD 中,底面ABCD 为平行四边形,AB =2AD =4,BD =23,PD ⊥底面ABCD .(1)证明:平面PBC ⊥平面PBD ;(2)若二面角P -BC -D 的大小为 π4,求AP 与平面PBC 所成角的正弦值.。
高中数学解题思维提升专题01集合与简易逻辑训练手册
专题01 集合与简易逻辑【训练目标】1、 掌握集合及相关的概念,注意集合的三个性质,注意空集的定义及性质;2、 掌握集合间的关系判断方法,会根据集合元素的个数求子集的个数,真子集的个数;会根据集合间的关系求参数的取值范围;3、 掌握集合的交并补运算,在运算时能正确的理解集合的含义,能看懂维恩图;4、 掌握四种命题的写法及相互间的关系;5、 理解充分条件,必要条件的含义,能正确的判断条件;掌握充分条件,必要条件与集合间的关系的联系;6、 能理解特称命题与全称命题,能正确的对它们进行否定;7、 能正确的判断复合命题的真假。
【温馨小提示】本专题虽然难度不大,但在高考中属于必考题,一般集合,简易逻辑各一题,拿下这10分是不容置疑的,需要同学们在训练时多总结,对照训练目标进行练习。
【名校试题荟萃】1、(“永安一中、德化一中、漳平一中”三校联考)已知集合,则AB =( ).A {1,3} .B {1,3,9} .C {3,9,27} .D {1,3,9,27}【答案】A2、(河北省承德市第一中学2019届高三上学期第三次月考)已知集合{}2,3,4A =,集合,则集合B 可能为( )A .{}1,2,3B .{}1,2,5C .{}2,3,5D .{}0,1,5【答案】B【解析】由于并集是指两集合的元素放在一起组成的集合,相同的元素只保留一个,显然只有B 符合。
3、(黑龙江省哈尔滨市第六中学2019届高三12月月考数学(文)试题)已知集合,,则=B A ( )A. {}1,0,1-B. {}2,1,0C. {}1,0D.{}2,1 【答案】C【解析】解指数不等式可确定集合,再根据交集的定义知由两集合的公共元素组成的集合=B A {}1,0。
4、(黑龙江省哈尔滨市第六中学2019届高三12月月考数学(理)试题)已知集合,集合,则图中的阴影部分表示的集合是( )A .[1,3]B .(1,3]C .{1,2,3}-D .{1,0,2,3}- 【答案】C5、(江西省吉安市遂川中学2018届高三上学期第六次月考文数试卷)设全集I 是实数集R,与都是I 的子集(如图所示),则阴影部分所表示的集合为( )A. B. C. D.【答案】A【解析】由于且10x -≠,则,则维恩图所表示的。
集合与简易逻辑训练题
第一章 集合与常用逻辑用语一一、选择题1.已知A ,B 均为集合U ={1,3,5,7,9}的子集,且A ∩B ={3},(∁U B )∩A ={9},则A =( )A .{1,3}B .{3,7,9}C .{3,5,9}D .{3,9} 2. 集合A ={x |11+-x x <0},B ={x || x -b|<a },若“a =1”是“A ∩B ≠φ”的充分条件, 则b 的取值范围是 ( )(A )-2≤b <0 (B )0<b ≤2 (C )-3<b <-1 (D )-1≤b <23、设P ,Q 为两个非空实数集合,定义集合P+Q={a+b|, a ∈P ,b ∈Q},若P={0,2,5},Q={1,2,6},则P+Q 中元素的个数是( )A.9B.8C.7D.64.已知},1|{},0|{,-≤=>==x x B x x A R U 则)()(A C B B C A U U =( )(A) φ (B) }0|{≤x x (C)}1|{->x x (D ) 0|{>x x 或}1-≤x5.若非空集合,,A B C 满足A B C ⋃=,且B 不是A 的子集,则 ( )A x C ∈是x A ∈的充分条件但不是必要条件B xC ∈是x A ∈的必要条件但不是充分条件C x C ∈是x A ∈的充要条件D x C ∈既不是x A ∈的充分条件也不是x A ∈的必要条件二、填空题6.已知集合A ={1,3,m },B ={3,4},A ∪B ={1,2,3,4},则m =________.7.设全集U =A ∪B ={x ∈N +|lg x <1}.若A ∩(∁U B )={m |m =2n +1,n =0,1,2,3,4},则集合B =________.8.已知命题p :1∈{x |x 2<a },q :2∈{x |x 2<a },则“p 且q ”为真命题时a 的取值范围是________.三、解答题9.设集合A ={x 2,2x -1,-4},B ={x -5,1-x,9},若A ∩B ={9},求A ∪B .10.已知A={x||x-a|<4},B={x||x-2|>3}.(1)若a=1,求A∩B;(2)若A∪B=R,求实数a的取值范围.第一章 集合与常用逻辑用语二一、选择题1.满足{}1234,,,,M a a a a ⊆且{}{}12312,,,M a a a a a ⋂=的集合M 的个数是( ) A .1 B .2 C .3D .4 2.命题“若一个数是负数,则它的平方是正数”的逆命题是( )A .“若一个数是负数,则它的平方不是正数”B .“若一个数的平方是正数,则它是负数”C .“若一个数不是负数,则它的平方不是正数”D .“若一个数的平方不是正数,则它不是负数”3.若向量a =(x,3)(x ∈R ),则“x =4”是“|a |=5”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件4.若集合A ={x ||x |≤1,x ∈R },B ={y |y =x 2,x ∈R },则A ∩B =( )A .{x |-1≤x ≤1}B .{x |x ≥0}C .{x |0≤x ≤1}D .∅5.设全集U ={x ∈N +|x ≤a },集合P ={1,2,3},Q ={4,5,6},则a ∈[6,7)是∁U P =Q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件二、填空题6.给定下列四个命题:①“x =π6”是“sin x =12”的充分不必要条件; ②若“p 或q ”为真,则“p 且q ”为真;③若a <b ,则am 2<bm 2;④若集合A ∩B =A ,则A ⊆B .其中为真命题的是________.(填上所有正确命题的序号)7、已知集合M ={x |1≤x ≤10,x ∈N },对它的非空子集A ,将A 中每个元素k ,都乘以(-1)k 再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对M 的所有非空子集,这些和的总和是 .8、要使函数)1()1(2-+-+=m x m mx y 的值恒为正数,则m 的取值范围是__________.三、解答题17.已知p :2x 2-9x +a <0,q :⎩⎪⎨⎪⎧x 2-4x +3<0,x 2-6x +8<0,且¬p 是¬q 的充分条件,求实数a 的取值范围.18.已知P ={x |x 2-8x -20≤0},S ={x ||x -1|≤m }.(1)是否存在实数m ,使x ∈P 是x ∈S 的充要条件,若存在,求出m 的范围;(2)是否存在实数m ,使x ∈P 是x ∈S 的必要条件,若存在,求出m 的范围.第一章 集合与常用逻辑用语三一、选择题1.已知M ={x |x -a =0},N ={x |ax -1=0},若M ∩N =N ,则实数a 的值为( )A .1B .-1C .1或-1D .0或1或-12.已知实数a 、b ,则“ab ≥2”是“a 2+b 2≥4”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知p :直线a 与平面α内无数条直线垂直,q :直线a 与平面α垂直,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.定义:A ⊗B =⎩⎨⎧⎭⎬⎫z ⎪⎪z =xy +x y ,x ∈A ,y ∈B ,设集合A ={0,2},B ={1,2},C ={1},则集合(A ⊗B )⊗C 的所有元素之和为( )A .3B .9C .18D .275.已知命题p :存在x ∈R ,使sin x -cos x =3,命题q :集合{x |x 2-2x +1=0,x ∈R }有2个子集,下列结论:①命题“p 且q ”是真命题;②命题“p 且¬q ”是假命题;③命题“¬p 或¬q ”是真命题,正确的个数是( )A .0B .1C .2D .3二、填空题6.对任意实数a ,b ,c ,给出下列命题:①“b a =”是“bc ac =”充要条件;②“5+a 是无理数”是“a 是无理数”的充要条件③“a >b ”是“a 2>b 2”的充分条件; ④“a <5”是“a <3”的必要条件.其中为真命题的是7、设二次函数,若(其中),则等于 _____.8、满足P⊆}1,0{{0,1,2,3,4}的集合P 的个数有____________个。
集合与简易逻辑练习题与答案
一、选择题(每小题5分,共25分)1.(2011·北京)已知集合P ={x |x 2≤1},M ={a }.若P ∪M =P ,则a 的取值范围是( ).A .(-∞,-1]B .[1,+∞)C .[-1,1]D .(-∞,-1]∪[1,+∞)析 由题设P ∪M =P ,可得M ⊆P ,∴a 2≤1,解得-1≤a ≤1.故选 C2.(2011·陕西)设集合M ={y |y =|cos 2x -sin 2x |,x ∈R },N =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪⎪⎪⎪x -1i <2,i 为虚数单位,x ∈R ,则M ∩N 为( ). A .(0,1) B .(0,1] C .[0,1) D .[0,1]解析 由题意得M ={y |y =|cos 2x |}=[0,1],N ={x ||x +i|<2}={x |x 2+1<2}=(-1,1),∴M ∩N =[0,1).故选 C3.(2011·山东)对于函数y =f (x ),x ∈R ,“y =|f (x )|的图象关于y 轴对称”是“y =f (x )是奇函数”的( ).A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件解析 若y =f (x )是奇函数,则f (-x )=-f (x ),∴|f (-x )|=|-f (x )|=|f (x )|,∴y =|f (x )|的图象关于y 轴对称,但若y =|f (x )|的图象关于y 轴对称,如y =f (x )=x 2,而它不是奇函数.故选 B4.已知命题“函数f (x )、g (x )定义在R 上,h (x )=f (x )·g (x ),若f (x )、g (x )均为奇函数,则h (x )为偶函数”的原命题、逆命题、否命题、逆否命题中正确命题的个数是( ).A .0B .1C .2D .3解析 由f (x )、g (x )均为奇函数,可得h (x )=f (x )·g (x )为偶函数,反之则不成立,如h (x )=x 2是偶函数,但函数f (x )=x 2e x ,g (x )=e x 都不是奇函数,故逆命题不正确,故其否命题也不正确,即只有原命题和逆否命题正确.故选C.故选 C5.下列命题错误的是( ).A .命题“若m >0,则方程x 2+x -m =0有实根”的逆否命题为:“若方程x 2+x -m =0无实根,则m ≤0”B .“x =1”是“x 2-3x +2=0”的充分不必要条件C .命题“若xy =0,则x ,y 中至少有一个为零”的否定是:“若xy ≠0,则x ,y 都不为零”D .对于命题p :∃x ∈R ,使得x 2+x +1<0;则綈p :∀x ∈R ,均有x 2+x +1≥0解析 对C 选项中命题的否定是“若xy =0,则x ,y 都不为零”,C 错.命题:“若p 则q ”的否命题是:“若綈p ,则綈q ”,命题的否定是:“若p 则綈q ”.故选 C二、填空题(每小题5分,共15分)6.(2010·重庆)设U ={0,1,2,3},A ={x ∈U |x 2+mx =0},若∁U A ={1,2},则实数m =________. 解析 ∵U ={0,1,2,3},∁U A ={1,2},∴A ={0,3},即方程x 2+mx =0的两根为0和3,∴m =-3.故填 -37.设p :方程x 2+2mx +1=0有两个不相等的正根;q :方程x 2+2(m -2)x -3m +10=0无实根,则使p 或q 为真,p 且q 为假的实数m 的取值范围是________.解析 令f (x )=x 2+2mx +1.则由f (0)>0,且-b 2a>0, 且Δ>0,求得m <-1,∴p :m ∈(-∞,-1).q :Δ=4(m -2)2-4(-3m +10)<0⇒-2<m <3. 由p 或q 为真,p 且q 为假知,p 、q 一真一假.①当p 真q 假时,⎩⎪⎨⎪⎧ m <-1,m ≤-2或m ≥3,即m ≤-2; ②当p 假q 真时,⎩⎪⎨⎪⎧m ≥-1,-2<m <3,即-1≤m <3. ∴m 的取值范围是m ≤-2或-1≤m <3.故填 (-∞,-2]∪[-1,3)8.已知命题p :∃x ∈R ,使sin x =52;命题q :∀x ∈R ,都有x 2+x +1>0,给出下列结论: ①命题“p ∧q ”是真命题;②命题“綈p ∨綈q ”是假命题;③命题“綈p ∨綈q ”是真命题;④命题“p ∧q ”是假命题.其中正确的是________.解析 命题p 是假命题,命题q 是真命题,故结论③④正确.故填 ③④三、解答题(每小题10分,共20分)9.设a ∈R ,二次函数f (x )=ax 2-2x -2a .设不等式f (x )>0的解集为A ,又知集合B ={x |1<x <3},A ∩B ≠∅,求a 的取值范围.解: 由f (x )为二次函数知,a ≠0.令f (x )=0,解得其两根为x 1=1a- 2+1a2, x 2=1a + 2+1a 2. 由此可知x 1<0,x 2>0.(1)当a >0时,A ={x |x <x 1或x >x 2}.A ∩B ≠∅的充要条件是x 2<3,即1a + 2+1a 2<3.∴a >67. (2)当a <0时,A ={x |x 1<x <x 2}.A ∩B ≠∅的充要条件是x 2>1,即1a+ 2+1a 2>1,解得a <-2. 综上,使A ∩B ≠∅成立的a 的取值范围是(-∞,-2)∪⎝⎛⎭⎫67,+∞.10.已知集合A ={y |y 2-(a 2+a +1)y +a (a 2+1)>0},B =⎩⎨⎧⎭⎬⎫y |y =12x 2-x +52,0≤x ≤3. (1)若A ∩B =∅,求a 的取值范围;(2)当a 取使不等式x 2+1≥ax 恒成立的a 的最小值时,求(∁R A )∩B .解:A ={y |y <a 或y >a 2+1},B ={y |2≤y ≤4}.(1)当A ∩B =∅时,⎩⎪⎨⎪⎧a 2+1≥4,a ≤2, ∴3≤a ≤2或a ≤- 3. ∴a 的取值范围是(-∞,-3]∪[3,2].(2)由x 2+1≥ax ,得x 2-ax +1≥0,依题意Δ=a 2-4≤0,∴-2≤a ≤2.∴a的最小值为-2.当a=-2时,A={y|y<-2或y>5}.∴∁R A={y|-2≤y≤5}.∴(∁R A)∩B={y|2≤y≤4}.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
限时训练(一) 集合与简易逻辑
一、选择题(每小题5分,共40分)
1. (2008年四川卷)设集合U ={1,2,3,4,5},A ={1,2,3},B ={2,3,4},则∁U (A ∩B )=( )
A .{2,3}
B .{1,4,5}
C .{4,5}
D .{1,5} 答案:B
解析:此题重点考察集合的交集,补集的运算;画韦恩氏图,数形结合;
∵A ={1,2,3},B ={2,3,4},∴A ∩B ={2,3}
又∵U ={1,2,3,4,5},∴∁U (A ∩B )={1,4,5}
2. (2010福建龙岩质检)已知集合A ={y |y =log 2x ,x >1},B ={y |y =(12
)x ,x >1},则A ∪B =( ) A .{y |0<y <12
} B .{y |y >0} C .∅
D .R 答案:B
解析:因为函数y =log 2x 是增函数,函数y =(12
)x 是减函数, 所以A =(0,+∞),B =(0,12
),从而A ∪B ={y |y >0}. 3.设全集U =R ,A ={x ∈N ︱1≤x ≤10},B ={x ∈R ︱x 2+x -6=0},则右图中阴影表示的
集合( )
A .{2}
B .{3}
C .{-3,2}
D .{-2,3} 答案:A
4. (2010年梧州模拟)若集合A ={1,m 2},集合B ={2,4},则“m =2”是“A ∩B ={4}”的
( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
答案:A
解析:A ∩B ={4}当且仅当m 2=4,即m =±2,而{2}⊆{-2,2}.
5. 定义A ⊗B ={z |z =xy +x y
,x ∈A ,y ∈B },设A ={0,2},B ={1,2},则A ⊗B 中所有元素和为 ( )
A .1
B .3
C .9
D .18
答案:C
解析:考查本题对集合概念的理解及表示A ⊗B ={z |z =xy +x y
,x ∈A ,y ∈B }={0,4,5}. 6. (2010惠州市第三次调研)设条件p :a >0;条件q :a 2+a ≥0,那么p 是q 的什么条件( )
A .充分非必要条件
B .必要非充分条件
C .充分 且必要条件
D .非充分非必要条件 答案:A 解析:条件q :a ≤-1,或a ≥0,明显(0,+∞)⊆(0,+∞)∪(-∞,-1)
7. 若命题“p 或q ”是真命题,“p 且q ”是假命题,则 ( )
A .命题p 和命题q 都是假命题
B .命题p 和命题q 都是真命题
C .命题p 和命题“非q ”的真值不同
D .命题p 和命题q 的真值不同
答案:D
8. 设M ,P 是两个非空集合,定义M 与P 的差集为M -P ={x |x ∈M 且x ∉P },则M -(M
-P )等于 ( )
A .P
B .M ∩P
C .M ∪P
D .M 答案:B
二、填空题(每小题5分,共30分)
9. 若集合A ={x | |x -1|>2},U =R ,则∁U A =__________.
答案:{x |-1≤x ≤3}
10.(2010年济南市高三模拟)若全集U =R ,集合M ={x |-2≤x ≤2},N ={x |x 2-3x ≤0},
则M ∩(∁U N )=________.
答案:{x |-2≤x <0}
解析:根据已知得M ∩∁U N ){x |-2≤x ≤2}∩{x |x <0或x >3}={x |-2≤x <0}.
11.(2010年苏、锡、常、镇四市调查)已知集合A ={x |x >5},集合B ={x |x >a },若命题“x
∈A ”是命题“x ∈B ”的充分不必要条件,则实数a 的取值范围是________.
答案:a <5
解析:命题“x ∈A ”是命题“x ∈B ”的充分不必要条件,∴A B ,∴a <5.
12.定义集合A *B ={x |x ∈A ,且x ∉B },若A ={1,3,5,7},B ={2,3,5},则A *B 的子集个数为
______.
答案:4
13.命题:若a ≥b ,则a 3≥b 3的逆命题是____________.
答案:若a 3≥b 3,则a ≥b
14.若集合M ={(x ,y )|y =16-x 2},N ={(x ,y )|y =x +a },若M ∩N =∅,则实数a 的取值
范围是________________.
答案:(-∞,-42)∪(42,+∞)
三、解答题(4小题,共50分,解答应写出文字说明,证明过程或演算步骤)
15.(12分)若集合A ={x |log a (x 2-x -2)>2,a >0且a ≠1}.
(1)若a =2,求集合A ;
(2)若94
∈A ,求a 的取值范围. 解析:(1)若a =2,log 2(x 2-x -2)>2,则x 2-x -2>4,
x 2-x -6>0,(x -3)(x +2)>0,得x <-2或x >3
所以A ={x |x <-2或x >3}
(2)因为94∈A ,所以log a [(94)2-94
-2]>2 log a 1316>2,因为log a 1316
>2>0, 所以0<a <1且1316<a 2,134
<a <1 ∴a 的取值范围为(134
,1) 16.(12分)(2010年浙江嘉兴质检)已知集合A ={x |x >1},集合B ={x |m ≤x ≤m +3}.
(1)当m =-1时,求A ∩B ,A ∪B ;
(2)若B ⊆A ,求m 的取值范围.
解析:(1)当m =-1时,B ={x |-1≤x ≤2},
∴A ∩B ={x |1<x ≤2},A ∪B ={x |x ≥-1}.
(2)若B ⊆A ,则m >1,即m 的取值范围为(1,+∞)
17.(12分)已知集合A ={a 1,a 2,a 3,…,a k }(k ≥2)其中a i ∈Z (i =1,2,…,k ),由A 中的元
素构成两个相应的集合S ={(a ,b )|a ∈A ,b ∈A ,a +b ∈A },T ={(a ,b )|a ∈A ,b ∈A ,a -b ∈A },其中(a ,b )是有序实数对,集合S 和T 的元素个数分别为m ,n .若对于任意的a ∈A ,总有-a ∉A ,则称集合A 具有性质P .
(1)检验集合{0,1,2,3}与{-1,2,3}是否具有性质P ,并对其中具有性质P 的集合写出相应的集合S 和T ;
(2)对任何具有性质P 的集合A ,证明:n ≤k (k -1)2
; (3)判断m 和n 的大小关系,并证明你的结论.
(1)解析:集合{0,1,2,3}不具有性质P ,{-1,2,3}具有性质P ,其相应的集合S 和T 是S ={(-1,3),(3,-1)},T ={(2,-1),(2,3)};
(2)证明:首先由A 中的元素构成的有序实数对共有k 2个,因为0∈A ,(a i ,a i )∈T (i =1,2,…,k ),又因为当a ∈A 时,-a ∉A ,
所以当(a i ,a i )∈T 时,(a i ,a i )∉T (i =1,2,…,k ),于是集合T 中的元素的个数最多为n
=12(k 2-k )=12k (k -1),即n ≤k (k -1)2
. (3)解析 :m =n ,证明如下:
①对于(a ,b )∈S ,根据定义a ∈A ,b ∈A ,
则a +b ∈A ,从而(a +b ,b )∈T
如果(a ,b )与(c ,d )是S 中的不同元素,那么a =c 与b =d 中至少有一个不成立,于是a +b =c +d 与b =d 中至少有一个不成立,故(a +b ,b )与(c +d ,d )也是T 中的不同元素.可见S 中的元素个数不多于T 中的元素个数,即m ≤n ;
②对于(a ,b )∈T ,根据定义a ∈A ,b ∈A ,
则a -b ∈A ,从而(a -b ,b )∈S
如果(a ,b )与(c ,d )是T 中的不同元素,那么a =c 与b =d 中至少有一个不成立,于是a -b =c -d 与b =d 中至少有一个不成立,故(a -b ,b )与(c -d ,d )也是S 中的不同元素.可见T 中的元素个数不多于S 中的元素个数,即n ≤m .由①②可知m =n .
18.(14分)集合A ={x |x 2-ax +a 2-19=0},B ={x |log 2(x 2-5x +8)=1},
C ={x |x 2+2x -8=0},求a 的值使A ∩B ∅,且A ∩C =∅同时成立.
解析:log 2(x 2-5x +8)=1,由此得x 2-5x +8=2,
∴B ={2,3}由x 2+2x -8=0得x =2或-4
∴C ={2,-4},又A ∩C =∅,
∴2和-4都不是关于x 的方程x 2-ax +a 2-19=0的解,
而A ∩B ∅,即A ∩B ≠∅,
∴3是关于x 的方程x 2-ax +a 2-19=0的解,
∴可得a =5或a =-2
当a =5时,得A ={2,3},∴A ∩C ={2},
这与A ∩C =∅不符合,所以a =5舍去;
当a =-2时,可以求得A ={3,-5},
符合A ∩C =∅,A ∩B ∅,∴a =-2。
