MATLAB控制系统各种仿真例题(包括simulink解法)
MATLAB与控制系统仿真练习题及答案 (2)
MATLAB与控制系统仿真练习题1、在同一坐标系内，画出一条正弦曲线和一条余弦曲线，要求正弦曲线用红色实线、数据点用“+”号显示；余弦曲线用黑色点线、数据点用“*”显示。
x=0:1 /10:2*pi;y=sin(x);plot(x,y,'r--+')hold ont=cos(x);plot(x,t,'k-.*')>>2、绘制单位圆。
a=0:1/10:2*pi;x=cos(a);y=sin(a);plot(x,y)axis squaregrid on3、使用极坐标函数绘制)3/ρ=的曲线。
8θsin10(t=0:0.01:2*pi;>> y=8*sin((10*t)/3);>> polar(t,y)4、绘制方程⎪⎩⎪⎨⎧===)cos()sin(t z t y t x 在[]π20，=t 区间的三维曲线。
t=0:pi/50:2*pi;x=t;y=sin(t);z=cos(t);plot3(x,y,z)5、用不同的线型和颜色在同一坐标内绘制曲线x 5.0e 21y -=、)2sin(2y x π=的图形。
x=0:1/10:10;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'r');>> hold onplot(x,y2,'b')6、绘制二维正态分布密度函数)(212221),(y x e y x f +-=π的三维图形。
syms x yz=(1/(2*pi))*exp(-0.5*(x.^2+y.^2));ezsurf(x,y,z)7、选择合适的步长绘制下列函数的图形。
（1）x y cos =，⎥⎦⎤⎢⎣⎡-∈2,2ππx （2）x xe y = x=-2/pi:1/20:2/pi; >> y=sqrt(cos(x)); >> plot(x,y)>> hold on>> y=x.*exp(x);>> plot(x,y)>>8、在同一坐标下绘制函数x 、2x 、3x -、)sin(x x 在()π,0的曲线。
matlab的simulink仿真建模举例 -回复
matlab的simulink仿真建模举例-回复Matlab的Simulink仿真建模举例Simulink是Matlab附带的一款强大的仿真建模工具，它能够帮助工程师们通过可视化的方式建立和调试动态系统模型。
Simulink通过简化传统的数学模型建立过程，使得工程师们能够更加直观地理解和分析复杂的系统。
在本文中，我们将介绍一个关于电机控制系统的Simulink仿真建模的例子。
一、了解电机控制系统在开始建模之前，我们首先需要了解电机控制系统的基本原理。
电机控制系统通常包括输入、电机和输出三个主要部分。
输入通常是来自于传感器或用户的命令信号，例如转速、位置或力矩。
电机是通过接受输入信号并根据特定的控制算法生成输出信号。
输出信号通常是电机的转速、位置或功率等。
控制算法通常采用比例-积分-微分（PID）控制或者其他控制算法。
二、建立Simulink模型1. 创建新的Simulink模型在Matlab主界面中，选择Simulink选项卡下的“New Model”创建一个新的Simulink模型。
2. 添加输入信号在Simulink模型中，我们首先需要添加输入信号模块。
在Simulink库浏览器中选择“Sources”类别，在右侧面板中找到“Step”模块，并将其拖放到模型中。
3. 添加电机模型接下来，我们需要将电机模型添加到Simulink模型中。
Simulink库浏览器中选择“Simscape”类别，在右侧面板中找到“Simscape Electrical”子类别，然后找到“Simscape模型”模块，并将其拖放到模型中。
4. 连接输入信号和电机模型将输入信号模块的输出端口与电机模型的输入端口相连，以建立输入信号与电机模型之间的连接。
5. 添加输出信号模块在Simulink模型中，我们还需要添加输出信号模块。
在Simulink库浏览器中选择“Sinks”类别，在右侧面板中找到“Scope”模块，并将其拖放到模型中。
matlab的控制系统仿真上机习题
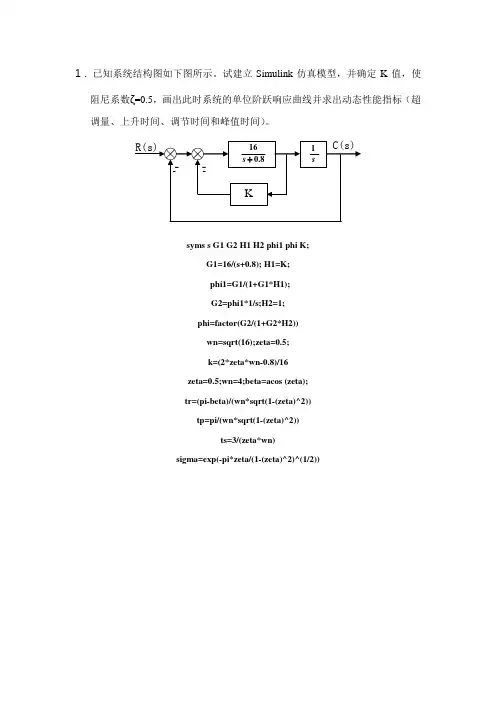
1．已知系统结构图如下图所示。
试建立Simulink 仿真模型，并确定K 值，使阻尼系数ζ=0.5，画出此时系统的单位阶跃响应曲线并求出动态性能指标（超调量、上升时间、调节时间和峰值时间）。
-R(s)C(s)K8.016s -s1syms s G1 G2 H1 H2 phi1 phi K;G1=16/(s+0.8); H1=K; phi1=G1/(1+G1*H1); G2=phi1*1/s;H2=1; phi=factor(G2/(1+G2*H2)) wn=sqrt(16);zeta=0.5; k=(2*zeta*wn-0.8)/16 zeta=0.5;wn=4;beta=acos (zeta); tr=(pi-beta)/(wn*sqrt(1-(zeta)^2)) tp=pi/(wn*sqrt(1-(zeta)^2))ts=3/(zeta*wn)sigma=exp(-pi*zeta/(1-(zeta)^2)^(1/2))--2． 试画出如图所示系统的零极点图，并确定系统的稳定性。
-C(s)4s()11.0302+s s -50R(s)syms s G1 G2 H1 H2 phi1 phi;G1=30/(0.1*s^3+s^2);H1=4*s; phi1=G1/(1+G1*H1);G2=50;H2=1;phi=factor(G2*phi1/(1+G2*phi1*H2))phi =15000/(s^3+10*s^2+1200*s+15000) closys=tf(15000,[1,10,1200,15000]);pzmap(closys)3．已知某系统开环传递函数为：()()()15.012102+++=sssssG，试用Bode图法判断闭环系统的稳定性，并用阶跃响应曲线加以验证；求出相位裕量和幅值裕量。
num=10;den=(conv(conv([1,0],[2,1]),[1,0.5,1]));sys=tf(num,den);subplot(1,2,1);bode(sys);grid onsubplot(1,2,2);step(sys);grid onsubplot(1,1,1);margin(sys); [wn,pm,wg,wc]=margin(sys)-140-120-100-80-60-40-200204060M a g n i t u d e (d B )10-210-110101102-360-315-270-225-180-135-90P h a s e (d e g )Bode DiagramGm = -22.5 dB (at 0.707 rad/sec) , P m = -136 deg (at 1.62 rad/sec)Frequency (rad/sec)wn =0.0750 pm =-136.3866 wg =0.7067 wc =1.62104．已知某系统开环传递函数为：()122+++=ssssG，试用Nyquist稳定判据判断闭环系统的稳定性，并用阶跃响应曲线加以验证。
控制系统matlab仿真设计题目
计算机学院自动化控制系统仿真实验题目1. 设计一个PID 调节器，对1025)(2++=s s G s 实行调节，通过仿真分析出最佳调节参数。
写出仿真步骤、过程、中间结果及结果分析。
2. 利用最小二乘递推算法，辨识系统参数，要求利用matlab 编程实现，假设初始参数都为0，I p 610)0(=，I 为单位阵。
)(k u 为（0,1）均匀分布的随机变量，)(k v 为（0,1）分布的白噪声，采样100次)()2(5.0)1(0.1)2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+--3. 求解解微分方程 1)0(2'=-=y y x y y要求利用matlab 编写S 函数求解4. 利用Matlab 编写M 文件实现控制系统仿真，要求1）输入传递函数，状态方程能够实现阶跃响应，2）能够绘制系统的bode 图，nquist 曲线图和根轨迹。
5. 已知控制系统传递函数)102.0)(12.0(20)(++=s s s s G ，性能指标要求 1） 超调量%40≤σ，2）过度时间s t S 1≤，3）70≥v K ，设计一个串联滞后校正环节，满足以上性能指标，手工计算出校正环节传递函数，利用Matlab 语言对系统进行仿真设计出结果，利用simulink 进行仿真出结果（以单位阶跃响应为输入）。
6. 已知单位负反馈系统的开环传递函数)12.0)(1()(2.0++=-s s s Ke s G s，性能指标要求 1） 静态误差系数1=v K ，2）045≥γ， 在前向通道中插入一相位超前校正，确定校正系统传函，利用matlab 画出未校正和校正系统的根轨迹，编程实现校正前后系统的阶跃响应，计算系统性能指标。
7. 单位负反馈系统的开环传递函数)12.0)(11.0()(0++=s s s K s G ，用相应的频率校正法对系统进行校正设计，使系统的性能指标达到：1)相角余度060≥γ，2）在单位斜坡下的稳态误差05.0<SS e ，3）系统的s rad C /3<ω。
MATLAB语言：Simulink系统仿真习题与答案
一、单选题1、将模块连接好之后，如果要分出一根连线，操作方法是（）。
A.把鼠标指针移到分支点的位置，按住鼠标左键拖曳到目标模块的输入端B.双击分支点的位置，按住鼠标左键拖曳到目标模块的输入端C.把鼠标指针移到分支点的位置，按下Ctrl键并按住鼠标拖曳到目标模块的输入端D.把鼠标指针移到分支点的位置，按下Shift键并按住鼠标拖曳到目标模块的输入端正确答案：C2、在一个模型窗口上按住一个模块并同时按Shift键移动到另一个模型窗口，则（）。
A.在两个模型窗口都有这个模块B.在后一个窗口有这个模块C.在前一个窗口有这个模块D.在两个窗口都有模块并添加连线正确答案：A3、为子系统定制参数设置对话框和图标，使子系统本身有一个独立的操作界面，这种操作称为子系统的（）。
A.包装B.封装C.集成D.组合正确答案：B4、使用S函数时，要在模型编辑窗口添加（）。
A.Sine Wave模块B.S-Program模块C.Subsystem模块D.S-Function模块正确答案：D二、多选题1、启动Simulink的方法有（）。
A.在命令行窗口中输入simulink命令B.在“主页”选项卡中单击SIMULINK命令组中的“Simulink”命令按钮C.在“主页”选项卡中单击“文件”命令组中的“新建”命令按钮D.在“主页”选项卡中单击“文件”命令组中的“新建脚本”命令按钮正确答案：A、B、C2、根据控制信号的控制方式不同，条件执行子系统分为（）。
A.事件驱动子系统B.使能子系统C.触发子系统D.使能加触发子系统正确答案：B、C、D3、以下关于S函数的描述中，正确的有（）。
A.利用S函数可以对Simulink模块库进行扩充B.S函数只能用MATLAB语言编写C.S函数有现成的模板程序D.S函数模块能够被封装正确答案：A、C、D三、判断题1、建立系统仿真模型是在Simulink模型编辑窗口中进行的。
正确答案：√2、利用触发子系统能够将锯齿波转换为方波。
MATLAB控制系统仿真-simulink
6 4 u 2 0
系统为一个两输入两输出系统 》A=[1 6 9 10; 3 12 6 8; 4 7 9 11; 5 12 13 14]; 》B=[4 6; 2 4; 2 2; 1 0]; 》C=[0 0 2 1; 8 0 2 2]; 》D=zeros(2,2);
第五节
一、模型的转换
• 举例应用： 1）exp3_2.m 系统1为：
0 x1 1 y 1 1
1 0 x1 u1 2 1 3 x 1 u 1
系统2为：
0 x2 1 y 2 1 1 0 x2 u2 3 1 4 x 2
0 . 25 i s 2i 2 s 1
2s 9s 1
3
k= 2
结果表达式： G ( s ) 2
0 . 25 i s 2i
第四节
状态空间描述
状态方程与输出方程的组合称为状态空间表达式，又称 为动态方程，经典控制理论用传递函数将输入—输出关 系表达出来，而现代控制理论则用状态方程和输出方程 来表达输入—输出关系，揭示了系统内部状态对系统性 能的影响。
零极点增益模型： G ( s ) 4 3 2 s 9 s 45 s 87 s 50 》num=[1,11,30,0]; 》den=[1,9,45,87,50]; [z,p,k]=tf2zp(num,den) 》 z= p= k= 0 -6 -5 -3.0000+4.0000i -3.0000-4.0000i -2.0000 1
用法举例： 0 1）已知系统状态空间模型为： x 1
y 1
1 0 x u 2 1 3 x u
》A=[0 1; -1 -2]; B=[0;1]; 》C=[1,3]; D=[1]; 》[num,den]=ss2tf(A,B,C,D,iu) ％iu用来指定第n个输入，当只有一个输入时可忽略。 》num=1 5 2; den=1 2 1; 》[z,p,k]=ss2zp(A,B,C,D,iu) 》z= -4.5616 p= -1 k=1 -0.4384 -1
MATLAB与控制系统仿真大作业
>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模（每题 10 分，共 20 分）
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
，试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括：（1）simulink 建模结构图；
（2）在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
，H
(s)
=
5(s + 2) s +10
求：建立 Simulink 仿真模型，并求出其系统在单位阶跃响应；
要求答案包括：（1）simulink 建模结构图；
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
《MATLABSimulink与控制系统仿真(第版)》的Simulink仿真详解18页PPT
•
29、在一切能够接受法律支配的人类 的状态 中，哪 里没有 法律， 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律，也可以废除 法律。 ——塞·约翰逊
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事，无字句处读书。——周恩来 5、阅读使人充实，会谈使人敏捷，写作使人精确。——培根
《MATLAB仿真详解 26、我们像鹰一样，生来就是自由的，但是为了生存，我们不得不为自己编织一个笼子，然后把自己关在里面。——博莱索
•
27、法律如果不讲道理，即使延续时 间再长 ，也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、 控制系统的模型与转换1． 请将下面的传递函数模型输入到matlab 环境。
]52)1)[(2(24)(32233++++++=s s s s s s s G )99.02.0)(1(568.0)(22+--+=z z z z z H ，T=0.1s >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5)); GTransfer function:s^3 + 4 s + 2 ------------------------------------------------------ s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3>> num=[1 0 0.56];den=conv([1 -1],[1 -0.2 0.99]); H=tf(num,den,'Ts',0.1)Transfer function: z^2 + 0.56 ----------------------------- z^3 - 1.2 z^2 + 1.19 z - 0.992． 请将下面的零极点模型输入到matlab 环境。
请求出上述模型的零极点，并绘制其位置。
)1)(6)(5()1)(1(8)(22+++-+++=s s s s j s j s s G )2.8()6.2)(2.3()(1511-++=----z z z z z H ，T=0.05s>>z=[-1-j -1+j]; p=[0 0 -5 -6 -j j];G=zpk(z,p,8)Zero/pole/gain: 8 (s^2 + 2s + 2) -------------------------- s^2 (s+5) (s+6) (s^2 + 1)>>pzmap(G)>> z=[0 0 0 0 0 -1/3.2 -1/2.6]; p=[1/8.2];H=zpk(z,p,1,'Ts',0.05)Zero/pole/gain:z^5 (z+0.3125) (z+0.3846) ------------------------- (z-0.122)Sampling time: 0.05>>pzmap （H ）二、 线性系统分析1. 请分析下面传递函数模型的稳定性。
221)(23+++=s s s s G 13)50600300(13)(22+++++=s s s s s s G>> num=[1];den=[1 2 1 2]; G=tf(num,den); eig(G)' ans =-2.00000.0000 - 1.0000i 0.0000 + 1.0000i可见，系统有两个特征根在虚轴上，一个特征根在虚轴左侧，所以系统是临界稳定的。
>> num=[3 1];den=[300 600 50 3 1];G=tf(num,den); eig(G)' ans =-1.9152 -0.14140.0283 - 0.1073i 0.0283 + 0.1073i可见，有两个特征根在虚轴右侧，所以系统是不稳定的。
2. 请判定下面离散系统的稳定性。
)05.025.02.0(23)(23+--+-=z z z z z H)34039.804.10215.20368.791.1576.1112.2)(1234512-++--++=-------z z z z z z z z H>> num=[-3 2];den=[1 -0.2 -0.25 0.05]; H=tf(num,den,'Ts',0.1); [eig(H) abs(eig(H))] ans =-0.5000 0.5000 0.5000 0.50000.2000 0.2000可以看出，由于各个特征根的模均小于1，所以可以判定闭环系统是稳定的。
>> z=tf('z',0.1);H=(2.12*z^-2+11.76*z^-1+15.91)/…;(z^-5-7.368*z^-4-20.15*z^-3+102.4*z^-2+80.39*z-1-340);[eig(H) abs(eig(H))] ans =0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4.1724 4.1724 0.3755 + 0.1814i 0.4170 0.3755 - 0.1814i 0.4170 -0.5292 0.5292 -0.2716 0.27160.1193 0.1193可以看出，由于4.1724这个特征根的模大于1，所以可以判定闭环系统是不稳定的。
3. 设描述系统的传递函数为4032010958411812467284224494536546364032018576022208812266436380598251418)(2345678234567+++++++++++++++=s s s s s s s s s s s s s s s s G ，假定系统具有零初始状态，请求出单位阶跃响应曲线和单位脉冲响应曲线。
>> num=[18 514 5982 36380 122664 22088 185760 40320]; den=[1 36 546 4536 22449 67284 118124 109584 40320]; G=tf(num,den)Transfer function:18 s^7 + 514 s^6 + 5982 s^5 + 36380 s^4 + 122664 s^3 + 22088 s^2 + 185760 s + 40320 -----------------------------------------------------------------------------------------s^8 + 36 s^7 + 546 s^6 + 4536 s^5 + 22449 s^4 + 67284 s^3 + 118124 s^2 + 109584 s + 40320>> step(G ,10) >> impulse(G ,10)单位阶跃响应：单位脉冲响应：三、线性系统Simulink仿真应用1. 请分析下面传递函数模型阶跃响应。
221)(23+++=s s s s G利用Simulink 建模，建立系统仿真模型如下：单击启动仿真按钮，双击示波器得到系统的阶跃响应如下：2. 请分析下面离散系统的脉冲响应。
13)50600300(143)(2223++++++=s s s s s s s G利用Simulink 建模，建立系统仿真模型如下：单击启动仿真按钮，双击示波器得到系统的脉冲响应如下：3. 对离散采样系统进行分析，并求出其阶跃响应。
其中：2373)(23++++=s s s s s G利用Simulink 建模，建立系统仿真模型如下：单击启动仿真按钮，双击示波器得到系统的阶跃响应如下：4. 设计控制器，使得下列系统稳定。
)2.1)(2)(3()3.2)(1()(+-+++=s s s s s s G利用Simulink 建模，未连入控制器时，仿真模型和响应如下：利用Simulink 建模，设计控制器：从响应输出图形可以看出，连入控制器后系统稳定，性能明显提高。
以下只做了解四、 基于MATLAB 的PID 控制器设计设计题目：1. 应用Ziegler — Nichols 算法设计PID 控制器，实现系统的闭环稳定，并比较对各个系统的控制效果。
3)1s (1G(s)+=未连入PID 控制器时的系统仿真及其性能指标如下：可见，未调节时的系统性能有待提高，需设计PID控制器连入。
输入：>> num=1;den=conv( [1,1],conv( [1,1],[1,1] ));Step(num,den);K=dcgain (num,den)得出：K =1根据图形，得出：L=1.86 T=4.4利用自定义的Ziegler_std函数求出Kp、Ti、Td输入：>> K=1;L=1.86;T=4.4;[num,den,Kp,Ti,Td]=Ziegler_std (3,[K,L,T])得出：num =2.6400 2.8387 1.5262den =10Kp =2.8387Ti =3.7200Td =0.9300根据得出的Kp 、Ti 、Td 值，设计PID 控制器，并利用利用Simulink 仿真建模。
仿真模型及其响应如下：可见，加入PID 控制器调节后，系统性能明显改善。
5)1s (1G(s)+=未连入PID 控制器时的系统仿真及其性能指标如下：输入：>> num=1;den=conv([1,1],conv([1,1],…;conv( [1,1],conv( [1,1],[1,1] ))));Step(num,den);K=dcgain (num,den)得出：K = 1根据图形，得出：L=3.4 T=6.8利用自定义的Ziegler_std函数求出Kp、Ti、Td输入：>> K=1;L=3.4;T=6.8;[num,den,Kp,Ti,Td]=Ziegler_std (3,[K,L,T])得出:num =4.0800 2.4000 0.7059den =1 0Kp =2.4000Ti =6.8000Td =1.7000根据得出的Kp、Ti、Td值，设计PID控制器，并利用利用Simulink仿真建模。
仿真模型及其响应如下：可见，加入PID控制器调节后，系统性能明显改善。
3)1 s(1-1.5s G(s)++=利用Simulink建模，未连入控制器时，仿真模型和响应如下：输入:>>num=[-1.5 1];den=conv( [1,1],conv( [1,1],[1,1] ));Step(num,den);K=dcgain (num,den)得出:K =1根据图形，得出：L=1.8 T=5.7利用自定义的Ziegler_std函数求出Kp、Ti、Td输入:>> K=1;L=1.8T=5.7;[num,den,Kp,Ti,Td]=Ziegler_std (3,[K,L,T])得出:num =3.4200 3.8000 2.1111den =10Kp =3.8000Ti =3.6000Td =0.9000根据得出的Kp、Ti、Td值，设计PID控制器，并利用利用Simulink仿真建模。