浙江大学 材料力学课件10-能量法(新)
合集下载
演示课件材料力学能量法.ppt
.精品课件.
14
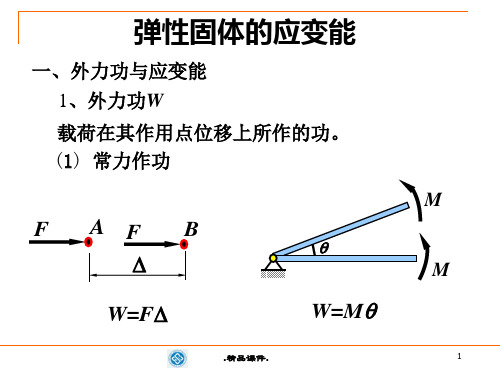
先加F1后加F2 F1
F2
先加F2后加F1 F1
F2
不同加载次序外力功均相同,若按比例同时加载, 外力同时达到最终值,即比例加载,外力功不变。
.精品课件.
15
三、克拉贝依隆(Clapeyron)原理 线弹性体上,作用有载荷F1,F2 , … Fi, … Fn 与外力方向相应的位移为D1, D2, … Di, … Dn 由线弹性体的叠加原理,各位移是载荷的线性函数
……
Di*= di1F1 * +di2 F2 * + … +diiFi * … +dinFn *= lDi
……
注意:带星号上标的载荷和位移都是中间值,所 以是变数,随着l的变化而变化。
.精品课件.
18
Ve
W
n i 1
1 2
Fi Di
线弹性体的外力功或变形能等于每一外力与其 对应位移乘积之半的总和。
20
组合变形
M
据Clapeyron原理,
微段dx上
dVe
dW
1 2
FNd (Dl )
1 Mdq
2
1 Tdj
2
FN2dx M 2dx T 2dx
dx
2EA 2EI 2GIP
整个杆件的应变能为
Ve
FN2
(
x
)
dx
l 2EA
M2 (x)
dx l 2EI
T2 (x)
dx l 2GIP
T
FN
.精品课件.
9
已知:EI = 常数,用功能原理
F
计算A点的挠度。
A
B
解:①建立坐标系
wA
第十章 能量法 材料力学课件

§10.2 杆件变形能计算
一. 杆件基本变形的变形能 U=W
F
F
线弹性 U W 1F
2
特殊情况
F
F UW1Fl FN2l
2
2EA
Me
Me UW12Me2M Gx2Ilp
Me 广义表达式
Me UW12Me2M E2lI
UW
1F
2
内力2
2刚度
l
注意:当内力或刚度发生变化时要用
积分或分段计算
(内力)2(x)
必须强调 U W 1F 只适用于线弹性结构 2
面积= 1 底高 2
对非线性材料 U=W=曲线下的面积
可利用积分计算
U uW 0d0Fd
未作特殊说明,均假定材料在 线弹性范围内
F
F
例10.2 已知d F E G
解
求 fc=? 1 U W 2Ffc
2U
A
2a
F
C
a
B
fc F
UUCBUBA
aM 1 2(x)d x2aM 2 2(x)d x2aM x2(x)d
l M x M x dx tan l xM x dx
tan x c
M c
Mx
C•
x
Mx
l
M
lMxMxdx
tanxM(x)dx
l
tanxc
M
x xc
.c
dx
x
M M ( x) M c xc l
lM xE M Ixdx E M cI
lM xE M Ixdx E M cI
若需要分段,则: i Mci
M(x) ql x qx2(0 x l) 22
A1
。。。
大学材料力学下能量方法教学课件

对未来研究的展望
随着科学技术的发展,材料力学中的问题越来越 复杂,需要更深入的研究。
在实际应用中,应结合数值计算方法和实验研究 ,进一步提高能量方法的实用性和可靠性。
未来研究可进一步探索能量方法的理论基础,完 善其应用范围和精度,以满足更广泛的工程需求 。
此外,可开展跨学科的研究,将能量方法与其他 分析方法相结合,以解决更复杂的工程问题。同 时,应注重培养具有创新思维和实践能力的人才 ,为未来的科学研究和技术发展做出贡献。
断裂能与裂纹扩展的能量关系:在断裂力学中,我们通 常将断裂能作为描述裂纹扩展的能量关系的主要参数。 断裂能是裂纹扩展单位面积所需的能量。
能量法在断裂力学中的应用实例
韧性材料的疲劳裂纹扩展:对于韧性材料,疲劳裂纹的 扩展通常是一个渐进的过程。使用能量法可以研究疲劳 裂纹的扩展规律,并预测结构的剩余寿命。
04
案例分析
悬臂梁的弯曲问题
总结词
悬臂梁弯曲问题是一个经典的材料力学问题,通过能量方法可以更深入地理解其 力学行为。
详细描述
悬臂梁在受到外力作用时会产生弯曲变形,通过应用能量方法,可以计算梁的弯 曲刚度、挠度以及应力分布情况。同时,还可以分析不同材料对梁弯曲的影响。
圆孔附近的应力集中问题
总结词
简化。
输标02入题
能量方法在解决弹性力学、塑性力学和断裂力学等领 域的问题时表现出色,为工程设计和科学研究提供了 有力支持。
01
03
能量方法的应用范围广泛,不仅可用于求解静力问题 ,还可用于分析动力学问题,以及研究材料的屈曲、
振动和稳定性等问题。
04
能量方法的基本原理包括虚功原理、最小势能原理和 哈密顿原理等,这些原理为解决各种材料力学问题提 供了基础。
材料力学--能量法

1、求内力
F
R
A
FA
R
M n
T
t
弯 矩:M () FR sin
扭矩:T () FR(1 cos) 12
2、变形能:
弯 矩:M () FR sin
扭矩:T () FR(1 cos)
U T 2 (x) dx M 2 (x) dx
l 2GI P
l 2EI
U1 U2
U U1 U2 F1 l2 U1 U2 F2 l1
结论:应变能与加载次序无关。
10
[例11-1-1] 用能量法求C点的挠度。梁为等截面直梁。
F
解:外力功等于应变能
A
C
B
W
1 2
FwC
a
a
U
L
M 2(x) 2EI
dx
利用对称性,得:
M (x)
L 2EA
L 2GIP
L 2EI
注意:应变能是力的二次函数,因此,引起同一 基本变形的一组外力在杆内所产生的应变能,并不等 于各力分别作用时产生的应变能的简单相加。
6
例如: 求图示简支梁的应变能。 解:设F和M同时由零按比 A 例加至终值。
(1)求支反力,列弯矩方程:
x
F
C
l 2
M1(x)
1 2
MFl2 16
M 2l 6
7
U
1 EI
F 2l3 96
MFl2 16
M 2l 6
(a)
A
FM
C
B
变形(a)式得
l
l
F
R
A
FA
R
M n
T
t
弯 矩:M () FR sin
扭矩:T () FR(1 cos) 12
2、变形能:
弯 矩:M () FR sin
扭矩:T () FR(1 cos)
U T 2 (x) dx M 2 (x) dx
l 2GI P
l 2EI
U1 U2
U U1 U2 F1 l2 U1 U2 F2 l1
结论:应变能与加载次序无关。
10
[例11-1-1] 用能量法求C点的挠度。梁为等截面直梁。
F
解:外力功等于应变能
A
C
B
W
1 2
FwC
a
a
U
L
M 2(x) 2EI
dx
利用对称性,得:
M (x)
L 2EA
L 2GIP
L 2EI
注意:应变能是力的二次函数,因此,引起同一 基本变形的一组外力在杆内所产生的应变能,并不等 于各力分别作用时产生的应变能的简单相加。
6
例如: 求图示简支梁的应变能。 解:设F和M同时由零按比 A 例加至终值。
(1)求支反力,列弯矩方程:
x
F
C
l 2
M1(x)
1 2
MFl2 16
M 2l 6
7
U
1 EI
F 2l3 96
MFl2 16
M 2l 6
(a)
A
FM
C
B
变形(a)式得
l
l
材料力学第10章-能量法

10-4 卡氏定理
(2)先加载dFi ,则力 dFi 在其相应的位移 di上做的功为
1
W1 dFi di
2
F1
再加载F1, F2 ,, Fn ,在相应
的位移 i 上所做的功为
1
n1
W2 i1 2 Fi i V
F2
2
dFi Fi
di
i
n
Fn
原来载荷 dFi 对位移i 上所做的功为
W3 dFi i
F A
F
在位移坐标轴上取了一个微段d ,
该微段对应的外力可视为常力。则常力作
功为
dW Fd k d
B
当外载荷和相应的位移由零缓慢增加 O
d
至F 和 时,在这个过程中外力作功
k 2 F
W kd 0
2
2
SOAB
线弹性范围内,外载荷所做的功等于力与位移乘积的一半。
10-2 外载荷做的功
二、多个力作用下的外力功
量的损失),弹性体内部所贮存的应变能,在数
值上等于外力所作的功,即满足:
V W
l
P
利用功和能的概念来求解可变形固体的位移、变形和内力
等的方法,通称为能量方法。
10-2 外载荷做的功
一、单个力作用下的外力功
材料服从胡克定律,即在线弹性范围内,弹性体在外力
作用下位移 与外载荷F 成正比,即
F k
横力弯曲时,弯矩为x的函数,则横力弯曲时的应变能为
M (x)2 dx dV
2EI
M (x)2 dx
V l 2EI
四、用广义力和广义位移表示的应变能
轴向压力
扭转
弯曲
F l V 2
V M e
材料力学第10章能量法介绍

A
(4)能量守恒:W=U
1 1 67 F 2 FvB 2 2 20 EA
67 F vB 20 EA
1.6m C 1.2m
B
F
U vB F
10.2 卡氏 (Castigliano)定理
10.2.1 卡氏第一定理
卡氏定理
1879年,意大利工程师Alerto Castigliano发表了两个 “内功的积分系数定理”—卡氏定理 建立应变能和外力、位移的关系
第一步:加增量dPn 应变能
1 dPn dn 2
n
第二步:施加外荷载。应变能 U ndPn 该步总能量
U 2total
1 U ndPn dPn dn U ndPn 2
3. 应变能与加载次序无关
U1total U 2total
U U dPn U ndPn Pn U n Pn
例10-2
图示悬臂刚架,已知F、a、EI,求应变能和C点竖直位 移(忽略AB杆段的压缩应变能)。
解:
(1)分段写弯矩函数
B
a
x2
F
x1 C
BA段:
M ( x2 ) Fa
a
A
CB段:
M ( x1 ) Fx1
(2)应变能
2 M 2 dx 2 a ( Fx ) dx a ( Fa) dx 1 1 U 2 l 2 EI 0 0 2EI 2 EI 2 F 2a3 3 EI
10.1 杆件的弹性应变能 10.2 卡氏定理 10.3 冲击应力与冲击韧性
功和能
弹性体在外力作用下产生变形,变形过程中外力所 做的功=外力功W 外力功转化为弹性势能存储于杆件内,该弹性势能= 应变能U(内力的功) 能量守恒: U = W
材料力学( 最新 )能量法

U W
• 10-2
杆件变形能的计算
P P
•轴向拉压 •轴力P与轴向变形成正比 •当轴力N沿轴向为变量时
N 2 ( x)dx dU udV dV Pl 2 2 EA N 2 ( x)dx dU 2 EA N 2 ( x)dx U dU l l 2 EA
' 4
1 1 U b P 3 P4 4 3 2 2
P3
P 4
A
B
1'
' 2
3
4
• 10-4
P 1
互等定理
P 2
A
P3
P 4
B
' 4 4
1
' 1
2
' 2
3
' 3
1 1 1 1 ' U1 P 1 P2 2 P 3 P4 4 P 1' P2 2 1 3 1 2 2 2 2 1 1 1 1 ' ' U 2 P 1 P2 2 P 3 P4 4 P 3 P4 4 1 3 3 2 2 2 2
U1 U 2
P 1' P2 2' P3 3' P4 4' 1
•功的互等定理
P P P P
' 1 1 ' 2 2 ' 3 3 ' 4 4
•第一组力在第二组力引起的位移上做的功,等 于第二组力在第一组力引起的位移上所做的功
' 当P2和P4等于零时 P 1' P3 3 1
V wA ε FP
FP2l 3 x 2dx 0 6 EI
l
FP l 3 wA () 3EI
材料力学 第2版 第10章 能量法

例1 已知 d, F, E, G
2a B
A
F
C
U UCB U BA
求 fc=?
解:
U
W
1 2
Ffc
fc
2U F
a
M
2 BC
(x)
d
x
2a
M
2 AB
(x)
d
x
2a
M
2 xAB
(x)
d
x
0 2EI
0 2EI
0 2GI p
15
10.2 杆件变形能计算
U
a
M
2 BC
(x)
d
x
2a
M
2 AB
任意结构 任意截面
任意载荷 任意方向的位移
U=W
(功能原理)
17
10.3 单位载荷法 • 莫尔积分
以平面刚架为例,求任意截面任意方向的位
移(A点沿a-a 方向)
F
aA a
设刚架在F、Me作用下任意截面
A' x的弯矩为M(x),
Me
变形能
U
M 2(x) 2EI
d
x
18
10.3 单位载荷法 • 莫尔积分
此时变形能为
U
M 2(x) 2EI
d
x
在此变形基础上再加F、Me,
变形能增加了 U
M 2(x) 2EI
d
x
Me ①
F aA
a A' Me ②
20
10.3 单位载荷法 • 莫尔积分
注意,此时单位力1在上作功1·,
aA
F
a A'
a 1A
F
a
Me
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十、能量法(Energy method)
1、应变能与余能
(1)应变能
F
F
F1
L
o
等直杆拉伸,非弹性变形情况下
应变能
1
Vε W Fd
0
应变能密度
vε
Vε AL
1
d
0
功
1
一般应力状态下,应变能密度
(ε1 ,γ1 )
vε ( xd x yd y zd z xyd xy xzd xz yzd yz )
——虚设外力法
例10-3. 题同例10-2,求铰B的水平与铅直位移。
A
F
B B
解:由铰B平衡,得两杆内力 C
FAB F(拉),FBC 2F(压)
应变能 V
Fi2 Li L (F 2 2 2F 2 ) 2EA 2EA
铅直位移
2
V F
(1 2
2) FL EA
水平位移
1
V Ft
0?
虚设力法:假定铰B还受水平向右的力Ft作用
例10-6 试分析下列结构的位移
A
BF
AB
B
V F
F A
B
F
AB
V F
或 V ? (2F )
F1 A
F2 B
AB
V F1
或 V F2
或?
q AB
C B ?
虚加一对力偶MB
B
MB
B
V M B
M B 0
思考:P83- 3-1,2,3,4,习题3-8(c),9,14
练习:P86- 习题3-7(c),8(a),15
F
C
A
D
B
F
解:二次超静定
基本静定系——解除铰D约束, 加反力F1,F2,F3,F4
铰D平衡:
F2 F4
F3 F1,F2 F4 F
F1
F3
D
结构对称性
F2
F4
F 2
一次超静定
F2 F4
F1 D
F3
F
D
变形相容 Dy 0 ——对称性已用
Dx 0
F1
F1
F 2
左半弯矩
1 M1 2 Fx
GA
d Tdx
GI p
d FNdx
EA
单位力法的表达式
1
(M
L
M EI
Fs
s Fs
GA
T
T GI p
FN
FN )dx EA
同一根杆的轴力和剪力所作功与弯矩所作功相比
一般较小,其中相应项可略去
思考:线弹性、小变形假设下,单位力法表达式
与卡氏第二定理表达式的关系
例10-7题同例10-3,求铰B的水平与铅直位移。 解:实际外力F相应的杆内力
(1)卡氏第一定理
应变能与功取决于荷载的最终值及相应的位移
——假定各力同时按比例加载至最终值
外力的功
i
W Fidi
0
应变能
F1 F2 Fn
A
B
1 2
n
i
V
Fidi V (i )
0
假设仅第i个位移有微小增量di,则应变能的变化
dV
V
i
di
外力功的变化 dW Fidi
外力功等值于应变能
由铰B平衡,得 FAB F,FBC 2F
(1)水平位移
去掉原外力,加水平单位力 A
B
1
相应内力 FAB 1,FBC 0
单位力法表达式
C
Bx
FN
L
FN dx EA
L EA
(
FAB
FAB
FL () EA
2FBC FBC )
(2)铅直位移
加铅直单位力,相应内力
1
FAB
1
FAB F
同一根杆的拉压应变能与弯曲应变能相比一般也较小
思考:组合变形杆应变能的叠加法
(2)余能
F 余功
F
F1
L
o
等直杆拉伸,非弹性变形情况下
1
余功
F1
Wc dF
余能
余能密度
0
vc
Vc AL
1
d
0
F1
Vc Wc dF
0
一般应力状态下,余能密度
(σ1 ,τ1 )
vc ( xd x yd y zd z xyd xy xzd xz yzd yz )
2 2
1
引起杆伸缩
2
L1 0,L2
2 2
2
L1 1 ,L2
2 2
(1
2
)
应变能 V
EAL2i 2Li
EA 2L
21
2
1 2
(1
2
)2
卡氏第一定理
0
V 1
EA 2L
21
2 2
1
2 2
2
F
V 2
EA 2L
2 2 1
2 2
2
解得
1
FL, EA
2
(1 2
2) FL EA
(2)余能定理与卡氏第二定理
解静定问题的方法:
选取基本静定系,适当解除约束,增加相应的 约束反力
建立相应约束处的变形协调关系,并用外力与 解除约束的反力表示,得到补充方程
再结合基本静定系的平衡方程,可求得该约束 反力,从而将超静定问题转化为静定问题求解
进一步可计算内力、应力、变形及强度、刚 度、稳定性等
用能量法解超静定问题的特点:
由铰B平衡,得 FAB F Ft,FBC 2F
应变能
V
L 2EA
(F Ft )2
2F 2
1 (Ft
)
V Ft
L
(F EA
Ft )
实际上,Ft 0 水平位移
1
FL EA
注:变形在弹性范围内
例10-4. 试求悬臂梁自由端的挠度与转角。
F
EI , L
MB
A
B
解:弯矩 M Fx
,
应变能
(注意:内力正负规定应一致)
单位力法
M
FL3
wB
M
L
EI
dx
3EI
M M dx
M 2 F dx
L F EI
L 2EI
V F
注:线弹性、小变形条件下,单位力法得到的 位移等于卡氏第二定理的结果,但两者的 概念与方法有所区别。
(2)转角
1
加单位力偶,相应内力
A
B
M 1
单位力法
B
M
M2
1 2
Fa
1 2
F sin 30 x
F1 sin 60 x
假定各力同时按比例加载至最终值
外力的余功
Fi
Wc
idFi
0
F1 F2 Fn
A
B
余能
Fi
Vc idFi Vc (Fi )
1 2
n
0
假设仅第i个外力有微小增量dFi,则余能的变化
dVc
Vc Fi
dFi
外力余功的变化 dWc idFi
外力余功等值于余能 dWc dVc
i
Vc Fi
余能定理
q
x
A w
B
y
解:线弹性、小变形条件下,弯矩 M 1 qLx 1 qx2
应变能
V
M 2 dx q2 L5
L 2EI
240EI
2
2
挠度 w q (L3 x 2Lx3 x4 )
24EI
外力功 W qdx w q2 L5
L
2 240EI
V W
思考:若计算梁弯曲的剪切应变能,功能相等 关系是否仍成立。
E3 A3
0
——补充方程
解得
FN 3
FD
1
F
2EAcos3
E3 A3
FN1 FN 2
F
2 cos
E3 A3
EAcos2
例10-1构0 架,各杆弹性模量均为E,横截面积 A1=2A,A2=3A,A3=4A,铰A受力F。 试求各杆应力(AD=L, =30, 60)
C2
B 1
3
D
A
F
解:一次超静定
内力虚功 dWi dWe (Md~ Fsd~) 一般情况下 dWi (Md~ Fsd~ Td~ FNd~)
杆内力的总虚功
Wi (Md~ Fsd~ Td~ FNd~)
L
Fi~i (Md~ Fsd~ Td~ FNd~)
L
适用非线弹性情况
虚位移原理
(2)单位力法
小变形假设下,结构因实际外力作用而产生的位移,
3. 虚位移原理与单位力法
(1)虚位移原理
变形体:约束—支座约束、变形的几何相容
虚位移——满足约束条件的微小的位移
平衡条件等价于 We Wi 0
杆外力的总虚功
We Fi~i
F1 F2 Fn
A
B
1 2
n
截取微段
平衡
M
M+dM d
d
dWe dWi 0
2
2
外力虚功
Fs dx
Fs+dFs
dWe Md~ Fsd~
F
B
A
解:杆AB,M Fx
C
杆BC,M Fa,FN F
应变能 V
a F 2 x 2 dx 0 2EI
2a F 2a 2 dx 0 2EI
2a F 2 dx 0 2EA
位移
Ay
V F
7Fa 3 3EI
2Fa EA
思考:在D处也作用有水平力F, B
1、应变能与余能
(1)应变能
F
F
F1
L
o
等直杆拉伸,非弹性变形情况下
应变能
1
Vε W Fd
0
应变能密度
vε
Vε AL
1
d
0
功
1
一般应力状态下,应变能密度
(ε1 ,γ1 )
vε ( xd x yd y zd z xyd xy xzd xz yzd yz )
——虚设外力法
例10-3. 题同例10-2,求铰B的水平与铅直位移。
A
F
B B
解:由铰B平衡,得两杆内力 C
FAB F(拉),FBC 2F(压)
应变能 V
Fi2 Li L (F 2 2 2F 2 ) 2EA 2EA
铅直位移
2
V F
(1 2
2) FL EA
水平位移
1
V Ft
0?
虚设力法:假定铰B还受水平向右的力Ft作用
例10-6 试分析下列结构的位移
A
BF
AB
B
V F
F A
B
F
AB
V F
或 V ? (2F )
F1 A
F2 B
AB
V F1
或 V F2
或?
q AB
C B ?
虚加一对力偶MB
B
MB
B
V M B
M B 0
思考:P83- 3-1,2,3,4,习题3-8(c),9,14
练习:P86- 习题3-7(c),8(a),15
F
C
A
D
B
F
解:二次超静定
基本静定系——解除铰D约束, 加反力F1,F2,F3,F4
铰D平衡:
F2 F4
F3 F1,F2 F4 F
F1
F3
D
结构对称性
F2
F4
F 2
一次超静定
F2 F4
F1 D
F3
F
D
变形相容 Dy 0 ——对称性已用
Dx 0
F1
F1
F 2
左半弯矩
1 M1 2 Fx
GA
d Tdx
GI p
d FNdx
EA
单位力法的表达式
1
(M
L
M EI
Fs
s Fs
GA
T
T GI p
FN
FN )dx EA
同一根杆的轴力和剪力所作功与弯矩所作功相比
一般较小,其中相应项可略去
思考:线弹性、小变形假设下,单位力法表达式
与卡氏第二定理表达式的关系
例10-7题同例10-3,求铰B的水平与铅直位移。 解:实际外力F相应的杆内力
(1)卡氏第一定理
应变能与功取决于荷载的最终值及相应的位移
——假定各力同时按比例加载至最终值
外力的功
i
W Fidi
0
应变能
F1 F2 Fn
A
B
1 2
n
i
V
Fidi V (i )
0
假设仅第i个位移有微小增量di,则应变能的变化
dV
V
i
di
外力功的变化 dW Fidi
外力功等值于应变能
由铰B平衡,得 FAB F,FBC 2F
(1)水平位移
去掉原外力,加水平单位力 A
B
1
相应内力 FAB 1,FBC 0
单位力法表达式
C
Bx
FN
L
FN dx EA
L EA
(
FAB
FAB
FL () EA
2FBC FBC )
(2)铅直位移
加铅直单位力,相应内力
1
FAB
1
FAB F
同一根杆的拉压应变能与弯曲应变能相比一般也较小
思考:组合变形杆应变能的叠加法
(2)余能
F 余功
F
F1
L
o
等直杆拉伸,非弹性变形情况下
1
余功
F1
Wc dF
余能
余能密度
0
vc
Vc AL
1
d
0
F1
Vc Wc dF
0
一般应力状态下,余能密度
(σ1 ,τ1 )
vc ( xd x yd y zd z xyd xy xzd xz yzd yz )
2 2
1
引起杆伸缩
2
L1 0,L2
2 2
2
L1 1 ,L2
2 2
(1
2
)
应变能 V
EAL2i 2Li
EA 2L
21
2
1 2
(1
2
)2
卡氏第一定理
0
V 1
EA 2L
21
2 2
1
2 2
2
F
V 2
EA 2L
2 2 1
2 2
2
解得
1
FL, EA
2
(1 2
2) FL EA
(2)余能定理与卡氏第二定理
解静定问题的方法:
选取基本静定系,适当解除约束,增加相应的 约束反力
建立相应约束处的变形协调关系,并用外力与 解除约束的反力表示,得到补充方程
再结合基本静定系的平衡方程,可求得该约束 反力,从而将超静定问题转化为静定问题求解
进一步可计算内力、应力、变形及强度、刚 度、稳定性等
用能量法解超静定问题的特点:
由铰B平衡,得 FAB F Ft,FBC 2F
应变能
V
L 2EA
(F Ft )2
2F 2
1 (Ft
)
V Ft
L
(F EA
Ft )
实际上,Ft 0 水平位移
1
FL EA
注:变形在弹性范围内
例10-4. 试求悬臂梁自由端的挠度与转角。
F
EI , L
MB
A
B
解:弯矩 M Fx
,
应变能
(注意:内力正负规定应一致)
单位力法
M
FL3
wB
M
L
EI
dx
3EI
M M dx
M 2 F dx
L F EI
L 2EI
V F
注:线弹性、小变形条件下,单位力法得到的 位移等于卡氏第二定理的结果,但两者的 概念与方法有所区别。
(2)转角
1
加单位力偶,相应内力
A
B
M 1
单位力法
B
M
M2
1 2
Fa
1 2
F sin 30 x
F1 sin 60 x
假定各力同时按比例加载至最终值
外力的余功
Fi
Wc
idFi
0
F1 F2 Fn
A
B
余能
Fi
Vc idFi Vc (Fi )
1 2
n
0
假设仅第i个外力有微小增量dFi,则余能的变化
dVc
Vc Fi
dFi
外力余功的变化 dWc idFi
外力余功等值于余能 dWc dVc
i
Vc Fi
余能定理
q
x
A w
B
y
解:线弹性、小变形条件下,弯矩 M 1 qLx 1 qx2
应变能
V
M 2 dx q2 L5
L 2EI
240EI
2
2
挠度 w q (L3 x 2Lx3 x4 )
24EI
外力功 W qdx w q2 L5
L
2 240EI
V W
思考:若计算梁弯曲的剪切应变能,功能相等 关系是否仍成立。
E3 A3
0
——补充方程
解得
FN 3
FD
1
F
2EAcos3
E3 A3
FN1 FN 2
F
2 cos
E3 A3
EAcos2
例10-1构0 架,各杆弹性模量均为E,横截面积 A1=2A,A2=3A,A3=4A,铰A受力F。 试求各杆应力(AD=L, =30, 60)
C2
B 1
3
D
A
F
解:一次超静定
内力虚功 dWi dWe (Md~ Fsd~) 一般情况下 dWi (Md~ Fsd~ Td~ FNd~)
杆内力的总虚功
Wi (Md~ Fsd~ Td~ FNd~)
L
Fi~i (Md~ Fsd~ Td~ FNd~)
L
适用非线弹性情况
虚位移原理
(2)单位力法
小变形假设下,结构因实际外力作用而产生的位移,
3. 虚位移原理与单位力法
(1)虚位移原理
变形体:约束—支座约束、变形的几何相容
虚位移——满足约束条件的微小的位移
平衡条件等价于 We Wi 0
杆外力的总虚功
We Fi~i
F1 F2 Fn
A
B
1 2
n
截取微段
平衡
M
M+dM d
d
dWe dWi 0
2
2
外力虚功
Fs dx
Fs+dFs
dWe Md~ Fsd~
F
B
A
解:杆AB,M Fx
C
杆BC,M Fa,FN F
应变能 V
a F 2 x 2 dx 0 2EI
2a F 2a 2 dx 0 2EI
2a F 2 dx 0 2EA
位移
Ay
V F
7Fa 3 3EI
2Fa EA
思考:在D处也作用有水平力F, B
