电磁场与电磁波理论(第二版)(徐立勤,曹伟)第4章习题解答
电磁场与电磁波课后习题及答案四章习题解答
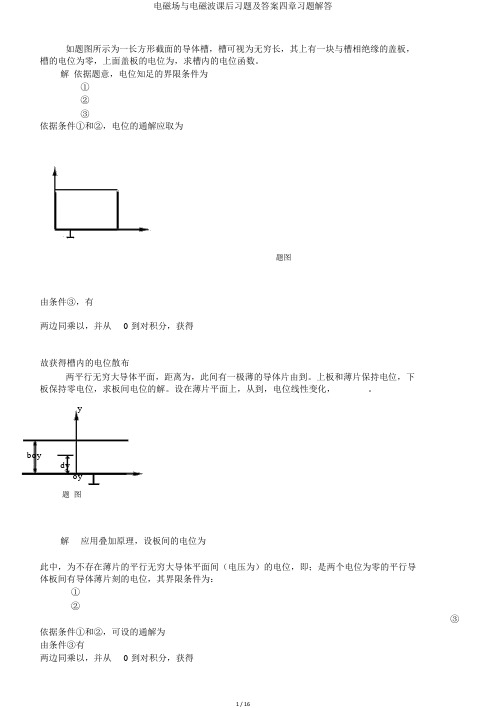
如题图所示为一长方形截面的导体槽,槽可视为无穷长,其上有一块与槽相绝缘的盖板,槽的电位为零,上面盖板的电位为,求槽内的电位函数。
解依据题意,电位知足的界限条件为①②③依据条件①和②,电位的通解应取为题图由条件③,有两边同乘以,并从0 到对积分,获得故获得槽内的电位散布两平行无穷大导体平面,距离为,此间有一极薄的导体片由到。
上板和薄片保持电位,下板保持零电位,求板间电位的解。
设在薄片平面上,从到,电位线性变化,。
yboydyoy题图解应用叠加原理,设板间的电位为此中,为不存在薄片的平行无穷大导体平面间(电压为)的电位,即;是两个电位为零的平行导体板间有导体薄片刻的电位,其界限条件为:①②③依据条件①和②,可设的通解为由条件③有两边同乘以,并从0 到对积分,获得故获得求在上题的解中,除开一项外,其余全部项对电场总储能的贡献。
并按定出边沿电容。
解在导体板()上,相应于的电荷面密度则导体板上(沿方向单位长)相应的总电荷相应的电场储能为其边沿电容为如题图所示的导体槽,底面保持电位,其余两面电位为零,求槽内的电位的解。
解依据题意,电位知足的界限条件为①题图②③依据条件①和②,电位的通解应取为由条件③,有两边同乘以,并从0 到对积分,获得故获得槽内的电位散布为一长、宽、高分别为、、的长方体表面保持零电位,体积内填补密度为的电荷。
求体积内的电位。
解在体积内,电位知足泊松方程( 1)长方体表面上,电位知足界限条件。
由此设电位的通解为代入泊松方程(1),可得由此可得或( 2)由式( 2),可得故如题图所示的一对无穷大接地平行导体板,板间有一与轴平行的线电荷,其地点为。
求板间的电位函数。
解因为在处有一与轴平行的线电荷,认为界将场空间切割为和两个地区,则这两个地区中的电位和都知足拉普拉斯方程。
而在的分界面上,可利用函数将线电荷表示成电荷面密度。
电位的界限条件为题图①②③由条件①和②,可设电位函数的通解为由条件③,有( 1)( 2)由式( 1),可得( 3)将式( 2)两边同乘以,并从到对积分,有(4)由式( 3)和( 4)解得故如题图所示的矩形导体槽的电位为零,槽中有一与槽平行的线电荷。
电磁场与电磁波理论第二版徐立勤,曹伟第2章习题解答

电磁场与电磁波理论第二版徐立勤,曹伟第2章习题解答第2章习题解答2.2已知半径为a 、长为l 的圆柱体内分布着轴对称的体电荷,已知其电荷密度()0Va ρρρρ=,()0a ρ≤≤。
试求总电量Q 。
解:2π200002d d d d π3laV VQ V z la aρρρρρ?ρ===?2.3 半径为0R 的球面上均匀分布着电荷,总电量为Q 。
当球以角速度ω绕某一直径(z 轴)旋转时,试求其表面上的面电流密度。
解:面电荷密度为 204πS QR ρ=面电流密度为 00200sin sin sin 4π4πS S S Q Q J v R R R R ωθρρωθωθ=?=== 2.4 均匀密绕的螺旋管可等效为圆柱形面电流0S S J e J ?=。
已知导线的直径为d ,导线中的电流为0I ,试求0S J 。
解:每根导线的体电流密度为 00224π(/2)πI I J d d== 由于导线是均匀密绕,则根据定义面电流密度为04πS IJ Jd d ==因此,等效面电流密度为04πS IJ e d=2.6 两个带电量分别为0q 和02q 的点电荷相距为d ,另有一带电量为0q 的点电荷位于其间。
为使中间的点电荷处于平衡状态,试求其位置。
当中间的点电荷带电量为-0q 时,结果又如何?解:设实验电荷0q 离02q 为x ,那么离0q 为x d -。
由库仑定律,实验电荷受02q 的排斥力为实验电荷受0q 的排斥力为要使实验电荷保持平衡,即21F F =,那么由00222114π4π()q q x d x εε=-,可以解得如果实验电荷为0q -,那么平衡位置仍然为d d x 585.0122=+=。
只是这时实验电荷与0q 和02q 不是排斥力,而是吸引力。
2.7 边长为a 的正方形的三个顶点上各放置带电量为0q 的点电荷,试求第四个顶点上的电场强度E 。
解:设点电荷的位置分别为()00,0,0q ,()0,0,0q a 和()00,,0q a ,由库仑定律可得点(),,0P a a 处的电场为2.9半径为0R 的半球面上均匀分布着面电荷,电荷密度为0S ρ,试求球心处的电场强度;若同样的电荷均匀分布在半径为0R 的半球内,再求球心处的电场强度。
电磁学第二版习题答案第四章

j
δ
=
ρ I 3.14 ×10−8 × 20 = = 0.2 V 2 −3 2 m πR 3.14 × (10 )
4.3.5 铜的电阻温度系数为 4.3 ×10−3 / 0C ,在 0 0C 时的电阻率为 1.6 ×10−8 Ω ⋅ m ,求直径为 5mm、长 为 160km 的铜制电话线在 25 0C 时的电阻。
b a
ρ dx ρ 1 1 ρ (b − a) = ( − )= 2 4π r 4π a b 4π ab
ρ dx 4π r 2
4.3.4 直径为 2mm 的导线由电阻率为 3.14 ×10−8 Ω ⋅ m 的材料制成,当 20A 的电流均匀地流过该导 体时,求导体内部的场强。
解:根据 j = δ E ,得 E =
lρ ⎡ 1 1 ⎤ lρ − = π (b − a) ⎢ ⎣a b⎥ ⎦ π ab lρ l =ρ 2 s πa
当 a = b 时: R =
4.3.3 球形电容器内外半径为 a 和 b,两极板间充满电阻率为 ρ 的均匀物质,试计算该电容器的漏 电电阻。 解:对漏电电阻,其内部电极电位差,电流沿径向从高电位向低电位流过,则有: dR = 积分得: R = ∫ dR = ∫
(a) Rab = 1K Ω , (b) Rab = 4.5Ω (c) Rab = 1.2Ω (d) Rab = 7.4Ω (e) Rab = 5Ω (f) Rab = 1.5Ω (g) Rab = 14Ω
4.2.3 当附图中的 R1 为何值时 A、B 间的总电阻恰等于 R0? 解:由 R总 = R1 +
U = 0.01× 103 = 10(V ) , U 额 = RW =
2 P 100 = 0.01 × 100 = 0.01(W )
电磁场理论 答案 习题4

( evr
2 cosθ
+
evθ
sin θ
)
4-5 接地无限大导体平板上有一个半径为 a 的半球形突起,在点 (0,0, d ) 处有一个
点电荷 q (如图 4-3),求导体上方的电
z
位。
d·q
解:计算导体上方的电位时,要保持导 体平板部分和半球部分的电位都为零。先找平
面导体的镜像电荷 q1 = −q ,位于 (0,0,−d )
k Q2
所以在整个过程中,外力作的总功为
8πε 0d
. 也可以用静电能计算,在移动以前,系统的静电能等于两个点电荷之间的相互 w 作用能:
wwW
=
1 2
q1ϕ1
+
1 2
q2ϕ
2
=
1 Q
2
4π
−Q ε0 (2d )
+
1 (−Q) 2 4π
−Q ε0 (2d )
=
− Q2 8π ε0d
移动点电荷到无穷远以后,系统的静电能为零。因此,在这个过程中,外力作
h 4-3 证明:一个点电荷 q 和一个带有电荷 Q 、半径为 R 的导体球之间的作用力为
.kF
=
q 4π ε 0
⎡ ⎢ ⎢ ⎢
Q
+ D
Rq
D
2
−
DRq (D2 − R2 )2
⎤ ⎥ ⎥ ⎥
w⎣
⎦
其中 D 是 q 到球心的距离 (D > R) 。
ww证明:使用镜像法分析。由于导体球不接地,本身又带电 Q ,必须在导体球内
om 处。再找球面镜像电荷 q2 = −aq / d ,位于
a b·q2 ·
-b·q3
电磁场与电磁波课后复习题与答案四章复习题解答
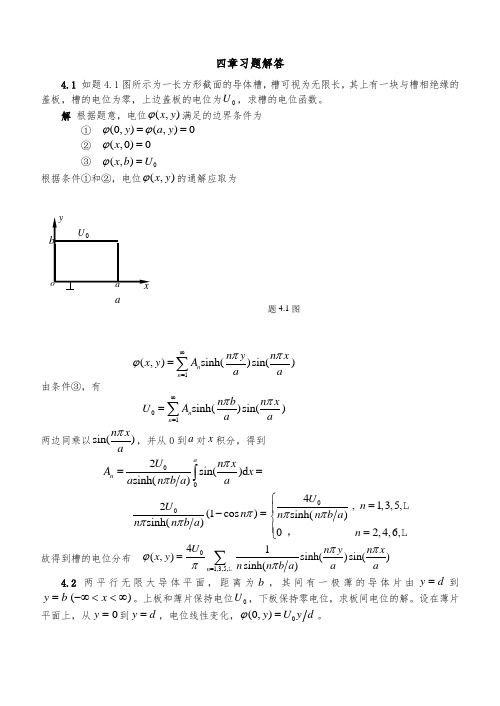
四章习题解答4.1 如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ=③ 0(,)x b U ϕ=根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a aππϕ∞==∑ 由条件③,有01sinh()sin()n n n b n x U A a aππ∞==∑ 两边同乘以sin()n xaπ,并从0到a 对x 积分,得到 002sin()d sinh()an U n xA x a n b a aππ==⎰ 02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩L L , 故得到槽的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑L 4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
a题4.1图解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:① 22(,0)(,)0x x b ϕϕ== ② 2(,)0()x y x ϕ=→∞③ 002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩根据条件①和②,可设2(,)x y ϕ的通解为 21(,)sin()e n x b n n n y x y A b ππϕ∞-==∑ 由条件③有 00100(0)sin()()n n U U y y d n y bA U U b y y d y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n yb π,并从0到b 对y 积分,得到 0002211(1)sin()d ()sin()d d bn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d bππ 故得到 (,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d n b b ππππ∞-=+∑ 4.3 求在上题的解中,除开0U y b 一项外,其他所有项对电场总储能的贡献。
电磁场与电磁波习题答案资料讲解

电磁场与电磁波习题答案第四章习题解答★【4.1】如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ==;② (,0)0x ϕ=; ③ 0(,)x b U ϕ= 根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a a ππϕ∞==∑ 由条件③,有 01sinh()sin()n n n b n xU A a a ππ∞==∑两边同乘以sin()n xa π,并从0到a 对x 积分,得到002sin()d sinh()an U n x A x a n b a a ππ==⎰ 02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩,故得到槽内的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:22(,0)(,)0x x b ϕϕ==① 2(,)0()x y x ϕ=→∞②③ 002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩; 根据条件①和②,可设2(,)x y ϕ的通解为21(,)sin()en x bn n n yx y A b ππϕ∞-==∑;由条件③有 00100(0)sin()()n n U U y y d n y b A U U b y yd y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n ybπ,并从0到b 对y 积分,得到 0002211(1)sin()d ()sin()d d bn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d bππ 故得到 (,)x y ϕ=0022121sin()sin()e n x b n U bU n d n y y b d nb b ππππ∞-=+∑ 4.4 如题4.4图所示的导体槽,底面保持电位0U ,其余两面电位为零,求槽内的电位的解。
电磁场与电磁波第二版课后答案

电磁场与电磁波第二版课后答案本文档为《电磁场与电磁波》第二版的课后答案,包含了所有章节的练习题的答案和解析。
《电磁场与电磁波》是电磁学领域的经典教材,它讲述了电磁场和电磁波的基本原理和应用。
通过学习本书,读者可以深入了解电磁学的基本概念和原理,并且能够解决一些相关问题。
第一章绪论练习题答案1.电磁场是由电荷和电流产生的一种物质性质,具有电场和磁场两种形式。
电磁波是电磁场的振动。
电磁辐射是指电磁波传播的过程。
2.对于一点电荷,其电场是以该点为中心的球对称分布,其强度与距离成反比。
对于无限长直导线产生的电场,其强度与距离呈线性关系,方向垂直于导线轴线。
3.电磁场的本质是相互作用力。
电场力是由于电荷之间的作用产生的,磁场力是由于电流之间的作用产生的。
解析1.电磁场是由电荷和电流产生的物质性质。
当电荷存在时,它会产生一个电场,该电荷周围的空间中存在电场强度。
同时,当电流存在时,它会产生一个磁场,该电流所在的区域存在磁场。
电磁波是电磁场的振动传播。
电磁波是由电磁场的变化引起的,相邻电磁场的振动会相互影响,从而形成了电磁波的传播。
电磁辐射是指电磁波在空间中的传播过程。
当电磁波从一个介质传播到另一个介质时,会发生折射和反射现象。
2.在一点电荷产生的电场中,电场强度与该点到电荷的距离成反比,即\(E = \frac{{k \cdot q}}{{r^2}}\),其中\(E\)为电场强度,\(k\)为电场常数,\(q\)为电荷量,\(r\)为距离。
对于无限长直导线产生的电场,其电场强度与离导线的距离呈线性关系。
当离无限长直导线的距离为\(r\)时,其电场强度可表示为\(E = \frac{{\mu_0 \cdot I}}{{2 \pi \cdot r}}\),其中\(E\)为电场强度,\(\mu_0\)为真空中的磁导率,\(I\)为电流强度。
3.电磁场的本质是相互作用力。
当两个电荷之间有作用力时,这个作用力是由于它们之间的电场力产生的。
电磁场与电磁波理论(第二版)(徐立勤-曹伟)第3章习题解答

第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇r r 和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+r r r0202εερA -=Φ∇-=(2) ()x y z E A e yz e xz e xy Φ=-∇=-++r r r r r020=Φ∇-=ερ(3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦r r r r20004sin sin 3sin Bz Bz A A A ρεΦεϕϕεϕρρ⎛⎫⎛⎫=-∇=-+-=-+ ⎪ ⎪⎝⎭⎝⎭(4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-r r r r r200cos 2cos cos 6sin cos sin sin A A A θϕϕρεΦεθϕθθ⎛⎫=-∇=-+- ⎪⎝⎭3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为22001111100()()22S S d R d R d ρρΦεε=+-=- 下顶面在球心产生的电位为22002222200()()22S S d R d R d ρρΦεε=+-=- 侧面在球心产生的电位为030014π4πS S SSRRρρΦεε==⎰式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为1230S R ρΦΦΦΦε=++=3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章习题解答4.1 电导率为的均匀、线性、各向同性的导体球,半径为,其表面的电位分布σR 为。
试确定表面上各点的电流密度。
0cos Φθ解:由于导体球的外部是空气,所有在导体球的表面只有切向分量,即0t t t 11sin sin J E e e e R R R θϕθσΦΦΦσσΦσθθθϕ⎛⎫∂∂==-∇=-+= ⎪∂∂⎝⎭4.2 如题4.2图所示平板电容器。
板间填充两种不同的导电媒质,其厚度分别为和,两平板的面积均为。
若在两极板上加上恒定的电压。
试求板间1d 2d S 0U 的电位、电场强度、电流密度以及各分界面上的自由电荷和电容器的漏ΦEJ 电导。
解:理想电容器,满足的定解问题为021==σσ 和 210 Φ∇=220Φ∇=以及12111112120121200x x d d x d x d x d x d V xxΦΦΦΦΦΦεε==+====∂∂====∂∂由直接积分法可以得到电位的通解为 和 1 Ax B Φ=+2Cx DΦ=+由和可以确定出及,则上式电位的表达式为10x Φ==1220x d d V Φ=+=0=B )(210d d C V D +-= 和 1 Ax Φ=2012()Cx V C d d Φ=+-+利用电位在介质分界面的边界条件,则确定出211201211202d d V C d d V A εεεεεε+=+=因此电位分布为和 2012112V x d d εΦεε=+102110221122112()V d Vx d d d d εεεΦεεεε-=+++而对应的电场强度和电位移矢量为和 2101221xE e V d d εεε=-+ 1201221xE e V d d εεε=-+以及和 12101221xD e d d εεεε=-+ 12201221x D e Vd d εεεε=-+ 根据静电比拟法得到对平板电容器内恒定电场的电位为()E ED J εσΦΦ⇔⇔⇔⇔和 2012112V x d d σΦσσ=+102110221122112()V d V x d d d d σσσΦσσσσ-=+++电场强度为和 2101221x E e d d σσσ=-+1201221x E e Vd d σσσ=-+电流密度矢量为和 12101221xJ e d d σσσσ=-+ 12201221x J e d d σσσσ=-+此时的电流称为电容器的漏电流,对应的电导称为电容器的漏电导,有G——极板的面积121221d d d d S SCCJ S E S S I G V d d E l E l σσσσσ⋅⋅====+⋅⋅⎰⎰⎰⎰ A A S 4.3 如题4.3图所示矩形导体片的电导率为,试求导电片上的电位分布σ以及导电片中各处的电流密度。
解:根据题意,定解问题为20Φ∇=以及 00π0 sin0 02nx x ay y byU bΦΦΦΦ====∂====∂于是可以将通解直接选为1212(,)(sinh||cosh||)(sin cos )y y y y x y C k x C k x D k y D k y Φ=++由得到,则0y Φ==02=D 12(,)(sinh ||cosh ||)sin y y y x y C k x C k x k yΦ=+由得到,即。
因此0y byΦ=∂=∂0cos =b k y (21)π,1,2,2y n k n b-== 1(21)π(21)π(21)π(,)sinhcosh sin 222n n n n x n x n yx y C D b b b Φ∞=---⎡⎤=+⎢⎥⎣⎦∑由得到,于是0y Φ==0=n D 1(21)π(21)π(,)sinhsin 22n n n x n yx y C b bΦ∞=--=∑再由可以得到0πsin2x ayU ybΦ=∂=∂01π(21)π(21)πsin sinh sin222n n y n a n yU C b b b ∞=--=∑比较系数法可以得到,而其余的系数均为零。
因此,导电片上电位分布为1πsinh2U C a b=0ππ(,)sinh sinπ22sinh 2U x yx y a b b bΦ=利用和可以计算出导电片上各处电流密度分布为E Φ=-∇ E Jσ=0ππππππcosh sin sinh cos π222222sh 2x y x y J E e e x y U x y x y e e a b b b b b b bΦΦσσΦσσ⎛⎫∂∂==-∇=-+ ⎪∂∂⎝⎭⎛⎫=-+ ⎪⎝⎭ 4.4 在电导率为的无限大导电媒质中流有电流密度的恒定电流。
今沿轴方向挖一半径为的无限σ0x J J e =z a 长圆孔。
试求空间各处的电位、电场强度和电流密度。
ΦEJ 解:在圆柱坐标系下,均匀电流密度产生的电位为,因此存在空腔的媒质中电位的定J ϕρσcos 0J-(,)Φρϕ解问题为20Φ∇=以及和 0aρΦρ=∂=∂0cos J ρΦρϕσ→∞=-根据分离变量法可以得到问题的通解为001(,)ln [(sin cos )(sin cos )]n n n n n n n A B A n B n C n D n Φρϕρρϕϕρϕϕ∞-==+++++∑代入边界条件可以得到,,即J A σ=-22a J B a A σ==-2(,)(cos J a Φρϕρϕσρ=-+而电流密度为220221(1cos (1)sin z J E e e e z a a J e e ρϕρϕΦΦΦσσΦσρρϕϕϕρρ⎛⎫∂∂∂==-∇=-++ ⎪∂∂∂⎝⎭⎡⎤=--+⎢⎥⎣⎦4.5 如题4.5图所示,厚度为的扇形弧片由两块大小相同但电导率不同的金属片构d 成。
弧片的内外半径分别为和。
当以和作为电极时,加上恒定的电1R 2R AB CD 压后,试求弧片上的电位分布、分界面上的面电荷密度以及极板间的电阻;若0U 以和作为电极,结果又如何?AAD A BC 解:弧片内电流只有分量,即,。
根据边界条件可以e ϕ 11J J e ϕ= 22J J e ϕ=1n 2n J J =得到,即。
而21JJ =2211E E σσ=π/4π/2021120π/4πd d d ()4CDAB U E e l E E E E ϕρϕρϕρ=-⋅=--=-+⎰⎰⎰ 可以解得 201012121244π()π()U U E e E e ϕϕσσσσρσσρ==++金属片1中的电位分布为10120124πd d 0π()4PABU E e l E ϕϕσΦρϕϕϕσσ=-⋅=-=≤≤+⎰⎰ 金属片2中电位分布为π/4201202210π/412124()ππd [d d ] π()()42PABU U E e l E E ϕϕσσσΦρϕρϕϕϕσσσσ-=-⋅=-+=+≤≤++⎰⎰⎰ 面电荷密度为 00021002121124()()()S U J E E εεεσσρεσσπσσρ⎛⎫-=-=-=⎪+⎝⎭电流为 21021021212144d d ln π()π()b S a U U RI J S d R σσσσρσσρσσ=⋅=⋅=++⎰⎰ 根据电阻的定义可得 1222101π()14ln U R R I U R σσσσ+==当电极改置于内圆弧和外圆弧,则,即,因此电位仅为的函数,21E E =12ΦΦ=Φr 1021d d 0() ()0d d R U R r ΦρΦΦρρ⎛⎫=== ⎪⎝⎭因此电位分布为 021221()ln(/) ln(/)U r R R R R R Φρρ=≤≤于是有 1020111122222121d()()ln(/)d ln(/)U U d J E r J E r d R R R R σσσσΦσσρρρρ==-===-=因此,总电流为12120121221π()ππd d 444ln(/)S S U d I J S J S J d J d R R σσρρ+=+=+=⎰⎰阻抗为211204ln(/)π()R R R U dσσ=+4.6 球形电容器的内球半径为,外球壳的内半径为。
将两种不同的 导电煤质分别填入两个半球,两种导电a b 煤质的 电导率分别为和。
求该电容器的漏电阻。
1σ2σ解:设在上电位为,上电位为零。
根据题意,电位仅为的函数,因此定解问题为a r =Ub r =Φr 221d d 0() ()0d d r a U b r r r ΦΦΦ⎛⎫=== ⎪⎝⎭因此,通解为C D rΦ=-+根据边界条件可以得到ba aU Db a abU C -=-=因此11abU b a r b Φ⎛⎫=- ⎪-⎝⎭在两种煤质中电流密度分别为2222221111r a b abU E J r a b abU E J σσσσ-==-==因此总电流为1212122πd d ()S S abUI J S J S b aσσ=+=+-⎰⎰于是电容器的漏电阻1212π()b a R ab σσ-=⋅+4.8 半径为的圆柱形导体内的磁场,试求导体中的总电流。
1a =cm 2424.77102210H e ϕρρ--⎛⎫=⨯- ⎪⨯⎝⎭A /m 解: J H =∇⨯ ()42134.77101210z z z ze e e H e e z H H H ρϕϕρϕρρρρρϕρρρ--∂∂∂∂⎛⎫===⨯- ⎪∂∂∂∂⨯⎝⎭2π0.0142003d 4.77101d 0210S I J S ρρρ--⎛⎫=⋅=⨯-= ⎪⨯⎝⎭⎰⎰⎰ 4.14 已知某一电流分布的矢量磁位为224x y z A e x y e y x e xyz=+-求该电流分布及其对应的。
B解:利用矢量磁位满足的泊松方程来求出电流分布为A222222222y x z x y z x y A A A J A e e e e y e xx y z ∂∂∂=-∇=---=--∂∂∂由可以求出磁感应强度为A B⨯∇=22244()y y x x z z x y z x y z A A A A A A B A e e y x e y z z x xy e xz e yz e y x ∂∂⎛⎫⎛⎫∂∂∂∂⎛⎫=∇⨯=-+-+- ⎪ ⎪⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭=--+-。
