明胶水溶液(2%,无菌)
4_3_2薄膜干涉

λ 明环: δ = 2e + = kλ r 2 e= 代入 2R λ λ 暗环:δ = 2e + = ( 2k + 1) 2 2 得 o · ( 2 k − 1) R λ R 明环半径: rk = λ 2 r 平凸透镜 e r = kR λ 暗环半径: k 平晶 条纹特点: (1) rk与环的级次的平方根成正比; (2)中心为0级暗斑,越往外级次越高; (3) 越向外环越密,即内疏外密。
肥皂膜显示的明亮颜色, 火玛瑙: 是什么原因造成的呢? 为什么会闪出火红色的晕 答案在本次讲课中。 彩,而称其为火玛瑙呢?
中国石油大学,冯金波
第3章
光的干涉
§3.2 相干光 §3.1 杨氏双缝干涉 §3.5 光程 §3.6 薄膜干涉(一)——等厚干涉 §3.7 薄膜干涉(二)——等倾干涉 §3.8 迈克尔孙干涉仪 §3.3 光的非单色性对干涉条纹的影响 §3.4 光源的大小对干涉条纹的影响
∆e 条纹间距:L = sin θ
λ L= 2 n sin θ λ ≈ 2 nθ
�等厚干涉条纹
劈尖
不规则表面
中国石油大学,冯金波
引子:五彩缤纷的肥皂膜(答案)
δ (e ) = kλ , k = 1,2 ,3 ,… 干涉相长 λ δ (e ) = ( 2k + 1) , k = 0 ,1,2 ,… 2 干涉相消 λ δ (e ) = 2ne + 2
f
λ n + ′ − δ = ( AB + BC ) n AD 2 e AB = BC = cos r
S
i
n′ n > n′ n′
·
i
1
i
2
i
A
· ·ri · ·
第四章 第2讲 同角三角函数的基本关系与诱导公式-2025年高考数学备考

第四章三角函数第2讲同角三角函数的基本关系与诱导公式课标要求命题点五年考情命题分析预测1.理解同角三角函数的基本关系式:sin 2x +cos 2x =1,sinHs =tan x .2.借助单位圆的对称性,利用定义推导出诱导公式(α±π2,α±π的正弦、余弦、正切)同角三角函数关系的应用2023全国卷乙T14;2021新高考卷ⅠT6;2021全国卷甲T9;2020全国卷ⅠT9本讲主要考查利用同角三角函数的基本关系与诱导公式化简与求值,常与三角恒等变换结合命题,考查基本运算能力.题型以选择题、填空题为主,难度中等偏下.在2025年高考复习备考时,要掌握公式并会灵活运用.诱导公式的应用2020北京T9;2019全国卷ⅠT7同角三角函数基本关系与诱导公式的综合应用学生用书P0751.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1.(2)商的关系:tan α=sinHs (α≠π2+k π,k ∈Z ).(3)公式常见变形:sin 2α=1-cos 2α;sin α=±1-cos 2;sin 2α=sin 2sin 2+c 2=ta 2tan 2r1,cos 2α=cos 2si 2+cos 2=①1tan 2r1;(sin α±cos α)2=1±2sin αcos α.注意利用平方关系时,若要开方,要注意判断符号.2.诱导公式公式一二三四五六角2k π+α(k ∈Z )π+α-απ-απ2-απ2+α正弦sin α②-sin α-sin α③sin αcos α④cos α余弦cos α⑤-cos αcos α⑥-cos αsin α⑦-sin α正切tan α⑧tan α-tan α⑨-tan α口诀奇变偶不变,符号看象限.1.[易错题]已知α是第二象限角,sinα=513,则cosα=(A)A.-1213B.-513C.513D.213解析因为α是第二象限角,所以cosα<0,又sin2α+cos2α=1,所以cosα=-1-sin2=-1213.2.[2023贵州联考]已知tanθ=-2,则sin+cos sin=(D)A.-1B.-3C.-12D.12解析因为tanθ=-2,则sin+cos sin=1+1tan=1-12=12.3.[2023上饶重点中学模拟]下面诱导公式使用正确的是(C)A.sin(θ-π2)=cosθB.cos(3π2+θ)=-sinθC.sin(3π2-θ)=-cosθD.cos(θ-π2)=-sinθ解析∵sin(θ-π2)=-sin(π2-θ)=-cosθ,∴A错误;∵cos(3π2+θ)=sinθ,∴B 错误;∵sin(3π2-θ)=-cosθ,∴C正确;∵cos(θ-π2)=cos(π2-θ)=sinθ,∴D错误.4.sin1050°=-12.解析sin1050°=sin(-30°)=-12.5.[2023成都八中模拟]已知tan(π+α)=2,则sin(π2+)+sin(π-)cos(3π2+)-2cos(π+)=34.解析因为tan(π+α)=tanα=2,所以sin(π2+)+sin(π-)cos(3π2+)-2cos(π+)=cos+sinsinr2cos=1+tan tanr2=1+22+2=34.学生用书P076命题点1同角三角函数关系的应用例1(1)[2024山东模拟]若tanθ=2,则1+sinθcosθ=(B)A.73B.75C.54D.53解析易知cosθ≠0,则1+sinθcosθ=1+sinvos1=si2+cos2+sinvossin2+cos2=tan 2+tanr1 tan2r1=22+2+122+1=75.(2)[2023全国卷乙]若θ∈(0,π2),tanθ=12,则sinθ-cosθ=-55.解析由tan =sin cos=12,sin 2+cos 2=1,且θ∈(0,π2),解得sin cos 故sin θ-cos θ方法技巧同角三角函数基本关系的应用技巧(1)利用sin 2α+cos 2α=1和tan α=sinHs ,可以解决sin α,cos α,tan α的知一求二的问题,注意判断角的终边所在的象限.(2)利用(sin α±cos α)2=1±2sin αcos α,可以解决sin α+cos α,sin αcos α,sin α-cos α知一求二的问题,注意方程思想的应用.(3)利用sin 2α+cos 2α=1可以实现角α的正、余弦互化;利用tan α=sinHs 可以实现角α的弦、切互化,主要考查齐次式的使用技巧以及“1”的变形.训练1[多选/2023江西省上饶市第一中学模拟]已知θ∈(-π,0),sin θ+cos θ=713,则下列结论正确的是(BD )A.θ∈(-π,-π2) B.cos θ=1213C.tan θ=512 D.sin θ-cos θ=-1713解析由sin θ+cos θ=713可得,cos θ=713-sin θ,则(713-sin θ)2+sin 2θ=1,解得sin θ=1213或sin θ=-513.由θ∈(-π,0),可得sin θ=-513,cos θ=1213,故B 正确;由sin θ=-513<0,cos θ=1213>0可得θ为第四象限角,又θ∈(-π,0),所以θ∈(-π2,0),故A 错误;tan θ=sinHs =-512,故C 错误;sin θ-cos θ=-513-1213=-1713,故D 正确.故选BD.命题点2诱导公式的应用例2(1)[全国卷Ⅲ]函数f (x )=15sin (x +π3)+cos (x -π6)的最大值为(A )A.65B.1C.35D.15解析因为cos (x -π6)=cos[(x +π3)-π2]=sin (x +π3),所以f (x )=65sin (x +π3),所以f (x )的最大值为65,故选A.(2)[北京高考]若函数f (x )=sin (x +φ)+cos x 的最大值为2,则常数φ的一个取值为π2(答案不唯一).解析易知当y=sin(x+φ),y=cos x同时取得最大值1时,函数f(x)=sin(x+φ)+cos x取得最大值2,故sin(x+φ)=cos x,则φ=π2+2kπ,k∈Z,故常数φ的一个取值为π2.方法技巧应用诱导公式的一般思路(1)化负角为正角,化大角为小角,直到化到锐角;(2)统一角,统一名;(3)角中含有π2的整数倍时,用公式去掉π2的整数倍.训练2(1)[2023山东省济宁市模拟]已知cos(π6-θ)=13,则cos(5π6+θ)+2sin(5π3-θ)的值为-1.解析原式=cos[π-(π6-θ)]+2sin[3π2+(π6-θ)]=-cos(π6-θ)-2cos(π6-θ)=-3cos(π6-θ)=-1.(2)已知sinα是方程5x2-7x-6=0的根,且α是第三象限角,则sin(--3π2)cos(3π2-)cos(π2-)sin(π2+)·tan2(π-α)的值为-916.解析原式=-sin(3π2+)cos(3π2-)sinvos·tan2α=-tan2α.解方程5x2-7x-6=0,sinvos·tan2α=-cosLin得x1=-35,x2=2.又α是第三象限角,∴sinα=-35,∴cosα=-45,∴tanα=34.故原式=-tan2α=-916.命题点3同角三角函数基本关系与诱导公式的综合应用例3(1)[2023陕西模拟]已知0<α<π2,cos(α+π3)=-23,则tan(2π3-α)=(A)B. D.解析由0<α<π2,得π3<α+π3<5π6,则sin(α+π3)tan(α+π3)=sin(+π3)Hs(+π3)=-tan(2π3-α)=tan[π-(α+π3)]=-tan(α+π3)故选A.(2)[全国卷Ⅰ]已知θ是第四象限角,且sin(θ+π4)=35,则tan(θ-π4)=-43.解析解法一因为sin(θ+π4)=35,所以cos(θ-π4)=sin[π2+(θ-π4)]=sin(θ+π4)=35.因为θ为第四象限角,所以-π+2kπ<θ<2kπ,k∈Z,所以-3π4+2kπ<θ-π4<2kπ-π4,k∈Z,所以sin(θ-π4)=-45,所以tan(θ-π4)=sin(-π4)cos(-π4)=-43.解法二因为θ是第四象限角,且sin (θ+π4)=35,所以θ+π4为第一象限角,所以cos (θ+π4)=45,所以tan (θ-π4)=sin (-π4)Hs (-π4)=-cos[π2+(-π4)]sin[π2+(-π4)]=-cos (+π4)sin (+π4)=-43.方法技巧利用同角三角函数基本关系与诱导公式解题的基本思路(1)分析结构特点,寻求条件及所求间的关系,尤其是角之间的关系;(2)选择恰当公式,利用公式灵活变形;(3)化简求值.注意(1)角的范围会影响三角函数值的符号,开方时要先判断三角函数值的符号.(2)化简过程是恒等变换.训练3[2024安徽省皖江名校联考]已知在平面直角坐标系中,点M (2,4)在角α终边上,则sin 3(π-)+cos 3(-)sin 3-2cos 3=(B )A.23B.32C.-35D.-53解析由题意可得tan α=2,所以原式=sin 3+cos 3si 3-2cos 3=tan 3r1tan 3-2=8+18-2=32.故选B.1.[命题点1/2023广州市一测]已知θ为第一象限角,sin θ-cos θtan 2θ=(D )C. D.解析由sin θ-cos θ1-2sin θcos θ=13,∴sin θcos θ=13,∴(sin θ+cos θ)2=1+2sin θ·cos θ=53.∵θ是第一象限角,∴sin θ+cos θ解法一易得sin θcos θ∴tan θ∴tan 2θ=-52]5 D.解法二易得sin θcos θ=13,∴sin 2θ=23,∵sin θ-cos θ>0,θ是第一象限角,∴π4<θ<π2,(易错警示:不知道求角θ的范围造成增解)∴π2<2θ<π,∴cos 2θ∴tan 2θ D.2.[命题点2/北京高考]已知α,β∈R ,则“存在k ∈Z 使得α=k π+(-1)k β”是“sin α=sin β”的(C)A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件解析若存在k∈Z使得α=kπ+(-1)kβ,则当k=2n,n∈Z时,α=2nπ+β,则sinα=sin(2nπ+β)=sinβ;当k=2n+1,n∈Z时,α=(2n+1)π-β,则sinα=sin(2nπ+π-β)=sin(π-β)=sinβ.若sinα=sinβ,则α=2nπ+β或α=2nπ+π-β,n∈Z,即α=kπ+(-1)kβ,k∈Z,故“存在k∈Z使得α=kπ+(-1)kβ”是“sinα=sinβ”的充分必要条件.3.[命题点3/2023广东惠州一模]若tanα=cos3-sin,则sin(2α+π2)=(D)A.23B.13C.89D.79解析因为tanα=cos3-sin,所以sin Hs=cos3-sin,即3sinα-sin2α=cos2α,所以3sinα=sin2α+cos2α=1,即sinα=13,所以sin(2α+π2)=cos2α=1-2sin2α=79,故选D.学生用书·练习帮P2921.若θ∈(π2,πA)A.sinθ-cosθB.cosθ-sinθC.±(sinθ-cosθ)D.sinθ+cosθ解析)=1-2sinBos=(sin-cos)2=|sinθ-cosθ|,因为θ∈(π2,π),所以sinθ-cosθ>0,所以原式=sinθ-cosθ.故选A.2.[2024北大附中模拟]在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于直线y=x对称,若sinα=45,则cosβ=(B)A.-45B.45C.-35D.35解析因为平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于直线y=x 对称,所以+2=π4+kπ,k∈Z,即α+β=π2+2kπ,k∈Z,所以β=π2-α+2kπ,k∈Z,因为sinα=45,所以cosβ=cos(π2-α+2kπ)=sinα=45(k∈Z),故选B.3.[2024江西联考]已知sin (α+π3)=-14,则cos (α+5π6)=(B )A.-14B.14解析因为sin (α+π3)=-14,所以cos (α+5π6)=cos[(α+π3)+π2]=-sin (α+π3)=14,故选B.4.[2024内蒙古包头模拟]若tan α=2,则sin α(sin α+cos α)=(D )A.25B.35C.45D.65解析sin α(sin α+cos α)=sin 2+sinvos sin 2+cos 2=tan 2+tan tan 2r1=22+222+1=65.故选D.5.[2023湖南衡阳模拟]已知θ为第三象限角,且tan (π2-θ)=43,则cos (θ+π2)=(C)A.-45B.-35C.35D.45解析tan (π2-θ)=sin (π2-)Hs (π2-)=Hs sin=43,即3cos θ=4sin θ,∵θ为第三象限角,∴sin θ<0,cos θ<0,又sin 2θ+cos 2θ=1,∴sin θ=-35,cos θ=-45,∴cos (θ+π2)=-sin θ=35.故选C.6.[2023深圳光明区一模]已知α为第一象限角,cos (α+10°)=13,则tan (170°-α)=(A)A.-22B.22C.-2D.2解析因为α为第一象限角,且cos (α+10°)=1>0,所以α+10°为第一象限角,所以sin (α+10°)=1-cos 2(+10°)=tan (α+10°)=sin (r10°)cos (r10°)=22,则tan (170°-α)=tan[180°-(α+10°)]=-tan (α+10°)=-22.故选A.7.[多选]在△ABC 中,下列结论正确的是(ABC )A.sin (A +B )=sin CB.sin+2=cos2C.tan (A +B )=-tan C (C ≠π2)D.cos (A +B )=cos C 解析在△ABC 中,有A +B +C =π,则sin (A +B )=sin (π-C )=sin C ,A 正确.sin+2=sin (π2-2)=cos 2,B 正确.tan (A +B )=tan (π-C )=-tan C (C ≠π2),C正确.cos (A +B )=cos (π-C )=-cos C ,D 错误.故选ABC.8.[2023四川省资阳市模拟]在△ABC 中,3sin (π2-A )=3sin (π-A ),cos A =-3cos (π-B ),则△ABC 为直角三角形.解析在△ABC 中,由3sin (π2-A )=3sin (π-A ),得3cos A =3sin A ,即tan A =3A ∈(0,π),∴A =π6,又cos A =-3cos (π-B ),=3cos B ,即cos B =12,又B ∈(0,π),∴B =π3,∴C =π-π6-π3=π2,∴△ABC 为直角三角形.9.已知sin θ+cos θ=15,θ∈(0,π),则tan θ=-43;2sinBosr2si 21-tG=24175.解析因为sin θ+cos θ=15,θ∈(0,π),所以(sin θ+cos θ)2=1+2sin θcos θ=125,所以sin θcos θ=-1225<0,所以sin θ>0,cos θ<0.由sin +Hs =15,si 2+c 2=1,得25sin 2θ-5sin θ-12=0,解得sin θ=45或sin θ=-35(舍去),所以sin θ=45,cos θ=-35,所以tan θ=-43.(或sin θ-cos θ>0,(sin θ-cos θ)2=sin 2θ+cos 2θ-2sin θcos θ=1+2425=4925,则sin θ-cos θ=75,由sin +cos =15,sin -cos =75,得sin =45,cos =-35,所以tan θ=-43)解法一2sinvosr2sin 21-tan=2sin (cos +sin )1-sin cos=2sinvos (cos +sin )cos -sin=-2425×15-75=24175.解法二2sin θcos θ+2sin 2θ=2sinvosr2sin 2sin 2+cos 2=2tanr2tan 2tan 2r1=2×(-43)+2×(-43)2(-43)2+1=825,故2sinvosr2sin 21-tan=8251-(-43)=24175.10.设f (x )=a sin (πx +α)+b cos (πx +β),其中a ,b ,α,β都是非零实数,若f (2024)=1,则f (2025)=(D)A.1B.2C.0D.-1解析f (2024)=a sin (2024π+α)+b cos (2024π+β)=a sin α+b cos β=1,f (2025)=a sin (2025π+α)+b cos (2025π+β)=a sin (π+α)+b cos (π+β)=-a sin α-b cos β=-(a sin α+b cos β)=-1.故选D.11.[数学探索/2023河南部分学校联考]“黑洞”是时光曲率大到光都无法从其事件视界逃脱的天体,在数学中也有这种神秘的“黑洞”现象.数字串是由一串数字组成的,如:743258….任意取一个数字串,长度不限,依次写出该数字串中偶数的个数、奇数的个数以及总的数字个数,把这三个数从左到右写成一个新的数字串.重复以上步骤,最后会得到一个反复出现的数字串,我们称它为“数字黑洞”,如果把这个数字串设为α,则cos (χ3+2π3)=(C)B. C.12 D.-12解析任取数字2023,经过第一步之后为314,经过第二步之后为123,再变为123,所以“数字黑洞”为123,即α=123,则cos(χ3+2π3)=cos(123π3+2π3)=cos(41π+2π3)=cos(π+2π3)=-cos2π3=cosπ3=12,故选C.12.已知-π<α<0,且满足.从①sinαcosα+sinαtanα=-2这三个条件中选择一个合适的,补充在上面的横线上,然后解答以下问题.(1)求cosα-sinα的值;(2)若角β的终边与角α的终边关于y轴对称,求Hs+sinHs-sin的值.解析方案一选择条件②.(1)由cosα+sinαcosα+sinα)2=15,则2sinαcosα=-45<0.又-π<α<0,所以sinα<0,cosα>0,所以cosα-sinα>0,所以cosα-sinα=1-2cosLin=(2)由题意得cosβ=-cosα,sinβ=sinα,所以cos+sin= 3.cos-sin=-cos+sin-cos-sin方案二选择条件③.(1)因为tanα=-2<0,且-π<α<0,所以sinα=-2cosα<0.又sin2α+cos2α=1,所以sinαcosα所以cosα-sinα(2)由题可得cosβ=-cosα,sinβ=sinα,所以Hs+sinHs-sin= 3.(注:若选择条件①,由-π<α<0,得sinα<0,与sinα①不符合题意.)。
二年级上册 100以内的加减法 《不退位减法》PPT课件

铁提尔美其提小学
8 9 - 5 ( 8 4)
铁提尔美其提小学
铁提尔美其提小学
第五关
铁提尔美其提小学
4、大猴子摘了65个桃子,送了23个给小 猴子后,大猴子还剩下几个桃子?
铁提尔美其提小学
我一定会回来 的!!
铁提尔美其提小学
例 十
36 - 23 =
பைடு நூலகம்
13
个
-
3 6 2 3
1 3
列竖式计算应注意什么?
铁提尔美其提小学
计算减法要注意 相同数位要对齐
铁提尔美其提小学
第一关
铁提尔美其提小学
做一做 P18.1 十 个
45
-
3
=
42
( -( (
4 5 3
4 2
) ) )
铁提尔美其提小学
做一做 P18.1 十 个
64
-
42
=
两位数减两位数
铁提尔美其提小学
1、35由(
3)个十和(
5 )个一组成。
2、46十位上的4表示4个( 6表示6个( )。
一
),个位上的
十
铁提尔美其提小学
铁提尔美其提小学
铁提尔美其提小学
美国36枚金牌
俄罗斯23枚金牌
美国比俄罗斯 多多少枚金牌?
代表团 美国 俄罗斯 金牌数 36 23
铁提尔美其提小学
22
( -( (
6 4 4 2
2 2
) ) )
铁提尔美其提小学
第二关
铁提尔美其提小学
做一做
48 – 18 =
4 - 1 3
P18.2
30
25 - 21 =
2 5 1 - 2
专项训练- 数字推理1000题

数字推理题725道详解【1】7,9,-1,5,( )A、4;B、2;C、-1;D、-3分析:选D,7+9=16; 9+(-1)=8;(-1)+5=4;5+(-3)=2 , 16,8,4,2等比?【2】3,2,5/3,3/2,( )A、1/4;B、7/5;C、3/4;D、2/5分析:选B,可化为3/1,4/2,5/3,6/4,7/5,分子3,4,5,6,7,分母1,2,3,4,5【3】1,2,5,29,()A、34;B、841;C、866;D、37分析:选C,5=12+22;29=52+22;( )=292+52=866【4】2,12,30,()A、50;B、65;C、75;D、56;分析:选D,1×2=2; 3×4=12; 5×6=30; 7×8=()=56【5】2,1,2/3,1/2,()A、3/4;B、1/4;C、2/5;D、5/6;分析:选C,数列可化为4/2,4/4,4/6,4/8,分母都是4,分子2,4,6,8等差,所以后项为4/10=2/5,【6】 4,2,2,3,6,()A、6;B、8;C、10;D、15;分析:选D,2/4=0.5;2/2=1;3/2=1.5; 6/3=2; 0.5,1,1.5, 2等比,所以后项为2.5×6=15【7】1,7,8,57,()A、123;B、122;C、121;D、120;分析:选C,12+7=8; 72+8=57; 82+57=121;【8】 4,12,8,10,()A、6;B、8;C、9;D、24;分析:选C,(4+12)/2=8;(12+8)/2=10; (8+10)/2=9【9】1/2,1,1,(),9/11,11/13A、2;B、3;C、1;D、7/9;分析:选C,化成 1/2,3/3,5/5 ( ),9/11,11/13这下就看出来了只能是(7/7)注意分母是质数列,分子是奇数列。
?【10】95,88,71,61,50,()A、40;B、39;C、38;D、37;分析:选A,思路一:它们的十位是一个递减数字 9、8、7、6、5 只是少开始的4 所以选择A。
人教版二下《语文园地四》教学设计(优秀模板13套)

人教版二下《语文园地四》教学设计(优秀模板13套)人教版二下《语文园地四》教学设计套1【我的发现】这一项训练旨在引导学生发现词语的特点,进一步体验祖国语言的丰富和发现的乐趣,积累词语。
其中包括两大组词语,它们的共同特点是每组词语的两个字都相同,只是交换了前后的位置。
第一大组都是表示事物名称的词,因为颠倒了字的顺序,所以表达的意思不同了。
第二大组的第一竖行是表示事物名称或地理位置的词,交换了字的位置,就变成了表示动作的词。
〖过程建议〗1、出示词语:奶牛牛奶图画画图蜜蜂蜂蜜牙刷刷牙水池池水山上上山2、自读词语,小组交流自己的发现。
3、全班交流发现。
4、你还能说出类似的词语吗?以小组竞赛的方式,看哪一组说得多。
5、随学生回答教师板书,然后用多种方法朗读。
【日积月累】这一部分包括“读读认认”、“我会填”和“我会读”三项内容。
其中“读读认认”教学重点是认识八个生字,积累由这些生字组成的新词。
“我会填”是选择近义词填空的练习。
“我会读”是阅读《鲁班造伞》这篇短文,目的是让学生增加阅读量,积累语言,激发动手创造的欲望。
〖过程建议〗1、自由读两组字:你发现了什么?(形声字;用熟字加熟字的方法识记新字。
)2、小组合作交流,说说你记住了哪个字?是怎么记住的?3、卡片认读──任意抽读──送信游戏──同桌互读4、任意选择喜欢的字进行扩词练习。
二、我会填1、读句子,说说每组的两个词语是什么关系?(近义词)2、结合生活分别用这两个词造句。
3、说说差别。
4、填空,互相检查。
三、我会读1、默读短文,自主识字。
2、朗读感悟:鲁班是什么样的人?(善于思考,动手创造)3、谈谈自己读完短闻后的心得和体会。
4、把这个故事讲给别人听。
【口语交际】这次训练是以“我们的小制作”为主题开展口语交际,是对本组专题的扩展和延伸。
旨在培养学生的创新思维和动手实践能力,同时在交际过程中提高学生的口语表达能力和与人协作的能力。
1、学生课前进行的小制作。
(如:用毛线编织蝴蝶结,用塑料瓶做成花篮等)2、把学生划分成若干个交际小组。
4m+2阶幻方

(2) 在A象限的中间行、中间格开始,按自左向右的方向,标出k格。
A象限的其它行则标出最左边的k格。
将这些格,和C象限相对位置上的数,互换位置。
6阶幻方第二步:
35* 1 6 | 26 19 24
3 32* 7 | 21 23 25
b[m][n] = 1;
x = m;
y = n;
}
}
}
void Exchange(int div)
{
int i,j,k,temp;
k = (div - 1) / 2; //需要交换位置的元素所需标出的格数
a[div+i][div/2+j] = temp;
}
else
{
temp = a[i][j];
a[i][j] = a[div+i][j];
a[div+i][j] = temp;
}
}
}
for(i=0;i<div;i++)
odd(div*(div+num),div,div,0);
Exchange(div); //对各个象限的数据进行交换
for(i=0;i<num;i++)
{
for(j=0;j<num;j++)
{
}
}
}
void main()
{
int num,div;
int i,j;
scanf("%d",&num);
while((num < 6) || (num%2 != 0) || (num%4 == 0))
魔方小站四阶魔方公式
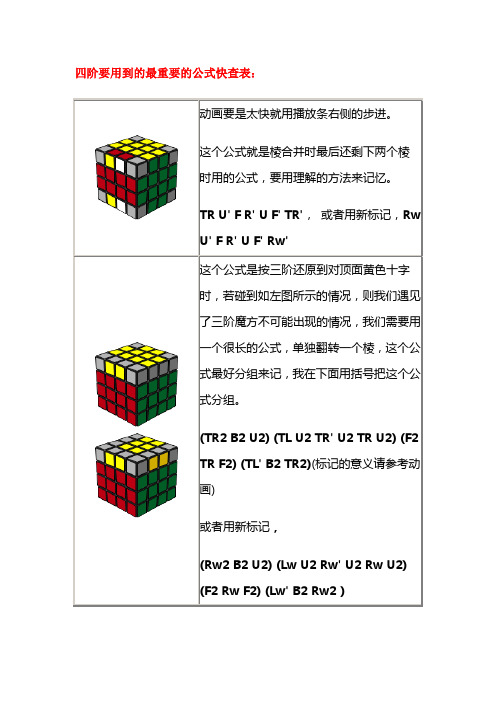
四阶要用到的最重要的公式快查表:
动画要是太快就用播放条右侧的步进。
这个公式就是棱合并时最后还剩下两个棱
时用的公式,要用理解的方法来记忆。
TR U' F R' U F' TR'
U' F R' U F' Rw'
这个公式是按三阶还原到对顶面黄色十字
时,若碰到如左图所示的情况,则我们遇见
了三阶魔方不可能出现的情况,我们需要用
一个很长的公式,单独翻转一个棱,这个公
式最好分组来记,我在下面用括号把这个公
式分组。
(TR2 B2 U2) (TL U2 TR' U2 TR U2) (F2
TR F2) (TL' B2 TR2)
画
或者用新标记
(Rw2 B2 U2) (Lw U2 Rw' U2 Rw U2)
(F2 Rw F2) (Lw' B2 Rw2
如果最后遇见只需要交换一对棱的情况,这对棱可能相邻、也可能相对。
这个公式很好记,就是不停的
U2
(
(
效于上面这种只需要交换一对棱的情况。
您就按照三阶入门还原方法第六步,
角同色的边放右边,
入门玩法第六步的公式,然后把四角颜色和。
4.2.4积化和差与和差化积公式-【新教材】北师大版高中数学必修第二册课件

��
+
·sin
��
− −
=−2sin ·sin=− s#43; 化为积的情势.
解:cosx+
=cosx+cos
=2cos
=2cos
+
cos
−
+ cos
−
.
综合练习
已知sinα+sin=,cosα+cos=,则tan(α+)
➢ 三角函数的和差化积
从积化和差的4个公式可以得出
sin(α+β)+ sin(α-β)=2sinαcosβ
sin(α+β)- sin(α-β)=2cosαsinβ
cos(α+β)+ cos(α-β)=2cosαcosβ
cos(α+β)- cos(α-β)=−2sinαsinβ
课文精讲
➢ 三角函数的和差化积
=.
综合练习
计算:
解:
°+°
=_____.
°
°+°
°
(°+°)+(°−°)
°
=
=
°°
°
= °= .
本课小结
三角函数的积化和差
积化和差与和差
化积公式
三角函数的和差化积
+
−
,β=
.
设α+β=x, α-β=y,则α=
这样,上一页得出的四个式子可以写成
+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京雷根生物技术有限公司
明胶水溶液(1%,无菌)
简介:
明胶(Gelatin)是以动物的皮、骨为主要原料,通过洗浸、水解、过滤、凝胶、粉碎等工序制成的一种粉末,明胶的主要组成为氨基酸以及组成相同而分子量分布很宽的多肽分子混合物,分子量一般在几万至十几万。
明胶是肽分子聚合物质,是胶原蛋白多级的水解产物,在食品、医药等工业领域有着广泛应用。
Leagene 明胶水溶液(2%,无菌)主要由高纯度明胶、去离子水组成,经无菌处理,室温下多呈淡黄色粘稠液体或胶冻状,加热后溶解使用,经常用作粘附剂和添加剂等。
组成:
操作步骤(仅供参考):
1、 加热后溶解使用。
注意事项:
1、 注意无菌操作,避免微生物污染。
2、 为了您的安全和健康,请穿实验服并戴一次性手套操作。
有效期:6个月有效。
相关:
编号 名称 R00502 Storage 明胶水溶液(2%,无菌) 100ml 4℃ 使用说明书 1份
编号
名称 CC0005 磷酸缓冲盐溶液(1×PBS,无钙镁) CC0022
D-Hanks 平衡盐溶液(1×,含酚红) IH0270
甘油明胶封固液 IH0305
柠檬酸钠抗原修复液(50×) NR0001
DEPC 处理水(0.1%) TC0699 植物总糖和还原糖检测试剂盒(硝基水杨酸法)。
