二自由度机械臂动力学分析
机械臂的动力学分析与控制

机械臂的动力学分析与控制近年来,随着科学技术的不断进步,机械臂在工业领域得到了广泛的应用。
机械臂以其优异的精度和灵活性,成为自动化生产的得力助手。
而要实现机械臂的高效工作,动力学分析与控制是不可或缺的关键。
动力学分析是研究机械臂在特定条件下的力学行为和运动规律。
通过对机械臂的动力学进行分析,可以深入了解机械臂在不同工作状态下的力学特性,有助于优化机械臂的设计和控制算法。
首先,动力学分析需要建立机械臂的动力学模型。
机械臂由多个关节和执行器组成,关节是机械臂的运动连接部件,执行器负责驱动机械臂的运动。
通过对机械臂的关节和执行器进行建模,可以得到机械臂的几何结构,质量分布以及关节间的连接关系。
接下来,动力学分析需要考虑机械臂的力学特性。
机械臂在工作时会受到多种力的作用,如重力、惯性力和外部负载力等。
这些力的作用会导致机械臂的加速度、速度和位置的变化。
通过对这些力进行分析,可以确定机械臂在特定工作状态下的动力学特性。
在动力学分析的基础上,控制机械臂的运动是十分重要的。
控制机械臂的目的是使其按照预设的路径和姿态进行精准的操作。
控制机械臂的方法有很多种,其中常用的是PID控制器和模糊控制器。
PID控制器是一种基于比例、积分和微分的控制策略。
通过对机械臂的误差进行测量和反馈,PID控制器可以根据误差的大小来调整机械臂的输出,从而使机械臂的位置和姿态接近预期值。
而模糊控制器则是一种基于模糊逻辑推理的控制方法,它可以处理复杂和模糊的输入条件,从而实现对机械臂的精确控制。
除了基本的控制方法,机械臂的轨迹规划也是控制的重要一环。
轨迹规划是指确定机械臂运动的路径和速度,使机械臂在运动过程中保持平稳和高效。
常见的轨迹规划方法有插值法和最小时间法。
插值法通过对机械臂的离散点进行插值,得到机械臂的路径和速度。
最小时间法则是通过确定机械臂的加速度、速度和位置的变化,使机械臂在最短时间内完成运动。
总结起来,机械臂的动力学分析与控制是实现机械臂高效工作的重要一环。
一种新型两自由度柔性并联机械手的动力学建模和运动控制_胡俊峰

一种新型两自由度柔性并联机械手的动力学建模和运动控制X DYNAMIC MODELING AND KINEMATIC CO NTROL OF A NOVEL 2-DOF FLEXIBLE PARALLEL MANIPULATOR胡俊峰X X1张宪民2(1.江西理工大学机电工程学院,赣州341000)(2.华南理工大学机械与汽车工程学院,广州510640)HU JunF eng1ZHAN G XianM in2(1.School o f Mechanical&Electrical Engineering,Jiangxi University o f Science andTechnolo gy,Ganzhou,341000,China)(2.School o f Mechanical&Automotive Engineering,South China University o f Technology,Guangzhou510640,China)摘要对一种新型两自由度柔性并联机械手的动力学模型和运动控制进行研究。
首先,考虑刚)柔耦合影响,利用假设模态法和Lagrange乘子法,推导出系统的动力学方程,该方程为微分)代数方程组。
为了设计控制器,采用坐标分块法将该微分)代数方程组化为二阶微分方程组。
然后,根据机械手的控制要求,采用滑模变结构方法设计控制器,该控制器能跟踪所期望的运动轨迹,同时柔性构件的弹性振动得到抑制。
仿真结果表明该控制器的可行性和有效性。
关键词并联机械手柔性构件滑模变结构控制假设模态法中图分类号TH112TH113Abstract For a novel2-DOF(degree of freedom)flexible parallel manipulator,i ts dynamic model and kinematic control were studied.Taking into account the effect of rigid-flexible coupling,the dynamic equations of the system were derived by using assu med mode method and Lagrange multiplier method.It is a differential algebraic equations.In order to design a controller,the coordinate-par-titioned method is used to convert the differen tial algebraic equations in to a second-order differential equations.According to the demand of control,the variable structure control method is applied to design the controller in order to acq uire desired trajectory and attenuate the elastic deformation of flexible parts.The si mulation resul ts show the feasi bility and effectivenss of the controller.Key words Parallel manipulator;Flexible part;Variable structure control;Assum ed mode methodCorrespon ding author:H U JunFen g,E-mail:h jf su per@,Tel:+86-20-87110345,Fax:+86-20-87110069The project supported by the National Natural Science Foundation of Chi na for Distinguished Young Scholars(No.50825504).Manuscript received20091009,in revi sed form20100104.引言并联机器人具有高速度、高精度、高承载能力等特点,在许多领域得到应用。
二自由度机器臂机械部分报告

目录一、实习目的、任务及要求 (1)(一)、目的 (1)(二)、任务及要求 (1)二、实习设备 (1)三、实习内容 (1)(一)、二自由度机械臂结构 (1)(二)、机械传动部分的结构分析 (2)(三)、机器人运动学分析 (4)(四)、谐波减速器的结构原理 (9)(五)、电磁铁工作原理 (11)(六)、机械臂实验系统其他部分介绍 (11)1、运动控制卡 (11)2、伺服驱动器 (11)3、增量式光电编码器 (11)4、交流伺服电机 (12)5、光电开关传感器 (13)(七)、二自由度机械臂设备的控制 (13)(八)机械臂绘图误差分析 (14)四、实习总结 (15)参考文献 (16)两自由度机械臂控制系统实习(机械部分)一、实习目的、任务及要求(一)、目的(1)、学习机电控制技术,了解机电一体化设备的基本结构,控制方式和工业机器人的基本控制原理。
(2)、学习研究系统基础硬件构成。
了解各部件名称、功能、选型依据和使用方法。
了解网络系统配置及操作特点。
(3)、学习研究系统基础软件,了解控制软件平台,了解示教再现控制方式及其演示软件。
学习对机器人控制中两种坐标空间运动模式的操作设计。
(4)、通过机械臂的操作使用,了解部分控制器件的功能、使用方法和基本控制原理。
了解机械臂素描绘图控制的图像处理技术。
(5)、通过编程训练,学习工业机器人控制绘图语言的基本编程方法,了解机械臂绘图的基本算法。
(6)、通过对儿自由度机械臂机械部分的重点研究,了解机械臂的动力传递和结构特点。
(二)、任务及要求(1)、测定机械臂结构,描述机械传动部分的结构形式、运动模式及减速器的结构原理。
绘出机构运动示意图。
(2)、了解机械臂控制系统电器控制部分的主要器件,绘制控制系统框图.标注各部件的主要功能、型号及参数。
(3)、学习使用鼠标、手写板和摄像头控制机械臂绘制图案文字和素描肖像。
(4)、学习编写控制程序。
设计绘图程序,控制机械臂绘出实际图形。
两自由度机械手动力学问题
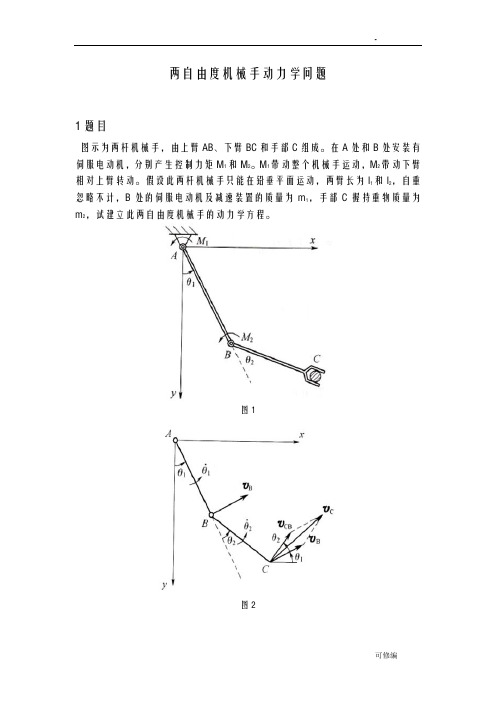
两自由度机械手动力学问题1题目图示为两杆机械手,由上臂AB、下臂BC和手部C组成。
在A处和B处安装有伺服电动机,分别产生控制力矩M1和M2。
M1带动整个机械手运动,M2带动下臂相对上臂转动。
假设此两杆机械手只能在铅垂平面运动,两臂长为l1和l2,自重忽略不计,B处的伺服电动机及减速装置的质量为m1,手部C握持重物质量为m2,试建立此两自由度机械手的动力学方程。
图1图22数值法求解2.1拉格朗日方程此两杆机械手可以简化为一个双摆系统,改双摆系统在B 、C 出具有质量m 1,m 2,在A 、B 处有控制力矩M 1和M 2作用。
考虑到控制力矩M 2的作用与杆2相对杆1的相对转角θ2有关,故取广义力矩坐标为2211,θθ==q q系统的动能为二质点m 1、m 2的动能之和,即由图2所示的速度矢量关系图可知以A 处为零势能位置,则系统的势能为由拉格朗日函数,动势为:广义力2211,M Q M Q ==求出拉格朗日方程中的偏导数,即代入拉格朗日方程式,整理得:2.2 给定条件 (1)角位移运动规律()231*52335.0*1163.0t t t +-=θ,()232*52335.0*1163.0t t t +-=θ21θθ和都是从0到90°,角位移曲线为三次函数曲线。
(2)质量m 1=4㎏ m 2=5kg (3)杆长l 1=0.5m l 2=0.4m2.3 MATLAB 程序t=0:0.1:3;theta1=-0.1163*t.^3+0.52335*t.^2; w1=-0.3489*t.^2+1.0467*t; a1=-0.6978*t+1.0467;theta2=-0.1163*t.^3+0.52335*t.^2; w2=-0.3489*t.^2+1.0467*t; a2=-0.6978*t+1.0467;m1=4; m2=5;l1=0.5; l2=0.4; g=9.8;D11=(m1+m2)*l1.^2+m2*l2.^2+2*m2*l1*l2*cos(theta2); D22=m2*l2.^2;D12=m2*l2.^2+m2*l1*l2*cos(theta2); D21=m2*l2.^2+m2*l1*l2*cos(theta2); D111=0;D122=-m2*l1*l2*sin(theta2); D222=0;D211=m2*l1*l2*sin(theta2); D112=-m2*l1*l2*sin(theta2); D121=-m2*l1*l2*sin(theta2); D212=0; D221=0;D1=(m1+m2)*g*l1*sin(theta1)+m2*g*l2*sin(theta1+theta2); D2=m2*g*l2*sin(theta1+theta2);M1=D11.*a1+D12.*a2+D111.*w1.^2+D122.*w2.^2+D112.*w1.*w2+D121.*w2.*w1+D1; M2=D21.*a2+D22.*a2+D211.*w1.^2+D222.*w2.^2+D212.*w1.*w2+D221.*w2.*w1+D2; T1=polyfit(t,M1,3) T2=polyfit(t,M2,3)subplot(2,1,1),plot(t,M1),grid on,xlabel('时间(s )'),ylabel('控制力矩(N ·m )'),title('motion1') subplot(2,1,2),plot(t,M2),grid on,xlabel('时间(s )'),ylabel('控制力矩(N ·m )'),title('motion2')2.4 数值计算结果()6167.1*7993.31*7329.3*5685.3t 231+++-=t t t M ()5449.1*9801.25*9481.8*0679.0t 232-+--=t t t M图3 M 1变化规律图图4 M2变化规律图3 ADAMS仿真3.1模型建立图5 模型图3.2 施加运动在两个关节处分别施加位移函数图6 关节运动施加图位移函数为:step(time,0,0,3,pi/2)运动规律如下图所示:图7 关节处运动规律图3.3 运动仿真设置仿真时间为3s,步数为300步,仿真结果如下图所示:图8 关节1处控制力矩仿真结果图图9 关节2处控制力矩仿真结果图4 结果对比图10 控制力矩M1结果对比图图11控制力矩M2结果对比图从函数规律上看,两种求解方法得出的结果几乎一样;从数值上看:t 0 0.5 1.0 1.5 2 2.5 3.0 数值计算M1 7.1699 14.3348 33.4367 49.4650 51.6557 44.8470 40.0971 仿真求解M1 7.4526 14.5646 33.5798 49.5093 51.5775 44.6398 39.8039表2 控制力矩M2数值结果对比由上两表可以看出:数值计算结果与仿真求解结果相差很小,误差围为0.437%-0.731%,出现这种结果的原因可能是因为两种方法计算的精度不同,或者是算法存在差异。
二自由度机械臂动力学分析

平面二自由度机械臂动力学分析姓名:黄辉龙 专业年级:13级机电 单位:汕头大学摘要:机器臂是一个非线性的复杂动力学系统。
动力学问题的求解比较困难,而且需要较长的运算时间,因此,这里主要对平面二自由度机械臂进行动力学研究。
拉格朗日方程在多刚体系统动力学的应用方法分析平面二自由度机械臂的正向动力学。
经过分析,得出平面二自由度机械臂的动力学方程,为后续更深入研究做铺垫。
关键字:平面二自由度 动力学方程 拉格朗日方程相关介绍机器人动力学的研究有牛顿-欧拉(Newton-Euler )法、拉格朗日(Langrange)法、高斯(Gauss )法等,但一般在构建机器人动力学方程中,多采用牛顿-欧拉法及拉格朗日法。
欧拉方程又称牛顿-欧拉方程,应用欧拉方程建立机器人机构的动力学方程是指研究构件质心的运动使用牛顿方程,研究相对于构件质心的转动使用欧拉方程,欧拉方程表征了力、力矩、惯性张量和加速度之间的关系。
在机器人的动力学研究中,主要应用拉格朗日方程建立机器人的动力学方程,这类方程可直接表示为系统控制输入的函数,若采用齐次坐标,递推的拉格朗日方程也可以建立比较方便且有效的动力学方程。
在求解机器人动力学方程过程中,其问题有两类:1)给出已知轨迹点上•••θθθ、及、,即机器人关节位置、速度和加速度,求相应的关节力矩矢量τ。
这对实现机器人动态控制是相当有用的。
2)已知关节驱动力矩,求机器人系统相应各瞬时的运动。
也就是说,给出关节力矩矢量τ,求机器人所产生的运动•••θθθ、及、。
这对模拟机器人的运动是非常有用的。
平面二自由度机械臂动力学方程分析及推导过程1、机器人是结构复杂的连杆系统,一般采用齐次变换的方法,用拉格朗日方程建立其系统动力学方程,对其位姿和运动状态进行描述。
机器人动力学方程的具体推导过程如下:1) 选取坐标系,选定完全而且独立的广义关节变量n r ,,2,1,r ⋅⋅⋅=θ。
2) 选定相应关节上的广义力r F :当r θ是位移变量时,r F 为力;当r θ是角度变量时,r F 为力矩。
两自由度机械系统动力学

x2 y2 l2
15
第15页/共143页
另外,可以积分的速度约束也是完整约束。例如:直 线纯滚动的圆盘,速度满足如下约束关系:
x r
为速度约束,但可以积分,因此还是完整约束。
x r c
本课程只考虑完整约束,而且通常只考虑定常约束情 况。
M e
(1)
拉格郎日方程为
d dt
E qi
E qi
Qi
(2)
需要证明(1)是(2)的特例。
65
第65页/共143页
证明:对于单自由度系统,拉格郎日方程应为
d E
dt
E
Me
E
1 2
J e
2
E
Je
( d )
W Fk rk 0
k
(3-3)
18
第18页/共143页
也可以写成分解形式,即
W (X kxk Ykyk Zkzk ) 0
k
(3-4)
19
第19页/共143页
说明: (1)虚位移也叫可能位移,是在约束允许 的条 件下可能实现的无限小位移。与时间无关,可 用变分符号表示。变分与微分很相似,但对时 间冻结。 (2)力在虚位移上作的功叫虚功,因此虚位移 原理也叫虚功原理。 (3)理想约束的约束力在虚位移上不做功,所 以约束力不在方程中出现。
1 2
m2l2222
46
第46页/共143页
47
第47页/共143页
48
第48页/共143页
机器人机械手臂运动学与动力学分析
机器人机械手臂运动学与动力学分析1.引言随着科技的不断进步,机器人技术已经广泛应用于生产制造、医疗卫生、军事防务等领域。
机器人的机械手臂是其重要组成部分,通过其灵活的运动能力,使机器人能够执行各种任务。
在机械手臂的设计和控制中,运动学和动力学是两个重要的方面。
本文将对机械手臂的运动学和动力学进行深入分析。
2.机械手臂的运动学机械手臂的运动学研究机器人手臂的位置和运动方式。
运动学分析通常包括正、逆运动学两个方面。
2.1 正运动学正运动学研究机器人手臂的运动学模型与其关节角度之间的关系。
对于n自由度的机械手臂,可以通过构建齐次变换矩阵的方法,将末端执行器的位置和姿态与关节角度联系起来。
2.2 逆运动学逆运动学研究机械手臂如何通过末端执行器的位置和姿态来确定关节角度。
逆运动学问题通常是非线性的,并且存在多解性。
通过使用几何方法、代数方法或数值方法,可以求解机械手臂的逆运动学问题。
3.机械手臂的动力学机械手臂的动力学研究机器人手臂受力和加速度之间的关系。
动力学分析可以帮助我们理解机械手臂的受力情况,为控制和优化机械手臂的运动提供基础。
3.1 机械手臂的运动方程机器人手臂的运动方程是描述手臂在特定坐标系下的加速度与外部力之间关系的方程。
通过运动方程,可以推导出机械手臂的动力学模型。
3.2 动力学优化动力学优化是基于机械手臂的动力学模型,通过优化算法来最小化手臂的能耗、提高执行效率或实现更加精确的运动。
通过对机械手臂的动力学特性进行深入分析,可以找到最佳的控制策略和参数设置。
4.机械手臂运动学与动力学的应用机器人机械手臂的运动学和动力学分析在实际应用中具有重要意义。
4.1 生产制造领域在生产制造领域,机械手臂的运动学和动力学分析可以帮助优化生产线的布局和工艺流程。
通过合理设计机械手臂的运动轨迹和力矩分配,可以实现高效率和高精度的自动化生产。
4.2 医疗卫生领域机械手臂在医疗卫生领域的应用越来越广泛,例如辅助手术机器人。
第二章两自由度机构动力学分析
r
17
F2 s2
M1
r
计算广义力:
动力学方程:
r 1 2m2 r Q1 J11q 2 J q m r Q2 2 22 2
18
1 J12 q 2 Q1 J11q 动力学方程: J q 2 Q2 21 1 J 22 q
差动轮系动力学方程,可以直接应用此结论式。
16
例5:已知:J1 A , m2 , J s 2 , M 1 , F2
重力略,建立运动方程。
s2
M1
F2
分析:选广义坐标: q1 , q2 r
方法1:
1 2 1 3 i21 , i22 2 2
2 0, 即H不动,则: 方法2: 令q
同理
1 0, 令q
1 i 即1轮不动,则: 2 H i22
3 i22 2
求:i31 , ห้องสมุดไป่ตู้32
1 1 ( ) 8
15
2 J H iH 2
计算广义力:
此为二阶非线性微分方程,用数值解法求解。
13
例4:已知差动轮系中:
,各轮质量略。
1 , H 求:
分析:取广义坐标: q1 1 , q 2 H
1 q1 2, 2 ', 3 q1 , q2
H q2
则:
1 H
14
求:i21 , i22
第二章 两自由度机构动力学分析
§2-1 两自由度机构的运动分析 例:五杆机构,取 q1 1 , q2 S 4
分析:构件1由 q1 (1 ) 控制,q2 0
构件4由 q2 ( s4 ) 控制,q1 0 件2、3由
二自由度机器人动力学控制及仿真研究
拉 格 朗 日函数 方 法 建 立 机 器 人 动 力 学 方 程 , 近 而确 立机 器人 动 力 学模 型 。基 于 永磁 同步 电机 建 立 伺 服 控 制 系统 , 利 用 机 器 人 的 位 置 控 制 与 电流 相 结 合 的 方 式 完 成 机 器 人 的 动 力 学控 制 。利 用 自适 应控 制 来 完成 机 器人 的 位 置 控 制 , 利 用滑 模 控 制 算 法 控 制 电机 。根 据 控 制 方 法 建 立 机 器人 和 伺服 控 制模 型 , 利 用 MA T L A B 中的 S i mu l i n k 模 块 进 行 仿 真 。仿 真 结 果 表 明 , 系统
by t he c om bi na t i o n o f t h e pos i t i on c on t r o l o f t h e r ob ot an d t he cu r r en t c on t r ol o f t h e mot or Us i n g a dap t i v e c on t r o l l er t O
・
对 机 器 人 控 制 的 研 究 一 般 是 将 驱 动 电机 控 制 和 机器 人 的 动
质 量表 示 整 个 杆 的质 量 ; 连杆的长度分别为 d 和d 。 根 据 机 器 人 求逆 解 的 方法 , 已知 C 点 的运 动轨 迹 , 可求得角位移 q 。 拉格朗 1 3函数 L = K — P 。其 中 , L是 拉 格 朗 1 3函数 , K是 系 统 动能 , P是 系 统 位 能 。
杨 彦 平 潘松 峰 周 真 诚 ( 青岛大学 自 动化与电气工程学院, 山东 青岛 2 6 6 0 7 1 )
摘要 : 根 据 所在 研 究 中 心机 器人 的 工作 模 式 , 把 二 自 由度 串联 型 机 器 人 的 关 节控 制 当成 经典 案 例 进 行 深入 探 讨 。 利 用
二自由度机械臂matlab
二自由度机械臂matlab二自由度机械臂是一种重要的工业机器人,它由两个旋转关节组成,可以完成简单的抓取和定位任务。
在进行机械臂的控制和运动分析时,我们可以使用Matlab 软件,它提供了强大的数学计算和图形界面,可以帮助我们快速构建模型和进行仿真。
首先,我们需要建立机械臂的运动学模型,包括关节尺寸、连杆长度等参数。
这些参数可以通过实际测量或理论计算得到。
然后,我们可以使用正运动学方法计算机械臂的末端坐标,也就是机械臂的位置和姿态。
正运动学模型可以表示为:T_{0n} = T_{01} T_{12} ... T_{n-1n}其中,T_{0n}表示机械臂的末端坐标,T_{ij}表示从第i个关节到第j个关节的变换矩阵。
关节的运动可以通过设置关节角度来实现,这些角度可以通过编程或手动输入。
接下来,我们可以使用逆运动学方法计算机械臂的关节角度,也就是根据末端坐标计算关节角度。
逆运动学模型可以通过解析法、数值法、优化法等多种方法得到。
解析法是最常用的方法,它可以得到解析解,但是只适用于特定的机械臂结构。
数值法和优化法可以得到数值解,适用于复杂的机械臂结构。
在Matlab中,我们可以使用symbolic toolbox来实现解析求解,也可以使用数值库和优化函数来实现数值求解。
例如,我们可以使用fsolve函数来求解非线性方程组,使用fmincon函数来进行优化问题的求解。
最后,我们可以对机械臂进行动力学分析,包括关节扭矩、惯性矩、作用力等。
动力学分析可以根据机械臂的运动学模型和质量参数得到。
在Matlab中,我们可以使用Simulink工具箱来进行动力学分析和控制设计。
总之,Matlab是一种非常有用的工具,可以帮助我们进行机械臂的建模、控制和分析。
通过Matlab,我们可以更加深入地了解机械臂的运动规律和机理,从而为机械臂的应用和设计提供重要的支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面二自由度机械臂动力学分析
姓名:黄辉龙 专业年级:13级机电 单位:汕头大学
摘要:机器臂是一个非线性的复杂动力学系统。
动力学问题的求解比较困难,而且需要较长的运算时间,因此,这里主要对平面二自由度机械臂进行动力学研究。
拉格朗日方程在多刚体系统动力学的应用方法分析平面二自由度机械臂的正向动力学。
经过分析,得出平面二自由度机械臂的动力学方程,为后续更深入研究做铺垫。
关键字:平面二自由度 动力学方程 拉格朗日方程
相关介绍
机器人动力学的研究有牛顿-欧拉(Newton-Euler )法、拉格朗日(Langrange)法、高斯(Gauss )法等,但一般在构建机器人动力学方程中,多采用牛顿-欧拉法及拉格朗日法。
欧拉方程又称牛顿-欧拉方程,应用欧拉方程建立机器人机构的动力学方程是指研究构件质心的运动使用牛顿方程,研究相对于构件质心的转动使用欧拉方程,欧拉方程表征了力、力矩、惯性张量和加速度之间的关系。
在机器人的动力学研究中,主要应用拉格朗日方程建立机器人的动力学方程,这类方程可直接表示为系统控制输入的函数,若采用齐次坐标,递推的拉格朗日方程也可以建立比较方便且有效的动力学方程。
在求解机器人动力学方程过程中,其问题有两类:
1)给出已知轨迹点上•
••θθθ、及、
,即机器人关节位置、速度和加速度,求相应的关节力矩矢量τ。
这对实现机器人动态控制是相当有用的。
2)已知关节驱动力矩,求机器人系统相应各瞬时的运动。
也就是说,给出关节力矩矢量τ,求机器人所产生的运动•
••θθθ、及、。
这对模拟机器人的运动是非常有用的。
平面二自由度机械臂动力学方程分析及推导过程
1、机器人是结构复杂的连杆系统,一般采用齐次变换的方法,用拉格朗日方程建立其系统动力学方程,对其位姿和运动状态进行描述。
机器人动力学方程的具体推导过程如下:
1) 选取坐标系,选定完全而且独立的广义关节变量n r ,,2,1,r ⋅⋅⋅=θ。
2) 选定相应关节上的广义力r F :当r θ是位移变量时,r F 为力;当r θ是角度变量时,r F 为力矩。
3)求出机器人各构件的动能和势能,构造拉格朗日函数。
4) 代入拉格朗日方程求得机器人系统的动力学方程。
2、下面以图1所示说明机器人二自由度机械臂动力学方程的推导过程。
1)如图1,设
2
1
,θ
θ是广义坐标,
2
1
,Q
Q是广义力。
2)分别求出两杆的动能和势能
1
1
1
1
2
1
1
1
1
1
1
sin
,
2
1
2
1
:1θ
θ
c
c
c
T
c
gl
m
U
I
v
v
m
E=
+
=
•
杆
(1-1)
]
sin
[
,
2
1
2
1
:2
2
1
1
2
2
2
2
1
2
2
2
2
2
)
(
)
(
杆θ
θ
θ
θ+
=
+
+
=
•
•
l
g
m
U
I
v
v
m
E
c
c
T
c
(1-2)
式中,
1c
v是杆1质心)
,
(
1
1
1c
c
y
x
C的速度向量,
2c
v是杆2质心)
,
(
2
2
2c
c
y
x
C的速度向量。
它们可以根据质心
2
1
,C
C的位置方程导出。
3)分别求出两杆的速度
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
)
sin
(
)
cos
(
1
1
1
1
1
1
1
θ
θ
l
dt
d
l
dt
d
dt
dy
dt
dx
v
c
c
c
(1-3)
[]
[]⎥⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
+
+
+
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
)
sin(
sin
)
cos(
cos
2
1
2
1
1
2
1
2
1
1
2
2
2
θ
θ
θ
θ
θ
θ
c
c
c
c
c
l
l
dt
d
l
l
dt
d
dt
dy
dt
dx
v
(1-4)
4)代入拉格朗日方程求得机械臂动力学方程
根据具有完整理想约束的有N 个广义坐标系统的拉格朗日方程 n r Q q U q E q E dt d r r r r ,2,1,⋅⋅⋅==∂∂+∂∂-⎪⎪⎪⎭
⎫ ⎝⎛∂∂• (1-5)
式中,r q 是第r 个广义坐标,E 是系统动能,U 是系统势能,r Q 是对第r 个广义坐标的广义力。
该问题为二自由度的动力学研究,所以n=2,由于势能函数U 与广义速度无关,即•∂∂r q U
=0。
由(1-5)式可写成: r r r Q q L q L dt d =∂∂-⎪⎪⎪⎭
⎫ ⎝⎛∂∂• (1-6)
其中,是拉格朗日算子L U E L ,-=
可知在这里拉格朗日算子为:2121U U E E L --+=
代入式(1-6)可导出相应的式子,经过整理得:
Q g C M =++•
••)(),()(θθθθθ (1-7)
式中 ⎥⎦
⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=•21212122211211,)(,),(,)(Q Q Q g g g C C C M M M M M θθθθ []⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎨⎧+=+++==+-=+==++=+++++=•
••)cos()cos(cos cos sin ),2(sin ,)cos ()cos 2(212222*********
22122212221212222221221222122221222122212121111θθθθθθθθθθθθθc c c c c c c c c c c c c gl m g l l g m gl m g l l m C l l m C I l m M M M I l l l m M I l l l l m I l m M 式(1-7)为机械臂在关节空间的动力学方程的一般结构形式,它反映了关节力矩和关节变量、速度、加速度之间的函数关系。
对于n 个关节的机
械臂,)(θM 是n n ⨯的正定对称矩阵,是θ的函数,称为机械臂的惯性矩阵;),(•
θθC 是nx1的离心力和科氏力矢量;)(θg 是nx1的重力矢量,与机械臂的形位θ有关。
