浙江省推理公式法计算设计洪水
浙江省推理公式计算方法的改进-2008.9.26

hS F ( 3) S hR F S ( 4)
当 t c [ S 时 , 属部分面积汇流 , Qm = 01 278
式中 : hS 为相应于 S 时段的最大净雨 ; h R 为单 一洪峰的 净雨。 在小流域设计洪水计算 过程中 , 净 雨历时 t c 一 般大于 汇流时间 S, 故以全面积汇流为主。 在全面积汇流条件 下 , ( 3) 式可 转化为 : Qm = 01 278( HS - L) F S ( 5)
4
收敛很快 , 取前 2 项 ( 1+ mx ) 略去高次项 , 得 Qm ( 1+ ( 16)
6
结
语
( 下转第 7 页 )
随着短历时 暴雨 资料的 不断 延长 , 采 用分段 概化 的方 法求 得暴雨衰减指数 , 从而进行暴雨时程
将 Q 0 = 01 278 L F 代入 ( 16) 式 得 :
# 5 #
再将 ( 6) 式代入 , 整理 可得 : Qm
4- n 4
表 2 设计洪水计算表
频率 P% A 01547 01540 B 7 645 11 707 C 1313 12165 D 614 6138 Qm 3081 2 4931 7 S 21 59 21 31
( 1+
Q0 ) = Qm
( 15)
1 0105
( Zhejiang Institute of Hydraulics & Estuary, Hangzhou 310020, China) Abstract: An approach that coupling Zhejiang rational formula and step - shaped formula of rainstorm improves the traditional interative solution method. Example of calculations reveals that the methed simplifies the calculations process, and the result precision meets the requirement. Key words: rational formula; calculation method; improvement 净雨 过程和汇流面积曲线形状的组合情况 , 表达式可写为 : Qm = 在计算山区 中小 流域 设计暴 雨洪 水时 , 推 理公式 以其 概念明确、计算简便 等特 点得 到了广 泛的 应用。浙 江省在 推理公式的应用实践过程中 , 从 20 世纪 60 年代的合理化公 式发展到目 前应用的 浙江 省推理 公式 , 在 考虑 降雨 时程分 配时 , 均采用一个统 一的暴 雨衰减 指数 n 进 行控 制。随着 短历时暴雨资料系列的不断增 加 , 浙江 省于 2003 年 编制颁 发了 5浙江省短历时 暴 雨6 图 集 , 增加 了短 历时 暴雨 统计 参数等值线 , 在使用 推理 公式 计算设 计洪 水时 , 应 尽可能 采用分段概化的 n 值 进行暴 雨时程分 配。本文 对浙 江省推 理公式与分 段暴雨公 式进 行耦合 处理 后 , 不需 试算 而求得 设计洪峰流 量 , 既满 足了 计算 精度的 要求 , 又 简化 了计算 过程。 式中 :
基于流量-面积比值的小流域设计洪水r计算方法对比研究

基于流量-面积比值的小流域设计洪水r计算方法对比研究叶永东【摘要】为了对小流域洪水设计过程中常用的推理公式法、分布式模型法和地区瞬时单位线法的适用性进行探讨,本文以浙江省宁波市甬江地区水系为研究对象,利用洪峰流量流域面积比值参数,对设计洪水分别采用3种方法进行计算,然后将各计算结果分别与宁波市洪峰流量100年一遇实测值进行对比分析.研究表明:推理公式法适用于面积小于10km2的流域,其假定条件均与流域的产、汇流条件相符,计算结果更加真实可靠;对于面积大于100km2的流域,采用不同方法的计算结果与实测结果表现出不同程度的偏差,而分布式模型法的计算准确性相对较高;对于面积为10~100km2的流域,其坡度较为平缓、河道较长,水动力在空间上可视为均匀分布态,采用地区瞬时单位线法和分布式模型法进行洪水设计较为合理,而后者的计算精确性更好.本文的研究成果有利于提高洪水设计计算法的适用性和准确性,并可为洪水设计方法的选择提供一定的数据支撑和决策依据.【期刊名称】《中国水能及电气化》【年(卷),期】2018(000)005【总页数】6页(P35-40)【关键词】流量面积比值;洪水设计;小流域;计算方法【作者】叶永东【作者单位】浙江省围海建设集团股份有限公司, 浙江宁波 315040【正文语种】中文【中图分类】TV122山洪是指具有破坏力大、暴涨暴落特征的强大快速的地表径流,往往发生在周期性流水的荒溪或面积较小的溪沟内,可引起山塘、水坝等水利设施的崩溃和道路桥梁的破坏,甚至可形成山洪灾害并造成人员财产的伤亡和损失。
山洪灾害经常发生在面积小于200km2的流域,因该特征流域的水文资料相对缺少,进而造成无法采用长时间序列的水文资料对洪水设计进行计算和预测。
当前,对小流域面积进行洪水设计的主要方法有推理公式法、分布式模型法和地区瞬时单位线法[1]。
分布式模型法是结合区域水文地形资料,按照土壤水径流、地下水径流和截流等多个径流的汇流特点将流域划分为若干个子流域计算单元,并沿各子单元逐级向流域的出口进行演算。
应用推理公式求解小流域设计暴雨洪水

应用推理公式求解小流域设计暴雨洪水(图解法)仅供内部参考使用编者:陆雪华2011.10.20为了统一和方便大家在应用推理公式求解小流域设计暴雨洪水,编者根据SL44-2006《水利水电工程设计洪水计算规范》有关要求及2005版《浙江省短历时暴雨集》推举设计暴雨点,面雨量。
暴雨衰减系数等计算方法,编写了本市水 利水电工程应用0.2780.278pm nS hQ FF ψττ==推理公式图解设计洪峰流量及其相应汇流时间τ计算一文,供同志们设计时参考使用,在应用过程中若发现有错误及不解之处请及时与本人联系以便修正和解释。
本文尽供本院内使用,切勿外传。
编者:陆雪华2011.10.20应用0.278pm nS Q F ψτ=推理公式图解Q m ,τ值式0.278pm nS Q F ψτ=,它与其它推理公式如0.278m Q F a a τ-=,0.278m hQ Fτ=计算原理是一样的,只不过是表现形式有所不同,今求证如下:在全面汇流(t B >t)情况下,式0.278m hQ Fτ=中h 是代表相应于τ时段的最大净雨,它也可用R τ来表示,因此0.278=0.278m R h Q FFτττ=。
而式_0.2780.278m R Q FF a a τττ==,参见《长江流域规划办公式水文处编写:(水利工程实用水文水利计算一书)P 70页式(2-85)》。
式_0.278m Q F a a τ=中:a 为洪峰径流系数,它与式0.278pm nS Q F ψτ=中ψ意义相同,只是使用符号不同而已,因此a ψ=。
_a τ为τ时段内最大(毛)雨量的平均强度,其值为_pna S ττ=,所以:0.2780.278pm nS Q F a a F τψτ-== (1)现就利用公式(1)图解计算设计洪峰流量Q m 及相应汇流时间τ举例如下,供大家设计时参考。
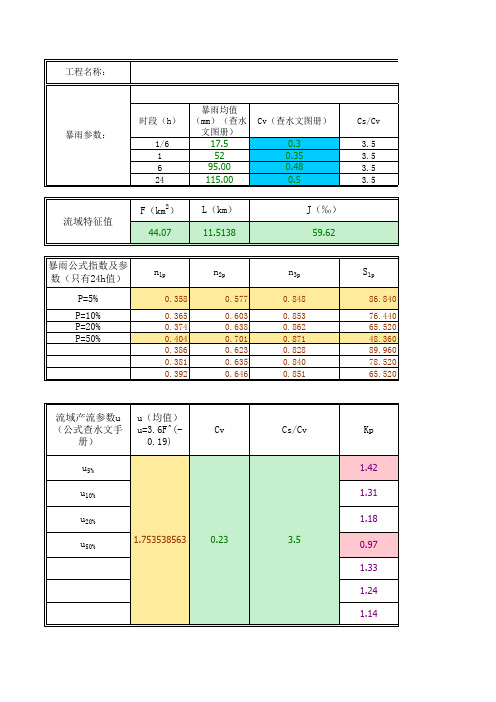
例:某工程流域面积21.13km F =,主流长 1.682km L =,平均坡度j 0.165=,求其20年一遇及200年一遇设计洪峰流量Q p 及相应汇流时间τ。
推理公式计算设计频率洪水、洪量标准版

设计频率的模比系数即Kp值查询
汇流参m表
,如大于150mm
降雨历时为24小时的迳流Array 1、优点:本方法计算公式为简化小流域推理公式,计算结果与原型公式比较,产生的
应用方便。
2、使用说明:输入流域面积F、干流长度L、河道平均坡降J、暴雨递减指数历时24小时的降雨迳流系数а24,即可自算出相应频率的洪峰流量和洪水总量。
3、汇、表2中查取。
4、先取n=n1(τ≤1),求出一个洪峰流量Q p和τ,当计算的τ≤1时,当设τ≤1,算出的τ>1,再设τ>1,计算出τ>1时,可取n=(n1+n2)/2,再进行计算见I12
数即Kp值查询表(Cs=3.5Cv)
汇流参数m表
70~150mm,如大于150mm时m值略有减小,小于70mm时m值略有增加。
Ф=L/J(1/3)
为24小时的迳流系数
结果与原型公式比较,产生的误差最大不超过百分之一,可直接求解,省去联解过程,道平均坡降J、暴雨递减指数n、n1、n2、年最大24小时降雨量均值H24、模比系数K P和流量和洪水总量。
3、汇流参数m和历时24小时的降雨迳流系数а24值,均可从表1和τ,当计算的τ≤1时,洪峰流量Q p即为所求。
如τ>1,则应取n=n2重新计算。
p
可取n=(n1+n2)/2,再进行计算。
5、tc>24时D8中的u值为D11中的值,洪峰流量结果。
小流域设计洪水计算(主讲推理公式法)

Qm——待求最大流量(m3/s);
m——汇流参数; J——流域平均纵比降;
σ、λ ——反映沿流程水力特性的经验指数。对于一般 山区河道采用σ=1/3,λ=1/4。
WUHEE
将σ=1/3,λ=1/4代入(8-12)式得:
0.278
L 1/ 4 m J1/ 3Qm
将上式代入 Qm 0.278
Qm,p=C p· Fn
式中,Cp——随频率变化的综合系数;n ——经验指数;各省、 市水文手册中可查。
WUHEE
例如湖南、江西的Cp、n值表
WUHEE
二、多因素公式
Qm, p Ch24 , p F n Qm, p Ch24 , p f F
n
n Qm, p Ch24 J f F ,p
第八章
8.1 8.2 8.3 8.4 8.5
小流域设计洪水计算
概述 小流域设计暴雨计算 设计洪峰流量的推理公式 计算洪峰流量的地区经验公式 设计洪水过程线的推求
WUHEE
8.1
概述
一、小流域设计洪水特点 1. 缺少实测资料(流量和暴雨资料)。
中、小型水库,涵洞,城市和工矿区的防洪工程
a、由实测暴雨资料分析得到; b、从水文手册中的n值分区图上查取。 (2)Sp的计算 t· it,P=Pt,p=Sp· t1-n
a、地区水文手册中的Sp等值线图插取; b、由式(8-2)知:Sp=Pt,p· tn-1 ∵ P24,p已知(t=24h) ∴ Sp=P24,p· 24n2 -1
WUHEE
概化过程线法 概化线型有三角形、五边形和综合概化过程线等形式。 一、三角形概化设计洪水过程线 已知:设计洪峰流量Qm,p;P24,p
洪水计算(推理公式法)
P=00
1.32
33.93
1.80
67.87
2.40
135.74
2.94
271.48
3.78
407.21
4.80
542.95
5.93
644.76
7.19
678.69
8.39
644.76
9.77
542.95
11.81
407.21
14.81
271.48
19.66
135.74
25.18
1.998 2.121 2.305 2.734 2.118 2.212 2.335
499.41 411.02 320.79 194.33 489.36 405.92 317.23
Qm
4.73 4.50 4.23 3.73 4.70 4.49 4.22
验算
ψ
τ
τn3
Qp
0.045936341 0.052548381 0.061999459 0.086334157 0.046416195 0.052274533 0.061536412
Htp
380.79 306.67 232.49 137.59 335.79 281.41 225.67
t=1-6h
Qp
499.41 411.02 320.79 194.33 489.36 405.92 317.23
Wp(万m ³)
1376.06 1094.70 819.68 479.04 1154.25 954.94 755.85
-0.274557823 3.0716779 -0.275104022 3.1915656 -0.275803928 3.3439505 -0.278095567 3.6870571 -0.276682603 3.065531 -0.276322519 3.1814113 -0.277180269 3.3635863
小流域设计洪水计算(主讲推理公式法).ppt

例如湖南、江西的Cp、n值表
二、多因素公式
Qm, p Ch24, p F n Qm, p Ch24, p f F n Qm, p Ch24, p J f F n
式中,f=F/L2——流域形状系数。 例如:安微省山区小河洪峰流量经验公式为:
QP
Ch F 1.21 0.73 24,P
同时把山区分为4类:深山区(C=0.0514)、浅山区(C=0.0285)、 高丘区(C=0.0239)、低丘区(C=0.0194)。
1. 暴雨公式
it , P
SP tn
(8-1)
式中,it.p—— 历时为t、频率为P的平均暴雨强度(mm/h);
Sp—— 单位时间的平均雨强(mm/h),又称雨力,随地区 和重现期而变;
n—— 暴雨参数或暴雨递减指数,随地区和历时长短而变 。
式(8-1)为水利电力部门广泛应用的暴雨公式。
意义:暴雨强度与历时成指数关系。见书图8-2。
简单到复杂,由计算洪峰流量到计算设计洪水过程线。
三、计算方法 1. 推理公式法 2. 经验公式法 3. 相似流域法 4. 综合单位线法
四、小流域设计洪水计算步骤 1. 小流域设计暴雨计算; 2. 设计洪峰流量计算; 3. 小流域设计洪水过程线拟定。
8.2 小流域设计暴雨计算
小流域面积较小,可忽略暴雨在地区上分布的不均匀, 由流域中心点处的点雨量作为流域面雨量。
1第八章小流域设计洪水计算81概述82小流域设计暴雨计算83设计洪峰流量的推理公式84计算洪峰流量的地区经验公式85设计洪水过程线的推求81概述一小流域设计洪水特点1
第八章 小流域设计洪水计算
8.1 概述 8.2 小流域设计暴雨计算 8.3 设计洪峰流量的推理公式 8.4 计算洪峰流量的地区经验公式 8.5 设计洪水过程线的推求
浙江省各城市暴雨强度公式表2008041801

200
43
1961-2006
年最大值
耿贝尔
43
武义
193
48
1957-2006
年最大值
耿贝尔
44
磐安
220
48
1956-2006
年最大值
耿贝尔
45
浦江
206
22
1980-2004
年最大值
耿贝尔
46
衢
州
市
衢州
199
46
1961-2006
年最大值
耿贝尔
47
江山
216
48
1958-2006
年最大值
耿贝尔
耿贝尔
32
德清
225
46
1957-2006
年最大值
耿贝尔
序
号
所在
地区
城市
名称
暴雨强度公式
TM=2a
q20
资料年数及起止年份
选样
方法
理论
分布
33
绍
兴
市
绍兴
213
45
1962-2006
年最大值
耿贝尔
34
诸暨
211
50
1957-2006
年最大值
耿贝尔
35
上虞
235
38
1957-2006
年最大值
耿贝尔
36
嵊州
215
45
1961-2006
年最大值
耿贝尔
37
新昌
225
48
1958-2006
年最大值
耿贝尔
38
金
华
市
