随机型时间序列
随机时间序列分析

参数模型
参数模型是指通过已知的参数来描述 时间序列的统计特性,如AR模型、 MA模型和ARMA模型等。
非参数模型
非参数模型是指通过数据本身来描述 时间序列的统计特性,如滑动平均模 型和自回归积分滑动模型等。
04 随机时间序列分析的方法 与技术
参数估计与模型选择
参数估计
利用已知数据估计模型中的未知参数,常用方法包括最小二乘法、极大似然估计法等。
的问题。
非线性过程的建模挑战
要点一
非线性动态
许多时间序列数据具有非线性动态,这意味着传统的线性 模型可能无法准确描述数据的复杂行为。因此,需要开发 更复杂的非线性模型来捕捉数据的非线性特征。
要点二
模型复杂度
为了更好地描述非线性动态,需要增加模型的复杂度。然 而,这可能导致模型过拟合和欠拟合问题,影响模型的泛 化能力和解释性。
提高数据利用效率
提高数据利用效率。
随机时间序列分析的应用场景
金融领域
气象领域
经济领域
用于股票价格、汇率等 金融时间序列的预测和
分析。
用于气温、降水等气象 时间序列的预测和分析。
用于GDP、消费、投资 等经济时间序列的预测
和分析。
交通领域
用于车流量、客流量等 交通时间序列的预测和
就业形势分析
通过分析历史就业数据,利用随机 时间序列模型预测未来就业形势, 为政府和企业的决策提供支持。
金融市场的随机时间序列分析
股票价格预测
通过对股票价格的历史数据进行随机时间序列分析,可以预测未 来股票价格的走势,有助于投资者做出更明智的投资决策。
利率变动预测
利用随机时间序列模型对利率变动进行建模,有助于金融机构制定 合理的贷款和存款利率政策。
ARMA模型

方差为 2 的正态分布.随机项与滞后变量不相关。
注2: 一般假定
X t 均值为0,否则令
X
t
Xt
1 时间序列分析模型【ARMA模型 】简介
记 Bk 为 k 步滞后算子, 即 Bk X t X tk , 则
模型【1】可表示为
Xt 1BXt 2B2 Xt pBp Xt ut
实际问题中, 常会遇到季节性和趋势性同时存在的情况, 这 时必须事先剔除序列趋势性再用上述方法识别序列的季节性, 否则季节性会被强趋势性所掩盖, 以至判断错误.
包含季节性的时间序列也不能直接建立ARMA模型, 需进 行季节差分消除序列的季节性, 差分步长应与季节周期一致.
1 时间序列分析模型【ARMA模型 】简介
式【5】称为( p, q)阶的自回归移动平均模型, 记为ARMA ( p, q)
注1: 实参数 1,2 , , p 称为自回归系数, 1,2 , ,q 为移动平均系数,
都是模型的待估参数
注2: 【1】和【3】是【5】的特殊情形 注3: 引入滞后算子,模型【5】可简记为
(B) Xt (B)ut
【6】
在实际中, 常见的时间序列多具有某种趋势, 但很多序列 通过差分可以平稳
判断时间序列的趋势是否消除, 只需考察经过差分后序列 的自相关系数
(3)季节性 时间序列的季节性是指在某一固定的时间间隔上, 序列重
复出现某种特性.比如地区降雨量、旅游收入和空调销售额等 时间序列都具有明显的季节变化. 一般地, 月度资料的时间序列, 其季节周期为12个月;
Xt 1 v1B v2B2
ut
vjB
j
ut
j0
随机时间序列分析

当滞后期大于q时,Xt的自协方差系数为0。 因此:有限阶移动平均模型总是平稳的。
3、ARMA(p,q)模型的平稳性
由于ARMA (p,q)模型是AR(p)模型与MA(q)模型的组合: Xt=1Xt-1+ 2Xt-2 + … + pXt-p + t - 1t-1 - 2t-2 - - qt-q 而MA(q)模型总是平稳的,因此ARMA (p,q)模型的平 稳性取决于AR(p)部分的平稳性。 当AR(p)部分平稳时,则该ARMA(p,q)模型是平稳的, 否则,不是平稳的。
1、时间序列模型的基本概念
随机时间序列模型(time series modeling)是指仅用它的 过去值及随机扰动项所建立起来的模型,其一般形式为 Xt=F(Xt-1, Xt-2, …, t) 建立具体的时间序列模型,需解决如下三个问题: (1)模型的具体形式 (2)时序变量的滞后期 (3)随机扰动项的结构 例如,取线性方程、一期滞后以及白噪声随机扰动项( t =t),模型将是一个1阶自回归过程AR(1): Xt=Xt-1+ t 这里, t特指一白噪声。
考虑p阶自回归模型AR(p) Xt=1Xt-1+ 2Xt-2 + … + pXt-p +t • 引入滞后算子(lag operator )L: LXt=Xt-1, L2Xt=Xt-2, …, LpXt=Xt-p
(*)
(*)式变换为 (1-1L- 2L2-…-pLp)Xt=t 记(L)= (1-1L- 2L2-…-pLp),则称多项式方程
2、时间序列分析模型的适用性
• • 经典回归模型的问题: 迄今为止,对一个时间序列 Xt 的变动进行解释或预测, 是通过某个单方程回归模型或联立方程回归模型进行的, 由于它们以因果关系为基础,且具有一定的模型结构,因 此也常称为结构式模型(structural model)。 • 然而,如果Xt波动的主要原因可能是我们无法解释的因 素,如气候、消费者偏好的变化等,则利用结构式模型来 解释Xt的变动就比较困难或不可能,因为要取得相应的量 化数据,并建立令人满意的回归模型是很困难的。 • 有时,即使能估计出一个较为满意的因果关系回归方程, 但由于对某些解释变量未来值的预测本身就非常困难,甚 至比预测被解释变量的未来值更困难,这时因果关系的回 归模型及其预测技术就不适用了。
时间序列的成分可以分为四种

时间序列的成分可以分为四种:趋势(T)、季节性或季节变动(S)、周期性或循环波动(C)、随机性或不规则波动(I)。
时间序列可以分为平稳序列和非平稳序列两大类。
平稳序列是基本上不存在趋势的序列。
这类序列中的各观察值基本上在某个固定的水平上波动,虽然在不同的时间段波动的程度不同,但并不存在某种规律,波动可以看成是随机的。
非平稳序列(non-stationary series)是包含趋势、季节性或周期性的序列,它可能只含有其中一种成分,也可能含有几种成分。
因此非平稳序列又可以分为有趋势的序列、有趋势和季节性的序列、几种成分混合而成的复合型序列。
趋势(Trend):是时间序列在长期内呈现出来的某种持续上升或持续下降的变动,也称长期趋势。
时间序列中的趋势可以是线性的,也可以是非线性的。
季节性(seasonality)也称季节变动(seasonal fluctuation),它是时间序列在一年内重复出现的周期性波动。
例如:在商业活动中,常常听到的“销售旺季”或“销售淡季”这类术语。
其本质上指的是一种周期性的变化。
含有季节成分的序列可能含有趋势,也可能不含有趋势。
周期性(cyclicity)也称循环波动(cyclical fluctuation),是时间序列中呈现出来的围绕长期趋势的一种波浪形或震荡式变动。
周期性通常是由商业和经济活动引起的,它不同于趋势变动,不是朝着单一方向的持续运动,而是涨落相同的交替波动;它也不同于季节变动,季节变动有比较固定的规律,而且变动周期大多为一年,循环波动则无固定规律,变动周期多在一年以上,且周期长短不一。
周期性通常是由经济环境的变化引起的。
除此之外,还有些偶然性因素对时间序列产生影响,致使时间序列呈现出某种随机波动。
时间序列中除去趋势、周期性和季节性之后的偶然性波动称为随机性(randomness),也称不规则波动(irregular variations)。
构成要素:长期趋势,季节变动,循环变动,不规则变动。
第五章_随机型时间序列预测方法

第5章 随机型时间序列预测方法随机时间序列分析方法的出现虽然有相当长的历史,但广泛用于经济、商业预测和经济分析还是第二次世界大战之后。
一方面计算机技术的迅速发展,为随机时间序列分析的建模和预测提供了强有力的工具;另一方面,是由于美国著名的统计学家博克斯(Box )和英国的詹金斯(Jenkins )于1968年在理论上提出了一整套的随机时间序列的模型识别、参数估计和诊断检验的建模方法,并于1970年出版了专著《时间序列分析——预测与控制》。
该书对随机序列的理论分析和应用作了系统的论述,尤其是1976年出第2版以后,其应用更为广泛。
优点:它能利用一套相当明确规定的准则来处理复杂的模式,预测精度也比较高。
缺点:但同时为了达到高的精确性,其计算过程复杂,计算工作量大,花费也大。
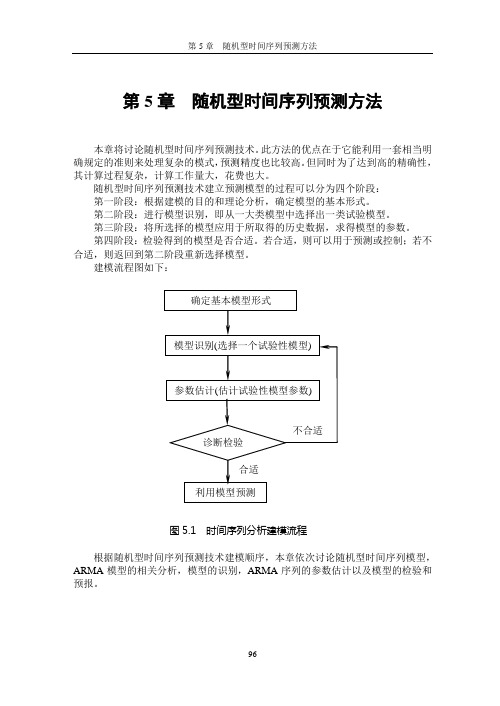
利用随机型时间序列预测方法建立预测模型的过程可以分为4个阶段: (1) 第一阶段:根据建模的目的和理论分析,确定模型的基本形式。
(2) 第二阶段:进行模型识别,即从一大类模型中选择出一类试验模型。
(3) 第三阶段:将所选择的模型应用于所取得的历史数据,求得模型参数。
(4) 第四阶段:检验得到的模型是否合适。
若合适,则可以用于预测和控制;若不合适,则返回到第二阶段重新选择模型。
5.1 随机型时间序列模型 1.时间序列随机时间序列是指{}n X ,对于每个n ,n X 都是一个随机变量。
定义:时间序列{}n X 是平稳的,如果它满足:(1)对于任一n ,()n E X C =,C 是与n 无关的常数;(2)对于任意的n 和k ,[()()]n k n k E X C X C γ+--=,其中k γ与n 无关。
k γ称为时间序列{}n X 的自协方差函数。
0/k k ργγ=称为自相关函数。
平稳性定义中的两条也就是说时间序列的均值和自协方差函数不随时间的变化而变化。
通常我们可以假设一个平稳时间序列{}n X 的均值为0。
如果均值不为零的话,我们可以对原有的时间序列进行一次平移变换,即令nn X X C '=-,则{}n X '是一个零均值的平稳序列。
第十一章SPSS的时间序列分析

3.1 AR(自回归)模型
一般地,如果和p个过去值有关则是p阶自回归模型, 记为AR(p),表达式为: xt 0 1 xt 1 2 xt 2 p xt p t
(B) xt t
或者
其中, (B) 1 1 B 2 B 2 p B p
1 - 12
第三节 时间序列的图形化观察
4、互相关图(CCF) 对两个互相对应的时间序列进行相关性分 析,检验一个序列与另一个序列的滞后 序列之间的相关性 Analyze>Forecasting>Cross Correlations 举例: GDP与通信业务收入,0阶滞后相关性最显 著
1 - 13
3.2 MA模型
(Moving Average Model)
3.3 ARMA模型
(Auto Regression Moving Average model)
3.4 ARIMA模型
( Autoregressive Integrated Moving Average Model )
1 - 22
3.1 AR(自回归)模型
1 - 15
第六节 ARIMA模型
ARIMA模型全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA),是由博克 思(Box)和詹金斯(Jenkins)于70年代初提出的著名时间序列 预测方法,所以又称为box-jenkins模型、博克思-詹金斯法。
第十一章 SPSS的时间序列分析
1-1
第一节 时间序列分析概述
一、相关概念 时间序列:有序的数列:y1,y2,y3,…yt 理解: 1、有先后顺序且时间间隔均匀的数列; 2、随机变量族或随机过程的一个“实现” ,即在每一个固定时间点t上,现象yt看 作是一个随机变量, y1,y2,y3,…yt是一系 列随机变量所表现的一个结果。
随机时间序列
第5章随机型时间序列预测方法本章将讨论随机型时间序列预测技术。
此方法的优点在于它能利用一套相当明确规定的准则来处理复杂的模式,预测精度也比较高。
但同时为了达到高的精确性,其计算过程复杂,计算工作量大,花费也大。
随机型时间序列预测技术建立预测模型的过程可以分为四个阶段:第一阶段:根据建模的目的和理论分析,确定模型的基本形式。
第二阶段:进行模型识别,即从一大类模型中选择出一类试验模型。
第三阶段:将所选择的模型应用于所取得的历史数据,求得模型的参数。
第四阶段:检验得到的模型是否合适。
若合适,则可以用于预测或控制;若不合适,则返回到第二阶段重新选择模型。
建模流程图如下:图5.1 时间序列分析建模流程根据随机型时间序列预测技术建模顺序,本章依次讨论随机型时间序列模型,ARMA模型的相关分析,模型的识别,ARMA序列的参数估计以及模型的检验和预报。
5.1 随机型时间序列模型本节讨论时间序列的几种常用模型。
从实用观点来看,这些模型能够表征任何模式的时间序列数据。
这几类模型是:1)自回归(AR)模型;2)移动平均(MA )模型;3) 自回归移动平均(ARMA)模型;4)求和自回归移动平均(ARIMA)模型。
5.1.1 时间序列所谓随机时间序列是指{|,1,2,,,}n X n o N =±±± ,这里对每个n ,n X 都是一个随机变量。
以下我们简称为时间序列。
定义5.1 时间序列{|0,1,2,}n X n =±± 称为平稳的,如果它满足: (1)对任一n ,()n E X C =,C 是与n 无关的常数;(2)对任意的n 和k ,()()n k n k E X C X C γ+--=其中k γ与n 无关。
k γ称为时间序列{}n X 的自协方差函数,0/k k ργγ=称为自相关函数。
平稳性定义中的两条也就是说时间序列的均值和自协方差函数不随时间的变化而变化。
随机型时间序列预测法概述

随机型时间序列预测法概述随机型时间序列预测法的核心思想是通过对历史观测值的统计分析,来获得对未来观测值的概率分布预测。
常用的方法包括随机游走模型、ARIMA模型和蒙特卡洛模拟等。
随机游走模型是基于随机游走过程的思想,认为未来的观测值仅仅取决于当前的观测值,而不受其他因素的影响。
随机游走模型假设未来观测值是当前观测值的随机扰动,因此只需要根据历史观测值的方差来预测未来的观测值的方差。
ARIMA模型是一种基于自回归移动平均的方法,可以对时间序列数据进行拟合和预测。
ARIMA模型的核心思想是通过对时间序列数据进行平稳化处理,然后利用自回归和移动平均的效应来对未来观测值进行预测。
蒙特卡洛模拟是一种基于随机采样的方法,通过对历史观测值的概率分布进行抽样,得到多个可能的未来观测值序列。
然后,可以通过对这些样本序列的统计分析来获得对未来观测值的概率分布预测。
总之,随机型时间序列预测法通过对时间序列数据的随机性特征进行建模和分析,可以得到对未来观测值的概率分布预测。
这些方法可以帮助我们更好地理解和预测时间序列数据的随机性,提供数据分析和决策支持。
随机型时间序列预测法的应用领域非常广泛。
它可以用于金融市场预测、天气预报、股票市场分析、经济指标预测等许多领域。
在这些领域中,时间序列数据经常呈现出一定的随机性,传统的预测方法往往无法准确捕捉到这种随机性,因此随机型时间序列预测法成为了一种有效的预测方法。
随机游走模型是一种简单而又直观的随机型时间序列预测方法。
它假设未来的观测值仅仅取决于当前的观测值,并且通过随机扰动来进行模拟。
这种方法的一个重要特点是不考虑任何外部因素对未来观测值的影响,因此被广泛应用于金融市场预测中。
例如,在股票市场中,随机游走模型被用来预测股票价格的波动范围,从而帮助投资者制定买卖策略。
ARIMA模型是一种比较常用的随机型时间序列预测方法。
它基于自回归和移动平均的效应,旨在通过对时间序列数据进行平稳化处理,然后根据历史观测值的自相关性和移动平均性来预测未来观测值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.5
2007
1.5
2
2008
1
1.5
2009
2
1
2010
1.5
2
2011
2.5
1.5
2.5
11
1.5
( yt y)(yt1 y)
t1
1
12
2
( yt y)2
t 1
2.5
10
2
( yt y)(yt2 y)
t1
2
12
1.5
( yt y)2
t 1
1
11
2
表中列出了2006年1 1
二、纯随机性检验 纯随机序列的定义 纯随机性的性质 纯随机性检验
4
一、平稳性检验
平稳时间序列的定义
严平稳
严平稳是一种条件比较苛刻的平稳性定义,它认为 只有当序列所有的统计性质都不会随着时间的推移 而发生变化时,该序列才能被认为平稳。
宽平稳
宽平稳是使用序列的特征统计量来定义的一种平稳 性。它认为序列的统计性质主要由它的低阶矩决定, 所以只要保证序列低阶矩平稳(二阶),就能保证 序列的主要性质近似稳定。
许多经济现象的变化并不是时间的确定函数,而是具有 随机性的,因此也就需要建立随机时间序列模型来预测。
随机时间序列
随机时间序列是指一串随机变量 Yt ,t T,T 1,2,3
所构成的序列。对每一个固定的时刻t,yt 是一个随机变量, 而对于一次特定的试验结果, y是t 一个确定的样本函数,
称为随机时间序列的一个实现。如果 是Yt 随t变化的一族 随机变量,t取 ,上的一切值,则称 Y为t 随机过程。
2008 450.0 514.7 540.7 488.4 588.2 568.1 384.4 516.9 513.6 510.9 390.3 489.0
2009 509.8 594.2 564.8 514.8 473.2 478.9 414.9 453.7 553.6 544.2 448.0 637.4
满足如下条件的序列称为宽平稳序列
1) EXt , 为常数,t T 2) (t, s) (k, k s t),t, s, k且k s t T
8
平稳时间序列的统计性质
常数均值
自协方差函数和自相关函数只依赖于时间的平移长度 而与时间的起止点无关
延迟k自协方差函数
(k) (t,t k), k为整数
p 0
E(
t
)
0,Var(
t
)
2
,
E(
t
s
)
0,
s
t
Exst 0,s t
特别当 0 0 时,称为中心化AR( p)模型
延迟k自相关系数
k
(k) (0)
自相关系数的性质 对称性
9
平稳性的检验(图检验方法)
时序图检验
根据平稳时间序列均值、方差为常数的性质, 平稳序列的时序图应该显示出该序列始终在 一个常数值附近随机波动,而且波动的范围 有界、无明显趋势及周期特征
自相关图检验
平稳序列通常具有短期相关性。该性质用自 相关系数来描述就是随着延迟期数的增加, 平稳序列的自相关系数会很快地衰减向零
检验中国纱年产量序列的平稳性
14
例1自相关图
15
例2时序图
检验1962年1月—1975年12月平均每头奶牛月产奶量序列的平稳性
16
例2.自相关图
17
例3时序图
检验1949年——1998年北京市每年最高气温序列的平稳性
18
例3自相关图
19
二、纯随机性检验
20
白噪声检验例题
对北京市城乡居民定期储蓄所占比例序列的平 稳性与纯随机性进行检验
月至2011年10月的电 2
话用户数,计算自 3
相关函数
456ຫໍສະໝຸດ 78910
11
12
2006 89.2 144.4 110.5 121.5 154.1 359.4 151.4 130.0 140.1 232.7 206.2 125.4
2007 177.7 270.3 242.7 280.8 310.6 322.8 188.3 202.2 186.5 217.3 216.4 158.6
自协方差
(t, s) E( X t t )( X s s )
自相关系数
(t, s) (t, s)
DXt DXs
7
平稳时间序列的统计定义
满足如下条件的序列称为严平稳序列
正整数m, t1,t2, ,tm T,正整数,有
Ft1,t2 tm ( x1 , x2 , , xm ) Ft1 ,t2 tm ( x1 , x2 , , xm )
2010 575.3 396.0 509.0 422.7 433.9 441.6 498.7 465.9 585.6 696.4 654.0 521.5
2011 810.7 553.0 798.0 544.0 580.9 472.4 493.5 488.2 491.7 496.3
12
13
例1时序图
10
自相关系数的计算
时间t 2000
原序列 滞后一期 滞后二期 2
k
Cov( yt , ytk ) Var( yt )Var( ytk )
2001
3
2
2002
2.5
3
2003
1.5
2.5
2 3
k
Cov( yt , ytk ) Var( yt )
rk r0
2004
2
1.5
2005
2.5
2
2006
2
对北京市每年最高气温序列的平稳性与纯随机 性进行检验
24
第二节 平稳随机序列模型的预测
平
计
稳
算
非
样
白
本
噪
相
声
关
序
系
列
数
模型 识别
参数 估计
模
序
N 模型 Y 型
列
检验
优
预
化
测
25
1.自回归模型
AR模型的定义
具有如下结构的模型称为 p 阶自回归模型,简
记为 AR( p)
xt 0 1xt1 2 xt2 p xt p t
随机时间序列也称为离散时间参数的随机过程。
随机型时间序列预测过程
1.确定模型的基本类型或形式 2.模型识别,从大类模型中选择子模型 3.拟合模型,求解参数 4.检验拟合效果 5.预测
2
第一节 随机型时间序列的检验 第二节 平稳随机序列模型的预测
3
第一节 随机型时间序列的检验
一、平稳性检验
平稳时间序列的定义 特征统计量 平稳时间序列的统计性质 平稳性的检验
5
严平稳-概率分布
概率分布的意义
随机变量族的统计特性完全由它们的联合分布函数 或联合密度函数决定
时间序列概率分布族的定义
{Ft1,t2, ,tm (x1, x2, , xm )} m(1,2, , m),t1,t2, ,tm T
实际应用的局限性
6
弱平稳-特征统计量
均值 方差
t EX t DX t E( X t t )2 2
