垂直平分线的证明.ppt
合集下载
线段的垂直平分线性质ppt课件
猜想：
反过来，如果PA =PB，那么点P 是否在线 段AB 的垂直平分线上呢？
P
点P 在线段AB 的垂直平分线上．
已知：如图，PA =PB．
求证：点P 在线段AB 的垂直平
分线上．
A
B
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
小结与作业：
（1）本节课学习了哪些内容？ （2）线段垂直平分线的性质和判定是如何得到的？
两者之间有什么关系？ （3）如何判断一条直线是否是线段的垂直平分线？
教科书习题13.1第6、9题．
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
拓展:
结论：三角形三边的垂直平分线交于一点， 并且这点到三个顶点的距离相等.
已知： △ABC中，边AB、 BC的垂直平分线交于点P.
求证：(1)PA=PB=PC.
(2)点P是否也在边AC的垂直平分线上?由此你
还能得出什么结论？
C
P
A
B
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
12.3 角的平分线
A DP C
O
EB
定理1 在角的平分线上的点到这 个角的两边的距离相等.
13.1 线段的垂直平分线
M P
A
B
N
定 理 线段垂直平分线上的点和 这条线段两个端点的距离相等.
定理2 到一个角的两边的距离相 等的点，在这个角的平分线上.
逆定理 和一条线段两个端点距离相 等的点，在这条线段的垂直平分线上.
反过来，如果PA =PB，那么点P 是否在线 段AB 的垂直平分线上呢？
P
点P 在线段AB 的垂直平分线上．
已知：如图，PA =PB．
求证：点P 在线段AB 的垂直平
分线上．
A
B
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
小结与作业：
（1）本节课学习了哪些内容？ （2）线段垂直平分线的性质和判定是如何得到的？
两者之间有什么关系？ （3）如何判断一条直线是否是线段的垂直平分线？
教科书习题13.1第6、9题．
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
拓展:
结论：三角形三边的垂直平分线交于一点， 并且这点到三个顶点的距离相等.
已知： △ABC中，边AB、 BC的垂直平分线交于点P.
求证：(1)PA=PB=PC.
(2)点P是否也在边AC的垂直平分线上?由此你
还能得出什么结论？
C
P
A
B
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
12.3 角的平分线
A DP C
O
EB
定理1 在角的平分线上的点到这 个角的两边的距离相等.
13.1 线段的垂直平分线
M P
A
B
N
定 理 线段垂直平分线上的点和 这条线段两个端点的距离相等.
定理2 到一个角的两边的距离相 等的点，在这个角的平分线上.
逆定理 和一条线段两个端点距离相 等的点，在这条线段的垂直平分线上.
线段的垂直平分线课件
定理应用
在几何作图和证明中，垂直平分线是重要的工具之一。通过 垂直平分线，我们可以找到一个点到线段两端点距离相等的 点，从而解决一些几何问题。
在实际生活中，垂直平分线的应用也十分广泛。例如，在建 筑、道路规划、通信等领域中，常常需要用到垂直平分线的 性质来解决问题。
PART 03
线段垂直平分线的作法
垂直平分线的判定
判定1
若一条直线过线段中点且与线段 所在直线垂直，则该直线为线段
的垂直平分线。
判定2
若一条直线与线段上的两点距离相 等，且该直线与线段所在直线垂直 ，则该直线为线段的垂直平分线。
判定3
若一条直线与线段所在直线垂直， 且该直线上的点到线段两端点的连 线形成的角均为直角，则该直线为 线段的垂直平分线。
详细描述
首先，确定已知线段和该线段的垂直 平分线。然后，使用直尺或三角板， 将垂直平分线与线段的两个端点连接 。最后得到的直线即为所求的垂直平 分线。
PART 04
线段垂直平分线的性质在 生活中的应用
REPORTING
三角形中的垂直平分线
总结词
三角形中的垂直平分线有助于确定顶点的位置和三角形的形状。
详细描述
在三角形中，垂直平分线通过顶点将相对边等分，有助于确定顶点的位置和三角形的形状。在几何学中，垂直平 分线的性质常用于解决与三角形相关的问题。
地球上的经纬线
总结词
地球上的经纬线是垂直平分线的应用实例，用于确定地理位置和方向。
详细描述
经纬线是地球表面上的垂直平分线系统，用于确定地球上任意地点的地理位置和方向。经纬线交汇的 点称为经纬度，是地理坐标的基础。
总结词：操作简单，适合快 速作图。
01
第一步，将三角板的一条直
垂直平分线的性质ppt课件
解:
∵DE是AB的垂直平分线 ∴EA=EB(线段垂直平分线上的点与这条线 段的两个端点的距离相等）
A D B
∵△BCE周长=CE+EB+BC 又∵AC=CE+EA=CE+EB
∴BC=△BCE周长-(CE+EB) =△BCE周长-AC =10cm
E C
21
做一做
已知：如图，P为∠MON内一点，OM⊥PA 于E，ON⊥PB于F，EA=EP，FB=FP，若AB 长为15cm，求△PCD的周长。
22
线段的垂直平分线
一、性质定理：线段垂直平分线上的点到这条线段两个端 点的距离相等。
二、逆定理：到线段两个端点距离相等的点，在这条 线段的垂直平分线上。
点P在线段 AB的垂直 平分线上
线段垂直平分线上的点到这 条线段两个端点的距离相等
到线段两个端点距离相等的点， 在这条线段的垂直平分线上
PA=PB
分析：
点P在线段AB的 垂直平分线上
点P在线段BC的 垂直平分线上
A M
M’
P
PA=PB
PB=PC
B
PA=PB=PC
∵PA=PC ∴点P在AC的垂直平分线上
C N N’
18
例2：
如图，在Rt△ABC中，∠C=90
度，DE是AB的垂直平分线，连
接AE，∠1：∠2=1：2，求∠B
的度数。
C
E
B
D
A
19
1题图
13
2、如图，在△ABC中，BC的
中垂线交斜边AB于D，图中相
等的线段有（ ）
A、1组
B、2组
C、3组
D、4组
1
2
14
∵DE是AB的垂直平分线 ∴EA=EB(线段垂直平分线上的点与这条线 段的两个端点的距离相等）
A D B
∵△BCE周长=CE+EB+BC 又∵AC=CE+EA=CE+EB
∴BC=△BCE周长-(CE+EB) =△BCE周长-AC =10cm
E C
21
做一做
已知：如图，P为∠MON内一点，OM⊥PA 于E，ON⊥PB于F，EA=EP，FB=FP，若AB 长为15cm，求△PCD的周长。
22
线段的垂直平分线
一、性质定理：线段垂直平分线上的点到这条线段两个端 点的距离相等。
二、逆定理：到线段两个端点距离相等的点，在这条 线段的垂直平分线上。
点P在线段 AB的垂直 平分线上
线段垂直平分线上的点到这 条线段两个端点的距离相等
到线段两个端点距离相等的点， 在这条线段的垂直平分线上
PA=PB
分析：
点P在线段AB的 垂直平分线上
点P在线段BC的 垂直平分线上
A M
M’
P
PA=PB
PB=PC
B
PA=PB=PC
∵PA=PC ∴点P在AC的垂直平分线上
C N N’
18
例2：
如图，在Rt△ABC中，∠C=90
度，DE是AB的垂直平分线，连
接AE，∠1：∠2=1：2，求∠B
的度数。
C
E
B
D
A
19
1题图
13
2、如图，在△ABC中，BC的
中垂线交斜边AB于D，图中相
等的线段有（ ）
A、1组
B、2组
C、3组
D、4组
1
2
14
线段的垂直平分线的性质PPT课件
你能再找一些到线段AB 两端点的距离相等的点吗？能找到多 少个到线段AB 两端点距离相等的点？
这些点能组成什么几何图形？
l
与A，B 的距离相等的点
都在直线l上，所以直线l 可
以看成与A、B两点 的距离
A
相等的所有点的集合.
P
C
B
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
C
求作：AB的垂线，使它经过点C .
作法：（1）任意取一点K，使点K和
点C在AB的两旁.
A
D
（2）以点C 为圆心，CK长为半径作弧，
K
交AB于点D和点E.
（3）分别以点D和点E为圆心，大于 1 DE 的长为半径作弧，两弧相交于点F. 2
E B
F
（4）作直线CF. 直线CF就是所求作的垂线.
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
二 线段垂直平分线的判定
合作探究
想一想：如果PA=PB,那么点P是否在线段AB的垂 直平分线上呢？
已知：如图，PA =PB．
求证：点P 在线段AB 的垂直
平分线上．
A
P B
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
作 用 见垂直平分线，得线段相等
内容
到线段的两个端点距离相等 的点在线段的垂直平分线上
作 用 判断一个点是否在线段的垂 直平分线上
这是判断一条直
u应用格式：
线段的垂直平分线PPT课件
把其中的字母去掉，全用文字来表述：
如果_有__一__个__点_为__线__段__垂__直_平__分__线__上__的_任__意__一__点____________， 那么_这__个__点__到_这__条__线__段__的_两__个__端__点__距_离__相__等______________
把如果与那么再去掉，又可简写为：
如果有一个点为线段垂直平分线上的任意一点， 那么这个点到线段的两个端点距离相等。 其中，题设是__有_一__个__点__为__线_段__垂__直__平__分_线__上__的__任__意_一__点_
结论是__这__个__点__到_线__段__的__两__个_端__点__距__离__相_等______ 逆命题是 如果__有__一__个__点_到__线__段__的__两__个_端__点__距__离__相_等____
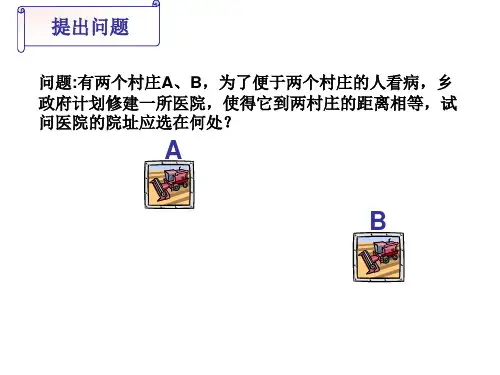
提出问题
问题:有两个村庄A、B，为了便于两个村庄的人看病，乡 政府计划修建一所医院，使得它到两村庄的距离相等，试 问医院的院址应选在何处？
A
B
图形展示
C P
A
E
D
已知CD是AB的垂直平 分线，P是CD上任意一点， 连接PA和PB,问PA=PB吗？
从图形上来看，随着P点上下 移动，PA=PBB你能用所学过的 Nhomakorabea识来证明吗？
A
C
B P L D
问题2:有三个村庄A、B、C，为了便于三个村庄的人看病，
乡政府计划修建一所医院，使得它到三个村庄的距离相等，
试问医院的院址P应选在何处？
A
F
D
P
B
E
想一想，P点与BC有怎样 的关系？
C
G
三角形三条边的中垂线是交 于一点的，这个点到三个顶 点距离相等
垂直平分线ppt课件
Love ,not time,heals all wounds. 治愈一切创伤的并非时间,而是爱.
Life is tough,but I'm tougher. 生活是艰苦的,但我应更坚强.
猜想得到结论： 线段垂直平分线上的点与这条线段两个端 点距离_相__等___.
你能证明这一结论吗?
M
P
已知:如图，P点在线段
我能行
判断：如图PA=PB， 则直线MN是线段AB的 垂直平分线。
精讲例2 已知:如 图,AC=AD，BC=BD。 A 求证：AB垂直平分CD。
C
O
B
D
两点确定一条直线。怎样的两点可以确定一条线段 的垂直平分线呢？
注意： 由“两点确定一条直线”可知， 到同一条线段两个端点距离相等的两点， 可确定这条线段的垂直平分线。
∴△APC≌△BPC(SSS)
∵∠PCA+∠PCB=180° ∴∠PCA=∠PCB=90°即 PC⊥AB
∴P点在AB的垂直平分线 上
精学
2
判定定理 到一条线段两个端点距离
相等的点,在这条线段的垂直平分线
上.
几何语言
M P
∵PA=PB
∴点P在AB的垂直平分线上
A
C
B
作用:仅用来证明一点在线段的垂
N
直平分线上。
∴ ∠ PMA=∠PMB=90°
在RtΔPAC和RtΔPBC中，
AP = BP
A
PM = PM
M
B
∴ RtΔPAC ≌ RtΔPBC(HL) ∴ MA=MB ∴ P点在线段AB的垂直平分线上
P
证法二：
证明：取AB的中点C， 连接PC。
A
C
Life is tough,but I'm tougher. 生活是艰苦的,但我应更坚强.
猜想得到结论： 线段垂直平分线上的点与这条线段两个端 点距离_相__等___.
你能证明这一结论吗?
M
P
已知:如图，P点在线段
我能行
判断：如图PA=PB， 则直线MN是线段AB的 垂直平分线。
精讲例2 已知:如 图,AC=AD，BC=BD。 A 求证：AB垂直平分CD。
C
O
B
D
两点确定一条直线。怎样的两点可以确定一条线段 的垂直平分线呢？
注意： 由“两点确定一条直线”可知， 到同一条线段两个端点距离相等的两点， 可确定这条线段的垂直平分线。
∴△APC≌△BPC(SSS)
∵∠PCA+∠PCB=180° ∴∠PCA=∠PCB=90°即 PC⊥AB
∴P点在AB的垂直平分线 上
精学
2
判定定理 到一条线段两个端点距离
相等的点,在这条线段的垂直平分线
上.
几何语言
M P
∵PA=PB
∴点P在AB的垂直平分线上
A
C
B
作用:仅用来证明一点在线段的垂
N
直平分线上。
∴ ∠ PMA=∠PMB=90°
在RtΔPAC和RtΔPBC中，
AP = BP
A
PM = PM
M
B
∴ RtΔPAC ≌ RtΔPBC(HL) ∴ MA=MB ∴ P点在线段AB的垂直平分线上
P
证法二：
证明：取AB的中点C， 连接PC。
A
C
垂直平分线课件
定理2
垂直平分线上的任意点与线段的两个端点的距 离相等。
推论2
垂直平分线与线段的垂直平分线相交于线段中 点。
实例应用
垂直平分线在几何题目求解中有很多应用，比如通过画垂直平分线证明等式。
几何题目求解
通过画垂直平分线，我们可以解决一些需要使用垂 直平分线的几何问题。
画垂直平分线证明等式
在一些几何证明中，我们可以通过画垂直平分线来 证明等式的成立。
如何作图？
以下是作图垂直平分线的步骤： 1. 以线段的两个端点为圆心，任选一个长度超过一半的半径画两个弧。 2. 两个弧交于两点，连接这两点得到的线即为垂直平分线。
接下来，我们通过一个例题分析具体的作图方法。
相关定理
定理1
垂直平分线将一条线段分成两段相等的部分。
推论1
垂直平分线与线段的延长线垂直。
总结
知识点回顾
垂直平分线将一条线段垂直平分，具有一些性质和 相关定理。
拓展思考
如何利用垂直平分线解决其他几何问题？你能发现 什么有趣的应用吗？
参考资料
图片来源
Unsplash、Pexels等网站提供的免费高质量图片。
参考文献
相关几何学教材和学术论文。 Nhomakorabea垂直平分线ppt课件
本课件介绍垂直平分线的概念、作图方法、相关定理以及实例应用。通过图 示和例题分析，帮助学生巩固知识点并提高解题能力。
什么是垂直平分线？
垂直平分线定义为将一条线段垂直平分的线。 它具有以下性质：
• 垂直平分线将一条线段分成两段相等的部分。 • 垂直平分线上的任意点与线段的两个端点的距离相等。
人教版八年级上册数学垂直平分线的证明课件PPT
B
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
N
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
证明: ∵MNAB（已知） M ∴PCA=PCB(垂直的定义)
P
在PCA和PCB中,
AC=CB(已知),
PCA=PCB(已证)
A C B PC=PC(公共边)
∵ PA=PB(已知)
∴ PAB是等腰三角形(等腰三角
形的定义)
AC
∴AC=BC(等腰三角形底边上
B 的高是底边上的中线)
∴PC是线段AB的垂直平分线. 即点P在线段AB的垂直 平分线MN上.
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
逆定理
和一条线段两个端 点距离相等的点,在 这条线段的垂直平 分线上.
线段垂直平分线上的点 和这条线段两个端点的 距离相等.
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
已知： 直线MNAB，垂足是C， 且AC=CB.点P在MN上.
M P
求证： PA=PB
AC
C
.Q
N
B
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
定理(线段垂直平分线的性质定理) 线段垂直平分线上的点 和这条线段两个端点的 距离相等.
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
人教版八年级上册数学13.1.2垂直平 分线的 证明课 件(共36 张PPT)
《线段的垂直平分线》课件
详细描述
线段垂直平分线是数学竞赛中常用的解题工具之一。在数学竞赛中，常常会遇到一些复杂的几何问题 ，需要利用线段垂直平分线的性质来解决。通过深入理解线段垂直平分线的性质和定理，可以更好地 解决数学竞赛中的几何问题，提高解题效率。
THANK YOU
《线段的垂直平分线》PPT 课件
目录
• 引言 • 线段垂直平分线的性质证明 • 线段垂直平分线的作法 • 线段垂直平分线的应用实例
01
引言
什么是线段的垂直平分线是一条 过线段中点且垂直于线段 所在直线的直线。
性质
垂直平分线上的任意一点 到线段两端点的距离相等 。
详细描述
首先，连接两个给定点并确定中点。 然后，同样使用直角三角板或量角器 ，过中点作与线段垂直的垂线。最后 ，标记垂足，完成作图。
通过三个给定点作已知线段的垂直平分线
总结词
通过三个给定点作已知线段的垂直平分线的方法较为复杂，需要先确定三个点 的中点，然后过中点作垂线。
详细描述
首先，连接三个给定点并确定其中两个点的中点。然后，使用直角三角板或量 角器，过中点作与线段垂直的垂线。接着，再确定第三个点与前两个点的中点 ，重复上述步骤。最后，标记所有垂足，完成作图。
04
线段垂直平分线的应 用实例
线段垂直平分线在几何图形中的应用
总结词
解决几何图形问题
详细描述
线段的垂直平分线在几何图形中有着广泛的应用。它可以用来解决与线段、三角 形、四边形等有关的几何问题，例如线段的等分、角度的确定等。通过利用线段 垂直平分线的性质，可以简化几何图形的解题过程。
线段垂直平分线在日常生活中的应用
在三角形中，垂直平分 线将三角形分为两个面
积相等的子三角形。
线段垂直平分线是数学竞赛中常用的解题工具之一。在数学竞赛中，常常会遇到一些复杂的几何问题 ，需要利用线段垂直平分线的性质来解决。通过深入理解线段垂直平分线的性质和定理，可以更好地 解决数学竞赛中的几何问题，提高解题效率。
THANK YOU
《线段的垂直平分线》PPT 课件
目录
• 引言 • 线段垂直平分线的性质证明 • 线段垂直平分线的作法 • 线段垂直平分线的应用实例
01
引言
什么是线段的垂直平分线是一条 过线段中点且垂直于线段 所在直线的直线。
性质
垂直平分线上的任意一点 到线段两端点的距离相等 。
详细描述
首先，连接两个给定点并确定中点。 然后，同样使用直角三角板或量角器 ，过中点作与线段垂直的垂线。最后 ，标记垂足，完成作图。
通过三个给定点作已知线段的垂直平分线
总结词
通过三个给定点作已知线段的垂直平分线的方法较为复杂，需要先确定三个点 的中点，然后过中点作垂线。
详细描述
首先，连接三个给定点并确定其中两个点的中点。然后，使用直角三角板或量 角器，过中点作与线段垂直的垂线。接着，再确定第三个点与前两个点的中点 ，重复上述步骤。最后，标记所有垂足，完成作图。
04
线段垂直平分线的应 用实例
线段垂直平分线在几何图形中的应用
总结词
解决几何图形问题
详细描述
线段的垂直平分线在几何图形中有着广泛的应用。它可以用来解决与线段、三角 形、四边形等有关的几何问题，例如线段的等分、角度的确定等。通过利用线段 垂直平分线的性质，可以简化几何图形的解题过程。
线段垂直平分线在日常生活中的应用
在三角形中，垂直平分 线将三角形分为两个面
积相等的子三角形。
线段垂直平分线的性质定理及逆定理课件
基础习题2
已知线段AB的垂直平分线为OM，点 C在直线OM上，AC=5cm， BC=3cm，则AB=多少cm。
进阶习题
进阶习题1
已知线段AB的垂直平分线为OM，点C在 直线OM上，AC=3cm，BC=5cm，求 AB的长度。
VS
进阶习题2
已知线段AB的垂直平分线为OM，点C在 直线OM上，AC=6cm，BC=4cm，求 AB的长度。
理，△AMP≌△MBN，所以PM=PN。
证明逆定理2
假设线段AB上有两点C、D到直线l的距离相等，即CL=DL，取AB的中点M，连接MC 、MD、MN，由于∠CML=∠DML=90°，ML=ML，CL=DL，根据三角形的全等定理
，△CML≌△DML，所以CM=DM，根据中点的性质，CM+MA=DM+MB，所以 AC=BD，即线段AB被直线l垂直平分。
定理证明的注意事项
注意证明的逻辑严推理都是正确的，避免出现 逻辑漏洞。
注意使用正确的几何语言
在书写证明过程时，要使用规范的几何语言，确保表达的准确性和 严谨性。
注意检查结论是否符合题意
在得出结论后，要再次核对结论是否符合题目的要求，确保结论正 确无误。
04 定理的应用
定理在数学竞赛中的解题策略中的应用
在数学竞赛中，利用线段垂直平分线性质定理可以设计出一些巧妙的解题策略， 如利用对称性质简化问题、利用中点性质构造辅助线等。
05 习题与解答
基础习题
基础习题1
已知线段AB的垂直平分线与AB交于 点O，点C在直线OM上，CA=CB， 若AB=6cm，则AC=多少cm。
定理在几何图形中的应用
定理在三角形中的应用
线段垂直平分线性质定理可以用于证明三角形中的一些重要 性质，如等腰三角形的三线合一、直角三角形斜边上的中线 性质等。
已知线段AB的垂直平分线为OM，点 C在直线OM上，AC=5cm， BC=3cm，则AB=多少cm。
进阶习题
进阶习题1
已知线段AB的垂直平分线为OM，点C在 直线OM上，AC=3cm，BC=5cm，求 AB的长度。
VS
进阶习题2
已知线段AB的垂直平分线为OM，点C在 直线OM上，AC=6cm，BC=4cm，求 AB的长度。
理，△AMP≌△MBN，所以PM=PN。
证明逆定理2
假设线段AB上有两点C、D到直线l的距离相等，即CL=DL，取AB的中点M，连接MC 、MD、MN，由于∠CML=∠DML=90°，ML=ML，CL=DL，根据三角形的全等定理
，△CML≌△DML，所以CM=DM，根据中点的性质，CM+MA=DM+MB，所以 AC=BD，即线段AB被直线l垂直平分。
定理证明的注意事项
注意证明的逻辑严推理都是正确的，避免出现 逻辑漏洞。
注意使用正确的几何语言
在书写证明过程时，要使用规范的几何语言，确保表达的准确性和 严谨性。
注意检查结论是否符合题意
在得出结论后，要再次核对结论是否符合题目的要求，确保结论正 确无误。
04 定理的应用
定理在数学竞赛中的解题策略中的应用
在数学竞赛中，利用线段垂直平分线性质定理可以设计出一些巧妙的解题策略， 如利用对称性质简化问题、利用中点性质构造辅助线等。
05 习题与解答
基础习题
基础习题1
已知线段AB的垂直平分线与AB交于 点O，点C在直线OM上，CA=CB， 若AB=6cm，则AC=多少cm。
定理在几何图形中的应用
定理在三角形中的应用
线段垂直平分线性质定理可以用于证明三角形中的一些重要 性质，如等腰三角形的三线合一、直角三角形斜边上的中线 性质等。
垂直平分线课件
详细描述
首先，将圆规的两脚分开，分别置于 已知线段的两个端点上。然后，将圆 规的笔头置于线段的中点，旋转圆规 即可得到垂直平分线。
利用尺规作图作垂直平分线
总结词
尺规作图是一种更为精确的作图方法 ，通过尺规作图可以作出更为精确的 垂直平分线。
详细描述
首先，用直尺画出已知线段。然后， 用圆规以线段的中点为圆心，分别在 已知线段的两侧画弧。接着，用直尺 连接两个交点，即可得到垂直平分线 。
02
垂直平分线也是一条直线，它经 过线段的中点，并且与线段垂直 。
垂直平分线的图形定义
在几何图形中，垂直平分线通常用一 条通过线段中点并与线段垂直的虚线 表示。
这条虚线将线段分为两个相等的部分 ，并且与线段垂直。
垂直平分线的性质
垂直平分线上的任意一点到线段两端的距离相等。 经过线段中点的直线是该线段的垂直平分线。
利用垂直平分线性质解决实际问题
要点一
总结词
要点二
详细描述
垂直平分线的性质在实际问题中有着广泛的应用，如解决 几何作图问题、确定物体的位置等。
在几何作图问题中，利用垂直平分线的性质可以确定对称 点的位置。在解决实际问题时，如建筑、机械设计等领域 ，垂直平分线的性质可以帮助确定物体的位置和方向，简 化问题的解决过程。
垂直平分线的逆定理
总结词
垂直平分线的逆定理是，如果一条直线是某点的垂直平分线，则这条直线上有两点到该点的距离相等。
详细描述
垂直平分线的逆定理是一个与判定定理相反的结论。如果一条直线是某点的垂直平分线，那么在这条直线上存在 两个点，它们到该点的距离是相等的。这个逆定理常常用于证明两条线段相等，或者确定一个点是否在某条直线 上。
质等来进行判定。
首先，将圆规的两脚分开，分别置于 已知线段的两个端点上。然后，将圆 规的笔头置于线段的中点，旋转圆规 即可得到垂直平分线。
利用尺规作图作垂直平分线
总结词
尺规作图是一种更为精确的作图方法 ，通过尺规作图可以作出更为精确的 垂直平分线。
详细描述
首先，用直尺画出已知线段。然后， 用圆规以线段的中点为圆心，分别在 已知线段的两侧画弧。接着，用直尺 连接两个交点，即可得到垂直平分线 。
02
垂直平分线也是一条直线，它经 过线段的中点，并且与线段垂直 。
垂直平分线的图形定义
在几何图形中，垂直平分线通常用一 条通过线段中点并与线段垂直的虚线 表示。
这条虚线将线段分为两个相等的部分 ，并且与线段垂直。
垂直平分线的性质
垂直平分线上的任意一点到线段两端的距离相等。 经过线段中点的直线是该线段的垂直平分线。
利用垂直平分线性质解决实际问题
要点一
总结词
要点二
详细描述
垂直平分线的性质在实际问题中有着广泛的应用，如解决 几何作图问题、确定物体的位置等。
在几何作图问题中，利用垂直平分线的性质可以确定对称 点的位置。在解决实际问题时，如建筑、机械设计等领域 ，垂直平分线的性质可以帮助确定物体的位置和方向，简 化问题的解决过程。
垂直平分线的逆定理
总结词
垂直平分线的逆定理是，如果一条直线是某点的垂直平分线，则这条直线上有两点到该点的距离相等。
详细描述
垂直平分线的逆定理是一个与判定定理相反的结论。如果一条直线是某点的垂直平分线，那么在这条直线上存在 两个点，它们到该点的距离是相等的。这个逆定理常常用于证明两条线段相等，或者确定一个点是否在某条直线 上。
质等来进行判定。
线段的垂直平分线的性质课件ppt
平移等距性
在平移变换中，垂直平分线上的 点到线段两个端点的距离相等， 且等于平移的距离。
旋转变换中应用
旋转不变性
垂直平分线在旋转变换下保持不变， 即旋转后的图形仍然保持垂直平分线 的性质。
旋转等角性
以垂直平分线上一点为旋转中心，旋 转任意角度后，所得图形与原图形关 于该点对称。
对称变换中应用
对称中心
思路拓展与延伸
拓展1
探究线段垂直平分线与三角形的关系。例如，已知三角形ABC 中，D是AB的中点，DE垂直于AC于点E，求证：DE是AB的垂 直平分线。
拓展2
将线段垂直平分线的性质应用于实际问题中。例如，在建筑 设计或工程测量中，如何利用线段的垂直平分线性质来确定 某点的位置或某线段的长度。
易错点提示与防范策略
THANKS
感谢观看
线段的垂直平分线是对称中心，即关于垂直平分线的对称点连线的中点就是垂 直平分线与线段的交点。
对称轴
线段的垂直平分线也是对称轴，即关于垂直平分线对称的两个图形是全等的。
05
典型例题解析与思路拓展
典型例题解析
例题1
已知线段AB和点C，D分别是AB，BC的中点，求证：CD是AB的垂直平分线。
解析
根据中点的定义，可知AC=CB，BD=DA。因为CD是AB的中线，所以CD垂直于AB。 又因为AC=CB，所以角ACD=角BCD，从而角ADC=角BDC。根据角平分线的性质， 可知CD平分角ADB，所以CD是AB的垂直平分线。
性质1
垂直平分线上的任意一点 到线段两端的距离相等。
性质2
线段的垂直平分线是其对 称轴，即线段关于垂直平 分线对称。
判定方法
判定定理
一条直线是某线段的垂直 平分线当且仅当该直线过 线段的中点且与该线段垂 直。
在平移变换中，垂直平分线上的 点到线段两个端点的距离相等， 且等于平移的距离。
旋转变换中应用
旋转不变性
垂直平分线在旋转变换下保持不变， 即旋转后的图形仍然保持垂直平分线 的性质。
旋转等角性
以垂直平分线上一点为旋转中心，旋 转任意角度后，所得图形与原图形关 于该点对称。
对称变换中应用
对称中心
思路拓展与延伸
拓展1
探究线段垂直平分线与三角形的关系。例如，已知三角形ABC 中，D是AB的中点，DE垂直于AC于点E，求证：DE是AB的垂 直平分线。
拓展2
将线段垂直平分线的性质应用于实际问题中。例如，在建筑 设计或工程测量中，如何利用线段的垂直平分线性质来确定 某点的位置或某线段的长度。
易错点提示与防范策略
THANKS
感谢观看
线段的垂直平分线是对称中心，即关于垂直平分线的对称点连线的中点就是垂 直平分线与线段的交点。
对称轴
线段的垂直平分线也是对称轴，即关于垂直平分线对称的两个图形是全等的。
05
典型例题解析与思路拓展
典型例题解析
例题1
已知线段AB和点C，D分别是AB，BC的中点，求证：CD是AB的垂直平分线。
解析
根据中点的定义，可知AC=CB，BD=DA。因为CD是AB的中线，所以CD垂直于AB。 又因为AC=CB，所以角ACD=角BCD，从而角ADC=角BDC。根据角平分线的性质， 可知CD平分角ADB，所以CD是AB的垂直平分线。
性质1
垂直平分线上的任意一点 到线段两端的距离相等。
性质2
线段的垂直平分线是其对 称轴，即线段关于垂直平 分线对称。
判定方法
判定定理
一条直线是某线段的垂直 平分线当且仅当该直线过 线段的中点且与该线段垂 直。
《线段的垂直平分线》PPT课件
练习
1. 如图，在△ABC中，AB的垂直平分线分别交 AB，BC于点D，E，∠B=30°，∠BAC= 80°， 求∠CAE的度数.
答：∠CAE=50°.
2.已知：如图，点C，D是线段AB外的两点，且 AC =BC，AD=BD，AB与CD相交于点O.
求证：AO=BO.
证明： ∵ AC =BC，AD=BD， ∴ 点C和点D在线段AB的垂直平分线上， ∴ CD为线段AB的垂直平分线.
练习
用尺规完成下列作图（只保留作图痕迹，不要 求写出作法）.
1. 如图，在直线l上求作一点P，使PA= PB.
已知：如图,在△ABC中,AB,BC的垂直平分线相交于点P,
求证：点P也在AC的垂直平分线上
证明：连接AP,BP,CP.
∵点P在线段AB的垂直平分线上, A
∴PA=PB
同理,PB=PC.
中考 试题
例
如图，在△ABC中，BC=8cm，AB的垂直
平分线交AB于点D，交边AC于点E，△BCE 的周长等于18cm，则AC的长等于（ C ）.
A.6cm B.8cm C.10cm D.12cm
解析 ∵DE是AB的垂直平分线， ∴AE=BE(线段垂直平分线上的点到线段两端点的距离相等).
又∵在△BCE中，
∴EB=EA ∴△AEC的周长
=AC+CE+EA
C E
=AC+CE+EB
=AC+BC
B
=4+5 =9
D A
做一做
已知：如图，P为∠MON内一点，OM⊥PA 于E，ON⊥PB于F，EA=EP，FB=FP，若AB 长为15cm，求△PCD的周长。
M A
E C
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
∴ 1= B 即 CAF= B.
35
如图,已知:AOB,点M、N. 求作:一点P,使点P到AOB两边的 距离相等,并且满足PM=PN.
∴ 2= 3(等量代换)
∴ AD ∥BC(内错角相等,两直线平行)
D 30
证明题:3.已知:如图,在ABC中, AB=AC,A=120o, AB的垂直平分线交AB于E,交BC于F. 求证:CF=2BF.
A
E
300
300
B
60O F
30O C
CF=2AF AF=BF CF=2BF
31
线段垂直平分线上的点和这条线 段
求证:D点在AB的垂直平分线上. A 证明: ∵ C=90o, A=30o(已知)
∴ ABC=60o(三角形内角和定理) ∵BD平分A BC(已知)
30o
∴ ABD=30o(角平分线的定义)
∴ A= ABD (等量代换)
D
∴ AD=BD(等角对等边)
30o
∴ D点在AB的垂直平分线上.(和一 条线段两个端点距离相等的点,在这
两 和一个条端线点段的两距个离端相点等距. 离相等的点, 在这条线段的垂直平分线上.
线段的垂直平分线可以看作是和线 段两个端点距离相等的所有点的集合.
32
作业: P95 2. 3. 4
33
证明题:4.已知:如图,AD平分BAC,EF垂直平分 AD交BC的延长线于F,连结AF. 求证: CAF= B.
P
在PCA和PCB中,
AC=CB(已知),
PCA=PCB(已证)
A C B PC=PC(公共边)
N ∴ PCA ≌ PCB(SAS)
∴PA=PB(全等三角形的对应边相等)
12
M
当点P与点C重合时,上述证 明有什么缺陷?
P
PCA与PCB将不存在.
AC
N
PA与PB还相等吗?
B 相等! 此时,PA=CA,PB=CB 已知AC=CB ∴PA=PB
点,在这条线段的垂直平分线上.
17
M
• •
• • •
A
•
•C
B
•
•
•
N
18
M
• •
• • •
A
•
•C
B
•
•
•
N
19
线段的垂直平分线可以看作是
和线段两个端点距离相等 的所有点的集合.
20
例 已知:如图ABC中,边AB、BC的
垂直平分线相交于点P.
A
求证:PA=PB=PC.
M
证明: ∵ 点A在线段
哈五中
1
问题:如图,A、B、C三个村庄合建 一所学校,要求校址P点距离三个村 庄都相等.请你帮助确定校址.
C•
A•
•B
2
M
P•
A
C
B
N
3
M
A
C
B
N •Q
4
M
P.
A
B
C
.Q
N
5
定理(线段垂直平分线的性质定理) 线段垂直平分线上的点 和这条线段两个端点的 距离相等.
6
定理 线段垂直平分线上的点 和这条线段两个端点的 距离相等.
A
3 21 E
4
B
D
C
F
34
A
E3 2 1
4
B
DC
F
证明:∵ EF垂直平分AD(已知) ∴ AF=DF(线段垂直平分线的性质定理) ∴ 1+ 2= 4(等边对等角)
又∵ 4= B+ 3(三角形的一个外角等于与它
不相邻的两个内角的和)
∴ 1+ 2= B+ 3 ∵ AD平分BAC(已知)
∴ 2= 3(角平分线的定义)
形的定义)
AC
∴AC=BC(等腰三角形底边上
B 的高是底边上的中线)
∴PC是线段AB的垂直平分线. 即点P在线段AB的垂直 平分线MN上.
15
逆定理
和一条线段两个端 点距离相等的点,在 这条线段的垂直平 分线上.
16
小结: 1.线段的垂直平分线上的点,和这条
线段两个端点的距离相等. 2.和一条线段两个端点距离相等的
7
定理 线段垂直平分线上的点 和这条线段两个端点的 距离相等.
8
定理 线段垂直平分线上的点 和这条线段两个端点的 距离相等.
9
定理 线段垂直平分线上的点 和这条线段两个端点的 距离相等.
10
已知： 直线MNAB，垂足是C， 且AC=CB.点P在MN上.
M P
求证： PA=PB
AC
B
N
11
证明: ∵MNAB（已知） M ∴PCA=PCB(垂直的定义)
13
M
P•
P• /
已知线段AB,有一 点P,并且PA=PB. 那么,点P是否一定 在AB的垂直平分 线上?
这样的点P /不存在
A
C
B
N 14
已知: 线段AB,且PA=PB 求证: 点P在线段AB的垂直
平分线MN上.
P 证明: 过点P作PCAB垂足为C.
∵ PA=PB(已知)
∴ PAB是等腰三角形(等腰三角
A
E
13cm
B
D
C
27
5.如图,CD、EF分别是AB、BC的垂直
平分线.请你指出图中相等的线段有哪些?
D
AD =BD AC = BC
3
CF = BF CE = BE F CF =DF
2
即:BF=CF=DF
1
A
CE B
28
证明题:1.已知:ABC中,C=90,A=30o,BD
平分ABC交AC于D.
•A
•B l
P 点P为所求作的点
23
填空： 1.已知:如图,AD是ABC的高,E为AD上一点, 且BE=CE,则ABC为 等腰 三角形.
A
1题图
E
B
D
C
24
填空：
1.已知:如图,AD是ABC的高,E为AD上一点, 且BE=CE,则ABC为 等腰 三角形. 2.已知: 等腰ABC,AB=AC,AD为BC边上的高,
AB的垂直平分线上
(已知)
B
M/ P N C
N/
∴ PA=PB(线段垂直平分线上的点
和这条线段两个端点距离相等)
同理 PB=PC
∴ PA=PB=PC.
21
问题:如图,A、B、C三个村庄合建 一所学校,要求校址P点距离三个村 庄都相等.请你帮助确定校址.
C•
P• A•
•B
点P为校址
22
作图题:如图,在直线 l 上求一点P,使PA=PB
E为AD上一点,则BE = EC.(填>、<或=号)
A
A
1题图
E
B
D
C
2题图
E
B
D
C
25
3.已知:如图,AB=AC,A=30o,AB的垂 直平分线MN交AC于D,则 1= 60o ,
2= 45o . A
30o
M
D
1N
30o
B 2 75o C
26
填空： 4.已知:如图,在ABC中,DE是AC的垂直平分线, AE=3cm, ABD的周长为13cm,则ABC 的周长 为 19 cm
条线段的垂直平分线上.)
C
B
29
证明题:
2.已知:如图,线段CD垂直平分AB,AB平分CAD.
求证:AD∥BC.
C 证明: ∵线段CD垂直平分AB(已知)
∴ CA=CB(线段垂直平分线的
性质定理)
∴ 1= 3(等边对等角)ALeabharlann 1 2O3
又∵ AB平分CAD(已知) B∴ 1= 2(角平分线的定义)