第四章晶体中的点缺陷与线缺陷第二讲
合集下载
第4章 晶体缺陷
刃位错的滑移
螺位错的滑移
刃、螺型位错的滑移特点
特征差异：
切应力方向不同 刃型：F⊥l；螺型：F∥l
位错运动方向与晶体滑移方向关系 刃型：运动方向与滑移 方向一致；螺型：运动方向与滑移方向垂直。 统一之处： 两者的滑移情况均与各自的b一致。
b) 位错环（混合型位错）的滑移
A、B处为刃型位错，C、D处为螺型位错，其余各处为 混合型位错。 位错环可以沿法线方向向外扩张而离开晶体；也可以反 向缩小而消失。
透射电镜下观察到的位错线
第三节 位错的能量及交互作用
位错线周围的原子偏离平衡位置，处于较高的能量状 态，高出的这部分能量称为位错的应变能（位错能）
一、位错的应变能
位错的应变能可分为：位错中心畸变能Ec和位错应 力场引起的弹性应变能Ee。 Ec：位错中心点阵畸变较大，需借助点阵模型直接考虑晶体
结构和原子间的相互作用，其能量约为总应变能的1/10～ 1/15，常予以忽略。
和间隙原子的“间隙-空位”对。
Frenkel defect
化合物离子晶体中的两种点缺陷 金属晶体：弗兰克尔缺陷比肖脱基缺陷少得多 离子晶体：结构配位数低-弗兰克尔缺陷较常见
结构配位数高-肖脱基缺陷较重要
间隙原子
定义：晶体中的原子进入晶格的间隙位置而形成 的缺陷。
Interstitial defect
b 2 r
Gb 2 r
b 2 r dr L L Gb
位错线
半原子面
刃型位错的特点
滑移面
a、属于线型位错，但在晶体中为狭长的管道畸变区；
b、是晶体中滑移区与未滑移区的分界线，不一定是 直线，也可以是折线或曲线； c、不能中断于晶体内部
《材料科学基础》课件之第四章----04晶体缺陷
41
刃位错：插入半原子面，位错上方，原子间距变小， 产生压应变，下方原子间距变大，拉应变。过渡处 切应变，滑移面处有最大切应力，正应力为0。x NhomakorabeaGb
2 (1 )
y(3x2 (x2
y2) y2 )2
y
Gb
2 (1
)
y(x2 y2) (x2 y2)2
z ( x y )
x
xy
Gb
2 (1 )
21
刃位错b与位错线 垂直
螺位错b与位错线 平行
bb
l
l
正
负
b
b
右旋
左旋
任意一根位错线上各点b相同，同一位错只有一个b。
有大小的晶向指数表示
b a [uvw] 模 n
b a u2 v2 w2 n
22
Burgers矢量合成与分解：如果几条位错线在晶体内
部相交（交点称为节点），则指向节点的各位错的伯氏矢量 之和，必然等于离开节点的各位错的伯氏矢量之和 。
不可能中断于晶体内部（表面露头，终止与 晶界和相界，与其他位错相交，位错环）
半原子面及周围区域统称为位错
18
2. 螺位错
晶体在大于屈服值的切应力作用下，以某晶面为滑移面发生滑移。由于位错线周围 的一组原子面形成了一个连续的螺旋形坡面，故称为螺位错。
几何特征：位错线与原子滑移方向相平行；位错线周围原子的配置是螺旋状的。
d
34
六、位错应变能
位错原子偏移正常位置，产生畸变应力， 处于高能量状态，但偏移量很小，晶格为弹 性应变。
位错心部应变较大，超出弹性范围， 但这部分能量所占比例较小， <10%，可以近似忽略。
35
1. 理论基础：连续弹性介质模型
第四章 晶体中的点缺陷和面缺陷
热平衡态点缺陷：纯净和严格化学配比的晶体中，由于体系能量涨落而形
成的，浓度大小取决于温度和缺陷形成能。
非平衡态点缺陷：通过各种手段在晶体中引入额外的点缺陷，形态和数量
完全取决于产生点缺陷的方法，不受体系温度控制。
晶体中引入非平衡态点缺陷的方法：
快速冷却 低温，形成过饱和点缺陷 （1）淬火 ：高温---------
23
P22
(a)M离子空位VM″ ；
· X离子空位VX·
· (b)M离子填隙Mi· ； ( c)M离子错位MX； X离子错位X X离子填隙Xi″ M 24
6．带电缺陷：
对于离子晶体 MX ，如果取走一个 M2+和取走一个 M原子相比，少取了二个电子。 因此，M空位必然和二个附加电子 2e′相联系，如果这二个附加电子被束缚在 M空位上，则M2+空位可写成VM″(=VM2+)； 同样，如果取走一个X2-，即相当于取走一个X原子加二个电子，则在X空位上留
16
表4-1为某些化合物的缺陷形成自由能。 目前，对缺陷形成自由能尚不能精确计算，但其大小与晶 体结构、离子极化等因素有关。
17
表2-7为由理论公式计算的缺陷浓度。由表中数据可见，随⊿Gf升高，温度降 低，缺陷浓度急剧下降。
当⊿Gf不太大，温度较高时，晶体中热缺陷的浓度可达百分之几。
18
§4-2 非热力学平衡态点缺陷
1
第四章 晶体中的点缺陷与线缺陷
理想晶体：热力学上最稳定的状态，内能最低，存在于０K。 真实晶体： 在高于 0K 的任何温度下，都或多或少地存在着对理想
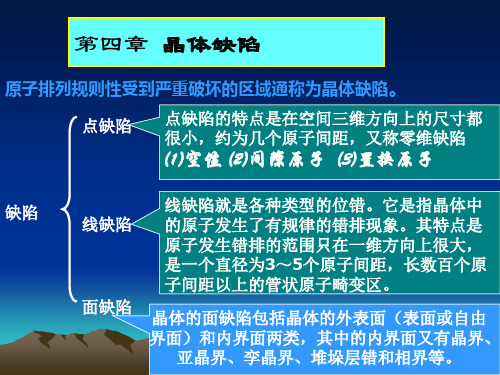
晶体结构的偏离。 实际晶体结构中和理想点阵结构发生偏离的区域，就是晶体结 构缺陷。或：造成晶体点阵结构的周期势场畸变的一切因素，都称 之为晶体缺陷。 晶体结构缺陷与固体的电学性质、机械强度、扩散、烧结、化 学反应性、非化学计量化合物组成以及对材料的物理化学性能都密 切相关。只有在理解了晶体结构缺陷的基础上，才能阐明涉及到质 点迁移的速度过程。掌握晶体结构缺陷的知识是掌握材料科学的基 础。
成的，浓度大小取决于温度和缺陷形成能。
非平衡态点缺陷：通过各种手段在晶体中引入额外的点缺陷，形态和数量
完全取决于产生点缺陷的方法，不受体系温度控制。
晶体中引入非平衡态点缺陷的方法：
快速冷却 低温，形成过饱和点缺陷 （1）淬火 ：高温---------
23
P22
(a)M离子空位VM″ ；
· X离子空位VX·
· (b)M离子填隙Mi· ； ( c)M离子错位MX； X离子错位X X离子填隙Xi″ M 24
6．带电缺陷：
对于离子晶体 MX ，如果取走一个 M2+和取走一个 M原子相比，少取了二个电子。 因此，M空位必然和二个附加电子 2e′相联系，如果这二个附加电子被束缚在 M空位上，则M2+空位可写成VM″(=VM2+)； 同样，如果取走一个X2-，即相当于取走一个X原子加二个电子，则在X空位上留
16
表4-1为某些化合物的缺陷形成自由能。 目前，对缺陷形成自由能尚不能精确计算，但其大小与晶 体结构、离子极化等因素有关。
17
表2-7为由理论公式计算的缺陷浓度。由表中数据可见，随⊿Gf升高，温度降 低，缺陷浓度急剧下降。
当⊿Gf不太大，温度较高时，晶体中热缺陷的浓度可达百分之几。
18
§4-2 非热力学平衡态点缺陷
1
第四章 晶体中的点缺陷与线缺陷
理想晶体：热力学上最稳定的状态，内能最低，存在于０K。 真实晶体： 在高于 0K 的任何温度下，都或多或少地存在着对理想
晶体结构的偏离。 实际晶体结构中和理想点阵结构发生偏离的区域，就是晶体结 构缺陷。或：造成晶体点阵结构的周期势场畸变的一切因素，都称 之为晶体缺陷。 晶体结构缺陷与固体的电学性质、机械强度、扩散、烧结、化 学反应性、非化学计量化合物组成以及对材料的物理化学性能都密 切相关。只有在理解了晶体结构缺陷的基础上，才能阐明涉及到质 点迁移的速度过程。掌握晶体结构缺陷的知识是掌握材料科学的基 础。
4.1-2晶体缺陷的基本类型and位错缺陷的性质
晶界： 两个空间位向不同 的相邻晶粒之间的 界面。
晶粒间界面缺陷分类:
大角度晶界： 晶 粒 位 向 差 大 于 10 度 的晶界。 其结构为几个原子范 围内的原子的混 乱排列， 可视为一个过渡区。
小角度晶界： 晶粒位向差小于 10度的晶界。
2.堆垛间界
我们知道金属晶体常采用立方密积的结构形式，而立方密积 是原子球以三层为一组，如果把这样的一组三层记为 ABC，则晶
4.1.2 线缺陷
当晶格周期性的破坏是发生在晶体内部一条线的周围近邻，
这就称为线缺陷。位错就是线缺陷。
刃型位错 螺旋位错 1.刃型位错 A A B
G
H
F b B E
刃型位错
设想晶体的上部沿ABEF平面向右推移， A B 原来与AB
重合，经过这样的推压后，相对于AB滑移一个原子间距b，EF
§4.1 晶体缺陷的基本类型
本节主要内容： 4.1.1 点缺陷 4.1.2 线缺陷 4.1.3 面缺陷
晶体缺陷（晶格的不完整性）：晶体中任何对完整周期性
结构的偏离就是晶体的缺陷。 结构缺陷： 没有杂质的具有理想的化学配比
的晶体中的缺陷，如空位，填隙
晶体的缺陷 原子，位错。 化学缺陷： 由于掺入杂质或同位素，或者化学 配比偏离理想情况的化合物晶体中 的缺陷，如杂质，色心等。
１．弗仑克尔缺陷和肖特基缺陷
弗仑克尔缺陷 当晶格中的原子脱离格点后，移到间隙位置形成填隙原 子时，在原来的格点位置处产生一个空位，填隙原子和空位成 对出现，这种缺陷称为弗仑克尔缺陷。
肖特基缺陷
当晶体中的原子脱离格点位置后不在晶体内部形成填隙原
子，而是占据晶体表面的一个正常位置，并在原来的格点位置 产生一个空位，这种缺陷称为肖特基缺陷。
第四章晶体缺陷
空位形成引起点阵畸变，亦会割断键力，故空位形成需能量， 空位形成能（ΔEV）为形成一个空位所需能量。
点缺陷是热力学稳定的缺陷： 点缺陷与线、面缺陷的区别 之一是后者为热力学不稳定的缺陷 。在一定温度下，晶体中
有一定平衡数量的空位和间隙原子，其数量可近似算出。
设自由能G=H－TS H为焓，S为系统熵（包括振动熵SV和排列熵SC） 空位的引入，一方面由于弹性畸变使晶体内能增加； 另一方面又使晶体中混乱度增加，使熵增加。而熵 的变化包括两部分： ① 空位改变它周围原子的振动频率引起振动熵，SV ② 空位在晶体点阵中的排列可有许多不同的几何 组态，使排列熵SC增加。
一些能量较大的质点 离开平衡位置后，进 入到间隙位置，形成间隙质点，而在原来位置上 形成空位
（2）肖特基空位： 如果正常格点上的 质点，在热起伏过程中 获得能量离开平衡位置迁移到晶体的表面，而在晶体
内部正常格点上留下空位
材料科学基础
2 间隙原子 原子或离子进入晶体中正常结点之间的间隙位置， 成为填隙原子（或离子）或间隙原子（或离子）。 从成分上看，填隙质点可以是晶体自身的质点，
Example 6.1 SOLUTION The lattice parameter of FCC copper is 0.36151 nm. The basis is 1, therefore, the number of copper atoms, or lattice points, per cm3 is:
Example 4.1 The Effect of Temperature on Vacancy Concentrations
Calculate the concentration of vacancies in copper at room temperature (25oC). What temperature will be needed to heat treat copper such that the concentration of vacancies produced will be 1000 times more than the equilibrium concentration of vacancies at room temperature? Assume that 20,000 cal are required to produce a mole of vacancies in copper.
4. 晶体缺陷
螺型位错的滑移：在图示的晶体上施加一切应力，当应力足够大 时，有使晶体的左右部分发生上下移动的趋势。假如晶体中有一 螺型位错，显然位错在晶体中向后发生移动，移动过的区间右边 晶体向下移动一柏氏矢量。因此，①螺位错也是在外加切应力的 作用下发生运动；②位错移动的方向总是和位错线垂直；③运动 位错扫过的区域晶体的两部分发生了柏氏矢量大小的相对运动 (滑移)；④位错移过部分在表面留下部分台阶，全部移出晶体 的表面上产生柏氏矢量大小的完整台阶。这四点同刃型位错。
第二节 位错的基本概念
一．位错概念的引入
★1926年 Frank计算了理论剪切强度，与实际剪切 强度相比，相差３~４个数量级，当时无法解释， 此矛盾持续了很长时间 。
★1934年 Taylor在晶体中引入位错概念，将位错与 晶体结构、晶体的滑移联系起来解释了这种差异 。
★ 1939年 Burgers提出柏氏矢量b以表征位错的特征， 阐述了位错弹性应力场理论。
例题
Cu晶体的空位形成能uv=0.9ev/atom或 1.44*10-19J/atom材料常数A取作1,k=1.38*10-23. 计算:
1)在５００℃下，每立方米中的空位数目; 2)５００ ℃下的平衡空位浓度 。
解：首先确定1m3体积内原子Cu原子总数 （已知Cu的摩尔质量MCu=63.54g/mol,500 ℃
螺型位错
τb
晶体的局部滑移
螺型位错的原子组态
混合型位错： 晶体的局部滑移
τ∧ b
混合型位错的原子组态
线缺陷：在三维空间的一个方向上的尺寸很大(晶粒数量级)，
另外两个方向上的尺寸很小(原子尺寸大小)的晶体缺陷。其 具体形式就是晶体中的位错Dislocation
一、位错的原子模型
第二讲 晶体缺陷、相图相变
•
金属晶体
• 堆积特征：面心立方和密排六方中，每个原子和 最近邻的原子间都相切；体心立方中，体心原子 与顶角八原子相切，八个顶角原子互不相切。 • 密排面：原子密排程度最高的晶面。是密排六方 的{0001}和面心立方的{111}，体心立方{110}。 • 密排面上原子排列方式：ABAB…(或ACAC…)的 顺序堆垛，是密排六方；ABCABC…的顺序堆垛， 是面心立方。 • 晶格常数与原子半径的关系： • 面心立方结构(a=b=c)： 体心立方结构(a=b=c)： 密排六方结构(a=b≠c)： a=2R
1 C Fs 2 k T ln C0 b
——C0：晶体中空位的平衡浓度为，C：实际浓度为 单位长度位错线所受的弹性攀移驱动力：
bdy Fc b dy
位错与缺陷的相互作用
• 位错之间的相互作用 • 1、位错间的弹性相互作用：位错的弹性应力场间发生的干涉和相互 作用，将影响到位错的分布和运动 • 两平行的螺型位错间的相互作用（滑移）：作用是中心力，位错同号 相斥，异号相吸，大小与位错间距成反比，和两条带电导线的相互作 用相似。 图2-37
• 螺型位错滑移特性：位错线向垂直于柏格斯矢量 （原子移动）方向（位错的侧向）滑移。见 图228，原子的移动量很小，位错移动所需的力也很 小。晶体因滑移而产生的台阶扩大一个原子间距， 滑过整个晶体产生台阶宽度为一个柏格斯矢量b。 见 图2-29
混合型位错滑移特性：分析圆环形，如 图2-30 ( 图2-31)。A、 B、C、D分别为正、负、右、左位错。切应力作用下，各位 错线分别向外扩展，一直到达晶体边缘。晶体滑移由柏格斯 矢量b决定，产生一个b的滑移
b
i
i
0
位错密度 位错密度：在单位体积晶体中所包含的位错线的总 长度 简便起见，位错密度等于穿过单位截面积的位错线数目
晶体缺陷-线缺陷讲解
（1）有一个额外的半原子面；
（2）刃型位错线可理解为晶体中已滑 移区与未滑移区的边界线；
（3）滑移面必定是同时包含有位错线 和滑移矢量的平面，在其他面上不 A 能滑移；
（4）晶体中存在刃型位错之后，位错 周围的点阵发生弹性畸变；
（5）在位错线周围的过渡区（畸变区 ）每个原子具有较大的平均能量。
H D
错中心附近的原子沿柏氏矢量方向在滑移面上不断 地作少量的位移（小于一个原子间距）而逐步实现 的。（刃型位错和螺型位错均可发生） 4.2 位错的攀移
刃型位错在垂直于滑移面的方向上运动，即发 生攀移。实质上就是构成刃型位错的多余半原子面 的扩大或缩小。（螺型位错没有多余的半原子面， 因此不会发生攀移运动）
12
三.柏氏矢量
(a) 实际晶体
(a) 理想晶体
13
三.柏氏矢量
3.2 右手法则（确定刃型位
错的正负）： 先人为的规定位错线方向，
用右手的拇指、食指和中指构 成直角坐标，以食指指向位错 线的方向，中指指向柏氏矢量 的方向，则拇指的指向代办多 余半原子面的位向，且规定拇 指向上者为正刃型位错；反之 为负刃型位错。
（2）线缺陷：特征是在两个方向上尺寸很小，另外一 个方向上延伸较长。如各种位错；
（3）面缺陷：特征是在一个方向上尺寸很小，另外两 个方向上扩展很大。如晶界、孪晶界等。
5
二.位错（dislocation)
2.1 位错的定义：晶体的线缺陷表现为各种
类型的位错。即晶体中某处一列或若干列原 子有规律的错排。
3.1 柏氏矢量的确定：柏氏矢量可通过
柏氏回路（Burgers circuit）来确定。 在含有位错的实际晶体中作一个包含位 错发生畸变的回路，然后将这同样大小 的回路置于理想晶体中，此时回路将不 能封闭，需引一个额外的矢量b连接回路 ，才能使回路闭合，这个矢量b就是实际 晶体中位错的柏氏矢量。如图所示： a ）实际晶体（b) 完整晶体
（2）刃型位错线可理解为晶体中已滑 移区与未滑移区的边界线；
（3）滑移面必定是同时包含有位错线 和滑移矢量的平面，在其他面上不 A 能滑移；
（4）晶体中存在刃型位错之后，位错 周围的点阵发生弹性畸变；
（5）在位错线周围的过渡区（畸变区 ）每个原子具有较大的平均能量。
H D
错中心附近的原子沿柏氏矢量方向在滑移面上不断 地作少量的位移（小于一个原子间距）而逐步实现 的。（刃型位错和螺型位错均可发生） 4.2 位错的攀移
刃型位错在垂直于滑移面的方向上运动，即发 生攀移。实质上就是构成刃型位错的多余半原子面 的扩大或缩小。（螺型位错没有多余的半原子面， 因此不会发生攀移运动）
12
三.柏氏矢量
(a) 实际晶体
(a) 理想晶体
13
三.柏氏矢量
3.2 右手法则（确定刃型位
错的正负）： 先人为的规定位错线方向，
用右手的拇指、食指和中指构 成直角坐标，以食指指向位错 线的方向，中指指向柏氏矢量 的方向，则拇指的指向代办多 余半原子面的位向，且规定拇 指向上者为正刃型位错；反之 为负刃型位错。
（2）线缺陷：特征是在两个方向上尺寸很小，另外一 个方向上延伸较长。如各种位错；
（3）面缺陷：特征是在一个方向上尺寸很小，另外两 个方向上扩展很大。如晶界、孪晶界等。
5
二.位错（dislocation)
2.1 位错的定义：晶体的线缺陷表现为各种
类型的位错。即晶体中某处一列或若干列原 子有规律的错排。
3.1 柏氏矢量的确定：柏氏矢量可通过
柏氏回路（Burgers circuit）来确定。 在含有位错的实际晶体中作一个包含位 错发生畸变的回路，然后将这同样大小 的回路置于理想晶体中，此时回路将不 能封闭，需引一个额外的矢量b连接回路 ，才能使回路闭合，这个矢量b就是实际 晶体中位错的柏氏矢量。如图所示： a ）实际晶体（b) 完整晶体
第四章 缺陷
混合位错：在实际晶体中可能同时产生刃错位和螺位错
┴
4.2.3 面缺陷
面缺陷的特征： 指二维尺度很大而第三维尺度
很小的缺陷。面缺陷的取向及分布与材料的断裂韧 性有关 ，如解理性。
面缺陷类型：
表面(surface) 内界面(interface)：层错、孪晶界、晶界
肖特基缺陷
弗仑克尔缺陷
（2）间隙原子：
在晶体中总是有少部分原子离开正常格点，跳到间隙 位置，形成间隙原子，或者说，间隙原子就是进入点阵间隙 中的原子。间隙原子可以是晶体中的正常原子离位产生，也 可以是外来杂质原子。
间隙原子
空位
图4-4 空位和间隙原子周围的弹性畸变
（3）杂质原子：
取代晶格中的原子，进入正常格点位置或进入间隙位置 的杂质原子。 如氧原子，在硅中主要占据间隙位置；特意掺入的B、 Al、Ga、P、As等杂质，则为替位原子，它们在硅中占据晶 格格点位置。原子半径较硅原子半径大的原子使晶格膨胀， 而原子半径比硅原子半径小的则使晶格收缩，造成晶格缺陷。
第四章 晶体缺陷
4.1 概述 4.2 晶体缺陷
第四章内容提要
1、点缺陷及点缺陷的运动：空位、间隙原子、替 位原子 2、线缺陷及位错运动：刃型位错、螺型位错、混 合型位错； 3、面缺陷：层错、表面、晶界和孪晶缺陷；
4、体缺陷：空隙与析出物。
概 述
前面章节都是就理想状态的完整晶体而 言，即晶体中所有的原子都在各自的平衡位 置，处于能量最低状态。然而在实际晶体中 原子的排列不可能这样规则和完整，而是或 多或少地存在离开理想的区域，出现不完整 性。正如我们日常生活中见到玉米棒上玉米 粒的分布。通常把这种偏离完整性的区域称 为晶体缺陷。
晶体缺陷：点缺陷,线缺陷,晶面缺陷,空穴Notes_2-34
3.091 – 固体化学导论课件（二）化学键* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *相关阅读资料：1．Pauling,L.,General Chemistry,W.H.Freeman and Co. San Francisco,1970,chapter 62．Gray H.B., Chemical Bonds, Benjamin, 19803．West, A.R.., Solid State Chemistry, J.Wiley, 19844．Borg, R.J. and G.R.Dienes, Physical Chemistry of Solids, Acdemic Press, 1992 5．Parker,S.B., Physical Chemistry Source Book, McGraw-Hill，1987* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *如第一章介绍，元素的电子结构只适用于独立的原子——这些原子隔了一定距离，在该距离内原子间无相互作用。
该条件对于凝聚相（如：固相和液相）永远得不到满足，这种情况只会出现在高真空下原子相隔很远的距离且无相互作用的情况下。
在正常情况下，尤其在前述的凝聚相中，原子间隔了一定距离，从本质上来看该距离由各自被填充的最外层电子轨道决定。
每当两个或两可以上原子的外电子壳层相互靠近时（部分发生重叠），便存在相互作用势。
当电子重组能够降低体系能量时，自发反应（包括电子轨道的重组和/或电子从一个原子向另一个原子的转移）将会发生。
这意味着彼此作用的驱动力和电子分布结构的重排在大多数（但不是所有）情况下通过向环境释放热（一种能量）表现出来。
晶体的缺陷
第四章 晶体的缺陷
4．1 晶体缺陷的基本类型
晶体缺陷按几何形态分，有点缺陷、线缺陷和面缺陷
4.1.1 点缺陷
( 1)．弗仑克尔(Frenkel)缺陷 正常格点上的原子，无时无刻 不在作围绕平衡点的振动．由 于存在热振动的涨落，振幅达 的原子就会摆脱平衡位置而进 入原子间隙位置．这种由一个 正常原子同时产生一个填隙原 子和一个空穴的缺陷称为弗仑 克尔缺陷。
τ1：空位从一个格点跳到相邻格点所需等待的时间 τ2：填隙从一个间隙跳到下一个间隙所需等待的时间
假设τ2》τ1， 与空位相邻的原子跳入空位所要等待的时间
可得出单位时间内一个原子由正常格点跳到间隙位置变 成填隙原子的几率为
当τ1》τ2时，即空位从一个格点跳到相邻格点所需等 待的时间比填隙原子从—个间隙位经跳到相邻间隙位置 所需等待的时间长得多时，可以近似把空位看作相对静 止．由类似的分析可得
从N个院子中取出n个原子形成n个空位的可能方式数目
N! W N n 形成间隙院子的方式数目为
' N ! W1'' ' N n !n!
有缺陷后晶格的微观状态数目为
' N ! N ! W W1'W1''W0 ' N n !N n(n!) 2
4．3 热缺陷的统计理论
4.3.1 热缺陷的产生几率
弗仑克尔缺陷和肖持基缺陷，存在产生、运动 和复合问题． 当温度一定时，热缺陷的产生和复合达到平衡， 热缺陷的统计平均数目为一定值，热缺陷在晶体内均 匀分布．设晶体是由N个原子构成，空位数目为nl，填 隙原子数目为n2； P代表在单位时间内，一个正常格点 上的原子跳到间隙位置的几率，τ＝l／P代表一个正常 格点上的原子成为填隙原子所需等待的时间．
4．1 晶体缺陷的基本类型
晶体缺陷按几何形态分，有点缺陷、线缺陷和面缺陷
4.1.1 点缺陷
( 1)．弗仑克尔(Frenkel)缺陷 正常格点上的原子，无时无刻 不在作围绕平衡点的振动．由 于存在热振动的涨落，振幅达 的原子就会摆脱平衡位置而进 入原子间隙位置．这种由一个 正常原子同时产生一个填隙原 子和一个空穴的缺陷称为弗仑 克尔缺陷。
τ1：空位从一个格点跳到相邻格点所需等待的时间 τ2：填隙从一个间隙跳到下一个间隙所需等待的时间
假设τ2》τ1， 与空位相邻的原子跳入空位所要等待的时间
可得出单位时间内一个原子由正常格点跳到间隙位置变 成填隙原子的几率为
当τ1》τ2时，即空位从一个格点跳到相邻格点所需等 待的时间比填隙原子从—个间隙位经跳到相邻间隙位置 所需等待的时间长得多时，可以近似把空位看作相对静 止．由类似的分析可得
从N个院子中取出n个原子形成n个空位的可能方式数目
N! W N n 形成间隙院子的方式数目为
' N ! W1'' ' N n !n!
有缺陷后晶格的微观状态数目为
' N ! N ! W W1'W1''W0 ' N n !N n(n!) 2
4．3 热缺陷的统计理论
4.3.1 热缺陷的产生几率
弗仑克尔缺陷和肖持基缺陷，存在产生、运动 和复合问题． 当温度一定时，热缺陷的产生和复合达到平衡， 热缺陷的统计平均数目为一定值，热缺陷在晶体内均 匀分布．设晶体是由N个原子构成，空位数目为nl，填 隙原子数目为n2； P代表在单位时间内，一个正常格点 上的原子跳到间隙位置的几率，τ＝l／P代表一个正常 格点上的原子成为填隙原子所需等待的时间．
晶体缺陷
杂质原子可形成间隙原子和替位原子
固溶体是以某一组元为溶剂，在其晶体点阵中溶 入其他组元原子（溶质原子）所形成的均匀混合 的固态溶体，它保持着溶剂的晶体结构类型。
固溶度:硅中能容纳杂质的最大数目 影响固溶度的因素有很多,主要有以下几个因素: ①杂质的种类。硅与杂质原子的晶体结构相同时， 杂质原子就可以连续不断地置换硅原子。如果两 种原子的晶体结构类型不同，固溶度是有限的。
一般把多出的半原子面在滑移面上边的称为正刃 型位错，记为“┻”；而把多出在下边的称为负 刃型位错，记为“┳”。正、负之分只具相对意 义而无本质的区别。
刃位错的几何特征:
位错线与原子滑移方向相垂直；
滑移面上部分位错线周围原子受压应力作用，原 子间距小于正常晶格间距； 滑移面下部分位错线周围原子受张应力作用，原 子间距大于正常晶格间距。
根据晶体缺陷的几何特征，可以分为四类：
点缺陷：其特征是在三维空间的各个方面上尺寸都很小， 尺寸范围约为一个或几个原子尺度， 故称零维缺陷，包 括空位、间隙原子、杂质或溶质原子等； 线缺陷：其特征是在两个方向上尺寸很小，另外一个方向 上延伸较长，也称一维缺陷，如各类位错；
面缺陷：其特征是在一个方向上尺寸很小，另外两个方向 上扩展很大，也称二维缺陷．晶界、相界、孪晶界和堆垛 层错等都属于面缺陷。
位错的爬升
位错爬升是靠原子或空位的转移来实现的。当原 子从多余半原子面下端转移到别处，或空位从别 处转移到半原子面下端时，位错线便向上爬升， 即正爬升；反之，当原子从别处转移到多余半原 子面下端时，或空位从这里转移到别处去时，位 错线就向下爬升，即负爬升。
刃位错爬升的实质就是构成刃位错的多余半原子 面的扩大或缩小。
位错运动不引起晶体体积的变化，这类运动称为位错的守 恒运动（滑移） 位错运动引起晶体体积的变化，这类运动称为位错的非守 恒运动（爬升）
固溶体是以某一组元为溶剂，在其晶体点阵中溶 入其他组元原子（溶质原子）所形成的均匀混合 的固态溶体，它保持着溶剂的晶体结构类型。
固溶度:硅中能容纳杂质的最大数目 影响固溶度的因素有很多,主要有以下几个因素: ①杂质的种类。硅与杂质原子的晶体结构相同时， 杂质原子就可以连续不断地置换硅原子。如果两 种原子的晶体结构类型不同，固溶度是有限的。
一般把多出的半原子面在滑移面上边的称为正刃 型位错，记为“┻”；而把多出在下边的称为负 刃型位错，记为“┳”。正、负之分只具相对意 义而无本质的区别。
刃位错的几何特征:
位错线与原子滑移方向相垂直；
滑移面上部分位错线周围原子受压应力作用，原 子间距小于正常晶格间距； 滑移面下部分位错线周围原子受张应力作用，原 子间距大于正常晶格间距。
根据晶体缺陷的几何特征，可以分为四类：
点缺陷：其特征是在三维空间的各个方面上尺寸都很小， 尺寸范围约为一个或几个原子尺度， 故称零维缺陷，包 括空位、间隙原子、杂质或溶质原子等； 线缺陷：其特征是在两个方向上尺寸很小，另外一个方向 上延伸较长，也称一维缺陷，如各类位错；
面缺陷：其特征是在一个方向上尺寸很小，另外两个方向 上扩展很大，也称二维缺陷．晶界、相界、孪晶界和堆垛 层错等都属于面缺陷。
位错的爬升
位错爬升是靠原子或空位的转移来实现的。当原 子从多余半原子面下端转移到别处，或空位从别 处转移到半原子面下端时，位错线便向上爬升， 即正爬升；反之，当原子从别处转移到多余半原 子面下端时，或空位从这里转移到别处去时，位 错线就向下爬升，即负爬升。
刃位错爬升的实质就是构成刃位错的多余半原子 面的扩大或缩小。
位错运动不引起晶体体积的变化，这类运动称为位错的守 恒运动（滑移） 位错运动引起晶体体积的变化，这类运动称为位错的非守 恒运动（爬升）
第四章 晶体缺陷与缺陷运动
第四章晶体缺陷与缺陷运动§4.1 晶体缺陷的基本类型§4.2 位错缺陷的性质、晶体滑移的本质§4.3 热缺陷数目的统计平衡理论§4.4 热缺陷的运动、产生和复合§4.5 晶体中的扩散过程§4.6 离子晶体中的点缺陷与导电性前言理想晶体的主要特征是原子(或分子)的严格规则排列、周期性实际晶体中的原子排列会由于各种原因或多或少地偏离严格的周期性，存在着偏离了理想晶体结构的区域，于是就形成了晶体的缺陷。
晶体中虽然存在各种各样的缺陷，但实际在晶体中偏离平衡位置的原子数目很少（相对于晶体原子总数），在最严重的情况下，一般不会超过原子总数的万分之一，因而实际晶体结构从整体上看还是比较完整的。
缺陷——偏离了晶体周期性排列的局部区域。
前言（续）晶体中缺陷的种类很多，它们分别影响着晶体的力学、热学、电学、光学等各方面的性质。
然而，尽管在晶体中缺陷的数目很少，它们的产生和发展、运动和相互作用、以及合并和消失，对晶体的性能有重要的影响。
因此，晶体缺陷是固体物理中一个重要的研究领域，它对于研究和理解一些不能用完整晶体理论解释和理解的现象具有重要的意义。
例如：塑性与强度、扩散、相变、再结晶、离子电导以及半导体的缺陷导电等现象。
§4.1 晶体缺陷的基本类型一、点缺陷点缺陷——发生在一个或几个晶格常数范围内的缺陷。
如：空位、填隙原子、杂质原子等。
这些空位、填隙原子是由热起伏原因而产生的，所以又称为热缺陷。
晶体中存在的缺陷种类很多，但由于晶体中的晶体结构具有规律性，因此晶体中实际出现缺陷的类型也不是无限制的。
根据晶体缺陷在空间延伸的线度，晶体缺陷可分为点缺陷、线缺陷、面缺陷和体缺陷。
几种重要的点缺陷：1）弗仑克尔缺陷和肖脱基缺陷原子（或离子）在格点平衡位置附近振动，由于存在这样的热振动的能量涨落，使得当某一原子能量大到某一程度时，原子就会克服平衡位置势阱的束缚，脱离格点，而到达邻近的原子空隙中，当它失去多余动能后，就会被束缚在那里，这样产生一个暂时的空位和一个暂时的填隙原子，当又经过一段时间后，填隙原子会与空位相遇，并同空位复合；也有可能跳到较远的间隙中去或跳到晶体边界上去。
大学材料科学基础第四章晶体缺陷
Point defects: (a) vacancy, (b) interstitial atom, © small substitutional atom, (d) large substitutional atom, (e) Frenkel defect-ionic cystals (f) Schottky defect- ionic crystals. All of these defects disrupt the perfect arrangement of the surrounding atoms.
第一节 点缺陷
一、点缺陷的类型 1．点缺陷的概念 指在三维方向上尺寸都很小的原子错排区 域，不能理解为一个几何点。
(1) vacancy; (2) selfinterstitial; (3) interstitial impurity; (4), (5) substitutional impurities. The arrows show the local stresses introduced by the point defects.
3830 6480 10960 2630
0.786 0.49 2.75 0.393
2．位错学说的提出
图5 位错滑动模型
位错理论发展进程 1934年，Talay和Orowa 度低于理论强度的现象。 1939 1939年，Burgers提出用柏氏矢量来表征位错 Burgers 类型，为用数学方法处理位错奠定了基础。 1947年，Cottrell提出柯氏气团钉扎模型，成 功地解释了低碳钢的屈服现象。 1950年，Frank和Read提出金属塑性变形中位 错增殖机制，即Frank－Read位错源学说。
刃型位错柏氏矢量确定
晶体中的点缺陷与线缺陷第二讲
式中 G为形成1摩尔弗仑克尔缺陷的自由焓变化。
（2）质量平衡：与化学反应方程式相同，缺 陷反应方程式两边的质量应该相等。需要注 意的是缺陷符号的右下标表示缺陷所在的位 置，对质量平衡无影响。（V的质量=0）
（3）电中性：电中性要求缺陷反应方程式两 边的有效电荷数必须相等，晶体必须保持电 中性 。
2. 缺陷反应实例
（1）杂质（组成）缺陷反应方程式 ──杂质在基质 中的溶解过程 杂质进入基质晶体时，一般遵循杂质的正负 离子分别进入基质的正负离子位置的原则，这样 基质晶体的晶格畸变小，缺陷容易形成。在不等 价替换时，会产生间隙质点或空位。
注意：
一． 位置关系强调形成缺陷时，基质晶体中正负离子格点 数之比保持不变，并非原子个数比保持不变。 二． 在上述各种缺陷符号中，VM、VX、MM、XX、MX、 XM等位于正常格点上，对格点数的多少无影响，而
Mi、Xi、e，、h· 等不在正常格点上，对格点数的多少
也无影响。 三． 形成缺陷时，基质晶体中的原子数会发生变化，外加 杂质进入基质晶体时，系统原子数增加，晶体尺寸增 大；基质中原子逃逸到周围介质中时，晶体尺寸减小。
例1· 写出NaF加入YF3中的缺陷反应方程式
以正离子为基准，反应方程式为：
NaF Na Y '' FF 2V
YF3
F
以负离子为基准，反应方程式为：
例2· 写出CaCl2加入KCl中的缺陷反应方程式
以正离子为基准，缺陷反应方程式为：
CaCl2 Ca ClCl Cli '
三、热缺陷浓度的计算
在一定温度下，热缺陷是处在不断地产生和消失的过程 中，当单位时间产生和复合而消失的数目相等时，系统 达到平衡，热缺陷的数目保持不变。
材料物理化学-第四章 晶体的点缺陷与线缺陷
第四章晶体结构缺陷晶体缺陷的产生与晶体的生长条件，晶体中原子的热运动以及对晶体的加工工艺等有关。
事实上，任何晶体即使在绝对零度都含有缺陷，自然界中理想晶体是不存在的。
既然存在着对称性的缺陷，平移操作不能复制全部格点，那么空间点阵的概念似乎不能用到含有缺陷的晶体中，亦即晶体理论的基石不再牢固。
但缺陷的存在只是晶体中局部的破坏。
作为一种统计，一种近似，一种几何模型，缺陷存在的比例毕竟只是一个很小的量(这指的是通常的情况），从占有原子百分数来说，晶体中的缺陷在数量上是微不足道的。
因此，整体上看，可以认为一般晶体是近乎完整的。
因而对于实际晶体中存在的缺陷可以用确切的几何图形来描述，这一点非常重要。
它是我们今后讨论缺陷形态的基本出发点。
事实上，把晶体看成近乎完整的并不是一种凭空的假设，大量的实验事实（X射线及电子衍射实验提供了足够的实验证据）都支持这种近乎理想的对称性。
当然不能否认，当缺陷比例过高以致于这种“完整性”无论从实验或从理论上都不复存在时，此时的固体便不能用空间点阵来描述，也不能被称之为晶体。
这便是材料中的另一大类别：非晶态固体。
对非晶固体和晶体，无论在原子结构理论上或是材料学家对它们完美性追求的哲学思想上都存在着很大差异，有兴趣的同学可以对此作进一步的理解。
缺陷是晶体理论中最重要的内容之一。
晶体的生长、性能以及加工等无一不与缺陷紧密相关。
因为正是这千分之一、万分之一的缺陷，对晶体的性能产生了不容小视的作用。
这种影响无论在微观或宏观上都具有相当的重要性。
4.1热力学平衡态点缺陷4.1.1 热缺陷的基本类型点缺陷形成的热力学平衡当晶体的温度高于绝对零度时，晶格内原子吸收能量，在其平衡位置附近温度越高，热振动幅度加大，原子的平均动能随之增加。
热振动的原子在某一瞬间可以获得较大的能量，挣脱周围质点的作用，离开平衡位置，进入到晶格内的其它位置，而在原来的平衡格点位置上留下空位。
这种由于晶体内部质点热运动而形成的缺陷称为热缺陷。
固体物理第四章_晶体的缺陷
刃位错
A
未滑动的晶面
EC
F
B
滑动前的晶格
D
刃位错的晶格
刃位错： F原子链。 EF是晶体的挤压区与未挤压区的分界线：
F以下原子间距变大，原子间有较强吸引力；
F的左右晶格被挤压，原子间的排斥力增大。
16
例：实际晶体的小角倾斜 晶体由倾斜角很小的两部分晶体结合而成。为了使 结合部的原子尽可能地规则排列，就得每隔一定距 离多生长出一层原子面，这些多生长出来的半截原 子面的顶端原子链就是刃错位。
添加Fe、Co、Mn等“硬性”添加物后，这些 原子占据Zr或Ti的格点，显著提高该铁电材料的 机械品质因数。
9
4、色心 能吸收光的点缺陷
完善的卤化碱晶体是无色透明的。众多的 色心缺陷能使晶体呈现一定的颜色。
例如：F心，把卤化碱晶体在相应的碱金 属蒸气中加热，然后骤冷到室温，则原来透明 的晶体就出现了颜色。
实验临界切应力比理 论值小的根源
30
2、螺位错的滑移 螺位错的滑移与刃位错的滑移相类似，只是螺位的 滑移方向与晶体所受切应力的方向相垂直。
BC原子 受到向 下的拉 力
螺位 错线 滑移
BC列原子受到右边原子的下拉力，BC原子有向下 位移的趋势，BC原子下移一定的距离； 使BC 变为螺错位。
31
二、螺位错与晶体生长
4
§4.1 晶体缺陷的基本类型
本章主要讨论单晶的缺陷：多晶体是由许多小晶粒 构成，每个晶粒可看成是小单晶。晶粒间界不仅原 子排列混乱，而且是杂质聚集的地方。因此晶粒间 界是一种性质复杂的晶体缺陷。
一、点缺陷
晶体中的填隙原子、空位、俘获电子的空位、杂质 原子等。这些缺陷约占一个原子尺寸，引起晶格周 期性在一到几个原胞范围内发生紊乱。
A
未滑动的晶面
EC
F
B
滑动前的晶格
D
刃位错的晶格
刃位错： F原子链。 EF是晶体的挤压区与未挤压区的分界线：
F以下原子间距变大，原子间有较强吸引力；
F的左右晶格被挤压，原子间的排斥力增大。
16
例：实际晶体的小角倾斜 晶体由倾斜角很小的两部分晶体结合而成。为了使 结合部的原子尽可能地规则排列，就得每隔一定距 离多生长出一层原子面，这些多生长出来的半截原 子面的顶端原子链就是刃错位。
添加Fe、Co、Mn等“硬性”添加物后，这些 原子占据Zr或Ti的格点，显著提高该铁电材料的 机械品质因数。
9
4、色心 能吸收光的点缺陷
完善的卤化碱晶体是无色透明的。众多的 色心缺陷能使晶体呈现一定的颜色。
例如：F心，把卤化碱晶体在相应的碱金 属蒸气中加热，然后骤冷到室温，则原来透明 的晶体就出现了颜色。
实验临界切应力比理 论值小的根源
30
2、螺位错的滑移 螺位错的滑移与刃位错的滑移相类似，只是螺位的 滑移方向与晶体所受切应力的方向相垂直。
BC原子 受到向 下的拉 力
螺位 错线 滑移
BC列原子受到右边原子的下拉力，BC原子有向下 位移的趋势，BC原子下移一定的距离； 使BC 变为螺错位。
31
二、螺位错与晶体生长
4
§4.1 晶体缺陷的基本类型
本章主要讨论单晶的缺陷：多晶体是由许多小晶粒 构成，每个晶粒可看成是小单晶。晶粒间界不仅原 子排列混乱，而且是杂质聚集的地方。因此晶粒间 界是一种性质复杂的晶体缺陷。
一、点缺陷
晶体中的填隙原子、空位、俘获电子的空位、杂质 原子等。这些缺陷约占一个原子尺寸，引起晶格周 期性在一到几个原胞范围内发生紊乱。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
摩尔肖特基缺陷的自由焓变化。
又[O]=1， [VCa''
]
1 34
exp(
G 3RT
)
Schottky缺陷： 例： MgO晶体
Mg Mg OO
VMg
V •• O
Mgs
Os
简写：0
VMg
V •• O
K s [VMg ][VO•• ]
[VMg ]
[VO•• ]
1
K2 s
Ks
K0
exp(
G f KT
)
[VMg
]
[VO•• ]
K
exp(
G f KT
)
若将缺陷浓度写成 n N ,并取N 1mol
则n K exp( G f ) 2KT
（2） 弗仑克尔缺陷浓度的计算
AgBr晶体形成弗仑克尔缺陷的反应方程式为：
AgAg Agi. VA' g
平衡常数K为：
K
[ Agi. ][VA'g ]
[ AgAg ]
式中 [AgAg]1。 又G=－RTlnK
[
Agi.
]
[VA' g
]
exp(
G 2RT
)
式中 G为形成1摩尔弗仑克尔缺陷的自由焓变化。
点缺陷的化学平衡
缺陷的产生和回复是动态平衡，可看作是一种化学平衡。
Franker缺陷：如AgBr晶体中
AgAg Vi Agi• VAg
KF
[ Agi • ][VAg ] [ AgAg ][Vi ]
2MgO Al2O3 2MgAl VO•• 2OO
(1－4)
3MgO Al2O3 2MgAl Mgi•• 3OO
(1－5)
（1－5〕较不合理。因为Mg2+进入间隙位置不易发生。
基本规律：
低价正离子占据高价正离子位置时，该位 置带有负电荷，为了保持电中性，会产生 负离子空位或间隙正离子。
高价正离子占据低价正离子位置时，该位 置带有正电荷，为了保持电中性，会产生 正离子空位或间隙负离子。
（2）热缺陷反应方程式
例3·MgO形成肖特基缺陷
MgO形成肖特基缺陷时，表面的Mg2+和O2-离子迁 移到表面新位置上，在晶体内部留下空位:
MgMg +OO
MgMg +OO
+
V'' Mg
VO
以零O（naught）代表无缺陷状态，则：
杂质进入基质晶体时，一般遵循杂质的正负 离子分别进入基质的正负离子位置的原则，这样 基质晶体的晶格畸变小，缺陷容易形成。在不等 价替换时，会产生间隙质点或空位。
例1·写出NaF加入YF3中的缺陷反应方程式
以正离子为基准，反应方程式为：
NaF
YF3
Na Y
''
FF
2V
• F
以负离子为基准，反应方程式为：
例2·写出CaCl2加入KCl中的缺陷反应方程式
以正离子为基准，缺陷反应方程式为：
CaCl2
KCl
Ca
• K
ClCl
Cli
'
以负离子为基准，则缺陷反应方程式为：
CaCl2
KCl
Ca
• K
VK
'
2ClCl
Ca2+进入晶格的间隙位置时：
CaCl2 KCl Cai•• 2VK 2ClCl
（2） MgO溶解到Al2O3晶格中
c
n
－ exp(
G s)
N
2kBT
△Gs为形成一对正负离子空位时系统自由焓的变化，△Gs>0 kB为玻尔兹曼因子常数，kB=1.38×10-23J/K
费仑克尔缺陷的成对出现 的，热缺陷浓度计算为：
c
n
－ exp(
G F)
N
2kBT
GF 为形成一对一个弗伦克尔缺陷时系统自由焓的变化，△Gs>0
注：对单质晶体 n / N exp( E ) kT
（2）质量平衡：与化学反应方程式相同，缺 陷反应方程式两边的质量应该相等。需要注 意的是缺陷符号的右下标表示缺陷所在的位 置，对质量平衡无影响。（V的质量=0）
（3）电中性：电中性要求缺陷反应方程式两 边的有效电荷数必须相等，晶体必须保持电 中性 。
2. 缺陷反应实例
（1）杂质（组成）缺陷反应方程式──杂质在基质 中的溶解过程
如：NaCl为1:1；TiO2为1:2；在氧不足的 气氛中制备氧化钛时，会形成TiO2-x， 此时Ti与O的原子比为1：2-x，但是位 置数之比仍然是 1:2，只是有x个氧空 位没有被氧原子点据而已。
注意：
一． 位置关系强调形成缺陷时，基质晶体中正负离子格点 数之比保持不变，并非原子个数比保持不变。
当缺陷浓度很小时，[Vi ] [ AgAg ] 1
因为填隙原子与空位成对出现，故有
[
Agi•
]
[V
Ag
]
K F [ Agi• ]2 K0 exp(G f / kT )
三、热缺陷浓度的计算
在一定温度下，热缺陷是处在不断地产生和消失的过程 中，当单位时间产生和复合而消失的数目相等时，系统 达到平衡，热缺陷的数目保持不变。
缺陷看作化学物质
热力学数据
化学反应
质量定律
热力学统计物理法
热缺陷浓度
化学平衡法
热力学统计物理方法计算热缺陷浓度
MX二元离子晶体Schottky 缺陷，热缺陷浓度计算为
二． 在上述各种缺陷符号中，VM、VX、MM、XX、MX、 XM等位于正常格点上，对格点数的多少无影响，而 Mi、Xi、e，、h·等不在正常格点上，对格点数的多少 也无影响。
三． 形成缺陷时，基质晶体中的原子数会发生变化，外加 杂质进入基质晶体时，系统原子数增加，晶体尺寸增 大；基质中原子逃逸到周围介质中时，晶体尺寸减小。
二、缺陷反应表示法
对于杂质缺陷而言，缺陷反应方程式的一般式：
1. 写缺陷反应方程式应遵循的原则
缺陷产生 复合 化学反应A B + C
三个原则：
（1）位置关系 （2）质量平衡 （3）电中性
（1）Байду номын сангаас置关系：
在化合物MaXb中，无论是否存在缺陷，其 正负离子位置数（即格点数）的之比始终 是一个常数a/b。
MgO形成肖特基缺陷：
O
V'' Mg
VO
例4·AgBr形成弗仑克尔缺陷
其 中 半 径 小 的 Ag+ 离 子 进 入 晶 格 间 隙 ， 在其格点上留下空位，方程式为：
AgAg Ag.i VA' g
一般规律：
当晶体中剩余空隙比较小，如NaCl型结构，容 易形成肖特基缺陷；当晶体中剩余空隙比较大时， 如萤石CaF2型结构等，容易产生弗仑克尔缺陷。
化学平衡方法计算热缺陷浓度
（1）MX2型晶体肖特基缺陷浓度的计算
CaF2晶体形成肖特基缺陷反应方程式为：
O VC'a' 2VF.
动态平衡
[VF. ] 2[VC''a ]
K [VC'a' ][VF. ]2 4[VCa'' ]3
[O]
[O]
因G=－RTlnK ，式中 R气体常数8.314， G为形成1