山东科技大学2015-2016高等数学期中考试试卷

合集下载

山东科技大学2015-2016高等数学期中考试试卷

f ( )
2 f ( ) 。 b 第 Nhomakorabea2 页/共
2 页
cos
4. 设
x ln 1 t 2 y arctan t
，求
d2y 。 dx 2
2
5. 设 y y ( x ) 由方程 e 6 xy x 1 0 所确定，求
y
y '' (0) 。
四、解答题（共 10 分）
设 f ( x ) ( x ) sin x ，其中 ( x ) 的一阶导数连续，且 (0) 0 ， (0) 0 ，试判断 f ( x ) 在
山东科技大学 2015—2016 学年第一学期
《高等数学》期中考试试卷
班级题号得分
一、填空题（每小题 5 分，共 15 分） 1. 设 lim ( x x 1 ax b) 0, 则 a _________， b ________。
x 2
姓名一二三四五总得分
3.已知 f (3) 2 ，则 lim
( A) 无穷小 (C ) 有界但不为无穷小
2. ( x )
( B ) 无穷大 ( D) 无界但不为无穷大
）
1 x ， ( x ) 1 3 x ，则当 x 1 时有（ 1 x
（A）是比高阶的无穷小
（B）是比低阶的无穷小
（C）与同阶无穷小，但不等价（D） ~ 3. sin x x
1 3 ) x R4 ( x) 其中 R4 ( x ) ( 6 cos 5 cos 5 （A）（B） x x 5! 5! sin 5 sin 5 （ C）（ D） x x （上述各式中介于 0 与 x 之间） 5! 5!

2015-2016学年度期中考试数学考卷-掌门1对1

第1页共4页 ◎ 第2页共4页2015-2016学年度期中考试数学考卷-掌门1对1全国Ⅱ卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题，共60分）一、选择题（本大题共12题，每小题5分）1．设集合}0)4)(1(|{},5,4,3,2,1{<--==x x x B A ，则B A ＝（） A.}4,3,2,1{ B.}3,2{ C.}3,2,1{ D.}4,3,2{2．已知a R ∈，则“2a >”是“22a a >”的（）A ．充分不必要条件 B．必要不充分条件C ．充要条件D ．既非充分也非必要条件3．已知函数⎩⎨⎧≤>=0,20,log )(3x x x xf x，则（）.A4．已知平面向量b a 与的夹角为）A ．1B ．2 D ．3 5．下列函数中，既是奇函数又是增函数的为（） A ．1y x =+ B ．3y x =-C ．||y x x = 6．设等差数列{}n a 的前项和为n S ，已知10100S =，则29a a +=（）．A．100 B ．40 C ．12 7．将函数()()ϕ+=xx f 2sin 的图象向左平移所得到的函数图象关于y轴对称，则ϕ的一个可能取值为（）A ．0 C 8．函数()ln xf x xe =+（e 为自然对数的底数）的零点所在的区间是（） A．()1,e D ．(),e +∞ 9图所示，则ω，φ的值分别是（） A ．2．2．4．410．函数x x x y sin cos +=的图象大致为( )11．在等差数列{}n a 中，前四项之和为20，最后四项之和为60，前n 项之和是100，则项数n 为（）A ．9B ．10C ．11D ．1212．已知函数)(x f 满足则当0>x 时，)(x f （）A ．有极大值，无极小值B ．有极小值，无极大值C ．既有极大值，也有极小值D ．既无极大值，也无极小值第3页共4页 ◎ 第4页共4页第II 卷（非选择题，共90分）二、填空题（共4个小题，每题5分）1314．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知，，则角B= ．15．设,x y R ∈，向量(,1)a x = ，(1,)b y =，(2,4)c =- 且a b ⊥ ，b ∥c ，______________．16．已知函数()f x 满足，且12,x x 均大于e ，其中e 为自然对数的底数，12()()1f x f x +=，则12()f ex x 的最小值为．三、解答题（解答应写出文字说明，证明过程或演算步骤） 17．（本题满分10分）在△ABC 中，角A ，B ，C 的对边分别为，b=5，△ABC 的面积为．（1）求a ，c 的值；（2）求的值． 18．（本小题满分12分）已知}{n a 是等差数列，满足143,,12a a == ，数列}{n b 满足20,441==b b ，且}{n n a b -为等比数列．（1）求数列}{}{n n b a 和的通项公式；（2）求数列}{n b 的前n 项和．19．（本题满分12,x ∈R ．（Ⅰ）求函数()f x 的最小正周期与单调增区间；（Ⅱ）求函数()f x 在 20．（本题满分12分）已知函数2()2ln ()f x ax x x a R =+-∈ ．（Ⅰ）若4a =，求函数()f x 的极值；（Ⅱ）若'()f x 在区间(0,1)内有唯一的零点0x ，求a 的取值范围．21．（本小题满分12分）已知函数()ln ()f x x a x a R =-∈ （Ⅰ）当2a =时，求曲线()y f x =在点(1,(1))A f 处的切线方程；（Ⅱ）讨论函数()f x 单调区间22．（本小题满分12分）已知函数()e x f x x a -=+⋅．（Ⅰ）当2e a =时，求()f x 在区间[1,3]上的最小值；（Ⅱ）求证：存在实数0[3,3]x ∈-，有0()f x a >．本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

山东科技大学20152016学年第一学期期末考试安排表

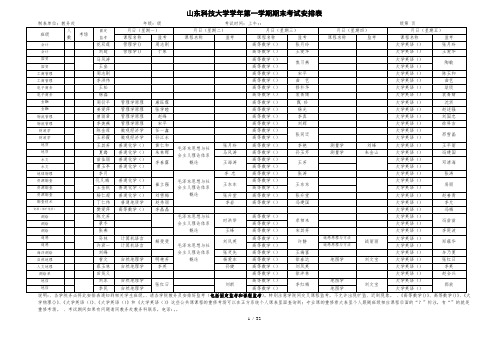
数监考课程名称监考课程名称监考课程名称监考课程名称监考课程名称监考会计花双莲管理学() 周志刚高等数学（）张月玲大学英语（）张月玲会计刘超管理学() 于泉高等数学（）王爱华大学英语（）王爱华国贸马风涛高等数学（）焦习燕大学英语（）陶敏国贸王垒高等数学（）大学英语（）工商管理周志刚高等数学（）宋平大学英语（）陈玉和工商管理李洪伟高等数学（）曲艺大学英语（）曲艺电子商务王松高等数学（）修朴华大学英语（）耿琰电子商务杨磊高等数学（）袁菁婧大学英语（）袁菁婧金融周衍平管理学原理康旺霖高等数学（）甄珍大学英语（）沈圳金融姜爱萍管理学原理张学睦高等数学（）杨光大学英语（）赵述强物流管理曾丽君管理学原理赵峰高等数学（）李真大学英语（）刘国忠物流管理李美燕管理学原理宋平高等数学（）刘辉大学英语（）徐科吉财政学陈金库微观经济学任一鑫高等数学（）张同迁大学英语（）邢雪晶财政学王彩霞微观经济学孙江永高等数学（）大学英语（）地质王其芳普通化学（）黄仁和毛泽东思想与社会主义理论体系概论张月玲高等数学（）李艳测量学刘峰大学英语（）王平丽地质夏璐普通化学（）朱林晖马风涛高等数学（）孙玉芹测量学朱金山大学英语（）冯建国水文苗佳丽普通化学（）李春露王海涛高等数学（）王芳大学英语（）邓清海水文曹玉亭普通化学（）高等数学（）大学英语（）地球物理李月毛泽东思想与社会主义理论体系概论李忠高等数学（）张涛大学英语（）张涛资源勘查孔凡梅普通化学（）崔立强王东东高等数学（）王东东大学英语（）房丽资源勘查王金凯普通化学（）高等数学（）大学英语（）资源勘查杨仁超普通化学（）刘雪梅张升堂高等数学（）张升堂大学英语（）赵善青勘查技术丁仁伟普通地质学赵秀丽李岩高等数学（）冯建国大学英语（）李允资源（煤矿地质）樊爱萍高等数学（）李晶晶大学英语（）冯梅测绘陈允芳毛泽东思想与社会主义理论体系概论时洪举高等数学（）卓相来大学英语（）冯苗苗测绘景冬高等数学（）大学英语（）测绘张燕王峰高等数学（）宋其芳大学英语（）李延波遥感孙林计算机语言解斐斐毛泽东思想与社会主义理论体系概论刘凤英高等数学（）许静遥感原理与方法战丽丽大学英语（）郑蕴华遥感许君一计算机语言高等数学（）遥感原理与方法大学英语（）海洋测绘刘峰张灵先高等数学（）王瑞富大学英语（）牟乃夏自然地理曾文自然地理学明艳芳杨爱东高等数学（）徐春达地图学刘文宝大学英语（）张红日人文地理蔡玉林自然地理学李英孙健高等数学（）刘凤英大学英语（）李英测绘单田茂义高等数学（）徐泮林大学英语（）赵会兴地信刘冰自然地理学张红日刘新高等数学（）李红梅地图学刘文宝大学英语（）郭放地信季民自然地理学高等数学（）地图学大学英语（）说明：、各学院务必将此安排表通知到相关学生班级。

2016-2017高等数学(2-1)期中考试试卷答案(3)

2016—2017学年第一学期《高等数学（2-1）》期中考试卷答案( 工科类)专业班级姓名学号开课系室基础数学系考试日期2016年11 月19 日注意事项：1．请在试卷正面答题，反面及附页可作草稿纸；2．答题时请注意书写清楚，保持卷面清洁；3．本试卷共七道大题，满分100分；试卷本请勿撕开，否则作废；4. 本试卷正文共7页。

正确 ? 在题后的括号内打“√”或“ ”，如果正确，请给出证明，如果不正确，请举一个反例进行说明。

1．如果数列{x n }有界，则数列{x n }收敛．（ ╳ ）………… 2分反例：数列 {x n }={(−1)n }有界，但是不收敛. ………… 2分 2．如果lim x→0|f(x)|=0，则lim x→0f(x)=0．（ √ ）………… 2分证明：∀ε>0, 由lim x→0|f(x)|=0，可得 ∃δ>0, 当x ∈U o (0,δ) 时，||f (x )|−0|<ε,即|f (x )−0|<ε, 故lim x→0f(x)=0. (2)3. 如果函数f (x )在x 0可导，则|f(x)|在x 0也可导．（ ╳ ）………… 2分反例：f (x )=x , 在x =0处可导，但|f(x)|在x =0处不可导． ………… 2分4. 如果函数f (x )在x 0处既存在左导数又存在右导数，则函数f(x)在x 0处连续．（ √ ） ………… 2分证明：由f′+(x 0)=lim x→x 0+f (x )−f(x 0)x−x 0可知lim x→x 0+f (x )=f(x 0),由f′−(x 0)=lim x→x 0−f (x )−f(x 0)x−x 0可知lim x→x 0−f (x )=f(x 0),故lim x→x 0f (x )=f(x 0), 即函数连续. ………… 2分1．求极限lim n→∞(1+n)1n.由海涅定理可得：原式=lim x→+∞(1+x)1x ………… 2分=lim x→+∞eln(1+x)x………… 2分=elimx→+∞11+x=e 0=1 (2)2. 求极限xx x x ⎪⎭⎫⎝⎛-+∞→3212lim .原式=lim x→∞(1+42x−3)2x−34∙4x2x−3………… 4分=e 2 ………… 2分3. 求极限1e 1cos lim 2--→x x x .原式=limx→0√cos x−1x 2 ………… 2分=limx→0−sin x 2√cos x2x=lim 4√cos x−１４…………三．（共3小题，每小题6分，共计18分）1．设函数⎩⎨⎧>+≤-+=1,1,1)(3x b ax x x x x f 在1=x 处可导，求常数a 和b .解. 因为函数在x=1处可导，所以连续，故lim x→1−(x 3+x −1)=1=lim x→1+(ax +b )=a +b ………… 2分因为在x=1处可导，可得：f +′(1)= f −′(1) ………… 2分而： f +′(1)=lim x→1+f (x )−f(1)x−1=a f −′(1)=lim x→1−f (x )−f(1)x−1=4故 a =4 , 从而ｂ＝−３ ………… 2分 2．指出函数325)(-=x x x f 的间断点及其类型．解. x=3 是间断点. ………… 3分因为lim x→3+f (x )=5limx→3+2x x−3=+∞所以x=3是无穷间断点. ………… 3分3. 设方程43=+x y y x (x >0,y >0)确定了隐函数y =y (x )，求)1(y '.解. 方程变形得：3e y ln x +e x ln y =4 ………… 2分两边同时关于x 求导得：3e y ln x (y ′ln x +yx )+e x ln y (ln y +xy y ′)=0 ………… 2分把x=1带入原方程可得y=1，把x=1,y=1带入上式可得：y ′(1)=−4 ………… 2分四．（共2小题，每小题6分，共计12分）1．求曲线2211x x e y e--+=-的所有渐近线方程．解. 因为 lim x→01+e −x21−e −x2=∞ 所以x=0是铅直渐近线.………… ３分a =limx→±∞f(x)x=0 b =lim x→±∞(f (x )−ax)=1所以有水平渐近线：y=1 ………… ３分2．设函数x x x f sin )1()(2+=，求f (50)(π2) ．解. 由莱布尼兹公式可得：f (50)(x )=(x 2+1)∙sin (x +50∙π2)+50∙2x ∙sin (x +49∙π2)+50∙492∙2∙sin(x +48∙π2)=−(x 2+1)∙sin x +100x ∙sin (x +π2)+2450∙sin x (4)所以f (50)(π2)=−(π24+1)+2450 ………… 2分1. 设参数方程⎪⎩⎪⎨⎧+=+=t y tt x tsin e 3确定了函数y =y (x )，求dx dy ，22dx y d . 解. dxdy=e t +cos t 3t 2+1 ………… 2分22dxyd =d dt (e t +cos t 3t 2+1)∙dt dx =(e t −sin t)(3t 2+1)−6t(e t +cos t)(3t 2+1)2∙13t 2+1 =(e t −sin t)(3t 2+1)−6t(e t +cos t)(3t 2+1)3 (4)2. 求()()32132--=x x x f 的单调区间和极值．解. 定义域是:R =(−∞,+∞)f ′(x )=23−23(x −1)−13x=1是不可导点，f ′(x )=0可得x=2 ………… 2分列表如下：极大值：f (1)=23 极小值：f (2)=13 ………… 1分1．讨论函数y =xe x 的凸性区间和拐点．解. y ′=(x +1)e x ,y ′′=(x +2)e x令y ′′=0, 得x =−2 ………… 2分列表如下：拐点是：(−2,−2e −2) ………… 1分 2．证明：当x <1时，e x ≤11−x．证明. 令 f (x )=e x (1−x), ………… 2分则 f ′(x )=−xe x =0,可得x=0所以当x <0时，f ′(x )>0, 当0<x <1时,f ′(x )<0 ………… 2分故函数在x=0处取得最大值，即f (x )≤f (0)=1 综上可得当x <1时，e x ≤11−x． (2)七．（共2小题，每小题6分，共计12分）1．加热一块半径为2cm 的金属圆形薄板，其半径以0.01cm/s 的速率增大，求当半径为2.1cm 时，面积的变化率．解. 设t 时刻圆形薄板得半径为r, 面积为S(r)则 S (r )=π∙r 2 ………… 2分两边关于t 求导可得 dSdt =2πr drdt ………… 2分所以当r=2.1时，ｄＳｄｔ＝２π∙２．１∙０．０１＝０．０４２π ｃｍ２／ｓ3．设函数f (x )在[0,b]上连续，在(0,b)内可导，且f (b )=0，证明存在一点ξ∈(0,b),使得f (ξ)+ξ∙f′(ξ)=0．解．令Ｆ(ｘ)＝ｘｆ（ｘ）， ………… 2分则Ｆ(ｘ)在［０，ｂ］上连续，在（０，ｂ）内可导，并且Ｆ(０)＝Ｆ(ｂ)＝０， ………… 2分由罗尔定理可知，∃ξ∈（０，ｂ）使得Ｆ′(ξ)＝０即f (ξ)+ξ∙f′(ξ)=0． ………… 2分。

高等数学大一上学期期中考试题-参考模板

山东大学2014-2015学年第一学期期中考试《高等数学（Ⅰ）》试卷姓名：________一、选择题（每题2分，共16分）1、下列极限存在的是…………………………………………………………( )（A ） x x 21lim ∞→（B ） 1310lim -→x x （C ） x e x 1lim ∞→ （D ） x x 3lim ∞→ 2x 22x 0-ax +bx+1x a b e →当时，若（）是比高阶的无穷小，则，的值是（）…( a )（A ）1／2， 1 （B ） 1，1（C ）-1／2， 1 （D ） -1，13、,0)(lim >=→A x f a x ,0)(lim <=→B x g ax 则下列正确的是…………………………( ) （A ） f (x )>0, （B ） g(x )<0, （C ） f (x )>g (x ) （D ）存在a 的一个空心邻域，使f (x )g (x )<0。

4、已知， ,2lim )(0=→x x f x 则=→)2x (sin3x 0lim f x ………………………………………………( )（A ） 2/3, （B ） 3/2 （C ） 3/4 （D ）不能确定。

5、函数f(x)在[a ，b]上有定义，在（a ，b ）内可导，则（）（A ）当f （a ）f （b ）＜0时，存在ξ∈（a ，b ），使f （ξ）=0（B ）对任何ζ∈（a ，b ），有（C ）当f （a ）=f （b ）时，存在ξ∈（a ，b ），使f ¹（ξ）=0（D ）存在ξ∈（a ，b ），使f （a ）-f （b ）=f ¹（ξ）（b-a ）6、下列对于函数y =x cos x 的叙述，正确的一个是………………………………………()（A ）有界，且是当x 趋于无穷时的无穷大，（B ）有界，但不是当x 趋于无穷时的无穷大，（C ）无界，且是当x 趋于无穷时的无穷大，（D ）无界，但不是当x 趋于无穷时的无穷大。

15~16高数期中考

(
oe
r
.
,
3
1 Bd x
y' =
x
( u r »)
>
t
2
/
T eo
)
< x 1 JL o · e 1
:1 I
c ,
a i f *o )
@ 354 b
.
,
壮舌汝 ·
·
乙
··
Lw
¥
1A
::
00
71 po
1乇亡 Q 呻 w /
飞弦直芍
币小结牡代 ·
A
0)= 0
五某地区防空洞的截面拟建成矩形加半圆 ( 见图) 截面的面积为 6 2 问底
则存在 C E (0, 1) 使 F (C) = 0
( 12 分)
> W W / e t * ,
Cor Ï J
· ·+ ° l+ x
六 +
·
千均
·!
彐
,
¢ I L Ë t
竹他 I r
°"
r{
4
3 当X
O 时 (1 C0 Sx ) l n (1+ 3× Z ) 是比X a r c t a n x ( n 为正整数 ) 高阶的无穷小而 X a r c t a n c x
是比 e 1高阶的无穷小则 n - 2
2
4 设 f (x ) =
, 贝rj l im f ( x )=
;:
lim f (x )=
睾 X ) 求
6
h
3× + 2
" 0旧
求y
:::
·
= y : =j

山东省平度市四校15—16学年上学期高一期中联考数学试题(扫描版)(附答案) (1)

2015—2016学年度第一学期第一学段学分认定高一数学试题 2015.11一、选择题：本大题共10小题．每小题5分，共50分．B A D BC CD C A A二、填空题：本大题共5小题，每小题5分，共25分． 11. 1412. 21x x -++ 13.1 14. [)(0,)0+∞+∞或写成， 15. ①③ 三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤．16.解：（1） =B {}x x x 2873|-≥-={}3|≥x x ………………………2分∴=B A {}42|<≤x x {}3|≥x x= {}43|<≤x x ………………………………………………4分（2）R B =ð{}3|<x x ……………………………………………………6分∴()R A B ð={}42|<≤x x {}3|<x x = {}4|<x x ……………………8分（3）集合=A {}42|<≤x x ,=C {}a x x <|，且A C ⊆∴4≥a ……12分17.解：…………………………………6分（2）(-（观察图象或根据解析式求解均可）…………………………………12分 18．解：（1）210321627198391113442ππ----+=--+-=-（（）（……………………………6分（2）71235555210025731710002542214log log log log .log log .-+++=-+++=…………………………………12分 19.解： 22(1)1,()22(1)1,a f x x x x =-=-+=-+当时对称轴为min max 1,()(1)1,()(5)37x f x f f x f ====-=∴max m ()37,()1in f x f x == …………………………………（6分）（2）对称轴为。

山东省烟台市2015-2016学年高一下学期期中学段检测数学试题含答案(1)

2015-2016学年度第二学期学段检测高一数学本试卷共4页，分第I 卷(选择题）和第Ⅱ卷（非选择题）两部分，共150分,考试时间120分钟.参考公式：如果事件A,B 互斥，那么P （A+B ）=P(A ）+P(B ）。

()2211211))((ˆx n x yx n y x x x y y x x bi ni i i ni i ni i i ni -∑-∑=-∑--∑=====，a x b y+=第I 卷（选择题共50分）注意事项：1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2.每题选出答案后，用2B 铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后,在改涂在其他答案标号。

一．选择题：本大题共10小题,每小题5分，共50分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1。

有20 位同学，编号从1至20，现在从中抽取4人作问卷调查,用系统抽样的方法确定的编号可能是A 。

5,10，15,20 B.2，6，10，14, C 。

2，4，6，8 D 。

5，8,11,14 2.圆0166822=++-+y x y x与圆1622=+y x 的位置关系是A 。

相交B 。

内切C 。

相离 D. 外切 3。

样本中共有五个个体，其值分别为a ，0，1，2，3,若该样本的平均值为1，则样本的标准差为A 。

56B 。

56 C 。

2 D 。

24。

某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示,规定不低于90分为优秀等级,则该校学生优秀等级，则该校学生优秀等级的人数是A.300B.30 C 。

150 D.155．若一口袋中装有4个白球3个红球,现在从中任取两球,则取出的两球中至少有一个白球的概率为（）A.31B.61 C 。

71 D 。

2126。

过点 P (4,2)做圆422=+y x的两条切线，切点分别为A,B ，O 为坐标原点,则AOB ∆的外接圆方程是A 。

2015届青岛市高三期中考试数学理科试题(附带详解答案)

青岛市高三学年度第一学期期中测试高三（理）数学试题注意事项：1．答题前，考生务必用0．5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上．2．第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试卷上．3．第Ⅱ卷必须用0．5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．4．填空题请直接填写答案，解答题应写出文字说明、演算步骤或推证过程．第I 卷(共50分)一、选择题：本大题共10小题，每小题5分，共50分． 1．已知集合(){}{}2lg 4,3,0=xA x y xB y y x A B ==-==⋂＞时，A.{}02x x ＜＜B.{}2x x 1＜＜C.{}12x x ≤≤D.∅2．设非空集合P Q ，满足P Q P =，则（）A ．P x Q x ∈∈∀有,B ．P x Q x ∉∉∀有,C ．Px Q x ∈∉∃00,使得D ．Qx P x ∉∈∃00,使得3.已知数列{}n a 的前n 项和为n S ，且22-=n n a S , 则2a =（） A. 4 B ．2 C ．1D ． -24．设向量(1,sin )θ=a ，(3sin ,1)θ=b ，且//a b ，则cos 2θ等于A ．31-B ．32-C ．32D ．315.下列各小题中，p 是q 的充要条件的是（）①p ：2m <-或6m >；q ：23y x mx m =+++有两个不同的零点． ②():1()f x p f x -=-；:()q y f x =是奇函数． ③:cos cos p αβ=；:tan tan q αβ=．④:p AB A =；AC B C q U U ⊆:．A ．①②B ．②③C ．③④D ．①④6．为得到函数)32sin(π+=x y 的导函数．．．图象，只需把函数sin 2y x =的图象上所有点的( ) A ．纵坐标伸长到原来的2倍，横坐标向左平移6πB ．纵坐标缩短到原来的12倍，横坐标向左平移3πC ．纵坐标伸长到原来的2倍，横坐标向左平移125πD ．纵坐标缩短到原来的12倍，横坐标向左平移65π7. 设y x ,满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ，若目标函数()0,0>>+=b a by ax z 的值是最大值为12，则23a b +的最小值为( ). A ．625 B ．38 C ． 311 D ． 48.函数()2tan 22f x x x ππ⎛⎫=--⎪⎝⎭在，上的图象大致为 ( )9．已知函数2()2f x x x =-，()()20g x ax a =+>，若1[1,2]x ∀∈-，2[1,2]x ∃∈-，使得()()21x g x f =，则实数a 的取值范围是A.1(0,]2B. 1[,3]2C.(0,3]D. [3,)+∞10.已知定义在R 上的函数()()()()311,11y f x f x f x x f x x =+=--≤=满足当＜时，，则函数()()x x f x g 6log -=的零点个数为（）A.4B.5C.6D.7密封线第II 卷（非选择题共100分）二、填空题：本大题共5小题，每小题5分，共25分.11.已知1(2)xa e x d x =+⎰(e 为自然对数的底数),函数l n ,0()2,0x x xf x x ->⎧=⎨≤⎩,则21()(log )6f a f +=__________.12．已知⎪⎭⎫ ⎝⎛∈=ππαα,2,53sin ，则cos sin 44ππαα⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭的值为________ ．13．若关于x 的不等式a x x ≥+++42的解集为实数集R ，则实数a 的取值范围是． 14．已知直线ex y =与函数x e x f =)(的图象相切，则切点坐标为 .15.定义方程()()f x f x '=的实数根o x 叫做函数()f x 的“新驻点”，如果函数()g x x =，()ln(1)h x x =+，()cos x x ϕ=（()x π∈π2，）的“新驻点”分别为α，β，γ，那么α，β，γ的大小关系是．三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

山东科技大学2015—2016学年第一学期
《高等数学》期中考试试卷
班级姓名学号
一、填空题（每小题5分，共15分）
1.
设lim )0,x ax b →-∞
-=则a =_________，b =________。

2. 设()sin
cos 22
x
f x x =+,(27)()f π=___________。

3.已知2)3(='f ，则h
f h f h 2)
3()3(lim
0--→= 。

二、单项选择题（每小题5分，共15分）
1. 当0x →时，变量211
sin x x
是（）
()A 无穷小 ()B 无穷大
()C 有界但不为无穷小 ()D 无界但不为无穷大
2. x
x
x +-=
11)(α，31)(x x -=β，则当1→x 时有（）（A ）α是比β高阶的无穷小（B ）α是比β低阶的无穷小（C ）α与β同阶无穷小，但不等价（D ）βα~
3. )(6
1sin 43
x R x x x +-
=其中=)(4x R ( ) （A ）
5!5cos x ξ- （B ）5
!5cos x ξ （C ）5!5sin x ξ （D ）5
!
5sin x ξ-（上述各式中ξ介于0与x 之间）
三、计算题（每小题8分，共40分）
1. 求极限 x x x e e x
x x cos sin lim tan 0--→。

2. 求极限 x
x x
x )121lim
2+-∞
→（。

3. 讨论2
cos
2(1)
x
y x x π=
-的连续性，若有间断点判断其类型，如是可去间断点补充定义使其连续。

4.
设ln arctan x y t
⎧⎪=⎨=⎪⎩ 22d y dx 。

5. 设()y y x =由方程2610y e xy x ++-=所确定，求
''(0)y 。

四、解答题（共10分）
设()()sin f x x x ϕ=，其中()x ϕ的一阶导数连续，且 (0)0ϕ=，'(0)0ϕ=，试判断()f x 在
0x =处是否二阶可导。

五、证明题（每小题10分，共20分）
1.设函数()f x 在(,)-∞+∞内二阶可导,且()1,f x ''>0
()
lim
2,x f x x
→= 试证明：2
1()22
f x x x ≥+。

2．设函数()f x 在[,]a b 上有二阶导数,()()f a f b =,试证：在(,)a b 内至少存在一点ξ,使得
2()
()f f b ξξξ
'''=
- 。

山东科技大学2015-2016高等数学期中考试试卷