利用Excel2000进行一元线性回归分析
Excel关于求解一元及多元线性回归方程 图解详细
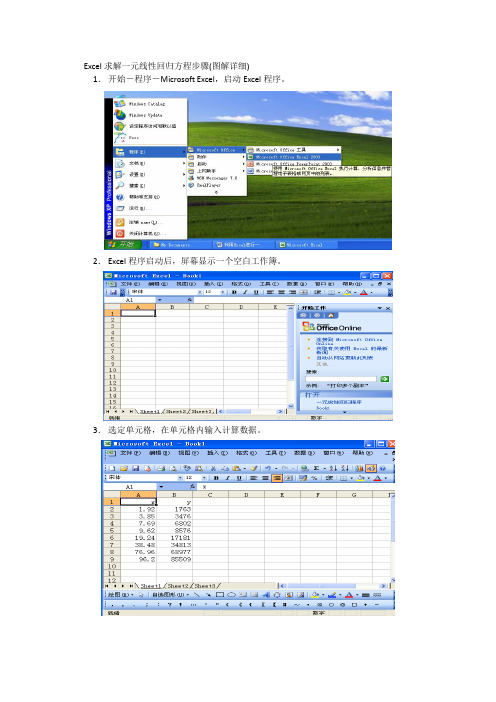
Excel求解一元线性回归方程步骤(图解详细)1.开始-程序-Microsoft Excel,启动Excel程序。
2.Excel程序启动后,屏幕显示一个空白工作簿。
3.选定单元格,在单元格内输入计算数据。
4.选中输入数据,点击“图表向导”按钮。
5.弹出图表向导对话窗,点击XY散点图,选择平滑线散点图,点击下一步。
6.选择系列产生在:列,点击下一步。
7.在图表标题中输入“硝基苯标准曲线”,数值(X)轴输入“硝基苯浓度”,数值(Y)轴输入“HPLC峰面积”。
此外还可以点击“坐标轴”,“网格线”,“图例”,“数据标志”下拉菜单,对其中选项进行选择。
8.点击完成后,即可得到硝基苯的标准曲线图。
9.将鼠标移至图表工作曲线上,单击鼠标右键,选择“添加趋势线”。
10.在“类型”选项中选择“线性”,“选项”中选择“显示公式”,“显示R平方值”,单击确定。
11.单击确定后即可得到附有回归方程的一元线性回归曲线。
12.至此,利用“图表向导”制作回归方程的操作步骤完毕。
利用Excel中“图表向导”制作标准曲线,使用者仅需按照向导说明填入相关信息即可完成图表的制作。
方法简单,适合对Excel了解不多的人员,如果你对Excel函数有一定的了解,那么你可以利Excel函数编制程序完成回归方程的计算。
4.4.2.2通过编制Excel程序计算一元线性回归方程1.打开一个新工作簿,以“一元线性回归方程”为文件名存盘。
2.单击插入,选择名称-定义。
3.在弹出的“定义名称”对话窗中“名称”栏输入“a”,“引用位置”栏输入“=$E$4”,然后按“添加”按钮;再在“名称”栏输入“b”,“引用位置”栏输入“=$E$3”,按“添加”按钮,依次输入下列内容,最后单击确定。
“名称”栏输入内容“引用位置”栏输入内容a =$E$4b =$E$3f =$G$4n =$G$3rf =$G$6rxy =$E$5x =$A$3:$A$888y =$B$3:$B$888aa=$G$2yi1 =$E$12yi2 =$E$134.完成命名后,在相关单元格内输入下列程序内容。
如何用Excel做数据线性拟合和回归分析

如何用Excel做数据线性拟合和回归分析我们已经知道在Excel自带的数据库中已有线性拟合工具,但是它还稍显单薄,今天我们来尝试使用较为专业的拟合工具来对此类数据进行处理。
在数据分析中,对于成对成组数据的拟合是经常遇到的,涉及到的任务有线性描述,趋势预测和残差分析等等。
很多专业读者遇见此类问题时往往寻求专业软件,比如在化工中经常用到的Origin和数学中常见的MATLA爵等。
它们虽很专业,但其实使用Excel就完全够用了。
我们已经知道在Excel自带的数据库中已有线性拟合工具,但是它还稍显单薄,今天我们来尝试使用较为专业的拟合工具来对此类婺选进行处理。
注:本功能需要使用Excel扩展功能,如果您的Excel尚未安装楚迪[分析,请依次选择“工具”-“加载宏”,在安装光盘支持下加载“分析婺此库”。
加载成功后,可以在“工具”下拉菜单中看到“塑ft分析”选项实例某溶液浓度正比对应于色谱仪器中的峰面积,现欲建立不同浓度下对应峰面积的标准曲线以供测试未知样品的实际浓度。
已知8组对应数据,建立标准曲线,并且对此曲线进行评价,给出残差等分析数迎这是一个很典型的线性拟合问题,手工计算就是采用最小二乘法求出拟合直线的待定参数,同时可以得出R的值,也就是相关系数的大小。
在Excel中,可以采用先绘图再添加趋势线的方法完成前两步的要求。
选择成对的数据列,将它们使用“X、丫散点图”制成散点图。
在数据点上单击右键,选择“添加趋势线”-“线性”,并在选项标签中要求给出公式和相关系数等,可以得到拟合的直线。
拟合的直线是y=15620x+6606.1,R2的值为0.9994。
因为R2>0.99,所以这是一个线性特征非常明显的实验模型,即说明拟合直线能够以大于99.99%地解释、涵盖了实测K,具有很好的一般性,可以作为标准工作曲线用于其他未知浓度溶液的测量。
为了进一步使用更多的指标来描述这一个模型,我们使用数据分析中的“回归”工具来详细分析这组数据。
一元线性回归法 excle操作

实验结果:实验一:一元线性回归在Excel中的实现一、实验过程描述1.录入数据打开EXCLE,录入实验数据,B列存放居民货币收入,C列存放居民消费品购买力,如下图所示:2.绘制散点图点击插入——图表——散点图——下一步,选择数据区域如下图:定义表名为消费能力表、X轴为收入、Y轴为购买力,形成生散点图:根据散点图可知,题中两个条件之间存在着线性关系,根据散点图可建立一次回归模型。
3.所需数据的计算一元线性回归系数的计算中,需要用到∑x、∑y、∑2x、∑2y及∑xy 的值,因此按下列步骤求出这些值。
在D2单元格中输入“=B2*B2”,下拉求出所有的值。
同上,在E2单元格中输入”=C2*C2”,在F2单元格中输入“=B2*C2”,依次下拉,得到所有值。
结果如下表所示:在B11单元格中输入“=SUM(B2:B10)”,依次右拉,求出各列的和∑x 、∑y 、∑2x 、∑2y 及∑xy ,依次存在B11,C11,D11,E11,F11.如下图所示:4. 一元线性回归系数的计算:根据系数公式x b y a x x n y x xy n b 22-=--=∑∑∑∑∑)(,在EXCLE 表格中进行计算如下: 在I2单元格中输入一元线性回归系数b 的公式“=(9*F11-B11*C11)/(9*D11-B11*B11)”,在I3单元格中输入系数a 的公式 “ =C11/9-I2*(B11/9)”结果如下图所示:由此得出回归方程:Y=-0.99464X+0.847206二、实验结果分析在进行线性回归分析之前,首先必须依据一定的经济理论、专业知识,对变量间是否存在一定的相关性进行分析。
本题中,应根据实际经验,确定居民货币收入为自变量,居民消费品购买力为因变量。
再次要绘制散点图,观察数据信息是否符合线性要求,在完成上述准备工作后,才能进行线性回归方程的计算。
利用Excel进行线性回归分析

利用Excel进行线性回归分析————————————————————————————————作者: ————————————————————————————————日期:ﻩ文档内容1.利用Excel进行一元线性回归分析2. 利用Excel进行多元线性回归分析1.利用Excel进行一元线性回归分析第一步,录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图(图1)。
图1第二步,作散点图如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在“插入”菜单中打开“图表(H)”。
图表向导的图标为。
选中数据后,数据变为蓝色(图2)。
图2点击“图表向导”以后,弹出如下对话框(图3):图3在左边一栏中选中“XY散点图”,点击“完成”按钮,立即出现散点图的原始形式(图4):灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩)图4第三步,回归观察散点图,判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时,才能采用线性回归分析方法。
从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。
回归的步骤如下:1. 首先,打开“工具”下拉菜单,可见数据分析选项(见图5):图5用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):图62.然后,选择“回归”,确定,弹出如下选项表(图7):图7进行如下选择:X 、Y 值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图(图8-1)。
或者:X 、Y 值的输入区域(B2:B11,C2:C11),置信度(95%),新工作表组,残差,线性拟合图(图8-2)。
注意:选中数据“标志”和不选“标志”,X 、Y 值的输入区域是不一样的:前者包括数据标志:最大积雪深度x (米) 灌溉面积y (千亩)后者不包括。
这一点务请注意(图8)。
图8-1包括数据“标志”图8-2不包括数据“标志”3.再后,确定,取得回归结果(图9)。
用Excel进行回归线分析操作

”
第4步:当对话框出现时
在“Y值输入区域”方框内键入Y的数据区域B3:B15 ,在“X值输入区域”方框内键入X的数据区域C3: C15。如果是多元线性回归,则X值的输入区就是除Y 变量以外的全部解释变量。 在“置信度”选项中给出所需的数值(这里我们使用 隐含值95%)。 在“输出选项”中选择输出区域(这里我们选择新工 作表组)。 在“残差”分析选项中选择所需的选项(这里我们暂 时未选)。 结果如下图所示。
下面给出利用Excel求线性回归方程的操作过程
首先,省94-2005年国内生产总值和固定资产 投资完成额资料到Excel工作表中的B3:C15单 元格。然后按下列步骤进行操作。 第1步:选择“工具”下拉菜单。 第2步:选择“数据分析”选项。
第3步:在分析工具中选择“回归”,然后选择“确定。
Excel输出的回归 分析结果回括以下几个部分
第一部分是“回归统计”,这部分主要是回归 分析中的一些常用统计量,包括相关系数( Multiple R)、判定系数(R Square)、调整 判定系数(Adjusted R Square)、估计标准误 差、观测值个数等。 第二部分是参数估计的内容。包括回归方程的 截距(Intercept)斜率(X Variabl)、截距和 斜率的标准误差、用于检验回归系数的统计量 (t Stat)和P-值(P-valu)以及截距和斜率的 置信区间(Lower 95%和Upper 95%)等。
线性回归excel

线性回归excel线性回归(LinearRegression)是机器学习中最基础的一种算法,它用于判断两种数据之间是否存在线性关系,以及模型中变量之间的相关性。
它使用了抛物线和线性函数来确定由一个或多个自变量对因变量的影响程度。
Excel中的线性回归功能提供了一种方法来识别线性关系,它可以帮助我们快速确定变量的相关性,并在此基础上建立预测模型。
用Excel来进行线性回归分析,第一步是收集好基础数据,确保所有数据都已经被输入到Excel表格中,在输入完成后,我们可以使用Excel中的Data Analysis ToolPak来进行线性回归分析。
重要的是,在工具包中,我们需要在“Analysis Tools”中选择“Regression”,然后在弹出窗口中输入因变量和自变量,并确定分析类型(即我们是否想要显示结果图形)以及输出结果的位置(如表格或新的工作表)。
线性回归的结果是一个参数矩阵,它含有一组参数,用来拟合我们的因变量。
矩阵中的一行定义了一个自变量,其中每列包含三个值:自变量的系数(Coefficient),参数的t值(t-value),和最低的可接受t值(Critical t Value)。
系数反映了自变量对因变量的影响程度,即自变量的变化或改变对因变量的影响程度。
t值表明由于这种联系,我们实际上测量到的结果是否具有统计学意义。
最后一列显示的是受试者可以接受的最低的t值,它表示我们的研究是有统计学意义的,即有显著性差异存在。
另外,Excel中的线性回归功能还可以帮助我们计算出残差分析(Residual Analysis),这是一种统计技术,用于分析线性回归模型的拟合情况。
残差分析可以帮助我们确定线性回归模型的准确性和可靠性,即它是否能很好地拟合数据。
总结而言,Excel中的线性回归功能是一个强大的工具,它可以节约时间,节省精力,帮助我们快速确定变量之间的相关性,并以此为基础建立预测模型。
它不仅可以提供线性回归模型,还提供了残差分析,这有助于我们更好地理解线性回归模型。
利用excel进行线性回归分析
LINEST 函数通过使用“最小二乘法”计算最符合您的数据的直线来计算直线的统计值,并返回描述该直线的 数组 。
因为此函数返回数值数组,所以必须以 数组公式 的形式输入。
直线的公式为 y = mx + b 或 y = m1x1 + m2x2 + ... + b (如果 x 值包含多个区域),其中因变量 y 值是自变量 x 值的函数。
m 值是与每个 x 指数值相对应的系数,b 为常量值。
请注意,y 、x 和 m 可以是向量。
LINEST 函数返回的数组为 {m n,m n-1,...,m 1,b}。
LINEST 函数还会返回附加回归统计值。
语法LINEST(known_y's, known_x's, const, stats ) 以下图示显示了附加回归统计值返回的顺序。
可以使用斜率和 y 轴截距描述任何直线:如果需要计算斜率(通常记为 m ),则选取直线上的两点 (x1,y1) 和 (x2,y2);斜率等于 (y2 - y1)/(x2 - x1)。
直线的 y 轴截距(通常记为 b )为直线与 y 轴交点的 y 值。
.直线的公式为 y = mx + b。
如果知道 m 值和 b 值,可以将 y 值或 x 值代入公式来计算直线上的任意点。
还可以使用TREND函数。
∙如果只有一个自变量 x,可以使用以下公式直接算出斜率和 y 轴截距值:计算斜率,使用=INDEX(LINEST(known_y's, known_x's), 1 )计算 Y 轴截距,使用=INDEX(LINEST(known_y's, known_x's), 2 )∙LINEST计算出的直线的精确度取决于数据的离散程度。
数据越接近线性,LINEST模型就越精确。
LINEST使用最小二乘法确定最适合数据的直线。
只有一个自变量 x 时,m 和 b 可根据以下公式算出:其中 x 和 y 是样本平均值,即,x =AVERAGE(known x's)和 y =AVERAGE(known_y's)。
2020年用Excel做线性回归分析
作者:空青山作品编号:89964445889663Gd53022257782215002时间:2020.12.13用Excel进行一元线性回归分析Excel功能强大,利用它的分析工具和函数,可以进行各种试验数据的多元线性回归分析。
本文就从最简单的一元线性回归入手.在数据分析中,对于成对成组数据的拟合是经常遇到的,涉及到的任务有线性描述,趋势预测和残差分析等等。
很多专业读者遇见此类问题时往往寻求专业软件,比如在化工中经常用到的Origin和数学中常见的MATLAB等等。
它们虽很专业,但其实使用Excel就完全够用了。
我们已经知道在Excel自带的数据库中已有线性拟合工具,但是它还稍显单薄,今天我们来尝试使用较为专业的拟合工具来对此类数据进行处理。
文章使用的是2000版的软件,我在其中的一些步骤也添加了2007版的注解.1 利用Excel2000进行一元线性回归分析首先录入数据.以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图(图1)。
图1第二步,作散点图如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在“插入”菜单中打开“图表(H)(excel2007)”。
图表向导的图标为。
选中数据后,数据变为蓝色(图2)。
图2点击“图表向导”以后,弹出如下对话框(图3):图3在左边一栏中选中“XY 散点图”,点击“完成”按钮,立即出现散点图的原始形式(图4):灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩)图4第三步,回归观察散点图,判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时,才能采用线性回归分析方法。
从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。
回归的步骤如下:⑴首先,打开“工具”下拉菜单,可见数据分析选项(见图5)(2007为”数据”右端的”数据分析”):图5用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):图6⑵然后,选择“回归”,确定,弹出如下选项表:图7进行如下选择:X、Y值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图。
回归方程excel
回归方程excel
在Excel中创建回归方程可以使用"线性回归"数据分析工具。
下面是一种使用Excel的方法:
1. 首先,确保你的数据集是正确的。
将自变量和因变量输入到Excel的两列中。
2. 在Excel的菜单栏中,点击"数据"选项,在下拉菜单中选择"数据分析"。
3. 在弹出的"数据分析"对话框中,选择"回归"选项,然后点击"确定"。
4. 在弹出的"回归"对话框中,将自变量范围和因变量范围输入到相应的输入框中。
确保选择了"标签"和"残差"选项,然后点击"确定"。
5. Excel将自动生成回归分析的结果,并将其显示在一个新的工作表中。
在这个工作表中,你将看到回归方程的参数、相关系数、显著性水平等。
请注意,使用回归方程进行预测时,要确保预测的自变量值在你的数据集范围内,否则结果可能不准确。
excel做回归分析的教程
excel做回归分析的教程Excel中经常需要对数据进行回归分析的一个操作,回归分析具体该如何进行操作呢?下面是由店铺分享的excel做回归分析的教程,以供大家阅读和学习。
excel做回归分析的教程(一)步骤1:首先将预处理的数据输到单元格里步骤2:“数据”里有一项“数据分析”,至于如何导入,详见我另外的经验步骤3:在一堆数据分析工具里找到回归这一项步骤4:对应框入Y值和X值,即可进行分析步骤5:点击确定后,即出现以下分析,常用的几个数据已圈出excel做回归分析的教程(二)步骤1:选择成对的数据列,将它们使用“X、Y散点图”制成散点图。
步骤2:在数据点上单击右键,选择“添加趋势线”-“线性”,并在选项标签中要求给出公式和相关系数等,可以得到拟合的直线。
步骤3:由图中可知,拟合的直线是y=15620x+6606.1,R2的值为0.9994。
步骤4:因为R2 >0.99,所以这是一个线性特征非常明显的实验模型,即说明拟合直线能够以大于99.99%地解释、涵盖了实测数据,具有很好的一般性,可以作为标准工作曲线用于其他未知浓度溶液的测量。
步骤5:为了进一步使用更多的指标来描述这一个模型,我们使用数据分析中的“回归”工具来详细分析这组数据。
步骤6:在选项卡中显然详细多了,注意选择X、Y对应的数据列。
“常数为零”就是指明该模型是严格的正比例模型,本例确实是这样,因为在浓度为零时相应峰面积肯定为零。
先前得出的回归方程虽然拟合程度相当高,但是在x=0时,仍然有对应的数值,这显然是一个可笑的结论。
所以我们选择“常数为零”。
步骤7:“回归”工具为我们提供了三张图,分别是残差图、线性拟合图和正态概率图。
重点来看残差图和线性拟合图。
步骤8:在线性拟合图中可以看到,不但有根据要求生成的数据点,而且还有经过拟和处理的预测数据点,拟合直线的参数会在数据表格中详细显示。
本实例旨在提供更多信息以起到抛砖引玉的作用,由于涉及到过多的专业术语,请各位读者根据实际,在具体使用中另行参考各项参数,此不再对更多细节作进一步解释。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 利用Excel2000进行一元线性回归分析
第一步,录入数据
以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图(图1)。
图1
第二步,作散点图
如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在
“插入”菜单中打开“图表(H)”。
图表向导的图标为。
选中数据后,数据变为蓝色(图2)。
图2
点击“图表向导”以后,弹出如下对话框(图3):
图3
在左边一栏中选中“XY 散点图”,点击“完成”按钮,立即出现散点图的原始形式
(图4):
灌溉面积y(千亩)
01020304050600
10
2030
灌溉面积y(千亩)
图4
第三步,回归
观察散点图,判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时,才能采用线性回归分析方法。
从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。
回归的步骤如下:
⑴首先,打开“工具”下拉菜单,可见数据分析选项(见图5):
图5
用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):
图6
⑵然后,选择“回归”,确定,弹出如下选项表:
图7
进行如下选择:X、Y值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图。
或者:X、Y值的输入区域(B2:B11,C2:C11),置信度(95%),新工作表组,残差,线性拟合图。
注意:选中数据“标志”和不选“标志”,X、Y值的输入区域是不一样的:前者包
括数据标志:
最大积雪深度x(米)灌溉面积y(千亩)
后者不包括。
这一点务请注意。
图8-1 包括数据“标志”
图8-2 不包括数据“标志”
⑶再后,确定,取得回归结果(图9)。
图9 线性回归结果
⑷最后,读取回归结果如下:
截距:356.2a
;斜率:813.1b
;相关系数:989.0R ;测定系数:
979.02
R
;F 值:945.371F。
⑸建立回归模型,并对结果进行检验模型为:x y 813.1356.2?至于检验,R 、R 2
和
F 值可以直接从回归结果中读出。
实际上,
8,05.0632
.0989416
.0R R
,检验通过。
有了
R 值,F 值和t 值均可计算出来。
F 值的
计算公式和结果为:
8
,05.02
2
2
2
32
.5945
.371)
989416.01(1
1
10
1989416
.0)
1
(1
1F R k
n
R F
显然与表中的结果一样。
t 值的计算公式和结果为:
8
,05.02
306.2286
.191
1
10
979416.01
979416.01
1t k
n
R R t
回归结果中给出了残差(
图10),据此可以计算标准离差。
首先求残差的平方
2
2)?(i i
i
y
y ,然后求残差平方和107.16174
.0724.110
1
2n i i
S
,于是标准
离差为
419
.18
107
.161)?(1
11
2
S
v
y
y k
n s
n
i i i
于是
15
.0~1.0%
15~100388
.053
.36419.1y
s 图10 y 的预测值及其相应的残差等
进而,可以计算DW 值(参见图11),计算公式及结果为
751
.0417
.0)
911.1()
313.1()833.0417.0()
313.1911.1()
(
DW
2
2
2
2
2
1
22
2
1
n
i i
n
i i i 取05.0,1k ,10n (显然81
1
10
v
),查表得
94.0l
d ,29.1u
d 。
显然,DW=0.75194.0l
d ,可见有序列正相关,预测的结果令人怀疑。
图11 利用残差计算DW 值
最后给出利用Excel 快速估计模型的方法:
⑴用鼠标指向图4中的数据点列,单击右键,出现如下选择菜单(图
12):
图12
⑵点击“添加趋势线(R)”,弹出如下选择框(图13):
图13
⑶在“分析类型”中选择“线性(L)”,然后打开选项单(图14):
图14
⑷在选择框中选中“显示公式(E)”和“显示R平方值(R)”(如图14),确定,立即得到回归结果如下(图15):
图表标题
y = 1.8129x + 2.3564
R 2
= 0.9789
01020304050600
10
20
30
灌溉面积y(千亩)线性 (灌溉面积y(千亩))
图15
在图15中,给出了回归模型和相应的测定系数即拟合优度。
