精选2019-2020年初中数学七年级下册7.7 几种简单几何图形及其推理北京课改版习题精选九
北京课改版数学七年级下册7.7《几种简单几何图形及其推理》同步练习1.doc
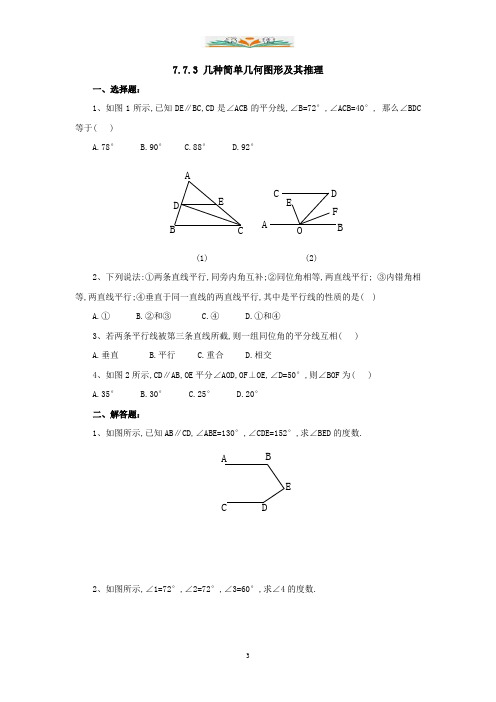
7.7.3 几种简单几何图形及其推理一、选择题:1、如图1所示,已知DE ∥BC,CD 是∠ACB 的平分线,∠B=72°,∠ACB=40°,•那么∠BDC 等于( )A.78°B.90°C.88°D.92°ED BA OF E D C BA(1) (2)2、下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;•③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )A.①B.②和③C.④D.①和④3、若两条平行线被第三条直线所截,则一组同位角的平分线互相( ) A.垂直 B.平行 C.重合 D.相交4、如图2所示,CD ∥AB,OE 平分∠AOD,OF ⊥OE,∠D=50°,则∠BOF 为( ) A.35° B.30° C.25° D.20° 二、解答题:1、如图所示,已知AB ∥CD,∠ABE=130°,∠CDE=152°,求∠BED 的度数.EDC BA2、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.ba34123、如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?4、如图所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数.参考答案一、选择题:1、C 2、A 3、B 4、C二、解答题:1、∠BED=78°.2、∠4=120°.3、可以判断EF∥BD。
因为∠AED=60°,EF平分∠AED,所以∠1=30°,又知∠2=30°,所以∠1=∠2.用内错角相等两直线平行得出EF∥BD.4、解:因为AD∥BC,∠2=40°所以∠ADB=∠2=40°又因为∠1=78°所以∠ADC=∠ADB+∠1=40°+78°=118°.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
2018北京课改版数学七下7.7《几种简单几何图形及其推理》ppt课件3

通过本节课的学习你收获了什么? 作业布置 课本P137 习题 4、5
同学们再见!
不难推出,因为AB∥CD,由“两直 线平行,同位角相等” 得∠1=∠2,又 因为∠1=∠3,所以∠2=∠3 .
A
C F
E 1
3
B
2
D 图7-30
由此得到平行线的另一个性质:
想一想
性质定理:两条平行线被第三条直线所截,得到的内错角相等(简 记为:两直线平行,内错角相等).
E 1
如图7-30,用符号语言表示: ∵ AB∥CD , ∴∠2=∠3.
A3
B
2
C
D
F 图7-30
思考
如图7-31,直线AB∥CD,它们被直线EF所截,那么同旁内角∠1与
∠2之间有什么关系?
不难发现:
E
性质定理:两条平行线被第三条直线所截,得到 A 的同旁内角互补(简记为:两直线平行,同旁内角互 补).
1B 2
C
D
如图7-31,用符号语言表示:
F 图7-31
∵ AB∥CD , ∴∠1=∠2.
达标检 测 1、已知∠3 =∠4,∠1=47°,求∠2的度数?
解:∵ ∠3 =∠4( 已知),
d
∴a∥b( 同位角相等,两直线平行).
a
3
∴∠1=∠2( 两直线平行,同位角相等).
又∵∠ 1 = 470 ( ), 已知
b
4
∴∠2=47°(
七年级数学几种简单几何图形及其推理测试题及答案

七年级数学几种简单几何图形及其推理测试题及答案以下是查字典数学网为您推荐的七年级数学几种简单几何图形及其推理测试题及答案,希望本篇文章对您学习有所帮助。
七年级数学几种简单几何图形及其推理测试题及答案【基础能力训练】一、余角、补角1.如果一个角的补角是150,那么这个角的余角是( )A.30B.60C.90D.1202.下列命题中的真命题是( )A.锐角大于它的余角B.锐角大于它的补角C.钝角大于它的补角D.锐角与钝角之和等于平角3.如图,ACB=90,CDAB,垂足为D,下列结论错误的是( )A.有三个直角三角形B.2C.1和B都是A的余角D.A(第3题)4.一个锐角的补角比它的余角大_________.5.1,2互为补角,且2,则2的余角是( )A. (2)B. 1C. (2)D. 26.一个角的补角比它的余角的2倍大42,求这个角的度数.二、对顶角7.下列说法正确的是( )A.若两个角是对角角,则这两个角相等;B.若两个角相等,则这两个角是对顶角C.若两个角不相等,则这两个角不是对顶角;D.以上判断都不对8.把命题对顶角相等写成如果那么的形式:________.9.如图,图中对顶角共有( )A.6对B.11对C.12对D.13对(第9题)10.下列各图的1和2是对顶角的是( )11.如图,已知直线a,b相交,2,求1,2,3,4的度数.12.如图,已知+=80,求,的度数.三、平行线13.下列语句正确的是( )A.有一条而且只有一条直线和已知直线平行;B.直线AB∥CD,那么直线AB也一定和EF平行;C.一条直线垂直于两条平行线中的一条,也一定垂直于另一条;D.两条永不相交的直线叫做平行线14.如果a∥b,b∥c,那么a∥c的根据是( )A.等量代换B.平行公理C.平行于同一条直线的两条直线平行;D.同位角相等,两直线平行15.如果两条平行线被第三条直线所截,则一对内错角的平分线互相( )A.平行B.平分C.相交但不垂直D.垂直16.如图,DH∥EG∥BC,DC∥EF.则与BFE相等的角(不包括BFE)的个数是( )A.2B.3C.4D.517.若两平行直线被第三条直线所截,则可构成( )A.对顶角和同位角各4对B.内错角2对,同位角2对C.同位角和同旁内角各2对D.同旁内角2对,内错角4对18.如图1,由2,可判定AB∥CD,是根据________,如图2,由1=•2可判定CD∥EF,是根据________;如图3,∵2(已知),DE∥______,•根据_________.(1) (2) (3)19.如图,∵1=130,2=50(已知)2=180(等式的性质)AB∥CD(_______).(第19题) (第20题) (第21题)20.如图,已知L1∥L2∥L3.①若1=70,则2=_____,理由是________;②若1=70,则3=_____,理由是________;③若1=70,则4=_____,理由是________.21.如图,直线DE经过点A,DE∥BC,B=44,C=57.那么:(1)DAB=_______( );(2)EAC=_______( );(3)BAC=_______( );(4)BAC+C=______( ).【综合创新训练】创新应用22.命题甲:同位角相等,两直线平行.命题乙:两直线平行,同位角相等下列说法正确的是( )A.命题甲、乙都是平行线的性质B.命题甲、乙都不是平行线的性质C.只有命题甲是平行线的性质D.只有命题乙是平行线的性质23.如图,如果AB∥CD,则①2,②4,③3=4.上述结论中正确的是( )A.只有①B.只有②C.只有③D.①②和③生活中的数学24.如图,是一座坚固的两面城墙,为了得出它的角度,我们既无法进到墙内,又不能把墙拆掉.问:用什么办法我们能得出它的度数呢.追根求源25.如图,2,EC∥AC,求证:4.证明:∵EC∥AD1=_______(______)2=_______(________)又∵2(_______)4(________).26.如图,已知:3=180,3=180.求证:AB∥CD证明:∵3=180(_________)1与3互补(________)∵3=180(________)2与3互补(________)1=_______(________)AB∥CD(________).27.已知:如图,FMN=C,FNM=B,求证:F.探究学习在同一平面内有2 005条直线a1,a2,,a2019,如果a1a2,a2∥a3,a3a4,a4∥a5,,那么a1与a2019的位置关系是怎样的?答案:【基础能力训练】1.B 解析:这个角是30.2.C 解析:反例:30的余角是60所以A错,30的补角是150,所以B错,•30+120=150不是平角,所以D错.3.B4.90 解析:设这个角的度数为x,180-x-(90-x)=180-x-90+x=905.C6.设这个角的度数为x,根据题意得:180-x-42=2(90-x)138-x=180-2xx=42所以,这个角的度数是42.7.A8.如果两个角是对顶角,那么这两个角相等9.A 10.D11.∵2=180,1=2222=1802=60,1=1201与3,2与4是对顶角1=120,2=60,3=120,4=60.12.∵与是对顶角,+=80==40又∵+=180=180=180-40=140=40,=140.13.C 14.C 15.A 16.D 17.A18.同位角相等,两直线平行内错角相等,两直线平行BC 同位角相等,两直线平行19.同旁内角互补,两直线平行20.①110 两直线平行,同旁内角互补②70 两直线平行,同位角相等③70 两直线平行,内错角相等21.(1)44 两直线平行,内错角相等(2)57 两直线平行,内错角相等(3)79 三角形内角和等于180(4)180 三角形内角和等于180【综合创新训练】22.D 解析:命题甲是平行线判定定理.23.D24.从墙角处向外延伸得到墙角的对顶角,即可.25.3 两直线平行,同位角相等4 两直线平行,内错角相等已知•等量代换26.已知补角定义已知补角定义2 等量代换内错角相等,•两直线平行27.∵FMN=C(已知),DF∥AC(内错角相等,两直线平行)FDB(两直线平行,同位角相等)又∵FNM=B(已知)NMF=DMB(对顶角相等)BDM=MFN(三角形内角和等于180)F(等量代换).我国古代的读书人,从上学之日起,就日诵不辍,一般在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。
初一数学(北京版)-简单几何图形与推理

三角形:不在同一直线上的三条线段首尾顺次相接组成的 图形叫做三角形.
由3条线段围成的图形(每相邻两条线段的端点 相连)叫做三角形.
概念反映对象的本质属性.
概念的内涵
具有该本质属性的所有对象呢?
概念反映对象的本质属性.
概念的内涵
具有该本质属性的所有对象
概念的外延
概念
概念的内涵 明确 下定义
题设
结论
等于同一个量的两个量相等.
等于同一个量的两个量相等. 如果两个量都与同一个量相等,那么这两个量也相等.
“如果……,那么……”形式.
题设
结论
成立 一定成立
成立 不一定成立
真命题 假命题
判断下列命题的真假. 如果直线a//b,那么直线a与直线b没有交点. 真命题 如果a=b,c=d,那么a+c=b+d. 真命题 等于同一个量的两个量相等. 真命题 两个锐角的和一定是钝角.
试一试 观察并说出下图中每个三角形区别于其他三角形 的特有属性.
1
5
7
9
11
图①三个角都是锐角 +三角形
锐角三角形
试一试 观察并说出下图中每个三角形区别于其他三角形 的特有属性.
1
5
7
9
11
图①三个角都是锐角 +三角形
锐角三角形
图⑤有一个角是钝角 +三角形
钝角三角形
特有属性 + 一般概念
特殊概念
霍布斯 17世纪 英国哲学家
霍布斯巧遇《几何原本》的故事
爱上几何学
概念
命题
推理
组成
组成
概念
命题
推理
组成
组成
北京版七年级数学下册 几种简单几何图形及其推理教案

《几种简单几何图形及其推理》教案3
教学目标
1.要求学生掌握互为余角,补角的定义
2.要会求一个角的余角和补角
3.掌握余角和补角的定理及其应用。
教学过程
1.余角与补角
①如果两个角的和等于( ),就说这两个角互为余角。
符号语言:如果∠α+∠β= ,那么∠α和∠β互为。
反之:如果∠α与∠β互为余角,那么∠α+∠β=。
②如果两个角的和等于( ),就说这两个角互为补角。
符号语言:如果∠α+∠β= ,那么∠α和∠β互为。
反之:如果∠α与∠β互为补角,那么∠α+∠β=。
想一想:1.如左图OC ⊥AB ,∠1=∠2,图中共有多少对互为余角的角? 2.如右图,O 是直线AB 上一点,∠1=∠2,图中共有多少对互为补角的角?
练习:已知:如图∠1+∠2=90°,∠1+∠3=90°,试判断∠2与∠3的关系。
例 一个角的补角比它的余角的2倍多8°,求这个角的余角及这个角的补角。
2.对顶角
例:已知:如图,直线AB
与直线CD 交于O 求证:
∠AOC=∠
BOD ,∠AOD=∠BOC
O
E
D
C
B A
2
1
O
D
C
B
A
2
1
D
C
B
A
4
3
2
1
3、课堂小结
1.没有熟悉的可以直接运用结论的图形时,可以作什么?
2.添加辅助线的目的是什么?构造新的平行线或三角形
3.构造三角形,应用三角和内角和定理。
精选2019-2020年初中数学七年级下册第七章 观察、猜想与证明7.7 几种简单几何图形及其推理北京课改版知识

精选2019-2020年初中数学七年级下册第七章观察、猜想与证明7.7 几种简单几何图形及其推理北京课改版知识点练习[含答案解析]第二十七篇第1题【单选题】甲,乙,丙三位先生是同一家公司的职员,他们的夫人,M,N,P也都是这家公司的职员,知情者介绍说:“M的丈夫是乙的好友,并在三位先生中最年轻;丙的年龄比P的丈夫大”.根据该知情者提供的信息,我们可以推出三对夫妇分别是( )A、甲﹣M,乙﹣N,丙﹣PB、甲﹣M,乙﹣P,丙﹣NC、甲﹣N,乙﹣P,丙﹣MD、甲﹣P,乙﹣N,丙﹣M【答案】:【解析】:第2题【单选题】在一次400米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是( )A、甲B、乙C、丙D、丁【答案】:【解析】:第3题【单选题】某班有50人,其中35人参加文学社,45人参加书画社,38人参加音乐社,42人参加体育社,则四个社都去参加的学生至少是多少人?( )A、10B、121C、14D、16【答案】:【解析】:第4题【单选题】下列推理正确的是( )A、因为a//d, b//c,所以c//dB、因为a//c, b//d,所以c//dC、因为a//b, a//c,所以b//cD、因为a//b, d//c,所以a//c【答案】:【解析】:第5题【填空题】一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是21°和32°.当检验工人量得的∠BDC的度数不等于______度时,就可判定此零件不合格?【答案】:【解析】:第6题【解答题】小红、小强和小华三名学生中,有一人把教室打扫得干干净净.事后,老师问他们三人是谁做的好事?小红说:“是小强做的.”小强说:“不是我做的.”小华说:“不是我做的.”如果他们三人中有两人说了假话,一人说了真话,那么老师能判定是谁做的吗?【答案】:【解析】:第7题【解答题】四个足球队进行单循环比赛,规定胜一场得3分,平一场得1分,负一场得0分,有一个队一场都没输过,排名却倒数第一,你觉得可能吗?如果可能,请举出这情况何时出现;如果不可能,请说明理由.【答案】:【解析】:第8题【解答题】某个参观团根据下列约束条件从A,B,C,D,E五个城市中选择参观地点:( 1 )若去A市,也必须去B市;( 2 )D,E两市至少去一市;( 3 )B,C两市只去一市;( 4 )C,D两市都去或者都不去;( 5 )若去E市,则A,D两市也必须去.试分析该参观团至多能去哪几个城市.【答案】:【解析】:第9题【解答题】附加题:收集4瓶空矿泉水瓶可以换一瓶矿泉水喝,现在有27个空矿泉水瓶子,最多能喝几瓶矿泉水?请表述你的方案.【答案】:【解析】:第10题【解答题】某班同学出去野营,其中n个人围成一圈,其余的人做观众.这几个人按顺时针方向依次编为1至n 号,从1号开始表演节目,以后每隔1个人表演,某人表演完后就退出圈子作观众,当n为下列各值时,求最后一个表演节目的人是几号?(1)n=32;(2)n=39.【答案】:【解析】:。
【课件】2022年北京版初中数学七年级下第七章 观察、猜想与证明几种简单几何图形及其推理
∵MG平分∠EMB,NH平分∠END(已知),
∴∠EMG= ∠1EMB,∠ENH= ∠END1(角平分线的定义).
2
2
∴∠EMG=∠ENH(等量代换).
∴MG∥NH(同位角相等,两直线平行).
小结
1. 余角、补角. 同角(或等角)的余角相等;同角(或等
角)的补角相等. 2. 对顶角.
对顶角相等. 3. 平行线.
过直线外一点有且只有一条直线与这条直线平行.
探究:同位角、内错角以及同旁内角. 图1是小亮所在学校周边的道路示意图,如 果把图中的道路都看做直线,就得到图2.
图1
图2
(1)在图2中,直线AB,CD被直线EF所截, 一共形成哪几个角?
(2)观察∠1与∠5,它们有怎样的位置关系?
回答问题并得出概念:
那么这两条直线平行. (简记为:内错角相等,两直线平行).
在下图中,∠1与∠2互补,直线a与直线b平
行吗?为什么?与同学交流.
c
3a
2
1
b
如果∠1+∠2=180°,因为∠2+∠3=180°,
所以∠1=∠3,因此a∥b.
两条直线被第三条直线所截,如果同旁内角相
等,那么这两条直线平行.
(简记为:同旁内角相等,两直线平行).
平行线的判定
怎样才能判定两条直线平行呢? 回想一下用三角尺和直尺画平行线的方法.
由画图过程可以看出,经过直线AB外的一点画AB的 平 行 线 , 是 通 过 画 ∠1=∠2 完 成 的 . 而 ∠1 和 ∠2 是 直 线 AB ,CD被直线EF截得的同位角.这就说明,如果同位 角∠1与∠2相等,那么直线AB ∥ CD.
2
1
1
3
2019-2020年北京课改版数学七年级下册第七章 观察、猜想与证明7.7 几种简单几何图形及其推理复习巩固四十
2019-2020年北京课改版数学七年级下册第七章观察、猜想与证明7.7 几种简单几何图形及其推理复习巩固四十第1题【单选题】下列推理正确的是( )A、因为a∥d,b∥c,所以c∥dB、因为a∥c,b∥d,所以c∥dC、因为a∥b,a∥c,所以b∥cD、因为a∥b,d∥c,所以a∥c【答案】:【解析】:第2题【单选题】如图,已知甲、乙两车分别从A、B两地同时相向出发,它们第1次相遇时距离B地54千米,甲、乙两车分别到达B、A两地后立即调头,它们第2次相遇时距离B地48千米,则A、B两地相距( )千米.A、102B、103C、104D、105【答案】:【解析】:第3题【单选题】气象爱好者孔宗明同学在x(x为正整数)天中观察到:①有7个是雨天;②有5个下午是晴天;③有6个上午是晴天;④当下午下雨时上午是晴天.则x等于( )A、7B、8C、9D、10【答案】:【解析】:第4题【单选题】如图游戏:人从格外只能进入第1格,在格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有( )种方法.A、6B、7C、8D、9【答案】:【解析】:第5题【单选题】在期中考试中,同学甲、乙、丙、丁分别获得第一、第二、第三、第四名.在期末考试中,他们又是班上的前四名.如果他们当中只有一位的排名与期中考试中的排名相同,那么排名情况有( )种可能.A、5B、6C、7D、8【答案】:【解析】:第6题【单选题】下列推理正确的是( )A、弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,因为弟弟的明年比今年长大了1岁B、如果a>b,b>c,则a>cC、∠A与∠B相等,原因是它们看起来大小也差不多D、因为对顶角必然相等,所以相等角也必是对顶角【答案】:【解析】:第7题【单选题】A、BABABB、BABBAC、AABABD、ABBAB【答案】:【解析】:第8题【填空题】夏洛特去山里寻宝,来到藏有宝藏的地方,发现这里有编号分为一,二,三,四,五的五扇大门,每扇门上都写有一句话:一,宝藏在五号大门的后面;二,宝藏或者在三号大门的后面,或者在五号的后面;三,宝藏不在五号大门的后面;四,宝藏不在此门后面;五,宝藏在二号大门的后面,夏洛特从当地人得到,五句话中只有一句是真的,那么夏洛特应该去______号大门后面寻找宝藏.【答案】:【解析】:第9题【填空题】我市教研室对2008年嘉兴市中考数学试题的选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:已知这n人中,平均每题有11人答错,同时第6题答错的人数恰好是第5题答错人数的1.5倍,且第2题有80%的同学答对.则第5题有______人答对.【答案】:【解析】:第10题【填空题】参加2008年北京第29届奥运会的A,B,C,D四名运动员国籍各不相同,分别是美,韩,法,日.当然这里的名字顺序不一定与上面写的国籍顺序相同.已知:A和美国运动员都是排球运动员,B和日本运动员都是柔道运动员且比韩国运动员高,C不是排球运动员,则A是______,B是______,C是______,D是______【答案】:【解析】:第11题【填空题】有5名新同学,如果每两个人都握手1次,那么他们握手的总次数是______次.【答案】:【解析】:第12题【解答题】160人站成一行,自1起至160依次报数.然后,所有报奇数的离开.留下的再从1起报数,报奇数者又离开.这样继续下去.最后留下一个人.问这个人第一次报的数是多少?【答案】:【解析】:第13题【解答题】有锁若干把,现有六个人各掌握一部分钥匙,已知任意两个人同时去开锁,有且恰有一把锁打不开,而任何三个人都可以把全部锁打开,问最少有多少把锁?【答案】:【解析】:第14题【解答题】请你参与亮亮在翻转扑克牌游戏时的思考.(1)亮亮同学把3张正面都朝上的扑克牌每次都翻转2张,改变它们的朝向.他发现无论经过多少次这样的操作都不能使3张扑克牌的正面全部朝下.他的结论对吗?(2)把4张正面都朝上的扑克牌每次都翻转2张,改变它们朝向,经过若干次操作,能否使4张扑克牌的正面都朝下呢?(3)把4张正面都朝上的扑克牌每次都翻转3张,改变它们朝向,经过若干次操作,能否使4张扑克牌的正面都朝下呢?若能,至少要经过几次这样的操作?若不能,请说明理由.【答案】:【解析】:第15题【解答题】11个学生到书店去买书,每人都买了若干本.其中买书最多的人买了100本书.证明:这11个学生中必有2人,他们买的书相差不到10本.【答案】:【解析】:。
北京课改版数学初中七年级(初一)下册7.7《几种简单几何图形及其推理》ppt课件2
基本事实:过直线外一点有且只有一条直线与这条直线 平行.
按上述方法作平行线的根据是什么呢?请你猜想它和图 7-22中的∠1=∠2是否有关.
两条直线AB、CD被第三条直线
EF所截,得到八个角(图7-23 ). E
其中∠1与∠2,∠3与∠4,∠5与
57
B
∠6,∠7与∠8分别叫做同位角; A
七年级下册
7.7.2 几种简单几何图形及其推理
回顾旧知
1、余角、补角的概念? 2、余角、补角的性质? 3、对顶角的概念及性质? 4、平行线的定义?
进行新课
我们在第三章中曾学过“在同一平面内不相交的两条直 线叫做平行线”平行线应用很广泛.怎样准确地作平行线呢? 可以利用三角尺与直尺,照图7-22的方法去做.
步骤: 第一步:做直线AB,并用三角尺的一边贴住直线AB; 第二步:用直尺紧靠三角尺的另一条边; 第三步:沿直尺下移三角尺; 第四步:沿三角尺的边作出直线CD. 这样,就得到AB∥CD.
同学们在练习本上实际操作.
实践
请你动手作一条直线AB,在直线AB外作一点C,然后过 点C作AB的平行线,你能作出几条?
31
∠3与∠8,∠1与∠6分别叫做内 错角;∠1与∠8,∠3与∠6分别 叫做同旁内角.
C
68
D
42
F
图723
下面我们利用计算机演示当“三线八角”满足什么条件时, AB∥C用D.计算机画出图7-24,直线AB,CD被直线EF所截,EF与 AB,CD的交点分别为点M,N.分别显示八个角的测量值,然后 让直线AB绕点M旋转, 各个角的测量值就会发生变化.观察图 形的变化,当这八个角的测量值具有哪些关系时,AB与CD平行?
∠1=∠C, 求证:AC∥FD.
精选2019-2020年北京课改版初中七年级下册数学第七章 观察、猜想与证明7.7 几种简单几何图形及其推理复习
精选2019-2020年北京课改版初中七年级下册数学第七章观察、猜想与证明7.7 几种简单几何图形及其推理复习特训第八十九篇
第1题【单选题】
世界杯足球赛小组赛,每个小组4个队进行单循环比赛,每场比赛胜队得3分,败队得0分,平局时两队各得1分,小组赛完以后,总积分最高的两个队出线进入下轮比赛,如果总积分相同,还要按净胜球排序,一个队要保证出线,这个队至少要积( )
A、6分
B、7分
C、8分
D、9分
【答案】:
【解析】:
第2题【单选题】
某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A、若甲对,则乙对
B、若乙对,则甲对
C、若乙错,则甲错
D、若甲错,则乙对
【答案】:
【解析】:
第3题【单选题】
某轮船往返于A、B两地之间,设船在静水中的速度不变,那么,当水的流速增大时,轮船往返一次所用的时间( )
A、不变
B、增加
C、减少
D、增加,减少都有可能
【答案】:
【解析】:
第4题【单选题】
老师问5个学生,昨天晚上你们有几个复习数学了
张:没有人
李:一个人
王:两个人
赵:三个人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精选2019-2020年初中数学七年级下册7.7 几种简单几何图形及其推理北京课改
版习题精选九
第1题【单选题】
气象爱好者孔宗明同学在x(x为正整数)天中观察到:①有7个是雨天;②有5个下午是晴天;③有6个上午是晴天;④当下午下雨时上午是晴天.则x等于( )
A、7
B、8
C、9
D、10
【答案】:
【解析】:
第2题【单选题】
如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
A、15粒
B、18粒
C、20粒
D、31粒
【答案】:
【解析】:
第3题【单选题】
七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )
A、甲、乙、丙、丁
B、甲、丙、乙、丁
C、甲、丁、乙、丙
D、甲、丙、丁、乙
【答案】:
【解析】:
第4题【单选题】
甲,乙,丙,丁,戊与小强六位同学参加乒乓球比赛,每两人都要比赛一场,到现在为止,甲已经赛了5场,乙已经赛了4场,丙已经赛了3场,丁已经赛了2场,戊已经赛了1场,小强已经赛了( )
A、1场
B、2场
C、3场
D、4场
【答案】:
【解析】:
第5题【单选题】
有8个小朋友围成一圈,按顺时针方向依次编为1﹣8号.现按如下方式发糖:给1号发1块;然后顺时针向隔过1人,给3号发1块;再顺时针向隔过2人给6号发1块;接着又顺时针向隔过1人后发1块糖;…;如此续行.问最先拿到10块糖的是( )号小朋友?
A、8
B、5
C、3
D、2
【答案】:
【解析】:
第6题【单选题】
如图是一个风景区,A,B,C,D,E,F是这一风景区内的五个主要景点,现观光者聚于A点.假若你是导游,要带领游客欣赏这五个景点后再回到A点,但又不想多走“冤枉路”(不能走重复的路线和经过同一个景点),你认为可选择行走路线有( )种.
A、4
B、5
C、6
D、7
【答案】:
【解析】:
第7题【单选题】
A,B,C,D四人参加某一期的体育彩票兑奖活动,现已知:如果A中奖,那么B也中奖:如果B中奖,那么C中奖或A不中奖:如果D不中奖,那么A中奖,C不中奖:如果D中奖,那么A也中奖则这四个人中,中奖的人数是( )
A、1
B、2
C、3
D、4
【答案】:
【解析】:
第8题【填空题】
有A、B、C、D四位员工做一项工作,每天必须是三位员工同时做,另一位员工休息,当完成这项工作时,D做了8天,比其他任何人都多,B做了5天,比其他任何人都少,那么A做了______天.
【答案】:
【解析】:
第9题【填空题】
老师问A、B、C、D、E五位学生:“昨天你们有几个人玩过游戏?”他们的回答分别为A:没有人;B:一个人;C:二个人;D;三个人;E:四个人。
老师知道:他们之中有人玩过游戏,也有人没有玩过游戏。
若没有玩过游戏的人说的是真话,那么他们5个人中有______个人玩过游戏。
【答案】:
【解析】:
第10题【解答题】
四个足球队进行单循环比赛,规定胜一场得3分,平一场得1分,负一场得0分,有一个队一场都没输过,排名却倒数第一,你觉得可能吗?如果可能,请举出这情况何时出现;如果不可能,请说明理由.
【答案】:
【解析】:
第11题【解答题】
某人说:“我从去年开始都在撒谎,从没说过真话.”请问这句话可信吗?
【答案】:
【解析】:
第12题【解答题】
设a、b、c都是实数,考虑如下3个命题:
①若a^2+ab+c>0,且c>1,则0<b<2;
②若c>1且0<b<2,则a^2+ab+c>0;
③若0<b<2,且a^2+ab+c>0,则c>1.
试判断哪些命题是正确的,哪些是不正确的,对你认为正确的命题给出证明;你认为不正确的命题,用反例予以否定.
【答案】:
【解析】:
第13题【解答题】
27颗珍珠,有一颗是假的,但外观和真的一样,只是比真的珍珠轻一点.你能用天平称3次(不用砝码)将假的珍珠找出来吗?
【答案】:
【解析】:
第14题【解答题】
某参观团依据下列约束条件,从A、B、C、D、E五个地方选定参观地点:
①如果去A地,那么也必须去B地;
②D、E两地至少去一处;
③B、C两地只去一处;
④C、D两地都去或都不去;
⑤如果去E地,那么A、D两地也必须去
依据上述条件,你认为参观团只能去哪些地方参观?
【答案】:
【解析】:
第15题【综合题】
如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。
试说明:
AE∥CF;
""
AB∥CD。
""
【答案】:【解析】:。
