量子力学课程总结
量子力学课程总结与反思

量子力学课程总结与反思在量子力学课程中,我学到了许多关于微观世界的新概念和理论。
这门课程不仅带给我新的知识,也让我对物质世界的认识有了更新和深化。
首先,我学到了量子力学的基本原理和数学框架。
量子力学是描述微观粒子行为的理论,它与经典力学有很大的区别。
在量子力学中,粒子的性质和行为是通过波函数来描述的,而波函数的演化则由薛定谔方程决定。
通过学习薛定谔方程和波函数的性质,我对量子力学的基本原理有了更深入的理解。
其次,我学到了量子力学的测量理论。
在量子力学中,测量的结果是概率性的,而且测量会导致波函数的坍缩。
这一概念在初学时可能比较难以理解,但通过学习测量理论的数学形式和实例,我逐渐理解了量子力学的测量过程和测量结果的统计分布。
此外,我还学到了一些重要的量子力学应用,如波粒二象性、不确定性原理和量子力学中的电子结构等。
这些应用不仅扩展了我对量子力学理论的认识,也帮助我理解了一些实际现象的量子本质。
在学习量子力学的过程中,我也遇到了一些困难和挑战。
量子力学的数学语言和抽象概念对初学者来说可能比较难以理解和应用。
我发现通过反复学习和解答习题,以及与同学和教师的讨论,可以逐渐克服这些困难。
此外,我也意识到在学习量子力学时需要有坚实的数学基础,尤其是线性代数和微积分的知识。
在反思自己的学习过程中,我意识到量子力学是一门需要重复学习和实践的课程。
只有通过反复学习和解题,才能真正理解和掌握其中的概念和技巧。
同时,我也认识到量子力学是一门前沿科学,它的理论和应用还有许多未解决的问题和待发展的领域。
因此,我希望在未来的学习中能够继续深入研究量子力学,探索更多有关微观世界的奥秘。
量子力学知识点总结

v
2mx
1.05 1034 2 9.1 1031 1010
0.6106 m/s
按经典力学计算
v2 m
r
k
e2 r2
v
ke2 mr
9109 (1.6 1019 )2 9.11031 0.5 1010
2.2106m/s
速度与其不确定度 同数量级。可见,对原 子内的电子,谈论其速 度没有意义,描述其运 动必须抛弃轨道概念, 代之以电子云图象。
Eˆ i 哈密顿算符 t
pˆ x
i
Hˆ
x
2
xˆ x 2 U
定态薛定谔方程(一维)
条件:U=U(x,y,z)
不随时间变化。
2 2m
2m 2Ψ x2 U( x)Ψ
i Ψ t
一般薛定谔方程(三维) 2 2 U i
2m
5. (1) 用 4 个量子数描述原子中电子的量子态,这 4 个 量子数各称做什么,它们取值范围怎样?
(2) 4 个量子数取值的不同组合表示不同的量子态, 当 n = 2 时,包括几个量子态?
(3) 写出磷 (P) 的电子排布,并求每个电子的轨道角 动量。
答:(1) 4 个量子数包括: ➢ 主量子数 n, n = 1, 2, 3,… ➢ 角量子数 l, l = 0, 1, 2,…, n-1 ➢ 轨道磁量子数 ml, ml = 0, 1, …, l ➢ 自旋磁量子数 ms, ms = 1/2
处单位体积元中发现一个粒子的概率,称为概率密度。
因此波函数 y 又叫概率幅。
六、不确定关系
位置动量不确定关系: xpx / 2 能量时间不确定关系: Et / 2
量子力学总结

2个费米子
A k1k2
q1,q2
12k1
q1k2
q2k1
q2k2
q1
Quantum Mechanics
1 k1 q1 k1 q2 2k2 q1 k2 q2
2个玻色子
s k1k2
q1,q2
cn 2an
A (rv)(rv)drv n cn2
n
对于归一的波函数此项为一。
Quantum Mechanics
矩阵表示
A
a1
c1
b1
d1
A ac11
b1 d1
*
a1 c1
db1112an12
A
n
Quantum Mechanics
解存在的条件
久期方程
a1 an
b 0
c d1 an
给出 a n ,一般是多值。 对应不同本征值 a n 代入本征方程中,在考虑归一化条件,
A B A B 1 [A ,B ] 1[A ,B ]
2
2
Quantum Mechanics
2、量子力学基本原理: (1)状态→数学上用波函数描述,波函数是
(r,t)的函数,
是希尔伯特空间中的矢量。
波函数满足标准化条件:单值、连续、有限(或平方可积)。
波函数|ψ(x,t)|2才有物理意义,解释为概率密度。 在t时刻,在x--x+dx区域发现粒子的概率:dp=|ψ(x,t)|2 dx
a* c* a b b* d* c d
Quantum Mechanics
② AB C C B A
③ 本征值为一些实数, ④ 计算的常用基本公式
也是体系中测量这些力学量得 到的测量值
[xi, pˆj ]iij (i, j 1,2,3)
量子力学课程总结

量子力学课程总结简介量子力学作为现代物理学的基石,对于理解微观世界中的粒子行为起着至关重要的作用。
本文将对量子力学课程进行总结,深入探讨量子力学的基本原理、数学形式以及一些经典实验与现象的量子解释。
通过这门课程的学习,我对量子世界有了更深入的了解,并且对于量子力学的应用也有了一定的认识。
量子力学基本原理波粒二象性量子力学的基本原理之一是波粒二象性。
根据量子力学理论,微观物体既可以表现出波的性质,又可以表现出粒子的性质。
这一观念颠覆了我们对自然界的认识,代表性实验是双缝干涉实验,通过对电子或光子的干涉实验观察到的干涉条纹,验证了物质或能量的波动性质。
不确定性原理量子力学的另一个基本原理是不确定性原理,由海森堡提出。
不确定性原理表明,在测量某个粒子的某个物理量时,无论采用什么样的实验手段,都无法同时准确测量出粒子的位置和动量,或者能量和时间的值。
这一原理对于我们认识到微观世界的局限性有着重要的意义。
波函数和量子态波函数是量子力学的核心概念,它用来描述微观粒子的量子态。
根据波函数的演化方程——薛定谔方程,我们可以确定一个粒子在任意时刻的量子态。
波函数通过对位置、动量、角动量等物理量的测量,给出了相应的概率密度分布,从而揭示了微观粒子的统计规律。
叠加原理和量子叠加态叠加原理是量子力学的重要原理之一。
它表明,当一个系统处于两个或多个互不干扰的状态时,该系统的总量子态是这些状态的叠加。
这一概念被广泛应用于量子计算、量子通信和量子模拟等领域。
量子叠加态的表达方式是态矢量,它可以用一个复数向量表示。
数学形式希尔伯特空间和算符希尔伯特空间是量子力学中描述量子态和物理量的数学框架。
它是一个无穷维度的线性向量空间,量子态用希尔伯特空间中的向量表示。
算符是希尔伯特空间中的线性算子,用来描述量子系统的物理量以及其演化。
常用的算符有位置算符、动量算符、角动量算符等。
薛定谔方程和定态解薛定谔方程是量子力学中描述物体运动的基本方程。
量子力学学习心得

量子力学学习心得量子力学是一门涉及微观世界的科学,它描述了微观粒子的行为和性质。
在我学习量子力学的过程中,我真正认识到了它的深度和复杂性。
在此,我想分享一些我的学习心得。
首先,量子力学需要放弃经典物理的直观观念。
我们在日常生活中习惯于观察和描述经典物理现象,而在量子世界中,我们必须用数学语言描述粒子的行为。
这需要我们逐渐接受和理解量子力学的数学框架,如波动函数、算符以及矩阵形式的表示。
通过学习数学工具,我们可以更准确地描述和预测量子粒子的行为。
其次,量子力学对观察者的影响非常大。
根据测量原理,观察者的行为会导致波动函数的塌缩,从而确定粒子处于一些状态。
这个观察和测量过程是量子力学的关键概念,而且与经典力学的测量方式截然不同。
我学习了双缝干涉实验以及薛定谔猫等思想实验,深刻体会到了观察者对量子系统的影响。
这对我们理解物质的本质以及测量的可靠性有着重要启示。
不确定性原理是量子力学中的另一个重要概念,它表明在一些情况下,我们无法准确确定粒子的位置和动量,这是由于测量的性质决定的。
这种不确定性的存在挑战了我们对自然界的认识和理解。
不确定性原理的提出不仅揭示了物质的本质,也对我们思考科学和世界观提出了新的问题。
此外,在学习量子力学的过程中,我还意识到了科学与哲学之间的关系。
量子力学的概念和实验结果引发了众多哲学问题,如关于自由意志、存在性和实在性的讨论。
量子力学的发展不仅引领了科学的进步,也影响了哲学思考和对人类认知的界限重新思考。
总而言之,学习量子力学是一项艰巨而复杂的任务,需要逐步熟悉数学工具和理论框架。
通过学习量子力学,我更加深入地理解了物质和粒子的本质,认识到观察者对量子系统的重要性,也思考了科学与哲学的关系。
量子力学作为一门前沿科学,不仅丰富了我们对自然界的认识,也挑战了我们思考和理解世界的方式。
大学物理-量子力学小结
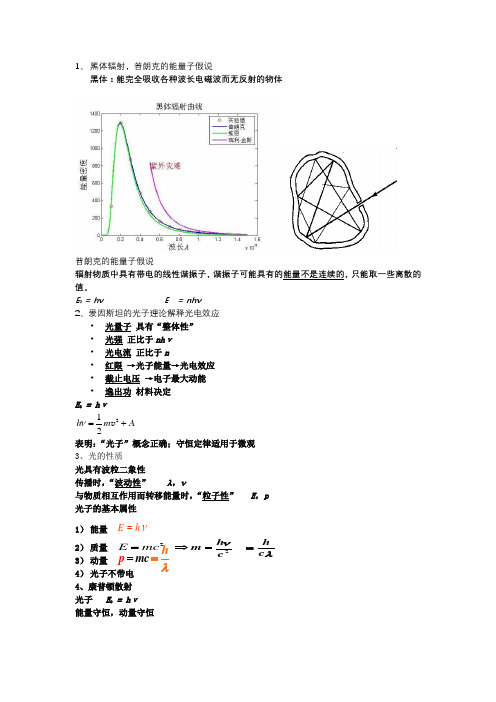
1、 黑体辐射,普朗克的能量子假说黑体:能完全吸收各种波长电磁波而无反射的物体普朗克的能量子假说辐射物质中具有带电的线性谐振子,谐振子可能具有的能量不是连续的,只能取一些离散的值。
E 0 = h ν E = nh ν2、爱因斯坦的光子理论解释光电效应•光量子 具有“整体性” •光强 正比于nh ν •光电流 正比于n •红限 →光子能量→光电效应 •截止电压 →电子最大动能 • 逸出功 材料决定E 0 = h ν212h m A ν=+v表明:“光子”概念正确;守恒定律适用于微观3、光的性质光具有波粒二象性传播时,“波动性” λ,ν与物质相互作用而转移能量时,“粒子性” E ,p光子的基本属性1) 能量 νh E =2) 质量 3) 动量 4) 光子不带电4、康普顿散射光子 E 0 = h ν能量守恒,动量守恒2mc E =2h m c ν⇒=λc h=p mc =λh =传递给反冲电子的能量等于光子损失的能量k 0E h h νν=-5、德布罗意波 微观粒子的波动性德布罗意假设 :实物粒子具有波粒二象性德布罗意公式h p λ= Eh ν= mvhp h ==λ h mc h E 2==ν6、 不确定关系用电子衍射说明不确定关系电子经过缝时的位置不确定x a ∆=电子经过缝后,x 方向动量不确定sin x p p p a λφ∆==hp λ= x hp a ∆=h p x x =∆∆考虑衍射次级有 h p x x ≥∆∆7、实物粒子的不确定关系对于微观粒子不能同时用确定的位置和确定的动量来描述量子力学精确计算:2x x p ∆∆⋅≥h2η≥∆⋅∆y p y 2η≥∆⋅∆z p z 8、物质波函数,及其统计诠释波函数 的解释——波恩(1926)统计解释:当测量用ψ 描写的状态下的粒子位置时,它在一点(x, y, z )附近的 d V 体积元中被发现的概率与 ψ *ψ d V 成正比Ψ 本身无意义|Ψ|2 代表粒子在某处单位体积中出现的概率——概率密度波函数的标准条件:单值、有限、连续还满足:归一化条件:*1ΨΨdV ∞=⎰ 9、薛定谔方程一维自由粒子波函数 (自由:势能函数U =0)()0(,)x i p x E t Ψx t Ψe -=h若粒子在势能为U 的势场中运动 E =E k +U含时薛定谔方程 (一维运动粒子)∂∂-+==∂∂222ΨΨU(x,t )Ψi E Ψ2m x t h h粒子的波函数 -=i Et Ψ(x,t )(x ) eψh定态薛定谔方程 (势场,一维运动粒子):波函数的空间部分方程亦常写作求解定态波函数典型步骤(一维无限深方势阱):• 1. 势能函数代入定态薛定谔方程,并讨论阱外• 2. 阱内,方程整理为如下形式,直接写出其通解• 3. 利用单值、有限、连续、归一化条件,确定通解中的三个参数,得到波函数• 4. 添加时间项,写出完整波函数(1) 一维无限深势阱中的粒子[]()()1,2nx kx k naπϕπ=+==概率密度2()nP xϕ=(2) 一维势垒隧道效应在势垒区域,粒子波函数不为零,表明粒子可以到达、甚至穿越势能高于其动能的势垒。
量子力学课程心得体会(2篇)
第1篇自接触到量子力学这门课程以来,我仿佛进入了一个充满神秘与奇妙的微观世界。
在这段学习旅程中,我不仅对物理学有了更深的理解,也对科学探索的精神有了更深刻的体会。
以下是我对量子力学课程的一些心得体会。
一、量子世界的奇妙之处1. 波粒二象性在量子力学中,微观粒子的行为既不像宏观物体那样简单,也不像经典物理学那样绝对。
波粒二象性是量子力学中最具代表性的特性之一。
通过学习,我了解到,微观粒子既可以表现出波动性,也可以表现出粒子性。
这种看似矛盾的现象,揭示了微观世界的复杂性和多样性。
2. 量子纠缠量子纠缠是量子力学中的另一个奇妙现象。
两个或多个粒子在量子态上相互关联,即使它们相隔很远,一个粒子的状态变化也会立即影响到另一个粒子的状态。
这种现象打破了经典物理学中信息传递的局限性,引发了我对量子信息领域的浓厚兴趣。
3. 量子隧穿效应量子隧穿效应是量子力学中的另一个重要现象。
当一个微观粒子受到势垒阻挡时,它有可能穿越这个势垒,这种现象被称为量子隧穿。
量子隧穿效应在纳米技术和量子计算等领域有着广泛的应用。
二、量子力学的方法论1. 矩阵力学和波动力学量子力学有两大基本形式:矩阵力学和波动力学。
矩阵力学采用矩阵运算来描述量子系统的状态和演化,而波动力学则用波动方程来描述。
学习这两种方法,使我更加深入地理解了量子力学的本质。
2. 变分法在量子力学中,变分法是一种常用的近似方法。
通过选取合适的试探波函数,可以近似求解出量子系统的基态能量。
学习变分法,使我掌握了求解量子力学问题的另一种思路。
3. 相对论量子力学相对论量子力学是量子力学与相对论相结合的产物。
在学习相对论量子力学时,我了解到量子力学在描述高速运动的微观粒子时,需要引入相对论效应。
这使我认识到,量子力学并非孤立的理论,而是与相对论等物理学分支相互关联。
三、科学探索的精神量子力学是一门揭示微观世界奥秘的学科,它的发展历程充满了科学探索的精神。
以下是我从量子力学课程中得到的几点启示:1. 勇于质疑在量子力学的发展过程中,许多科学家都曾对经典物理学提出质疑。
(完整版)量子力学总结
量子力学总结第一部分 量子力学基础(概念)量子概念所谓“量子”英文的解释为:a fixed amount (一份份、不连续),即量子力学是用不连续物理量来描述微观粒子在微观尺度下运动的力学,量子力学的特征简单的说就是不连续性。
描述对象:微观粒子微观特征量以原子中电子的特征量为例估算如下:○1“精细结构常数”(电磁作用常数),1371~10297.732-⨯==c e α○2原子的电子能级 eV a e me c e mc E 27~~0224222==⎪⎪⎭⎫ ⎝⎛ 即:数10eV 数量级○3原子尺寸:玻尔半径: 53.0~220mea =Å,一般原子的半径1Å○4速率:26~~ 2.210/137e c V c m s c ⋅-⨯ ○5时间:原子中外层电子沿玻尔轨道的“运行”周期秒1600105.1~2~-⨯v at π秒角频率160102.4~~⨯a vc ω,即每秒绕轨道转1016圈(电影胶片21张/S ,日光灯频率50次/S )○6角动量:=⋅⋅2220~~em me mv a J基本概念:1、光电效应2、康普顿效应3、原子结构的波尔理论波尔2个假设:定态轨道定态跃迁4、物质波及德布洛意假设(德布洛意关系)“任何物体的运动伴随着波,而且不可能将物质的运动和波的传播分开”,认为物体若以大小为P 的动量运动时,则伴随有波长为λ的波动。
Ph =λ,h 为普朗克常数 同时满足关系ω ==hv E因为任何物质的运动都伴随这种波动,所以称这种波动为物质波(或德布罗意波)。
称Ph h E v ==λ 德布罗意波关系 例题:设一个粒子的质量与人的质量相当,约为50kg ,并以12秒的百米速度作直线运动,求粒子相应的德布罗意波长。
说明其物理意义。
答:动量v p μ=波长m v h p h 3634101.1)1250/(1063.6)/(/--⨯=⨯⨯===μλ晶体的晶格常数约为10-10m ,所以,题中的粒子对应的德布罗意波长<<晶体的晶格常数,因此,无法观测到衍射现象。
量子力学的工作总结
量子力学的工作总结
量子力学是一门研究微观世界的物理学科,它探讨了微观粒子的行为和性质。
自从20世纪初以来,量子力学一直是物理学领域中最引人注目的研究方向之一。
在过去的几十年里,科学家们在量子力学领域取得了许多重大突破,这些突破不仅深刻影响了我们对世界的理解,也为未来的科技发展带来了巨大的潜力。
量子力学的工作总结可以从多个方面来展开。
首先,量子力学的基本原理包括了波粒二象性、不确定性原理、量子纠缠等重要概念。
这些原理的提出和发展,为我们理解微观世界的奇异现象提供了重要的理论基础。
其次,量子力学在技术和工程领域的应用也日益广泛。
量子计算、量子通信、量子传感等新兴技术的发展,为人类社会带来了前所未有的机遇和挑战。
最后,量子力学的研究也为我们揭示了自然界的奥秘,让我们对宇宙的本质有了更深刻的认识。
在未来,量子力学的研究将继续深入发展。
科学家们将继续探索量子世界的奥秘,寻找新的量子现象和量子技术的应用。
同时,量子力学也将与其他学科相互交叉,为人类社会的发展带来更多的创新和进步。
总的来说,量子力学的工作总结是一项重要的任务,它不仅可以总结过去的成就,也可以为未来的研究和发展指明方向。
量子力学的发展将继续为我们的生活和科技带来新的可能性,我们期待着在这个领域取得更多的突破和进展。
量子力学课程总结
量子力学
10
量子力 学
波函数和薛定谔方程
量子力学课程总结
V(x) a 0 x
一维线性谐振子
1 2 2 x 2
结论
V0
1 En = n+ 2 , n 0,1, 2,... 2 2 N e H n n n
算 符 的 本 征 值 和 本 征 函 数
3、动能的本征值和本征函数
T x Ae Be
ix
ix
Ae
i
2T
2
x
Be
i
2T
2
x
4、角动量的本征值
ˆ Lz -ih
2 1 1 ˆ2 2 [ L (sin ) ] 2 2 sin sin
1900年普朗克引入量子概念才 很好地解释黑体辐射
量子论的生日—1900年12月14日 柏林物理学会
/μm
量子力学
4
量子力 学
绪论
量子力学课程总结
1905年,爱因斯坦对光电效应做出了解释:
1 2 me vm =h -W0 2
量子力学
5
量子力 学
绪论
量子力学课程总结
1913年,玻尔提出了量子化条件解释了 经典理论在原子结构上遇到的困难
ˆ ˆ ˆ S S i S ˆ ,S ˆ ]i S ˆ [S x y z ˆ ,S ˆ ]i S ˆ [S y z x ˆ ,S ˆ ]i S ˆ [S z x y
ˆ ,L ˆ ]i L ˆ [L y z x ˆ ,L ˆ ]i L ˆ [L z x y
所以
ˆ S x
ˆ S y
ˆ S z
ˆ ˆa ˆ N a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2
0
1 2
0
1
S x 的本征函数
1
'
2
2 1
2
1
1 2
'
2 1
2
1
S y 的本征函数
1
''
2
2 1
2
i
1 2
''
2 1
2
i
量子力学
29
量子力 学
自旋与全同粒子
量子力学课程总结
两电子自旋波函数
χ ( s 1 z , s 2 z ) = χ α 1 ( s 1 z ) χ α 2 ( s 2 z ) ( α 1 , α 2 = ± 2 1 )
量子力学课程总结
厄米算符的对易
F ,G
FGGF
若式子为零,则 Fµ 和 Gµ
易,否则,不对易
对
测不准关系
F F F 均方差可以描述对本征态的偏离程度
(Fˆ )2 • (Gˆ )2 (k )2 4
量子力学
17
量子力 态和力学量的表象 学
量子力学课程总结
算符的矩阵表示,在G表象中
F11 F12 L
F21
F22
L
F1m L
F2m
L
Fµ L L L L L
Fn1 Fn2 L
Fnm L
L
L
L
L
L
在自身表象中,是对角矩阵,对角线上的值 是本征值
量子力学
18
量子力 态和力学量的表象 学
量子力学公式的矩阵表示 1、平均值
量子力学课程总结
F11 F12 F1n a1(t)
F21 F22 F2n a2(t)
量子力 学
量子力学课程总结
合肥工业大学微电子12-1班
量子力学
1
量子力 学
主 要 内 容
量子力学课程总结
1、绪论 2、波函数和薛定谔方程 3、量子力学中的力学量 4、态和力学量的表象 5、微扰论 7、自旋与全同粒子
量子力学
2
量子力 学
量子力学课程总结
量子力学
3
量子力
学 绪论
量子力学课程总结
经典力学的困难:无法解释黑体辐射、光电效应 等
量子力学
33
量子力 学
量子力学课程总结
量子计算机
量子计算机(quantum computer)是一类遵循量子力 学规律进行高速数学和逻辑运算、存储及处理量子信 息的物理装置。低功耗,散热好、速度极快。量子算 法代替经典算法。
量子力学
34
量子力 学
量子力学课程总结
国内量子科学的发展处于世界领先水平
波函数在空间中某一点的强度和在该点找到粒子 的概率成正比例,按照这种解释,描写粒子的波 乃是概率波。
态叠加原理一般表述:
若Ψ1 ,Ψ2 ,..., Ψn ,...是体系的一系列可能的状态,则这些态的 线性叠加 Ψ= C1Ψ1 + C2Ψ2 + ...+ CnΨn + ... 也是体系的一个可能状态。 (其中 C1 , C2 ,...,Cn ,...为复数)。
n
E (2)
(1)
n
n
E (1)
(2)
n
n
(0) n
LLLL LLLLLL LLLLLL LLLLLL LLLLLL
[Hˆ (0)
En(0)]
(0) n
0
[Hˆ (0)
En(0)]
(1) n
[Hˆ (1)
En(1)]
(0) n
[Hˆ(0) En(0)]
(2) n
[Hˆ (1)
En(1)]
量子力学
27
量子力 学
自旋与全同粒子
泡 利
S
x
2
x
算
S
y
2
y
符
S z
2
z
量子力学课程总结
因为Sx, Sy, Sz的本征值都是± /2 , 所以σx,σy,σz的本征值都是±1; σx2,σy2,σZ2 的本征值都是1 。
反
对 易 关
ˆ xˆ y ˆ yˆ x 0 ˆ yˆz ˆzˆ y 0 ˆzˆ x ˆ xˆz 0
r
uur
r 0 ur
征函数
uur r0
r r0
本 征 值 和 本
2、动量的本征值和本征函
数
u µ p r P 0 u pu r0 , P 0
ceh iu pu0 r•rr
P 0
征
函 数
箱归一化
1 ur
e p
3
i
ur r p•r
h
L2
归一化成δ
1 函数
ur
2h e p
i
ur r p•r
[
1 2
(s1z
)
1 2
(s2
z
)
1 2
(s2z
)
1 2
(s1z
)]
A
1 2
[1
2
(s1z
)
1 2
(s2
z
)
1
2
(s2
z
)
1 2
(s1z
)]
量子力学
30
量子力 学
量子力学课程总结
量子力学
31
量子力
量子力学课程总结
学
当前量子力学的重要应用
• 量子生物学 • 量子生命科学 • 量子神经网络 • 量子化学 • 量子材料科学 • 量子信息科学 • 量子计算机科学 • BEC器件、原子器件
h
3 2
量子力学
14
量子力 量子力学中的力学量
量子力学课程总结
学算
符
的
3、动能的本征值和本征函数
本
征 值
TxA eixB e ixA ei 2 h 2 TxB e i 2 h 2 Tx
和
本 征
4、角动量的本征值
函 数
Lˆ z
-ih
L ˆ2h2[sin 1 (sin )sin 1 2 22]
目前,它正在向材料 科学、化学、生物学、 信息科学、计算机科学 大规模渗透。 预计不久的将来它将 会成为
整个近代科学共 同的理论基础
量子力学
32
量子力 学
量子力学课程总结
量子通讯(Quantum communication)是指利用量子纠缠 效应进行信息传递的一种新型的通讯方式,具有高效,绝 对安全等特点。是国际量子物理和信息科学研究的热点
an
an
F11 F12
F21 F22
F1n F2n
0 久期行列式
Fn1
Fn2
Fnn
量子力学
20
量子力 态和力学量的表象 学
量子力学课程总结
狄拉克符号
右矢:|n > ψn(x);左矢:< |是右矢的共轭
1:*d
2:F|Fˆ|
量子力学
21
量子力 态和力学量的表象 学 线性谐振子与占有数表象
E (1)
(2)
n
n
(0) 学
量子力学课程总结
(2)非简并定态微扰 (本章简并微扰不是重点)
En
E(0) n
Hnn
mn
' | Hnm |2
E(0) n
Em(0)
L
n
(0) n
mn
'
Hmn
E(0) n
Em(0)
(0) m
L
Hm n
E(0) n
Em (0)
L)(
(0)
n
(1)
2
n
(2) n
L)
量子力学
23
量子力 微扰理论 学
量子力学课程总结
0 :
Hˆ(0)
E (0)
(0)
n
n
(0) n
1: 2 :
Hˆ(0)
(1) n
Hˆ(1)
E (0)
(0)
n
n
E (1)
(1)
n
n
(0) n
Hˆ(0)
(2) n
Hˆ(1)
E (1)
(0)
n
量子力学
22
量子力 微扰理论 学
量子力学课程总结
微扰体系的Schrödinger方程
H ˆ H ˆ(0) H ˆ(1)
En En(0)
E(1) n
E 2 (2) n
L
(H ˆ(0)
H ˆ(1))(
(0)
n
(1)
2
n
(2) n
L)
(En (0)
E(1) n
E 2 (2) n
1900年普朗克引入量子概念才 很好地解释黑体辐射
量子论的生日—1900年12月14日 柏林物理学会
量子力学
/μm
4
量子力
学 绪论
量子力学课程总结
1905年,爱因斯坦对光电效应做出了解释:
1 2
mevm 2
=h
-W0
量子力学
5
量子力
学 绪论
量子力学课程总结
1913年,玻尔提出了量子化条件解释了 经典理论在原子结构上遇到的困难
中国科学技术大学潘建伟院士及其团队与中 科院上海微系统所和清华大学合作,将可以抵御 黑客攻击的远程量子密钥分发系统的安全距离扩 展至200公里,创下新的世界纪录。
“量子科学实验卫星”现已完成关键部件的研制 与交付,卫星有望先于欧美在2016年左右发射, 在轨设计寿命为2年。
量子力学
35
量子力 学
