《高等数学辅导讲义》
高等数学辅导讲义
第一部分函数极限连续历年试题分类统计及考点分布本部分常见的题型1.求分段函数的复合函数。
2.求数列极限和函数极限。
3.讨论函数连续性，并判断间断点类型。
4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数 例1 (1988, 5分) 设2(),[()]1x f x e f x xϕ==-且()0x ϕ≥,求()x ϕ及其定义域。
解: 由2()x f x e =知2()[()]1x f x e xϕϕ==-,又()0x ϕ≥,则()0x x ϕ=≤.例2 (1990, 3分) 设函数1,1()0,1x f x x ⎧≤⎪=⎨>⎪⎩,则[()]f f x =1.练习题: (1)设1,1,()0,1,(),1,1,xx f x x g x e x ⎧<⎪===⎨⎪->⎩求[()]f g x 和[()]g f x ,并作出这两个函数的图形。
(2)设20,0,0,0,()(),,0,,0,x x f x g x x x x x ≤≤⎧⎧==⎨⎨>->⎩⎩求[()],[()],[()],[()]f f x g g x f g x g f x .二、 求数列的极限方法一 利用收敛数列的常用性质一般而言,收敛数列有以下四种常用的性质。
性质1(极限的唯一性) 如果数列{}n x 收敛,那么它的极限唯一。
性质2(收敛数列的有界性)如果数列{}n x 收敛,那么数列{}n x 一定有界。
性质3(收敛数列的保号性) 如果lim nn xa→∞=,且0a >(或0a <),那么存在0n N+∈,使得当0n n >时,都有0n x >(或0n x <).性质4(数列极限的四则运算法则) 如果,,lim lim nn n n xa yb →∞→∞==那么(1)()lim nn n xy a b →∞±=±;(2)lim nn n xy a b→∞∙=∙;(3)当0()nyn N +≠∈且0b ≠时,limn n nx a y b→∞=.例3 若 lim nn xa→∞=,则 limn n x a→∞=.注: 例3的逆命题是不对的, 例如我们取(1)nnx =-, 显然1limn n x →∞=,但数列(1)nnx=-没有极限。
高等数学辅助教材哪个好
高等数学辅助教材哪个好高等数学是大学数学教育中的重要组成部分，对学生的数学思维和分析能力的培养至关重要。
为了更好地理解和应用高等数学知识，许多学生会选择使用辅助教材。
然而，市面上有各种各样的高等数学辅助教材，学生常常面临选择困难。
本文旨在探讨几种常用的高等数学辅助教材，并提供一些建议，帮助学生选购适合自己的辅助教材。
一、《高等数学辅导讲义》《高等数学辅导讲义》是一本经典的辅助教材，由数学教育专家编写。
该讲义以简明扼要的方式解释了高等数学的核心概念和方法，并提供了大量的例题和习题，帮助学生巩固所学知识。
讲义内容全面，循序渐进，适合对高等数学有一定基础的学生使用。
此外，该讲义还提供了详细的解题思路和方法，有助于学生培养数学分析和解决问题的能力。
二、《高等数学解析教程》《高等数学解析教程》是一本理论与应用相结合的辅助教材。
该教程以严谨的数学理论为基础，通过大量实际问题的分析和解答，帮助学生将理论知识应用到实际问题中。
教程中的案例涵盖了不同领域的应用，如物理、经济学等，使学生能够更好地理解高等数学的实际应用场景。
此外，教程还提供了详细的推导过程和解题步骤，帮助学生理清数学思路，提高解题效率。
三、《高等数学习题集》《高等数学习题集》是一本专门用于练习和巩固高等数学知识的辅助教材。
该习题集包含了大量的练习题和解析，涵盖了高等数学各个重要的章节和知识点。
习题的难度逐渐增加，有助于学生逐步提升数学解题的能力。
此外，习题集还提供了详细的解题思路和方法，帮助学生理解题目的解法和解题思路。
综上所述，选择一本适合自己的高等数学辅助教材非常重要。
对于有一定基础的学生来说，可以选择《高等数学辅导讲义》或《高等数学解析教程》，这两本教材内容详尽，涵盖了高等数学的核心概念和方法。
而对于需要更多练习和巩固的学生来说，可以选择《高等数学习题集》，通过大量的练习提升自己的数学解题能力。
无论选择哪种教材，学生都应该注重理解和应用数学知识，培养自己的数学思维和解决问题的能力。
(完整word版)高等数学辅导讲义
第一部分函数极限连续历年试题分类统计及考点分布本部分常见的题型1.求分段函数的复合函数。
2.求数列极限和函数极限。
3.讨论函数连续性，并判断间断点类型。
4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数例1 (1988, 5分) 设2(),[()]1x f x e f x x ϕ==-且()0x ϕ≥,求()x ϕ及其定义域。
解: 由2()x f x e =知2()[()]1x f x e x ϕϕ==-,又()0x ϕ≥,则()0x x ϕ=≤.例2 (1990, 3分) 设函数1,1()0,1x f x x ⎧≤⎪=⎨>⎪⎩,则[()]f f x =1.练习题: (1)设 1,1,()0,1,(),1,1,x x f x x g x e x ⎧<⎪===⎨⎪->⎩求[()]f g x 和[()]g f x , 并作出这两个函数的图形。
(2)设20,0,0,0,()(),,0,,0,x x f x g x x x x x ≤≤⎧⎧==⎨⎨>->⎩⎩求[()],[()],[()],[()]f f x g g x f g x g f x .二、 求数列的极限方法一 利用收敛数列的常用性质一般而言,收敛数列有以下四种常用的性质。
性质1(极限的唯一性) 如果数列{}n x 收敛,那么它的极限唯一。
性质2(收敛数列的有界性)如果数列{}n x 收敛,那么数列{}n x 一定有界。
性质3(收敛数列的保号性) 如果lim n n x a →∞=,且0a >(或0a <),那么存在0n N +∈,使得当0n n >时,都有0n x >(或0n x <).性质4(数列极限的四则运算法则) 如果,,lim lim n n n n x a y b →∞→∞==那么(1)()lim n n n x y a b →∞±=±;(2)lim n n n x y a b →∞•=•;(3)当0()n y n N +≠∈且0b ≠时,limn n n x a y b→∞=.例3 若lim nn xa →∞=,则lim nn xa →∞=.注: 例3的逆命题是不对的, 例如我们取(1)n n x =-, 显然1lim n n x →∞=,但数列(1)n n x =-没有极限。
2024高等数学辅导讲义零基础篇pdf
2024高等数学辅导讲义零基础篇pdf
2024高等数学辅导讲义零基础篇（PDF）是一部针对零基础者的高等
数学辅导讲义，旨在帮助这部分人及时掌握新的数学知识，更好地理
解和学习高等数学。
1.本讲义全面覆盖了高等数学的基本概念和原理，包括集合论、代数学、几何学、解析学、概率论、非标准分析和微积分学等。
2.每一章节都以问题为导向，紧扣考试大纲和学习要求，涵盖了完备的理论知识点，以简洁明了的公式、实例和例题介绍，以便更好地理解
概念。
3.讲义附有大量练习题，侧重检验题，帮助学生加深对知识点的理解和掌握，更好地掌握知识的技能。
4.本讲义分为三大块内容：数学基本概念、基本技能和实用技能。
5.数学基本概念章节介绍了数学相关必备概念，它讨论了基本概念、基本公式以及基本定理，以帮助学生更好地理解基本知识。
6.基本技能章节介绍了常见的数学知识的解决方法，包括求导和积分技巧，以及如何利用转换求解定义域上的特征方程、曲线或增减相关的
问题。
7.实用技能章节介绍了一些有用的数学方法，包括曲线拟合、算法和数值计算、抽样理论和概率分布等，这些内容将有助于学生收集数据，建立数学模型，从而分析实际问题。
本讲义是一本入门级的高等数学辅导讲义，既可以作为学习高等数学的入门教材，也可以作为复习用途，以应对高考等考试。
本讲义附有完整的知识点理论介绍和大量实例、习题，有助于学习者及时理解新的数学结论，熟练应用数学方法求解实际问题。
2023高等数学辅导讲义
2023高等数学辅导讲义摘要：一、引言1.高等数学的重要性2.2023 高等数学辅导讲义的编写目的二、高等数学的主要内容1.函数与极限2.导数与微分3.积分4.多元函数微分学5.常微分方程三、2023 高等数学辅导讲义的特点1.系统性与完整性2.理论与实践相结合3.注重思维能力的培养4.丰富的例题与习题四、如何使用2023 高等数学辅导讲义1.结合教材进行学习2.制定合理的学习计划3.勤于练习，善于总结4.参加课后讨论与辅导五、总结1.2023 高等数学辅导讲义的价值2.对学习者的期望正文：一、引言高等数学是理工科专业学生的重要基础课程，涉及到函数、极限、导数、积分等基本概念，以及微分方程、多元函数微分学等高级内容。
为了帮助广大学习者更好地掌握这门课程，我们编写了2023 高等数学辅导讲义。
二、高等数学的主要内容高等数学主要包括以下五个部分：1.函数与极限：研究变量之间的关系以及变量在某一范围内的变化情况。
2.导数与微分：研究函数在某一点处的变化率，以及利用微分研究函数的局部性质。
3.积分：研究函数在某一区间上的累积效应，以及利用积分求解有关问题。
4.多元函数微分学：研究多元函数的导数、微分以及方向导数等概念，了解多元函数的局部性质。
5.常微分方程：研究微分方程的解法及应用，涉及诸如一阶、二阶微分方程的求解等问题。
三、2023 高等数学辅导讲义的特点2023 高等数学辅导讲义具有以下特点：1.系统性与完整性：讲义按照教材的章节安排，系统地介绍了高等数学的各个知识点，保证学习者全面掌握课程内容。
2.理论与实践相结合：讲义在讲解理论知识的同时，注重结合实际问题进行讲解，培养学习者的实际问题解决能力。
3.注重思维能力的培养：讲义在例题与习题的选择上，注重启发学习者的思维，提高学习者的逻辑推理能力。
4.丰富的例题与习题：讲义提供了大量典型例题与习题，帮助学习者巩固知识点，提高解题技巧。
四、如何使用2023 高等数学辅导讲义1.结合教材进行学习：学习者应将讲义与教材相结合，充分利用教材中的例题与习题进行学习。
(完整word版)高等数学辅导讲义.doc
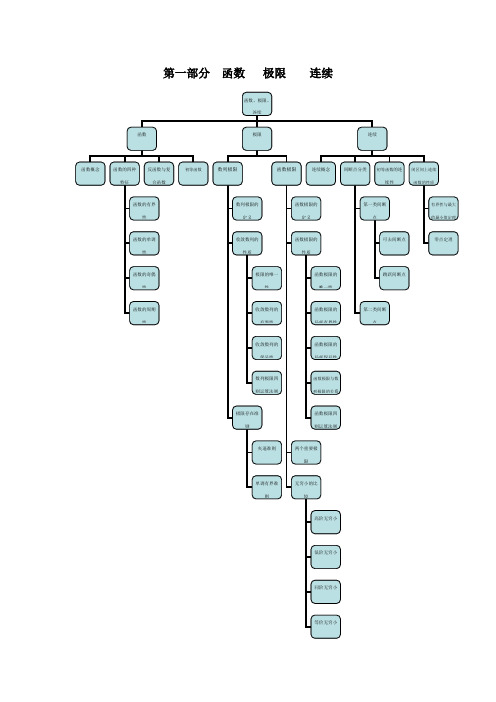
第一部分函数极限连续函数、极限、连续函数极限连续函数概念函数的四种反函数与复初等函数数列极限函数极限连续概念间断点分类初等函数的连闭区间上连续特征合函数续性函数的性质函数的有界数列极限的函数极限的第一类间断有界性与最大性定义定义点值最小值定理函数的单调收敛数列的函数极限的可去间断点零点定理性性质性质函数的奇偶极限的唯一函数极限的跳跃间断点性性唯一性函数的周期收敛数列的函数极限的第二类间断性有界性局部有界性点收敛数列的函数极限的保号性局部保号性数列极限四函数极限与数则运算法则列极限的关系极限存在准函数极限四则则运算法则夹逼准则两个重要极限单调有界准无穷小的比则较高阶无穷小低阶无穷小同阶无穷小等价无穷小历年试题分类统计及考点分布考点复合函数极限四则两个重要单调有界无穷小的合计运算法则极限准则阶年份19871988 5 3 8 19891990 3 3 6 1991 5 3 8 1992 3 3 1993 5 3 8 1994 3 3 1995 3 3 1996 3 6 3 12 1997 3 3 199819992000 5 5 200120022003 4 4 8 2004 4 4 20052006 12 3 15 2007 4 4 2008 4 4 2009 4 4 2010 4 4 2011 10 10 20 合计8 18 37 32 27本部分常见的题型1.求分段函数的复合函数。
2.求数列极限和函数极限。
3.讨论函数连续性，并判断间断点类型。
4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数 例 1 (1988, 5 分) 设 f (x)e x2, f [ (x)]1 x 且 ( x) 0 求 (x) 及其定义,域。
解: 由 f (x) e x 2知 f [ ( x)] e2( x)1x ,又 (x) 0 ,则 ( x)ln(1 x), x 0 .例 2 (1990, 3 分) 设函数 f ( x)1, x1则 f [ f ( x)]10, x 1, .1, x1,练习题 : (1)设f (x)0, x1, g ( x)e x , 求f [ g( x)] 和 g[ f (x)] , 并作出这1, x 1,两个函数的图形。
高数辅导讲义
高数辅导讲义引言高等数学作为一门基础学科，对于理工科学生来说具有重要的地位。
然而，由于其抽象、理论性强以及计算方法繁琐等特点，很多学生都觉得高数难以理解和掌握。
因此，本讲义旨在通过系统的学习和辅导，帮助读者掌握高等数学的基本概念、理论和计算方法，提高其对高数的理解和应用能力。
一、基础概念1.1 实数与复数实数是指包括有理数和无理数的全体数。
有理数包括整数、分数和有限小数，无理数包括无限不循环小数，如π和√2等。
复数由实部和虚部组成，形如a+bi，其中a和b均为实数，i为虚数单位。
1.2 函数和极限函数是一种特殊的关系，它描述了自变量和因变量之间的对应关系。
极限是函数的重要概念，用于描述自变量无限接近某个数值时，函数取值的变化趋势。
1.3 导数和微分导数是描述函数变化快慢的工具，表示函数在某一点处的变化率。
微分是导数的几何意义，用于刻画函数曲线的切线斜率。
二、重要理论2.1 微分中值定理微分中值定理是微分学中的一组重要定理，包括罗尔定理、拉格朗日中值定理和柯西中值定理。
它们揭示了函数在一定条件下的性质和规律，应用广泛。
2.2 泰勒展开泰勒展开是将函数用无穷多项式逼近的方法，利用一阶导数和高阶导数来描述函数的性质。
泰勒展开在数学分析以及物理、工程等领域都有广泛的应用。
三、计算方法3.1 极限的计算计算极限是高等数学的基本技能之一，有多种方法可以计算极限，如代数运算法、夹逼定理、洛必达法则等。
3.2 导数的计算导数的计算是高数中的重要内容，通过基本导数公式和求导法则，可以计算各种函数的导数，如多项式函数、三角函数、指数函数等。
3.3 积分的计算积分是导数的逆运算，也是高数中的重要概念和计算方法。
凭借基本积分公式和换元积分法、分部积分法等技巧，可以计算各种函数的积分。
四、应用领域4.1 物理学中的应用高等数学在物理学中有广泛的应用，如描述物体运动的微积分、解析几何在力学中的应用等。
4.2 工程学中的应用工程学中的各种应用问题，如电路分析、信号处理、控制系统等，都离不开高等数学的支持和应用。
金榜时代高等数学辅导讲义
金榜时代高等数学辅导讲义摘要：一、金榜时代高等数学辅导讲义概述二、高等数学的重要性三、金榜时代高等数学辅导讲义的特点四、金榜时代高等数学辅导讲义的内容及亮点五、金榜时代高等数学辅导讲义的使用建议正文：一、金榜时代高等数学辅导讲义概述《金榜时代高等数学辅导讲义》是一本针对高等数学课程的同步辅导教材，适用于各类本专科院校的学生。
该书旨在帮助学生更好地掌握高等数学的基本概念、理论知识和方法技巧，提高学生的数学素养和解决实际问题的能力。
二、高等数学的重要性高等数学是现代科学的基础，其重要性不言而喻。
在工程技术、自然科学、经济学、生物学等各个领域，高等数学都扮演着关键角色。
掌握高等数学，不仅能够帮助学生更好地理解相关专业知识，还能够提高学生的逻辑思维和分析问题的能力。
三、金榜时代高等数学辅导讲义的特点1.系统性强：该书按照高等数学的课程体系进行编排，从基本概念到方法技巧，内容系统完整，便于学生全面掌握高等数学知识。
2.实用性强：书中例题丰富，贴近实际，有利于学生将所学知识应用于解决实际问题。
同时，习题部分也有针对性地进行了设计，帮助学生巩固所学内容。
3.辅导性强：该书注重辅导学生掌握高等数学的学习方法和技巧，以及解决各类题型的思路和策略，有利于提高学生的学习效果。
四、金榜时代高等数学辅导讲义的内容及亮点《金榜时代高等数学辅导讲义》主要包括函数与极限、导数与微分、微积分基本定理、多元函数微分法、重积分等内容，涵盖了高等数学的主要知识点。
亮点一：书中例题丰富，解析详细，能够帮助学生更好地理解高等数学的基本概念和方法技巧。
亮点二：课后习题部分有针对性地进行了设计，有利于学生巩固所学内容，并提高学生的实际解题能力。
亮点三：该书注重辅导学生掌握高等数学的学习方法和技巧，以及解决各类题型的思路和策略，有利于提高学生的学习效果。
五、金榜时代高等数学辅导讲义的使用建议1.建议学生按照课程进度使用该书，同步学习，以达到更好的辅导效果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
44 页 最后一行
45 页 第1行
1 1 ( f ′(ξ ) + f ′(η )) − (ξ 2 + η 2 ) = 0 2 2
= F ′(a ) 0, F ′′( x) > 0
49 页例 1 证 = f ′(a ) 0, f ′′( x) > 0 明第 1 行
f ′(a ) = 0, f ′′( x) > 0( x > a) 得 f ′( x) > 0( x > a ) F (a ) = 0, 49 页例 1 证 再由 明第 3 行 x) 0( x > a ) f ′(= f ′( x) < 0, 0 < x < 1, 52 页 例 12 得 证明第 5 行 x > 1, f ′( x) > 1,
1 1 F ( ) − F (0) = f ′(ξ ), 2 2 1 1 F (1) − F ( ) = f ′(η ) 2 2
1 ) ex ≠ 0
1 = F ( ) − F (0) 2 1 F (1) − F ( )= 2 1 ) F ′(ξ = 2 1 F ′(η )= 2 1 ( f ′(ξ ) − ξ 2 ), 2 1 ( f ′(η ) − η 2 ) 2
49 页例 1 证 明第 2 行 由
F ′(a ) = 0, F ′′( x) > 0( x > a ) 得 F ′( x) > 0( x > a ) F (a ) = 0, 再由 x) 0( x > a ) F ′(= f ′( x) < 0, 0 < x < 1, 得 x > 1, f ′( x) > 0,
2014全程包括基础班+强化班+冲刺班+押题班持续不断更新中，QQ：756294099，有条件请积极购买正版
文都汤家凤《2014 高等数学辅导讲义》勘误表 1
位置 书中错误 更正为
n
15 页 第2行
2
4n + n 4n + 1 4n + 2 n n + ≤ 4n 2 + n 4n 2 + 1
2 2
由
52 页 例 13 证明第 1 行
′( x) f=
1 ≠0 1+ x
′( x) F=
1 ≠0 1+ x
因为左右极限 则 f ( x) 在 x = a 处可导； 则 f ( x) 在 x = a 处不可导。
f (0) + f (1) + f (2) = 3 f (0)
在 (a, b) 内可导
f (0) + f (1) + f (2) = 3 f (c )
在 (0, a ) 内可导
f ′( x= ) ex ≠ 0
≤
1
+
2
+
n
4n 2 + n 4n 2 + 1 4n 2 + 2 1 n + ≤ 2 4n + n 4n 2 + 1
因为左右导数 则 f ( x) 在 x = a 处可导； 则 f ( x) 在 x = a 处不可导。
≤
1
+
1
+
21 页 注 解 （3）第 3 行 29 页 最后一行 38 页 第4行 41 页 第1行 44 页例 3 证 明第 1 行