钢筋混凝土粘结滑移问题的单弹簧联结单元法

合集下载

钢筋混凝土粘结滑移相关问题

2 3 3
2
- 0. 478 ! 10 s )f ts
4 4
c /d ∀ F (x )
2 2
( 4)
式中:
为局部粘结应力 ( N /mm ), s 为局部滑移
( mm ) , f ts为混凝土劈位强度 ( N /mm ) , c /d 为混凝土保护层和钢筋直径比; F ( x ) 为粘结刚度分布函数, x 为至最接近的横向裂缝的距离 ( mm ) 。 5) 狄生林从梁式试件剪跨内测点的试验数据拟合的公式 = 6. 59 ! 10 s - 2 . 13 ! 10 s + 0. 22 ! 10 s
2 4 2 2 6 3
( 5)
式中, 为粘结应力 ( N /mm ), s 为滑移量 ( mm )。 6) 中国建筑科学研究院徐有邻等人做了一系列试验, 系统地研究了混凝土强度、保护层厚度、锚固长度、配箍率、钢筋直径对粘结锚固性能的影响, 将粘结滑移曲线分成 5段 (微滑移段、滑移段、劈裂段、下降段、残余段 ) 进行描述, 曲线上有 4 个转折点, 通过实测结果得出一分段函数表达式, 并用一个位置函数同时考虑不同锚固深度处的变化, 建立了 - s 关系: = 式中: ( s) ∀ (x ) ( 6) ( s)即用 ( x )是用来描述粘结滑移关系随不同锚固深度
K ey w ord s : re inforced concrete; bond slip; constitutive m ode;l spring e lem en t
在钢筋混凝土结构中, 钢筋和混凝土两种性质完全不同的材料能共同工作, 主要是依靠钢筋与混凝土间的粘结应力, 也就是两者接触面上的剪应力。钢筋与混凝土的粘结强度主要由水泥凝胶体与钢筋表面的化学胶着力、混凝土与钢筋之间的摩擦力以及机械咬合力三部分组成。混凝土硬化后通过粘结作用, 钢筋与混凝土可以实现应力传递, 并达到变形协调。本文主要从试验方法、影响因素、本构关系、粘结单元等方面对钢筋混凝土粘结滑移研究中的相关问题进行了探讨。 1 粘结滑移试验方法结构中钢筋粘结部位的受力状态复杂, 很难准确模拟。采用不同形状和受力状态的试件, 目前主要发展了 3种试验方法, 即拔出试验、梁式试验和轴拉试验

ansys弹簧单元的使用

ansys弹簧单元的使⽤【问题1】ANSYS中弹簧的设置现在做机床分析，在原有螺栓的地⽅要加弹簧单元，每个弹簧单元有三个⽅向的⾃由度。

为了⽅便添加弹簧单元，模型应该如何建⽴呢（⽐如，为了⽅便在将机床与地⾯连接的螺栓处添加弹簧单元，我现在建模时会建⽴凸台，将凸台与机床连接添加三个⽅向的弹簧单元）；另外就是导轨与床⾝连接处添加弹簧单元时，是否需要添加三个⽅向的⾃由度呢（因为如果不加凸台的话，沿导轨的⽅向不⽅便加弹簧）；最后，假如我的机床中共有20处需要添加弹簧，每个弹簧有三个⽅向添加参数，不知⼤家的参数如何设置⽐较⽅便（我以前没做过弹簧，现在是建⽴⼀个combin14单元，添加该单元的刚度和阻尼系数，⽐较⿇烦。

如果弹簧的X ⽅向系数都⼀样的话，是否有简便⽅法呢）。

⾮常感谢⼤家的帮助，如果答案满意的话，愿追加50分【最佳答案】第⼀，如果建弹簧单元⽅便的问题：你可以⽤⼀些命令流来建⽴，⽐如你知道具体位置时想得到node编号，可以⽤Nnum=node(x,y,z)，其中Nnum就是返回得到的(x,y,z)位置的node编号；如果知道该位置的关键点号k1，你想得到该位置的节点编号，可以⽤Nnum=node(kx(k1),ky(k1),kz(k1)) 得到了节点号后，⽤E,Nnum1,Nnum2建⽴连接单元，很⽅便。

这样做的好处，⼀是减⼩了重复操作的⼯作量；⼆是，如果⼿动加单元，万⼀mesh重做后，要重新去找点、⼿动建单元，很⿇烦。

第⼆，如果想建三⽅向的连接属性，建议从同⼀点建3个不同⽅向的连接单元。

尽量⽤命令流操作（可以局部写命令流，然后输⼊到命令窗⾥），可以减⼩很多重复⼯作量，以及⽅便⾁眼难以分辨的内部点选取。

【问题2】ansys中弹簧阻尼单元的设置请教⼤家⼀个问题，在ansys中进⾏机床的静动态分析，机床的导轨和导轨滑块设置硬点之后，连接对应的硬点要建⽴弹簧阻尼单元。

请问弹簧阻尼单元具体应该怎样建⽴呢，包括如何将硬点连接起来，如何设置弹簧阻尼单元的参数（参考下图）。

一种用于在钢管混凝土有限元模型中添加弹簧单元的方法

一种用于在钢管混凝土有限元模型中添加弹簧单元的方法我折腾了好久一种用于在钢管混凝土有限元模型中添加弹簧单元的方法，总算找到点门道。

我刚接触这个的时候，真的是一头雾水，就像在黑暗里摸索一样。

一开始我是按照一些书上的标准步骤来尝试的，比如说先创建钢管和混凝土的有限元模型，这个虽然不简单，但也还算是有章可循，就好比你搭积木一样，一块一块把这个基本框架搭好。

但是一到添加弹簧单元就出问题了。

我开始就想当然地直接把弹簧单元按照普通单元的添加方式弄进去，根本没考虑到钢管混凝土的特殊性。

结果模型运行起来错误百出，不是这儿不匹配就是那儿受力分析完全不对。

这可把我愁坏了，后来我就重新梳理思路，我想弹簧单元不就是用来模拟一些特殊的连接关系嘛。

所以我就先仔细研究钢管和混凝土之间的连接特性。

我做了好多小的测试模型，就像是小试牛刀。

比如说我单独建立一个很简单的钢管和混凝土小块连接的模型，只添加一个弹簧单元，慢慢去调整弹簧的参数，什么刚度啦、阻尼之类的。

但是这里面也有很多不确定的东西，刚度该设成多少呢？我当时就很懵，只能一点点试，我从很小的值开始，逐步加大，观察模型的反应。

就像你炒菜放盐一样，先放一点尝尝，不够再放。

然后我又想到一个问题，弹簧的布置方式。

我开始不确定是按照均匀分布好还是集中在某些特殊点上好。

我两种都试了试，发现均匀分布对于一些整体受力均匀的模型表现还行，但要是有局部受力特殊的地方，集中布置在这些点附近效果更好。

比如说对于有外力集中作用在钢管某个局部的模型，就在那个局部对应的混凝土和钢管连接部分集中多布置些弹簧单元。

而且在添加弹簧单元的时候，节点的选择可重要了。

我之前就犯过错，选错了节点，那就感觉整个模型的弹簧就像长错了地方，完全发挥不了作用。

这个节点要选在能够准确反映钢管和混凝土相互作用的地方，就像是两个人手拉手，你的手得拉对地方才有那种传递力的效果。

这里我还有个小经验，一定要多参考相似的成功案例。

我当时找了好多论文、实际工程案例中的有限元模型，看看人家是怎么添加弹簧单元的。

2016新编火灾后钢筋混凝土节点钢筋粘结滑移模拟

2016新编火灾后钢筋混凝土节点钢筋粘结滑移模拟火灾后钢筋混凝土节点钢筋粘结滑移模拟钢筋混凝土节点在受到火灾作用后，钢筋与混凝土之间的粘结力出现了大幅度的下降，这就导致了两者之间较大的粘结滑移现象。

在进行钢筋混凝土节点抗震性能研究的时候，其滞回曲线出现了大的滑移现象，这与两者之间粘结力下降导致的滑移量增大有着直接的关系。

在ABAQUS中利用非线性弹簧单元来模拟两者间的粘结滑移是比较合适的，下面介绍弹簧单元及在本次模拟中的应用。

第一部分:弹簧单元弹簧单元时一种连接单元，在ABAQUS中它具有以下的性质:1.能够将力和相对位移联系起来2.在ABAQUS/CAE中能够将相对转角和弯矩联系起来3.可以是线性的也可以是非线性的4.如果是线性弹簧，可以基于频率直接进行稳态动力分析5.也可以基于温度和其他场变量的求解6.可以通过虚拟的弹簧刚度来模拟理想状态下的结构阻尼因子弹簧单元始终利用力和位移来描述。

当弹簧与某一自由度上的位移相关时，相对位移和力这些变量就在弹簧单元中表现。

如果弹簧单元与某一自由度上的转角相关，它就是扭转弹簧，相对转角通过弹簧转化成弯矩。

粘滞性弹簧的行为在ABAQUS/CAE中可以通过频变弹簧和频变阻尼的组合成功模拟。

典型应用弹簧单元被用来模拟实际的物理弹簧和理想化的轴向扭转组件。

还可以模拟阻止刚体运动的反力。

它们还可以通过假设的弹簧刚度指定结构阻尼系数来模拟结构的阻尼。

选择适当的单元类型Spring1，Spring2单元可以应用在隐式分析中，Spring1用在定义点和区域之间，Spring2用在定义点和点之间，这两种单元作用的都是以特定的方向。

SpringA可以应用在显示分析也可以应用在显式分析中，通过连接两个节点的作用线产生作用，因此在大的位移相应分析中这个作用线可能会产生旋转。

Spring1，Spring2弹簧单元都能够定义位移和旋转的自由度(后种情况被称为扭转弹簧)。

然而，在大位移响应分析时应用扭转弹簧需要仔细考虑在节点上整体的转动情况。

Combin39使用经验

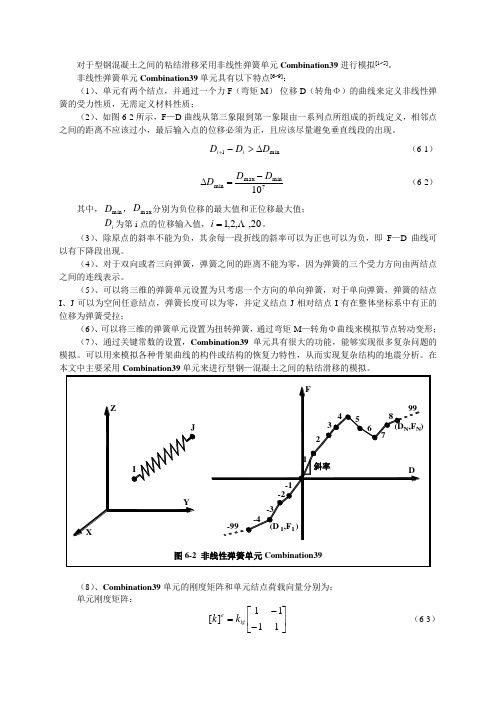
对于型钢混凝土之间的粘结滑移采用非线性弹簧单元Combination39进行模拟[1~5]。

非线性弹簧单元Combination39单元具有以下特点[6~9]：
（1）、单元有两个结点，并通过一个力F （弯矩M ）-位移D （转角Φ）的曲线来定义非线性弹簧的受力性质，无需定义材料性质；
（2）、如图6-2所示，F —D 曲线从第三象限到第一象限由一系列点所组成的折线定义，相邻点之间的距离不应该过小，最后输入点的位移必须为正，且应该尽量避免垂直线段的出现。

min 1D D D i i ∆>-+ （6-1）
7min max min
D D D -=∆ （6-2）
单元结点荷载向量：
⎥⎦
⎤⎢⎣⎡-=11][F F e （6-4）其中弹簧单元的刚度系数tg k 取值如图6-3所示。

基于ANSYS接触分析的粘结-滑移数值模拟

基于ANSYS接触分析的粘结-滑移数值模拟赵卫平【摘要】Contact analysis of pull-out specimen was carried out by using finite element program ANSYS 10. 0. A series of numerical simulation techniques, such as defining material model, establishing finite element model (FEM), generating contact element and post-processing were studied. The practical method of setting up 3-D contact pair with element Targel70 and Contal74 was emphatically introduced. Both friction coefficients of Coulomb friction model and adhesion strength were recommended. Finally, bond-slip numerical simulation was achieved based on ANSYS contact analysis. Results show that contact friction, contact pressure and contact state in the process of steel bar pull-out can be studied by this method, which makes up the deficiency of macro test. This method is feasible to simulate bond-slip relationship during pull-out test.%采用通用有限元程序ANSYS 10.0对拔出试件进行了接触分析,对数值模拟中的材料模型定义、有限元模型的建立、接触单元生成及后处理等关键技术进行了系统的研究；重点介绍了使用Targe170和Conta174单元建立三维接触对的实用方法,建议了库仑摩擦模型中摩擦因数和胶着强度的取值,最终实现了基于ANSYS接触分析的粘结-滑移数值模拟.结果表明:该方法可对钢筋拔出过程中的接触摩擦力、接触压力及接触状态等问题进行研究,弥补了宏观试验的不足,模拟拔出试验中的粘结-滑移关系具有一定的可行性.【期刊名称】《建筑科学与工程学报》【年(卷),期】2011(028)002【总页数】8页(P44-51)【关键词】高强混凝土；细晶粒钢筋；粘结-滑移；数值模拟；ANSYS；高温【作者】赵卫平【作者单位】同济大学建筑工程系，上海200092【正文语种】中文【中图分类】TU3750 引言1967年Ngo等［1］建立了第1个关于钢筋与混凝土粘结问题的有限元模型。

钢筋混凝土黏结滑移曲线研究与数值模拟_刘运林

钢筋混凝土黏结滑移曲线研究与数值模拟
刘运林
1， 2
*
叶献国
1
种
迅
1
丁克伟
2
（ 1．安徽建筑大学，合肥 230601 ； 2. 合肥工业大学，合肥 230009 ）摘要：现有具有代表性的黏结滑移曲线可以分为两大类，一类为单一曲线表达式，另一类为多段表达
式。不同的单一表达式黏结滑移曲线变化较大，峰值黏结应力和峰值滑移量均有较大差别；多段表达式明确地表达了上升段、峰值滑移段和残余变形段，不同表达式的峰值应力也有所不同。在比较分析的基础上，提出修正黏结滑移曲线，并采用有限元软件对其进行验证，模拟曲线与参考文献试验曲线符合较好，表明模型和数值模拟的可靠性。关键词：黏结滑移曲线；弹簧单元；双弹簧连接模型 DOI： 10. 13204 / j． gyjz201503015
［1 － 4］
供数值模拟计算使用。 1 不同黏结滑移曲线的比较图 1 中列出了前述几种单一曲线表达式得到的黏结应力－滑移量关系曲线（其中列出了 C Kankam 曲线不同位置处的黏结滑移关系）。由图 1 中可以看出，由于试验方法、试验条件的不同，不同的黏结滑移曲线变化较大，不同曲线的峰值黏结应力和峰值滑移量均有较大差别。图 1 中还列出了 GB 50010 —2010 规范建议的部分曲线，结合图 2 可以看出，单一表达式的黏结应力峰值对应的滑移量远
Fig． 3 图3 修正黏结滑移模型 proposed by LY
New bond stressslip relationship （ monotonic loading）
适用条件如下。劈裂破坏：保护层厚度大于纵筋直径，且箍筋面 n 为受到箍筋约束的纵筋数量，积不小于 0. 25 nA s ， A s 为纵筋截面积。

单弹簧联结单元法的改进算法

ｃｖｈｅｂｄｓｒｓ — ｌｐｒｌｔｏｈｉｆｔｅｎｆｒｅｏｒｔ，ｗｈｃｋｅｈｅｍｅｈｍｐｏｖｄＴｈｅｕｒｅｏｆｔｏｎｔｅｓｓｉｅａｉｎｓｐｏｈｅｒｉｏｃｄｃｎｃｅｅｉｈｍａｓｔｔｏｄｉｒｅ．
ＩｒｖｍｅｔｏｉｇｅＳｒｎｏｎ —ｌｍｅｔＭｅｈｄｍｐｏｅｎｆＳｎｌｐｉｇＪｉｔｅｅｎｔｏ
ＹａａｏｕｎＴｉｎｙＬｉＴｏｇｃｕｎｎｈＺｈｏＬａｈａ。ａｎｏ
（．ＣｈｎｊａｇＳｒｅ，Ｐａｎｎ１ａｇｉｎｕｖｙｌｎｉｇ，ＤｅｉｎａｄＲｅｅｒｈＬｉｔｄＬａｉｔｍｐｎ，Ｗｕａ３００ｓｇｎｓａｃｍｉｅｉｂｌｙＣｏａｙｉｈｎ４０１，Ｃｈｎ；ｉａ２．ＣｏｌｇｆＷａｅｏｓｒａｃｌｅｏｔｒＣｎｅｖｎｙ＆ＨｙｒｐｗｅｎｉｅｒｎｅｄｏｏｒＥｇｎｅｉｇ，Ｈｏａｉ．，Ｎａｊｇ２０９，Ｃｈｎ）ｈｉＵｎｖｎｉ１０８ｎｉａ
ＡｂｔａｔＳｎｌｐｉｇｊｉｔｅｅｎｔｏｓｔａｉｇｅｓｒｎｏｎｌｍｅｔｓｓｔａｏｇｔｅｔｎｅｔｉｅ — ｓｒｃｉｇｅｓｒｎｏｎ —ｌｍｅｔｍｅｈｄｉｈｔｓｎｌｐｉｇｊｉｔｅｅｎｅｌｎｈａｇｎｒｃｉｄ
度大大提高．关键词：弹簧联结单元法；粘结滑移；全量曲线；非线性迭代解法单

钢筋混凝土的粘结滑移

几种粘结滑移关系的经验公式钢筋混凝土有限元分析中粘结滑移关系表达式主要是从试验数据归纳拟合出的粘结滑移曲线，但这些曲线之间也有相当差异，常用的描述局部粘结应力一滑移关系的经验公式主要有如下几种：(1)1968年，Nilson根据Bresler、Bertero所做的钢筋混凝土在重复荷载下的试验结果，提出局部τ～s非线性关系表达式τ=9.78×102s-5.72×104s2+8.35×10５s３式中τ单位为 N/mm2，s的单位为 mm（2）Houde和 Mirza公式Houde和 Mirza认为粘结力与混凝土标号有关系，他们由62个变形钢筋模拟缝间粘结强度的试件和6个模拟锚固粘结强度的梁端试验结果回归出的经验公式：式中τ单位为 N/mm2，s的单位为 mm（3）清华大学土木系在滕智明指导下进行了92个短埋拔出式试件和12个轴拉混凝土试件的试验研究，发现粘结滑移关系与混凝土强度、钢筋外围的保护层厚度、测点所处位置到裂缝的距离有关。

在试验的基础上，得出如下公式：(2.5)式中，τ为局部粘结应力（N/mm2），s为局部滑移（mm），fts为混凝土劈位强度（N/mm2），c/d为混凝土保护层和钢筋直径比；F(x)为粘结刚度分布函数，x为至最接近的横向裂缝的距离。

（4）中国建筑科学研究院徐有邻等人做了一系列试验，系统地研究了混凝土强度、保护层厚度、锚固长度、配箍率、钢筋直径对粘结锚固性能的影响，将粘结滑移曲线分成五段（微滑移段、滑移段、劈裂段、下降段、残余段）进行描述，曲线上有四个转折点，通过实测结果得出一分段函数表达式，并用一个位置函数同时考虑不同锚固深度处的变化，建立了如下的τ～s关系：τ=φ(s)·Ψ(x) (2.6)式中，Ψ(x)是用来描述粘结滑移关系随不同锚深变化的位置函数，它可用锚固深度x来表示，具体参见文献[3]，φ(s)即是用控制点描述的粘结滑移分段表达式。

Combin39使用经验

对于型钢混凝土之间的粘结滑移采用非线性弹簧单元Combination39进行模拟[1~5]。

min 1D D D i i ∆>-+ （6-1）
7min max min
D D D -=∆ （6-2）
单元结点荷载向量：
⎥⎦
⎤⎢⎣⎡-=11][F F e （6-4）其中弹簧单元的刚度系数tg k 取值如图6-3所示。

基于ANSYS软件的钢筋砼间粘结滑移分析

基于ANSYS软件的钢筋砼间粘结滑移分析刘继鹏【摘要】钢筋混凝土是由钢筋和混凝土两种具有不同物理力学性质的材料组合而成的复合材料,其本构模型比较复杂.钢筋与混凝土两者之间的粘结滑移关系,虽然历经近百年的试验研究,对钢筋混凝土机理的认识水平日益深刻,但在有限元分析中还不是很完善.通过选用合适的材料本构模型和粘结滑移模型,建立有限元分析模型,从而进行全过程的模拟分析.%RC is a composite material with rebar and concrete that have different physical mechanics characters, and its constitutive relationship is relatively complex. Although through experimental study in almost a century,it is increasingly understanded in cognition about mechanism of RC,the bond-slip relationship between rebar and concrete has not been deeply studied in finite element analysis. In this paper, through selecting proper material constitutive relationship and bond梥lip model.finite element analysis model is established,and simulate analysis in all process is completed.【期刊名称】《河南科学》【年(卷),期】2012(030)006【总页数】5页(P750-754)【关键词】粘结滑移;分离式模型;弹簧单元;ANSYS【作者】刘继鹏【作者单位】河南工程学院,郑州 451191【正文语种】中文【中图分类】TU852钢筋与混凝土两种材料共同工作使两者具有很好的粘结强度，能承受由于变形差（相对滑移）沿钢筋与混凝土接触面上产生的剪应力，通常把这种剪应力称为粘结应力.研究钢筋混凝土间的粘结锚固，对于了解钢筋混凝土构件或结构的开裂、承载力以及钢筋锈蚀后的承载力具有重要的价值.目前对于静力作用和动力作用下以及钢筋锈蚀后的钢筋与混凝土间的粘结锚固，已进行了大量的试验和理论分析研究.这些传统的分析方法，通过大量的试验方法把试验数据回归统计得到一些经验公式来计算和设计，但是至今仍没有对粘结机理和粘结滑移关系形成共识.随着有限元法和钢筋混凝土力学的发展和计算机水平的提高，目前采用非线性有限元分析钢筋与混凝土之间的本构关系、有限元模型和裂缝处理，已经成为研究的热点.目前钢筋混凝土结构的有限元模型主要有三种：整体式、分离式和组合式[1-3].本课题采用分离式模型，将混凝土和钢筋各自划分成较小的单元，按照混凝土和钢筋不同的力学性能，选择不同的单元形式.对于混凝土材料采用八结点等参单元，考虑到钢筋几何形状相对于混凝土是细长的，可采用三维杆件单元，这样大大减少单元和结点数目，还可以避免钢筋单元划分过细，在钢筋和混凝土的交界面采用过多的过渡单元.为了模拟钢筋与混凝土间的粘结约束和相对滑移，可插入三向弹簧的联结单元.钢筋混凝土之间的粘结锚固问题一般分为筋端锚固和缝间粘结两大类.为了探讨钢筋混凝土的粘结应力与相对滑移的关系，许多学者进行了大量的试验研究和理论分析[1-9].由于钢筋与混凝土之间的粘结作用受混凝土强度、钢筋埋长、混凝土所受的约束等诸多因数的影响，再加上试验手段不同，试验结果有较大差异.国内外目前比较公认的具有代表性的粘结－滑移关系如下：3.1 本构关系3.1.1 混凝土的本构关系3.1.1.1 混凝土单轴受压应力应变关系 ANSYS非线性有限元分析中需要输入混凝土单轴受压应力应变关系，可采用多线性等向强化模型（MISO）.本课题采用美国E.Hognestad建议的模型[7]式中：fc为峰值应力（棱柱体极限抗压强度）；ε0为相应于峰值应力时的应变，取ε0=0.002；εu为极限压应变，取εu=0.003 8.3.1.1.2 混凝土单轴受拉应力应变关系通常认为混凝土受拉时，应力应变关系基本是线性的，达到极限应力fc以后，强度迅速降低.ANSYS默认的混凝土单轴受拉应力应变模型如图1.3.1.1.3 混凝土多轴应力应变关系和强度准则由于试验手段、加载路径的影响等因素，迄今为止没有较为完整的混凝土多轴应力应变模型，混凝土多轴应力应变关系的理论一直在发展中.ANSYS程序中的混凝土材料模型采用Willam－Warnke （1975）的五参数模型，该模型属于相关流塑性本构关系模型中理想弹塑性本构模型一类.Willam－Warnke的五参数模型表达式为当σm=ρ，τmt＝τmc＝0，θ=0°～60°，r（σm，θ）=f（rt，rc，θ）. Willam－Warnke五参数强度准则的参数由下列条件确定：①弹性摸量EX；②泊松比PRXY；③开裂的剪力传递系数βt；④闭合的剪力传递系数βc；⑤单轴受压强度fc；⑥单轴受拉强度ft；⑦极限双轴抗压强度；⑧周围静水应力状态；⑨静水应力状态下单轴压缩的极限强度；⑩双轴压缩的极限强度；○11断裂发生时刚度因子.在ANSYS程序中，①～⑥参数必须输入，⑦～○1 1参数可以采用默认值.3.1.2 钢筋的本构关系钢筋材料模型采用理想弹塑性模型，在ANSYS程序中可采用双线性随动强化模型（KISO）.3.2 单元的选取和划分3.2.1 SOLID65单元采用ANSYS程序提供的专用钢筋混凝土单元SOLID65来模拟混凝土.SOLID65是三维实体单元，有八个结点，每个节点有三个自由度：X、Y、Z方向的平移，单元能够发生塑性变形，可以在三个正交方向开裂和压溃，见图2. 钢筋混凝土单元SOLID65的实常数中可以以体积配箍率的形式输入钢筋的信息，可以按Willam－Warnke的五参数破坏曲面考虑混凝土在三轴受力状态下的开裂和压溃.本文在分析中仅考虑混凝土的开裂，不考虑混凝土的压溃.3.2.2 LINK8单元可用LINK8单元来模拟受压和受拉的钢筋（锚筋）.LINK8单元为三维空间实体，有两个结点，每个结点由三个自由度：X、Y、Z方向的平移，承受单轴拉力和压力，不能承受力矩，包含有塑性徐变膨胀应力强化大变形等性能.3.2.3 联结单元如果要考虑钢筋与混凝土之间的相对滑移，必须在钢筋和混凝土两者间界面创建联结单元.联结单元能沿着与联结面垂直方向传递压应力，也能沿着与联结面平行方向传递剪应力，但不传递拉应力.可以采用三向弹簧联结单元.这组弹簧是假想的力学模型，具有弹性刚度，但并无实际几何尺寸，可以放置在需要设置联系的任何位置.平行于两种单元接触面的弹簧用以计算相对滑移和粘结力，垂直于两种单元接触面的弹簧用以考虑钢筋的销拴作用.三个弹簧刚度分别为kh、kv1和kv2，其中弹簧单元的平面图见图3.3.2.3.1 粘结单元的非线性刚度[3，9]弹簧单元刚度的确定比较困难，其刚度值与所采用的粘结滑移关系密切相关，而粘结滑移关系又受到许多因素的影响而难有统一的表达式.分析结果的准确程度取决于弹簧刚度的取值.通常对垂直于钢筋锚长的弹簧刚度取值无限大，平行于锚固方向的弹簧可按τ－s关系表达式对s求导的方法得到.①平行于钢筋方向的弹簧刚度kh.有关kh的计算，不同的研究者根据各自的试验提出关系表达式，再通过微分求导出不同计算公式，目前较为流行的有Nilson公式和Houde和Mirza公式.Houde和Mirza公式为A是从属于一个弹簧的钢筋面积.②垂直于钢筋方向的弹簧刚度kv.kv的取值较复杂，弹簧刚度可以取无限大.本文按Houde－Mirza公式确定kh，另外取kv1=kv2=1012[10].3.2.3.2 Matrix27刚度矩阵 Matrix27是一种能代表任意单元的矩阵单元，但其几何特征无定义，但其弹性运动学响应可用刚度、阻尼或质量系数来指定.它内部有一种变量用以表明使用的是哪一种响应（刚度、质量或阻尼）.矩阵单元连接两个结点，每个节点有6个自由度：沿结点坐标系X、Y、Z方向的平动和绕结点坐标系X、Y、Z的转动.可以用这个单元来模拟双向（平面单元）或三向弹簧单元，刚度值可依据单元刚度矩阵的物理意义设定.在不同的荷载步下根据滑移值，依据粘结滑移关系修正弹簧的刚度.这些可以用FORTAN语句编写一个循环程序输入到ANSYS程序中.在Matrix27刚度矩阵为12×12的对称刚度矩阵，其实常数中需定义C1～C78，见图4.在沿钢筋方向某一位置i有一结点对（钢筋上结点bari和混凝土上结点hnti），取钢筋上结点bari对应的位移UZbari，混凝土上结点hnti对应的位移UZhnti.相对位移ΔUZi=UZbari－UZhnti，则此处滑移S=UZi.代入Matrix27单元对称刚度矩阵形（如下所示）成初始刚度矩阵，然后在不同的荷载步下根据滑移值，依据粘结滑移关系修正弹簧的刚度.3.2.3.3 创建联结单元采用非线性有限元方法分析钢筋混凝土之间粘结问题，一般的做法是对钢筋和混凝土分别划分单元，然后在钢筋和混凝土单元在同一坐标位置的节点之间增设虚拟的三向弹簧单元.具体作法：沿钢筋方向的某一位置，在钢筋上拾取i结点，在混凝土上拾取j结点，把这两个结点创建为联结单元（见图2），并赋予这个联结单元相对应的刚度矩阵.这样沿着每根钢筋依次从上到下，分别创建赋予刚度矩阵的联结单元.某预埋钢构件，有4Φ25钢筋埋入钢筋混凝土梁，混凝土为C60.混凝土的EX=3.6e4 N/mm2，PRXY=0.2，ft=2.04 N/mm2，fc=27.5 N/mm2.在混凝土裂缝处理中，采用开裂的剪力传递系数βt来反映剪切面上裂缝张开状态下剪切刚度的变化；又采用闭合的剪力传递系数βc来反映裂缝闭合状态下开裂面的剪切刚度.参考相关文献［1，2，8］以及试算收敛情况，取βt=0.5，βc=0.8. 钢筋为Ⅲ级，弹性模量 EX=2e5 N/mm2，泊松比 PRXY=0.3，屈服强度400 MPa，切向摸量0.钢筋混凝土梁内的钢筋（主筋和箍筋）按离散钢筋处理，在SOLID65单元中x、y、z方向的体积配箍率分别为1.2%、0.7%、1.5%.根据文献［10］，令 C1=C58=1012，C7=－1012，C13=C64=1012，C19=－1012，C24=C69=Kh，C30=－Kh，其它系数均设置为零.这样把C1～C78参数化来定义的Matrix27单元刚度矩阵.采用荷载增量法和Newton-Raphson相结合，线性搜索技术、应用预测、自适应下降等加速收敛技术有机结合建立的非线性平衡方程求解方法.影响求解方程的因素主要有网格密度、子步数、收敛准则.如果F范数曲线走形很长，可以考虑增大子步数NSUBST.采用力收敛准则，精度比默认0.5%可以适当放大，设置为5%.破坏准则为Kupfer准则.一根受拉钢筋的计算结果见图4和图5.在ANSYS软件中，钢筋混凝土结构或构件可采用分离式的模型，合理选取钢筋与混凝土的本构模型和粘结滑移关系经验公式，可以进行钢筋与混凝土间的粘结滑移非线性有限元分析.合理选取单元和划分网格，如混凝土采用SOLID65单元，钢筋采用LINK8单元，粘结滑移采用创建并付属性Matrix27的三向弹簧单元；合理设置Willam-Warnke五参数强度准则的6个参数，尤其是开裂和闭合的剪力传递系数.需要在ANSYS软件现有的基础上进行材料本构关系以及粘结滑移关系的二次开发，从而能深入地开展钢筋混凝土非线性的研究.［1］过镇海.钢筋混凝土原理［M］.北京：清华大学出版社，1999.［2］宋启根，单炳梓.钢筋混凝土力学［M］.南京：南京工学院出版社，1986. ［3］朱伯芳.有限元单元法原理与应用［M］.北京：中国水利水电出版社，2000. ［4］ Nilson A H.Nonlinear analysis of reinforced concrete by the finite element method［J］.ACI Journal，1968，65（9）：757-766.［5］ Houde J.Study of force－displacement relationships for the finite element analysis of reinfoeced concrete［D］.Montreal：Mc Gill University，1973.［6］徐有邻.变性钢筋－混凝土粘结锚固性能的试验研究［R］.北京：清华大学，1990.［7］朱伯龙，董振祥.钢筋混凝土非线性分析［M］.上海：同济大学出版社，1985.［8］江见鲸.混凝土结构工程学［M］.北京：中国建筑工业出版社，1998.［9］吕西林，金国芳，吴晓涵.钢筋混凝土结构非线性有限元理论与应用［M］.上海：同济大学出版社，1996.［10］刘龙强，吴胜兴，周继红.ANSYS软件分析钢筋混凝土粘结滑移关系的二次开发实践［J］.工程力学：增刊，2001（A2）：85-89.Abstract：In this paper，a global algorithm is proposed for solving generalized quadratic fractional programs with nonconvex quadratic constraints（P1）.Due to its intrinsic difficulty，less work has been devoted to globally solving this problem.The proposed algorithm is based on the recently developed theory of monotonic optimization，and it turns out that the optimal solution which is provided by the algorithm isadequately guaranteed to be feasible and to be close to the actual optimal solution.Convergence of the algorithm is shown and the numerical experiments is reported to show the feasibility and effectiveness of the proposed algorithm.Key words：global optimization；fractional programming；monotonic optimizationConsider the following generalized quadratic fractional programs with nonconvex quadratic constraints：where Q，P，Gmare N×N matrixes，q，p，wmare N－vectors，q0，p0，hmare real constants，for m＝1，…，M.Then it follows that the constraint set is nonconvex to problem（P1）.We assume throughout thatyTpy+pTy+p0＞0，y∈Ω0.Most of the theoretical and algorithmic work in fractional programming ［1-4］applies only to concave fractional programs or to special cases of concave fractional programs.To our knowledge，there exist few algorithms for globally solving problem（P1）.Recently，a few algorithms have been proposed for solving special cases of problem（P1）.For instance，algorithmic and computational results for convex－convex quadratic fractional programming can be found in［5-6］.In this section we show that problem（P1）can be transformed into an equivalent monotonic optimization problem，which is equivalent to（P1）. By solving two quadratic programming problems，we can obtain positive constants L and U such that 0＜L≤yTpy+pTy+p0≤U，∀y∈Ω0.Next，by introducing an additional variablew，one can convert the problem（P1）intoThe key equivalence result for problems（P1）and（P2）is given bythe following Theorem 1.Theorem 1 If（y*，w*） is a global optimal solution for problem （P2），then y*is a global optimal solution for problem（P1）.Conversely，if y*is a global optimal solution for problem（P1），then（y*，w*）is a global optimal solution for problem（P2），where w*=1/（yTQy+qTy+q0）. ProofThe proof is similar to Theorem 1 in Ref.［7］，it is omitted here. Note that the objective function and the constrained functions of problem （P2）are all polynomials inRN+1.Let G（y，w）=G+（y，w）－G－（y，w），Fm（y）=Fm+（y）－Fm－（y）and H（y，w）=H+（y，w）－H－（y，w）be the d.m.representations of G（y，w），F（y），H（y，w）as described in the problem（P2）.Then by introducing an additional variable z∈Rto（P2），we can obtain the following equivalent problem：Clearly the objective function of（P3）is increasing and each constrained function is a d.m.function.The validity of this approach follows from the following result.Theorem 2If（y*，w*，z*）is a global optimal solution for problem（P3），then（y*，w*）is a global optimal solution for problem（P2）.Conversely，if（y*，w*）is a global optimal solution for problem（P2），then（y*，w*，z*）is a global optimal solution for problem（P3），where，z*=－G－（y*，w*）.Proof The proof of this theorem follows easily from the definitions of problems（P2）and（P3），therefore，it is omitted.Based on the above discussion，here，from now on we assume that theoriginal problem（P1）has been equivalently converted to the monotonic optimization problem.Algorithm StatementStep 0 Initialization.Given convergence tolerance ε＞0.If no feasible solution is known，let V=g（xu）+ε with X0=[xl， x u ]；Otherwise，letxˆbe the best nonisolated feasible solution available，V=g（xˆ）.Letq=0. Step 1 Reduction cut.For each rectangle X∈Q，compute its valid reduction red X，which we can obtain by using the reduction cut.Then，if red X= ○ ，then delete X；Otherwise，replace X by red X，and compute an upper bound UB（X）for h（x）over the feasible solutions in X and delete X if UB （X）＜0.Step 2 Fathoming step.Let Qq′be the collection of rectangles that results from Qqafter completion of Step 1.Let Fq′=Fq∪Qq′.If Fq′= ○ then terminate：xˆis an essential ε－optimal solution of（P）if V=g（xˆ），or the problem（P） is nonisolated infeasible if V=g（xu）+ε；Otherwise，let ［aq，bq］：=Xq∈arg max｛UB（X）│X∈Fq′｝，and let UBq=UB（Xq）. Step 3 Optimality check.If UBq＜ε，then terminate：xˆis an essential ε－optimal solution of（P）if V=g（xˆ），or the problem（P）is ε－nonisolated infeasible if V=g（xu）+ε.Step 4Updating feasible solution.If UBq≥ε，and g（bq）＞V－ε，then compute xq=aq+γq（bq－aq）with g（xq）=V－ε；If UBq≥ε，and g（bq）≤V－ε，then let xq=aq.（4.1）If h（xq）≥0 then xqis a new nonisolated feasible solution of（P）with g（xq）≤V－ε.Reset xˆ←xq，V←g（xˆ）.Go to Step 5.（4.2）If h（xq）＜0，go to Step 5，with xˆunchanged.Step 5 Partitioning step.Divided Xqinto two subrectangles by the branching process.Let Qq+1be the collection of these two subrectanglesof Xq，Fq+1=Fq′\｛Xq｝.Reset q←q+1，and return to Step 1.Theorem 3 （Convergence result）.The above algorithm terminates after finitely many steps，yielding either an essential ε－optimal solution of （P），or an evidence that the problem is nonisolated infeasible. ProofSee Theorem 5.1 in Ref.［8］.To verify the performance of the proposed global optimization algorithm，there exists one computational issue to be considered in the following.The algorithm is coded in Matlab and some test problems are implemented on a Pentium （R）4 CPU 2.66 GHz with 512 MB memory microcomputer.Numerical results show that the proposed algorithm can globally solve the problem（P1）.Below we only describe some of these sample problems and the corresponding computational results.For these problems，the numerical results are illustrated in Tab.1 and Tab.2.Clearly，the upper and lower bounds of y32+5y1y2are U=49 and L=6，respectively.With ε=0.001，the algorithm found an es sential ε －optimal minimum 0.610 331 791 388 32 after 35 iterations at the essential ε －optimal solution yˆ=（1.258 840 471 299 51，1.523 388 209 853 02，1.030 851 968 215 46）.Example 3In Tab.1，the notations have been used for column headers：Ref.：reference；Iter：the number of algorithm iteration.Example 4 Consider the problemAll elements of Q，P Gmwere randomly generated between 0 and 1；The vectors p，q and wmare generated by using random numbers in the interval［－t，t］，where t is the average of the elements of P，Q，respectively，and p0，q0，hmare the average of p，q，wm，respectively. Numerical results are summarized in Tab.2，where average CPU seconds denoted by T are obtained by running the proposed algorithm for 20 tests problems.Tab.2 shows the average performance of the proposed algorithm when the convergence tolerance ε was fixed at 0.05.Through four examples and some randomly produced examples，it is shown that the proposed algorithm is effective.【相关文献】［1］ Charnes A，Cooper W W.Programming with linear fractional functions［J］.Nav Res Logist Q，1962，9：181－186.［2］ Schaible S.Fractional programming II，on Dinkelbachs algorithm［J］.Manag Sci，1976，22：868－873.［3］ Dinkelbach W.On nonlinear fractional programming［J］.Manag Sci，1967，13：492－498.［4］ Lo A W，MacKinlay A C.Maximizing predictability in the stock and bond markets ［J］.Macroeconomic Dynamics，1997，1：102－134.［5］ Benson H P.Fractional programming with convex quadratic forms and functions ［J］.Europ J Oper Res，2006，173：351－369.［6］ Yamamoto R，Konno H.An effcient algorithm for solving convexconvex quadratic fractional programs［J］.Optim J Theory Appl，2007，133：241－255.［7］ Benson H P.Global optimization algorithm for the nonlinear sum of ratios problem ［J］.J Optim Theory Appl，2002，112：1－29.［8］ Chen Yongqiang，Jiao Hongwei.A nonisolated optimalsolution of general linear multiplicative programming problems［J］.Computers and Operations Research，2009，36（9）：2573－2579.。

钢筋混凝土粘结滑移问题的单弹簧联结单元法

钢筋混凝土粘结滑移问题的单弹簧联结单元法赵兰浩;李同春;牛志伟【摘要】在传统双弹簧联结单元法的基础上,提出了求解钢筋与混凝土粘结滑移问题的～种新的方法一单弹簧联结单元法.在混凝土实体单元与钢筋粱单元的切向设置单弹簧联结单元,模拟钢筋与混凝土切向的相互作用,通过建立二者间法向自由度约束方程的方式保证钢筋与混凝土之间法向变形协调,避开了人为选择法向刚度系数的困难,能够很方便的考虑钢筋对混凝土的销拴效应.【期刊名称】《土木工程与管理学报》【年(卷),期】2008(025)004【总页数】3页(P147-149)【关键词】混合坐标系;单弹簧联结单元;钢筋混凝土;粘结滑移【作者】赵兰浩;李同春;牛志伟【作者单位】河海大学水利水电工程学院,江苏,南京,210098;河海大学水利水电工程学院,江苏,南京,210098;河海大学水利水电工程学院,江苏,南京,210098【正文语种】中文【中图分类】TV332在分析钢筋与混凝土的相互作用时，所采用的有限元模型主要有三种：分离式、组合式和整体式[1]。

采用分离式模型时，常用的联结单元有双弹簧单元[2]、无厚度四边形粘结单元[3]、粘结区单元[4]等。

这些模型在一定程度上较好的解决了粘结滑移问题的力学分析，但也存在一些固有的缺点。

在利用联结单元描述钢筋与混凝土的相互作用时，一般需要确定两个参数：一个是平行于钢筋方向的切向刚度系数kH和垂直于钢筋方向的法向刚度系数kV。

kH反映了钢筋与混凝土粘结滑移性能，kV反映了钢筋对混凝土间的销拴挤压作用，到目前为止对其取值还缺乏研究[3]。

一般情况下，为了反映钢筋与混凝土的相互作用，保证钢筋与混凝土之间法向变形协调，需要给一个大的法向刚度系数。

理论上kV越大越能代表真实的情况，但过大的取值将会给计算引起麻烦和带来计算误差，而过小的取值会发生单元相互嵌入问题，致使结构分析模型与实际几何形态有一定的偏差[5]。

本文基于双弹簧联结单元方法，提出一种新的钢筋与混凝土联合作用的分析方法—单弹簧联结单元法。

基于混合坐标系的单弹簧联结单元法

基于混合坐标系的单弹簧联结单元法赵兰浩;李同春;牛志伟;颜天佑【期刊名称】《河海大学学报（自然科学版）》【年(卷),期】2008(036)006【摘要】在传统双弹簧联结单元法的基础上,提出了一种求解钢筋与混凝土黏结滑移问题的新方法--基于混合坐标系的单弹簧联结单元法.在混凝土实体单元与钢筋梁(杆)单元的切向设置单弹簧联结单元,模拟钢筋与混凝土切向的相互作用,其切向刚度同样是由钢筋与混凝土之间黏结力与滑移量的关系确定.混凝土实体单元在整体坐标系内求解,而为了方便建立法向自由度之间的关系,钢筋梁单元在局部坐标系内求解,通过建立法向自由度约束方程保证钢筋与混凝土的法向变形协调,避开了人为选择法向刚度系数的困难,能够很方便地考虑钢筋对混凝土的销拴效应,并且也适用于钢筋单元在混凝土中任意布置的情况.数值算例表明,该方法是正确和有效的.【总页数】5页(P796-800)【作者】赵兰浩;李同春;牛志伟;颜天佑【作者单位】河海大学水利水电工程学院,江苏,南京,210098;河海大学水利水电工程学院,江苏,南京,210098;河海大学水利水电工程学院,江苏,南京,210098;河海大学水利水电工程学院,江苏,南京,210098【正文语种】中文【中图分类】TV33【相关文献】1.钢筋混凝土粘结滑移问题的单弹簧联结单元法 [J], 赵兰浩;李同春;牛志伟2.基于单弹簧联结单元法的白鹤滩拱坝孔口配筋非线性有限元分析 [J], 殷鸣;李同春;赵兰浩;张伟3.基于有限单元法的C型弹簧管载荷与位移关系的分析 [J], 吴振亭;赵伟阁4.基于几何非线性有限单元法的温控器用片弹簧优化设计 [J], 陈文华;李小辉;潘骏;贺青川;陈晓英;王孟5.单弹簧联结单元法的改进算法 [J], 颜天佑;李同春;赵兰浩因版权原因，仅展示原文概要，查看原文内容请购买。

刚体弹簧元法在钢筋混凝土构件动力分析中的应用

刚体弹簧元法在钢筋混凝土构件动力分析中的应用王路喜;赵平平【摘要】为分析钢筋混凝土结构在动力作用下的性能,采用刚体弹簧元法将结构离散为多段刚体,刚体间的变形通过块体间的弹簧变形来体现。

弹簧元模型与实际结构之间满足刚度、荷载和强度三个方面的等效准则,实现非连续介质力学模型模拟连续介质模型,为钢筋混凝土的力学性能计算提供了一种有效的分析方法。

【期刊名称】《安徽建筑》【年(卷),期】2012(019)005【总页数】2页(P159-160)【关键词】离散单元法;刚体弹簧;钢筋混凝土;中心差分法【作者】王路喜;赵平平【作者单位】山东科技大学土木建筑学院,山东青岛266590;山东科技大学土木建筑学院,山东青岛266590【正文语种】中文【中图分类】TU311.30 引述离散单元法是由Cundall于1971年提出来的，适用于准静力或动力条件下的节理或块体集合的力学问题。

离散单元法的理论基础是牛顿第二定律，将结构视为离散的快体的集合，在受力变形、运动过程中单元之间存在相互的接触关系，其力学行为被模拟为一个动力过程[7]，特别适合于大变形和不连续问题的求解[8]。

1 刚体弹簧元法刚体弹簧元法是在离散元的基础上发展起来模拟离散介质破坏的一种方法，它假设每个离散单元都是刚体，刚体之间通过弹簧相连接，并以单元型心位移作为基本未知量，单元间的作用力完全反映在弹簧上，根据计算力学原理建立按位移求解的支配方程[10]。

为了反映结构内阻尼的影响，可与弹簧并联一个粘滞阻尼器。

该模型基于牛顿第二定律采用动态松弛法求解块体运动方程，使用显式时步步进的中心差分方法求解块体运动，对于稳态问题，通过阻尼使系统运动衰减至稳定平衡状态。

刚体弹簧元与传统的离散元相比更适合分析静态、小变形问题。

2 模型计算2.1 模型的建立假定钢筋与混凝土间无相对滑移，把钢筋混凝土试件（如图1所示）切割为n个块体[2]，每一个块体为一个不发生变形的刚体单元，块体之间用弹簧组相连接，每一组弹簧分混凝土弹簧和钢筋弹簧，每一组弹簧代表相邻单元质心长度范围内的力学性能[3]，混凝土弹簧位于块体的轴心位置，钢筋弹簧的数量根据构件的配筋情况来确定，位于块体钢筋的中心位置。

添加钢筋混凝土弹簧单元

在inp里修改弹簧单元设置之前，先要做2件事。

1、在cae中建设弹簧单元。

建模后进入interaction，special→springs/dashpots→create，在connectivity type 选择connect two points,如以下列图：分别选择混凝土和钢筋上面各1个点，或者随便选，后面都可以在inp中修改。

选好以后按以下列图修改弹簧参数，1,1,900也是随便的，后面都可以在inp中修改，含义在后面解释。

2、找出混凝土和钢筋弹簧单元节点处的节点编号。

建模完成后提交运算，运算出现几步的结果后，进入results，options→common →labels→show node labels即可显示单元的节点。

假设钢筋和混凝土节点重合，想单独查看钢筋或混凝土的节点，tools→display group→create→part instances，选择钢筋或混凝土，remove，即可隐藏需查看混凝土内部的节点编号，可以用切片功能以下是修改inp的方法，转载：ABAQUS在inp里添加弹簧单元全过程，天天飞ABAQUS在inp里添加弹簧单元全过程模拟钢筋混凝土粘结滑移，以我现在的水平来看，大概有三个思路，一个是用cohesive，一个是用Spring2弹簧单元，再有就是Umat了。

我先学习的是弹簧单元。

ABAQUS里有三种弹簧单元，Spring1，Spring2和SpringA。

其中，ABAQUS 文档的解释如下：Spring2有两个节点，每个节点只有一个自由度。

钢筋采用Wire建模，Truss 单元，混凝土实体单元。

mesh之后会出节点，所以尽量mesh成一样的节点，用钢筋和混凝土重合的节点，在三个方向分别建设弹簧。

垂直于钢筋纵向的两个弹簧设置成刚度较大，弹性。

沿钢筋方向的弹簧，需要确定粘结滑移本构，定义力和滑移位移的关系。

比照一下：Spring1是弹性的,只有一个节点，而SpringA的作用是沿两点连线的，每个点有三个自由度。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

筋与混凝土在法线方向的关系。有了上一小节的
坐标变换关系之后，由（2）式可以直接得到钢筋法向位移插值方程：
∑ ui* = n riju j （i=2,3）
(5)
j =1
其中，n 为所求问题的维数，而插值系数 rij 即为
坐标转换矩阵的元素。
3 混凝土与钢筋的相互作用
若记 f * 为节点局部坐标系 x* y*z* 内混凝土
在分析钢筋与混凝土的相互作用时，所采用的有限元模型主要有三种：分离式、组合式和整体式[1]。采用分离式模型时，常用的联结单元有双弹簧单元[2]、无厚度四边形粘结单元[3]、粘结区单元[4]等。这些模型在一定程度上较好的解决了粘结滑移问题的力学分析，但也存在一些固有的缺点。在利用联结单元描述钢筋与混凝土的相互作用时，一般需要确定两个参数：一个是平行于钢筋方向的切向刚度系数 kH 和垂直于钢筋方向的法向刚度系数 kV。kH 反映了钢筋与混凝土粘结滑移性能，kV 反映了钢筋对混凝土间的销拴挤压作用，到目前为止对其取值还缺乏研究[3]。一般情况下，为了反映钢筋与混凝土的相互作用，保证钢筋与混凝土之间法向变形协调，需要给一个大的法向刚度系数。理论上 kV 越大越能代表真实的情况，但过大的取值将会给计算引起麻烦和带来计算误差，而过小的取值会发生单元相互嵌入问题，致使结构分析模型与实际几何形态有一定的偏差[5]。
[4] 吕西林, 金国芳, 吴晓涵. 钢筋混凝土结构非线性
有限元理论与应用[M]. 上海 : 同济大学出版社,
1996.
(c) 三级加载
[5] 戚乐磊, 赵鸿铁, 梁若筠, 等. 粘结滑移问题的界面应力元模型[J]. 河海大学学报, 2004, 32(2): 188-191.
[6] 李同春, 李淼, 温召旺, 等. 局部非协调网格在高
对钢筋的作用力，则由作用力与反作用力的关系
可知，在整体坐标系 xyz 内钢筋对混凝土的作用
力为 −rT f * 。可以建立混凝土和钢筋的增量有限
元平衡方程：混凝土：
kΔu = ΔF − rTΔf *
(6)
钢筋：
k*Δu* = ΔF * + Δf *
(7)
由于节点的法向自由度已通过强迫相等的方式保证了钢筋与混凝土之间法向变形协调，即混凝土与钢筋之间的法向作用力已变成内力，不需
要在平衡方程中出现，则 f * 仅仅为混凝土与钢筋
之间的切向粘结力。
与文献[7]相同，本文以 Shima 的 10 号拉伸构件[8]作为研究对象，说明本文方法的有效性。
试件为半径 R=500 mm、长度为 760 mm 的圆柱形混凝土构件，直径 D=19 mm 的钢筋位于试件中心。混凝土弹性模量 33 GPa，泊松比 0.167，抗压强度 fc′ 为 21.6 MPa；钢筋弹性模量 190 GPa，泊松比 0.23。五级加载时钢筋端部的应变值分别为：0.786×10-3、1.471×10-3、2.286×10-3、2.886×10-3、 3.586×10-3。粘结滑移本构关系采用 Shima 提出的将粘结应力表示为滑移量的函数与钢筋应变的函数之乘积，其表达式为[7]：
(d) 四级加载图 2 不同加载步钢筋应变沿构件长度分布
the Faculty of Engineering, 1987, 39(2):133-94.
Single-spring Joint Element Method for Reinforced Concrete
Bond-slip Problem
协调，梁、杆单元在局部坐标系内求解，避开了人为选择法向刚度系数的困难，能够很方便的考虑钢筋对混凝土的销拴效应。
1 坐标变换
为了计算方便，本文所采用的混合坐标系统
如图 1 所示，考查位于整体坐标系 xyz 内的钢筋与混凝土的相互作用问题。 x′y′z′ 为某一个梁单元局部坐标系，x′ 布置在梁的轴向。考虑到实际
吻合的较好，尤其在低应力水平下，计算结果与
实验结果几乎完全吻和，而随着拔拉荷载的增大，
本文方法得到的钢筋应变值在数值上比实测值要
小，但分布规律却接近。分析其原因，一方面由
于计算所采用的计算模型可能与实际有一定出
入，另一方面在高应力水平下，所采用的粘结滑
移的本构关系的适用性受到影响。图中同时还给
出了相同计算条件下双弹簧模型联结单元的计算
τ
(ε
s
,
s)
=
0.73
fc′[ln(1
+
105
s
/
D)]3
×
1
+
1 10ε
s
其中 εs 为钢筋应变，D 为钢筋直径，s 为滑移量(单
位为 mm)，τ 为粘结力(单位为 MPa)。
用本文方法计算得到的四级荷载作用下，钢
筋应变沿构件长度的分布与实测值的对比见图 2 所示。从图中可以看出，本文计算结果与实测值
deformation compatibility was ensured by letting the deformations of the normal direction degree-of-freedoms
for concrete and steel bar be identical, in this way, the difficulty of choosing the normal stiffness coefficient is
overcome.
Key words: mixed coordinate system; single-spring joint element; reinforced concrete; bond-slip
上式即为求解钢筋与混凝土粘结滑移问题的单弹簧联结单元法有限元方程。
2 法向自由度的约束方程
4 数值算例
为了建立钢筋与混凝土在法线方向的关系，
同样需要在二者相交处设置双节点。但与双弹簧
联结单元不同的是，单弹簧联结单元不需要定义
法向弹簧，而是应用不协调位协调位移解法[6]的
思想，令双节点的法向自由度相等来直接建立钢
第25卷第4期 2008 年 12 月
华中科技大学学报（城市科学版） J. of HUST.（Urban Science Edition）
Vol.25 No.4 Dec. 2008
钢筋混凝土粘结滑移问题的单弹簧联结单元法
赵兰浩，李同春，牛志伟
（河海大学水利水电工程学院，江苏南京 210098）摘要：在传统双弹簧联结单元法的基础上，提出了求解钢筋与混凝土粘结滑移问题的一种新的方法—单弹簧联结单元法。在混凝土实体单元与钢筋梁单元的切向设置单弹簧联结单元，模拟钢筋与混凝土切向的相互作用，通过建立二者间法向自由度约束方程的方式保证钢筋与混凝土之间法向变形协调，避开了人为选择法向刚度系数的困难，能够很方便的考虑钢筋对混凝土的销拴效应。关键词：混合坐标系；单弹簧联结单元；钢筋混凝土；粘结滑移中图分类号：TV332 文献标识码：A 文章编号：1672-7037(2008)04-0147-03
结果。由于本例为轴向拉伸构件，实际上不存在
法向刚度的选择及相互嵌入问题，计算结果几乎
与本文方法的计算结果完全吻和，这也从另一个
角度验证了本文方法的正确性和有效性。
第4期
赵兰浩等：钢筋混凝土粘结滑移问题的单弹簧联结单元法
5 结语
·149·
(a) 一级加载
在双弹簧联结单元方法的基础上，提出一种求解钢筋与混凝土粘结-滑移的分析方法—基于混合坐标系的单弹簧联结单元法。该方法只在钢筋切向设置单弹簧，通过建立钢筋与混凝土法向自由度的约束方程反映二者在法向方向的相互作用力，避开了人为选择法向刚度系数的困难，能够很方便的考虑钢筋对混凝土的销拴效应。数值算例的计算结果与实测值吻合的较好，说明了本文方法的正确性和有效性。
问题中钢筋可能不在一条直线上，在每一个梁单
元节点上建立节点局部坐标系 x* y*z* ，由相邻梁
单元的局部坐标系平均得到。各个坐标系之间的
坐标转换矩阵规定如下：R 为整体坐标系 xyz 与梁单元局部坐标系 x′y′z′ 的坐标转换矩阵；r 为整体坐标系 xyz 与每个定点的局部坐标系
钢筋直径。将（8）式代入至（6）,（7）式，并
写成矩阵的形式：
⎡ ⎢ ⎣
k+ −ks
r r
T
ks
r
−r k*
T ks + ks
⎤ ⎥ ⎥⎦
⎧Δu ⎨⎩Δu*
⎫ ⎬ ⎭
=
⎧ΔF ⎨⎩ΔF
*
⎫ ⎬ ⎭
(9)
其中，k* = rkrT = rRTk′RrT ，为梁单元在节点局部
坐标系 x* y*z* 中的刚度矩阵。
参考文献
[1] 江见鲸. 钢筋混凝土结构非线性有限元分析[M]. 西
(b) 二级加载
安: 陕西科学技术出版社, 1994. [2] 董哲仁. 钢筋混凝土非线性有限元法原理与应用
[M]. 北京: 中国水利水电出版社, 2002.
[3] 沈聚敏, 王传志, 江见鲸. 钢筋混凝土有限元与板
壳极限分析[M]. 北京: 清华大学出版社, 1993.
is proposed for reinforced concrete bond-slip problems. The single spring joint element is set along the tangent
direction of solid element for concrete and beam element for steel bar to simulate the tangential interaction. The