固体物理 5_4晶体热容的量子理论
合集下载
固体物理课件
e 2 晶体中有3N个振动模 晶体中有 个振动模 C = k ( ∑ B k T ) (eℏω j / kBT − 1)2 V 1) 爱因斯坦模型 ) j =1 B 假设N个原子构成的晶体 个原子构成的晶体, 假设 个原子构成的晶体,
所有的原子以相同的频率 ω0振动 2) 德拜模型 ) 以连续介质的弹性波来代表格 波,将晶格看作是各向同性的 连续介质
V (r + R) = V (r )
布洛赫定理
具有晶格周期性时, 布洛赫定理 —— 势场 V ( r ) 具有晶格周期性时,电子的波 函数满足薛定谔方程 ℏ2 2 [− ∇ + V ( r )]ψ ( r ) = E ψ ( r ) 2m —— 方程的解具有以下性质
ψ ( r + Rn ) = e ik ⋅R ψ ( r )
ω = 2
−
− i (ωt − naq )
2
β
m
ω
aq sin m 2
−π a
β
π π < q ≤ a a
q=
µn = µn+ N 2π
Na
× h —— h为整数 为整数
π a o 晶格振动波矢的数 目=晶体的原胞数 晶体的原胞数
能量本征值 ε n = ( n q + 1 ) ℏ ω q
q
晶格振动的能量量子; 声子 —— 晶格振动的能量量子;或格波的能量量子 当这种振动模处于 系统能量本征值
原子的振动 —— 晶格振动在晶体中形成了各种模式的波
模型 运动方程 试探解
m µ n = − β (µ n − µ n−1 ) − β (µ n − µ n+1 )
..
一维晶格振动 一维无限长原子链, , , 一维无限长原子链,m,a,β
《固体物理基础》晶格振动与晶体的热学性质

一、三维简单格子
二、三维复式格子
三、第一布里渊区
四、周期性边界条件
◇一个原胞内有P
个不同原子,则
有3P个不同的振
动模式,其中3支 声学波。
◇具有N个原胞的 晶体中共有3PN个
振动模式,其中
3N个声学波, 3N(P-1)个光学波。
四、周期性边界条件 总结
§ 3.4 声子
声子:晶格振动中格波的能量量子
二、一维单原子链的振动
格波
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
周期性边界条件
玻恩—卡曼边界条件
二、一维单原子链的振动
周期性边界条件
即q有N个独立的取值—晶格中的原胞数第一布
◇非弹性X射线散射、非弹性中子散射、可见光 的非弹性散射。
§ 3.4 声子
§ 3.4 声子
90K下钠晶体沿三个方向的色散关系
§ 3.5 晶格热容
一、晶格振动的平均能量
热力学中,固体定容热容:
根据经典理论,每一个自由度的平均能量是kBT, kBT/2为平均动能,kBT/2为平均势能,若固体有
N个原子,总平均能量: 取N=1摩尔原子数,摩尔热容是:
二、一维单原子链的振动
一维单原子链的振动
二、一维单原子链的振动
简谐近似下的运动方程
二、一维单Hale Waihona Puke 子链的振动简谐近似下的运动方程
在简谐近似下,原子的相互作用像一个弹 簧振子。一维原子链是一个耦合谐振子,各原 子的振动相互关联传播,形成格波。
固体物理总复习

gap
2 )q 一维双原子链的长声学波 ( a mM B 长声学波中相邻原子的振动 ( A ) 1
光学波 长波极限
2
mM B m , ( ) - mM A M
§3.4
1. 三维复式格子
三维晶格的振动
l i [ t R l k q ] 格波的一般形式 A e k k
ab c
§5 晶体的宏观对称性
点对称操作 1. 绕轴旋转 2.旋转-反演(反演,镜面) 对称操作
1. 绕轴旋转
2.旋转-反演 3.空间平移
晶体的宏观对称性只有8种独立的对称操作: 1,2,3,4,6, 1 ( i ),
2 (m)
和
4
能证明为何晶体中没有5次对称性?
第二章
• 晶体结合的类型? • 晶体结合的物理本质? • 固体结合的类型与固体性质之间的联系?
T —— 电子对比热的贡献, 即电子热容
AT 3—— 晶格振动对比热的贡献, 即晶格热容
温度不太低时,可以忽略电子的贡献 爱因斯坦模型与德拜模型 爱因斯坦温度和德拜温度
§3.9 晶格振动模式密度
晶格振动模式密度 —— 单位频率间隔的振动模式数目
n g ( ) lim 0
在q空间,晶格振动模是均匀分布的,状态密度
本课程的主要内容
晶格动力学
原子核的运动规律 核外电子的运动规律
固体物理
固体电子论
晶格动力学
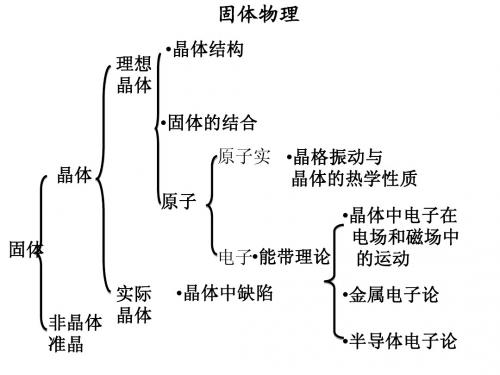
1. 晶体结构 2. 固体的结合 3. 晶格振动和热学性质
固体电子论
4. 能带理论 5. 外场中电子的运动 6. 金属电子论
第一章 摘
§1-1 §1-2 §1-3 §1-4 §1-5 §1-6 §1-7 §1-8 §1-9
固体物理-固体热容

03_08_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
在热力学中, 在热力学中,热容反映固体中原子热振动能量状态 改变时需要的能量,是固体的内能对温度求导。 改变时需要的能量,是固体的内能对温度求导。 ∂E CV = ( )V ∂T E------固体的平均内能 (晶格热振动)晶格热容,增加 晶格热振动)晶格热容, 离子的振动能量 固体的热容 (电子的热运动)电子热容,增 电子的热运动)电子热容, 加自由电子的动能。 加自由电子的动能。
晶体热容
hω0 CV = 3NkB fB ( ) kBT
hω0 hω0 2 ehω0 / kBT fB ( ) =( ) hω0 / kBT kBT kBT (e −1)2
—— 爱因斯坦热容函数 爱因斯坦特征温度
hω0 θE = kB
CV = 3NkB (
—— 大多数固体
θE
T
)
2
e
θE /T /T
• 定压热容 • 定容热容 • 定压摩尔热容和定容摩尔热容的关系:
Cp − Cv =
α v2 v m T
K
dV α v , 体膨胀系数, α v = , K −1 ; VdT dV K , 压缩系数, K = − ,m2 / N; Vdp V m , 摩尔体积, m 3 / mol ; K T , 物体的热力学温度,
调查结果
强调科普性的东西 强调固体物理的应用 倾向的专题: 超导体和半导体;生物材料;纳米 材料;磁性材料;记忆合金;热电 材料;石墨烯(碳纳米管);隐形 材料;光电材料;液晶材料 爱因斯坦相对论,宇宙大爆炸,时 空,黑洞
计算机在材料上的应用;碳纤维;萤光材料;耐高温冲击陶瓷;固体穿 透材料;晶体物理的基础;晶体学中的惯习现象;通信、电子材料原理 (电子材料及技术)轻合金材料及精密成型;军事和国防材料(黑体、灰 体、白体)等等
固体物理基础第3章-晶格振动与晶体的热学性质

3-2 一维单原子链模型
格波的色散关系 4 2 2 aq sin ( )
m 2 • ω取正值,则有 (3)
(q)
aq 2 sin( ) m 2 • 频率是波数的偶函数
• 色散关系曲线具有周期性, 仅取简约布里渊区的结果即可 • 由正弦函数的性质可知,只有满足 0 2 / m 的格波 才能在一维单原子链晶体中传播,其它频率的格波将被强
原子n和原子n+1间的距离
非平衡位置
原子n和原子n+1间相对位移
a n1 n
n1 n
3-2 一维单原子链模型
• 忽略高阶项,简谐近似考虑原子 振动,相邻原子间相互作用势能 1 d 2v v(a ) ( 2 ) a 2 2 dr • 相邻原子间作用力 dv d 2v f , ( 2 )a d dr • 只考虑相邻原子的作用,第n个原 子受到的作用力
• 连续介质中的波(如声波)可表示为 Ae ,则可看出 • 格波和连续介质波具有完全类似的形式 • 一个格波表示的是所有原子同时做频率为ω的振动 • 格波与连续介质波的主要区别在于(2)式中,aq取值任意加减 2π的整数倍对所有原子的振动没有影响,所以可将波数q取值 限制为 q a a
V
O
a
r
• 第n个原子的运动方程
(n1 n ) (n n1 ) (n1 n1 2n )
(1)
平衡位置
d 2 n m 2 ( n1 n 1 2n ) dt
非平衡位置
——牛顿第二定律F=ma
3-2 一维单原子链模型
• 上述(1)式的解(原子振动位移)具有平面波的形式
a
)
高二物理竞赛课件:晶体热容的量子理论

得到 Cv
定义德拜温度
有
9R
m3
m
0
(
k BT
)2
e
(e
/ k BT
/ k BT
1)
2
d
2
ΘD m / k B ,并令 m / k B
T 3 ΘD / T 4e
Cv 9R( )
d
2
0
Θ
(e 1)
R Nk B
晶体热容的量子理论
爱因斯坦模型忽略了各格波的频率差别
金刚石
11
晶体热容的量子理论
德拜模型
• 德拜模型的晶格振动假设方案:
• 以各向同性连续介质的弹性波来代表格波,非单一频率,
即 ω∝ q
• 格波包含有1个纵波和2个独立的横波
• 三种格波的波矢 q 在倒易空间均匀(准连续)分布
• 假设晶体中只存在小于某一ωm的长波以保证结果收敛
• 与实验结果相符合
j
Cv k B
k BT
/ k T
e j B
/ k T
j
B
1) 2
(e
2
2
1
/ k T 0
j
B
e
量子理论表明,晶体热容与晶格振动频率和温度有关系
晶体热容的量子理论
爱因斯坦模型
• 爱因斯坦模型的晶格振动假设方案:
2
j
B
1)
(e
2
与经典理论符合:振子的能量远远大于能量的量子
ℏ时,量子化效应可忽略,即
CV k B
与杜隆- 珀替定律相符
晶体热容的量子理论
定义德拜温度
有
9R
m3
m
0
(
k BT
)2
e
(e
/ k BT
/ k BT
1)
2
d
2
ΘD m / k B ,并令 m / k B
T 3 ΘD / T 4e
Cv 9R( )
d
2
0
Θ
(e 1)
R Nk B
晶体热容的量子理论
爱因斯坦模型忽略了各格波的频率差别
金刚石
11
晶体热容的量子理论
德拜模型
• 德拜模型的晶格振动假设方案:
• 以各向同性连续介质的弹性波来代表格波,非单一频率,
即 ω∝ q
• 格波包含有1个纵波和2个独立的横波
• 三种格波的波矢 q 在倒易空间均匀(准连续)分布
• 假设晶体中只存在小于某一ωm的长波以保证结果收敛
• 与实验结果相符合
j
Cv k B
k BT
/ k T
e j B
/ k T
j
B
1) 2
(e
2
2
1
/ k T 0
j
B
e
量子理论表明,晶体热容与晶格振动频率和温度有关系
晶体热容的量子理论
爱因斯坦模型
• 爱因斯坦模型的晶格振动假设方案:
2
j
B
1)
(e
2
与经典理论符合:振子的能量远远大于能量的量子
ℏ时,量子化效应可忽略,即
CV k B
与杜隆- 珀替定律相符
晶体热容的量子理论
固体物理学之晶格热容

晶格热容计算的简化模型 ---德拜模型
由周期性边界条件,q的取值为分立的,允许 的q值在q空间形成均匀分布的点子,在体积 元dk=dkxdkydkz中数目为:
V dk 3 (2π ) V V为晶体体积,上式表明, 3 是均匀分 (2π ) 布的q值的“密度”。
对于准连续分布的振动,可以把包含在ω+d ω内 的振动数目写成: Δn = g (ω )Δω 称为振动的频率分布函数(振动模的态密度函数)。 由于振动的热容只决定于它的频率:
2× ( V 2π 2Ct
ω 2 dω ) 3
总的频率分布为:
3V 2 g (ω ) = ω dω 2 3 2π C 1 1 1 1 = ( 3 + 3) 3 C 3 Cl Ct
根据弹性理论,ω可取0至无穷大地任意值,则:
∫
∞
0
g (ω )d ω
振动模的数量是发散的(因为理想介质的自由度是 无限的)。 在德拜模型中假设:频率大于某一个值ωm的短波 实际上是不存在的,而对ωm 以下的振动都可以用 弹性波近似, ωm则由自由度确定如下:
ξ
= 3R
辅助理解的课题思考题
1、爱因斯坦模型在低温下与实验存在偏差的物理根源是 什么? 2、在甚低温下,德拜模型为什么与实验相符?
CV (T / Θ D ) = 9 R ∫
Θ D /T
ξ 4 eξ
(e − 1)
ξ
2
0
dξ
T 3 ∞ ξ 4 eξ dξ ⇒ CV (T / Θ D ) = 9 R( ) ∫ 0 (eξ − 1) 2 ΘD T 3 12π 4 R( = ) 15 ΘD (T → 0)
Θ D = hω / k B
R = Nk B , ξ = hω / k BT
03_06_晶格热容的量子理论

实际晶体 态密度:
金属铝
• 总态密度是两 支横波(T1,T2) 和一支纵波 (L) 的叠加。 • 低频部分都近 似为抛物线。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
习题3.1
• 固体物理教程--王矜奉 习题 3.10
V ds g (w ) (2 )3 qw ( q)
假设1:N个原子构成的晶体,原子以相同频率 w0 振动;
假设2:谐振子能量是量子化的
温度T下,平衡后谐振子平均能量:
总能量
热容
w0 CV 3NkB f B ( ) —— 爱因斯坦热容函数 k BT
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
—— 爱因斯坦热容函数
爱因斯坦温度
定容比热
在较高温下,该理论与实验符合很好; 但在低温下,与实验结果差别很大,低温下测量有 Cv~ T 3
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
实验表明 —— 在低温时热容量随温度迅速趋于零 。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
2. 爱因斯坦模型
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
上面推导使用积分公式
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
T T 3 CV ( ) 9 NkB ( ) D D
D /T
0
x 4e x dx x 2 (e 1)
徳拜公式的比热容曲线
金属镱实验结果与 徳拜模型比较。
2
为简化,做变量代换,令
T T 3 CV ( ) 9 NkB ( ) D D
D /T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
e
j / k B T
1
j k BT )
2
CV k B (
T 0
1 e
j / k BT
CV 0
—— 与实验结果相符
5-2晶体热容的量子理论(Einstein、Debye模型)
一个频率为ωj振动模对CV贡献 C (
j V
dE j (T ) dT
( )V k B
m
m
g ( ) d
0
2 e / kBT 晶体总的热容 CV k B ( ) g ( )d / k BT 2 k BT ( e 1) 0 3 V 2 e / k T 3 kB ( ) 2 d 2 2 C 0 k BT ( e / k T 1) 2
E
(2)低温情况(T<<θE):
因为 : e T 1 所以, CV 3 Nk B (
E
结论:
E
T
) e
2
E
T
(1)T处于低温段时实验
值与理论不符;
(2)T趋近于0时理论结
—— 按温度的指数形式降低
T 0时, e
E
T
果与实际符合较好;
0,CV 0
5-2晶体热容的量子理论(Einstein、Debye模型)
5-2晶体热容的量子理论(Einstein、Debye模型)
对纵波:ω=Clq
q空间q的分布密度
qz
q dq
q q dq
范围的模式数: dnl
V ( 2 )
V 2 2 C
2 3 l
3
4q dq
2
q
qx
g t ( )
qy
d Cl dq
g l ( ) dnl d
计算晶格热容CV的理论模型 Ⅰ. Einstein模型
模型要点:
即忽略 q 存在.
(1)认为晶体中所有原子都以相同的频率振动,设为ω0 (2)晶格振动能量是量子化的。
体系规定: N个原子组成,共3N个频率为ω0的振动。
5-2晶体热容的量子理论(Einstein、Debye模型)
j 一个振动模的平均能量 E (T ) 1 j j j / k B T 2 e 1
如何确定振动频率分布函数 g ( ) 和m?
5-2晶体热容的量子理论(Einstein、Debye模型)
g ( ) 确定?
dn
频率在 d 之间振动模式的数目
单位频率间隔内的振动模式数目 g ( )
dn d
Debye 模型将晶体作为弹性连续介质处理,
C l q (纵波一支) N个原子组成晶体的色散关系: C t q (横波两支)
同理,对横波ω=Ctq
V 2 2 2 C t3
g ( ) g l ( ) 2 g t ( )
令
V 2 2 3
C
3
2
(
1 Cl 3
Cl
3
2 Ct 3
Ct
3
)
g ( )
V 2 2
2
3 C
3
3
3
5-2晶体热容的量子理论(Einstein、Debye模型)
m确定?格波总数目3 N
j
CV k B
—— 与杜隆- 珀替定律相符
5-2晶体热容的量子理论(Einstein、Debye模型)
一个频率为ωj振动模对CV贡献 C (
j V
dE j (T ) dT
( )V k B
j k BT
j
j
) 2 e k BT
( e k BT 1) 2
低温极限
k B T j
E j T
振动模
)V
先计算平均能量
一个频率为ωj谐振子(振动模)
再计算对CV贡献
5-2晶体热容的量子理论(Einstein、Debye模型)
一个频率为ωj的谐振子能级 占据 E j 概率:Pn j Ce
E j ( n j ) j 2
e
nj n j / k B T n j / k B T
E
Einstein模型讨论:
E
(1)高温情况(T>>θE):
E
e
2T
1
1
E
2T
( )2 T
eT
E
2
1
E
(e
T
1)
(e
2T
e
E 2T
)
2
(
E
2T
E
2T
E
)
2
C V 3 Nk B
5-2晶体热容的量子理论(Einstein、Debye模型)
e E / T 2 晶体热容 CV 3 Nk B ( ) E /T 2 T (e 1)
问题1:晶体比热的实验规律?如何利用理论解释? 一、晶体比热的实验规律 经典?量子?
1、高温时,晶体的比热为3NkB(N为晶体中原子个数);
2、低温时,晶体的比热按T3趋于零。
二、求解CV的一般方法 CV (
a e CV CV CV
E
)V E 指晶体的平均内能 T
晶格振动比热
晶体电子比热
120
115
D
110
105
100 0 5 10 15 20 25
T(K)
金属铟的Debye温度随T的变化
5-2晶体热容的量子理论(Einstein、Debye模型)
Debye模型评价:
(1)忽略晶体的各向异性; (2)忽略光学波和高频声学波对热容的贡献。
5-2晶体热容的量子理论(Einstein、Debye模型)
Einstein理论与实验比较图
6 5 4 3 2 1 0 0.0
Cp(J/mol.K)
0.2
0.4
T/
0.6
0.8
1.0
圆点为金刚石实验值,温度以θE=ω0/ħ为单位。
5-2晶体热容的量子理论(Einstein、Debye模型)
Einstein模型评价:
前提假设过于简单,忽略各格波的频率差别. Ⅱ. P.Debye模型 模型要点:
2
0 k BT
E
T
E C V 3 Nk B T
E
eT ( e T 1) 2
E
金刚石 E 1320 K
ቤተ መጻሕፍቲ ባይዱ大多数固体
E 100 K ~ 300 K
理论计算和实验结果比较
5-2晶体热容的量子理论(Einstein、Debye模型)
e E / T 2 晶体热容 CV 3 Nk B ( ) E /T 2 T (e 1)
( e 1)
2
d
12 T 3 CV (T / D ) R( ) 即Debye的T3定律 15 D
结论(1)德拜模型高温下或甚低温下,与实验相符;—T3成正比
(2)Debye理论得不同温度下ΘD同(实验上ΘD应该是与T有关)
5-2晶体热容的量子理论(Einstein、Debye模型)
m B B
N 1/ 3 m C [6 ( )] V
2
令
德拜温度 D m k BT kB
D
CV (T / D ) 9 R(
T 3 ) 3( ) 德拜热容函数 f D ( T D
D / T
T
D /T
0
D 4 e
)3
2
0
4 e
(e 1)
0 CV 3NkB f B ( ) k BT
fB (
0 k BT
)(
0 k BT
)2
e 0 / k B T (e
0 / k B T
1)
2
—— 爱因斯坦热容函数
5-2晶体热容的量子理论(Einstein、Debye模型)
令
0 kB
E (称爱因斯坦温度),则
2
d
( e 1)
d
CV (T / D ) 3Rf D (
5-2晶体热容的量子理论(Einstein、Debye模型)
D T
)
T 3 ) 3( ) 德拜热容函数 f D ( T D
D
D / T
0
4 e
( e 1)
2
d
Debye模型讨论:
在高温极限下 1 k BT
j k BT
j k BT
j
) 2 e k BT 1)
2
(e
晶格总热容
设晶体中包括N个原子,共3N个简谐振动模式,则总热容:
CV
CV
j
3N
j
可见, j C V C V
j
对于具体晶体,计算3N个简正频率十分复杂.
5-2晶体热容的量子理论(Einstein、Debye模型)
e (e
j / k B T
j / k B T
1) 2
j
物理上,遇到以下这一类求和问题时,可变为积分
f (
j
j
) g ( ) f ( ) d
其中g(ω)表示单位频率间隔内的振动模式数目,称态密度.
m
CV
0
2 e / kBT kB ( ) g ( )d / k BT 2 k BT ( e 1)
j 3 3 N 0 晶体总能量 E ( 1 ) N 0 / k T j j / k B T e 1 2 e 0 B 1 j 1 2
