高等数学教学有限与无限过程的划分
高等数学1-2极限的概念、无穷小与无穷大(上)
A3 , A4 , An ,
S
极限的概念
二、数列 及其极限
1.数列的概念 整标函数： 定义域为全体正整数的函数 y f (n) 称为整标函数。 f (1) x1 , f (2) x2 , f (3) x3 , 数列： 按照自然数的顺序排列的一列数 x1 , x2 , xn , 简记为{ xn }, 其中xn称为数列 { xn }的通项 或者一般项.
1 1 1 1 1 (1). , , , , n ,; 2 4 8 16 2
(1)n1 1 (2)1, 0, 1, 0,, ; 2
(3) 1, 2, 3,n,
1 1 1 1 1 解：(1). x1 , x2 , x3 ,, xn n ,. { xn } { n } 2 4 8 2 2
y y 1 x
1
y x2 1
o
x
解
观察可知:
x0
lim f ( x ) lim (1 x ) 1
x0
左极限
x 0
lim f ( x ) lim ( x 2 1) 1
x 0
x 0 x 0
右极限
因为 lim f ( x ) lim f ( x ) 1
极限的概念
3.2. 唯一性
性质2 每个收敛的数列只有一个极限.
3.3. 保号性
x n A, 且 A 0 ( A 0), 则N 0, 性质3 如果 lim n
当n N , 有xn 0 ( xn 0).
推论 如果数列 xn 从某项起有 xn 0 ( xn 0),
xn f (n)
13
n1 （n 1,2,3， ） 例如 (1) 、x n n 3 4 n1 ,} { xn } {2, , ,, 2 3 n
第六讲：有限与无限
i1
1 2
i
1
an an1 d ,
a1 = *
5）因子链条件（抽象代数中的术语）
34
3. 数学中的无限在生活中的反映
1）大烟囱是圆的：每一块砖都是直的 （整体看又是圆的）
(大家的经验：公园中通幽的“曲径”是“条石”修成的； 圆形的石拱桥；家中弧形的拱形装饰） 2）锉刀锉一个光滑零件： 每一锉锉下去都是直的 （许多刀合在一起的效果又是光滑的）
↙ ↙↙ 二团： 2.1 2.2 2.3 2.4 ……
↙↙ 三团： 3.1 3.2 3.3 3.4 …… ……………………………………
16
法II.
让每个旅游团占据某固定素数的方幂
由于素数有无穷多个，正整数又 “唯一析因”，
知，能安排住下，且还有空房，
一团
p
1 1
二团
p
1 2
p
2 1
p
3 1
…
p
4 1
n
a i 是个确定的数
i1
无穷级数一定有“和”。 ×
( 1)i
则不是个确定的数。称为该
i1
级数“发散”。反之称为“收敛”。
31
有限多个无穷小量的乘积一定还是无穷 小量。 (所以，高等数学中学习“无穷小量”性质时应 注意“有限个”的条件）
无穷多个无穷小量的乘积未必是无穷小量（ 甚至可以是无穷大量）。
7
1. 四个芝诺悖论之一： 阿基里斯追不上乌龟。
a1
a2
a3 a4
A1
A2
A3 A4 … An
2. 症结：
无限段长度的和，可能是有限的； 无限段时间的和，也可能是有限的。
例：“一尺之棰，日取其半，万世不竭”，每天取得的产度构成无穷 递缩等比数列{an} ½,1/4,1/8,1/16,1/32,…
《高等数学》分层次教学大纲
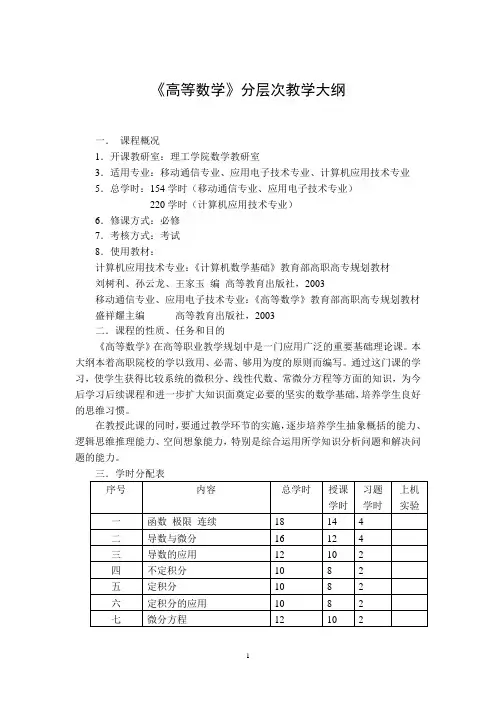
《高等数学》分层次教学大纲一．课程概况1．开课教研室：理工学院数学教研室3．适用专业：移动通信专业、应用电子技术专业、计算机应用技术专业5．总学时：154学时（移动通信专业、应用电子技术专业）220学时（计算机应用技术专业）6．修课方式：必修7．考核方式：考试8．使用教材：计算机应用技术专业：《计算机数学基础》教育部高职高专规划教材刘树利、孙云龙、王家玉编高等教育出版社，2003移动通信专业、应用电子技术专业：《高等数学》教育部高职高专规划教材盛祥耀主编高等教育出版社，2003二．课程的性质、任务和目的《高等数学》在高等职业教学规划中是一门应用广泛的重要基础理论课。
本大纲本着高职院校的学以致用、必需、够用为度的原则而编写。
通过这门课的学习，使学生获得比较系统的微积分、线性代数、常微分方程等方面的知识，为今后学习后续课程和进一步扩大知识面奠定必要的坚实的数学基础，培养学生良好的思维习惯。
在教授此课的同时，要通过教学环节的实施，逐步培养学生抽象概括的能力、逻辑思维推理能力、空间想象能力，特别是综合运用所学知识分析问题和解决问题的能力。
上述知识模块的教学顺序按序号中所标次序进行，*号部分为选学内容，计算机应用技术专业选学十三-----十八模块，移动通信专业、应用电子技术专业选学十二模块，数学软件的教学可结合高等数学的教学内容同步进行，也可以在课程最后进行。
四．课程基本要求 A 层：（一） 函数 极限 连续 1．教学要求理解函数的概念，了解函数的有界性，单调性，周期性与奇偶性，理解反函数与复合函数的概念，熟练掌握基本初等函数的性质与图形，能建立简单实际问题中的函数关系。
了解极限δεε--，N 的定义，在整个学习过程中，逐步加深对极限思想的理解，掌握极限的四则运算法则，了解夹逼准则和单调有限准则，会用两个重要极限求极限，了解无穷小，无穷大的概念，掌握无穷小的比较，会用等价无穷小的代换求极限，理解在一点连续的概念，会判断间断点的类型，了解初等函数的连续性，知道在闭区间上连续函数的性质。
浅谈高等数学教学创新思维
浅谈高等数学教学创新思维作者：陈争来源：《科技创新导报》2011年第06期摘要:本文就辨证逻辑思维是微积分的思维方法的主要力量,高等数学教学理应重视辨证逻辑思维,自觉运用唯物辨证法作指导,才能让学生深刻领会微积分思想方法的精髓和实质。
关键词:微积分辩证法逻辑思维中图分类号:O13-4 文献标识码:A 文章编号:1674-098X(2011)02(c)-0152-011 微积分学习中的问题就微积分是关于“无限数学”的科学,“无限”概念本属哲学范畴,处理“无限”问题,必须讲有限与无限的辩证关系,因此,微积分是数学思维与哲学辩证思维交互作用的产物,它以严格的形式逻辑和精确的数学语言表达了宇宙运动变化规律。
由于微积分是形式逻辑体系,其辩证逻辑蕴含于形式逻辑体系之中,这就给微积分思想方法的教与学增加了难度,微积分解决问题时常常使用常量与变量互易方法,但运用形式逻辑思维也同样无法理解的。
总之,他们明显觉得学习高等数学与学习初等数学的思维方法有别,但知其然而不知其所以然。
那么,作为教师,我们如何让学生领悟其中的辩证思想,充分发挥微积分学在科学世界观与方法论形成中的作用。
笔者认为,微积分思想方法的教学,关键是要让学生掌握辩证逻辑思维这把钥匙。
2 形式逻辑思维与辩证逻辑思维的区别与连系数学是在逻辑范围内活动的,数学逻辑包括形式逻辑与辩证逻辑。
形式逻辑它以思维形式结构及其规律性为其主要研究对象。
辩证逻辑思维规律与形式逻辑思维规律的关系是“前者是高级的思维规律,后者是低级的思维规律。
”辩证逻辑思维规律是以形式逻辑思维规律为基础的,辩证逻辑思维规律是动态下的逻辑思维规律,而动态是由一个个静态组成的,由静态所表现和度量的,因而辩证逻辑思维规律在相对静态下时,就变成了静态下的形式逻辑思维规律了。
形式逻辑思维规律是辩证逻辑从动态到静态后的有机的一环。
微积分学科的建立和发展,虽离不开形式逻辑这个使数学保持自身健康的卫生规则,然而微积分学一些重大的、原创性的思想方法的获得是源于形式逻辑思维以外的辩证逻辑思维。
《高等数学A》学习指南
课程学习指南一百多年前，恩格斯曾经说“数学是研究现实世界中的数量关系与空间形式的科学”，而现代数学的发展使得其研究对象已经大大超出了“数”与“形”的范畴。
一般说来，数学的研究对象可以包括现实中的任何形式和关系。
数学是自然科学的基本语言，是应用模式去探索现实世界物质运动机理的主要手段，更是现代技术与工程必不可少的工具。
历史上物理学、天文学、力学的许多重大发现，例如牛顿力学、爱因斯坦相对论、电磁波和光的本质的发现、海王星和冥王星的发现、量子力学的诞生等等，无不与数学的进步息息相关。
20世纪最伟大的技术成就电子计算机的发明和应用也都是以数学为基础的。
现代的许多“高科技”本质上就是数学技术，例如医学上的CT技术、指纹的存储和识别技术、飞行器的模拟设计、石油地震勘探的数据处理分析、信息安全技术、保险精算、金融风险分析和预测等等。
当今的数学不再只是通过其他学科间接地而是直接地、广泛地应用于各技术领域中。
数学来源于实践，又由本身的矛盾运动而不断发展，今天的数学作为一门科学，高度的抽象性、严密的逻辑性和应用的普遍性成为它的三大特征。
我们学习的《高等数学》课程，其主要内容是微积分。
从十七世纪60年代牛顿、莱布尼茨创立微积分起，逐步形成了一门逻辑严密、系统完整的学科，不仅成为其他许多数学分支的重要基础，而且在自然科学、工程技术、生命科学、社会科学、经济管理等众多领域获得了十分广泛的应用，成为处理有关连续量问题的强有力的数学工具。
在高等学校里，《高等数学》是大学生熟练掌握数学工具的主要平台，是培养大学生理性思维的重要载体，是学生获得数学素养的一条重要途径。
高等数学已成为大学理工学科、经济管理学科各专业以及其他许多专业最重要的数学基础课。
《高等数学》课程在大学一年级分上下两个学期讲授，包括函数与极限、函数的导数与微分、一元函数微分学的应用、定积分与不定积分、定积分的应用、向量代数与空间解析几何、多元函数的微分学及其应用、多元函数的积分学（重积分、曲线积分、曲面积分）及其应用以及无穷级数和常微分方程等教学内容。
高教社2024高等数学第五版教学课件-1.4 无穷小与无穷大
1
因为
→∞
=0
2．无穷大量
定义2
如果函数 = ()的绝对值在自变量的某一变化过
程中无限增大，则称函数 = ()为无穷大量，记作 () = ∞.
例如，因为 = ∞，所以 是 → ∞时的无穷大；因为
→+∞
1
→0
=
1
示()的绝对值无限变大且都是负值，而后者表示()的绝对值无限
变小，趋于零.
3．无穷小与无穷大的关系
定理1
1
在自变量的同一变化过程中，如果()是无穷大，则
是
()
无穷小；反之，如果()是无穷小，且() ≠
例如，当 →
1时， 2
1
0，则
是无穷大.
()
1
− 1是无穷小，而 2 是无穷大.
⑴称一个函数()是无穷小，必须指明自变量的变化趋势，如
3 + 1是当 → −1时的无穷小，但当 → 0时就不是无穷小.
⑵ 不要把一个绝对值很小的非零常数(如10−100 )说成是无穷小，
因为这个数的极限不为0.
⑶ 数“0”可以看成无穷小.（是唯一可作为无穷小的常数）
1
⑷ 无穷小的定义对数列也适用，例如数列{ }，当 → ∞时，就
∞，所以 是
→ 0时的无穷大.
这里，虽然使用了极限的符号 () = ∞，但并不意味着
()有极限. 因为，根据极限的定义，极限值必须是常数. 然而∞不
是常数，它只表示()的绝对值无限变大的一种变化趋势.
注意：⑴ 称一个函数()是无穷大，必须指明自变量的变化趋势，
1
是当
′
′
《高等数学》课程的思政元素挖掘与融入
《高等数学》课程的思政元素挖掘与融入发布时间：2021-09-28T01:42:00.137Z 来源：《教育学文摘》2021年第15期作者：王涛[导读] 本文从下面6个方面归纳总结了《高等数学》课程中的思政元素。
王涛长沙民政职业技术学院通识教育中心湖南长沙410004摘要:本文从下面6个方面归纳总结了《高等数学》课程中的思政元素；1，从课程内容的起源和发展融入思政教育；2，在教学内容中自然的融入思政教育；3，结合课程教学的特点融入思政教育；4，在体会和欣赏数学美中融入思政教育；5,通过介绍数学史融入思政教育6，通过培养学生的“数学精神”融入思政教育；并且指出这个融入过程应该是自然地，恰到好处地，画龙点睛地。
好的思政教育的融入可以使这堂课更有吸引力，可以使得这堂课达到更好的效果。
关键词:思政；融入一、问题的提出“课程思政”概念是由上海教育领域于2016年率先提出。
它不是一门课程，也不是一项活动，而是一种教育理念，是旨在将思想政治教育融入课程教学和教学改革的各个环节，实现与思政课程的同向同行，形成协同效应，达到润物无声，立德树人的目标。
在学校思想政治理论课教师座谈会上，总书记进一步指出：“要加大对学生认知规律和接受特点的研究，要坚持灌输性与启发性相统一，要坚持显性教育与隐形教育相统一，挖掘其他课程和教学方式中蕴含的思想政治教育资源，实现全员、全程、全方位育人。
”有人说；在《高等数学》课程中挖掘思政元素有点牵强附会，不自然，效果不好。
但我认为《高等数学》课程中有很多思政元素可以挖掘，并且可以很自然地融入到教学中，可以收到意想不到的好效果。
二、在《高等数学》课程教学中有效融入“思政元素”1，从课程内容的起源和发展融入思政教育（1）在讲解极限概念这一内容时，当讲到割圆术；割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体而无所失矣。
我国古代刘徽以极限思想为指导提出用割圆术求圆周率比西方早1000多年。
挖掘哲学思想,提高教学效果——谈级数中对立与统一的辩证观点
赤 峰 学 院 学 报（ 自 然 科 学 版 ） Journal of Chifeng University（Natural Science Edition）
Vol. 28 No. 6 Jun. 2012
挖掘哲学思想，提高教学效果
— ——谈级数中对立与统一的辩证观点
∞
∞
Σ Σ 下有 （－１）ｋ－１ｋ＝ｌｉｍ （－１）ｋ－１ｋｘｋ－１＝ｌｉｍ （１＋ｘ）－２＝ １ ，故此时该
ｋ＝１
ｘ＝１－ ｋ ＝ １
ｘ＝１－
４
级数收敛．由此可见，级数的收敛与发散之间既是对立关系，
又有统一关系．
２．３ 有限与无限的对立与统一
瑞士数学家伯努利（Ｂｅｒｎｏｕｌｌｉ，１６５４－１７０５）曾经说：“正
法国数学家努瓦利斯曾经说过“数学是朴素的哲学”，
而捷克的数学家、哲学家波尔达斯则说“没有哲学，难以得
知数学的深度”，这两句话充分表明了数学的本质是哲学，
数学与哲学之间是一个相互依存的关系．级数作为高等数学
的一个重要内容，是无限个常量或变量之和的数学模型，级
数是表示函数、研究函数性态以及进行数值计算的一种有
要讨论的问题．根据实际问题的需要，收敛性和发散性的也
有多种定义，每种定义中的收敛与发散概念是相互对立的，
而不同定义之间的收敛或发散，有时候却是统一的．我们知
道，级数的收敛或发散是依赖于所用的求和方法，在级数理
论中，有通常意义下的 Ｃａｕｃｈｙ 与广义 Ａｂｅｌ 两种求和法，其
中 Ｃａｕｃｈｙ 求和法即定义 ３ 中的方法，而广义 Ａｂｅｌ 求和的定
次用加号连接起来的表达式 ｕ１＋ｕ２＋…＋ｕｎ＋…，称为常数项无
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高等数学教学有限与无限过程的划分
[摘要] 高等数学教学中有限与无限量的变化规律及有联系又有区别,在教学中要时刻注意区分,这样才不致于出现把有限量的法则,规律用于无限量.
[关键词] 教学;有限;无限;区分.
高等数学是由极限的思想和理论产生发展起来的,并以极限为工具刻划了微分和积分以及无穷级数等无限过程的概念.通过有限到无限变化过程的描述,把直与曲,方与圆,变与不变等矛盾从代数与几何的双重角度分析,归纳使之化为辩证的统一.那么有限与无限过程是如何演变的,在教学中又如何区分呢,下面举例说明.
一. 圆的面积.
三国时代我国著名数学家刘徽创造了”割圆术”,从而解决了求圆面积的问题他首
先做圆内接正六边形 ,再做正12边形,正24边形……一直做下去,虽然边数越来越多,但是无论是正几边形,哪怕是成千上万边形,它都不是圆,仍然是正多边形,只有当边数无限增大时,这个无限就成为转折点把有限过程转化为无限过程,从而发生了质的变化,直边演变成了曲边,内接正多边形演变成了圆,从而得到正多边形面积当边数无限增大时的极限就是圆的面积.这个过程经过了若干年,这样随着圆面积的求法产生了极限的概念,这是无限过程的硕果,这个发明充分的体现出人类无限的想象力和非凡的创造力.经过极限这个无限过程,使正多边形发生了质的变化,演变成一个圆.使几何上直线与曲线得到辩证统一.其实在解析几何里直线本来就是曲线的特例,化直为曲这是无限过程的非凡作用.是有限过程做不到的.同时以直代曲也是重要的数学思想.有限到无限是数学发展的一个飞跃.标志着数学发展到一个高级阶段.
二. 有限集,无限集.
我们每个人都知道整体大于部分这个事实,但在集合论中整体大于部分这条古老的公理却发生了矛盾.众所周知当两个集合的元素有一一对应关系时,其元素个数相等,比如集合A={1,2,3,4}和B={}4,3,2,12222它们可建立一一对应关系,所以它们的元素个数相等.但是对于自然数集N={1,2,3,4…}和其平方数集M={...}4,3,2,12222就不那么简单了,显然M 是N 的部分元素构成的集合,比如2N ∈但2M ∉,然而N 与M 两个集合的元素也可建立一一对应关系,因此它们的元素个数应该相等.这使我们很难理解,整体既然大于部分,它怎么又等于部分呢?这是否具有普遍性呢?经过分析,在有限集中整体总大于部分,看来是无限集惹得祸,确实在无限集中整体大于部分就失灵了,我们不能简单的说两个无限集的元素谁多谁少.这个事实提醒我们在教学中有限集和无限集的理论不能混为一谈,有限集的有些理论,法则,公理不能直接用到无限集.
三. 定积分的概念
我们知道定积分⎰b
a
dx x f )(是一个积和式的极限.由于
=⎰b a dx x f )(i
n i i x f ∆∑=→)(1
0lim ξλ,所以定积分可理解为无限多个无穷小的代数和,
这个无限项代数和与有限项代数和有什么区别和联系呢,关于有限项的和对我们来说并不陌生,比如在极限里学过有限多个无穷小的代数和为无穷小,在微分里,有限个函数代数和的导数等于函数导数的代数和,在积分里,有限个函数代数和的积分等于函数积分的代数和等等,都特别强调了有限项.对于定积分来说它是无限项的和,能否沿用有限项和的性质与法则呢?如果用有限个无穷小的代数和为无穷小的性质,定积分是无穷小和的极限其值为零,这显然是错误的.否则就没有必要研究定积分的计算了,通过对定积分的研究发现其值可能是常数也可能不存在,这就是说有限项和与无限项和是有区别的,对于有限项代数和的法规,性质等 ,不能直接用到无限项上去,这说明有限项与无限项和的法则不通用,这也是我们在讲极限,微分,积分运算法则时强调有限项的必要性.要时刻注意区分有限与无限这两个概念不能混淆.
四. 无穷级数的和
众所周知有限项的代数和满足交换律,结合律在我们头脑中以是根深蒂固,但 对于无限项和是否满足交换律和结合律呢,我们还是以实例来说明吧,例如无穷级 数X=1-1+1-1+1-…求和时.
由于(a) X=1-1+1-1+…=(1-1)+(1-1)+…=0+0+…=0.所以X=0.
(b)X=1-1+1-1+1-…=1-(1-1)-(1-1)-…=1-0-0-…=1.所以X=1.
(c)X=1-1+1-1+1…=1-(1-1+1-1+1…)=1-X. 2X=1.所以X=2
1 综上所述0=2
1=1.两端同乘以任何数得,0=任何数.这显然是不正确的,错误的原因是什么呢,我们很难发现,那么也只能归结为无限项和的原因,分析上述三种算法都用到了加法的结合律,而对于无穷级数来说不一定满足加法结合律.其实该级数是发散的.对于上述错误都是由于把加法的结合律搬到了无限项和上去,因此区分有限与无限项的和就显得非常重要.加法的结合律只是满足有限项的和,当我们把加法的项数推广到无限项的时候,同时失去了加法结合律.在进行代数和运算时要特别加以重视,不然我们就会犯类似错误.
五. 无穷大的运算
我们学过两个无穷小的比较,有高阶,低阶,同阶和等价之分.对于
无穷
大其实我们也可用无穷小阶的定义方法,用其商的极限进行比较,来定义无穷大的阶数,但对于两无穷大的代数和是什么,又如何进行运算呢?由于无穷大不是具体的数它描述的是变量的一个无限变化趋势是不确定的,因此两无穷大的和也不确定,特别是∞-∞它可能是无穷大也可能不是,但是它不一定是零,因为两无穷大的变化速度不一定相同,因此无穷大的代数和的运算,只能用极限方法先变形在计算,因此我们在遇到无穷大的运算时要给予足够的重视它不是具体数而是一变化过程,因此不能代数运算法则进行运算.
总之在进行高等数学教学中,要时刻注意变量的有限与无限的变化过程,要注意它们及有区别又有联系和它们对立的统一,有的量经过无限变化过程可以发生质的变化.使原来的面目全非,而有限量的运算规律不一定适合无限量,特别是我
们熟悉的四则运算有限项适用对无限项就不一定适用,然而无限过程又是由有限过程演变,抽象而来.就是这种从特殊到一般,从具体到抽象的变化过程把我们认为可以推广的理论确不能推广,表面上看可以归纳猜想的理论却是错误的,就是因为无限变化过程与有限变化过程存在着本质区别.如果我们准确的理解掌握并时刻注意有限与无限过程的联系与区别,那么高等数学中变量的无限的变化规律就在我们掌握之中,使有限与无限产生的矛盾得到解决,成为一个辩证的统一体.
[参考文献]
[1]同济大学数学教研室主编[高等数学]
[2]王庚著[数学文化与数学教育]。