2021年高中数学第6章幂函数指数函数和对数函数6.1幂函数课件苏教版必修一.ppt
指数函数、幂函数、对数函数增长的比较(45张PPT)——高中数学必修第一册
一次函数y＝kx(k＞0)，指数函数y＝ax(a＞1)和对数函数y＝logbx(b＞1)的增长有何差异？
一般地，无论k(k＞0)、a(a＞1)、b(b＞1)如何取值，三种函数在区间(0，＋∞)上都单调递增，但一次函数总是保持固定的增长速度；指数函数的增长速度都会越来越快，并且指数函数的函数值最终总会大于一次函数的函数值；对数函数的增长速度都会越来越慢，并且对数函数的函数值最终总会小于一次函数的函数值．
401
626
901
y2
2
32
1024
32768
1.05×106
3.36×107
1.07×109
y3
2
10
20
30
40
50
60
y4
2
4.322
5.322
5.907
6.322
6.644
6.907
【解析】(1)由于指数型函数的增长式为爆炸式增长，则当x越来越大时，函数y=的增长速度最快，故选A.
(2)从表格中可以看出，四个变量y1，y2，y3，y4均是从2开始变化，变量y1，y2，y3，y4都是越来越大，但是增长速度不同，其中变量y2的增长速度最快，可知变量y2关于x呈指数函数变化.
x
y=2x
y=2x
0
1
0
2
4
4
4
16
8
6
64
12
8
256
16
10
1024
20
12
4096
24
…
…
…
可以看到，当自变量x越来越大时，y＝2x的图象就像与x轴垂直一样，2x的值快速增长；而函数y＝2x的增长速度依然保持不变，与函数y＝2x的增长速度相比几乎微不足道．
苏教版高中学案数学必修第一册 第6章 幂函数、指数函数和对数函数 幂函数、指数函数与对数函数的综合
函数，且 = ( − )在(, +∞)上是增函数，所以()在(, +∞)上是增函数.
∣ + ∣> ,
由( + ) < ()得(| + |) < (||)，所以ቐ∣ ∣> ,
所以
∣ + ∣<∣ ∣,
( + ) > ,
第6章 幂函数、指数函数和对数函数
午练23 幂函数、指数函数与对数函数的综合
1
1.当0 < ≤ 时，4 < log ，则实数的取值范围是() B
2
A.(0,
2
2
)B.( , 1)C.(1,
2
2
2)D.( 2, 2)
[解析]易知 < < ，则函数 = 与 = 的图象大致如图所示，只需满足
C.()在定义域内是偶函数D.()的图象关于直线 = 1对称
[解析]由| − | > ，得函数 = | − |的定义域为{| ≠ }.设
− , > ,
() =∣ − ∣= ቊ
则()在(−∞, )上单调递减，在(, +∞)上单调递
或 = .当 = 时，得 = ，解得 = .当 = 时，得 = ，即 = .
所以函数的定义域为[, ]( ≤ )，
所以当 = ， = 时， + 最大为3.
9.已知()是定义在[−2,2]上的奇函数，当 ∈ (0,2]时，() = 2 − 1，函数
1
2
1
4
因为() = log 2 (2 − 4 ) = log 2 [−(2 )2 + 2 ] = log 2 [−(2 − )2 + ]，所以当
苏教版高中数学必修一课件第3章-指数函数、对数函数和幂函数3.1.1+56张
【答案】 (1)－8 (2)10 (3)π－3 (4)m－n
根式与分数指数幂的互化
【思路探究】 各小题中均含有根式，可将根式化为分 数指数幂形式，根据分数指数幂的运算性质求解．
【自主解答】
1．此类问题应熟练应用 ＝n am(a>0，m，n∈N*，且 n>1)求解．当所求根式含有多重根号时，要搞清被开方数， 由里向外用分数指数幂写出，然后再用性质进行化简．
2．一般来说，应化根式为分数指数幂，利用幂的运算性 质运算．
用分数指数幂的形式表示下列各式(a>0 ，b>0)：
3 (1)
8－4；(2)4
－260；(3)a33
a2；(4)
a
a；(5)
ab3 ab5.
【解】
利用分数指数幂的运算性质化简求值
【思路探究】 先化简各个分数指数幂，然后再进行四 则运算，注意一般先将小数化为分数．
3．已知 a>0 且 a＋a－1＝2，则 a2＋a－2＝________. 【解析】 a2＋a－2＝(a＋a－1)2－2＝4－2＝2. 【答案】 2
【解】
课时作业（十一）
【思路探究】 令 pa3＝qb3＝rc3＝k，用等量代换分别表 示出所证等式左、右两边的量，最后化简判断．
【自主解答】
对于“恒等式”，如本例，我们往往令它等于一个常数 k，然后以 k 为“媒介”化简，这样可以使问题很容易解决．
计算下列各式的值
3 (1)
－83＝________；(2)
－102＝________；
4 (3)
3－π4＝________；(4)
m－n2(m>n)＝________.
【解析】 3 －83＝－8； －102＝ 102＝10；
高中数学第3章指数函数对数函数和幂函数3.3幂函数课件苏教版必修1
重点突破
解析答案
(2)已知函数 f(x)＝(a2－3a＋3) x a2 5 a 5 (a 为常数)为幂函数，且在(0，＋∞)
上单调递减，求实数 a 的值.
解 ∵f(x)为幂函数， ∴a2－3a＋3＝1，得a＝1或a＝2. 当a＝1时，f(x)＝x，在(0，＋∞)上单调递增，不合题意. 当a＝2时，f(x)＝x－1，在(0，＋∞)上单调递减，符合题意. 综上，得a的值为2.
解析答案
题型三 比较幂的大小
例3 比较下列各组数的大小.
5
5
(1) 3 2 和 3.1 2 ；
5
解 函数 y x 2 在(0，＋∞)上为减函数，
又3<3.1，所以 3
5 2
>
3
5
.1 2
.
(2)
8
89
和
(
1
)
8 9
9
；
8
解 函数 y x9 在(0，＋∞)上为增函数，
又18>19，
解析答案
返回
当堂检测
1.下列给出的函数中，是幂函数的是___③_____.
①y＝3x
②y＝2x3
③y＝x－3
④y＝x3－1
12345
答案
12345
2.若函数y＝(k2－k－5)x2是幂函数，则实数k的值为__3_或__－__2_. 解析 由幂函数的概念可知k2－k－5＝1， 即k2－k－6＝0，得k＝－2，或k＝3.
解 ∵3 y＝x3是1 R上的增函数，且3.14＜π，∴3.143＜π3，∴－3.143＞－π3.
(3)12 4
与34 2 .
3
1
解 ∵y＝12x 是减函数，∴12 4 ＜12 2 .
单元复习第6章幂函数、指数函数与对数函数-高一数学(苏教版必修第一册)课件
题型探究
一、直观想象
在本章中，函数图象的识别及应用均突出体现了直观想象的核心素养.
图象的识别
[例 1]
m
n
(1)已知函数 y＝x (m，n∈N *，且互质)的图象如图所示，
那么下面说法正确的是
(
)
m
A．m，n 是奇数， n <1
m
B．m 是偶数，n 是奇数， n >1
m
C．m 是偶数，n 是奇数， n <1
)
答案 (1)C (2)B
1 -1
解析 (1)函数 y=log2x 的反函数为 y=2 ,故 f(x)=2 ,于是 f(1-x)=2 = 2
,此函
x
x
1-x
数在 R 上为减函数,其图象过点(0,2),所以 C 中的图象符合要求.
8
8
39 -3-9
3-9
(2)由 f(1)=3>0 可排除 D,由 f(-1)=-3<0 可排除 A,又 f(9)= 4 =3- 4 >f(1),所
3.函数与方程
(1)实系数一元二次方程当Δ＞0时有两个不等实根；当Δ＝0时有两个相
等实根；当Δ＜0时无实数根.
(2)方程f(x)＝0的解就是函数y＝f(x)的图象和x轴交点的横坐标，也叫作
函数的零点；方程f(x)＝g(x)的解也就是两个函数y＝f(x)和y＝g(x)图象
交点的横坐标.
(3)可以用二分法或其他近似方法求得函数零点的近似值.
1
2
由于 f(x)是奇函数,从而 f(x)=- −
1
在(-∞,0)上为增函数.
2 -1
归纳提升对于形如y=af(x)或y=f(ax)的复合函数,要注意转化思想的应用,将
(完整版)指数函数、对数函数和幂函数知识点归纳
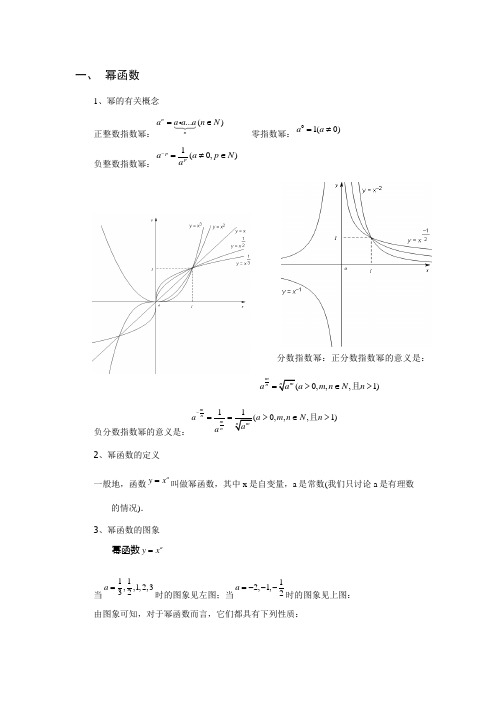
一、幂函数1、幂的有关概念正整数指数幂：...()nna a a a n N=∈零指数幂：01(0)a a=≠负整数指数幂：1(0,)ppa a p Na-=≠∈分数指数幂：正分数指数幂的意义是：(0,,,1)mn mna a a m n N n=>∈>且负分数指数幂的意义是：11(0,,,1) mnm n mna a m n N naa-==>∈>且2、幂函数的定义一般地，函数ay x=叫做幂函数，其中x是自变量，a是常数(我们只讨论a是有理数的情况)．3、幂函数的图象幂函数ay x=当11,,1,2,332a=时的图象见左图；当12,1,2a=---时的图象见上图：由图象可知，对于幂函数而言，它们都具有下列性质：a y x =有下列性质： (1)0a >时：①图象都通过点(0,0)，(1,1)；②在第一象限内，函数值随x 的增大而增大，即在(0,)+∞上是增函数． (2)0a <时：①图象都通过点(1,1)；②在第一象限内，函数值随x 的增大而减小，即在(0,)+∞上是减函数； ③在第一象限内，图象向上与y 轴无限地接近，向右与x 轴无限地接近． (3)任何幂函数的图象与坐标轴至多只有一个交点； (4)任何幂函数图象都不经过第四象限； (5)任何两个幂函数的图象最多有三个交点．二、指数函数①定义：函数)1,0(≠>=a a a y x且称指数函数， 1）函数的定义域为R ； 2）函数的值域为),0(+∞；3）当10<<a 时函数为减函数，当1>a 时函数为增函数. 4）有两个特殊点：零点(0,1)，不变点(1,)a .5）抽象性质： ()()(),()()/()f x y f x f y f x y f x f y +=⋅-=三、对数函数如果b a N =（0a >，1a ≠），那么b 叫做以a 为底N 的对数，记作log a N b =log b a a N N b =⇔=（0a >，1a ≠，0N >）． 1．对数的性质()log log log a a a MN M N =+． log log log aa a MM N N=-．log log n a a M n M =．（00M N >>，，0a >，1a ≠）（ a, b > 0且均不为1）2．换底公式：log log log m a m NN a=( a > 0 , a ≠ 1 ；0,1m m >≠) 常用的推论：（1）log log 1a b b a ⨯= ； ．（2）log log m na a nb b m=（a 、0b >且均不为1）．1log log 1N N a a mn n m==． （3）， （4）对数恒等式．一、对数函数的图像及性质① 函数log a y x =（0a >，1a ≠）叫做对数函数② 对数函数的性质：定义域：(0,)+∞； 值域：R ； 过点(1,0)，即当1x =时，0y =．当0a >时，在（0，+∞）上是增函数；当01a <<时，在（0，+∞）上是减函数．二、对数函数与指数函数的关系对数函数log a y x =与指数函数x y a =图像关于直线y x =对称． 指数方程和对数方程主要有以下几种类型：()()log ,log ()()f x b a a a b f x b f x b f x a =⇔==⇔=（定义法）b mnb a n am log log =1log log log =⋅⋅a c b c b a 01log =a 1log =a a N a N a =log()()()(),log ()log ()()()0f x g x a a a a f x g x f x g x f x g x =⇔==⇔=>（转化法） ()()()log ()log f x g x m m a b f x a g x b =⇔= (取对数法)。
苏教版高中数学必修1第6章幂函数、指数函数和对数函数章末复习课课件
1a
跟踪训练1 已知函数f(x)＝ x 3 在(－∞，0)上是增函数，在(0，＋∞)上是减函 数，则最小的正整数a＝___3__.
∵f(x)在(0，＋∞)上是减函数， 1－a
∴ 3 <0，∴a>1. 又∵f(x)在(－∞，0)上是增函数，且在(0，＋∞)上是减函数， ∴f(x)为偶函数， ∴1－a为负偶数，∴a为奇数， ∴最小的正整数a＝3.
例2 (1)已知a>0且a≠1，则函数f(x)＝ax和g(x)＝ loga－1x 的图象只可能是
√
函数g(x)的定义域是(－∞，0)，排除A，B， 若0<a<1，则f(x)＝ax是减函数， 此时 g(x)＝loga－1x是减函数，C，D 都不满足； 若a>1，则f(x)＝ax是增函数， 此时 g(x)＝loga－1x是增函数，C 满足.
(2)已知函数f(x)＝ 2|lnx－x－1，1x|，≤x1>，1，若方程f(x)－k＝0有3个根，则实数k的 取值范围是
A.[0,1]
√C.(0,1]
B.(0,1) D.[1，＋∞)
方程f(x)－k＝0有3个根，即函数f(x)的图象与直线y＝k有3个不同的交点. 作出函数f(x)的图象，如图. 根据图象可得，当0<k≤1时，函数f(x)的 图象与直线y＝k有3个不同的交点，所以 当方程f(x)－k＝0有3个根时，0<k≤1.
反思感悟
指数函数、对数函数图象既是直接考查的对象，又是数形结合求 交点、最值、解不等式的工具，所以要能熟练画出这两类函数图 象，并会进行平移、对称、翻折等变换.
跟踪训练2 (1)对数函数y＝logax(a>0且a≠1)与二次函数y＝(a－1)x2－x在同一 坐标系内的图象可能是
第6章-6.1-幂函数高中数学必修第一册苏教版
(2 − 1 )[ 2 − 1 ] < 0.请写出满足这两个性质的一个幂函数的表达式：
− （答案不唯一）
=
__________________________．
【解析】由题意知幂函数 满足性质：对定义域中任意的,有 = − ，则
调递增，且0 < 0.31 < 0.35，∴ 0.31 < 0.35 ，即 −0.31
6
5
6
5
< 0.35 .
【学会了吗丨变式题】
2.若 =
1
2
2
3
1
5
， =
A. < <
2
3
， =
1
2
1
3
，则,,的大小关系是( D
B. < <
2
3
【解析】 = 在[0, +∞)上单调递增，∴
间 0, +∞ 上单调递减，对应图象①；函数3 在区间[0, +∞)上单调递增，对应图象②；
函数4 在区间 0, +∞ 上单调递减，对应图象④.
例10 已知点
2, 2 在幂函数 的图象上，点
当为何值时：
（1） > ；
（2） = ；
（3） < .
则( B
)
A. > > >
B. > > >
C. > > >
D. > > >
图6.1-3
【解析】由幂函数的图象特征可知， < 0， > 0， > 0， > 0.
第6章-6.3-对数函数高中数学必修第一册苏教版
A.
B.
)
C.
D.
【解析】
若0 < < 1,则函数 = 的图象下降且过点 0,1 ，而函数
= log − 的图象上升且过点 −1,0 ，与题中所给图象均不符合.若 > 1,
首先函数 = 的图象只可能在轴上方，函数 = log − 的图象只可能
在轴左侧，从而A,D中图象不正确；再看单调性， = 与 = log − 的单调性
∴ = + 1.
又 的图象过点 1,3 ,
∴ 3 = + 1,即 = 2,
∴ = 2 + 1（【另解】至此,也可令2 + 1 = 9,解得 = 3,即 −1 9 = 3）.
∴ −1 = log 2 − 1 , > 1.
故 −1 9 = log 2 8 = 3.
（1） = lg − 1 + lg − 2 ;
【解析】要使函数式有意义，需满足ቊ
− 1 > 0,
解得 > 2.
− 2 > 0,
所以函数 = lg − 1 + lg − 2 的定义域是{| > 2}.
（2） = log
1−
5;
【解析】要使函数式有意义，需满足ቊ
所以函数 = log
log 0.5 4 − 3
ln 4−
−3
3
的定义域是{|
4
< ≤ 1}.
.
4 − > 0,
【解析】要使函数式有意义，需满足ቊ
解得 < 4且 ≠ 3.
− 3 ≠ 0,
所以函数 =
ln 4−
−3
高中数第3章指数函数、对数函数和幂函数3.4.1.2用二分法求方程的近似解课件苏教版必修1
x 0
0.5
0.531 25 0.562 5 0.625 0.75 1
f(x) -1.307 -0.084 -0.009
0.066 0.215 0.512 1.099
由二分法求得方程ln(x+1)+2x-m=0的近似解(精确度0.05)可能是
(
). (导学号51790116)
高中数第3章指数函数、对数函
数和幂函数3.4.1.2用二分法求方
程的近似解课件苏教版必修1
学习目标
重点难点
1.会用二分法求方程的近似
解.
重点:用二分法求方程的
近似解.
2.明确函数零点的近似值的
判断方法.
难点:零点近似值的判定
方法.
1.二分法的含义
(1)满足的条件:函数y=f(x)在区间(a,b)上连续不断且f(a)·f(b)<0.
1
则当 x∈(-∞,0)时,x >0, <0,
2
1
所以- >0,所以
2 1
2 1
f(x)=x - >0 恒成立.
所以 x - =0 在(-∞,0)内无实数解.
(导学号
典例导学
即时检测
一
二
1.准确理解“二分法”的含义:
二分法就是通过不断地将所选区间一分为二,使区间的两个端点逐
步逼近零点,直至找到零点附近足够小的区间,根据所要求的精确
零点,都能用二分法求函数零点,故选A.
典例导学
即时检测
一
二
1.下列图象表示的函数中,能用二分法求零点的是(
).
答案:C
解析:由题图知,只有C中有变号零点,能用二分法求零点.
(2021年整理)高中数学必修一幂函数及其性质
（完整）高中数学必修一幂函数及其性质编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）高中数学必修一幂函数及其性质）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）高中数学必修一幂函数及其性质的全部内容。
幂函数及其性质专题一、幂函数的定义一般地，形如y x α=（x ∈R)的函数称为幂孙函数,其中x 是自变量，α是常数.如11234,,y x y x y x -===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数。
二、函数的图像和性质（1）y x = （2）12y x = （3)2y x = （4）1y x -= （5）3y x =用描点法在同一坐标系内画出以上五个函数图像,通过观察图像，可以看出：y x = 2y x =3y x =12y x =1y x -=定义域奇偶性在第Ⅰ象限单调增减性定点（公共点）3．幂函数性质（1)所有的幂函数在（0，+∞）都有定义,并且图象都过点（1,1）;(2)x ＞0时，幂函数的图象都通过原点,并且在[0,+∞]上，是增函数（3）α＜0时,幂函数的图象在区间（0，+∞）上是减函数.三．两类基本函数的归纳比较： ① 定义对数函数的定义:一般地,我们把函数log a y x =（a ＞0且a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是(0，+∞）．幂函数的定义：一般地,形如y x α=（x ∈R ）的函数称为幂孙函数，其中x 是自变量，α是常数。
②性质对数函数的性质：定义域:（0，+∞）；值域:R; 过点（1,0)，即当x =1,y =0；在(0，+∞）上是增函数；在（0，+∞）是上减函数 幂函数的性质:所有的幂函数在（0，+∞）都有定义， 图象都过点(1，1）x ＞0时,幂函数的图象都通过原点, 在[0，+∞]上，y x =、2y x =、3y x =、12y x =是增函数，在(0，+∞）上， 1y x -=是减函数. 【例题选讲】例1．已知函数()()2531m f x m m x --=--，当 m 为何值时,()f x ：(1）是幂函数;(2)是幂函数,且是()0,+∞上的增函数；（3）是正比例函数;(4）是反比例函数；（5）是二次函数；简解：（1）2m =或1m =-（2）1m =-（3）45m =-（4）25m =-（5）1m =-变式训练：已知函数()()2223m m f x m m x--=+，当 m 为何值时,()f x 在第一象限内它的图像是上升曲线.简解：220230m m m m ⎧+>⎪⎨-->⎪⎩解得：()(),13,m ∈-∞-+∞例2．比较大小：（1）11221.5,1.7 （2）33( 1.2),( 1.25)--（3）1125.25,5.26,5.26---（4）30.530.5,3,log 0.5例3．已知幂函数223m m y x --=（m Z ∈)的图象与x 轴、y 轴都无交点，且关于原点对称,求m 的值．解:∵幂函数223m m y x --=（m Z ∈)的图象与x 轴、y 轴都无交点， ∴2230m m --≤，∴13m -≤≤；∵m Z ∈，∴2(23)m m Z --∈,又函数图象关于原点对称, ∴223m m --是奇数，∴0m =或2m =． 例4、设函数f （x ）＝x 3，（1）求它的反函数；（2)分别求出f －1(x )＝f （x ），f －1(x )＞f （x ),f －1（x )＜f (x )的实数x 的范围．解析：（1)由y ＝x 3两边同时开三次方得x ＝3y ，∴f －1（x )＝x 31．(2）∵函数f （x ）＝x 3和f －1（x ）＝x 31的图象都经过点（0，0）和（1，1)．∴f －1（x ）＝f (x )时，x ＝±1及0；在同一个坐标系中画出两个函数图象，由图可知 f －1（x ）＞f （x ）时,x ＜－1或0＜x ＜1；f －1（x ）＜f （x )时，x ＞1或－1＜x ＜0．点评：本题在确定x 的范围时，采用了数形结合的方法，若采用解不等式或方程则较为麻烦．例5、求函数y ＝52x ＋2x 51＋4(x ≥－32）值域．解析：设t ＝x 51，∵x ≥－32，∴t ≥－2，则y ＝t 2＋2t ＋4＝(t ＋1)2＋3．当t ＝－1时，y min ＝3．∴函数y ＝52x ＋2x 51＋4（x ≥－32）的值域为［3,＋∞）．【同步练习】1. 下列函数中不是幂函数的是（ ）Ａ．y x = Ｂ．3y x = Ｃ．2y x = Ｄ．1y x -= 2。
新教材高中数学第6章第2课时对数函数的图象与性质的应用ppt课件苏教版必修第一册
的值域是
．
(2)若函数 f(x)＝ax＋loga(x＋1)在[0,1]上的最大值和最小值之和为
a，则 a 的值为
．
(3)求函数 f(x)＝log2(－x2－4x＋12)的值域．
[思路点拨] (1)中利用 f(x)＝2log1x 在定义域[2,4]上为减函数求
2
解．
(2)中 y＝ax 与 y＝loga(x＋1)在[0,1]上具有相同的单调性，所以 f(x) ＝ax＋loga(x＋1)在[0,1]上是单调函数．
第6章 幂函数、指数函数和对数函数
6.3 对数函数 第2课时 对数函数的图象与性质的应用
学习目标 1．能正确判断图象之间的变换关 系．(重点) 2．理解并掌握对数函数的单调 性．(重点) 3．会用对数函数的相关性质解综 合题．(难点)
核心素养
通过学习本节内容，提升 学生的直观想象、逻辑推 理、数学运算的核心素 养．
要得到y＝loga 1x的图象，应将y＝loga x的图象关于 x轴 对称．
为了得到函数y＝lg x＋103的图象，只需把函数y＝lg x的图象上所
有的点
．
向左平移3个单位，再向下平移1个单位 [y＝lg x＋103＝lg (x＋3)
－1，故将y＝lgx向左平移3个单位，再向下平移1个单位．]
合作 探究 释疑 难
(3)[解] ∵－x2－4x＋12＞0， 又∵－x2－4x＋12＝－(x＋2)2＋16≤16， ∴0＜－x2－4x＋12≤16， 故log2(－x2－4x＋12)≤log216＝4， ∴函数的值域为(－∞，4]．
求函数值域或最大小值的常用方法 1直接法,根据函数解析式的特征，从函数自变量的变化范围 出发，通过对函数定义域、性质的观察，结合解析式，直接得出函 数值域. 2配方法,当所给的函数是二次函数或可化为二次函数形式的 形如y＝a[fx]2＋bfx＋c，求函数值域问题时，可以用配方法.
幂函数、指数函数和对数函数对数及其运算法则教案
幂函数、指数函数和对数函数对数及其运算法则教案第一章：幂函数1.1 幂函数的定义与性质学习幂函数的定义：f(x) = x^a，其中a为常数。
探讨幂函数的性质，如奇偶性、单调性等。
1.2 幂函数的图像与解析式绘制常见的幂函数图像，如f(x) = x^2，f(x) = x^-1等。
学习如何从图像得出幂函数的解析式。
第二章：指数函数2.1 指数函数的定义与性质学习指数函数的定义：f(x) = a^x，其中a为正常数。
探讨指数函数的性质，如单调性、特殊点等。
2.2 指数函数的图像与解析式绘制常见的指数函数图像，如f(x) = 2^x，f(x) = 3^x等。
学习如何从图像得出指数函数的解析式。
第三章：对数函数3.1 对数函数的定义与性质学习对数函数的定义：f(x) = log_a(x)，其中a为正常数。
探讨对数函数的性质，如单调性、特殊点等。
3.2 对数函数的图像与解析式绘制常见的对数函数图像，如f(x) = log_2(x)，f(x) = log_3(x)等。
学习如何从图像得出对数函数的解析式。
第四章：对数运算法则4.1 对数的基本运算法则学习对数的加法、减法、乘法和除法法则。
4.2 对数的复合运算法则学习对数的乘方和除方法则。
第五章：对数函数的应用5.1 对数函数在实际问题中的应用探讨对数函数在实际问题中的应用，如人口增长、放射性衰变等。
5.2 对数函数在其他数学领域的应用探讨对数函数在其他数学领域的应用，如微积分中的对数微分等。
第六章：指数函数的应用6.1 指数函数在实际问题中的应用探讨指数函数在实际问题中的应用，如复利计算、生物种群增长等。
6.2 指数函数在其他数学领域的应用探讨指数函数在其他数学领域的应用，如概率论中的指数分布等。
第七章：幂函数和指数函数的综合应用7.1 幂函数和指数函数在实际问题中的应用探讨幂函数和指数函数在实际问题中的应用，如物理学中的能量公式、经济学中的需求函数等。
7.2 幂函数和指数函数在其他数学领域的应用探讨幂函数和指数函数在其他数学领域的应用，如图论中的指数时间算法等。
幂指对函数的增长比较ppt课件
比较大小
[例 2] 比较下列各组值的大小：
(1)log1
2
45与
log1
2
67；
(2)0.8－0.1 与 1.250.2；
(3)log32.5 与 log52.5； (4)(lgm)1.7 与(lgm)2.1(m>1)．
[分析] 充分利用函数的图像和性质(如单调性等)来比较
两数的大小．
12
[解析] (1)y＝log1 x 在(0，＋∞)上递减，
1 o 1234 x
4
一般地，对于指数函数 y=ax (a>1)和幂函数 y=xn (n>0),在区间
（x0，0+∞）10 上，无20论n比a大30多少，尽4管0 在x的一5定0 变化范围
y内=2，x a1x会10小24于x1.n0,5但×由10于6 a1x.0的7×增1长09 快1.于10x×n1的01增2 长1.1，3×因10此15 总存在
2.列表并在同一坐标系中画出上面这三个函数的图像.
x
0.2 0.6 1.0 1.4
y
y=x2 y=2x
y=2x 1.149 1.516 2 2.639
5
y=x2 0.04 0.36 1 1.96
4
y=log2 x -2.322 -0.737 0 0.485
3
1.8 2.2 2.6 3.0 3.4 …
6
知能自主梳理
7
在区间(0，＋∞)上，尽管函数 y＝ax(a>1)，y＝logax(a>1)， y＝xn(n>0)都是________(填“增”或“减”)函数，但它们的 增长速度不同，而且在不同的“档次”上，随着 x 的增大，y ＝ax(a>1)的增长速度越来越快，会超过并会远远大于 y＝ xn(n>0)的增长速度，而 y＝logax(a>1)的增长速度会越来越 慢 ． 因 此 ， 总 会 存 在 一 个 x0 ， 当 x>x0 时 ， 就 有 logax________xn________ax.
2021_2022学年新教材高中数学第6章幂函数指数函数和对数函数6.1幂函数课件苏教版必修第一册
1．本题在解答过程中易出现忽略对底数的分类讨论而产生漏解． 2．求解此类题目的关键是弄清幂函数的概念及幂函数的性质． 解决此类问题可分为两大步： 第一步，研究幂函数的奇偶性(图象对称性)、第一象限的图象的单 调性求出 m 的值或范围； 第二步，利用分类讨论的思想，结合函数的图象求出参数 a 的取 值范围．
在同一平面直角坐标系中，幂函数 y＝x，y＝x2，y＝x3，y＝x ，y ＝x－1 的图象如图所示：
2．幂函数的性质
y＝x
y＝x2
定义域 _R_
_R _
值域
_R_ _[_0_，__＋__∞_)_
奇偶性 _奇__函__数_ 偶__函__数__
y＝x3 _R _ _R _
奇__函__数__
y＝x
y＝x－1
1234 5
回顾本节知识，自我完成以下问题．
1．判断函数为幂函数的标准是什么？ [提示] 底数是自变量，指数是常数，只有一项，系数为 1. 2．幂函数在第一象限内的图象有何特点？ [提示] α>0 时，幂函数的图象经过(0,0)，(1,1)，在(0，＋∞)上图 象上升．
α<0 时，幂函数的图象经过(1,1)，在(0，＋∞)上图象下降．
，∴α＝－12.
∴f(x)＝x ，
∴f(100)＝100 ＝ 1100＝110.]
类型 2 比较大小 【例 2】 比较下列各组数中两个数的大小： (1)31 与14 ；(2)－23－1 与－35－1； (3)0.25 与 6.25 ；(4)1.20.6 与 0.30.4；
(5)(－3) 与(－2) . [思路点拨] 可以借助幂函数 y＝x2 的单调性或化为同指数或借助 于中间量进行比较．
[解] (1)因为函数 y＝x 在(0，＋∞)内是减函数，所以 3 ＞
高一数学必修教学课件第三章指数函数幂函数对数函数增长的比较
THANK YOU
感谢聆听
计算、经济增长模型等。通过比较这些函数的增长差异，可以帮助学生
更好地理解经济学中的相关概念和原理。
02
生物学
在生物学中，这些函数可用于描述生物种群的增长、疾病的传播等。例
如，指数增长模型可用于描述某些生物种群的爆炸式增长，而对数增长
模型则适用于描述种群增长逐渐趋于稳定的情况。
03
物理学
在物理学中，幂函数可用于描述物体之间的万有引力、电场强度等物理
根据平均变化率的定义，可以 计算出f(x)=x^3在区间[1,2]上 的平均变化率为(f(2)-f(1))/(21)=(2^3-1^3)/1=7。
04
对数函数增长特性
对数函数定义及图像
对数函数定义
对数函数是以幂为自变量，指数为因变量，底数为常数的函数。
对数函数图像
对数函数的图像是一条经过原点的曲线，其形状与底数有关。当底数大于1时，图像向右上方倾斜；当底数小于1 时，图像向右下方倾斜。
与其他函数的比较
与一次函数、二次函数等相比，指数 函数的增长速度更快。当x足够大时， 指数函数的值将远远超过这些函数的 值。
典型例题解析
解析
对于(1)，由于1.1<1.2且2.5>2.3，因此1.1^2.5<1.2^2.3；对于(2)，由于 0.8<0.9且-0.7<-0.6，因此0.8^-0.7>0.9^-0.6。
量的变化规律。通过比较不同函数的增长特性，可以帮助学生深入理解
物理现象的本质。
在其他学科领域的应用举例
化学
在化学动力学中，反应速率常数与温度的关系通常可以用指数函数或幂函数来描述。比较 不同函数的增长差异有助于理解化学反应速率的变化规律。
高中数学第6章幂函数指数函数和对数函数6.3第1课时对数函数的概念图象与性质课件苏教版必修第一册
[解] (1)中真数不是自变量 x， ∴不是对数函数； (2)中对数式后减 1， ∴不是对数函数； (3)中 log8x 前的系数是 2，而不是 1， ∴不是对数函数； (4)中底数是自变量 x，而不是常数 a， ∴不是对数函数．
一个函数是对数函数，必须是形如 y＝logax(a＞0 且 a≠1)的形式， 即必须满足以下条件：
A．a>c>b
B．b>c>a
C．c>b>a
D．c>a>b
D [a＝log32<log33＝1，c＝log23>log22＝1.由对数函数的性质可知
log52<log32，∴ b<a<c.]
1 2 3 45
3．函数 y＝ln x 的单调增区间是________，反函数是________． (0，＋∞) y＝ex [y＝ln x 的底为 e>1，故 y＝ln x 在(0，＋∞)上 单调递增，其反函数为 y＝ex.]
图 象
0<a<1
a>1
0<a<1
定义域：_(_0_，__＋__∞_)__
值域：__R__
性
图象过定点__(_1_,0_)__
质 在_(_0_，__＋__∞_)_上是增函数
在_(_0_，__＋__∞_)_上是减函数
当__0_<_x_<_1__时，y<0；
当 0<x<1 时，__y_>_0__；
当_x_>_1__时，y>0
⇒0≤x<1.
∴函数的定义域为[0,1)．
(3)由题知xlo－g21x>－0 1≠0， ⇒xx－ >11，≠1，
高中数学第6章幂函数指数函数和对数函数6.2第1课时指数函数的概念图象与性质课件苏教版必修第一册
1．处理函数图象问题的策略 (1)抓住特殊点：指数函数的图象过定点(0,1)． (2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)． (3)利用函数的性质：奇偶性与单调性． 2．指数型函数图象过定点问题的处理方法 求指数型函数图象所过的定点时，只要令指数为 0，求出对应的 y 的值，即可得函数图象所过的定点．
第6章 幂函数、指数函数和 对数函数
6.2 指数函数 第1课时 指数函数的概念、图象
与性质
学习任务 1．理解指数函数的概念．(重点)
核心素养 1．通过学习指数函数的图
2．掌握指数函数的图象和性质．(重点) 象，培养直观想象的数学素
3．能够利用指数函数的图象和性质解 养．
题．(重点、难点)
2．借助指数函数的定义域、
A．f(x)＝x3
B．f(x)＝2x
C．f(x)＝21x
D．f(x)＝x
B [设 f(x)＝ax(a>0 且 a≠1)，则由 f(3)＝8 得 a3＝8，∴ a＝2，∴ f(x)
＝2x，故选 B.]
NO.2
合作探究·释疑难
类型1 指数函数的概念 类型2 利用单调性比较大小 类型3 利用指数函数的单调性解不等式 类型4 图象变换及其应用
(1)② (2)一 (3)(－1，－1) [(1)y＝3－x＝13x 为单调递减的指数函 数，其图象为②.
(2)函数 y＝ax(0＜a＜1)在 R 上单调递减，图象过定点(0,1)，所以 函数 y＝ax＋b 的图象在 R 上单调递减，且过点(0,1＋b)．因为 b＜－1， 所以点(0,1＋b)在 y 轴负半轴上，故图象不经过第一象限．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
必备知识·自主学习
导思
1.除了一次函数、二次函数、反比例函数外还有哪些常见函数? 2.幂函数有哪些特征?
1.幂函数的概念 一般地,我们把形如_y_=_x_α_的函数称为幂函数,其中_x_是自变量,_α__是常数.
2.常见幂函数的图象与性质
解析式
【变式探究】
把本例的各组数据更换如下,再比较其大小关系:
（1）（ 2 ）0.5与（1 ）0.5；（2）（ 2 ）1与（ 3 ）1.
5
3
3
5
【解析】(1)因为幂函数y=x0.5在[0,+∞)上是单调递增的,又 2 1，所以
53
（ 2 ）0.5 （1 ）0.5.
5
3
(2)因为幂函数y=x-1在(-∞,0)上是单调递减的,又 2＜所 以3，
【思考】 在区间(0,+∞)上,幂函数有怎样的单调性? 提示:幂函数在区间(0,+∞)上,当α>0时,y=xα是增函数;当α<0时,y=xα是减函 数.
【基础小测】
1.辨析记忆(对的打“√”,错的打“×”)
(1)幂函数的图象必过点(0,0)和(1,1). ( )
(2)幂函数的图象都不过第二、四象限. ( )
2
【解题策略】 判断一个函数是否为幂函数的方法 判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即 函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量; (3)系数为1.
【补偿训练】
下列函数中是幂函数的是
()
①y= 1 ； ②y=axm(a,m为非零常数,且a≠1);
【解析】选C.只有y=3x不符合幂函数y=xα的形式.
3.已知幂函数 f（x）（m2－3）x－m 在（0, ）上为增函数,则实数m的值为 ()
A. 3
B.±2
C.2
D.-2
【解析】选D.由于 f（x）为幂函数,所以m2-3=1,m=±2,当m=2时, f（x）=x-2在
（0, ）上为减函数,不符合题意,当m=-2时 f（x）=x2在（0, ）上为增函数,符
35
（ 2 ）1 3
（ 3 ）1. 5
角度2 幂函数性质的综合应用 【典例】已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称且在(0,+∞)上单调递减, 求满足 （a 1）m3 <（3 2a）m3 的a的取值范围. 【思路导引】根据函数的图象关于y轴对称且在(0,+∞)上单调递减及m∈N*求出 m的值,代入不等式解不等式即可,解不等式时注意幂函数的定义域.
x2
【补偿训练】 在同一坐标系内,函数y=xa(a≠0)和y=ax- 1 的图象可能是
a
()
类型三 幂函数性质的综合应用(数学抽象、逻辑推理)
角度1 比较大小
【典例】比较下列各组中幂值的大小:
(1)0.213,0.233;(2)
1
1
1.22 ,0.9 2
,
1.1.
【思路导引】构造幂函数,借助其单调性求解.
(3)y=
3
x2
与y=
6
x4
定义域相同. (
)
提示:(1)×,幂函数y= 不1 过点(0,0).
x
(2)×,幂函数y=x2过第二象限.
(3)×,y= 的3 定义域为[0,+∞),而y=
x2
的x定64 义域为R.
2.下列函数中不是幂函数的是 ( )
A.y= x C.y=3x
B.y=x3 D.y=x-1
x3
③y=
1
x5
+x4;④y=xn;⑤y=(x-6)3;⑥y=8x2;⑦y=x2+x.
A.①②③
B.①④
C.③④⑤⑥ D.②④⑦
【解析】选B.由幂函数的定义:形如y=xα(α∈R)的函数才是幂函数,则y= 1
x3
=x-3,y=xn是幂函数.
类型二 幂函数图象的应用(数学抽象、直观想象) 【题组训练】 1.函数y= 1 的图象是 ( )
合题意.
关键能力·合作学习
类型一 幂函数的概念(数学抽象) 【题组训练】 1.在函数y= 1 ，y=3x2,y=x2+2x,y=1中,幂函数的个数为 ( )
x4
A.0 B.1 C.2 D.3 2.(2020·吉林高一检测)函数f(x)=(2m-3) xm23 是幂函数,则m的值为 () A.2 B.-1 C.0 D.1 3.已知幂函数f(x)=xα的图象过点（2， 2 ），则f(4)=________.
函数
解析式 y=x
增区间
_R_
减区间
无
定点
y=x2 _[_0_,_+_∞__)_ _(_-_∞__,_0_)_
y=x3
y= 1
x
_R_
无
_(_-_∞__,_0_)_,_
无
_(_0_,_+_∞__)_
_(_1_,_1__)_
无
(1)本质:幂函数的图象是函数的图形表示,幂函数的性质是根据函数图象总结 得到的. (2)应用:①求定义域;②求值域;③比较大小;④求单调区间.
y=x
y=x2
y=x3
y= 1
x
y=
1
x2
图象
定义域 值域
奇偶性
R R _奇__函数
R _[_0_,_+_∞__)_ _偶__函数
R R _奇__函数
_{_x_|_x_≠__0_}_ _{_y_|_y_≠__0_}_
_奇__函数
_[_0_,_+_∞__)_ _[_0_,_+_∞__)_ _非__奇__非__偶__
x3
2.若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的 大小关系是 ( )
A.d>c>b>a C.a>b>c>d
B.d>c>a>b D.a>b>d>c
3.已知幂函数f(x)=(m2-2m+1) xm2m2 的图象不过原点,则m的值为 ( ) A.0 B.-1 C.2 D.0或2 【解析】选A.由幂函数定义可知m2-2m+1=1, 所以m=0或m=2; 当m=0时,f(x)=x-2,定义域为(-∞,0)∪(0,+∞); 当m=2时,f(x)=x4定义域为R; 又因为f(x)=(m2-2m+1x)m2m2 的图象不过原点; 所以m2+m-2<0,所以m=0.
【解题策略】 解决幂函数图象问题应把握的两个原则 (1)依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图 象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴 (简记为指大图高). (2)依据图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图 象(类似于y=x-1或y= 1 或y=x3)来判断.