2008-20009线性代数试卷A及答案
武汉理工2008年末-线代-A

武汉理工大学教务处试题标准答案及评分标准用纸| 课程名称——线性代数—— ( A 卷) |一、填空题:(每小题3分,共15分)1.6;2.⎪⎪⎪⎪⎪⎭⎫⎝⎛--233421(未写出的元素为0);3.-128;4.2;5..3535<<-t二、选择题: 1.B ; 2.C ; 3.B ; 4.C ; 5.A (每小题3分,共15分)三、计算题: 1.()20092008000020082008000200920091200800020092008000020092008200820082007⨯⨯-+⨯=D (5分)=2007200720092008+ (10分)2.首先,11)(6---=E A B (3分)其次,⎪⎪⎪⎭⎫⎝⎛=-7431A , (5分)⎪⎪⎪⎭⎫ ⎝⎛=--6321E A , (7分)()⎪⎪⎪⎭⎫ ⎝⎛=---6/13/12/111EA, (9分) 最后, .123⎪⎪⎪⎭⎫ ⎝⎛=B (10分) 注:矩阵中未写出的元素为0。
3.方程组的系数行列式()()⇒≠+-=---=012111111λλλλλA (3分) (1)21≠-≠λλand,时,方程组有唯一解; (5分)(2)当2=λ时,方程组的增广矩阵)()(100021104211~B R A R B <⇒⎪⎪⎪⎭⎫ ⎝⎛--此时方程组无解; (7分)(3)当1-=λ时,方程组的增广矩阵⇒<=⇒⎪⎪⎪⎭⎫ ⎝⎛3)()(000000001111~B R A R B此时方程组有无穷多个解,其通解为.),(0011010112121R k k k k X ∈⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-= (10分)4.解:观察知,矩阵A 的第一列加上第二列的(-1)倍,然后再交换第二列和第三列即得B ,(4分)根据初等方阵的定义,两次初等 列变换所对应的初等方阵分别为:⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-1111111,;(8分) 再根据初等行变换的实质得,⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-=11111111111X . (10分)注:矩阵中未写出的元素为0。
2008-2009学年线性代数试卷A及答案
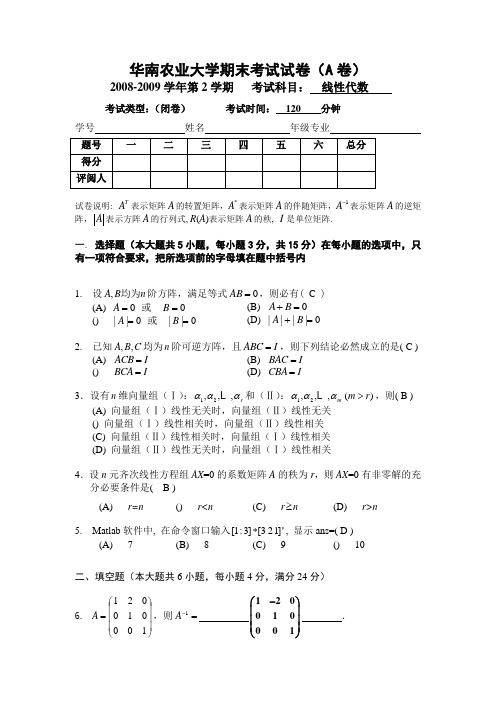
华南农业大学期末考试试卷(A 卷)2008-2009学年第2学期 考试科目: 线性代数考试类型:(闭卷) 考试时间: 120 分钟学号 姓名 年级专业 题号 一 二 三 四 五 六 总分 得分 评阅人试卷说明: T A 表示矩阵A 的转置矩阵,*A 表示矩阵A 的伴随矩阵,1A -表示矩阵A 的逆矩阵,A 表示方阵A 的行列式, R (A )表示矩阵A 的秩, I 是单位矩阵.一. 选择题(本大题共5小题,每小题3分,共15分)在每小题的选项中,只有一项符合要求,把所选项前的字母填在题中括号内1. 设n B A 均为,阶方阵,满足等式0=AB ,则必有( C )(A) 0=A 或 0=B(B) 0=+B A () 0||=A 或 0||=B(D) 0||||=+B A2. 已知,,A B C 均为n 阶可逆方阵,且ABC I =,则下列结论必然成立的是( C )(A) ACB I = (B) BAC I = () BCA I = (D) CBA I =3.设有n 维向量组(Ⅰ):12,,,r ααα 和(Ⅱ):12,,,()m m r ααα> ,则( B )(A) 向量组(Ⅰ)线性无关时,向量组(Ⅱ)线性无关() 向量组(Ⅰ)线性相关时,向量组(Ⅱ)线性相关 (C) 向量组(Ⅱ)线性相关时,向量组(Ⅰ)线性相关 (D) 向量组(Ⅱ)线性无关时,向量组(Ⅰ)线性相关4.设n 元齐次线性方程组AX =0的系数矩阵A 的秩为r ,则AX =0有非零解的充分必要条件是( B )5. Matlab 软件中, 在命令窗口输入[1:3][321]'*, 显示ans=( D )二、填空题(本大题共6小题,每小题4分,满分24分)6. ⎪⎪⎪⎭⎫ ⎝⎛=100010021A ,则=-1A120010001-⎛⎫⎪ ⎪ ⎪⎝⎭. (A) r=n() r<n(C) r ≥n(D) r>n(A) 7 (B) 8 (C) 9 () 107. 设t ηηη,,,21 及t t ηληληλ+++ 2211都是非齐次线性方程组b A =X 的解向量,则=+++t λλλ 21______1__________.8. 矩阵20002023A a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与矩阵10002000B b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦相似, 则a b += . 9. 设123,1,1),0,2,3),1,0,1),k ααα===(((则当k = 时,α1,α2,α3 线性相关.10.设A 为三阶方阵,其特征值2,1,3,- 则*A = .11.已知二次型222123112132233(,,)2245f x x x x tx x x x x x x x =+-+++正定, 则t 的取值范围为 .三、计算题12.(7分) 已知100110,021A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭131011,002B ⎛⎫⎪=- ⎪ ⎪⎝⎭求:2T A AB +13.(8分)计算下列行列式3214214314324321四、解方程组14. (10分)求方程组123412341234311232x x x xx x x xx x x x⎧⎪--+=⎪-+-=⎨⎪⎪--+=-⎩的通解.五、解答题15.(10分)求下列向量组的秩,并求一个最大无关组:a1=(1, 2,-1, 4)T,a2=(9, 100, 10, 4)T, a3= (-2,-4, 2,-8)T.16. (8分) 已知1121 342 012A--⎛⎫⎪= ⎪⎪-⎝⎭,求A的伴随矩阵*A.17.(12分) 设212122221A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,求一个正交阵P ,使1P AP -=Λ为对角阵.六、证明题18.(6分) 设向量组322211,a a b a a b +=+= 433,a a b += 144,a a b +=, 证明向量组4321,,,b b b b 线性相关.2008—2009第二学期《线性代数》(A )参考答案和评分标准一. 选择题(本大题共5小题,每小题3分,共15分)1. C2. C3. B4. B5. D二、填空题(本大题共6小题,每小题4分,满分24分)6. 120010001-⎛⎫⎪ ⎪⎪⎝⎭ 7. 18. 8 9. -1/2 10. 36 11. 405t -<<三、计算题12.T T A AB A E B 2(2)+=+=1001001001102010310021001112⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪-+⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦3分100300110330021114⎛⎫⎛⎫ ⎪⎪=- ⎪⎪ ⎪⎪-⎝⎭⎝⎭ 5分 300030754⎛⎫ ⎪= ⎪ ⎪⎝⎭7分 13.将行列式第2、3、4列加到第1列上,得3214214314324321=32110214101431043210=101110222031104321------ 4分=10400440311--- 6分=160 8分14.11110111101111011131002410024111231/200121/200000⎛⎫⎛⎫⎛⎫------ ⎪ ⎪ ⎪--→-→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭⎝⎭ 4分 x x x x x x 1234340241--+=⎧⎨-=⎩,x x x x x x x x 1324132431-=-⎧⎨+=++⎩, 5分 取x x 2400⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,得*120120η⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭, 6分取x x 2410,01⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,x x 1311,02⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 8分 得齐次方程组基础解系为121110,0201ξξ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 9分通解为x x k kx x 12123411120101022010⎛⎫⎪⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭10分 15. 192192192210040820010110201900004480320000A ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦6分rank(A)=2 7分 所以向量组的秩为2. 8分 a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T 不成比例,所以 a 1,a 2为最大无关组. 10分16. 因为1*1,||A A A -=2分*1111||||A A AA A ---==4分 1||1A -=- 6分*1||1*A A -=-=121342012--⎛⎫ ⎪--- ⎪ ⎪-⎝⎭8分17.123(1)(1)(5),1,1,5A E λλλλλλλ-=-+--=-==, 3分对应于11λ=-,由 ()0A E x += 得111122ξ-⎛⎫ ⎪=- ⎪ ⎪⎝⎭,单位化,得111162p -⎛⎫ ⎪=- ⎪ ⎪⎝⎭; 6分 对应于21λ=,由 ()0A E x -= 得2110ξ-⎛⎫ ⎪= ⎪ ⎪⎝⎭,单位化,得211120p -⎛⎫⎪= ⎪ ⎪⎝⎭ 8分 对应于35λ=,由 (5)0A E x -= 得3111ξ⎛⎫ ⎪= ⎪ ⎪⎝⎭,单位化,得311131p ⎛⎫⎪= ⎪ ⎪⎝⎭. 10分 11162311162321063P ⎛⎫-- ⎪ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭,有1100010005TP AP P AP --⎛⎫⎪==Λ= ⎪ ⎪⎝⎭. 12分18. 设有4321,,,x x x x 使得044332211=+++b x b x b x b x即0)()()()(144433322211=+++++++a a x a a x a a x a a x 3分整理得 01100011000111001)(43214321=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛x x x x a a a a 4分而011000110001110014321=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛x x x x 有非零解,所以结论成立 6分。
线性代数2008A答案

上海财经大学成人高等教育线性代数试题参考 答案(2008A 卷)姓名 学号 专业 班级一、 单选题(每小题2分,共计10分)1. 设,A B 均为方阵,且0AB =, 则以下结论中正确的是 ( 4 ) .(1) 0AB = (2) 0,0A B == (3) 0A =或0B = (4) 0A =或0B =2. 以下矩阵中是对称矩阵的是 ( 2 ).(1) 123212025⎛⎫ ⎪-- ⎪ ⎪-⎝⎭ (2)123204341⎛⎫⎪ ⎪ ⎪-⎝⎭ (3) 123211301⎛⎫⎪ ⎪ ⎪⎝⎭ (4) 111011001⎛⎫⎪ ⎪ ⎪⎝⎭3. 以下矩阵中是初等矩阵的是 ( 2 ).(1) 100010000⎛⎫ ⎪- ⎪ ⎪⎝⎭ (2)100010001⎛⎫⎪ ⎪ ⎪-⎝⎭ (3) 101010001⎛⎫⎪ ⎪ ⎪-⎝⎭ (4) 101011001⎛⎫⎪ ⎪ ⎪⎝⎭4. 下列不是n 阶矩阵A 可逆的充分必要条件的为 ( 1 ) .(1) 0A ≠ (2) 0A ≠ (3) ()R A n = (4) A 与单位阵E 等价5. 下列矩阵中是分块矩阵00A B ⎛⎫⎪⎝⎭的逆矩阵为 ( 4 ). (1) 1100A B --⎛⎫⎪⎝⎭ (2) 1100B A --⎛⎫⎪⎝⎭(3) 1100A B--⎛⎫⎪⎝⎭(4) 1100B A --⎛⎫ ⎪⎝⎭二、 填选题(每小题3分,共计30分)6. 行列式 111253_____.4259= (- 6)7. 设4阶行列式的第三行元素为1,2,3,4,其对应的余子式为4,3,2,1,则该行列式的值等于______.( 0 )……………………………………………………………装订线…………………………………………………8. 设A 是3阶方阵,TA 是A 的转置矩阵且 2,A =则 3____.T A =; ( 54 )9. 设211123223,322141113A B ⎛⎫⎛⎫⎪⎪=-=- ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭, 则 _____________AB =; (487731112514⎛⎫ ⎪- ⎪ ⎪-⎝⎭)10.设矩阵 120340002A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则1A -=__________. ; (312212210000--⎛⎫⎪ ⎪ ⎪⎝⎭) 11. 设矩阵 200030004A ⎛⎫⎪= ⎪ ⎪⎝⎭,则*A =__________.(*A 是A 的伴随矩阵); (12000800012⎛⎫⎪ ⎪ ⎪⎝⎭) 12. 设矩阵 123024003A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则*1()A -=__________; (12310246003⎛⎫⎪ ⎪ ⎪⎝⎭)13. 设矩阵 121211212112121,a a a a a A b b B b b b c c c c c -⎛⎫⎛⎫⎪ ⎪==- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,且AP B =,则初等阵P _____________;(1101-⎛⎫ ⎪⎝⎭) 14. 设 123(1,1,1),(2,3,4),(3,4,5)ααα===,则 123,,ααα的秩等于_______.;( 2 ) 15. 设123(1,1,1),(1,3,4),(3,4,5)ααα===,则 123,,ααα的极大无关组的个数为 _____.( 3 )三、 计算题(共计47分)16. 求解方程:2452450245x x x++=+ (本题满分10分)解:由于311113111132245(1)024500(1)47245(1)245047x r r x xx x x x x x c c x x a A x xx r r x x ++-+--+=-+-==-++-+++则原方程即2(11)0x x += 因而原方程的解为:120,11x x ==。
【免费下载】历年全国自考线性代数经管类试题及答案更新至4月

24.设向量组 α1,α2,α3 线性无关,令 β1=-α1+α3,β2=2α2-2α3,β3=2α1-5α2+3α3.
试确定向量组 β1,β2,β3 的线性相关性.
25.已知线性方程组
xx11
x2 x3 x2 x3
x1 x2 x3 3
(1)讨论 λ 为何值时,方程组无解、有惟一解、有无穷多个解.
1,则 ( A*)1
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
线性代数试题及答案解析

线性代数试题及答案解析一、选择题(每题4分,共40分)1. 矩阵A和矩阵B相乘,得到的结果矩阵的行列数为()。
A. A的行数乘以B的列数B. A的行数乘以B的行数C. A的列数乘以B的列数D. A的列数乘以B的行数答案:D解析:矩阵乘法中,结果矩阵的行数等于第一个矩阵的行数,列数等于第二个矩阵的列数。
2. 向量α和向量β线性相关,则下列说法正确的是()。
A. α和β可以是零向量B. α和β可以是任意向量C. α和β中至少有一个是零向量D. α和β中至少有一个是另一个的倍数答案:D解析:线性相关意味着存在不全为零的系数,使得这些系数乘以对应的向量和为零向量,因此至少有一个向量是另一个向量的倍数。
3. 对于n阶方阵A,下列说法不正确的是()。
A. A的行列式可以是0B. A的行列式可以是负数C. A的行列式可以是正数D. A的行列式一定是正数答案:D解析:方阵的行列式可以是正数、负数或0,因此选项D不正确。
4. 矩阵A和矩阵B相等,当且仅当()。
A. A和B的对应元素相等B. A和B的行数相等C. A和B的列数相等D. A和B的行数和列数都相等答案:A解析:两个矩阵相等,必须满足它们具有相同的行数和列数,并且对应元素相等。
5. 向量组α1,α2,…,αn线性无关的充分必要条件是()。
A. 由这些向量构成的矩阵的行列式不为0B. 这些向量不能构成齐次方程组的非零解C. 这些向量不能构成齐次方程组的非平凡解D. 这些向量可以构成齐次方程组的平凡解答案:C解析:向量组线性无关意味着它们不能构成齐次方程组的非平凡解,即唯一的解是零向量。
6. 矩阵A可逆的充分必要条件是()。
A. A的行列式不为0B. A的行列式为1C. A的行列式为-1D. A的行列式为任何非零数答案:A解析:矩阵可逆当且仅当其行列式不为0。
7. 矩阵A的特征值是()。
A. 矩阵A的行数B. 矩阵A的列数C. 矩阵A的对角线元素D. 满足|A-λI|=0的λ值答案:D解析:矩阵的特征值是满足特征方程|A-λI|=0的λ值。
08年7月全国自考线性代数试题

08年7月全国自考线性代数试题t; FONT-STYLE: italic; FONT-FAMIL Y: ‘宋体’; mso-spacerun: ‘yes’”>A=,则二次型f(x1,x2)=xTAx是()A.正定B负定C.半正定D.不定二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确安全。
错填、不填均无分。
11.设A=,B=,则AB=________.12.已知α=(1,2,3),则|αTα|=________.13.设A=,则A*=________.14.设A为4×5的矩阵,且秩(A)=2,则齐次方程Ax=0的基础解系所含向量的个数是________.15.设有向量α1=(1,0,-2),α2=(3,0,7),α3=(2,0,6).则α1,α2,α3的秩是________.16.方程x1-x2+x3=0的结构解是________.17.设A满足3E+A-A2=0,则A-1=________.18.设三阶方阵A的三个特征值为1,2,3.则|A+E|=________.19.设α与β的内积(α,β)=2,||β||=2,则内积(2α+β,-β)=________.20.矩阵A=所对应的二次型是________.三、计算题(本大题共6小题,每小题9分,共54分)21.计算6阶行列式22.已知矩阵A=,且ABA-1=BA-1+2E,求B.23.求向量组α1=(1,2,1,3),α2=(4,-1,-5,-6),α3=(1,-3,-4,-7)的秩和其一个最大无关组.24.当a,b为何值时,方程组有无穷多解?并求出其结构解.25.已知A=,求其特征值与特征向量.26.用正交变换化二次型f(x1,x2,x3)=为标准型,并给出所用的正交变换.四、证明题(本大题共1小题,6分)27.已知向量组α1,α2,α3线性无关,且β1=α1-α2,β2=2α1+2α2+α3,β3=α1-α2+2α3.证明向量组β1,β2,β3线性无关.。
线性代数四套真题答案详解

⎡2 / 3⎤ ⎢ −1 ⎥ ⎢ ⎥ 故齐次方程组基础解为 ξ = ⎢ 1 ⎥ ⎢ 2⎥ − ⎢ ⎣ 3⎥ ⎦ ⎡ 1⎤ ⎢− 3 ⎥ ⎢ ⎥ 1 令 X3=0;得 ξ = ⎢ 0 ⎥ ⎢ 0 ⎥ ⎢1 / 3⎥ ⎣ ⎦ ⎡2 / 3⎤ ⎡− 1 ⎤ ⎢ −1 ⎥ ⎢ 3 ⎥ ⎢ ⎥ ⎢ 0 ⎥ 方程组通解为 X = k ⎢ 1 ⎥+⎢ ⎥ ⎢ 2⎥ ⎢ 0 ⎥ − ⎢ ⎥ ⎢ ⎣ 3⎥ ⎦ ⎣1 / 3⎦
R(A)=r( A )=3 有解 令 X3=1
⎡2 / 3⎤ ⎢ −1 ⎥ ⎧ 2 X 3 + 3X 4 = 0 ⎪ ⎢ ⎥ 则 ⎨ − X 2 − X 3 = 0 ⇒ξ = ⎢ 1 ⎥ ⎪X + X + X + X ⎢ 2⎥ 2 3 4 ⎩ 1 − ⎢ ⎣ 3⎥ ⎦
6
For Perfect
线性代数四套真题答案详解
(2)矩阵 A 为实对称矩阵,则 P1P2P3 正交
⎡1 1 − 1⎤ ⎡1 ⎤ ⎢ ⎥ ⎢ −1 T = ⎢2 0 0 ⎥; T AT = ⎢ 3 ⎥ ⎥ ⎢1 − 1 − 1⎥ ⎢ ⎥ 4⎦ ⎣ ⎦ ⎣
7
For Perfect
线性代数四套真题答案详解
南华大学 2009-2010 年第一学期(船山)线性代数 B 卷
七、(1)特征方程
3− λ A − λE = − 1 0
−1 0 1 λ −2 1 2 2 − λ − 1 = 0 λ − 5λ + 5 λ − 3 = (3 − λ )(λ − 1)(λ − 4) = 0 −1 3 − λ 0 −1 3− λ
λ1 = 1; λ2 = 3; λ3 = 4
⎡ 2 −1 0 ⎤ ⎡1 ⎤ ⎢ ⎥ ⎥ 当λ1 = 1时,A − E = ⎢− 1 1 − 1⎥得P1 = ⎢ ⎢2⎥ ⎢ ⎢ ⎣ 0 −1 2 ⎥ ⎦ ⎣1 ⎥ ⎦ ⎡ 0 −1 0 ⎤ ⎡1⎤ ⎢ ⎥ ⎥ 当λ2 = 3时;A − 3E = ⎢− 1 − 1 − 1⎥ P2 = ⎢ ⎢0⎥ ⎢ ⎢ ⎣ 0 −1 0 ⎥ ⎦ ⎣− 1⎥ ⎦ ⎡− 1 − 1 0 ⎤ ⎡− 1⎤ ⎢ ⎥ ⎥ 当λ3 = 4时,A − 4 E = ⎢− 1 − 2 − 1⎥得P3 = ⎢ ⎢1⎥ ⎢ ⎢ ⎣ 0 − 1 − 1⎥ ⎦ ⎣− 1⎥ ⎦
线性代数试题(试题与答案)

线性代数试题(试题与答案)一、选择题(每题5分,共25分)1. 设矩阵 \( A = \begin{bmatrix} 1 & 2 \\ 3 & 4\end{bmatrix} \),则 \( A^2 \) 的特征值是()A. 5, 9B. 1, 16C. 5, -5D. 10, -102. 设 \( \alpha_1, \alpha_2, \alpha_3 \) 是线性无关的向量组,则下列向量组线性无关的是()A. \( 2\alpha_1 + \alpha_2 - \alpha_3 \)B. \( \alpha_1 + 2\alpha_2 + 3\alpha_3 \)C. \( \alpha_1 - \alpha_2 + \alpha_3 \)D. \( 3\alpha_1 - 2\alpha_2 + \alpha_3 \)3. 设 \( A \) 是一个 \( n \) 阶可逆矩阵,则 \( A^{-1} \) 的行列式等于()A. \( \frac{1}{|A|} \)B. \( |A| \)C. \( |A^{-1}| \)D. \( -|A| \)4. 设 \( A \) 是一个 \( n \) 阶实对称矩阵,则下列结论正确的是()A. \( A \) 的特征值都是实数B. \( A \) 的特征值都是正数C. \( A \) 的特征值都是负数D. \( A \) 的特征值既有正数也有负数5. 设 \( A \) 是一个 \( n \) 阶矩阵,且 \( A \) 的秩为\( n \),则下列结论正确的是()A. \( A \) 是可逆矩阵B. \( A \) 的行列式不为0C. \( A \) 的特征值不全为0D. \( A \) 的任意一行都可以作为主行二、填空题(每题5分,共25分)6. 若 \( A \) 是一个 \( n \) 阶矩阵,且 \( |A| = 0 \),则称 \( A \) 为________矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华南农业大学期末考试试卷(A 卷)
2008-2009学年第2学期 考试科目: 线性代数
考试类型:(闭卷) 考试时间: 120 分钟
学号 姓名 年级专业
试卷说明: T A 表示矩阵A 的转置矩阵,*A 表示矩阵A 的伴随矩阵,1
A -表示矩阵A 的逆矩阵,A 表示方阵A 的行列式, R (A )表示矩阵A 的秩, I 是单位矩阵.
一. 选择题(本大题共5小题,每小题3分,共15分)在每小题的选项中,只有一项符合要求,把所选项前的字母填在题中括号内
1. 设n B A 均为,阶方阵,满足等式0=AB ,则必有( )
(A) 0=A 或 0=B
(B) 0=+B A (C) 0||=A 或 0||=B
(D) 0||||=+B A
2. 已知,,A B C 均为n 阶可逆方阵,且ABC I =,则下列结论必然成立的是( )
(A) ACB I = (B) BAC I = (C) BCA I = (D) CBA I =
3.设有n 维向量组(Ⅰ):12,,,r ααα 和(Ⅱ):12,,,()m m r ααα> ,则( )
(A) 向量组(Ⅰ)线性无关时,向量组(Ⅱ)线性无关
(B) 向量组(Ⅰ)线性相关时,向量组(Ⅱ)线性相关 (C) 向量组(Ⅱ)线性相关时,向量组(Ⅰ)线性相关 (D) 向量组(Ⅱ)线性无关时,向量组(Ⅰ)线性相关
4.设n 元齐次线性方程组AX =0的系数矩阵A 的秩为r ,则AX =0有非零解的充分必要条件是( )
5. Matlab 软件中, 在命令窗口输入[1:3][321]'*, 显示ans=( )
二、填空题(本大题共6小题,每小题4分,满分24分)
6. ⎪⎪⎪
⎭
⎫ ⎝⎛=100010021A ,则=-1A .
(A) r=n
(B) r<n
(C) r ≥n
(D) r>n
(A) 7 (B) 8 (C) 9 (D) 10
7. 设t ηηη,,,21 及t t ηληληλ+++ 2211都是非齐次线性方程组b A =X 的解向量,则=+++t λλλ 21________________.
8. 矩阵20002023A a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与矩阵10002000B b ⎡⎤
⎢⎥=⎢⎥
⎢⎥⎣⎦
相似, 则a b += . 9. 设123,1,1),0,2,3),1,0,1),k ααα===(((则当k = 时,α1,α2,α3 线性相关.
10.设A 为三阶方阵,其特征值2,1,3,- 则*A = .
11.已知二次型222
123112132233(,,)2245f x x x x tx x x x x x x x =+-+++正定, 则t 的取值范围为 .
三、计算题
12.(7分) 已知100110,021A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭131011,
002B ⎛⎫
⎪=- ⎪ ⎪⎝⎭
求:2T A AB +
13.(8分)计算下列行列式
3
214
214314324321
四、解方程组
14. (10分)求方程组
1234
1234
1234
31
1
23
2
x x x x
x x x x
x x x x
⎧
⎪--+=
⎪
-+-=
⎨
⎪
⎪--+=-
⎩
的通解.
五、解答题
15.(10分)求下列向量组的秩,并求一个最大无关组:a1=(1, 2,-1, 4)T,
a2=(9, 100, 10, 4)T, a3= (-2,-4, 2,-8)T.
16. (8分) 已知1121 342 012
A-
-
⎛⎫
⎪
= ⎪
⎪
-
⎝⎭
,求A的伴随矩阵*A.
17.(12分) 设212122221A ⎛⎫ ⎪
= ⎪ ⎪⎝⎭
,求一个正交阵P ,使1P AP -=Λ为对角阵.
六、证明题
18.(6分) 设向量组322211,a a b a a b +=+= 433,a a b += 144,a a b +=, 证明向
量组4321,,,b b b b 线性相关.
2008—2009第二学期《线性代数》(A )参考答案和评分标准
一. 选择题(本大题共5小题,每小题3分,共15分) 1. C 2. C 3. B 4. B 5. D
二、填空题(本大题共6小题,每小题4分,满分24分)
6. 120010001-⎛⎫
⎪ ⎪
⎪⎝⎭ 7. 1 8. 8 9. -1/2 10. 36
11. 4
05
t -<<
三、计算题 12.
T T A AB A E B 2(2)+=+=1001001001102010310021001112⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥
⎪ ⎪ ⎪-+⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦
3分
100300110330021114⎛⎫⎛⎫ ⎪⎪
=- ⎪⎪ ⎪⎪-⎝⎭⎝⎭ 5分 300030754⎛⎫ ⎪
= ⎪ ⎪⎝⎭
7分
13.
将行列式第2、3、4列加到第1列上,得
32
14214314324321=
32
1
10214101431043210=101
110222*********------ 4分 =104
004403
1
1
--- 6分
=160 8分
14.
11110111101111011131002410024111231/200121/200000⎛⎫⎛⎫⎛⎫------ ⎪ ⎪ ⎪--→-→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭⎝⎭ 4分 x x x x x x 1234340241--+=⎧⎨
-=⎩
,x x x x x x x x 1324
132431-=-⎧⎨+=++⎩, 5分 取x x 2400⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,得*120120η⎛⎫ ⎪ ⎪
⎪
= ⎪ ⎪ ⎪ ⎪⎝⎭
, 6分
取x x 2410,01⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,x x 1311,02⎛⎫⎛⎫⎛⎫
= ⎪ ⎪ ⎪⎝⎭⎝⎭
⎝⎭, 8分 得齐次方程组基础解系为121110,0201ξξ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭
, 9分 通解为x x k k x x 12
123411120101
022010⎛⎫
⎪⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭
⎪⎝⎭
10分
15. 1
921921922100408200
10110201900004480320000A ---⎡⎤⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥-⎢
⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥
-⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦
6分 rank(A)=2 7分 所以向量组的秩为2. 8分 a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T 不成比例,所以 a 1,a 2为最大无关组. 10分
16. 因为1
*
1,||
A
A A -=
2分
*1
11
1
||||
A A A
A A ---==
4分 1||1A -=- 6分
*1||1*A A -=-=121342012--⎛⎫ ⎪
--- ⎪ ⎪-⎝⎭
8分
17.
123(1)(1)(5),1,1,5A E λλλλλλλ-=-+--=-==, 3分 对应于11λ=-,由 ()0A E x += 得
111122ξ-⎛⎫ ⎪=- ⎪ ⎪⎝⎭
,单位化,得1112p -⎛⎫⎪=-⎪⎪
⎭
; 6分 对应于21λ=,由 ()0A E x -= 得
2110ξ-⎛⎫ ⎪
= ⎪ ⎪
⎝⎭
,单位化,得2110p -⎛⎫
⎪=⎪⎪⎭ 8分 对应于35λ=,由 (5)0A E x -= 得
3111ξ⎛⎫ ⎪
= ⎪ ⎪⎝⎭
,单位化,得3111p ⎛⎫
⎪=⎪⎪
⎭
. 10分
0P ⎛ = ⎝,有1100010005T
P AP P AP --⎛⎫
⎪==Λ= ⎪ ⎪⎝⎭
. 12分
18. 设有4321,,,x x x x 使得044332211=+++b x b x b x b x
即0)()()()(144433322211=+++++++a a x a a x a a x a a x 3分
整理得 011000110
0011
1001)(43214321=⎪⎪⎪
⎪
⎪
⎭
⎫
⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝
⎛x x x x a a a a 4分
而0110001100011100143
21=⎪⎪⎪⎪
⎪
⎭
⎫
⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝
⎛x x x x 有非零解,所以结论成立 6分。
