混凝土构件截面的弯矩-曲率关系
弯矩 曲率关系

c0 0.00,2cu0.0033
11.0
1
0.8, 0.7,
fcu 50Mpa fcu 50Mpa
线性插值(《混凝土结构设计
规范》GB50010 )
六、受弯构件正截面简化分析
1. 压区混凝土等效矩形应力图形(极限状态下)
定义:
x h0
xn=nh
0
1c0
yc C
x=1xn
对试验梁,已知b、h0、As、fc、fy、Es, Mu
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
sAs
s= fyAs
y
fyAs s>y
四、受弯构件的试验研究
2. 试验结果
结论
•适筋梁具有较好的变形能力,超筋梁和少筋梁的破坏具有突然性,设计 时应予避免
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢筋屈服的同 时,混凝土压碎
二、骨架曲线的弯矩-曲率关系
1. 基本假定
P
平截面假定----平均应变意义上
As’
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
as b
s
b c
(1-n)h0
忽略剪切变形对梁、柱构件变形的影响
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的相容关系
as h/2as h h/2as
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
As
as 1
h/2-
名师名校勘测设计注册工程师讲义【土木工程材料考前复习指导】第83讲第十六章结构设计(二十九)

二、受弯构件(梁)1.强度计算1)抗弯强度在主平面内受弯的实腹构件,其抗弯强度应按下式计算(17-204)式中:M x、M y——分别为同一截面绕x轴和y轴的弯矩(对工字形截面,x轴为强轴,y轴为弱轴);M nx、M ny——分别为对x轴和y轴的净截面模量;当截面板件宽厚比等级为S1、S2、S3或S4级时,应取全截面模量,当截面板件宽厚比等级为S5级时,应取有效截面模量,均匀受压翼缘有15ε,腹板有效截面可按《钢结构设计标准》第8.4.2条的规定采用(mm3);效外伸宽度可取kγx、γy——分别为沿x轴、y轴的截面塑性发展系数,对工字形截面,γx=1.05,γy=1.20,对箱形截面γx=γy=1.05,对需要计算疲劳的梁,宜取γx=γy=1.0,对其他截面,可按《钢结构设计标准》中6.1.2条采用。
2)抗剪强度(17-205)式中:V——计算截面沿腹板平面作用的剪力;S——计算剪应力处以上毛截面对中和轴的面积矩;I——毛截面惯性矩;t w——腹板厚度;ƒv——钢材的抗剪强度设计值。
3)局部抗压强度当梁上翼缘作用有沿腹板平面的集中荷载,且该荷载又未设置支承加劲肋时,腹板计算高度上边缘的局部抗压强度按下式计算:(17-206)式中:F——集中荷载,对动力荷载应考虑动力系数;ψ——集中荷载增大系数,对重级工作制吊车梁,ψ=l.35,对其他梁,ψ=l.O;l z——集中荷载按45°扩散在腹板计算高度上边缘的假定分布长度,其值应根据支座具体尺寸确定。
梁的支座处,当不设置支承加劲肋时,也应按式(17-206)计算腹板计算高度下边缘的局部压应力,但ψ取1.0。
【例17-17/2014真题】设计一悬臂钢架,最合理的截面形式是:解:根据悬臂梁的受力特点可知,上翼縁承受拉应力,下翼縁承受压应力,钢材的抗拉、抗压强度相同,故应选择上、下翼縁面积相同的截面形式。
答案:B2.截面板件宽厚比等级截面板件宽厚比是指截面板件平直段的宽度和厚度之比,受弯或压弯构件腹板平直段的高度与腹板厚度之比也可称为板件高厚比。
第二章弯矩曲率关系

(1)
如记刚发生卸载时下边缘的应变为1
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理—考虑“拉伸硬化” 受拉区 域
注意!!!
M
钢筋 M
同时应用裸钢筋的应力-应变关系和开裂后混 凝土的平均受拉应力-应变关系会导致概念上 的错误
采用钢筋和混凝土考虑裂缝影响的平均应变即 可计入粘结作用的影响
二、骨架曲线的弯矩-曲率关系
a
2
b
]
a
2
b
b],
4) 重复13步骤直至满足精度要求
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
注意!!!
当外插法的计 算公式中的分 母g1过小时, 计算机可能会 “溢出”
g( )
AB两点的
割线
A
B
二分法的逼近值是围绕
正确值上下波动的,若
2 1
g1 3 1 m
2) 假定和 值
n
X 0 ,
c i A is 'A s ' sA s N 0
i 1
M 0 , M i n 1c A iiZ i sA s ( h 2 a s ) s A s ( a s h 2 ) = 0
3) 由相容方程求出各条带混凝土的应变及钢筋的应变;
4) 由物理关系求出相应的应力,拉区混凝土条带的应变 超过其极限受拉应变时,应对其进行处理;
?
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理--Considère(1899)试验
N (kN)
200
混凝土:fc=30.8MPa; ft=1.97MPa;
《弯矩曲率关系》课件

曲率的定义
曲率:描述曲线弯曲程度的量, 定义为曲线上任一点处切线方向 角的变化量与经过的弧长的比值
。
在数学上,曲率是用来衡量曲线 上某一点附近的小弧段弯曲程度
的量。
对于直线,其曲率为0;对于圆 ,其曲率是一个常数,等于圆的
半径倒数。
曲率的计算
曲率计算公式:K = lim(Δs->0) [Δs / (Δt)^2] / lim(Δt>0) [Δs / Δt]
在机械工程中的应用
传动系统设计
在机械传动系统中,弯矩曲率关系对于齿轮、轴等部件的设计和优化具有指导意义。了解弯矩与曲率的关系有助 于提高传动系统的效率和稳定性。
疲劳分析
在机械部件的疲劳分析中,弯矩曲率关系是评估其疲劳寿命的重要因素之一。通过对弯矩和曲率的变化规律进行 分析,可以预测部件的疲劳寿命和潜在的疲劳断裂风险。
在工程结构中,弯矩和曲率是密切相关的。例如,在桥梁、建筑和机械设计中,需 要考虑到结构的弯曲程度和弯矩之间的关系。
当结构受到外力作用时,会发生弯曲变形,曲率会发生变化,同时弯矩也会随之改 变。因此,在设计时需要考虑到结构的承载能力和稳定性。
了解弯矩与曲率的关系有助于工程师更好地设计结构,确保其安全性和稳定性。
需要研究弯矩曲率关系在不同温度、湿度等环境 条件下的变化规律。
需要探索弯矩曲率关系在复合材料、智能材料等 新型材料中的应用。
对学习者的建议
学习者应该深入理解弯矩和曲 率的定义及测量方法。
学习者应该掌握弹性力学和 材料力学的基本原理,以便 更好地理解弯矩曲率关系。
学习者可以通过实验和实践来 加深对弯矩曲率关系的理解和
应用。THANΒιβλιοθήκη S感谢观看详细描述
弯矩是材料力学中一个重要的概念,用于描述弯曲变形过程 中截面所受到的力矩作用。在材料受到弯曲时,截面上会产 生剪力和弯矩,弯矩的大小与剪力和中性轴距离有关。
弯矩曲率关系
1. 基本假定
混凝土受压时的应力-应 变关系
n
2
1 60
(
fcu
50),当n
2时,取n
2
当应力较小时,如 c 0.3 fc时,可取 c Ecc
c fc
c
f
c
1
1
c 0
n
o
0
0 0.002 0.5 fcu 50105
四、受弯构件的试验研究
2. 试验结果
最小配筋率
四、受弯构件的试验研究
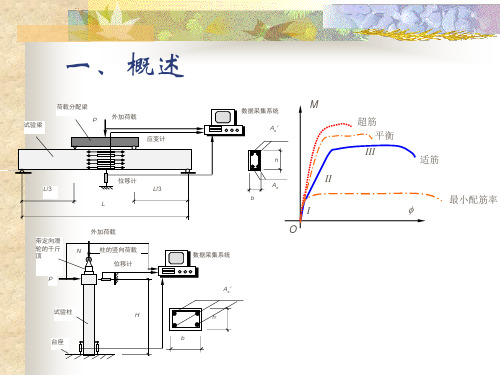
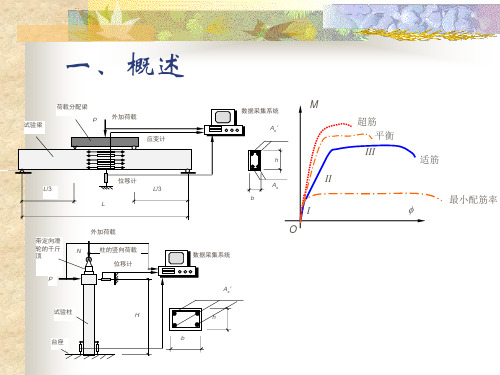
2. 试验结果 P
M
超筋 平衡
III
适筋
L/3 L
II 少筋 I O
最小配筋率
c
c
c
c
L/3
(c’<u) c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
As
as
h/2as h h/2as
as
1
i
Zi
截面中心线 s n
As
b
c1 s ci M
N
X 0,
n
ci Ai
' s
As'
s As
N
0
i 1
sAs ci
sAs
M 0,
荷载分 配梁 P
第二章弯矩曲率关系
n
i 1
ci
Ai s' As' s As N 0
n
2) 假定和 值
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )=0 2 2
3) 由相容方程求出各条带混凝土的应变及钢筋的应变; 4) 由物理关系求出相应的应力,拉区混凝土条带的应变 超过其极限受拉应变时,应对其进行处理;
2) 假定 值
X 0,
n
i 1
ci
Ai s' As' s As N 0
n
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )=0 2 2
3) 由相容方程求出各条带混凝土的应变及钢筋的应变; 4) 由物理关系求出相应的应力,拉区混凝土条带的应变 超过其极限受拉应变时,应对其进行处理;
5) 将各应力值代入第一平衡方程,判断是否满足平衡条件: 如不满足,需要调整 值直至满足为止,如满足平衡条件, 则由第二平衡方程求出M,然后重复步骤1~5
6) 当符合破坏条件时,停止计算。
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
M - 关系的计算方法之二 :分级加荷载法
1) 取M=M+M
h h/2as
as b
n
As
对钢筋混凝土柱, 有时也可能会出现 s < 0
s s ( s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
as h/2as h h/2as as b 1 i Zi 截面中心线 n As As
第3章钢筋混凝土受弯构件习题和思考题及答案

第三章钢筋混凝土受弯构件问答题1. 适筋梁正截面受弯全过程可划分为几个阶段?各阶段的主要特点是什么?与计算有何联系?1。
答:适筋梁正截面受弯全过程可划分为三个阶段—混凝土开裂前的未裂阶段、混凝土开裂后至钢筋屈服前的裂缝阶段和钢筋开始屈服前至截面破坏的破坏阶段.第Ⅰ阶段的特点是:1)混凝土没有开裂;2)受压区混凝土的应力图形是直线,受拉区混凝土的应力图形在第Ⅰ阶段前期是直线,后期是曲线;3)弯矩与截面曲率基本上是直线关系.a I 阶段可作为受弯构件抗裂度的计算依据。
第Ⅱ阶段的特点是:1)在裂缝截面处,受拉区大部分混凝土推出工作,拉力主要由纵向受拉钢筋承担,但钢筋没有屈服;2)受压区混凝土已有塑性变形,但不充分,压应力图形为只有上升段的曲线;3)弯矩与截面曲率是曲线关系,截面曲率与挠度的增长加快了.阶段Ⅱ相当于梁使用时的受力状态,可作为使用阶段验算变形和裂缝开展宽度的依据。
第Ⅲ阶段的特点是:1)纵向受拉钢筋屈服,拉力保持为常值;裂缝截面处,受拉区大部分混凝土已退出工作,受压区混凝土压应力曲线图形比较丰满,有上升曲线,也有下降段曲线;2)由于受压区混凝土合压力作用点外移使内力臂增大,故弯矩还略有增加;3)受压区边缘混凝土压应变达到其极限压应变实验值0cu 时,混凝土被压碎,截面破坏;4)弯矩—曲率关系为接近水平的曲线。
第Ⅲ阶段末可作为正截面受弯承载力计算的依据。
2. 钢筋混凝土梁正截面受力全过程与匀质弹性材料梁有何区别?2.答:钢筋混凝土梁正截面受力全过程与匀质弹性材料梁的区别有:钢筋混凝土梁从加载到破坏的全过程分为三个阶段;从第Ⅱ阶段开始,受拉区混凝土就进入塑性阶段,梁就开始带裂缝工作,受拉区拉力都由钢筋来承担,直到第Ⅲ阶段末整个梁破坏,而匀质弹性材料梁没有这两个阶段,始终是在弹性阶段内工作的.3.钢筋混凝土梁正截面有哪几种破坏形态?各有何特点?3。
答:钢筋混凝土梁正截面有适筋破坏、超筋破坏和少筋破坏三种。
混凝土结构设计原理复习资料(大纲重点)

混凝土结构设计原理复习资料(大纲重点)混凝土结构设计原理复资料第1章绪论钢筋与混凝土的共同工作原理钢筋与混凝土之间有着良好的粘结力,使它们能够结合成一个整体,在荷载作用下能够共同变形,完成其结构功能。
此外,钢筋与混凝土的温度线膨胀系数也较为接近,不会产生较大的温度应力而破坏两者之间的粘结。
同时,包围在钢筋外面的混凝土还能保护钢筋免遭锈蚀,从而保证了钢筋与混凝土的共同作用。
混凝土的优缺点混凝土作为建筑结构材料具有以下优点:材料利用合理、可模性好、耐久性和耐火性较好、现浇混凝土结构的整体性好、刚度大、阻尼大、易于就地取材。
但混凝土也有缺点,主要表现在自重大、抗裂性差、承载力有限、施工复杂、施工周期较长、修复、加固、补强较困难等方面。
建筑结构的功能和荷载分类建筑结构的功能包括安全性、适用性和耐久性三个方面。
荷载按时间的变异可分为永久作用、可变作用、偶然作用。
结构的极限状态包括承载力极限状态和正常使用极限状态。
结构的目标可靠度指标与结构的安全等级和破坏形式有关。
荷载的标准值应小于荷载设计值,而材料强度的标准值应大于材料强度的设计值。
第2章钢筋与混凝土材料物理力学性能混凝土的强度混凝土的立方体抗压强度(fcu,k是用150mm×150mm×150mm的立方体试件作为标准试件,在温度为(2±3)℃,相对湿度在90%以上的潮湿空气中养护28d,按照标准试验方法加压到破坏,所测得的具有95%保证率的抗压强度。
(fcu,k是确定混凝土强度等级的依据)。
混凝土的强度还包括强度轴心抗压强度(fc和轴心抗拉强度(ft其中,强度轴心抗压强度由150mm×150mm×300mm的棱柱体标准试件经标准养护后用标准试验方法测得。
(f ck0.67 fcu,k轴心抗拉强度相当于fcu,k的1/8~1/17,fcu,k越大,这个比值越低。
混凝土在复合应力下的强度表现为三向受压时,可以提高轴心抗压强度和轴心受压变形能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.3.1.1截面的弯矩曲率关系
第一个方面是柱截面的受弯性能,即截面弯矩M -截面曲率ϕ的关系。
在截面受弯过程中,钢筋混凝土构件截面一般经历三个阶段:截面弹性受力状态→截面受拉边缘混凝土纤维开裂→截面受拉边钢筋拉屈→截面受压边混凝土达到极限压应变。
随着弯矩的增加,截面受弯刚度趋势变小,一般配筋截面在进入屈服阶段后都存在一个明显的屈服平台,即截面的极限弯矩稍大于屈服弯矩,但是截面的极限曲率远远大于屈服曲率。
现在常用截面条带模型计算截面的M -ϕ全过程曲线。
截面条带模型程序分析中用到的基本假定有以下几条[32]:
(1)截面从受力开始到破坏,截面始终保持平面变形。
(2)钢筋和混凝土材料在标准试验中测定的本构关系可以用于程序分析。
(3)忽略由于时间因素引起的材料变化,例如:混凝土的收缩、徐变。
(4)截面的变形比较小,变形后的状态不影响受力体系计算图形和内力值。
根据以上的基本假定,程序中可以使用以下三个基本条件:
(1)几何变形条件:由假定(1)可以确定在截面分析过程中,以下公式始终成立。
ϕ =
h s
c εε+ 其中ϕ是截面曲率,c ε是受压边缘混凝土应变,s ε是受拉钢筋应
变,0h 是截面有效高度。
(2)物理本构关系:通过这个条件可以由混凝土或钢筋的应变推得相应的应力c σ和s σ。
本文采用了混凝土和钢筋典型的应力—应变曲线,如图3-2所示:
图3-2混凝土和钢筋的本构关系曲线
混凝土受压的本构关系采用了Hognestad 模型,数学表达式为:
⎪⎪⎭
⎪⎪⎬⎫---=-=cp
cp
cu cp
cp cp cp σεεεεσσεεεεσ)](15.01[])()(2[2
上升段
(3-1)
下降段 其中混凝土的受压峰值应变cp ε取为0.002,而极限应变u ε取为0.0033。
混凝土受拉的本构关系采用了简化模型,数学表达式为:
⎪⎭⎪
⎬⎫==tp
tp tp
σσσεεσ)(
上升段
(3-2)
水平段
其中混凝土的受拉峰值应变tp ε取为0.0001,而极限应变tu ε取为0.0002。
钢筋的本构曲线采用了典型的弹塑性模型,屈服应力y σ和屈服应变y ε根据钢材的性能取定。
(3)力平衡关系:将截面划分为若干个条带后,可以分别计算出每个条带的轴力和弯
矩。
由于截面受力是平衡的,所有条带的轴向力和弯矩的总和始终要满足平衡方程,具体可以用以下公式进行判断:
∑X =0 N A A A s s s n
i i ci
+++∆∑=σσσ
'
'1
=0 (3-3)
∑M =0 M h a A a h A Z A s s s s s n
i i i ci +-+-+∆∑=)2/()2/('''
1
σσσ=0 (3-4) 根据以上假定,本文编写了考虑截面轴力N 作用的M -ϕ全过程计算程序。
程序的计算是按照逐渐加大截面曲率ϕ的顺序进行的,在每一个ϕ阶段需要寻找到截面受力平衡对应的受压混凝土应变c ε。
而判定寻找到的c ε是否准确的标准是截面的平衡方程,即基本条件(3)∑X =0,具体程序如图3-3如下:
图3-3 考虑轴力作用的M-ϕ求解
程序在给定截面曲率ϕ时寻找对应平衡cε往往要通过二分法多次循环,而在N绝对值
ε时出现发散的情况,即按照二分法寻找时出特别大的时候,有时会出现按照二分法寻找
c
ε不断朝一个方向变化,而不是收敛向一个定值。
这是因为在给定ϕ条件下,截面所能现
c
承受的轴力N与cε并不是呈现单调递增或递减关系,而是呈现曲线关系,如图3-4所示。
ε的情况。
而二分法只能用于具有单调关系的线段,所以会出现寻找不到对应的
c
ε与N的关系曲线
图3-4 在φ确定条件下
c
所以在程序中必须加一个函数将曲线关系的线段截断成单调关系的线段,然后才能用二
分法循环寻找c ε。
具体的函数操作如下:在给定的ϕ条件,找到截面最大轴力max N 对应的截面上边缘纤维应变max c ε以及截面最小轴力min N 对应的截面上边缘纤维应变min c ε,[min c ε,max c ε]的范围就是保证c ε寻找收敛的范围。
如果外力N 超过了截面所能承受的范围[min N ,max N ],函数应该返回轴力“越界”的消息,也就是截面受到的轴外力N 已经超过了它的承受范围,如图3-4所示。
所以有了这个函数,就可以处理任意轴力作用下截面的M -ϕ关系。
为了节省后续程序的计算工作量,用程序计算出的M -ϕ全过程曲线可以用三折线模型替代,三个特征点是:截面开裂点、截面钢筋屈服点、截面混凝土压碎点。
从图3-5可以看出原曲线和替代曲线之间的偏差并不大,但是经过替代之后,后续程序的计算量却可以大大减小。
图3-5 M -ϕ的精确曲线和等效折线。
