弯矩曲率计算示例[详细]
弯矩计算公式总结

弯矩计算公式总结什么是弯矩?在物理学中,弯矩是指施加在物体上的扭曲力。
当一个物体受到弯曲力时,会在其横截面上形成一对反向的力,被称为弯矩。
弯矩可以是正的或负的,取决于力的方向和应力。
弯矩计算公式弯矩计算是工程力学中的一个重要计算问题,它涉及到力、距离和物体的特性。
下面将介绍几个常见的弯矩计算公式。
1. 单点弯矩计算公式单点弯矩计算公式用于计算在物体上施加单个点力时的弯矩。
假设我们有一个直杆,其中施加了一个点力F,作用点到杆的一端的距离为d。
单点弯矩计算公式可以表示为:M = F * d其中,M表示弯矩,F表示力,d表示作用点到杆的距离。
2. 弯矩分布计算公式当一个物体上存在多个力时,我们需要使用弯矩分布计算公式。
这种情况下,我们将物体划分为多个小段,每个小段的长度为∆x,施加在小段上的力为∆F,小段的位置为x。
弯矩分布计算公式可以表示为:dM = ∆F * x通过对小段进行积分,我们可以得到整个物体上的弯矩分布。
计算公式为:M = ∫(∆F * x)dx3. 具有弯曲系数的弯矩计算公式在实际应用中,物体的材料通常具有弯曲系数(弹性模量),该系数表示物体被弯曲时的抵抗性。
弯曲系数用E表示。
具有弯曲系数的弯矩计算公式可以表示为:M = (F * d) / E在这种情况下,力F和距离d与材料的弯曲系数E相关。
4. 轴向力和弯曲力的共同作用计算公式当物体同时受到轴向力和弯曲力时,我们需要综合考虑它们的影响。
这种情况下,我们需要使用联立公式来计算弯矩。
联立公式可以表示为:M = F * d + P * e其中,M表示弯矩,F表示施加的点力,d表示点力的距离,P表示轴向力,e表示轴向力作用点到杆的距离。
注意事项在使用弯矩计算公式时,有几个注意事项需要牢记:1.弯矩的单位通常为牛顿-米(N·m)或磅-英尺(lb·ft)。
2.力和距离的单位要一致,例如,如果力的单位是磅(lb),距离的单位应为英尺(ft)。
弯矩 曲率关系

c0 0.00,2cu0.0033
11.0
1
0.8, 0.7,
fcu 50Mpa fcu 50Mpa
线性插值(《混凝土结构设计
规范》GB50010 )
六、受弯构件正截面简化分析
1. 压区混凝土等效矩形应力图形(极限状态下)
定义:
x h0
xn=nh
0
1c0
yc C
x=1xn
对试验梁,已知b、h0、As、fc、fy、Es, Mu
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
sAs
s= fyAs
y
fyAs s>y
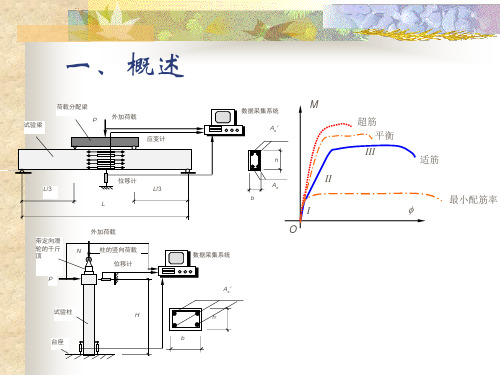
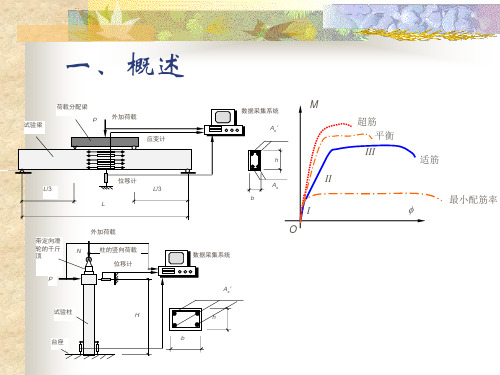
四、受弯构件的试验研究
2. 试验结果
结论
•适筋梁具有较好的变形能力,超筋梁和少筋梁的破坏具有突然性,设计 时应予避免
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢筋屈服的同 时,混凝土压碎
二、骨架曲线的弯矩-曲率关系
1. 基本假定
P
平截面假定----平均应变意义上
As’
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
as b
s
b c
(1-n)h0
忽略剪切变形对梁、柱构件变形的影响
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的相容关系
as h/2as h h/2as
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
As
as 1
h/2-
利用弯矩-曲率(M-Φ)曲线评价截面性能

复制和粘贴
| 输入钢筋 |
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
11
05.任意形状截面性能评价
2. 弯矩-曲率关系曲线
计算已经输入了钢筋的矩形截面的弯矩-曲率曲线。
在主菜单中选择模型 > 材料和截面特性 > 弯矩-曲率曲线 1. 勾选“显示理想模型”选项 2. 在“用户自定义曲率(理想化模型)”选项中输入‘0.002’ 3. 点击“计算”键
1. 点击主菜单的文件> 打开项目打开名称为‘M-Phi_Model.mcb’ 的模型文件。 2. 点击主菜单的模型> 材料和截面特性 > 截面确认已定义的两个截面
| 确认矩形截面 |
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
| 确认任意形状截面 |
5
03.选择材料本构模型
1. 混凝土材料本构
2. 钢材 1) Menegotto-Pinto Model 2) Bilinear Model 3) Asymmetrical Bilinear Steel Model 4) Trilinear Steel Model
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
3
01.概要
利用下面的弯矩-曲率曲线计算截面的屈服和极限承载力、屈服和极限位移。 M
STEP 1. 选择非线性材料本构模型
STEP 2. 输入钢筋
STEP 3. 计算弯矩-曲率曲线
STEP 4. 利用弯矩-曲率曲线计算截面特性
STEP 5. 利用理想化的弯矩-曲率曲线评价截面性能
| 截面性能评价过程 |
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
《弯矩曲率关系》课件

曲率的定义
曲率:描述曲线弯曲程度的量, 定义为曲线上任一点处切线方向 角的变化量与经过的弧长的比值
。
在数学上,曲率是用来衡量曲线 上某一点附近的小弧段弯曲程度
的量。
对于直线,其曲率为0;对于圆 ,其曲率是一个常数,等于圆的
半径倒数。
曲率的计算
曲率计算公式:K = lim(Δs->0) [Δs / (Δt)^2] / lim(Δt>0) [Δs / Δt]
在机械工程中的应用
传动系统设计
在机械传动系统中,弯矩曲率关系对于齿轮、轴等部件的设计和优化具有指导意义。了解弯矩与曲率的关系有助 于提高传动系统的效率和稳定性。
疲劳分析
在机械部件的疲劳分析中,弯矩曲率关系是评估其疲劳寿命的重要因素之一。通过对弯矩和曲率的变化规律进行 分析,可以预测部件的疲劳寿命和潜在的疲劳断裂风险。
在工程结构中,弯矩和曲率是密切相关的。例如,在桥梁、建筑和机械设计中,需 要考虑到结构的弯曲程度和弯矩之间的关系。
当结构受到外力作用时,会发生弯曲变形,曲率会发生变化,同时弯矩也会随之改 变。因此,在设计时需要考虑到结构的承载能力和稳定性。
了解弯矩与曲率的关系有助于工程师更好地设计结构,确保其安全性和稳定性。
需要研究弯矩曲率关系在不同温度、湿度等环境 条件下的变化规律。
需要探索弯矩曲率关系在复合材料、智能材料等 新型材料中的应用。
对学习者的建议
学习者应该深入理解弯矩和曲 率的定义及测量方法。
学习者应该掌握弹性力学和 材料力学的基本原理,以便 更好地理解弯矩曲率关系。
学习者可以通过实验和实践来 加深对弯矩曲率关系的理解和
应用。THANΒιβλιοθήκη S感谢观看详细描述
弯矩是材料力学中一个重要的概念,用于描述弯曲变形过程 中截面所受到的力矩作用。在材料受到弯曲时,截面上会产 生剪力和弯矩,弯矩的大小与剪力和中性轴距离有关。
弯矩 计算公式

弯矩计算公式
弯矩的计算公式可以根据不同的情境和需求进行选择。
以下是一些常用的弯矩计算公式:
1.均布荷载弯矩计算公式:M=(q*L^2)/8,其中q为均布荷载的重量,L为均
布荷载作用的长度。
2.点荷载弯矩计算公式:M=(PL^3)/3E,其中P为点荷载的集中力,L为集中
力作用的长度,E为材料的弹性模量。
3.梁的弯矩计算公式:M=F*L,其中F为梁受到的力,L为力臂。
4.简支梁的弯矩计算公式:M=(PL^2)/4,其中P为简支梁受到的集中力,L
为简支梁的跨度。
5.斜梁的弯矩计算公式:M=FLsinθ,其中F为斜梁受到的力,L为斜梁的长
度,θ为斜梁与水平面的夹角。
需要注意的是,不同的弯矩计算公式适用于不同的情境和条件,具体应用需要根据实际情况进行选择。
同时,还需要考虑材料的物理性质、几何形状和受力状态等因素的影响。
均布荷载的弯矩

均布荷载的弯矩弯矩是指在物体上施加荷载时产生的弯曲力矩。
均布荷载则是指施加在物体上的载荷均匀分布。
在工程领域中,了解均布荷载的弯矩计算方法对于设计和分析结构的稳定性至关重要。
本文将介绍均布荷载的弯矩及其计算方法。
一、均布荷载的概念均布荷载是指施加在物体上的荷载均匀分布的载荷形式。
例如,在桥梁设计中,自重荷载、行车荷载等都可以视为均布荷载。
均布荷载的弯矩计算可以帮助工程师确定结构的最大变形和最大应力,从而确保结构的稳定性和安全性。
二、均布荷载的弯矩计算方法1. 杆件弯曲方程在计算均布荷载的弯矩之前,需要先了解杆件的弯曲方程。
弯曲方程可以描述杆件在弯曲过程中的变形情况。
对于一个杆件,其弯矩可以通过以下方程计算:M = E * I * κ / R其中,M表示弯矩,E表示杨氏模量,I表示截面惯性矩,κ表示截面位置的曲率,R表示曲率半径。
2. 均布荷载的弯矩计算公式对于均布荷载,弯矩的计算公式如下:M = (w * L^2) / 8其中,M表示弯矩,w表示均布荷载的大小,L表示杆件的长度。
三、示例分析为了更好地理解均布荷载的弯矩计算方法,下面以一个简单的梁结构为例进行分析。
假设有一根梁,长度为L,宽度为b,高度为h。
该梁受到均布荷载w的作用。
根据上述公式,计算该梁的弯矩。
首先,计算截面惯性矩I和曲率κ。
对于矩形截面,截面惯性矩I可以通过以下公式计算:I = (b * h^3) / 12曲率κ可以通过以下公式计算:κ = M / (E * I)其中,E表示杨氏模量。
然后,根据弯曲方程,计算弯矩M。
将均布荷载w代入公式,得到:M = (w * L^2) / 8最后,将计算得到的M代入曲率公式,计算得到曲率κ。
通过曲率,可以进一步分析梁的变形情况和应力分布。
四、结论均布荷载的弯矩计算对于工程设计和结构分析非常重要。
通过了解弯曲方程和计算公式,工程师可以计算出结构在均布荷载作用下的弯矩,评估结构的稳定性和安全性。
弯矩曲率关系
1. 基本假定
混凝土受压时的应力-应 变关系
n
2
1 60
(
fcu
50),当n
2时,取n
2
当应力较小时,如 c 0.3 fc时,可取 c Ecc
c fc
c
f
c
1
1
c 0
n
o
0
0 0.002 0.5 fcu 50105
四、受弯构件的试验研究
2. 试验结果
最小配筋率
四、受弯构件的试验研究
2. 试验结果 P
M
超筋 平衡
III
适筋
L/3 L
II 少筋 I O
最小配筋率
c
c
c
c
L/3
(c’<u) c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
As
as
h/2as h h/2as
as
1
i
Zi
截面中心线 s n
As
b
c1 s ci M
N
X 0,
n
ci Ai
' s
As'
s As
N
0
i 1
sAs ci
sAs
M 0,
荷载分 配梁 P
第二章弯矩曲率关系
n
i 1
ci
Ai s' As' s As N 0
n
2) 假定和 值
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )=0 2 2
3) 由相容方程求出各条带混凝土的应变及钢筋的应变; 4) 由物理关系求出相应的应力,拉区混凝土条带的应变 超过其极限受拉应变时,应对其进行处理;
2) 假定 值
X 0,
n
i 1
ci
Ai s' As' s As N 0
n
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )=0 2 2
3) 由相容方程求出各条带混凝土的应变及钢筋的应变; 4) 由物理关系求出相应的应力,拉区混凝土条带的应变 超过其极限受拉应变时,应对其进行处理;
5) 将各应力值代入第一平衡方程,判断是否满足平衡条件: 如不满足,需要调整 值直至满足为止,如满足平衡条件, 则由第二平衡方程求出M,然后重复步骤1~5
6) 当符合破坏条件时,停止计算。
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
M - 关系的计算方法之二 :分级加荷载法
1) 取M=M+M
h h/2as
as b
n
As
对钢筋混凝土柱, 有时也可能会出现 s < 0
s s ( s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
as h/2as h h/2as as b 1 i Zi 截面中心线 n As As
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.933106
-4.36
P A
-7.84
Pey I
-9.06 -10.89
-12.2
P Pey AI
应力图
ce 0.324 103
s 0.389 103
0.436 103
c c / Ec
应变图
1 初始阶段
当外力矩(包括自重)M 0 时,截面曲率:
0.993106 rad/mm
f pu f p0.2 1540 MPa
预应力筋有效预应力
f pe 1000 MPa
弹性模量
Ep Es 2 105 MPa
Ap 784 mm2 As 402 mm2
Ap As
300 mm
弯矩曲率计算
Ⅰ
Ⅱ
Ⅲ
仅预应力 筋有效力 作用
梁底混凝 土达到抗 拉强度, 裂缝出现
给定顶部 应变,计 算弯矩曲 率
4 非线性阶段
假定截面顶纤维混凝土应变 c 0.001
截面开裂时,顶部纤维应变为:
c 0.464 103
0.464103 0.001 因此,在本阶段采用开裂截面分析。 即,假设中性轴以下混凝土不起作用。
4 非线性阶段
应力应变关系符如右图所
示,符合二次抛物线形曲
线
开裂后,截面扔符合平截面 假定。根据应力应变关系得 到应力图。
3 开裂阶段
由ΔM 对非预应力筋产生的拉应力为:
s
ns
My I
11.5 106 250 7.14 5.4 109
3.8MPa
因此开裂弯矩下,非预应力筋中的应力为:
s 12.7 3.8 16.5MPa
3 开裂阶段
由纤维应力0.64MPa而增加的曲率如图所示:
-0.64
-0.229 104
0
4 非线性阶段
求压应力合力,对应力
图积分,计算出合力大
小及位置。
顶部纤维应变 c
C0
bfc
0
c2 (1
c 3 0
)
x 0.35c
C X
中性轴
应变图
中性轴
应力图
4 非线性阶段
进行试算,确定中性轴高度。
1
假定中性轴高度 c=300mm c
受压区总压力为:
c
C0 4375c 4375 300 1312.5kN
混凝土:
本构关系
c
2
f
c
0
0
2
抗压抗拉强度
fc 35MPa ft 3.7MPa
550 mm 480 mm
600 mm
预应力混凝土梁
Ap 784 mm2 As 402 mm2
Ap As
300 mm
预应力混凝土梁
550 mm 480 mm
600 mm
钢筋:
假定预应力高强高筋的极限强 度和其屈服强度相等
2 加载阶段
加载阶段,是指在外弯矩开始作 用,直到预应力钢筋处的混凝土 应变为零的阶段。
0.123 103
0.933106
预应力钢筋除混凝土应变为零时 ,预应力筋的应力为:
ps Ep ps 2 105 5.324 103 1064.8MPa
此时,预应力筋中的拉力为:
P Ap ps 784 1064 .8 834 .8kN
ce 0.324 103
s 0.389 103
0.436 103
c c / Ec
应变图
2 加载阶段
-4.64 +8.35
+3.71
-4.64
P A
-8.35
Pey I
(P 834.8kN)
-9.64 -11.60
-13.0
P Pey AI
+3.71
2 加载阶段
-16.06
-12.35
600
弯矩为: M I 5.4 103 9.64 289 .0kNm
e
180
3 开裂阶段
截面开裂点将为截面弯矩曲率线弹性关系的终点
在上个阶段,截面底纤维已经存在3.06MPa的拉应力, 由于混凝土出现裂缝的抗拉强度为3.7MPa。
3.7 3.06 0.64MPa
M I 5.4 109 0.64 11.5kNm
弯矩曲率计算示例
北京交通大学
主要内容
弯矩曲率一般分为两个阶段进行:
梁未开裂
阶
段
一般假定为弹性阶段
一
梁开裂
阶
段
应力应变关系为非线性
二
弯矩曲率曲线
破坏
开裂
弯矩曲率曲线
曲线上的6个控制点
1.初始阶段,即外弯矩为零, f pe 1000 MPa 2.预应力筋水平处混凝土的应变为零。 3.裂缝出现,即混凝土达到其抗拉强度, ft 3.7MPa 4.梁截面顶纤维混凝土压应变达到 0.001 5.梁截面顶纤维混凝土压应变达到 0.002 6.梁截面顶纤维混凝土压应变达到 0.003
y
300
开裂弯矩为: M cr 289 11.5 300 .5kNm
3 开裂阶段
由ΔM 对预应力筋产生的拉应力为:
ps
n p c
np
Me I
7.14
11
.5 106 180 5.4 109
2.7MPa
因此开裂弯矩下,预应力筋中的应力为: ps 1064 .8 2.7 1067 .8MPa
0.441103
-9.64 -11.60
-13.0
-16.06
+9.64 +13.38
P Pey AI
M
+1.78 +3.06
应力图
0.317 106 0.0636 103
0.109 103
应变图
此阶段结束时,曲率为: (0.441 0.109) 103 0.917 106 rad/mm
1 初始阶段
无外力作用,仅考虑有80 103 mm2 I 5.4 109 mm4
Pe Ap f pe 784 1000 784 kN
计算有效预应力及偏心距引起的应力应变
Pe 784 kN
e 180mm
-4.36 +7.84
1 初始阶段
+3.48
0.123 103
p
(
480 c
c
)
c
s
(550 c
c )e
5.324 103
0.123 103
0.933106
普通钢筋的压应力:
Es s 2 105 0.389 3 77.8MPa
预应力筋在有效应力下的应变:
ps pe ce 5.324103
ce 0.324 103
s 0.389 103
0.436 103
c c / Ec
应变图
pe f pe Ep 1000/ 200000 5 103
+0.64
应力图
0.076 106
+0.229 104
应变图
3 开裂阶段
在开裂弯矩作用下, 截面的开裂曲率等于阶段(2)的曲率与开裂增加曲率之和, 也就是:
cr (0.917 0.076 ) 10 6 0.993 10 6 rad/mm
开裂弯矩为:
M cr 289 11.5 300 .5kNm
