钢结构基础第四章课后习题答案
陈绍蕃 钢结构第四章答案

第四章4. 1有哪些因素影响轴心受压杆件的稳定系数? 答:①残余应力对稳定系数的影响;②构件的除弯曲对轴心受压构件稳定性的影响; ③构件初偏心对轴心轴心受压构件稳定性的影响; ④杆端约束对轴心受压构件稳定性的影响;4.3影响梁整体稳定性的因素有哪些?提高梁稳定性的措施有哪些? 答:主要影响因素:①梁的侧向抗弯刚度y EI 、抗扭刚度t GI 和抗翘曲刚度w EI 愈大,梁越稳定; ②梁的跨度l 愈小,梁的整体稳定越好;③对工字形截面,当荷载作用在上翼缘是易失稳,作用在下翼缘是不易失稳; ④梁支撑对位移约束程度越大,越不易失稳; 采取措施:①增大梁的侧向抗弯刚度,抗扭刚度和抗翘曲刚度; ②增加梁的侧向支撑点,以减小跨度;③放宽梁的受压上翼缘,或者使上翼缘与其他构件相互连接。
4.6简述压弯构件中等效弯矩系数mx β的意义。
答:在平面内稳定的计算中,等效弯矩系数mx β可以把各种荷载作用的弯矩分布形式转换为均匀守弯来看待。
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N =1500kN 。
解:由支承条件可知0x 12m l =,0y 4m l =23364x 1150012850025012225012476.610mm 12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012500810000mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cm i ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa 0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
钢结构基础第四章课后习题答案
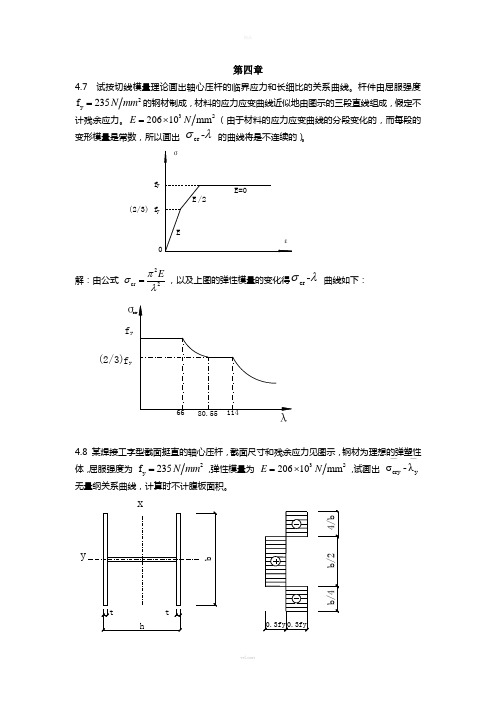
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cry y σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为0.6f yfyλσ0.20.40.60.81.0cryN=1500KN 。
解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构基础第四章课后习题答案

第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cryy σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500KN 。
0.6f yfyλσ0.20.40.60.81.0cry解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构基础(第二版)课后习题第四章答案
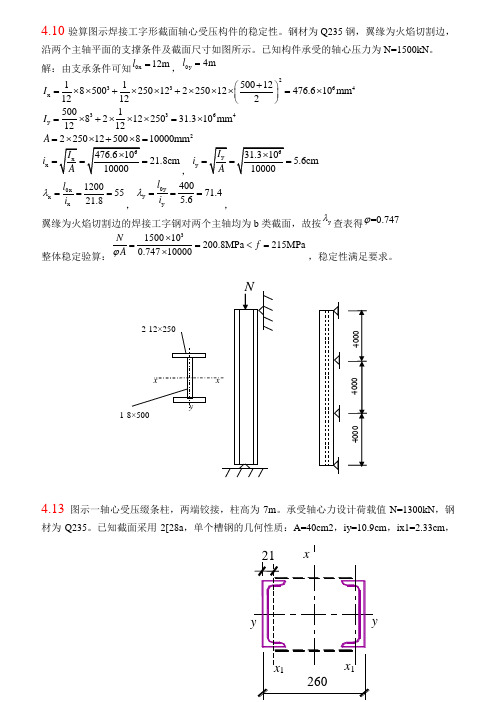
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500kN 。
解:由支承条件可知0x 12m l =,0y 4ml =23364x 1150012850025012225012476.610mm12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭ 3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012*********mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cmi ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m 。
承受轴心力设计荷载值N=1300kN ,钢材为Q235。
已知截面采用2[28a ,单个槽钢的几何性质:A=40cm2,iy=10.9cm ,ix1=2.33cm ,Ix1=218cm4,y0=2.1cm ,缀条采用∟45×5,每个角钢的截面积:A1=4.29cm2。
试验算该柱的整体稳定性是否满足?解:柱为两端铰接,因此柱绕x 、y 轴的计算长度为:0x 0y 7ml l ==224x x10262221840 2.19940.8cm 22b I I A y ⎡⎤⎡⎤⎛⎫⎛⎫=+-=+-=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦x 11.1cm i === 0x xx 70063.111.1l i λ=== 0y y y 70064.210.9l i λ===0x 65.1λ===格构柱截面对两轴均为b 类截面,按长细比较大者验算整体稳定既可。
钢结构-第四章课后答案

P1084.1解: 示意图要画焊缝承受的剪力V=F=270kN ;弯矩M=Fe=270300=81kN.mI x =[0.8(38-20.8)3]/12+[(15-2)119.52]2=13102cm 4=腹板A e =0.8(38-20.8)=29.12 cm 2截面最大正应力max M/W= 81106200/13102104=123.65 N/mm 2f t w =185N/mm 2剪力全部由腹板承担=V/A w =270103/2912=92.72 N/mm 2 =f v w =125N/mm 2腹板边缘处”1”的应力 1(M/W)(190/200) =123.65(190/200)=210.19=117.47腹板边缘处的折算应力应满足 2213 1.1w zs t f σστ=+≤22117.47392.72=+⨯=198..97N/mm 2 1.1f t w =203.5N/mm 2焊缝连接部位满足要求4.2解:(1) 角钢与节点板的连接焊缝“A ”承受轴力N=420kN连接为不等边角钢长肢相连 题意是两侧焊肢背分配的力N 1=0.65 420=273 kN肢背分配的力N 2=0.35 420=147 kNh fmin =1.5(t max )1/2=1.5(10)1/2=4.74mmh fmax =1.2(t min )=1.2(6)=7.2mm取h f =6mm 肢背需要的焊缝长度l w1=273103/(20.76160)+26=203.12+12=215.13mm 肢尖需要的焊缝长度l w2=147103/(20.76160)+26=109.38+12=121.38mm 端部绕角焊2h f 时,应加h f (书中未加)取肢背的焊缝长度l w1=220mm ;肢尖的焊缝长度l w2=125mm 。
l wmax =60h f =360mm ;l wmin =8h f =48mm ;焊缝“A ”满足要求4.3解:节点板与端板间的连接焊缝“B ”承受拉力N 对焊缝“B ”有偏心,焊缝“B ”承受拉力N=(1.5/1.8) 420=350kN ;剪力V=(1/1.8) 420=233.33 kN ;弯矩M=35050=17.5 kN.mh fmin =1.5(t max )1/2=1.5(20)1/2=6.71mm h fmax =1.2(t min )=1.2(10)=12mm焊缝“B ”h f =7mm焊缝“B ”A 点的力最大焊缝“B ”承受的剪应力=233.33103/(20.77386)=61.68 N/mm 2焊缝“B ”承受的最大正应力 =N/Ae+M/W=350103/(20.77386)+17.5106200/(20.773863/12) =92.52+71.91 =164.43 N/mm 2验算焊缝“B ”的强度=148.19 N/mm 2<f f w 焊缝“B ”满足要求。
钢结构第四章习题答案

截面轮廓尺寸 h =
两个槽钢翼缘间净距为 300 − 2 × 84 = 132mm > 100mm ,满足构造要求。 分肢形心轴之间的间距 a = 300 − 2 × 20.2 = 259.6mm (3)绕 y 轴整体稳定检算 分肢形心轴与 y 轴的间距 x1 = a / 2 = 259.6 / 2 = 129.8mm 绕 y 轴名义惯性距: I y = 2( I1 + x1 A1 ) =2(241.5+12.98 ×45.6) =15849cm
58.8
= 122.4mm
2 iy − 2i12 = 122.42 − 2 × 20.22 = 119mm
分肢形心至 y 轴: x1 =
分肢间距: b = 2( x1 + z0 ) = 2(119 + 20.2) = 278.4mm , 取 b = 300mm ,则实际分肢间距为 300-20.2×2=259.6mm 也可根据截面与回转半径的近似关系确定。 b=122.4/0.44=278mm,取 b=300mm (3)绕 y 轴整体稳定检算 分肢形心至 y 轴: x1 =300/2-20.2=129.8mm 绕 y 轴名义惯性距: I y = 2( I1 + x1 A1 ) =2(241.5+12.98 ×45.6) =15849cm
解:lox=9m,loy=3m,可选择窄翼缘热轧 H 型钢。 截面类型:绕 X 轴截面为 a 类截面, 绕 Y 轴截面为 b 类截面 假定长细比 λ = 100 ,查表 4.5(a)和 4.5(b),得 ϕ x = 0.638, ϕ y = 0.555 所需截面 A =
N 400 × 103 = = 33.52cm 2 ϕ f 0.555 × 215
第三版钢结构课后题答案第四章

4.1 验算由2∟63×5组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270kN ,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼,用于螺栓承压型连接。
钢材为Q235钢。
如截面尺寸不够,应改用什麽角钢?计算时忽略连接偏心和杆件自重的影响。
解:拉杆2L63×5,查附表7.4单角钢毛面积为:6.14 cm 2故:22n cm 28.10228.1210205214.62A =-=⨯⨯⨯-⨯=-钢材Q235,2215mmN f =强度验算:22232156.2621028.1010270mm N f mm N A N n =>=⨯⨯==σ该拉杆强度不满足。
试改用2∟70×6单角钢毛面积为:8.16 cm 2故:221392240163262021016.82mm A n =-=⨯⨯-⨯⨯=强度验算:223215194139210270mm N f mm N A N n =<=⨯==σ强度满足要求。
静力作用只需验算竖向平面内的长细比,按一般建筑结构系杆考虑,容许长细比为400 (或按其他构件300、350); 由附表7.4cm i x 15.2=长细比验算:[]4005.13915.2300=<===λλx o i l长细比满足要求。
点评:1、实际设计应多方案,在满足要求的方案中选重量最轻的。
如果选用的规格是所有角钢规格中最轻的就是最优设计。
OK4.3 验算图示高强螺栓摩擦型连接的钢板净截面强度。
螺栓直径20mm ,孔径22mm ,钢材为Q235-A.F ,承受轴心拉力N=600kN (设计值)。
解:钢板厚度14mm ,拼接板厚度2×10mmQ235—A.F 查表得2mm N 215f =钢板最外列螺栓处:()224369243360142234080804014mm A n =-=⨯⨯-+++⨯=()n n 5.01N N 1-='==600(1-0.5×3/9)=500kN验算净截面强度:2232153.205243610500mm N f mm N A N n =<=⨯='=σ钢板净截面强度满足要求。
钢结构第4章习题答案资料

2) 若杆长为6.5m 则 l0 0.7 6.5 4.55m
则
max
lo iy
4.55 4.99
91.2 < [] 150
b类 查表 0.612
N fA 0.612 215 64.28102 845.8kN
3)比较一下 4.8m时 按 λ 336 4.99 67.3 查表0.767
186.7kN
强度: N fA 215 21.6102 464.4kN
(2)Q345
强度: N fA 310 21.6102 669.6kN
刚度:
x
lox ix
36.5 150
y
loy iy
x
127 150
满足
稳定: 型钢构件,局部稳定无需验算
b 88 0.55 0.8 查表, x a y b
(1)几何参数
A 205002 5008 24000
Ix
1 12
8 5003
20 500 2602
2
1.435 109
Iy
1 12
20 5003
2
0.417 109
ix
Ix 244.5 A
iy
Ix 131.8 A
x
lox ix
10103 244.5
40.9
y
loy iy
10103 131.8
75.9
Q345 N=3000kN L=10m
(2)强度:
1
N A
3000 103 24000
125
310
(3)刚度:
x
lox ix
10103 244.5
40.9 150
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度 2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cry y σ-λ——无量纲关系曲线,计算时不计腹板面积。
解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =截面的平均应力 二者合并得cry y σ-λ——的关系式画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500KN 。
解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度oy =400cm l 。
抗压强度设计值 2215f N mm =。
(1) 计算截面特性毛截面面积 22 1.2250.850100A cm =⨯⨯+⨯=截面惯性矩 3240.850122 1.22525.647654.9x I cm =⨯+⨯⨯⨯=截面回转半径 ()()121247654.910021.83x x i I A cm ===(2) 柱的长细比 (3) 整体稳定验算从截面分类表可知,此柱对截面的强轴屈曲时属于b 类截面,由附表得到 0.833x ϕ=,对弱轴屈曲时也属于b 类截面,由附表查得 0.741y ϕ=。
经验算截面后可知,此柱满足整体稳定和刚度是要求。
4.11一两端铰接焊接工字形截面轴心受压柱,翼缘为火焰切割边,截面如图所示,杆长为12m ,设计荷载N=450KN ,钢材为Q235钢,试验算该柱的整体稳定及板件的局部稳定性是否满足?解:已知 N=450KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =900cm l 。
抗压强度设计值 2215f N mm =。
(1) 计算截面特性毛截面面积 221250.62062A cm =⨯⨯+⨯=截面惯性矩 3240.62012212510.55912.5x I cm =⨯+⨯⨯⨯=截面回转半径 ()()12125912.5629.77x x i I A cm ===(2) 柱的长细比(3) 整体稳定验算从截面分类表可知对截面的强轴屈曲时属于b 类截面,由附表得到 0.422x ϕ=,对弱轴屈曲时也属于b 类截面,由附表查得 0.741y ϕ=。
经验算截面后可知,此柱满足整体稳定和刚度是要求。
(4) 板件局部稳定性的验算 1) 翼缘的宽厚比1b t=12210=12.2 , (10+0.1+λ⨯(100.1100。
(110+0.1b t λ< 2) 腹板的高厚比0200633.33w h t ==, (()250.5250.510075λ+=+⨯= (0250.5w h λ<+。
即满足局部稳定的要求。
4.12 某两端铰接轴心受压柱的截面如图所示,柱高为6m ,承受轴心力设计荷载值 N=6000KN (包括柱身等构造自重),钢材为 Q235B F 钢,试验算该柱的整体稳定性是否满足?解:已知 N=6000KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =600cm l ,对弱轴的计算长度 oy =600cm l 。
抗压强度设计值 2215f N mm =。
(1) 计算截面特性毛截面面积 2250 1.6245 1.6304A cm =⨯⨯+⨯⨯=截面惯性矩 3242 1.645122 1.65023.3111162.4x I cm =⨯⨯+⨯⨯⨯=截面回转半径 ()()1212111162.419.12x x i I A cm ===(2) 柱的长细比 (3) 整体稳定验算从截面分类表可知,此柱对截面的强轴屈曲时属于b 类截面,由附表得到0.931x ϕ=,对弱轴屈曲时也属于b 类截面,由附表查得 0.934y ϕ=。
经验算截面后可知,此柱满足整体稳定和刚度是要求。
4.13 图示一轴心受压缀条柱,两端铰接,柱高为7m 。
承受轴心力设计荷载值 N=1300KN ,钢材为 Q235。
已知截面采用 2 [28a ,单个槽钢的几何性质: 10.9,cm =y i 1 2.33,x i cm = 41218,x I cm = 0 2.1y cm =,缀条采用 455L ⨯,每个角钢的截面积:21 4.29A cm =。
试验算该柱的整体稳定性是否满足?解:柱的计算长度在两个主轴方向均为7m 。
(1) 当构件绕实轴发生弯曲时: 已知:N=1300KN , 10.9,cm =y i则 =700010964.2y y l i λ==,从截面分类表可知,此柱对截面的实轴屈曲时属于b 类截面,由附表得0.785y ϕ=。
即此柱绕实轴满足整体稳定和刚度是要求。
(2) 当构件绕虚轴发生弯曲时:已知:N=1300KN 2=40cm A , 1 2.33,x i cm = 41218,x I cm = 0 2.1y cm =则构件绕虚轴的惯性矩为考虑剪切变形的影响,换算长细比得从截面分类表可知,此柱对截面的虚轴屈曲时属于b 类截面,由附表得 0.781x ϕ=。
即此柱绕虚轴满足整体稳定和刚度是要求。
4.14 某两端铰接的轴心压杆,截面由剖分T 型钢 2503001115⨯⨯⨯ 组成,钢材为235Q 钢,杆长 6m ,承受的轴心压力 1000N KN =。
试验算该柱的整体稳定性是否满足?解:已知 N=1000KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =600cm l ,对弱轴的计算长度 oy =600cm l 。
抗压强度设计值 2215f N mm =。
(1) 计算截面特性毛截面面积 230 1.5 1.123.570.85A cm =⨯+⨯=截面惯性矩 3241.123.51230 1.512.58220.89x I cm =⨯+⨯⨯=截面回转半径 ()()12128820.8970.8511.16x x i I A cm ===(2) 柱的长细比600111.653.8x x x l λ===,6006987y y y l λ===(3) 整体稳定验算从截面分类表可知,此柱对截面的强轴屈曲时属于b 类截面,由附表得到 0.839x ϕ=,对弱轴屈曲时也属于b 类截面,由附表查得 0.641y ϕ=。
经验算截面后可知,此柱不满足整体稳定的要求。
4.15 某压弯格构式缀条柱如图所示,两端铰接,柱高为 8m 。
承受压力设计荷载值 600N KN =,弯矩100M KN m =,缀条采用单角钢 455L ⨯,倾角为 45,钢材为 235Q ,试验算该柱的整体稳定性是否满足?已知:I22a ,2A=42cm 43400,x I cm = 41225;y I cm =解:1)当弯矩绕实轴作用时:(1)在弯矩作用平面内,此格钩式构件的计算与实腹式构件相同。
已知:600N KN = 100M KN m =。
从截面分类表可知,此柱对截面的实轴屈曲时属于b 类截面,由附表得到 0.619x ϕ=222322x =EA 1.1=3.142061073.810 1.190.3=1671.1KN Ex N πλ⨯⨯⨯⨯⨯、。
又查表得 m =1.0β, x =1.0λ,3W=218+309=527cm 则'1(10.8/)mx x x x x Ex M NA W N N βϕγ+- 即不满足整体稳定的要求。
(2)弯矩作用平面外的整体稳定的验算已知:600N KN = 100M KN m =,24231.873.8A cm =+=,通过静距计算得0112x mm =(形心到工字型钢形心的距离)。
换算长细比得从截面分类表可知,此柱对截面的虚轴屈曲时属于b 类截面,由附表得到0.752y ϕ=,又由 1.0b ϕ=,代入公式得:即不满足整体稳定的要求。
2) 当弯矩绕虚轴作用时: (1)在弯矩作用平面内,已知:600N KN = 100M KN m =,24231.873.8A cm =+=,m =1.0β,0800013857.97y y y l λ===,b 类截面查表得 0.818y ϕ=。
310/12616.95/11.21127y y W I x cm ===。
由公式得:即满足整体稳定的要求。
(2) 单肢计算: 左肢承受的压力 右肢承受的压力所以右肢承受拉力无需计算其稳定性。
已知: 18.99x i cm =, 800ox l cm =,189x ox x l λ== 1 2.31y i cm =,26oy l cm =,11.3y oy y l λ==从截面分类表可知,此柱对截面的x 轴屈曲时属于a 类截面,由附表得到 0.721x ϕ=,对y 轴屈曲时属于b 类截面,由附表查得 0.994y ϕ=。
由轴心受压公式得:即 构件满足整体稳定的要求。
(3) 缀条稳定因斜缀条长于横缀条,且前者的计算内力大于后者,故只需验算斜缀条。
柱段计算剪力 一个斜缀条受力 斜缀条长细比 02626.8cos 45 1.37λ==⨯ 由截面形式得是b 类截面,查附表得 0.947ϕ=。
折减系数 00.60.001526.80.64γ=+⨯= 则2013201.650.8215/0.9474290.64N N mm A ϕγ==<⨯⨯ 即 缀条满足稳定要求。
4.16 两端铰接的焊接工字形截面轴心受压构件,截面分别采用如图所示的两种尺寸。
柱高 10m ,钢材为 235Q 钢,翼缘为火焰切割以后又经过焊接,试计算:①柱所能承受的轴心压力?②板件的局部稳定是否满足要求? 解:已知,由支撑体系知对截面强轴弯曲的计算长度 ox =1000cm l ,对弱轴的计算长度 oy =1000cm l 。
抗压强度设计值 2215f N mm =。
1第一种截面尺寸 (1) 计算截面特性毛截面面积 2250 1.60.850200A cm =⨯⨯+⨯=截面惯性矩 3240.850122 1.65025.8114835.7x I cm =⨯+⨯⨯⨯=截面回转半径 ()()121114835.720023.96x x i I A cm ===(2) 柱的长细比 (3) 柱的轴心压力计算从截面分类表可知,此柱对截面的强轴屈曲时属于b 类截面,由附表得到 0.892x ϕ=,对弱轴屈曲时也属于b 类截面,由附表查得 0.704y ϕ=。
