机械原理 瞬心例题
机械原理课件瞬心例题
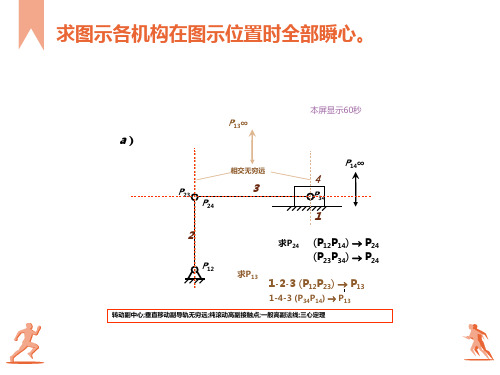
b)
P13
求P24
(P12P14) P24 (P23P34) P24
本屏显示60秒
P34 3
2
4
P12
P14∞
P24
求P13
1
1-2-3 (P12P23) P13
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
水平方向无穷远处有P12,通过P12作竖线连接P14
比1/ 3 。
解: 1. 绘机构运动简图 2.求瞬心P13 3.求1/ 3
1 P36 P13 3 P16 P13
求P13
1-2-3 (P12P23) P13
1-6-3 (P36P16) P13
2
P23
P12 4
P13
P36 5
ห้องสมุดไป่ตู้
3
6
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
求P24
(P12P14) P24
(P23P34) P24
c)
P13
M
P23
2
P12
P14
4
3
P24
求P13 1-2-3 (P12P23) P13
1
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
在图示的齿轮-连杆组合机构中, 试用瞬心法求齿轮1和3的传动
该线与通过P23P34的斜线相交于倾斜方向无穷远点
P12∞
c)
求P24
(P12P14) P24
机械原理50分题详解
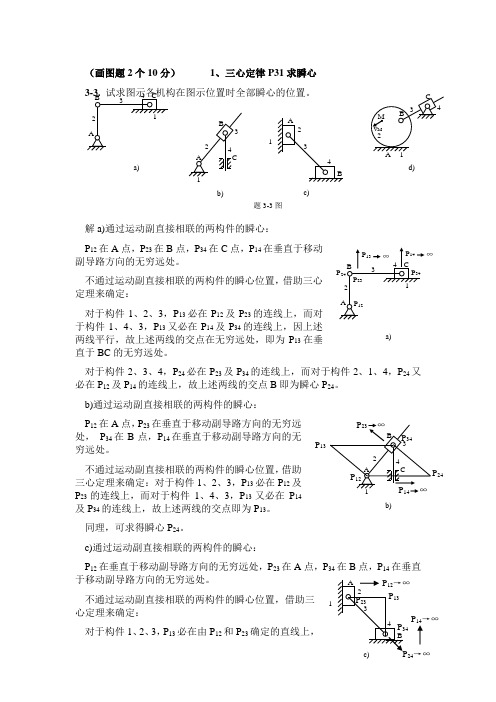
(画图题2个10分) 1、三心定律P31求瞬心解a)通过运动副直接相联的两构件的瞬心:P 12在A 点,P 23在B 点,P 34在C 点,P 14在垂直于移动副导路方向的无穷远处。
不通过运动副直接相联的两构件的瞬心位置,借助三心定理来确定:对于构件1、2、3,P 13必在P 12及P 23的连线上,而对于构件1、4、3,P 13又必在P 14及P 34的连线上,因上述两线平行,故上述两线的交点在无穷远处,即为P 13在垂直于BC 的无穷远处。
对于构件2、3、4,P 24必在P 23及P 34的连线上,而对于构件2、1、4,P 24又必在P 12及P 14的连线上,故上述两线的交点B 即为瞬心P 24。
b)通过运动副直接相联的两构件的瞬心: P 12在A 点,P 23在垂直于移动副导路方向的无穷远处, P 34在B 点,P 14在垂直于移动副导路方向的无穷远处。
不通过运动副直接相联的两构件的瞬心位置,借助三心定理来确定:对于构件1、2、3,P 13必在P 12及P 23的连线上,而对于构件1、4、3,P 13又必在P 14及P 34的连线上,故上述两线的交点即为P 13。
同理,可求得瞬心P 24。
c)通过运动副直接相联的两构件的瞬心:P 12在垂直于移动副导路方向的无穷远处,P 23在A 点,P 34在B 点,P 14在垂直于移动副导路方向的无穷远处。
不通过运动副直接相联的两构件的瞬心位置,借助三心定理来确定:对于构件1、2、3,P 13必在由P 12和P 23确定的直线上,a)b)d) 题3-3图a)b)P 13P 24 AB1234 c)1P 14→∞24→∞而对于构件1、4、3,P 13又必在由P 14和P 34确定的直线上,故上述两直线的交点即为P 13。
对于构件2、3、4,P 24必在由P 23和P 34确定的直线上,而对于构件2、1、4,P 24又必在由P 12及P 14确定的直线上(两个无穷远点确定的直线),故上述两线的交点即为P 24,即P 24在直线AB 上的无穷远处。
中南大学 机械原理 习题 (2)

√
n
2
3B
√
ω32×BD
√
﹖
√
ω32×BD
﹖
√
ω12×AB 2ω2×VB3B
﹖
√
√
τ B3
a B3 pb μa a 3
n a C3 ω3 CD 2
n b μa 3
a 3 α3= α2 = B BD
√
2
√
a r 3B 2 B
τ a C3 α3CD
n τ a c3 a c3 a c 3
VD=VB2+VDB2 V =pb μ ω = ω = VB3 (转向)
B3 3 v 3 2
VE=VB2+VEB2
VDB2=ω2 BD VEB2=ω2 BE VD=pd μv P d
CB
V
B3B2
=b2b3 μv
V =pe μ
E
b3
b2
B47
v
ω2= ω3
α3 =α2 k′ b2′ (2)、加速度分析
﹖ √
3-9、试判断在图示的两机构所在位置中,B点是否都存在哥氏加 速度?又在何位置时其哥氏加速度为零?作出其中一个机构位置 的位置图。并思考下列问题: 1)、在什么条件下才存在哥氏加速度? 2)、根据上一条,请检查一下所有哥氏加速度为零的位 置是否已全部找出?
k aB2 B3 22VB2 B3 3)、在图a中, ,对吗?为什么?
VB 2 AB
VB
VB 3 BP13
VC 3 CP13
P13
解: (1)、当φ=165°时,点C的速度VC ;
(2)、当φ=165°时,构件3的BC线上(或其延长线上) 速 度最小的一点E的位置及其速度的大小; E VE
机械原理典型例题(第三章运动分析)12-9-23

P14+∞
4
(P24 ) P12
P34
C 1
3
P13
4 C 3
M
P23 +∞ P13
2 3 B
P24+∞ P34
B P23
P14
νm
4 C
P12
A 1
2 P12
P24
1
P34+∞
P24
P14+∞
A
3-6:所示四杆机构中,LAB=60mm,LCD=90mm,LAD=LBC=120mm, ω2=10rad/S。试用瞬心法求:1)当φ =165°时,点C的速度VC; 2)当 VC=0时,φ 角之值; 3)当φ =165 °时,构件3的BC线上(或其延长线上)的 速度最小的一点E的位置及其速度。
n t k r aC 3 aC 3 aC 2 aC 3C 2 aC 3C 2
得:VB3=0,ω 3= 0 =ω 2,
VC3= ω 3LCD=0
a a a a a
n C3 t C3 n B t B
n C 2B
a
t C 2B
a
k C 3C 2
a
?
r C 3C 2
方:C→D ⊥CD B→A ⊥BD C→B ⊥CB √ 大:0 ? √ 0 0 ? 0 n t t 得: aC 3 aC 3 aC 3 aC 3 (p’ →c3’)
P12
1
ω2
P23 O
R C
=10×24×2=0.48m/s(右)
P14
ω1
A
4
∴ω2= ω1×LP12P14
/LP23P24=7.1rad/s(逆时)
VI=0=VP24,I 就是 P24
瞬心法运动分析
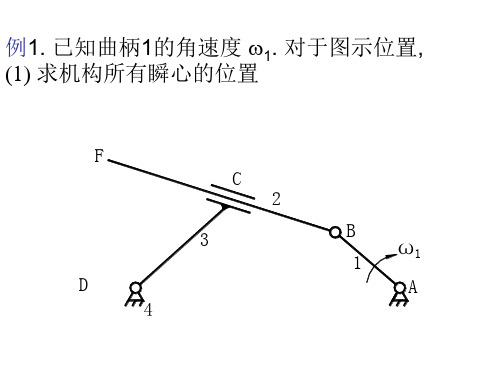
∞P14
E (P13) VE3 VE1 D
于是, 3 =V1/LCE
逆时针
VD = 3 *LCD
G (P23)
=V1*LCD /LCE.
V1
B
2
3
C (P )
A
1
F (P ) 12
根据三心定理,P24 应在P12P14连线上。 根据三心定理,P24 还应在P23P34连线上。 P12P14 和 P23P34 的交点G就是瞬心 P24.
G(P24) F C 2 3 D(P34) 4 B( P ) 12 1 E( P ) 13 P23
ω1
A(P14 )
(2) 求速比 3 /1. 利用机架4!! P34、P13、P14 在一直线上.
G(P24) F C 2 3 D(P34) 4 B( P ) 12 1 E( P ) 13 P23
ω1
A(P14 )
(2) 求速比 3 /1. 利用机架4!! P34、P13、P14 在一直线上. VE1=VE3, 1LAE=3LDE, 3=1LAE/LDE. 3为逆时针
F G(P24) P23
因为构件2与3组成移动副,所以 2 3. (此时, 都是逆时针)
G(P24) F P23
ω2 ω3
3
C 2 V E1 V E3 B( P ) 12 1
ω1
A(P14 )
D(P34) 4
E( P ) 13
(3) 求构件2上点F的速度VF 构件2绕绝对瞬心P24(G)相对机架4转动, 所以 VF= 2LGF
ω2
VF
C 2 3 B( P ) 12 1
ω3
D(P34) 4
V E1 V E3
ω1
A(P14 )
机械原理瞬心法求速度习题

机械原理瞬心法求速度习题引言机械原理是工程力学的一部分,研究物体的运动及力学效应。
在机械原理中,瞬心法是一种常用的分析方法,用于求解物体的速度和加速度。
本文将通过解答一些瞬心法求速度的习题,加深对机械原理的理解。
问题一有一个直径为1m的转盘,上面有一个固定在轴上的活动滑块。
滑块到轴的距离为0.5m。
转盘以5 rad/s的角速度逆时针旋转。
求滑块上某点P的速度。
首先,我们需要确定滑块上的点P的位置。
由于滑块到轴的距离为0.5m,而转盘的直径为1m,因此点P的位置位于滑块上与轴对称的位置,距离轴0.5m。
我们可以使用瞬心法来求解滑块上点P的速度。
瞬心法的基本原理是,在运动过程中,物体的速度等于通过瞬时转动中心与物体上的某一点所作的相对速度。
在本题中,我们可以选择转盘的轴作为瞬时转动中心。
因此,我们需要确定点P相对于转动中心的位置向量和其相对于转动中心的速度向量。
点P相对于转动中心的位置向量为[0.5, 0],即P的横坐标为0.5m,纵坐标为0,代表距离转动中心0.5m。
点P相对于转动中心的速度向量为[0, R * ω],其中R 为转盘的半径,即0.5m,ω为转盘的角速度,即5 rad/s。
代入数值计算,得到速度向量为[0, 2.5],即P点的速度大小为2.5 m/s,方向为垂直于转盘的切线方向。
问题二一个直径为0.8m的小车以2 rad/s的角速度逆时针旋转。
小车上有一根长1.2m的杆,杆上距离小车中心0.6m处有一个质量为1kg的小球。
求小球的速度大小和方向。
我们可以使用瞬心法来求解小球的速度。
同样地,选择小车的中心作为瞬时转动中心。
首先,我们需要确定小球相对于转动中心的位置向量和其相对于转动中心的速度向量。
小球相对于转动中心的位置向量为[0.6, 0],即小球距离转动中心0.6m。
小球相对于转动中心的速度向量为[0, R * ω],其中R为小车直径的一半,即0.4m,ω为小车的角速度,即2 rad/s。
机械原理习题答案第五六章
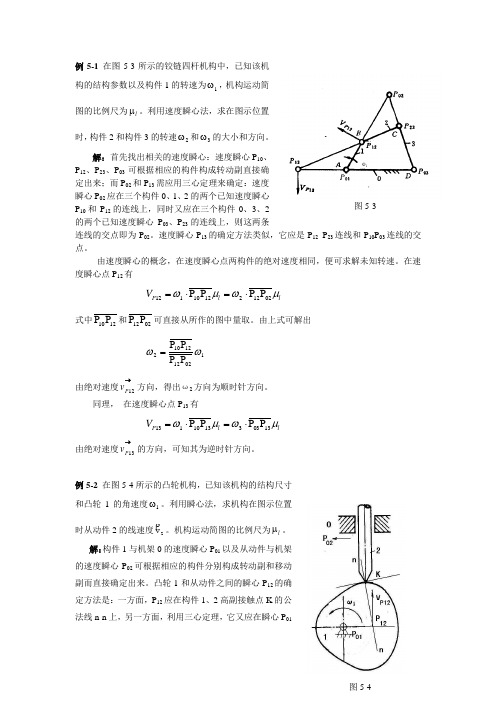
例5-1 在图5-3所示的铰链四杆机构中,已知该机构的结构参数以及构件1的转速为1ω,机构运动简图的比例尺为l μ。
利用速度瞬心法,求在图示位置时,构件2和构件3的转速2ω和3ω的大小和方向。
解:首先找出相关的速度瞬心:速度瞬心P 10、P 12、P 23、P 03可根据相应的构件构成转动副直接确定出来;而P 02和P 13需应用三心定理来确定:速度瞬心P 02应在三个构件0、1、2的两个已知速度瞬心P 10和P 12的连线上,同时又应在三个构件0、3、2的两个已知速度瞬心P 03、P 23的连线上,则这两条连线的交点即为P 02。
速度瞬心P 13的确定方法类似,它应是P 12 P 23连线和P 10P 03连线的交点。
由速度瞬心的概念,在速度瞬心点两构件的绝对速度相同,便可求解未知转速。
在速度瞬心点P 12有l l P V μωμω021*********P P P P ⋅=⋅= 式中1210P P 和0212P P 可直接从所作的图中量取。
由上式可解出1021212102P P P P ωω=由绝对速度→12P v 方向,得出ω2方向为顺时针方向。
同理, 在速度瞬心点P 13有l l P V μωμω130331310113P P P P ⋅=⋅= 由绝对速度→13P v 的方向,可知其为逆时针方向。
例5-2 在图5-4所示的凸轮机构,已知该机构的结构尺寸和凸轮1的角速度1ω。
利用瞬心法,求机构在图示位置时从动件2的线速度2v。
机构运动简图的比例尺为l μ。
解:构件1与机架0的速度瞬心P 01以及从动件与机架的速度瞬心P 02可根据相应的构件分别构成转动副和移动副而直接确定出来。
凸轮1和从动件之间的瞬心P 12的确定方法是:一方面,P 12应在构件1、2高副接触点K 的公法线n-n 上,另一方面,利用三心定理,它又应在瞬心P 01图5-4图5-3和P 02的连线上,即又应在过点P 01而垂直于从动件2与机架移动副导路的直线上。
机械原理课件瞬心例题

结论和总结
通过学习瞬心的例题和应用,我们对机械原理有了更深入的理解。瞬心是机 械系统中一个重要且复杂的问题,但它也为我们设计和优化机械系统提供了 丰富的信息。
机械Байду номын сангаас理课件瞬心例题
通过这个课件,我们来学习机械原理中的瞬心问题。了解如何计算瞬心,解 决瞬心问题,并探讨瞬心在机械系统中的应用和与平衡的关系。
题目瞬心分析
通过这个例题,我们将深入研究一个机械系统的瞬心问题。通过分析瞬心的 位置和大小,我们可以预测系统的运动和平衡状态。
计算瞬心的方法
了解瞬心的计算方法对于解决机械系统中的问题至关重要。我们将学习如何利用几何和力学原理来计算瞬心的 位置和大小。
解决瞬心问题的策略
当机械系统出现瞬心问题时,我们需要采取一些策略来解决它们。这些策略 可能涉及平衡调整、轴向调整或其他方法。
瞬心在机械系统中的应用
瞬心在机械系统中有许多重要应用。它可以帮助我们设计更稳定和高效的机械系统,提高性能和可靠性。
瞬心与平衡的关系
瞬心与机械系统的平衡有着密切的关系。深入理解瞬心的概念和计算方法可 以帮助我们更好地理解和控制机械系统的平衡状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P13∞
a)
本屏显示60秒
P23 P24
相交无穷远
3
P14∞
4
P34
1
2
求P24 (P12P14) P24
P12
(P23P34) P24 求P13 1-2-3 (P12P23) P13
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯实滚用文动档高副接触点;一般高副法线;三心定理
在图示的齿轮-连杆组合机构中,
本屏显示60秒
试用瞬心法求齿轮1和3的传动比1/ 3 。
解: 1. 绘机构运动简图
2.求瞬心P13
3.求1/ 3
1 P36 P13 3 P16 P13
求P13 1-2-3 (P12P23) P13 1-6-3 (P36P16) P13
2
P23
P12 4
P13
转动副中心;垂直移动副导轨无穷远;纯实滚用文动档高副接触点;一般高副法线;三心定理
本屏显示60秒
c)
求P24
(P12P14) P24 (P23P34) P24
P13
P14 4
3
M P23
P24
2 P12
求P13 1-2-3 (P12P23) P13
1
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯实滚用文动档高副接触点;一般高副法线;三心定理
c)
P12∞
水平方向无穷远处有P12,通过P12作竖线连接P14
该线与通过P23P34的斜线相交于倾斜方向无穷远
点
求P24 (P12P14) P24
1
2 P23 P13
(P23P34) P24
P12
3
P14∞ 无穷远处的P12和竖直线
4 P34
求P13 1-2-3 (P12P23) P13 1-4-3 (P34P14) P13
b)
P13
求P24 (P12P14) P24 (P23P34) P24
本屏显示60秒
P34 3
2 P12
4 P14∞
P24
求P13 1-2-3 (P12P23) P113
1-4-3 (P34P14) P1副接触点;一般高副法线;三心定理
本屏显示60秒
P36 5
1 P16
3
6
转动副中心;垂直移动副导轨无穷远;纯实滚用文动档高副接触点;一般高副法线;三心定理
