机械原理 瞬心及位置确定讲课ppt
合集下载
机械原理课件瞬心例题
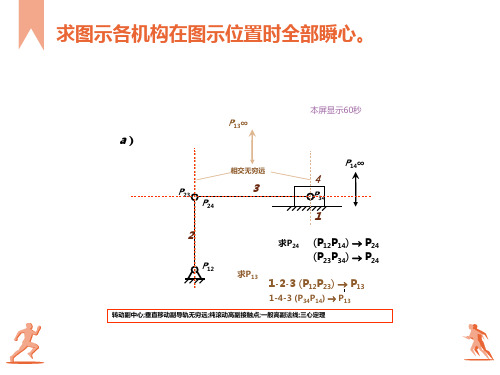
b)
P13
求P24
(P12P14) P24 (P23P34) P24
本屏显示60秒
P34 3
2
4
P12
P14∞
P24
求P13
1
1-2-3 (P12P23) P13
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
水平方向无穷远处有P12,通过P12作竖线连接P14
比1/ 3 。
解: 1. 绘机构运动简图 2.求瞬心P13 3.求1/ 3
1 P36 P13 3 P16 P13
求P13
1-2-3 (P12P23) P13
1-6-3 (P36P16) P13
2
P23
P12 4
P13
P36 5
ห้องสมุดไป่ตู้
3
6
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
求P24
(P12P14) P24
(P23P34) P24
c)
P13
M
P23
2
P12
P14
4
3
P24
求P13 1-2-3 (P12P23) P13
1
1-4-3 (P34P14) P13
转动副中心;垂直移动副导轨无穷远;纯滚动高副接触点;一般高副法线;三心定理
本屏显示60秒
在图示的齿轮-连杆组合机构中, 试用瞬心法求齿轮1和3的传动
该线与通过P23P34的斜线相交于倾斜方向无穷远点
P12∞
c)
求P24
(P12P14) P24
机械原理第三章优秀课件 (2)

机械原理课件第三章
§3-2 用速度瞬心法作机构的速度分析
一、速度瞬心及其位置的确定 1、速度瞬心的定义
A
vA2A1 B
若构件2相对固定的构件1运动,可求得 瞬心P12,有:
vB1B2
P12
பைடு நூலகம்
2
v v
P1
P2
0,
vP2P1 vP2 vP1 0
1
vP1 vP2 0,但 vP2P1 vP2 vP1 0
vCvP24 2P 1P 224 L
P12
1
vC
P13
C P34
4
利用瞬心P13---构件1和3的等速重合点。
P14
构件1为机架,则vP13=0, P13为构件3的瞬时转动中心,则有
3
vC P34P13L
vD3D1P3L
§3-3 矢量方程图解法(相对运动图解法)
一、同一构件上两点间的速度和加速度
2
且为绝对瞬心。
若构件1不固定,
P12
则P12为相对瞬心。
1
§3-2 用速度瞬心法作机构的速度分析
2、瞬心数目
若机构中有N个构件,则: ∵每两个构件就有一个瞬心 ∴根据排列组合,瞬心有 :
K N(N1) 2
P13
1 23
P12 P23
构件数 4 瞬心数 6
56
8
10 15 28
§3-2 用速度瞬心法作机构的速度分析
③另外2个用三心定理求出。
P13
P12 P23
1 2 3 P14 P34
PP2244
3 P23
P23 2
1
P13
“下标同号消去 P12 P23 法P”13在P12 P23的连线上。
§3-2 用速度瞬心法作机构的速度分析
一、速度瞬心及其位置的确定 1、速度瞬心的定义
A
vA2A1 B
若构件2相对固定的构件1运动,可求得 瞬心P12,有:
vB1B2
P12
பைடு நூலகம்
2
v v
P1
P2
0,
vP2P1 vP2 vP1 0
1
vP1 vP2 0,但 vP2P1 vP2 vP1 0
vCvP24 2P 1P 224 L
P12
1
vC
P13
C P34
4
利用瞬心P13---构件1和3的等速重合点。
P14
构件1为机架,则vP13=0, P13为构件3的瞬时转动中心,则有
3
vC P34P13L
vD3D1P3L
§3-3 矢量方程图解法(相对运动图解法)
一、同一构件上两点间的速度和加速度
2
且为绝对瞬心。
若构件1不固定,
P12
则P12为相对瞬心。
1
§3-2 用速度瞬心法作机构的速度分析
2、瞬心数目
若机构中有N个构件,则: ∵每两个构件就有一个瞬心 ∴根据排列组合,瞬心有 :
K N(N1) 2
P13
1 23
P12 P23
构件数 4 瞬心数 6
56
8
10 15 28
§3-2 用速度瞬心法作机构的速度分析
③另外2个用三心定理求出。
P13
P12 P23
1 2 3 P14 P34
PP2244
3 P23
P23 2
1
P13
“下标同号消去 P12 P23 法P”13在P12 P23的连线上。
机械原理PPT

2
D
2
p'(a') d'
3
c'
1
A
1
x
6
C
x
n2' b'
n t a C a B a CB a CB
方向: 沿xx 大小: ? √ √ C→ B 22lAB ⊥CB ?
用加速度影像法求出d'点 作Δb'c'd' ~ ΔBCD aD= μa p'd'
t aCB n 'c ' a 2 2 l BC l BC
课堂练习
图示机构,已知各构件尺寸和ω1,用瞬心法求v5 解题思路:
1
求3 求v5
C D
3
E
4
A
1 2
ω1
5 6
F
利用P13
利用P35
B
机械原理 —— 平面机构的运动分析
P15
求P13
求P35
P56→∞
求P15
v5 v P15 1 P16 P15 l
P35
E P 34
3 4
1 AP13 3 DP13
2 P13 vP13 B 1 AP
1 P13P14L = 3 P13P34 L
4
P34
D
P13 P14 3 1 逆时针 P13 P34
机械原理 —— 平面机构的运动分析
3 平面高副机构
3 2 1 1 1 2 3
P23
vP12 P12 P23
P13
P12 vP12
P23
P13
取μa= aB/ p'b'作加速度图 aC= μa p'c'
平面机构速度分析的瞬心法机械原理
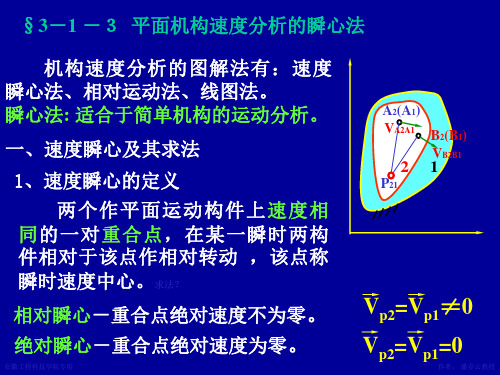
一、速度瞬心及其求法
1、速度瞬心的定义
两个作平面运动构件上速度相 同的一对重合点,在某一瞬时两构 件相对于该点作相对转动 ,该点称 瞬时速度中心。求法?
相对瞬心-重合点绝对速度不为零。 绝对瞬心-重合点绝对速度为零。
安徽工程科技学院专用
A (A ) 作者:潘存2 云教1授 VA2A1
2
P21
B2(B1)
56
8
10 15 28
安徽工程科技学院专用
作者: 潘存云教授
3、机构瞬心位置的确定
(1)直接观察法 (利用定义) 适用于求通过运动副直接相联的两构件瞬心位置。
P12
1
2
P12 ∞
1
n
1
2
2
P12 t
1t 2 V12
n
(2有三个瞬 心,且它们位于同一条直线上。此法特别适用 于两构件不直接相联的场合。
如右图所示的三个构件组成的一个机构若p23不与p12p13共线同一直线而在任意一点c则c点在构件2和构件3上的绝对速度的方向不可能相3上的绝对速度的方向不可能相同即绝对速度不相等
§3-1 -3 平面机构速度分析的瞬心法
机构速度分析的图解法有:速度 瞬心法、相对运动法、线图法。 瞬心法: 适合于简单机构的运动分析。
安徽工程科技学院专用
作者: 潘存云教授
用反证法证明:
如右图所示的三个构件组成 的一个机构,若P23不与P12、 P13共线(同一直线),而在任 意一点C,则C点在构件2和构件 3上的绝对速度的方向不可能相 同,即绝对速度不相等。二只有 C点在P12、P13连成的直线上, 才能使绝对速度的方向相同。
安徽工程科技学院专用
作者: 潘存云教授
VB2B1
1、速度瞬心的定义
两个作平面运动构件上速度相 同的一对重合点,在某一瞬时两构 件相对于该点作相对转动 ,该点称 瞬时速度中心。求法?
相对瞬心-重合点绝对速度不为零。 绝对瞬心-重合点绝对速度为零。
安徽工程科技学院专用
A (A ) 作者:潘存2 云教1授 VA2A1
2
P21
B2(B1)
56
8
10 15 28
安徽工程科技学院专用
作者: 潘存云教授
3、机构瞬心位置的确定
(1)直接观察法 (利用定义) 适用于求通过运动副直接相联的两构件瞬心位置。
P12
1
2
P12 ∞
1
n
1
2
2
P12 t
1t 2 V12
n
(2有三个瞬 心,且它们位于同一条直线上。此法特别适用 于两构件不直接相联的场合。
如右图所示的三个构件组成的一个机构若p23不与p12p13共线同一直线而在任意一点c则c点在构件2和构件3上的绝对速度的方向不可能相3上的绝对速度的方向不可能相同即绝对速度不相等
§3-1 -3 平面机构速度分析的瞬心法
机构速度分析的图解法有:速度 瞬心法、相对运动法、线图法。 瞬心法: 适合于简单机构的运动分析。
安徽工程科技学院专用
作者: 潘存云教授
用反证法证明:
如右图所示的三个构件组成 的一个机构,若P23不与P12、 P13共线(同一直线),而在任 意一点C,则C点在构件2和构件 3上的绝对速度的方向不可能相 同,即绝对速度不相等。二只有 C点在P12、P13连成的直线上, 才能使绝对速度的方向相同。
安徽工程科技学院专用
作者: 潘存云教授
VB2B1
机械原理-速度分析-PPT

已知:曲柄导杆机构,曲柄的角速度为ω1(常数) 求:导杆3的角速度 3 。
2
1 A B
例2
分
析
1
3 C
取构件3为动参考系,则构件2的运动=
构件3的牵连运动+相对于构件3的相对运动
2005---2006第一学期
1
vCB 的下角标与 bc 方向相反。
速度影像只适用同一构件,△BCD与△bcd为相
第三章
平面机构速度分析
2005---2006第一学期
第一节 速度瞬心法 进行平面机构的速度分析
2005---2006第一学期
• 一、速度瞬心的概念
Aபைடு நூலகம்
B
vA
vB
1 2
1
定义:做平面运动的两构件上其 瞬时速度相等的重合点Pij 。
P 12
2
分类: 绝对速度瞬心:速度瞬心的绝对速度为零。 相对速度瞬心:速度瞬心的绝对速度不为零。
2005---2006第一学期
利用两构件同速点求解。
求构件上速度为零的点
全部同速点中,凡是其右下角数码中含有 固定件的,其速度均为零,因此k个构件组成 的机构中,速度为零的点共有k-1个。
2005---2006第一学期
第二节 用相对运动图解 法作平面机构的速度分析
2005---2006第一学期
理论基础:理论力学的刚体平面运动和点的复合运动。
N ( N 1) 2
3
瞬心数目:构件数为K,组成的瞬心数为K,K =
2005---2006第一学期
• 二、瞬心位置的确定
直接成副的瞬心位置
1
两构件构成转动副——铰链回转中心
2005---2006第一学期
2
1 A B
例2
分
析
1
3 C
取构件3为动参考系,则构件2的运动=
构件3的牵连运动+相对于构件3的相对运动
2005---2006第一学期
1
vCB 的下角标与 bc 方向相反。
速度影像只适用同一构件,△BCD与△bcd为相
第三章
平面机构速度分析
2005---2006第一学期
第一节 速度瞬心法 进行平面机构的速度分析
2005---2006第一学期
• 一、速度瞬心的概念
Aபைடு நூலகம்
B
vA
vB
1 2
1
定义:做平面运动的两构件上其 瞬时速度相等的重合点Pij 。
P 12
2
分类: 绝对速度瞬心:速度瞬心的绝对速度为零。 相对速度瞬心:速度瞬心的绝对速度不为零。
2005---2006第一学期
利用两构件同速点求解。
求构件上速度为零的点
全部同速点中,凡是其右下角数码中含有 固定件的,其速度均为零,因此k个构件组成 的机构中,速度为零的点共有k-1个。
2005---2006第一学期
第二节 用相对运动图解 法作平面机构的速度分析
2005---2006第一学期
理论基础:理论力学的刚体平面运动和点的复合运动。
N ( N 1) 2
3
瞬心数目:构件数为K,组成的瞬心数为K,K =
2005---2006第一学期
• 二、瞬心位置的确定
直接成副的瞬心位置
1
两构件构成转动副——铰链回转中心
2005---2006第一学期
3机械原理课件

α3
=
a
t CB
l BC
= n ′3 c ′μ a BC μ l
α4
=
a
t CD
l CD
= n 4′ c ′μ a CD μ l
3. 加速度分析(续) e3(e5)
(4) 求aE6和α6
A
2 B
ω2
ω 3
a3
x 5
n4'
c' n6'
n3' b'
p' (a'、d'、f ')
e6 b
c D ω4
3
C
α4
ω 2 = P14 P 24
3
ω4
P12 P 24
ω 2 ω 4 称为机构传动比 且等于该两构件绝对瞬心
P23
至其相对瞬心距离的反比
2
P12
ω2
1
P24
P13 返回
P34 4
ω4 P14
速度瞬心法应用例题分析二
返回
如图所示的带有一移动副的平面四杆机构中, 已知原动件2 以角速度ω2等速度转动, 现需确定机构在图示位置时从动件 4的速度v4。
?
方向:C→D ⊥CD √ √ ∥AB
A
a = 2ω v 4 k C 2C1
1 C 2C1
科氏加速度方向是将vC2C1沿牵 连角速度ω1转过90o的方向。
四、典型例题分析
如图所示为一偏心轮机构。设已知机构各构件的尺寸, 并知原动件2以角速度ω2等速度转动。现需求机构在图示位 置时,滑块5移动的速度vE、加速度aE及构件3、4、6的角速 度ω3、ω4、ω6和角加速度α3、a4、α6。
x
ω3 4 x
机械原理第三章3-8速度瞬心法培训课件

正确应用瞬时心法是至关重要的。我们将介绍一些使用瞬时心法的实际步骤和注意事项,以确 保准确分析和解决机械系统速度相关的问题。
瞬时心法在机械工程中的重要 性和作用
瞬时心法在机械工程中扮演着重要角色。它不仅帮助我们理解和优化机械运 动,还可以用于设计和改进各种机械系统。了解瞬时心法的重要性将使您成 为卓越的机械工程师。
机械原理第三章3-8速度 瞬心法培训课件
欢迎来到机械原理第三章培训课件!本课程将深入介绍瞬时心法的概念、原 理、应用案例和步骤,并探讨其在机械工程中的重要性和未来发展方向。
瞬时心法的概念与原理
瞬时心法是一种基于瞬时速度和运动属性的分析方法,可用于解决机械系统中的速度相关问题。它通过考虑系 统中每个点的速度和方向,帮助我们更好地理解运动轨迹和动力学特性。
瞬时心法的基本公式与计算方 法
瞬时心法的核心公式即速度瞬心公式,可以通过计算速度和位置矢量之间的 叉积来确定瞬时心的位置。同时,我们将介绍一些常用的计算方法和工具, 以便准确地应用和计算。
瞬时心法的应用案例分析
我们将通过一些实际案例来演示瞬时心法的应用。这些案例将涉及各种机械 系统,例如连杆机构、齿轮传动和曲柄机构。通过分析这些案例,我们将展 示瞬时心法在解决实际工程问题中的有效性。
瞬时心法的发展趋势与前景展 望
随着科技的进步和工程需求的变化,瞬时心法也在不断发展和演进。我们将 探讨当前的发展趋势,并展望瞬时心法在未来的应用和创新领域,为您提供 关于瞬时心法的未来前景的洞察。
总结和结论
通过学习本课程,您将全面了解瞬时心法的概念、原理和应用。我们希望本课程能够帮助您在机械工程领域取 得更大的成就,并为您的职业发展提供有力的支持。
瞬心位置的确定

接相
1
联
P12
纯滚动
∞ ∞
2 P12
1
绝对瞬心
P12
v12
1
2
n
2
t
1
n
t
非纯滚动
你能证明吗?
两构
P14→∞
件运
动副 直接
P23
相联
瞬
心
P12
2
位
3
4
P34
置
的
确
1
定
两构 件非 运动
N n(n 1) 4 (4 1) 6
2
2
副直 接相
P12、P23、P34、P14、P13、P24
联
1
P24
P12
P13
P34 4 P14
消元法
P12、P23、P34、P14、P13、P24
P13
3
P34
P23
4
2
1
P24
P12
P14
小结
瞬心位置求解的步骤:
1)求出瞬心数目 N n(n 1) 2
2)确定直接联接构件的瞬心位置
3)用三心定理求非直接联接构件的瞬心位置 枚举法用于构件数较少的机构,构件较多用点元法求解。
如何求?
两构
P14→∞
件运
动副 直接
P23
相联
瞬心P12Fra bibliotek2位
3
4
P34
置
的
确
1
定
两构 件非 运动
N n(n 1) 4 (4 1) 6
2
2
副直 接相
P12、P23、P34、P14、P13、P24
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
构件1、2之间用 P12 表示
精选课件
5
位置确定—— ① 由瞬心定义确定
❖两构件组成纯滚动高副 接触点就是其瞬心
❖ 两构件组成滚动兼滑动高副
瞬心在接触点处两高副元素的 公法线上。
精选课件
6
位例置:确定—图—示铰②链借四助杆三机心构定的理瞬确心定
❖三心定理:
作平面运动的三个构件的三个
瞬心位于同一直线上。
3
4
P34
P13
➢同理,两直线P12P14 和P23P34的交点就是P24 。
精选课件
8
谢谢观看
精选课件
9
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
机械原理
瞬心及其位置确定
精选课件
1
瞬心的概念
瞬心
瞬
心
的
数目
概
念
位置
精选课件
2
瞬心
瞬心就是两构件上瞬时速度相同的重合点(即 等速重合点)。
精选课件
3
数目
精选课件
4
位置确定—— ① 由瞬心定义确定
❖两构件组成转动副 转动副的中心就是其瞬心;
❖两构件组成移动副 其瞬心在垂直于导路 方向的无穷远处;
B
P121A Fra bibliotek14❖ 瞬心P12、P23、P34、P14的位置可
直观地确定,标在图中。
2 P23
C
3
4
D
P34
精选课件
7
瞬心P13、P24的位置需用三心定理确定
P24
➢ P24与P12、P14在同一直
线上 P24又与P23、P34 在同一直
P12
12
P23
线上 故两直线P12P14 和P23P34的 P14 交点就是P24。
