2020年湖北省仙桃市、潜江市、天门市、江汉油田中考数学试卷【含答案;word版本试题;可编辑】
2020年湖北省潜江天门仙桃江汉油田中考数学试卷
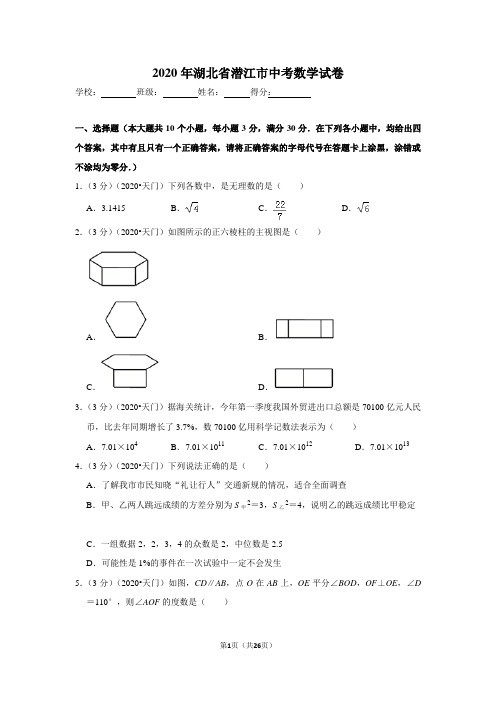
2020年湖北省潜江市中考数学试卷学校:班级:姓名:得分:一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)1.(3分)(2020•天门)下列各数中,是无理数的是()A.3.1415B.C.D.2.(3分)(2020•天门)如图所示的正六棱柱的主视图是()A.B.C.D.3.(3分)(2020•天门)据海关统计,今年第一季度我国外贸进出口总额是70100亿元人民币,比去年同期增长了3.7%,数70100亿用科学记数法表示为()A.7.01×104B.7.01×1011 C.7.01×1012 D.7.01×1013 4.(3分)(2020•天门)下列说法正确的是()A.了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查B.甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定C.一组数据2,2,3,4的众数是2,中位数是2.5D.可能性是1%的事件在一次试验中一定不会发生5.(3分)(2020•天门)如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D =110°,则∠AOF的度数是()A.20°B.25°C.30°D.35°6.(3分)(2020•天门)不等式组的解集在数轴上表示正确的是()A.B.C.D.7.(3分)(2020•天门)若方程x2﹣2x﹣4=0的两个实数根为α,β,则α2+β2的值为()A.12B.10C.4D.﹣48.(3分)(2020•天门)把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有()A.3种B.4种C.5种D.9种9.(3分)(2020•天门)反比例函数y=﹣,下列说法不正确的是()A.图象经过点(1,﹣3)B.图象位于第二、四象限C.图象关于直线y=x对称D.y随x的增大而增大10.(3分)(2020•天门)如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC,直线CD交BA的延长线于点E,连接BD.下列结论:①CD是⊙O的切线;②CO⊥DB;③△EDA∽△EBD;④ED•BC=BO•BE.其中正确结论的个数有()A.4个B.3个C.2个D.1个二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.)11.(3分)(2020•天门)分解因式:x4﹣4x2=.12.(3分)(2020•天门)75°的圆心角所对的弧长是 2.5πcm,则此弧所在圆的半径是cm.13.(3分)(2020•天门)矩形的周长等于40,则此矩形面积的最大值是.14.(3分)(2020•天门)一个不透明的口袋中有四个完全相同的小球,其上分别标有数字1,2,4,8.随机摸取一个小球后不放回,再随机摸取一个小球,则两次取出的小球上数字之积等于8的概率是.15.(3分)(2020•天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6m,则旗杆AB的高度为m.16.(3分)(2020•天门)如图,在平面直角坐标系中,四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,点A1,A2,A3,…都在x轴上,点C1,C2,C3,…都在直线y=x+上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是.三、解答题(本大题共8个小题,满分72分.)17.(12分)(2020•天门)(1)计算:(﹣2)2﹣|﹣3|+×+(﹣6)0;(2)解分式方程:=.18.(6分)(2020•天门)请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.19.(7分)(2020•天门)为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.(1)填空:样本容量为,a=;(2)把频数分布直方图补充完整;(3)若从该地随机抽取1名学生,估计这名学生身高低于160cm的概率.20.(8分)(2020•天门)某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为x千克,付款金额为y元.(1)求y关于x的函数解析式;(2)某农户一次购买玉米种子30千克,需付款多少元?21.(8分)(2020•天门)如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:(1)AE⊥BF;(2)四边形BEGF是平行四边形.22.(10分)(2020•天门)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O (0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.(1)直接写出y关于t的函数解析式及t的取值范围:;(2)当PQ=3时,求t的值;(3)连接OB交PQ于点D,若双曲线y=(k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.23.(10分)(2020•天门)已知△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,连接DB,DC.(1)如图①,当∠BAC=120°时,请直接写出线段AB,AC,AD之间满足的等量关系式:;(2)如图②,当∠BAC=90°时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求的值.24.(11分)(2020•天门)在平面直角坐标系中,已知抛物线C:y=ax2+2x﹣1(a≠0)和直线l:y=kx+b,点A(﹣3,﹣3),B(1,﹣1)均在直线l上.(1)若抛物线C与直线l有交点,求a的取值范围;(2)当a=﹣1,二次函数y=ax2+2x﹣1的自变量x满足m≤x≤m+2时,函数y的最大值为﹣4,求m的值;(3)若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.2020年湖北省潜江市中考数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)1.(3分)(2020•天门)下列各数中,是无理数的是()A.3.1415B.C.D.【分析】根据无理数的定义:无限不循环小数进行判断,=2是有理数;【解答】解:=2是有理数,是无理数,故选:D.2.(3分)(2020•天门)如图所示的正六棱柱的主视图是()A.B.C.D.【分析】主视图是从正面看所得到的图形即可,可根据正六棱柱的特点作答.【解答】解:正六棱柱的主视图如图所示:故选:B.3.(3分)(2020•天门)据海关统计,今年第一季度我国外贸进出口总额是70100亿元人民币,比去年同期增长了3.7%,数70100亿用科学记数法表示为()A.7.01×104B.7.01×1011 C.7.01×1012 D.7.01×1013【分析】把一个很大的数写成a×10n的形式.【解答】解:70100亿=7.01×1012.故选:C.4.(3分)(2020•天门)下列说法正确的是()A.了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查B.甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定C.一组数据2,2,3,4的众数是2,中位数是2.5D.可能性是1%的事件在一次试验中一定不会发生【分析】全面调查与抽样调查的优缺点:①全面调查收集的到数据全面、准确,但一般花费多、耗时长,而且某些调查不宜用全面调查.②抽样调查具有花费少、省时的特点,但抽取的样本是否具有代表性,直接关系到对总体估计的准确程度.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.一组数据中出现次数最多的数据叫做众数.【解答】解:A.了解我市市民知晓“礼让行人”交通新规的情况,适合抽样调查,A错误;B.甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明甲的跳远成绩比乙稳定,B错误;C.一组数据2,2,3,4的众数是2,中位数是2.5,正确;D.可能性是1%的事件在一次试验中可能会发生,D错误.故选:C.5.(3分)(2020•天门)如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D =110°,则∠AOF的度数是()A.20°B.25°C.30°D.35°【分析】根据平行线的性质解答即可.【解答】解:∵CD∥AB,∴∠AOD+∠D=180°,∴∠AOD=70°,∴∠DOB=110°,∵OE平分∠BOD,∴∠DOE=55°,∵OF⊥OE,∴∠FOE=90°,∴∠DOF=90°﹣55°=35°,∴∠AOF=70°﹣35°=35°,故选:D.6.(3分)(2020•天门)不等式组的解集在数轴上表示正确的是()A.B.C.D.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式x﹣1>0得x>1,解不等式5﹣2x≥1得x≤2,则不等式组的解集为1<x≤2,故选:C.7.(3分)(2020•天门)若方程x2﹣2x﹣4=0的两个实数根为α,β,则α2+β2的值为()A.12B.10C.4D.﹣4【分析】根据根与系数的关系可得α+β=2,αβ=﹣4,再利用完全平方公式变形α2+β2=(α+β)2﹣2αβ,代入即可求解;【解答】解:∵方程x2﹣2x﹣4=0的两个实数根为α,β,∴α+β=2,αβ=﹣4,∴α2+β2=(α+β)2﹣2αβ=4+8=12;故选:A.8.(3分)(2020•天门)把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有()A.3种B.4种C.5种D.9种【分析】可列二元一次方程解决这个问题.【解答】解:设2m的钢管b根,根据题意得:a+2b=9,∵a、b均为整数,∴,,,.故选:B.9.(3分)(2020•天门)反比例函数y=﹣,下列说法不正确的是()A.图象经过点(1,﹣3)B.图象位于第二、四象限C.图象关于直线y=x对称D.y随x的增大而增大【分析】通过反比例图象上的点的坐标特征,可对A选项做出判断;通过反比例函数图象和性质、增减性、对称性可对其它选项做出判断,得出答案.【解答】解:由点(1,﹣3)的坐标满足反比例函数y=﹣,故A是正确的;由k=﹣3<0,双曲线位于二、四象限,故B也是正确的;由反比例函数的对称性,可知反比例函数y=﹣关于y=x对称是正确的,故C也是正确的,由反比例函数的性质,k<0,在每个象限内,y随x的增大而增大,不在同一象限,不具有此性质,故D是不正确的,故选:D.10.(3分)(2020•天门)如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC,直线CD交BA的延长线于点E,连接BD.下列结论:①CD是⊙O的切线;②CO⊥DB;③△EDA∽△EBD;④ED•BC=BO•BE.其中正确结论的个数有()A.4个B.3个C.2个D.1个【分析】由切线的性质得∠CBO=90°,首先连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线,根据全等三角形的性质得到CD=CB,根据线段垂直平分线的判定定理得到即CO⊥DB,故②正确;根据余角的性质得到∠ADE=∠BDO,等量代换得到∠EDA=∠DBE,根据相似三角形的判定定理得到△EDA∽△EBD,故③正确;根据相似三角形的性质得到,于是得到ED•BC=BO•BE,故④正确.【解答】解:连结DO.∵AB为⊙O的直径,BC为⊙O的切线,∴∠CBO=90°,∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD.又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠COB.在△COD和△COB中,,∴△COD≌△COB(SAS),∴∠CDO=∠CBO=90°.又∵点D在⊙O上,∴CD是⊙O的切线;故①正确,∵△COD≌△COB,∴CD=CB,∵OD=OB,∴CO垂直平分DB,即CO⊥DB,故②正确;∵AB为⊙O的直径,DC为⊙O的切线,∴∠EDO=∠ADB=90°,∴∠EDA+∠ADO=∠BDO+∠ADO=90°,∴∠ADE=∠BDO,∵OD=OB,∴∠ODB=∠OBD,∴∠EDA=∠DBE,∵∠E=∠E,∴△EDA∽△EBD,故③正确;∵∠EDO=∠EBC=90°,∠E=∠E,∴△EOD∽△ECB,∴,∵OD=OB,∴ED•BC=BO•BE,故④正确;故选:A.二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.)11.(3分)(2020•天门)分解因式:x4﹣4x2=x2(x+2)(x﹣2).【分析】先提取公因式再利用平方差公式进行分解,即x4﹣4x2=x2(x2﹣4)=x2(x+2)(x﹣2);【解答】解:x4﹣4x2=x2(x2﹣4)=x2(x+2)(x﹣2);故答案为x2(x+2)(x﹣2);12.(3分)(2020•天门)75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是6 cm.【分析】由弧长公式:l=计算.【解答】解:由题意得:圆的半径R=180×2.5π÷(75π)=6cm.故本题答案为:6.13.(3分)(2020•天门)矩形的周长等于40,则此矩形面积的最大值是100.【分析】设矩形的宽为x,则长为(20﹣x),S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,当x=10时,S最大值为100.【解答】解:设矩形的宽为x,则长为(20﹣x),S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,当x=10时,S最大值为100.故答案为100.14.(3分)(2020•天门)一个不透明的口袋中有四个完全相同的小球,其上分别标有数字1,2,4,8.随机摸取一个小球后不放回,再随机摸取一个小球,则两次取出的小球上数字之积等于8的概率是.【分析】列表将所有等可能的结果列举出来,然后利用概率公式求解即可.【解答】解:列表如下1248 12482281644832881632由表知,共有12种等可能结果,其中两次取出的小球上数字之积等于8的有4种结果,所以两次取出的小球上数字之积等于8的概率为=,故答案为:.15.(3分)(2020•天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6m,则旗杆AB的高度为14.4m.【分析】作DE⊥AB于E,则∠AED=90°,四边形BCDE是矩形,得出BE=CD=9.6m,∠CDE=∠DEA=90°,求出∠ADC=120°,证出∠CAD=30°=∠ACD,得出AD=CD=9.6m,在Rt△ADE中,由直角三角形的性质得出AE=AD=4.8m,即可得出答案.【解答】解:作DE⊥AB于E,如图所示:则∠AED=90°,四边形BCDE是矩形,∴BE=CD=9.6m,∠CDE=∠DEA=90°,∴∠ADC=90°+30°=120°,∵∠ACB=60°,∴∠ACD=30°,∴∠CAD=30°=∠ACD,∴AD=CD=9.6m,在Rt△ADE中,∠ADE=30°,∴AE=AD=4.8m,∴AB=AE+BE=4.8m+9.6m=14.4m;故答案为:14.4.16.(3分)(2020•天门)如图,在平面直角坐标系中,四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,点A1,A2,A3,…都在x轴上,点C1,C2,C3,…都在直线y=x+上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是(47,32).【分析】根据菱形的边长求得A1、A2、A3…的坐标然后分别表示出C1、C2、C3…的坐标找出规律进而求得C6的坐标.【解答】解:∵OA1=1,∴OC1=1,∴∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,∴C1的纵坐标为:sin60°•OC1=,横坐标为cos60°•OC1=,∴C1(,),∵四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,∴A1C2=2,A2C3=4,A3C4=8,…,∴C2的纵坐标为:sin60°•A1C2=,代入y=x+求得横坐标为2,∴C2(,2,),C3的纵坐标为:sin60°•A2C3=2,代入y=x+求得横坐标为5,∴C3(5,4),∴C4(11,8),C5(23,16),∴C6(47,32);故答案为(47,32).三、解答题(本大题共8个小题,满分72分.)17.(12分)(2020•天门)(1)计算:(﹣2)2﹣|﹣3|+×+(﹣6)0;(2)解分式方程:=.【分析】(1)先计算乘方、取绝对值符号、计算二次根式的乘法及零指数幂,再计算加减可得;(2)去分母化分式方程为整式方程,解之求得x的值,再检验即可得.【解答】解:(1)原式=4﹣3+4+1=6;(2)两边都乘以(x+1)(x﹣1),得:2(x+1)=5,解得:x=,检验:当x=时,(x+1)(x﹣1)=≠0,∴原分式方程的解为x=.18.(6分)(2020•天门)请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.【分析】(1)连接AC,AC所在直线即为对称轴m.(2)延长BA,CD交于一点,连接AC,BC交于一点,连接两点获得垂直平分线n.【解答】解:(1)如图①,直线m即为所求(2)如图②,直线n即为所求19.(7分)(2020•天门)为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.(1)填空:样本容量为100,a=30;(2)把频数分布直方图补充完整;(3)若从该地随机抽取1名学生,估计这名学生身高低于160cm的概率.【分析】(1)用A组的频数除以它所占的百分比得到样本容量,然后计算B组所占的百分比得到a的值;(2)利用B组的频数为30补全频数分布直方图;(3)计算出样本中身高低于160cm的频率,然后利用样本估计总体和利用频率估计概率求解.【解答】解:(1)15÷=100,所以样本容量为100;B组的人数为100﹣15﹣35﹣15﹣5=30,所以a%=×100%=30%,则a=30;故答案为100,30;(2)补全频数分布直方图为:(3)样本中身高低于160cm的人数为15+30=45,样本中身高低于160cm的频率为=0.45,所以估计从该地随机抽取1名学生,估计这名学生身高低于160cm的概率为0.45.20.(8分)(2020•天门)某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为x千克,付款金额为y元.(1)求y关于x的函数解析式;(2)某农户一次购买玉米种子30千克,需付款多少元?【分析】(1)根据题意,得①当0≤x≤5时,y=20x;②当x>5,y=20×0.8(x﹣5)+20×5=16x+20;(2)把x=30代入y=16x+20,即可求解;【解答】解:(1)根据题意,得①当0≤x≤5时,y=20x;②当x>5,y=20×0.8(x﹣5)+20×5=16x+20;(2)把x=30代入y=16x+20,∴y=16×30+20=500;∴一次购买玉米种子30千克,需付款500元;21.(8分)(2020•天门)如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:(1)AE⊥BF;(2)四边形BEGF是平行四边形.【分析】(1)由SAS证明△ABE≌△BCF得出AE=BF,∠BAE=∠CBF,由平行线的性质得出∠CBF=∠CEG,证出AE⊥EG,即可得出结论;(2)延长AB至点P,使BP=BE,连接EP,则AP=CE,∠EBP=90°,证明△APE ≌△ECG得出AE=EG,证出EG=BF,即可得出结论.【解答】证明:(1)∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠BCD=90°,∴∠ABE=∠BCF=90°,在△ABE和△BCF中,,∴△ABE≌△BCF(SAS),∴AE=BF,∠BAE=∠CBF,∵EG∥BF,∴∠CBF=∠CEG,∵∠BAE+∠BEA=90°,∴∠CEG+∠BEA=90°,∴AE⊥EG,∴AE⊥BF;(2)延长AB至点P,使BP=BE,连接EP,如图所示:则AP=CE,∠EBP=90°,∴∠P=45°,∵CG为正方形ABCD外角的平分线,∴∠ECG=45°,∴∠P=∠ECG,由(1)得∠BAE=∠CEG,在△APE和△ECG中,,∴△APE≌△ECG(ASA),∴AE=EG,∵AE=BF,∴EG=BF,∵EG∥BF,∴四边形BEGF是平行四边形.22.(10分)(2020•天门)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O (0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.(1)直接写出y关于t的函数解析式及t的取值范围:y=25t2﹣80t+100(0≤t≤4);(2)当PQ=3时,求t的值;(3)连接OB交PQ于点D,若双曲线y=(k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.【分析】(1)过点P作PE⊥BC于点E,由点P,Q的出发点、速度及方向可找出当运动时间为t秒时点P,Q的坐标,进而可得出PE,EQ的长,再利用勾股定理即可求出y 关于t的函数解析式(由时间=路程÷速度可得出t的取值范围);(2)将PQ=3代入(1)的结论中可得出关于t的一元二次方程,解之即可得出结论;(3)连接OB,交PQ于点D,过点D作DF⊥OA于点F,利用勾股定理可求出OB的长,由BQ∥OP可得出△BDQ∽△ODP,利用相似三角形的性质结合OB=10可求出OD =6,由CB∥OA可得出∠DOF=∠OBC,在Rt△OBC中可求出sin∠OBC及cos∠OBC 的值,由OF=OD•cos∠OBC,DF=OD•sin∠OBC可求出点D的坐标,再利用反比例函数图象上点的坐标特征即可求出k值,此题得解.【解答】解:(1)过点P作PE⊥BC于点E,如图1所示.当运动时间为t秒时(0≤t≤4)时,点P的坐标为(3t,0),点Q的坐标为(8﹣2t,6),∴PE=6,EQ=|8﹣2t﹣3t|=|8﹣5t|,∴PQ2=PE2+EQ2=62+|8﹣5t|2=25t2﹣80t+100,∴y=25t2﹣80t+100(0≤t≤4).故答案为:y=25t2﹣80t+100(0≤t≤4).(2)当PQ=3时,25t2﹣80t+100=(3)2,整理,得:5t2﹣16t+11=0,解得:t1=1,t2=.(3)经过点D的双曲线y=(k≠0)的k值不变.连接OB,交PQ于点D,过点D作DF⊥OA于点F,如图2所示.∵OC=6,BC=8,∴OB==10.∵BQ∥OP,∴△BDQ∽△ODP,∴===,∴OD=6.∵CB∥OA,∴∠DOF=∠OBC.在Rt△OBC中,sin∠OBC===,cos∠OBC===,∴OF=OD•cos∠OBC=6×=,DF=OD•sin∠OBC=6×=,∴点D的坐标为(,),∴经过点D的双曲线y=(k≠0)的k值为×=.23.(10分)(2020•天门)已知△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,连接DB,DC.(1)如图①,当∠BAC=120°时,请直接写出线段AB,AC,AD之间满足的等量关系式:AB+AC=AD;(2)如图②,当∠BAC=90°时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求的值.【分析】(1)在AD上截取AE=AB,连接BE,由条件可知△ABE和△BCD都是等边三角形,可证明△BED≌△BAC,可得DE=AC,则AB+AC=AD;(2)延长AB至点M,使BM=AC,连接DM,证明△MBD≌△ACD,可得MD=AD,证得AB+AC=;(3)延长AB至点N,使BN=AC,连接DN,证明△NBD≌△ACD,可得ND=AD,∠N=∠CAD,证△NAD∽△CBD,可得,可由AN=AB+AC,求出的值.【解答】解:(1)如图①在AD上截取AE=AB,连接BE,∵∠BAC=120°,∠BAC的平分线交⊙O于点D,∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,∴△ABE和△BCD都是等边三角形,∴∠DBE=∠ABC,AB=BE,BC=BD,∴△BED≌△BAC(SAS),∴DE=AC,∴AD=AE+DE=AB+AC;故答案为:AB+AC=AD.(2)AB+AC=AD.理由如下:如图②,延长AB至点M,使BM=AC,连接DM,∵四边形ABDC内接于⊙O,∴∠MBD=∠ACD,∵∠BAD=∠CAD=45°,∴BD=CD,∴△MBD≌△ACD(SAS),∴MD=AD,∠M=∠CAD=45°,∴MD⊥AD.∴AM=,即AB+BM=,∴AB+AC=;(3)如图③,延长AB至点N,使BN=AC,连接DN,∵四边形ABDC内接于⊙O,∴∠NBD=∠ACD,∵∠BAD=∠CAD,∴BD=CD,∴△NBD≌△ACD(SAS),∴ND=AD,∠N=∠CAD,∴∠N=∠NAD=∠DBC=∠DCB,∴△NAD∽△CBD,∴,∴,又AN=AB+BN=AB+AC,BC=5,BD=4,∴=.24.(11分)(2020•天门)在平面直角坐标系中,已知抛物线C:y=ax2+2x﹣1(a≠0)和直线l:y=kx+b,点A(﹣3,﹣3),B(1,﹣1)均在直线l上.(1)若抛物线C与直线l有交点,求a的取值范围;(2)当a=﹣1,二次函数y=ax2+2x﹣1的自变量x满足m≤x≤m+2时,函数y的最大值为﹣4,求m的值;(3)若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.【分析】(1)点A(﹣3,﹣3),B(1,﹣1)代入y=kx+b,求出y=x﹣;联立y=ax2+2x﹣1与y=x﹣,则有2ax2+3x+1=0,△=9﹣8a≥0即可求解;(2)根据题意可得,y=﹣x2+2x﹣1,当y=﹣4时,有﹣x2+2x﹣1=﹣4,x=﹣1或x=3;①在x=1左侧,y随x的增大而增大,x=m+2=﹣1时,y有最大值﹣4,m=﹣3;②在对称轴x=1右侧,y随x最大而减小,x=m=3时,y有最大值﹣4;(3))①a<0时,x=1时,y≤﹣1,即a≤﹣2;②a>0时,x=﹣3时,y≥﹣3,即a≥,直线AB的解析式为y=x﹣,抛物线与直线联立:ax2+2x﹣1=x﹣,△=﹣2a>0,则a<,即可求a的范围;【解答】解:(1)点A(﹣3,﹣3),B(1,﹣1)代入y=kx+b,∴,∴,∴y=x﹣;联立y=ax2+2x﹣1与y=x﹣,则有2ax2+3x+1=0,∵抛物线C与直线l有交点,∴△=9﹣8a≥0,∴a≤且a≠0;(2)根据题意可得,y=﹣x2+2x﹣1,∵a<0,∴抛物线开口向下,对称轴x=1,∵m≤x≤m+2时,y有最大值﹣4,∴当y=﹣4时,有﹣x2+2x﹣1=﹣4,∴x=﹣1或x=3,①在x=1左侧,y随x的增大而增大,∴x=m+2=﹣1时,y有最大值﹣4,∴m=﹣3;②在对称轴x=1右侧,y随x最大而减小,∴x=m=3时,y有最大值﹣4;综上所述:m=﹣3或m=3;(3)①a<0时,x=1时,y≤﹣1,即a≤﹣2;②a>0时,x=﹣3时,y≥﹣3,即a≥,直线AB的解析式为y=x﹣,抛物线与直线联立:ax2+2x﹣1=x﹣,∴ax2+x+=0,△=﹣2a>0,∴a<,∴a的取值范围为≤a<或a≤﹣2;。
2020湖北省仙桃市中考数学试卷及答案解析

2020年湖北省仙桃市、潜江市、天门市、江汉油田中考数学试卷一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)1.(3分)下列各数中,比﹣2小的数是()A.0B.﹣3C.﹣1D.|﹣0.6|2.(3分)如图是由4个相同的小正方体组成的立体图形,它的俯视图为()A.B.C.D.3.(3分)我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为()A.0.3×106B.3×107C.3×106D.30×1054.(3分)将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是()A.15°B.20°C.25°D.30°5.(3分)下列说法正确的是()A.为了解人造卫星的设备零件的质量情况,选择抽样调查B.方差是刻画数据波动程度的量C.购买一张体育彩票必中奖,是不可能事件D.掷一枚质地均匀的硬币,正面朝上的概率为16.(3分)下列运算正确的是( )A .√4=±2B .(12)﹣1=﹣2C .a +2a 2=3a 3D .(﹣a 2)3=﹣a 67.(3分)对于一次函数y =x +2,下列说法不正确的是( )A .图象经过点(1,3)B .图象与x 轴交于点(﹣2,0)C .图象不经过第四象限D .当x >2时,y <48.(3分)一个圆锥的底面半径是4cm ,其侧面展开图的圆心角是120°,则圆锥的母线长是( )A .8cmB .12cmC .16cmD .24cm9.(3分)关于x 的方程x 2+2(m ﹣1)x +m 2﹣m =0有两个实数根α,β,且α2+β2=12,那么m 的值为( )A .﹣1B .﹣4C .﹣4或1D .﹣1或410.(3分)如图,已知△ABC 和△ADE 都是等腰三角形,∠BAC =∠DAE =90°,BD ,CE交于点F ,连接AF .下列结论:①BD =CE ;②BF ⊥CF ;③AF 平分∠CAD ;④∠AFE =45°.其中正确结论的个数有( )A .1个B .2个C .3个D .4个二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.)11.(3分)已知正n 边形的一个内角为135°,则n 的值是 .12.(3分)篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了 场.13.(3分)如图,海中有个小岛A ,一艘轮船由西向东航行,在点B 处测得小岛A 位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D 处,测得小岛A 在它的北偏西60°方向,此时轮船与小岛的距离AD 为 海里.14.(3分)有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为 .15.(3分)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为 元.16.(3分)如图,已知直线a :y =x ,直线b :y =−12x 和点P (1,0),过点P 作y 轴的平行线交直线a 于点P 1,过点P 1作x 轴的平行线交直线b 于点P 2,过点P 2作y 轴的平行线交直线a 于点P 3,过点P 3作x 轴的平行线交直线b 于点P 4,…,按此作法进行下去,则点P 2020的横坐标为 .三、解答题(本大题共8个小题,满分72分.)17.(12分)(1)先化简,再求值:a 2−4a+4a 2−2a ÷a 2−42a ,其中a =﹣1.(2)解不等式组{3x +2>x −2x−33≤7−53x ,并把它的解集在数轴上表示出来.18.(6分)在平行四边形ABCD 中,E 为AD 的中点,请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图1,在BC 上找出一点M ,使点M 是BC 的中点;(2)如图2,在BD 上找出一点N ,使点N 是BD 的一个三等分点.19.(7分)5月20日九年级复学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.学生体温频数分布表组别温度(℃)频数(人数)甲36.36乙36.4a丙36.520丁36.64请根据以上信息,解答下列问题:(1)频数分布表中a=,该班学生体温的众数是,中位数是;(2)扇形统计图中m=,丁组对应的扇形的圆心角是度;(3)求该班学生的平均体温(结果保留小数点后一位).20.(8分)把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.(1)直接写出抛物线C2的函数关系式;(2)动点P(a,﹣6)能否在抛物线C2上?请说明理由;(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.21.(8分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.(1)求证:DF是⊙O的切线;(2)当CF=2,BE=3时,求AF的长.22.(9分)如图,直线AB与反比例函数y=kx(x>0)的图象交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.(1)填空:反比例函数的关系式为;(2)求直线AB的函数关系式;(3)动点P在y轴上运动,当线段P A与PB之差最大时,求点P的坐标.23.(10分)系统找不到该试题24.(12分)小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为t (分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段AB表示小华和商店的距离y1(米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:(1)填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是.(2)直接写出妈妈和商店的距离y2(米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)求t为何值时,两人相距360米.2020年湖北省仙桃市、潜江市、天门市、江汉油田中考数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)1.(3分)下列各数中,比﹣2小的数是()A.0B.﹣3C.﹣1D.|﹣0.6|【解答】解:∵|﹣0.6|=0.6,∴﹣3<﹣2<﹣1<0<|﹣0.6|.故选:B.2.(3分)如图是由4个相同的小正方体组成的立体图形,它的俯视图为()A.B.C.D.【解答】解:俯视图就是从上面看到的图形,因此选项C的图形符合题意,故选:C.3.(3分)我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为()A.0.3×106B.3×107C.3×106D.30×105【解答】解:3000000=3×106,故选:C.4.(3分)将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是()A .15°B .20°C .25°D .30°【解答】解:∵∠B =90°,∠A =45°,∴∠ACB =45°.∵∠EDF =90°,∠F =60°,∴∠DEF =30°.∵EF ∥BC ,∴∠EDC =∠DEF =30°,∴∠CED =∠ACB ﹣∠EDC =45°﹣30°=15°.故选:A .5.(3分)下列说法正确的是( )A .为了解人造卫星的设备零件的质量情况,选择抽样调查B .方差是刻画数据波动程度的量C .购买一张体育彩票必中奖,是不可能事件D .掷一枚质地均匀的硬币,正面朝上的概率为1【解答】解:为了解人造卫星的设备零件的质量情况,应选择全面调查,即普查,不宜选择抽样调查,因此选项A 不符合题意;方差是刻画数据波动程度的量,反映数据的离散程度,因此选项B 符合题意;购买一张体育彩票中奖,是可能的,只是可能性较小,是可能事件,因此选项C 不符合题意;掷一枚质地均匀的硬币,正面朝上的概率为12,因此选项D 不符合题意; 故选:B .6.(3分)下列运算正确的是( )A .√4=±2B .(12)﹣1=﹣2C .a +2a 2=3a 3D .(﹣a 2)3=﹣a 6【解答】解:A .因为√4=2,所以A 选项错误;B .因为(12)﹣1=2, 所以B 选项错误;C .因为a 与2a 2不是同类项,不能合并,所以C 选项错误;D .因为(﹣a 2)3=﹣a 6,所以D 选项正确.故选:D .7.(3分)对于一次函数y =x +2,下列说法不正确的是( )A .图象经过点(1,3)B .图象与x 轴交于点(﹣2,0)C .图象不经过第四象限D .当x >2时,y <4【解答】解:∵一次函数y =x +2,∴当x =1时,y =3,∴图象经过点(1,3),故选项A 正确;令y =0,解得x =﹣2,∴图象与x 轴交于点(﹣2,0),故选项B 正确;∵k =1>0,b =2>0,∴不经过第四象限,故选项C 正确;∵k =1>0,∴函数值y 随x 的增大而增大,当x =2时,y =4,∴当x >2时,y >4,故选项D 不正确,故选:D .8.(3分)一个圆锥的底面半径是4cm ,其侧面展开图的圆心角是120°,则圆锥的母线长是( )A .8cmB .12cmC .16cmD .24cm【解答】解:圆锥的底面周长为2π×4=8πcm ,即为展开图扇形的弧长,由弧长公式得,120×π×R 180=8π,解得,R=12,即圆锥的母线长为12cm.故选:B.9.(3分)关于x的方程x2+2(m﹣1)x+m2﹣m=0有两个实数根α,β,且α2+β2=12,那么m的值为()A.﹣1B.﹣4C.﹣4或1D.﹣1或4【解答】解:∵关于x的方程x2﹣2(m﹣1)x+m2=0有两个实数根,∴△=[2(m﹣1)]2﹣4×1×(m2﹣m)=﹣4m+4≥0,解得:m≤1.∵关于x的方程x2+2(m﹣1)x+m2﹣m=0有两个实数根α,β,∴α+β=﹣2(m﹣1),α•β=m2﹣m,∴α2+β2=(α+β)2﹣2α•β=[﹣2(m﹣1)]2﹣2(m2﹣m)=12,即m2﹣3m﹣4=0,解得:m=﹣1或m=4(舍去).故选:A.10.(3分)如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE 交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE =45°.其中正确结论的个数有()A.1个B.2个C.3个D.4个【解答】解:如图,作AM⊥BD于M,AN⊥EC于N.∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB =AC ,AD =AE , ∴△BAD ≌△CAE (SAS ),∴EC =BD ,∠BDA =∠AEC ,故①正确 ∵∠DOF =∠AOE , ∠DFO =∠EAO =90°, ∴BD ⊥EC ,故②正确,∵△BAD ≌△CAE ,AM ⊥BD ,AN ⊥EC , ∴AM =AN , ∴F A 平分∠EFB ,∴∠AFE =45°,故④正确,若③成立,则∠AEF =∠ABD =∠ADB ,推出AB =AD ,显然与条件矛盾,故③错误, 故选:C .二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.)11.(3分)已知正n 边形的一个内角为135°,则n 的值是 8 . 【解答】解:∵正n 边形的一个内角为135°, ∴正n 边形的一个外角为180°﹣135°=45°, ∴n =360°÷45°=8. 故答案为:8.12.(3分)篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了 9 场. 【解答】解:设该队胜了x 场,负了y 场,依题意有 {x +y =142x +y =23, 解得{x =9y =5.故该队胜了9场. 故答案为:9.13.(3分)如图,海中有个小岛A ,一艘轮船由西向东航行,在点B 处测得小岛A 位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D 处,测得小岛A 在它的北偏西60°方向,此时轮船与小岛的距离AD 为 20√2 海里.【解答】解:如图,过点A 作AC ⊥BD 于点C ,根据题意可知:∠BAC =∠ABC =45°,∠ADC =30°,AB =20, 在Rt △ABC 中,AC =BC =AB •sin45°=20×√22=10√2,在Rt △ACD 中,∠ADC =30°, ∴AD =2AC =20√2(海里).答:此时轮船与小岛的距离AD 为20√2海里. 故答案为:20√2.14.(3分)有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为 49.【解答】解:画树状图得:∵共有9种等可能的结果,两次取出的数字之和是奇数的有4种结果, ∴两次取出的数字之和是奇数的概率为49,故答案为:49.15.(3分)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为70元.【解答】解:设每顶头盔的售价为x元,获得的利润为w元,w=(x﹣50)[200+(80﹣x)×20]=﹣20(x﹣70)2+8000,∴当x=70时,w取得最大值,此时w=8000,故答案为:70.16.(3分)如图,已知直线a:y=x,直线b:y=−12x和点P(1,0),过点P作y轴的平行线交直线a于点P1,过点P1作x轴的平行线交直线b于点P2,过点P2作y轴的平行线交直线a于点P3,过点P3作x轴的平行线交直线b于点P4,…,按此作法进行下去,则点P2020的横坐标为21010.【解答】解:∵点P(1,0),P1在直线y=x上,∴P1(1,1),∵P1P2∥x轴,∴P2的纵坐标=P1的纵坐标=1,∵P2在直线y=−12x上,∴1=−12x,∴x=﹣2,∴P2(﹣2,1),即P2的横坐标为﹣2=﹣21,同理,P3的横坐标为﹣2=﹣21,P4的横坐标为4=22,P5=22,P6=﹣23,P7=﹣23,P8=24…,∴P4n=212n,∴P2020的横坐标为212×2020=21010,故答案为:21010.三、解答题(本大题共8个小题,满分72分.) 17.(12分)(1)先化简,再求值:a 2−4a+4a 2−2a÷a 2−42a,其中a =﹣1.(2)解不等式组{3x +2>x −2x−33≤7−53x,并把它的解集在数轴上表示出来.【解答】解:(1)原式=(a−2)2a(a−2)•2a (a+2)(a−2)=2a+2,当a =﹣1时,原式=2−1+2=2;(2){3x +2>x −2①x−33≤7−53x②, ∵解不等式①得:x >﹣2, 解不等式②得:x ≤4,∴不等式组的解集是:﹣2<x ≤4,在数轴上表示为:.18.(6分)在平行四边形ABCD 中,E 为AD 的中点,请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图1,在BC 上找出一点M ,使点M 是BC 的中点; (2)如图2,在BD 上找出一点N ,使点N 是BD 的一个三等分点.【解答】解:(1)如图1,F 点就是所求作的点: (2)如图2,点N 就是所求作的点:19.(7分)5月20日九年级复学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.学生体温频数分布表组别温度(℃)频数(人数)甲36.36乙36.4a丙36.520丁36.64请根据以上信息,解答下列问题:(1)频数分布表中a=10,该班学生体温的众数是36.5,中位数是36.5;(2)扇形统计图中m=15,丁组对应的扇形的圆心角是36度;(3)求该班学生的平均体温(结果保留小数点后一位).【解答】解:(1)20÷50%=40(人),a=40×25%=10;36.5出现了20次,次数最多,所以众数是36.5;40个数据按从小到大的顺序排列,其中第20、21个数据都是36.5,所以中位数是(36.5+36.5)÷2=36.5.故答案为:10,36.5,36.5;(2)m%=640×100%=15%,m=15;360°×440=36°. 故答案为:15,36;(3)该班学生的平均体温为:36.3×6+36.4×10+36.5×20+36.6×440=36.455≈36.5(℃).20.(8分)把抛物线C 1:y =x 2+2x +3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C 2.(1)直接写出抛物线C 2的函数关系式;(2)动点P (a ,﹣6)能否在抛物线C 2上?请说明理由;(3)若点A (m ,y 1),B (n ,y 2)都在抛物线C 2上,且m <n <0,比较y 1,y 2的大小,并说明理由.【解答】解:(1)∵y =x 2+2x +3=(x +1)2+2,∴把抛物线C 1:y =x 2+2x +3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C 2:y =(x +1﹣4)2+2﹣5,即y =(x ﹣3)2﹣3, ∴抛物线C 2的函数关系式为:y =(x ﹣3)2﹣3. (2)动点P (a ,﹣6)不在抛物线C 2上,理由如下: ∵抛物线C 2的函数关系式为:y =(x ﹣3)2﹣3, ∴函数的最小值为﹣3, ∵﹣6<﹣3,∵动点P (a ,﹣6)不在抛物线C 2上;(3)∵抛物线C 2的函数关系式为:y =(x ﹣3)2﹣3, ∴抛物线的开口向上,对称轴为x =3, ∴当x <3时,y 随x 的增大而减小,∵点A (m ,y 1),B (n ,y 2)都在抛物线C 2上,且m <n <0<3, ∴y 1>y 2.21.(8分)如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 交BC 于点D ,过点D 的直线EF 交AC 于点F ,交AB 的延长线于点E ,且∠BAC =2∠BDE . (1)求证:DF 是⊙O 的切线;(2)当CF =2,BE =3时,求AF 的长.【解答】解:(1)连接OD ,AD , ∵AB 是直径, ∴∠ADB =90°, ∴AD ⊥BC , ∵AB =AC , ∴∠BAC =2∠BAD , ∵∠BAC =2∠BDE , ∴∠BDE =∠BAD , ∵OA =OD , ∴∠BAD =∠ADO , ∵∠ADO +∠ODB =90°, ∴∠BDE +∠ODB =90°, ∴∠ODE =90°, 即DF ⊥OD , ∵OD 是⊙O 的半径, ∴DF 是⊙O 的切线. (2)∵AB =AC ,AD ⊥BC , ∴BD =CD , ∵BO =AO , ∴OD ∥AC , ∴△EOD ∽△EAF , ∴OD AF=EO EA,设OD =x , ∵CF =2,BE =3,∴OA=OB=x,AF=AC﹣CF=2x﹣2,∴EO=x+3,EA=2x+3,∴x2x−2=x+32x+3,解得x=6,经检验,x=6是分式方程的解,∴AF=2x﹣2=10.22.(9分)如图,直线AB与反比例函数y=kx(x>0)的图象交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.(1)填空:反比例函数的关系式为y=6x;(2)求直线AB的函数关系式;(3)动点P在y轴上运动,当线段P A与PB之差最大时,求点P的坐标.【解答】解:(1)解:(1)将点A坐标(6,1)代入反比例函数解析式y=k x,得k=1×6=6,则y=6 x,故答案为:y=6 x;(2)过点A作AC⊥x轴于点C,过B作BD⊥y轴于D,延长CA,DB交于点E,则四边形ODEC是矩形,设B (m ,n ), ∴mn =6,∴BE =DE ﹣BD =6﹣m ,AE =CE ﹣AC =n ﹣1, ∴S △ABE =12AE ⋅BE =12(n −1)(6−m),∵A 、B 两点均在反比例函数y =k x(x >0)的图象上, ∴S △BOD =S △AOC =12×6×1=3, ∴S △AOB =S 矩形ODEC ﹣S △AOC ﹣S △BOD ﹣S △ABE =6n ﹣3﹣3−12(n −1)(6−m)=3n −12m , ∵△AOB 的面积为8, ∴3n −12m =8, ∴m =6n ﹣16, ∵mn =6, ∴3n 2﹣8n ﹣3=0, 解得:n =3或−13(舍), ∴m =2, ∴B (2,3),设直线AB 的解析式为:y =kx +b ,则{6k +b =12k +b =3,解得:{k =−12b =4, ∴直线AB 的解析式为:y =−12x +4;(3)如图,根据“三角形两这边之差小于第三边可知: 当点P 为直线AB 与y 轴的交点时,P A ﹣PB 有最大值是AB , 把x =0代入y =−12x +4中,得:y =4, ∴P (0,4).23.(10分)系统找不到该试题24.(12分)小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为t (分钟),图1表示两人之间的距离s (米)与时间t (分钟)的函数关系的图象;图2中线段AB 表示小华和商店的距离y 1(米)与时间t (分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:(1)填空:妈妈骑车的速度是 120 米/分钟,妈妈在家装载货物所用时间是 5 分钟,点M 的坐标是 (20,1200) .(2)直接写出妈妈和商店的距离y 2(米)与时间t (分钟)的函数关系式,并在图2中画出其函数图象;(3)求t 为何值时,两人相距360米.【解答】解:(1)妈妈骑车的速度为120米/分钟, 妈妈在家装载货物时间为5分钟, 点M 的坐标为(20,1200). (2)y 2={120t(0≤t <15)1800(15≤t <20)−120t +4200(20≤t ≤35),其图象如图所示,(3)由题意可知:小华速度为60米/分钟,妈妈速度为120米/分钟,①相遇前,依题意有60t+120t+360=1800,解得t=8分钟,②相遇后,依题意有,60t+120t﹣360=1800,解得t=12分钟.③依题意,当t=20分钟时,妈妈从家里出发开始追赶小华,此时小华距商店为1800﹣20×60=600米,只需10分钟,即t=30分钟,小华到达商店.而此时妈妈距离商店为1800﹣10×120=600米>360米,∴120(t﹣5)+360=1800×2,解得t=32分钟,∴t=8,12或32分钟时,两人相距360米第21 页共21 页。
2020年湖北潜江 仙桃 天门 江汉油田中考数学试卷

正面A .B .C .D .数 学 试 卷本卷共6页,满分120分,考试时间120分钟注意事项:1. 答题前,考生务必将自己的姓名、准考证号填写在试卷第1页装订线内和答题卡上,并在答题卡的规定位置贴好条形码,核准姓名和准考证号.2. 选择题的答案选出后,必须使用2B 铅笔把答题卡上对应的答案标号涂黑.如需改动,先用橡皮擦干净后,再选涂其他答案标号. 非选择题答案必须使用0.5毫米黑色墨水签字笔填写在答题卡对应的区域内,写在试卷上无效.3. 考试结束后,请将本试卷和答题卡一并上交.一、选择题(本大题共10个小题,每小题3分,满分30分)在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分. 1.31-的倒数是 A .31 B .-3 C .3 D .31-2.如图所示,该几何体的俯视图是3.第六次人口普查的标准时间是2020年11月1日零时.普查登记的大陆31个省、自治区、直辖市和现役军人的人口共1 339 724 852人.这个数用科学记数法表示为(保留三个有效数字)A .1013310.⨯ B .1013410.⨯ C .910331⨯. D .910341⨯. 4.某不等式组的解集在数轴上表示如图,则这个不等式组可能是 A .23x x -⎧⎨⎩≥≤ B .23x x -⎧⎨<⎩≥ 03-2(第4题图)•ο潜江市 天门市 仙桃市 江 汉 油 田2020年初中毕业生学业考试BA DCEF ο154ο46(第5题图)C .⎩⎨⎧<->32x x D .23x x >-⎧⎨⎩≤5.如图,AB ∥EF∥CD ,∠ABC =ο46,∠CEF =ο154,则∠BCE 等于A .ο23B .ο16C .ο20D .ο266.化简)2()242(2+÷-+-m mm m 的结果是A .0B .1C .-1D .2)2(+m7.如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A 、B 、C 为格点.作△ABC 的外接圆⊙O ,则»AC 的长等于 A .π43B .π45C . π23D .π258.小英早上从家里骑车上学,途中想到社会实践调查资料忘带了,立刻原路返回,返家途中遇到给她送资料的妈妈,接过资料后,小英加速向学校赶去.能反映她离家距离s 与骑车时间t 的函数关系图象大致是9.如图,已知直线l :y=33x ,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;…;按此作法继续下去,则点A 4的坐标为 A .(0,64) B .(0,128) C .(0,256) D .(0,512)10.如图是近年来我国年财政收入同比(与上一年比较)增长率的折线统计图,其中2020年我国财政收入约为61330亿元.下列命题:A .B .C .D .(第7题图)(第9题图) 年度(第10题图)①2020年我国财政收入约为61330(1-19.5%)亿元; ②这四年中,2020年我国财政收入最少;③2020年我国财政收入约为61330(1+11.7%)(1+21.3%)亿元.其中正确的有 A .3个 B .2个 C .1个 D .0个 二、填空题(本大题共5个小题,每小题3分,满分15分)将结果直接填写在答题卡相应的横线上. 11.分解因式: =+-962a a .12.西周戎生青铜编钟是由八个大小不同的小编钟组成,其中最大编钟高度比最小编钟高度的3倍少5cm ,且它们的高度相差37 cm .则最大编钟的高度是 cm . 13.将点A (-3,-2)先沿y 轴向上平移5个单位,再沿x 轴向左平移4个单位得到点A ′,则点A ′的坐标是 .14.张凯家购置了一辆新车,爸爸妈妈商议确定车牌号,前三位选定为8ZK 后,对后两位数字意见有分歧,最后决定由毫不知情的张凯从如图排列的四个数字中随机划去两个,剩下的两个数字从左到右 组成两位数,续在8ZK 之后,则选中的车牌号为8ZK86的概率是 . 15.已知□ABCD 的周长为28,自顶点A 作AE ⊥DC 于点E ,AF ⊥BC 于点F . 若AE =3,AF =4,则 CE -CF = . 三、解答题(本大题共9个小题,满分75分) 16.(满分6分)计算:165)1(2011+---.17.(满分6分)若关于x 的一元二次方程0342=-+-k x x 的两个实数根为1x 、2x ,且满足213x x =,试求出方程的两个实数根及k 的值.18.(满分7分)五月石榴红,枝头鸟儿歌.一只小鸟从石榴树上的A 处沿直线飞到对面一房屋的顶部C 处.从A 处看房屋顶部C 处的仰角为ο30,看房屋底部D 处的俯角为ο45,石榴树与该房屋之间的水平距离为33米,求出小鸟飞行的距离AC 和房屋的高度CD .19.(满分8分)为迎接市教育局开展的“创先争优”主题演讲活动,某校组织党员教师进行演讲预赛.学校将所有参赛教师的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:观察图表信息,回答下列问题:(1)参赛教师共有 人;(2)如果将各组的组中值视为该组的平均成绩,请你估算所有参赛教师的平均成绩; (3)成绩落在第一组的恰好是两男两女四位教师,学校从中随机挑选两位教师参加市教育局组织的决赛.通过列表或画树状图求出挑选的两位教师是一男一女的概率.20.(满分8分)如图,BD 是⊙O 的直径, A 、C 是⊙O 上的两点,且AB =AC ,AD 与BC的延长线交于点E .(1)求证:△ABD ∽△AEB ;(2)若AD =1,DE =3,求BD 的长.21.(满分8分)如图,已知直线AB 与x 轴交于点C ,与双曲线x k y =交于A (3,320)、B (-5,a )两点.AD ⊥x 轴于点D ,BE ∥x (1)求点B 的坐标及直线AB 的解析式;(2)判断四边形CBED 的形状,并说明理由第一组 第四组 第二组 40% 第三组32%ABEO •C D22.(满分10分)2020年4月25日,全国人大常委会公布《中华人民共和国个人所得税法修正案(草案)》,向社会公开征集意见.草案规定,公民全月工薪不超过3000元的部分不必纳税,超过3000元的部分为全月应纳税所得额.此项税款按下表分段累进计算.(1)李工程师的月工薪为8000元,则他每月应当纳税多少元?(2)若某纳税人的月工薪不超过10000元,他每月的纳税金额能超过月工薪的8%吗? 若能,请给出该纳税人的月工薪范围;若不能,请说明理由.23.(满分10分)两个大小相同且含ο30角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转ο30得到图②,点F、G分别是CD、DE 与AB的交点,点H是DE与AC的交点.(1)不添加辅助线,写出图②中所有与△BCF全等的三角形;(2)将图②中的△DEC绕点C逆时针旋转ο45得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I=CI.DBE图①D DD1BCEFGHBCEFG1H图③H11IGF124.(满分12分)在平面直角坐标系中,抛物线32++=bx ax y 与x 轴的两个交点分别为A (-3,0)、B (1,0),过顶点C 作CH ⊥x 轴于点H .(1)直接填写:a = ,b = ,顶点C 的坐标为 ; (2)在y 轴上是否存在点D ,使得△ACD 是以AC 为斜边的直角三角形?若存在,求出点D 的坐标;若不存在,说明理由;(3)若点P 为x 轴上方的抛物线上一动点(点P 与顶点C 不重合),PQ ⊥AC 于点Q ,CA 图②A原版录入,曹禺中学 陈玉平数学试卷参考答案及评分说明说明:本试卷中的解答题一般只给出一种解法,对于其它解法,只要推理严谨、运算合理、结果正确,均给满分.对部分正确的,参照本评分说明酌情给分. 一.选择题(每小题3分,共30分) 1——10 BADBC BDDCC 二.填空题(每小题3分,共15分)11.2)3(-a 12.58 13.(-7,3) 14.3115. 3714-或32-(答对前者得2分,答对后者得1分) 三.解答题(共75分)16.解:原式=-1-5+4 ………………………………………………………………… 3分 =-2………………………………………………………………………… 6分 17.解:由根与系数的关系得:421=+x x ① ,=⋅21x x 3-k ②………………… 2分又∵213x x =③,联立①、③,解方程组得⎩⎨⎧==1321x x ……………………… 4分∴6313321=+⨯=+=x x k ……………………………………………… 5分 答:方程两根为12=3,=1;=6x x k .……………………………………… 6分18.解:作AE ⊥CD 于点E .由题意可知:∠CAE =30°,∠EAD =45°,AE =33米. ………………… 1分 在Rt △ACE 中,tan ∠CAE =AE CE,即tan30°=33CE . 潜江市 天门市 仙桃市 江 汉 油 田2020年初中毕业生学业考试∴CE =ο30tan 33=3=(米),…………………………………… 3分 ∴AC =2CE=2×3 =6(米). …………………………………………………… 4分 在Rt △AED 中,∠ADE =90°-∠EAD =90°-45°= 45°, ∴DE =AE =33(米). ……………………………………………………… 5分∴DC =CE+DE =(3+33)米. …………………………………………… 6分 答:AC =6米,DC =(3+33)米. ………………………………………… 7分 19.解:(1)25. ……………………………………………………………………… 2分 (2)x =81253658751085495=⨯+⨯+⨯+⨯.………………………………4分分总共有12种结果,每种结果出现的可能性相同.挑选的两位教师恰好是一男一女的结果有8种,其概率为32128=. ……………………………………………… 8分 20.(1)证明:∵AB =AC , ∴»»AB AC =. ∴∠ABC =∠ADB . …………………… 2分又∠BAE =∠DAB ,∴ △ABD ∽△AEB . ………………………………… 4分(2)解:∵△ABD ∽△AEB , ∴ABADAE AB =. ∵ AD =1, DE =3, ∴AE =4. ∴ AB 2=AD ·AE =1×4=4.∴ AB =2. ……………………………………………………………………6分 ∵ BD 是⊙O 的直径, ∴∠DAB =90°.在Rt △ABD 中,BD 2=AB 2+AD 2=22+12=5,∴BD =5.………………………………………………………………… 8分21.解:(1)∵双曲线xk y =过A (3,320),∴20=k .把B (-5,a )代入x y 20=,得4-=a . ∴点B 的坐标是(-5,-4). ……………………………… 2分设直线AB 的解析式为n mx y +=,将 A (3,320)、B (-5,-4)代入得, ⎪⎩⎪⎨⎧+-=-+=nm nm 543320, 解得:38,34==n m . ∴直线AB 的解析式为:3834+=x y .………………………………… 4分 (2)四边形CBED 是菱形.理由如下: ………………………………… 5分点D 的坐标是(3,0),点C 的坐标是(-2,0). ∵ BE ∥x 轴, ∴点E 的坐标是(0,-4).而CD =5, BE=5, 且BE ∥CD .∴四边形CBED 是平行四边形. ………………………………………… 6分 在Rt △OED 中,ED 2=OE 2+OD 2, ∴ ED =2243+=5,∴ED =CD . ∴□CBED 是菱形. ……………………………………………………… 8分22.解:(1)李工程师每月纳税:1500×5% +3000×10% +(8000-7500)×20%=75+300+100= 475(元)…………………………………………… 4分(2)设该纳税人的月工薪为x 元,则当x ≤4500时,显然纳税金额达不到月工薪的8% ………………5分 当4500<x ≤7500时,由1500×5% +(x -4500)×10%>8%x得x >18750,不满足条件;………………………………………… 7分 当7500<x ≤10000时,由1500×5% +3000×10%+(x -7500)×20%>8%x 解得x >9375,故9375<x ≤10000………………………………… 9分 答:若该纳税人月工薪大于9375元且不超过10000元时,他的纳税金额能超过月工薪的8%.………………………………………………………… 10分23.解:(1)图②中与△BCF 全等的有△GDF 、 △GAH 、△ECH .……………3分(2)11F D =1AH …………………………………………………………… 4分证明:∵⎪⎩⎪⎨⎧∠==∠=∠公共111130CH F CD CA D A ο∴△AF 1C ≌△D 1H 1C . ………………… 5分 ∴ F 1C = H 1C , 又CD 1=CA ,∴CD 1- F 1C =CA - H 1C .即111AH F D =………………………………… 6分(3)连结CG 1.在△D 1G 1F 1和△AG 1H 1中,∵111111111H AHF D AG F G D A D ⎪⎩⎪⎨⎧=∠=∠∠=∠,∴△D 1G 1F 1 ≌△AG 1H 1. ∴G 1F 1=G 1H 1 ……………………………………7分 又∵H 1C =F 1C ,G 1C=G 1C ,∴△CG 1F 1 ≌△CG 1H 1. ∴∠1=∠2. ……………………………………8分 ∵∠B =60°,∠BCF =30° ,∴∠BFC =90°.又∵∠DCE =90°,∴∠BFC =∠DCE ,∴B A ∥CE , ∴∠1=∠3, ∴∠2=∠3,C 1∴G 1I=CI …………………………………………………………………… 10分24.解:(1)2,1-=-=b a ,顶点C 的坐标为(-1,4)………………………… 3分(2)假设在y 轴上存在满足条件的点D , 过点C由∠CDA =90°得,∠1+∠2=90°. 又∠2+∠∴∠3=∠1. 又∵∠CED =∠DOA =90°,∴△CED ∽△DOA ,∴AO DOED CE =. 设D (0,c ),则341cc =-. 变形得0342=+-c c ,解之得1231c ,c ==.综合上述:在y 轴上存在点D (0,3)或(0,1使△ACD 是以AC 为斜边的直角三角形.(3)①若点P 在对称轴右侧(如图①),只能是△PCQ ∽△CAH ,得∠QCP =∠CAH . 延长CP 交x 轴于M ,∴AM =CM , ∴AM 2=CM 2. 设M (m ,0),则( m +3)2=42+(m +1)2,∴m =2,即M (2,0). 设直线CM 的解析式为y=k 1x+b 1, 则⎩⎨⎧=+=+-0241111b k b k , 解之得341-=k ,381=b .∴直线CM 的解析式3834+-=x y .…………………………………………… 8分 联立⎪⎩⎪⎨⎧+--=+-=3238342x x y x y ,解之得13209x y ⎧=⎪⎪⎨⎪=⎪⎩或14x y =-⎧⎨=⎩(舍去).∴)92031(,P .…… 9分②若点P 在对称轴左侧(如图②),只能是△PCQ ∽△ACH ,得∠PCQ =∠ACH .过A 作CA 的垂线交PC 于点F ,作FN ⊥x 轴于点N .由△CF A ∽△CAH 得2==AHCHAF CA , 由△FNA ∽△AHC 得21===CA AF HC NA AH FN .∴12==FN AN ,, 点F 坐标为(-5,1). …………………………………10分设直线CF 的解析式为y=k 2x+b 2,则⎩⎨⎧=+-=+-1542222b k b k ,解之得419,4322==b k .∴直线CF 的解析式41943+=x y . ……………………………………………11分 联立 ⎪⎩⎪⎨⎧+--=+=32419432x x y x y ,解之得⎪⎪⎩⎪⎪⎨⎧=-=165547y x 或 14x y =-⎧⎨=⎩(舍去). ∴)165547(,-P .∴满足条件的点P 坐标为)92031(,或)165547(,- ………………………………12分。
2020年湖北省仙桃市、潜江市、天门市、江汉油田中考数学试卷和答案解析

2020年湖北省仙桃市、潜江市.天门市、江汉油田中考数学试卷和答案解析一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分•)1.(3分)下列各数中,比・2小的数是()D . I - 0.61解析:先计算I・0.61 ,再比较大小.参考答案:解:..1・0.61 = 0.6 ,- 3 < - 2 < - 1 < 0 < I - 0.61 .点拨:本题考查了绝对值的化简及有理数大小的比较.掌握有理数大小的比较方法是解决本题的关健.有理数大小的比较:正数大于0 , 0大于一切负数・两个负数比较大小,绝对值大的反而小.2.(3分)如图是由4个相同的小正方体组成的立体图形,它的俯视图为()解析:从上面看物体所得到的图形即为俯视图,因此选项C的图形符合题意.参考答案:解:俯视图就是从上面看到的图形,因此选项C的图形符合题意,故选:c.点拨:本题考查简单几何体的三视图,主视图、左视图、俯视图实际上就是从正面、左面、上面对该几何体正投影所得到的图形. 3.(3分)我国自主研发的“北斗系统"现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为()A . 0.3X106B . 3X107C . 3X106D . 30X105解析:科学记数法的表示形式为axl0«的形式,其中l<lal<10r n为整数・确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同・当原数绝对值210时, n是正数;当原数的绝对值< 1时,n是负数・参考答案:解:3000000 = 3X106 ,故选:C.点拨:此题考查了科学记数法的表示方法.科学记数法的表示形式为axion的形式,其中10 , n为整数,表示时关键要正确确定a的值以及n的值.4.(3分)将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EFIIBC , ZB = ZEDF = 90° , ZA = 45° , ZF = 60°,贝!J ZCED的度数是()B C DA . 15°B . 20°C . 25°D . 30°解析:由匕B = ZEDF = 90。
湖北省天门、仙桃、潜江、江汉油田2020年中考数学试题(Word版,含答案与解析)

湖北省天门、仙桃、潜江、江汉油田2020年中考数学试卷一、选择题(共10题;共20分)1.下列各数中,比-2小的数是()A. 0B. -3C. -1D. |−0.6|【答案】B【考点】有理数大小比较【解析】【解答】解:|−0.6|=0.6,∵−3<−2<−1<0<0.6,∴比−2小的数是-3,故答案为:B.【分析】根据有理数的大小比较法则“正数大于负数;0大于负数;0小于正数;两个正数比较大小,绝对值大的数就大;两个负数比较大小,绝对值大的数反而小”即可求解.2.如图是由4个相同的小正方体组成的立体图形,它的俯视图为()A. B. C. D.【答案】C【考点】简单组合体的三视图【解析】【解答】解:这个由4个相同的小正方体组成的立体图形:从上方可以看到前后两排正方形,后排有两个正方形,前排左边有一个正方形,即C选项符合.故答案为C.【分析】俯视图是从物体上面看所得到的图形;认真观察实物图,按照三视图的要求画图即可,其中看得到的棱长用实线表示,看不到的棱长用虚线的表示.3.我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为()A. 74.9×106 B. 3×107 C. 3×106 D. 10nn+1【答案】C【考点】科学记数法—表示绝对值较大的数【解析】【解答】科学记数法:将一个数表示成a×10n的形式,其中1≤|a|<10,n为整数,这种记数的方法叫做科学记数法则3000000=3×106故答案为:C.【分析】科学记数法是指,任何一个绝对值大于或等于1的数可以写成a×10n的形式,其中,n=整数位数-1.根据科学记数法的意义即可求解.4.将一副三角尺如图摆放,点E在AC上,点D在BC的延长线上,EF//BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是()A. 15°B. 20°C. 25°D. 30°【答案】A【考点】平行线的性质【解析】【解答】解:由三角板的特点可知∠ACB=45°、∠DEF=30°∵EF//BC∴∠CEF=∠ACB=45°,∴∠CED=∠CEF-∠DEF=45°-30°=15°.故答案为:A.【分析】根据三角板的特点可知∠ACB=45°、∠DEF=30°,根据EF//BC可知∠CEF=∠ACB=45°,最后运用角的和差即可解答.5.下列说法正确的是()A. 为了解人造卫星的设备零件的质量情况,选择抽样调查B. 方差是刻画数据波动程度的量C. 购买一张体育彩票必中奖,是不可能事件D. 掷一枚质地均匀的硬币,正面朝上的概率为1【答案】B【考点】方差【解析】【解答】解:A. 为了解人造卫星的设备零件的质量情况,选择普查,故A选项不符合题意;B. 方差是刻画数据波动程度的量,故B选项符合题意;C. 购买一张体育彩票必中奖,是随机事件,故C选项不符合题意;D. 掷一枚质地均匀的硬币,正面朝上的概率为0.5, 故D选项不符合题意.故答案为B.【分析】(1)为了解人造卫星的设备零件的质量情况,应选择全面调查,即普查,不宜选择抽样调查;(2)方差是刻画数据波动程度的量,反映数据的离散程度;(3)购买一张体育彩票中奖,是可能的,只是可能性较小,是随机事件;(4)掷一枚质地均匀的硬币,可能正面朝上,也可能反面朝上,所以正面朝上的概率为.6.下列运算正确的是()A. √4=±2B. (12)−1=−2 C. a+2a2=3a3 D. (−a2)3=−a6【答案】 D【考点】算术平方根,负整数指数幂的运算性质,合并同类项法则及应用,幂的乘方【解析】【解答】解:A、√4=2,故本选项错误;B、(12)−1=2,故本选项错误;C、a+2a2=a+2a2,故本选项错误;D、(−a2)3=−a6,故本选项正确;故答案为:D.【分析】根据算术平方根,负整数指数幂,幂的乘方和合并同类项的运算法则进行判断即可.7.对于一次函数y=x+2,下列说法不正确的是()A. 图象经过点(1,3)B. 图象与x轴交于点(−2,0)C. 图象不经过第四象限D. 当x>2时,y<4【答案】 D【考点】一次函数的性质【解析】【解答】A.图象经过点(1,3),正确;B.图象与x轴交于点(−2,0),正确C.图象经过第一、二、三象限,故错误;D.当x>2时,y>4,故错误;故答案为:D.x【分析】(1)把坐标代入解析式计算,若左、右两边的值相等,则可判断点在直线上;反之不在直线上;(2)由题意令y=0可得关于x的方程,解这个方程即可求得图象与x轴的交点;(3)由解析式知:k=1>0,则直线过一、三象限;b=2>0,直线交在y轴的正半轴,所以图像经过第一、二、三象限;(4)因为k=1>0,由一次函数的性质当k>0时,y随x的增大而增大。
湖北省天门、仙桃、潜江、江汉油田2020年中考数学试题

A.15°
B.20°
C.25°
5.下列说法正确的是( )
A.为了解人造卫星的设备零件的质量情况,选择抽样调查
B.方差是刻画数据波动程度的量
C.购买一张体育彩票必中奖,是不可能事件
D.掷一枚质地均匀的硬币,正面朝上的概率为 1
6.下列运算正确的是( )
试卷第 1 页,总 7 页
D.30°
A. 4 = ±2
东北方向,此时轮船与小岛相距 20 海里,继续航行至点 D 处,测得小岛 A 在它的北偏
西 60°方向,此时轮船与小岛的距离 AD 为________海里.
试卷第 2 页,总 7 页
14.有 3 张看上去无差别的卡片,上面分别写着 2,3,4.随机抽取 1 张后,放回并混
在一起,再随机抽取 1 张,则两次取出的数字之和是奇数的概率为_________.
说明理由.
21.如图,在 ABC 中, AB = AC ,以 AB 为直径的⊙O 交 BC 于点 D,过点 D 的直 线 EF 交 AC 于点 F,交 AB 的延长线于点 E,且 ∠BAC = 2∠BDE .
(1)求证: DF 是⊙O 的切线;
(2)当= CF 2= , BE 3 时,求 AF 的长.
17.(1)先化简,再求值:
a2 − a2
4a + − 2a
4
÷
a2 − 2a
4
,其中
a
=
−1 .
3x + 2 > x − 2
(2)解不等式组
x
− 3
3
≤
7
−
5 3
x
,并把它的解 ABCD 中,E 为 AD 的中点,请仅用无刻度的直尺完成下列画图,
2020年湖北省仙桃市、潜江市、天门市、江汉油田中考数学试题和答案
2020年湖北省仙桃市、潜江市、天门市、江汉油田中考数学试卷一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)1.(3分)下列各数中,比﹣2小的数是()A.0B.﹣3C.﹣1D.|﹣0.6| 2.(3分)如图是由4个相同的小正方体组成的立体图形,它的俯视图为()A.B.C.D.3.(3分)我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为()A.0.3×106B.3×107C.3×106D.30×105 4.(3分)将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是()A.15°B.20°C.25°D.30°5.(3分)下列说法正确的是()A.为了解人造卫星的设备零件的质量情况,选择抽样调查B.方差是刻画数据波动程度的量C.购买一张体育彩票必中奖,是不可能事件D.掷一枚质地均匀的硬币,正面朝上的概率为16.(3分)下列运算正确的是()A.=±2B.()﹣1=﹣2C.a+2a2=3a3D.(﹣a2)3=﹣a67.(3分)对于一次函数y=x+2,下列说法不正确的是()A.图象经过点(1,3)B.图象与x轴交于点(﹣2,0)C.图象不经过第四象限D.当x>2时,y<48.(3分)一个圆锥的底面半径是4cm,其侧面展开图的圆心角是120°,则圆锥的母线长是()A.8cm B.12cm C.16cm D.24cm 9.(3分)关于x的方程x2+2(m﹣1)x+m2﹣m=0有两个实数根α,β,且α2+β2=12,那么m的值为()A.﹣1B.﹣4C.﹣4或1D.﹣1或4 10.(3分)如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有()A.1个B.2个C.3个D.4个二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.)11.(3分)已知正n边形的一个内角为135°,则n的值是.12.(3分)篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了场.13.(3分)如图,海中有个小岛A,一艘轮船由西向东航行,在点B 处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为海里.14.(3分)有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为.15.(3分)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为元.16.(3分)如图,已知直线a:y=x,直线b:y=﹣x和点P(1,0),过点P作y轴的平行线交直线a于点P1,过点P1作x轴的平行线交直线b于点P2,过点P2作y轴的平行线交直线a于点P3,过点P3作x轴的平行线交直线b于点P4,…,按此作法进行下去,则点P2020的横坐标为.三、解答题(本大题共8个小题,满分72分.)17.(12分)(1)先化简,再求值:÷,其中a=﹣1.(2)解不等式组,并把它的解集在数轴上表示出来.18.(6分)在平行四边形ABCD中,E为AD的中点,请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图1,在BC上找出一点M,使点M是BC的中点;(2)如图2,在BD上找出一点N,使点N是BD的一个三等分点.19.(7分)5月20日九年级复学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.学生体温频数分布表组别温度(℃)频数(人数)甲36.36乙36.4a丙36.520丁36.64请根据以上信息,解答下列问题:(1)频数分布表中a=,该班学生体温的众数是,中位数是;(2)扇形统计图中m=,丁组对应的扇形的圆心角是度;(3)求该班学生的平均体温(结果保留小数点后一位).20.(8分)把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.(1)直接写出抛物线C2的函数关系式;(2)动点P(a,﹣6)能否在抛物线C2上?请说明理由;(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.21.(8分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.(1)求证:DF是⊙O的切线;(2)当CF=2,BE=3时,求AF的长.22.(9分)如图,直线AB与反比例函数y=(x>0)的图象交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.(1)填空:反比例函数的关系式为;(2)求直线AB的函数关系式;(3)动点P在y轴上运动,当线段PA与PB之差最大时,求点P 的坐标.23.(10分)实践操作:第一步:如图1,将矩形纸片ABCD沿过点D的直线折叠,使点A 落在CD上的点A'处,得到折痕DE,然后把纸片展平.第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C′处,点B落在点B'处,得到折痕EF,B'C′交AB于点M,C′F交DE于点N,再把纸片展平.问题解决:(1)如图1,填空:四边形AEA'D的形状是;(2)如图2,线段MC′与ME是否相等?若相等,请给出证明;若不等,请说明理由;(3)如图2,若AC′=2cm,DC'=4cm,求DN:EN的值.24.(12分)小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段AB表示小华和商店的距离y1(米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:(1)填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是.(2)直接写出妈妈和商店的距离y2(米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)求t为何值时,两人相距360米.答案一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)1.参考答案:解:∵|﹣0.6|=0.6,∴﹣3<﹣2<﹣1<0<|﹣0.6|.故选:B.2.参考答案:解:俯视图就是从上面看到的图形,因此选项C的图形符合题意,故选:C.3.参考答案:解:3000000=3×106,故选:C.4.参考答案:解:∵∠B=90°,∠A=45°,∴∠ACB=45°.∵∠EDF=90°,∠F=60°,∴∠DEF=30°.∵EF∥BC,∴∠EDC=∠DEF=30°,∴∠CED=∠ACB﹣∠EDC=45°﹣30°=15°.故选:A.5.参考答案:解:为了解人造卫星的设备零件的质量情况,应选择全面调查,即普查,不宜选择抽样调查,因此选项A不符合题意;方差是刻画数据波动程度的量,反映数据的离散程度,因此选项B 符合题意;购买一张体育彩票中奖,是可能的,只是可能性较小,是可能事件,因此选项C不符合题意;掷一枚质地均匀的硬币,正面朝上的概率为,因此选项D不符合题意;故选:B.6.参考答案:解:A.因为=2,所以A选项错误;B.因为()﹣1=2,所以B选项错误;C.因为a与2a2不是同类项,不能合并,所以C选项错误;D.因为(﹣a2)3=﹣a6,所以D选项正确.故选:D.7.参考答案:解:∵一次函数y=x+2,∴当x=1时,y=3,∴图象经过点(1,3),故选项A正确;令y=0,解得x=﹣2,∴图象与x轴交于点(﹣2,0),故选项B正确;∵k=1>0,b=2>0,∴不经过第四象限,故选项C正确;∵k=1>0,∴函数值y随x的增大而增大,当x=2时,y=4,∴当x>2时,y>4,故选项D不正确,故选:D.8.参考答案:解:圆锥的底面周长为2π×4=8πcm,即为展开图扇形的弧长,由弧长公式得,=8π,解得,R=12,即圆锥的母线长为12cm.故选:B.9.参考答案:解:∵关于x的方程x2﹣2(m﹣1)x+m2=0有两个实数根,∴△=[2(m﹣1)]2﹣4×1×(m2﹣m)=﹣4m+4≥0,解得:m≤1.∵关于x的方程x2+2(m﹣1)x+m2﹣m=0有两个实数根α,β,∴α+β=﹣2(m﹣1),α•β=m2﹣m,∴α2+β2=(α+β)2﹣2α•β=[﹣2(m﹣1)]2﹣2(m2﹣m)=12,即m2﹣3m﹣4=0,解得:m=﹣1或m=4(舍去).故选:A.10.参考答案:解:如图,作AM⊥BD于M,AN⊥EC于N.∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴EC=BD,∠BDA=∠AEC,故①正确∵∠DOF=∠AOE,∠DFO=∠EAO=90°,∴BD⊥EC,故②正确,∵△BAD≌△CAE,AM⊥BD,AN⊥EC,∴AM=AN,∴FA平分∠EFB,∴∠AFE=45°,故④正确,若③成立,则∠AEF=∠ABD=∠ADB,推出AB=AD,显然与条件矛盾,故③错误,故选:C.二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.)11.参考答案:解:∵正n边形的一个内角为135°,∴正n边形的一个外角为180°﹣135°=45°,∴n=360°÷45°=8.故答案为:8.12.参考答案:解:设该队胜了x场,负了y场,依题意有,解得.故该队胜了9场.故答案为:9.13.参考答案:解:如图,过点A作AC⊥BD于点C,根据题意可知:∠BAC=∠ABC=45°,∠ADC=30°,AB=20,在Rt△ABC中,AC=BC=AB•sin45°=20×=10,在Rt△ACD中,∠ADC=30°,∴AD=2AC=20(海里).答:此时轮船与小岛的距离AD为20海里.故答案为:20.14.参考答案:解:画树状图得:∵共有9种等可能的结果,两次取出的数字之和是奇数的有4种结果,∴两次取出的数字之和是奇数的概率为,故答案为:.15.参考答案:解:设每顶头盔的售价为x元,获得的利润为w元,w=(x﹣50)[200+(80﹣x)×20]=﹣20(x﹣70)2+8000,∴当x=70时,w取得最大值,此时w=8000,故答案为:70.16.参考答案:解:∵点P(1,0),P1在直线y=x上,∴P1(1,1),∵P1P2∥x轴,∴P2的纵坐标=P1的纵坐标=1,∵P2在直线y=﹣x上,∴1=﹣x,∴x=﹣2,∴P2(﹣2,1),即P2的横坐标为﹣2=﹣21,同理,P3的横坐标为﹣2=﹣21,P4的横坐标为4=22,P5=22,P6=﹣23,P7=﹣23,P8=24…,∴P4n=2,∴P2020的横坐标为2=21010,故答案为:21010.三、解答题(本大题共8个小题,满分72分.)17.参考答案:解:(1)原式=•=,当a=﹣1时,原式==2;(2),∵解不等式①得:x>﹣2,解不等式②得:x≤4,∴不等式组的解集是:﹣2<x≤4,在数轴上表示为:.18.参考答案:解:(1)如图1,M点就是所求作的点:(2)如图2,点N就是所求作的点:19.参考答案:解:(1)20÷50%=40(人),a=40×25%=10;36.5出现了20次,次数最多,所以众数是36.5;40个数据按从小到大的顺序排列,其中第20、21个数据都是36.5,所以中位数是(36.5+36.5)÷2=36.5.故答案为:10,36.5,36.5;(2)m%=×100%=15%,m=15;360°×=36°.故答案为:15,36;(3)该班学生的平均体温为:=36.455≈36.5(℃).20.参考答案:解:(1)∵y=x2+2x+3=(x+1)2+2,∴把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2:y=(x+1﹣4)2+2﹣5,即y=(x ﹣3)2﹣3,∴抛物线C2的函数关系式为:y=(x﹣3)2﹣3.(2)动点P(a,﹣6)不在抛物线C2上,理由如下:∵抛物线C2的函数关系式为:y=(x﹣3)2﹣3,∴函数的最小值为﹣3,∵﹣6<﹣3,∴动点P(a,﹣6)不在抛物线C2上;(3)∵抛物线C2的函数关系式为:y=(x﹣3)2﹣3,∴抛物线的开口向上,对称轴为x=3,∴当x<3时,y随x的增大而减小,∵点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0<3,∴y1>y2.21.参考答案:(1)证明:连接OD,AD,∵AB是直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴∠BAC=2∠BAD,∵∠BAC=2∠BDE,∴∠BDE=∠BAD,∵OA=OD,∴∠BAD=∠ADO,∵∠ADO+∠ODB=90°,∴∠BDE+∠ODB=90°,∴∠ODE=90°,即DF⊥OD,∵OD是⊙O的半径,∴DF是⊙O的切线.(2)解:∵AB=AC,AD⊥BC,∴BD=CD,∵BO=AO,∴OD∥AC,∴△EOD∽△EAF,∴,设OD=x,∵CF=2,BE=3,∴OA=OB=x,AF=AC﹣CF=2x﹣2,∴EO=x+3,EA=2x+3,∴=,解得x=6,经检验,x=6是分式方程的解,∴AF=2x﹣2=10.22.参考答案:解:(1)将点A坐标(6,1)代入反比例函数解析式y=,得k=1×6=6,则y=,故答案为:y=;(2)过点A作AC⊥x轴于点C,过B作BD⊥y轴于D,延长CA,DB交于点E,则四边形ODEC是矩形,设B(m,n),∴mn=6,∴BE=DE﹣BD=6﹣m,AE=CE﹣AC=n﹣1,∴S△ABE==,∵A、B两点均在反比例函数y=(x>0)的图象上,∴S△BOD=S△AOC==3,∴S△AOB=S矩形ODEC﹣S△AOC﹣S△BOD﹣S△ABE=6n﹣3﹣3﹣=3n﹣m,∵△AOB的面积为8,∴3n﹣m=8,∴m=6n﹣16,∵mn=6,∴3n2﹣8n﹣3=0,解得:n=3或﹣(舍),∴m=2,∴B(2,3),设直线AB的解析式为:y=kx+b,则,解得:,∴直线AB的解析式为:y=﹣x+4;(3)如图,根据“三角形两边之差小于第三边可知:当点P为直线AB与y轴的交点时,PA﹣PB有最大值是AB,把x=0代入y=﹣x+4中,得:y=4,∴P(0,4).23.参考答案:解:(1)∵ABCD是矩形,∴∠A=∠ADC=90°,∵将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,∴AD=AD′,AE=A′E,∠ADE=∠A′DE=45°,∴∵AB∥CD,∴∠AED=∠A′DE=∠ADE,∴AD=AD′,∴AD=AE=A′E=A′D,∴四边形AEA′D是菱形,∵∠A=90°,∴四边形AEA′D是正方形.故答案为:正方形;(2)MC′=ME.证明:如图1,连接C′E,由(1)知,AD=AE,∵四边形ABCD是矩形,∴AD=BC,∠EAC′=∠B=90°,由折叠知,B′C′=BC,∠B=∠B′,∴AE=B′C′,∠EAC′=∠B′,又EC′=C′E,∴Rt△EC′A≌Rt△CEB′(HL),∴∠C′EA=∠EC′B′,∴MC′=ME;(3)∵Rt△EC′A≌Rt△CEB′,∴AC′=B′E,由折叠知,B′E=BD,∴AC′=BE,∵AC′=2cm,DC′=4cm,∴AB=CD=2+4+2=8(cm),设DF=xcm,则FC′=FC=(8﹣x)cm,∵DC′2+DF2=FC′2,∴42+x2=(8﹣x)2,解得,x=3,即DF=3cm,如图2,延长BA、FC′交于点G,则∠AC′G=∠DC′F,∴tan∠AC′G=tan∠DC′F=,∴,∴,∵DF∥EG,∴△DNF∽△ENG,∴.24.参考答案:解:(1)妈妈骑车的速度为120米/分钟,妈妈在家装载货物时间为5分钟,点M的坐标为(20,1200).故答案为:120,5,(20,1200).(2),其图象如图所示,(3)由题意可知:小华速度为60米/分钟,妈妈速度为120米/分钟,①相遇前,依题意有60t+120t+360=1800,解得t=8分钟,②相遇后,依题意有,60t+120t﹣360=1800,解得t=12分钟.③依题意,当t=20分钟时,妈妈从家里出发开始追赶小华,此时小华距商店为1800﹣20×60=600米,只需10分钟,即t=30分钟,小华到达商店.而此时妈妈距离商店为1800﹣10×120=600米>360米,∴120(t﹣5)+360=1800×2,解得t=32分钟,∴t=8,12或32分钟时,两人相距360米。
2020年中考湖北潜江仙桃天门江汉油田数学卷
B
C
D.
9.如图,已知直线 l:y=
3 x,过点. A(0,1)作 y 轴的垂线.交直线 l 于点 B,过点 B 作直线 l
3
的垂线交 y 轴于点 A1。过点 A1 作 y 轴的垂线交直线 l 于点 B1,过点 B1 作直线 l 的垂线
交 y 轴于点 A2。…。按此作法继续下去,则点 A4 的坐标为
年我国财政收入约为 61330 亿元.下列命题:
①2007 年我国财政收入约为 61330(1-19.5%)亿元。
②这四年中,2009 年我国财政收入最少。
③2010 年我国财政收入约为 61330(1+11.7%)(1+21.3%)亿元.其中正确的有
A.3 个
B.2 个
C.1 个
D.0 个
2
二、填空题(本大题共 5 个小题,每小题 3 分,满分 15 分)
6.化简 ( m2 4 ) (m 2) 的结果是 m2 2m
A.0
B.1
C.-1
D. (m 2)2
A 46 B
E
F
154
C
D
(第 5 题图)
7.如图,在 6×6 的方格纸中,每个小方格都是边长为 1 的正方形, 其中 A、B、C 为格点.作△ABC 的外接圆⊙ O ,则 AC 的长等于
A O
3. 考试结束后,请将本试卷和答题卡一并上交.
一、选择题(本大题共 10 个小题,每小题 3 分,满分 30 分)
在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代
号在答题卡上涂黑,涂错或不涂均为零分. 1. 1 的倒数是
3
A. 1 3
B.- 3
C. 3
2020年仙桃市、潜江市、天门市、江汉油田中考数学试题及答案
2020年仙桃市、潜江市、天门市、江汉油田中考数学试卷一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.) 1.(3分)下列各数中,比﹣2小的数是( ) A .0B .﹣3C .﹣1D .|﹣0.6|2.(3分)如图是由4个相同的小正方体组成的立体图形,它的俯视图为( )A .B .C .D .3.(3分)我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( ) A .0.3×106B .3×107C .3×106D .30×1054.(3分)将一副三角尺按如图摆放,点E 在AC 上,点D 在BC 的延长线上,EF ∥BC ,∠B =∠EDF =90°,∠A =45°,∠F =60°,则∠CED 的度数是( ) A .15°B .20°C .25°D .30°5.(3分)下列说法正确的是( )A .为了解人造卫星的设备零件的质量情况,选择抽样调查B .方差是刻画数据波动程度的量C .购买一张体育彩票必中奖,是不可能事件D .掷一枚质地均匀的硬币,正面朝上的概率为1 6.(3分)下列运算正确的是( ) A .√4=±2B .(12)﹣1=﹣2C .a +2a 2=3a 3D .(﹣a 2)3=﹣a 67.(3分)对于一次函数y =x +2,下列说法不正确的是( ) A .图象经过点(1,3)B .图象与x 轴交于点(﹣2,0)C .图象不经过第四象限D .当x >2时,y <48.(3分)一个圆锥的底面半径是4cm ,其侧面展开图的圆心角是120°,则圆锥的母线长是( ) A .8cmB .12cmC .16cmD .24cm9.(3分)关于x 的方程x 2+2(m ﹣1)x +m 2﹣m =0有两个实数根α,β,且α2+β2=12,那么m 的值为( ) A .﹣1B .﹣4C .﹣4或1D .﹣1或410.(3分)如图,已知△ABC 和△ADE 都是等腰三角形,∠BAC =∠DAE =90°,BD ,CE 交于点F ,连接AF .下列结论:①BD =CE ;②BF ⊥CF ;③AF 平分∠CAD ;④∠AFE =45°.其中正确结论的个数有( ) A .1个B .2个C .3个D .4个二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.) 11.(3分)已知正n 边形的一个内角为135°,则n 的值是 .12.(3分)篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了 场.13.(3分)如图,海中有个小岛A ,一艘轮船由西向东航行,在点B 处测得小岛A 位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D 处,测得小岛A 在它的北偏西60°方向,此时轮船与小岛的距离AD 为 海里.14.(3分)有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为 .15.(3分)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为 元.16.(3分)如图,已知直线a :y =x ,直线b :y =−12x 和点P (1,0),过点P 作y 轴的平行线交直线a 于点P 1,过点P 1作x 轴的平行线交直线b 于点P 2,过点P 2作y 轴的平行线交直线a 于点P 3,过点P 3作x 轴的平行线交直线b 于点P 4,…,按此作法进行下去,则点P 2020的横坐标为 . 三、解答题(本大题共8个小题,满分72分.) 17.(12分)(1)先化简,再求值:a 2−4a+4a −2a÷a 2−42a,其中a =﹣1.(2)解不等式组{3x +2>x −2x−3≤7−5x ,并把它的解集在数轴上表示出来.18.(6分)在平行四边形ABCD中,E为AD的中点,请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图1,在BC上找出一点M,使点M是BC的中点;(2)如图2,在BD上找出一点N,使点N是BD的一个三等分点.19.(7分)5月20日九年级复学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.学生体温频数分布表组别温度(℃)频数(人数)甲36.36乙36.4a丙36.520丁36.64请根据以上信息,解答下列问题:(1)频数分布表中a=,该班学生体温的众数是,中位数是;(2)扇形统计图中m=,丁组对应的扇形的圆心角是度;(3)求该班学生的平均体温(结果保留小数点后一位).20.(8分)把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.(1)直接写出抛物线C2的函数关系式;(2)动点P(a,﹣6)能否在抛物线C2上?请说明理由;(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.21.(8分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.(1)求证:DF是⊙O的切线;(2)当CF=2,BE=3时,求AF的长.22.(9分)如图,直线AB与反比例函数y=kx(x>0)的图象交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.(1)填空:反比例函数的关系式为;(2)求直线AB的函数关系式;(3)动点P在y轴上运动,当线段P A与PB之差最大时,求点P的坐标.23.(10分)实践操作:第一步:如图1,将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,然后把纸片展平.第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C′处,点B落在点B'处,得到折痕EF,B'C′交AB于点M,C′F交DE于点N,再把纸片展平.问题解决:(1)如图1,填空:四边形AEA'D的形状是;(2)如图2,线段MC′与ME是否相等?若相等,请给出证明;若不等,请说明理由;(3)如图2,若AC′=2cm,DC'=4cm,求DN:EN的值.24.(12分)小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段AB表示小华和商店的距离y1(米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:(1)填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是.(2)直接写出妈妈和商店的距离y2(米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)求t为何值时,两人相距360米.参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.) 1.B .2.C .3.C .4.A .5.B .6.D .7.D .8.B .9.A .10.C .二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.) 11.8.12.9.13.20√2.14.49.15.70.16.21010.三、解答题(本大题共8个小题,满分72分.)17.【解答】解:(1)原式=(a−2)2a(a−2)•2a (a+2)(a−2)=2a+2, 当a =﹣1时,原式=2−1+2=2; (2){3x +2>x −2①x−33≤7−53x②, ∵解不等式①得:x >﹣2, 解不等式②得:x ≤4,∴不等式组的解集是:﹣2<x ≤4,在数轴上表示为:.18.【解答】解:(1)如图1,M 点就是所求作的点: (2)如图2,点N 就是所求作的点:19.【解答】解:(1)20÷50%=40(人),a =40×25%=10; 36.5出现了20次,次数最多,所以众数是36.5(℃);40个数据按从小到大的顺序排列,其中第20、21个数据都是36.5,所以中位数是(36.5+36.5)÷2=36.5(℃).故答案为:10,36.5℃,36.5℃;(2)m %=640×100%=15%,m =15; 360°×440=36°. 故答案为:15,36;(3)该班学生的平均体温为:36.3×6+36.4×10+36.5×20+36.6×440=36.455≈36.5(℃).20.【解答】解:(1)∵y =x 2+2x +3=(x +1)2+2,∴把抛物线C 1:y =x 2+2x +3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C 2:y =(x +1﹣4)2+2﹣5,即y =(x ﹣3)2﹣3, ∴抛物线C 2的函数关系式为:y =(x ﹣3)2﹣3. (2)动点P (a ,﹣6)不在抛物线C 2上,理由如下: ∵抛物线C 2的函数关系式为:y =(x ﹣3)2﹣3, ∴函数的最小值为﹣3, ∵﹣6<﹣3,∴动点P (a ,﹣6)不在抛物线C 2上;(3)∵抛物线C 2的函数关系式为:y =(x ﹣3)2﹣3, ∴抛物线的开口向上,对称轴为x =3, ∴当x <3时,y 随x 的增大而减小,∵点A (m ,y 1),B (n ,y 2)都在抛物线C 2上,且m <n <0<3, ∴y 1>y 2.21.【解答】(1)证明:连接OD ,AD , ∵AB 是直径, ∴∠ADB =90°, ∴AD ⊥BC , ∵AB =AC , ∴∠BAC =2∠BAD , ∵∠BAC =2∠BDE , ∴∠BDE =∠BAD , ∵OA =OD , ∴∠BAD =∠ADO , ∵∠ADO +∠ODB =90°,∴∠BDE +∠ODB =90°, ∴∠ODE =90°, 即DF ⊥OD , ∵OD 是⊙O 的半径, ∴DF 是⊙O 的切线.(2)解:∵AB =AC ,AD ⊥BC , ∴BD =CD , ∵BO =AO , ∴OD ∥AC , ∴△EOD ∽△EAF , ∴OD AF=EO EA,设OD =x , ∵CF =2,BE =3, ∴OA =OB =x , AF =AC ﹣CF =2x ﹣2, EO =x +3,EA =2x +3, ∴x 2x−2=x+32x+3,解得x =6,经检验,x =6是分式方程的解, ∴AF =2x ﹣2=10.22.【解答】解:(1)将点A 坐标(6,1)代入反比例函数解析式y =kx , 得k =1×6=6, 则y =6x, 故答案为:y =6x;(2)过点A 作AC ⊥x 轴于点C ,过B 作BD ⊥y 轴于D ,延长CA ,DB 交于点E ,则四边形ODEC 是矩形, 设B (m ,n ), ∴mn =6,∴BE =DE ﹣BD =6﹣m ,AE =CE ﹣AC =n ﹣1,∴S △ABE =12AE ⋅BE =12(n −1)(6−m),∵A 、B 两点均在反比例函数y =k x(x >0)的图象上, ∴S △BOD =S △AOC =12×6×1=3, ∴S △AOB =S 矩形ODEC ﹣S △AOC ﹣S △BOD ﹣S △ABE =6n ﹣3﹣3−12(n −1)(6−m)=3n −12m , ∵△AOB 的面积为8, ∴3n −12m =8, ∴m =6n ﹣16, ∵mn =6, ∴3n 2﹣8n ﹣3=0, 解得:n =3或−13(舍), ∴m =2, ∴B (2,3),设直线AB 的解析式为:y =kx +b ,则{6k +b =12k +b =3,解得:{k =−12b =4, ∴直线AB 的解析式为:y =−12x +4;(3)如图,根据“三角形两边之差小于第三边可知: 当点P 为直线AB 与y 轴的交点时,P A ﹣PB 有最大值是AB , 把x =0代入y =−12x +4中,得:y =4, ∴P (0,4).23.【解答】解:(1)∵ABCD 是矩形, ∴∠A =∠ADC =90°,∵将矩形纸片ABCD 沿过点D 的直线折叠,使点A 落在CD 上的点A '处,得到折痕DE , ∴AD =A ′D ,AE =A ′E ,∠ADE =∠A ′DE =45°, ∵AB ∥CD ,∴∠AED =∠A ′DE =∠ADE , ∴AD =AE ,∴AD =AE =A ′E =A ′D ,∴四边形AEA′D是菱形,∵∠A=90°,∴四边形AEA′D是正方形.故答案为:正方形;(2)MC′=ME.证明:如图1,连接C′E,由(1)知,AD=AE,∵四边形ABCD是矩形,∴AD=BC,∠EAC′=∠B=90°,由折叠知,B′C′=BC,∠B=∠B′,∴AE=B′C′,∠EAC′=∠B′,又EC′=C′E,∴Rt△EC′A≌Rt△C′EB′(HL),∴∠C′EA=∠EC′B′,∴MC′=ME;(3)∵Rt△EC′A≌Rt△C′EB′,∴AC′=B′E,由折叠知,B′E=BE,∴AC′=BE,∵AC′=2cm,DC′=4cm,∴AB=CD=2+4+2=8(cm),设DF=xcm,则FC′=FC=(8﹣x)cm,∵DC′2+DF2=FC′2,∴42+x2=(8﹣x)2,解得,x=3,即DF=3cm,如图2,延长BA、FC′交于点G,则∠AC′G=∠DC′F,∴tan∠AC′G=tan∠DC′F=AGAC′=DFDC′=34,∴AG=32 cm,∴EG=32+6=152cm,第11页(共11页) ∵DF ∥EG ,∴△DNF ∽△ENG ,∴DN EN =DF EG =3152=25. 24.【解答】解:(1)妈妈骑车的速度为120米/分钟,妈妈在家装载货物时间为5分钟,点M 的坐标为(20,1200).故答案为:120,5,(20,1200).(2)y 2={120t(0≤t <15)1800(15≤t <20)−120t +4200(20≤t ≤35), 其图象如图所示,(3)由题意可知:小华速度为60米/分钟,妈妈速度为120米/分钟,①相遇前,依题意有60t +120t +360=1800,解得t =8分钟,②相遇后,依题意有,60t +120t ﹣360=1800,解得t =12分钟.③依题意,当t =20分钟时,妈妈从家里出发开始追赶小华, 此时小华距商店为1800﹣20×60=600米,只需10分钟, 即t =30分钟,小华 到达商店.而此时妈妈距离商店为1800﹣10×120=600米>360米, ∴120(t ﹣5)+360=1800×2,解得t =32分钟,∴t =8,12或32分钟时,两人相距360米。
2020年湖北省天门、仙桃、潜江、江汉油田中考数学试题
天门仙桃潜江江汉油田2020年初中学业水平考试(中考)数学试卷一、选择题(本大题共10个小题,在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)1.下列各数中,比2-小的数是( )A. 0B. 3-C. 1-D. 0.6- B根据有理数的大小比较法则比较即可. 解:.0.606-=,∵32100.6-<-<-<<,∴比2-小的数是3-,故选:B .2.如图是由4个相同的小正方体组成的立体图形,它的俯视图为( )A. B. C. D. C根据俯视图是从立体图形上方看得到的图形解答即可.解:这个由4个相同的小正方体组成的立体图形:从上方可以看到前后两排正方形,后排有两个正方形,前排左边有一个正方形,即C 选项符合.故答案为C .3.我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )A.60.310⨯ B. 7310⨯ C. 6310⨯ D. 53010⨯ C根据科学记数法的定义即可得.科学记数法:将一个数表示成10n a ⨯的形式,其中110a ≤<,n 为整数,这种记数的方法叫做科学记数法则6⨯=故选:C.30000003104.将一副三角尺如图摆放,点E在AC上,点D在BC的延长线上,∠=∠=︒∠=︒∠=︒,则CED//,90,45,60EF BC B EDF A F∠的度数是()A. 15°B. 20°C. 25°D. 30°AEF BC可知∠CEF=∠ACB=45°,最后运用角的和差即根据三角板的特点可知∠ACB=45°、∠DEF=30°,根据//可解答.解:由三角板的特点可知∠ACB=45°、∠DEF=30°EF BC∵//∴∠CEF=∠ACB=45°,∴∠CED=∠CEF-∠DEF=45°-30°=15°.故答案为A.5.下列说法正确的是()A. 为了解人造卫星的设备零件的质量情况,选择抽样调查B. 方差是刻画数据波动程度的量C. 购买一张体育彩票必中奖,是不可能事件D. 掷一枚质地均匀的硬币,正面朝上的概率为1B根据抽样调查和普查、方差的意义、随机事件等知识逐项排除即可.解:A. 为了解人造卫星的设备零件的质量情况,选择普查,故A选项不符合题意;B. 方差是刻画数据波动程度的量,故B选项符合题意;C. 购买一张体育彩票必中奖,是随机事件,故C选项不符合题意;D. 掷一枚质地均匀的硬币,正面朝上的概率为0.5, 故D选项不符合题意.故答案为B.6.下列运算正确的是()A. 2=±B. 1122-⎛⎫=- ⎪⎝⎭ C. 2323a a a += D. ()326a a -=-D根据算术平方根,负整数指数幂,幂的乘方和合并同类项的运算法则进行判断即可.A 、2=,故本选项错误;B 、1122-⎛⎫= ⎪⎝⎭,故本选项错误;C 、2222a a a a +=+,故本选项错误;D 、()326a a -=-,故本选项正确;故选:D .7.对于一次函数2y x =+,下列说法不正确的是( )A . 图象经过点()1,3 B. 图象与x 轴交于点()2,0-C. 图象不经过第四象限D. 当2x >时,4y <D根据一次函数的图像与性质即可求解.A.图象经过点()1,3,正确;B.图象与x 轴交于点()2,0-,正确C.图象经过第一、二、三象限,故错误;D.当2x >时,y >4,故错误;故选D .8.一个圆锥的底面半径是4cm ,其侧面展开图的圆心角是120°,则圆锥的母线长是( )A. 8cmB. 12cmC. 16cmD. 24cmB根据题意求出圆锥的底面周长,根据弧长公式计算即可.解:圆锥的底面周长=2×π×4=8π,∴侧面展开图的弧长为8π, 则圆锥母线长=1808120ππ⨯=12(cm ),故选:B .9.关于x 的方程222(1)0x m x m m +-+-=有两个实数根α,β,且2212αβ+=,那么m 的值为()A. 1-B. 4-C. 4-或1D. 1-或4A通过根与系数之间的关系得到22m αβ,2m m αβ,由()2222αβαβαβ+=+-可求出m 的值,通过方程有实数根可得到[]()222(1)40m m m --≥-,从而得到m 的取值范围,确定m 的值.解:∵方程222(1)0x m x m m +-+-=有两个实数根α,β, ∴21221m m αβ, 221m m m m αβ, ∵()2222αβαβαβ+=+-,2212αβ+=∴()()2222212m m m -+-=-,整理得,2340m m --=,解得,11m =-,23m =,若使222(1)0x m x m m +-+-=有实数根,则[]()222(1)40m m m --≥-, 解得,1m ,所以1m =-,故选:A .10.如图,已知ABC 和ADE 都是等腰三角形,90BAC DAE ∠=∠=︒,,BD CE 交于点F ,连接AF ,下列结论:①BD CE =;②BF CF ⊥;③AF 平分CAD ∠;④45AFE ∠=︒.其中正确结论的个数有( )A. 1个B. 2个C. 3个D. 4个C ①证明△BAD ≌△CAE,再利用全等三角形的性质即可判断;②由△BAD ≌△CAE 可得∠ABF=∠ACF ,再由∠ABF+∠BGA=90°、∠BGA=∠CGF 证得∠BFC=90°即可判定;③分别过A 作AM ⊥BD 、AN ⊥CE,根据全等三角形面积相等和BD=CE ,证得AM=AN,即AF 平分∠BFE,即可判定;④由AF 平分∠BFE 结合BF CF ⊥即可判定.解:∵∠BAC=∠EAD∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE 在△BAD和△CAE中AB=AC, ∠BAD=∠CAE,AD=AE∴△BAD≌△CAE∴BD=CE故①正确;∵△BAD≌△CAE∴∠ABF=∠ACF∵∠ABF+∠BGA=90°、∠BGA=∠CGF∴∠ACF+∠BGA=90°,∴∠BFC=90°故②正确;分别过A作AM⊥BD、AN⊥CE垂足分别为M、N ∵△BAD≌△CAE∴S△BAD=S△CAE,∴1122BD AM CE AN ⋅=⋅∵BD=CE ∴AM=AN∴AF 平分∠BFE ,无法证明AF 平分∠CAD .故③错误;∵AF 平分∠BFE ,BFCF ⊥∴45AFE ∠=︒故④正确.故答案为C . 二、填空题(本大题共6个小题,请将结果直接填写在答题卡对应的横线上)11.正n 边形的一个内角等于135°,则边数n 的值为_________.8先根据多边形的外角与相邻的内角互补求出外角的度数,再根据外角和求边数即可.多边形的外角是:180﹣135=45°,∴n =36045=8. 12.篮球联赛中,每玚比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了_________场.9设该对胜x 场,则负14-x 场,然后根据题意列一元一次方程解答即可.解:设该对胜x 场由题意得:2x+(14-x )=23,解得x=9.故答案为9.13.如图,海中有个小岛A ,一艘轮船由西向东航行,在点B 处测得小岛A 位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D 处,测得小岛A 在它的北偏西60°方向,此时轮船与小岛的距离AD 为________海里.202过点A作AC⊥BD,根据方位角及三角函数即可求解.如图,过点A作AC⊥BD,依题意可得∠ABC=45°∴△ABC是等腰直角三角形,AB=20(海里)∴AC=BC=ABsin45°=102(海里)在Rt△ACD中,∠ADC=90°-60°=30°∴AD=2AC=202(海里)故答案为:202.14.有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为_________.49根据题意列出表格,找出所有可能结果和满足条件的结果即可求出.依题意列的表格如下:由表格看出共有9种结果,奇数的结果是4种. 故答案是49. 15.某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为_______元.70设降价x 元,利润为W ,根据题意得出方程,然后求出取最大值时的x 值即可得到售价.解:设降价x 元,利润为W ,由题意得:W=(80-50-x)(200+20x),整理得:W=-20x 2+400x+6000=-20(x-10)2+8000,∴当x=10时,可获得最大利润,此时每顶头盔的售价为:80-10=70(元),故答案为:70.16.如图,已知直线:a y x =,直线1:2b y x =-和点()1,0P ,过点1P 作y 轴的平行线交直线a 于点1P ,过点1P 作x 轴的平行线交直线b 于点2P ,过点2P 作y 轴的平行线交直线a 于点3P ,过点3P 作x 轴的平行线交直线b 于点4P ,…,按此作法进行下去,则点2020P 的横坐标为____.10102根据题意求出P 1,P 5,P 9…的坐标,发现规律即可求解.∵()1,0P ,1P 在直线:a y x =上∴1P (1,1); ∵过点1P 作x 轴的平行线交直线b 于点2P ,2P 在直线1:2b yx =-上 ∴2P (-2,1)同理求出P 3(-2,-2),P 4(4,-2),P 5(4,4),P 6(-8,4),P 7(-8,-8),P 8(16,-8),P 9(16,16)… 可得P 4n+1(22n , 22n )(n≥1,n 为整数)令4n+1=2021解得n=505∴P 2021(10102,10102 )∴2020P 的横坐标为10102.三、解答题(本大题共8个小题)17.(1)先化简,再求值:22244422a a a a a a-+-÷-,其中1a =-. (2)解不等式组32235733x x x x +>-⎧⎪-⎨≤-⎪⎩,并把它的解集在数轴上表示出来.(1)22a +,2;(2)24x -<≤,数轴见解析 (1)首先把分式的分子和分母分解因式,把除法去处转化成乘法运算,再把a 代入计算即可;(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.(1)22244422a a a a a a-+-÷- 2(2)2(2)(2)(2)a a a a a a -=⋅-+- 22a =+, 当1a =-时,原式2212==-+; (2)解:由322x x +>-得:2x >-, 由35733x x --得:4x ≤, ∴不等式组的解集为:24x -<≤.在数轴上表示如下:18.在平行四边形ABCD 中,E 为AD 的中点,请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图1,在BC 上找出一点M ,使点M 是BC 的中点;(2)如图2,在BD 上找出一点N ,使点N 是BD 的一个三等分点.(1)见解析;(2)见解析(1)连接对角线AC,BD ,再连接E 与对角线的交点,与BC 的交点即为M 点;(2)连接CE 交BD 即为N 点,根据相似三角形的性质可得12ND DE NB BC ==,于是DN=13BD . 解:(1)如图1,点M 即为所求;(2)如图2,点N 即为所求.19.5月20日九年级复学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.学生体温频数分布表:组别 温度(℃) 频数(人数)甲36.3 6乙36.4 a丙36.5 20丁36.6 4请根据以上信息,解答下列问题:(1)频数分布表中a=__________,该班学生体温的众数是_______,中位数是_________;(2)扇形统计图中m=__________,丁组对应的扇形的圆心角是_________度;(3)求该班学生的平均体温(结果保留小数点后一位).(1)10,36.5,36.5;(2)15,36;(3)36.5℃【分析】(1)先求出调查的学生总人数,再分别减去各组人数即可求出a,再根据众数、中位数的定义即可求解;(2)分别求出甲、丁的占比即可求解;(3)根据加权平均数的定义即可求解.解:(1)调查的学生总人数为20÷50%=40(人)频数分布表中40620410a=---=,该班学生体温的众数是36.5,中位数是36.5;故答案为:10,36.5,36.5;(2)扇形统计图中64010015m=÷⨯=,丁组对应的扇形的圆心角是436040⨯︒=36度;故答案为:15,36;(3)该班学生的平均体温为36.3636.41036.52036.6436.45536.5610204⨯+⨯+⨯+⨯=≈+++(℃). 20.把抛物线21:23C y x x =++先向右平移4个单位长度,再向下平移5个单位长度得到抛物线2C .(1)直接写出抛物线2C 的函数关系式;(2)动点(),6Pa -能否在拋物线2C 上?请说明理由; (3)若点()()12,,,A m y B n y 都在抛物线2C 上,且0m n <<,比较12,y y 的大小,并说明理由.(1)2(3)3y x =--;(2)不在,见解析;(3)12y y >,见解析(1)先求出抛物线1C 的顶点坐标,再根据向右平移横坐标加,向下平移纵坐标减求出平移后的抛物线的顶点坐标即可;(2)根据抛物线2C 的顶点的纵坐标为3-,即可判断点()6Pa -,不在拋物线2C 上; (3)根据抛物线2C 的增减性质即可解答.(1)抛物线221:23(1)2C y x x x =++=++,∴抛物线1C 的顶点坐标为(-1,2),根据题意,抛物线2C 的顶点坐标为(-1+4,2-5),即(3,-3),∴抛物线2C 的函数关系式为:2(3)3y x =--;(2)动点P 不在抛物线2C 上.理由如下:∵抛物线2C 的顶点为()3,3-,开口向上,∴抛物线2C 的最低点的纵坐标为3-.∵63P y =-<-,∴动点P 不在抛物线2C 上;(3)12y y >.理由如下:由(1)知抛物线2C 的对称轴是3x =,且开口向上,∴在对称轴左侧y 随x 的增大而减小.∵点()()12,,,A m y B n y 都在抛物线2C 上,且03m n <<<,∴12y y >.21.如图,在ABC 中,AB AC =,以AB 为直径的⊙O 交BC 于点D ,过点D 的直线EF 交AC 于点F ,交AB 的延长线于点E ,且2BAC BDE ∠=∠.(1)求证:DF 是⊙O 的切线;(2)当2,3CF BE ==时,求AF 的长.(1)见解析;(2)10(1)连接OD ,AD ,由AB 是直径可得到90ADB ∠=︒,然后通过题中角的关系可推出90ODE ∠=︒,即可得证;(2)通过EOD EAF ∽,得到OD EO AF EA=,然后设OD x =,列分式方程即可解得x ,从而得到AF 的长. (1)证明:如图,连接OD ,AD ,∵AB 是直径,∴90ADB ∠=︒.∴AD BC ⊥.∵AB AC =,∴2BAC BAD ∠=∠,∴2BAC BDE ∠=∠,∴BDE BAD ∠=∠.∵OA OD =,∴BAD ADO =∠∠.∵ADO ODB 90∠+∠=︒,∴90BDE ODB ∠+∠=︒.∴90ODE ∠=︒,即DFOD ⊥. 又OD 是O 的半径, ∴DF 是O 的切线.(2)解:∵,=⊥AB AC AD BC ,∴BD CD =.∵BO AO =,∴//OD AC .∴EOD EAF ∽, ∴OD EO AF EA=. 设OD x =,∵2CF =,3BE =,∴OA OB x ==,22AFAC CF x =-=-,3EO x =+,23EA x =+. ∴32223x x x x +=-+. 解得6x =.经检验6x =是所列分式方程的解.∴2210AF x =-=.【分析】本题考查了切线的判定,相似三角形的判定和性质,熟练掌握切线的判定方法是解题的关键. 22.如图,直线AB 与反比例函数(0)k y x x=>的图象交于A ,B 两点,已知点A 的坐标为()6,1,AOB 的面积为8.(1)填空:反比例函数的关系式为_________________;(2)求直线AB 的函数关系式;(3)动点P 在y 轴上运动,当线段PA 与PB 之差最大时,求点P 的坐标.(1)6y x =;(2)142y x =-+;(3)()0,4 (1)把点()6,1代入解析式,即可得到结果;(2)过点A 作AC x ⊥轴于点C ,过点B 作BD y ⊥轴于点D ,,CA DB 交于点E ,则四边形OCED 为矩形,设点B 的坐标为(),m n ,表示出△ABE 的面积,根据△AOB 得面积可得616m n =-,得到点B 的坐标,代入即可的到解析式;(3)根据“三角形两边之差小于第三边”可知,当点P 为直线AB 与y 轴的交点时,PA PB -有最大值为AB ,代入即可求值.解:(1)把点()6,1A 代入(0)k y x x =>可得6k =, ∴反比例函数的解析式为6y x=; (2)如图,过点A 作AC x ⊥轴于点C ,过点B 作BD y ⊥轴于点D ,,CA DB 交于点E ,则四边形OCED 为矩形.设点B 的坐标为(),m n ,∴6mn =. ∵点A 的坐标为()6,1, ∴6,1BEDE BD m AE CE AC n =-=-=-=-. ∴11(1)(6)22ABE S AE BE n m =⋅=--. ∵A ,B 两点均在双曲线6(0)y x x=>上, ∴16132BOD AOC S S ==⨯⨯=.∴AOB AOC BOD ABE OCED S S S S S =---矩形 11633(1)(6)322n n m n m =-----=-. ∵AOB 的面积为8,∴1382n m -=,整理得616m n =-. ∴23830n n --=.解得1213,3n n ==-(舍去). ∴2m =.∴点B 的坐标为(2,3).设直线AB 的函数关系式为(0)y kx b k =+≠,则6123k b k b +=⎧⎨+=⎩.解得124k b =-=⎧⎪⎨⎪⎩.∴直线AB 的函数关系式为142y x =-+.(3)如上图,根据“三角形两边之差小于第三边”可知,当点P 为直线AB 与y 轴的交点时,PA PB -有最大值为AB ,把0x =代入142y x =-+,得4y =. ∴点P 的坐标为()0,4.23.实践操作:第一步:如图1,将矩形纸片ABCD 沿过点D 的直线折叠,使点A 落在CD 上的点A '处,得到折痕DE ,然后把纸片展平.第二步:如图2,将图1中的矩形纸片ABCD 沿过点E 的直线折叠,点C 恰好落在AD 上的点C '处,点B 落在点B '处,得到折痕EF ,B C ''交AB 于点M ,C F '交DE 于点N ,再把纸片展平.问题解决:(1)如图1,填空:四边形AEA D '的形状是_____________________;(2)如图2,线段MC '与ME 是否相等?若相等,请给出证明;若不等,请说明理由;(3)如图2,若2cm,'4cm AC DC '==,求:DN EN 的值.(1)正方形;(2)MC ME '=,见解析;(3)25(1)有一组邻边相等且一个角为直角的平行四边形是正方形;(2)连接EC ',由(1)问的结论可知,90AD BC EAC B '=∠=∠=︒,,又因为矩形纸片ABCD 沿过点E 的直线折叠,可知折叠前后对应角以及对应边相等,有B B '∠=∠,B C BC ''=,90AE B C EAC B ''''=∠=∠=︒,,可以证明Rt EC A '和Rt C EB ''全等,得到C EA EC B '''∠=∠,从而有MC ME '=;(3)由Rt EC A Rt C EB '''≌,有AC B E ''=;由折叠知,AC BE '=,可以计算出()8cm AB =;用勾股定理计算出DF 的长度,再证明DNF ENG ∽得出等量关系,从而得到:DN EN 的值. (1)解:∵ABCD 是平行四边形,∴'////AD BC EA ,'//AE DA∴四边形'AEA D 是平行四边形∵矩形纸片ABCD 沿过点D 的直线折叠,使点A 落在CD 上的点A '处∴'AED A ED ≌∴'AE A E =∵90A ∠=∴四边形AEA D '的形状是正方形故最后答案为:四边形AEA D '的形状是正方形;(2)MC ME '=理由如下:如图,连接EC ',由(1)知:AD AE =∵四边形ABCD 是矩形,∴90AD BC EAC B '=∠=∠=︒,由折叠知:B C BC B B '''=∠=∠,∴90AE B C EAC B ''''=∠=∠=︒,又EC C E ''=,∴Rt EC A Rt C EB '''≌∴C EA EC B '''∠=∠∴MC ME '=(3)∵Rt EC A Rt C EB '''≌,∴AC B E ''=由折叠知:B E BE '=,∴AC BE '=∵2(cm)4(cm)AC DC ''==,∴()2428cm AB CD ==++= 设cm DF x =,则()8cm FC FC x '==-Rt DC F '中,由勾股定理得:2224(8)x x +=-解得:3x =,即()3cm DF =如图,延长BA FC ',交于点G ,则AC G DC F ''∠=∠ ∴3tan tan 4AG DF AC G DC F AC DC ''∠=∠==='' ∴3(cm)2AG =∴3156(cm)22EG=+=∵//DF EG,∴DNF ENG∽∴152::3:25DN EN DF EG===24.小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段AB表示小华和商店的距离1y(米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:(1)填空:妈妈骑车的速度是___________米/分钟,妈妈在家装载货物所用时间是__________分钟,点M的坐标是___________;(2)直接写出妈妈和商店的距离2y(米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)求t为何值时,两人相距360米.(1)120,5,()20,1200;(2)2120(015)1800(1520)1204200(2035)t ty tt t≤<⎧⎪=≤<⎨⎪-+≤≤⎩,见解析;(3)当t为8,12或32(分钟)时,两人相距360米.(1)先求出小华步行的速度,然后即可求出妈妈骑车的速度;先求出妈妈回家用的时间,然后根据小华到达商店比妈妈返回商店早5分钟,即可求出装货时间;根据题意和图像可得妈妈在M点时开始返回商店,然后即可求出M的坐标;(2)分①当0≤t<15时,②当15≤t<20时,③当20≤t≤35时三段求出解析式即可,根据解析式画图即可;(3)由题意知,小华速度为60米/分钟,妈妈速度为120米/分钟,分①相遇前,②相遇后,③在小华到达以后三种情况讨论即可.解:(1)由题意可得:小华步行的速度为:180030=60(米/分钟), 妈妈骑车的速度为:1800601010-⨯=120(米/分钟); 妈妈回家用的时间为:1800120=15(分钟), ∵小华到达商店比妈妈返回商店早5分钟,∴可知妈妈在35分钟时返回商店,∴装货时间为:35-15×2=5(分钟),即妈妈在家装载货物的时间为5分钟;由题意和图像可得妈妈在M 点时开始返回商店, ∴M 点的横坐标为:15+5=20(分钟),此时纵坐标为:20×60=1200(米),∴点M 的坐标为()20,1200;故答案为:120,5,()20,1200; (2)①当0≤t <15时y 2=120t ,②当15≤t <20时y 2=1800,③当20≤t≤35时,设此段函数解析式为y 2=kx+b ,将(20,1800),(35,0),代入得180020035k b k b =+⎧⎨=+⎩, 解得1204200k b =-⎧⎨=⎩,∴此段的解析式为y 2=-120x+4200,综上:2120(015)1800(1520)1204200(2035)t t y t t t ≤<⎧⎪=≤<⎨⎪-+≤≤⎩; 其函数图象如图,21;(3)由题意知,小华速度为60米/分钟,妈妈速度为120米/分钟, ①相遇前,依题意有601203601800t t ++=,解得8t=(分钟); ②相遇后,依题意有601203601800t t +-=,解得12t=(分钟); ③依题意,当20t =分钟时,妈妈从家里出发开始追赶小华,此时小华距商店180********-⨯=(米),只需10分钟, 即30t =分钟时,小华到达商店,而此时妈妈距离商店为180010120600-⨯=(米)360>(米), ∴()120536018002t -+=⨯,解得32t =(分钟), ∴当t 为8,12或32(分钟)时,两人相距360米.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年湖北省仙桃市、潜江市、天门市、江汉油田中考数学试卷
一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给
出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)
1. 下列各数中,比−2小的数是()
A.0
B.−3
C.−1
D.|−0.6|
2. 如图是由4个相同的小正方体组成的立体图形,它的俯视图为()
A. B. C. D.
3. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多
项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为()
A.0.3×106
B.3×107
C.3×106
D.30×105
4. 将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF // BC,∠B=∠EDF=90∘,∠A=45∘,∠F=60∘,则∠CED的度数是()
A.15∘
B.20∘
C.25∘
D.30∘
5. 下列说法正确的是()
A.为了解人造卫星的设备零件的质量情况,选择抽样调查
B.方差是刻画数据波动程度的量
C.购买一张体育彩票必中奖,是不可能事件
D.掷一枚质地均匀的硬币,正面朝上的概率为1
6. 下列运算正确的是()
A.√4=±2
B.(1
2
)−1=−2 C.a+2a2=3a3 D.(−a2)3=−a6
7. 对于一次函数y=x+2,下列说法不正确的是()
A.图象经过点(1, 3)
B.图象与x轴交于点(−2, 0)
C.图象不经过第四象限
D.当x>2时,y<4
8. 一个圆锥的底面半径是4cm,其侧面展开图的圆心角是120∘,则圆锥的母线长是()
A.8cm
B.12cm
C.16cm
D.24cm
9. 关于x的方程x2+2(m−1)x+m2−m=0有两个实数根α,β,且α2+β2=12,那么m的值为()
A.−1
B.−4
C.−4或1
D.−1或4
10. 如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90∘,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45∘.其中正确结论的个数有()
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共6个小题,每小题3分,满分18分.请将结果直接填写在答题卡对应的横线上.)
11. 已知正n边形的一个内角为135∘,则n的值是________.
12. 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了________场.
13. 如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的
东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏
西60∘方向,此时轮船与小岛的距离AD为________海里.
14. 有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混
在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为________.
15. 某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头
盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为________元.16. 如图,已知直线a:y=x,直线b:y=−1
2
x和点P(1, 0),过点P作y轴的平行线交
直线a于点P1,过点P1作x轴的平行线交直线b于点P2,过点P2作y轴的平行线交直线a
于点P3,过点P3作x轴的平行线交直线b于点P4,…,按此作法进行下去,则点P2020的
横坐标为________.
三、解答题(本大题共8个小题,满分72分.)
17.
(1)先化简,再求值:a 2−4a+4
a2−2a
÷a2−4
2a
,其中a=−1.
(2)解不等式组{
3x+2>x−2
x−3
3
≤7−5
3
x,并把它的解集在数轴上表示出来.
18. 在平行四边形ABCD中,E为AD的中点,请仅用无刻度的直尺完成下列画图,不
写画法,保留画图痕迹.。
