福建省石狮市七级数学上册 第三章 整式的加减导学案(无答案)(新版)华东师大版
2023七年级数学上册第3章整式的加减3.3整式1单项式教案(新版)华东师大版

3. 信息化资源:多媒体教学课件、动画演示、互动软件、在线练习题库。
4. 教学手段:讲解法、示范法、练习法、小组合作法、讨论法、反馈法。
教学流程
一、导入新课(用时5分钟)
同学们,今天我们将要学习的是《整式的加减》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要合并同类项的情况?”(举例说明)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索整式加减的奥秘。
请同学们认真对待课后拓展,这将有助于巩固本节课所学知识,并提高自己的数学素养。如有需要,我会提供必要的指导和帮助,期待同学们的进步!
反思改进措施
(1)引入实际问题:在教学中,我通过引入实际问题,如小明买苹果和橙子的例子,使学生能够将数学知识与实际生活联系起来,提高了学生的学习兴趣和参与度。
(2)鼓励学生提问:我鼓励学生在课堂上提问,并通过小组讨论和合作,促进学生之间的交流和互动,从而提高学生的思维能力和团队合作能力。
为了巩固本节课所学内容,请同学们完成以下检测题目:
(1)合并同类项:
a. 2x + 3x = _______
b. 4y^2 - 5y^2 = _______
c. 7z^3 - 2z^3 = _______
(2)处理不同类项:
a. 合并以下整式:2x^2 + 3xy - 4y^2 + 5x - 2y
b. 合并以下整式:4a^3 - 5a^2b + 3ab^2 - 2a
8. 培养学生的创新思维能力,通过解决实际问题,学生能够学会运用所学知识进行创新性的思考和解决问题。
华师版七年级数学上册(HS)导学案 第三章 整式的加减 整式的加减

4. 整式的加减学习目标:1.能熟练正确地运用合并同类项、去括号的法则进行整式的加减运算(重点);2.能用整式加减运算解决实际问题(难点).自主学习一、知识链接1.在3222112,3,1,,,,4,,43xy x x y m n x ab x x --+---+,π2b 中,单项式有:____________________________________; 多项式有: ; 整式有: . 2.同类项:必须同时具备的两个条件(缺一不可): ①所含的 相同;②相同 也相同. 合并同类项,就是把多项式中的同类项合并成一项.方法:把同类项的 相加,而 不变. 3.去括号法则:(1)括号前面是“+”号,把括号和它前面的“+”号去掉,原括号里的各项都 正负号.(2)括号前面是“-”号,把括号和它前面的“-”号去掉,原括号里的各项都 正负号.二、新知预习(预习课本P109-111)完成练习:练习:计算:(1)2n-5mn).合作探究一、要点探究探究点1:整式的加减运算问题:小亮和小莹到希望小学去看望小同学,小亮买了10支钢笔和5本字典作为礼物;小莹买了6支钢笔、4本字典和2个文具盒作为礼物.已知钢笔的售价为每支a元,字典的售价为每本b元,文具盒的售价为每个c元.请你计算:(1)小亮花了________元;小莹花了__________元;小亮和小莹共花______________元.(2)小亮比小莹多花_______________元.想一想:如何把上述的整式的化简?【要点归纳】整式加减运算的一般步骤是先去括号,再合并同类项.求整式ab-a-b与整式-2ab-a+b的和.计算:3(2x2-y2)-2(3y2-2x2).【方法总结】先运用去括号法则去括号,然后合并同类项.去括号时,如果括号前面是负号,那么括号中的每一项都要变号,注意不要漏乘;合并同类项时,只把系数相加减,字母与字母的指数不变.【针对训练】计算:(1)2(2ab+3a)﹣3(2a﹣ab);(2)a2﹣[﹣4ab+(ab﹣a2)]﹣2ab.化简求值:3x2﹣[x2﹣2(3x﹣x2)],其中x=﹣7;【针对训练】化简求值:12a -2(a -13b 2)-(32a —13b 2)+1,其中a =2,b =-32.【方法总结】化简求值时,一般先将整式进行化简,当代入求值时,要适当添上括号,否则容易发生计算错误,同时还要注意代数式中同一字母必须用同一数值代替,代数式中原有的数字和运算符号都不改变.已知ab=3,a+b=4,求3ab -[2a - (2ab-2b)+3]的值.【方法总结】 运用整体思想,将需要求值的整式用已知的整式表示,然后整体代入求值.【针对训练】已知xy =﹣2,x+y =3,求整式(3xy+10y )+[5x ﹣(2xy+2y﹣3x)]的值.探究点2:整式加减的应用一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本4本,买圆珠笔3支;小强买这种笔记本3本,买圆珠笔2支.(1)买这些笔记本和圆珠笔,两人一共花费多少钱?(2)请结合生活实际选取适当的x,y值,计算两人的总花费.【针对训练】某校七年级(1)(2)(3)(4)四个班的学生在植树节这9x+5)棵.其中(1)班植树x棵,(2)班植树的棵数比(1)天共植树(2班的2倍少40棵,(3)班植树的棵数比(2)班的一半多30棵.(1)求(1)(2)(3)班共植树多少棵;(2)若x=40,求(4)班植树多少棵?二、课堂小结整式的加减当堂检测1.比2a2﹣3a﹣7少3﹣2a2的多项式是()A.﹣3a﹣4 B.﹣4a2﹣3a+10 C.4a2﹣3a﹣10 D.﹣3a﹣102.若m=2>n B.m=n C.m<n D.不能确定3.长方形的一边长等于3a+2b,另一边长等于4a+b,那么这个长方形的周长是()A.14a+6bB.7a+3bC.10a+10bD.12a+8b4.已知m-n=100,-y)的值是( )A.99B.101C.-99D.-101 5.多项式32281x x x -+-与多项式323253x mx x +-+的和不含二次项,则m 的值为( )A.2B.-2C.4D.-46.已知220a ab -=,212ab b -=-,则22a b -=_______;222a ab b -+=_______.7.先化简,再求值.(1),其中;(2)2,23),3123()3141(222-==+-+--y x y x y x x 其中;8.做大小两个长方体纸盒,尺寸如下(单位:cm ):长 宽 高 小纸盒 a b c 大纸盒1.5a2b2c2223(421)2(31)a a a a a +----+12a =-(1)做这两个纸盒共用料多少平方厘米? (2)做大纸盒比做小纸盒多用料多少平方厘米?参考答案自主学习 一、知识链接1.单项式有:22,3,,,xy m n ab --π2b ;多项式有:3211,,44x x y x -+--;整式有:32221,3,1,,,4,,4xy x x y m n x ab --+---π2b .2.字母 字母的指数 系数 字母和字母的指数3.①不改变 ②改变 二、新知预习练习:解:(1)原式=x-5y-32n+5mn=3m 2n. 合作探究 一、要点探究探究点1:整式的加减运算问题 (1)(10a+5b ) (6a+4b+2c ) (10a+5b+6a+4b+2c )(2)[10a+5b-(6a+4b+2c )]解:由题意得ab-a-b+(-2ab-a+b )=-ab-2a.解:原式=6x 2-3y 2-6y 2+4x 2=10x 2-9y 2. 【针对训练】解:(1)原式=4ab+6a ﹣6a+3ab =7ab.(2)原式=a 2﹣(﹣4ab+ab ﹣a 2)﹣2ab =a 2+4ab ﹣ab+a 2﹣2ab =2a 2+ab.解:原式=3x 2﹣(x 2﹣6x+2x 2)=3x 2﹣3x 2+6x =6x ,当x =﹣7时,原式=6×(﹣7)=﹣42.【针对训练】解:原式=12a -2a+32b 2-32a+13b 2+1=-3a+b 2+1.当a =2,b=-32时,原式=-3×2+(-32)2+1=411.解:原式=3ab -2a + 2ab-2b-3=5ab -2a -2b-3=5ab -2(a+b )-3,当ab=3,a+b=4时,原式=5×3-2×4-3=4.【针对训练】解:原式=3xy+10y+(5x ﹣2xy ﹣2y+3x )=3xy+10y+5x ﹣2xy ﹣2y+3x =xy+8(y+x ).当xy =﹣2,x+y =3时,原式=﹣2+8×3=22. 探究点2:整式加减的应用解:(1)小红的花费为(4x+3y )元,小强的花费为(3x+2y )元, 两人一共花费4x+3y+3x+2y =(7x+5y )元.(2)答案不唯一,如:当x =3,y =1时,原式=7×3+5×1=26(元). 答:两人的总花费为26元.【针对训练】解:(1)x+2x-40+21(2x-40)+30=(4x-30)(棵). 故(1)(2)(3)班共植树(4x-30)棵.(2)(29x+5)-(4x-30)=29x+5-4x+30=(21x+35)(棵), 当x=40时,原式=20+35=55. 故(4)班植树55棵. 当堂检测1.C2.A3.A4.D5.C6.8 327.解:(1)原式=2223421622a a a a a +---+-=23a -.将12a =-代入上式,原式=2111()324--=-.(2)原式=2212312323x x y x y -+-+=2x y -+.将3,22x y ==-代入上式,原式=235(2)22-+-=.8.解:(1)2(1.5a ×2b+2b ×2c+1.5a ×2c )+2(ab+bc+ac )=6ab+8bc+6ac+2ab+2bc+2ac =(8ab+10bc+8ac)(cm 2). 答:做这两个纸盒共用料(8ab+10bc+8ac )cm 2.(2)2(1.5a ×2b+2b ×2c+1.5a ×2c )﹣2(ab+bc+ac )=6ab+8bc+6ac ﹣(2ab+2bc+2ac)=(4ab+6bc+4ac)(cm 2).答:做大纸盒比做小纸盒多用料(4ab+6bc+4ac )cm 2.。
七年级数学上册 3.4.4 整式的加减导学案 (新版)华东师大版

4.整式的加减学前温故计算:(1)3x+3(1-x);(2)(5a2-3b)-3(a2-2b).新课早知1.整式加减的一般步骤是:先______,再__________.2.求x3+x2y与x3+2x2y-y3的差.3.先化简,再求值:(1)5x2-(3y2+7xy)+(2y2-5x2),其中x=1,y=2.(2)(2a2b-3ab+8a3)+2(2ab-4a3-3a2b),其中a=-2,b=4.答案:学前温故解:(1)原式=3x+3-3x=3.(2)原式=5a2-3b-3a2+6b=2a2+3b.新课早知1.去括号合并同类项2.解:x3+x2y-(x3+2x2y-y3)=x3+x2y-x3-2x2y+y3=-x2y+y3.3.解:(1)原式=5x2-3y2-7xy+2y2-5x2=-y2-7xy.当x=1,y=2时,-y2-7xy =-22-7×1×2=-18;(2)原式=2a2b-3ab+8a3+4ab-8a3-6a2b=(2a2b-6a2b)+(-3ab+4ab)+(8a3-8a3)=-4a2b+ab.当a=-2,b=4时,-4a2b+ab=-4×(-2)2×4+(-2)×4=-72.1.利用整式的加减比较整式的大小【例1】已知:M=4x2-3x-2,N=6x2-3x+6,试比较M与N的大小.分析:M-N>0,则M>N;M-N<0,则M<N.解:∵M-N=(4x2-3x-2)-(6x2-3x+6)=4x2-3x-2-6x2+3x-6=-2x2-8<0,∴M<N.比较两数(或整式)的大小时,可以采用作差与0比较大小,当差大于零时,被减数较大;差小于零时,被减数较小.2.整式的加减与有理数有关概念的综合【例2】有理数a、b、c在数轴上的位置如图所示,化简|a|+|b|+|a-b|+|b-c|.分析:由数轴可知,a<0,b>0,c>0,a<b<c.解:|a|+|b|+|a-b|+|b-c|=-a+b-(a-b)-(b-c)=-a+b-a+b-b+c=-2a+b+c.(1)正数的绝对值等于它本身,负数的绝对值等于它的相反数.(2)“数形结合”是解决数学问题的重要方法.1.计算-(a-b)-3(a-b)的结果是( ).A.-4a+4b B.-4a-2bC.-4a-4b D.-4a+2b2.下列各式化简正确的是( ).A.a-(2a-b+c)=-a-b+cB.(a+b)-(-b+c)=a+2b+cC.3a-[5b-(2c-a)]=2a-5b+2cD.a-(b+c)-d=a-b+c-d3.计算6a2-5a+3与5a2+2a-1的差,结果正确的是( ).A.a2-3a+4 B.a2-3a+2C.a2-7a+2 D.a2-7a+44.代数式2(x-2y)与(2x+y)的差为__________.5.若多项式x2-7x-2减去m的差为3x2-11x-1,则m=__________.6.化简:5(a2b-3ab2)-2(a2b-7ab2).答案:1.A2.C A中a-(2a-b+c)=-a+b-c;B中(a+b)-(-b+c)=a+2b-c;D中a-(b+c)-d=a-b-c-d.3.D 6a2-5a+3-(5a2+2a-1)=6a2-5a+3-5a2-2a+1=a2-7a+4.4.-5y2(x-2y)与(2x+y)的差是2(x-2y)-(2x+y)=2x-4y-2x-y=-5y.5.-2x2+4x-1 由题意,得m=(x2-7x-2)-(3x2-11x-1)=x2-7x-2-3x2+11x+1=-2x2+4x-1.6.分析:应先去括号,再合并同类项.解:5(a2b-3ab2)-2(a2b-7ab2)=5a2b-15ab2-2a2b+14ab2=3a2b-ab2.。
福建省石狮市七年级数学上册第三章整式的加减导学案(无答案)(新版)华东师大版

复习:整式的加减【学习目标】 .扎实掌握代数式、单项式、多项式、同类项的定义,会用合并同类项法则、去括号法则将整式化简. .提升运用数学知识解决实际问题的能力。
.养成良好的学习学习习惯,超越自我。
【使用说明与学法指导】请同学们结合学习目标用分钟时间复习课本的内容,用分钟时间认真独立完成学案,注意书写规范,保持卷面整洁。
知识梳理 一、构建知识树 二、我的疑惑 典型例题 探究点一:去括号、合并同类项 例.先去括号,再合并同类项: )43(4)1(b a a -+ )22(3)2(a ab ab +-- )()3(c a b a --- )2(34)4(y x x -- 探究点二:整式的加减运算 例.先化简,再求值: 2222()3()4,1,1x y xy x y xy x y x y +---==-其中 【针对性练习】.下列去括号中错误的是( )2-(-)2--. d c b a a d c b a a 2332)23()3(222+---=----+. b x x b x x --=+-33)(3322. –22222)()2(y x y x y x y x -++-=+--- 、下列各组中,不是同类项的是( ) 、 与 、y x 213 与224yx、与 21、n n y x 23+- 与22+n n x y .下列各式中与c b a --的值不相等的是 ( )。
.)(c b a +-; .)(c b a --; .)()(c b a -+-; .)()(a b c ---、已知y x 625和y x m 25是同类项,的值为( ) 、 、 、 、或.先去括号,再合并同类项:)54()106)(1(b a b a +-+- )75()53)(2(b a b a +--+-)3(27)3(n m m -+ 【拓展提升】化简:3()2()4()5()a b a b a b a b +-+-+++【拓展小结】1、 知识方面:、数学思想方法:。
【初中教育】2019最新华师版新版初中数学七年级上册:3-4整式的加减导学案

——教学资料参考参考范本——【初中教育】2019最新华师版新版初中数学七年级上册:3-4整式的加减导学案______年______月______日____________________部门教学过程设计 分析备注 1 同类项教学目的:1、使学生能掌握同类项的概念,并能在多项式中找到同类项;2、能逆向运用同类项的概念,确定某些指数的值。
教学分析:重点:作为同类项所必须满足的条件; 难点:同类项概念的逆向运用。
教学过程: 一、知识导向:本节课是结合乘方、单项式、多项式的一个全新的知识,在新课的讲解中,应突出“同”字,即必须抓住“两同”:必须含有相同的字母,相同的字母的指数也必须相同。
二、新课拆析: 1、知识引入:其一:多项式的项。
如多项式“5253432222+++--xy y x xy y x ” 的项中有y x 23、24xy -、3-、y x 25、22xy 、5,其二:我们常常把具有相同特征的事物归为一类。
所以在多项式中,也可以把具有相同特征的项归为一类,如:y x 23与y x 25、24xy -与22xy 、3-与5。
2、知识形成:概括:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项。
注:(1)同类项中要注意到两相同:字母相同及相同的字母的指数也相同;(2)所有的常数项都是同类项;(3)同类项的判断是以它的总体特征来判断,而不能仅仅看它们的位置。
复习多项式的知识应该是全方位的,而不能仅仅在项上,还应包括项的系数与次数。
引导学生思考这些所谓相同特征的项有什么相同的特征。
教学过程设计分析备注 如:系数 字母指数 y x 23 3 x2 y 1 y x 255x2 y1从上我们很容易发现,这两个所谓的同类项,只有系数不同, 而字母是相同,而且相同的字母的指数也相同。
例1:指出下列多项式中的同类项: (1)523123--++-x y y x(2)yx xy xy y x 2222233123-+-例2:k 取何值时,y x k 3与y x 2-是同类项?三、巩固训练: P102 练习题 四、知识小结:在学习同类项的概念后,必须知道,同类项必须具有“两同”,并能对同类项的知识进行扩充性的开放运用。
七年级数学上册 第3章 整式的加减 第3节 整式《单项式》导学案(无答案)(新版)华东师大版
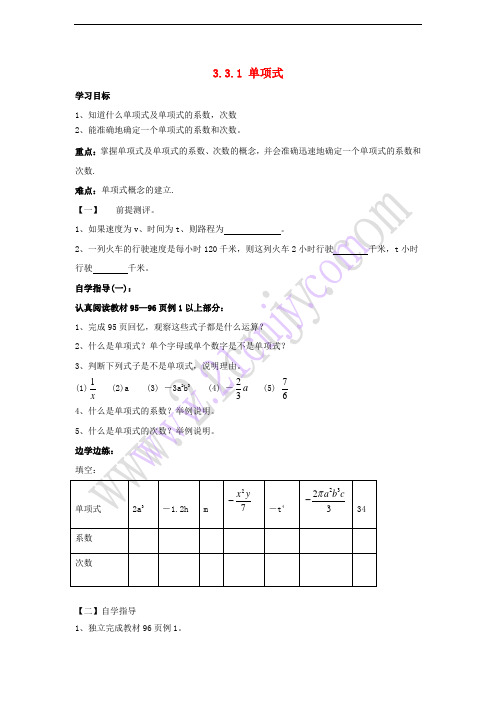
3.3.1 单项式学习目标1、知道什么单项式及单项式的系数,次数2、能准确地确定一个单项式的系数和次数。
重点:掌握单项式及单项式的系数、次数的概念,并会准确迅速地确定一个单项式的系数和次数.【二】自学指导1、独立完成教材96页例1。
22、边学边练:教材96页练习1、2题 【三】当堂检测: 1、 下列式子中: ①m ②-23a ③216x y ④2x y + ⑤abc⑥3a b + ⑦0 是单项式的是 (只填序号).2、单项式-22x y的系数是 ,次数是 。
3A C 4A C 5678 9(5)y +x ; (6)-xy 2; (7)-5; (8)b/a 。
10、填空(1)6m 的数字部分是 ;字母部分是 ;字母部分的指数的和是 。
(2)2.5x 的数字部分是 ;字母部分是 ;字母部分的指数的和是 。
(3) 6a 2的数字部分是 ;字母部分是 ;字母部分的指数的和是 。
(4) a 3的数字部分是 ;字母部分是 ;字母部分的指数的和是 。
(5)- n 的数字部分是 ;字母部分是 ;字母部分的指数的和是 。
(6)-5a b 2的数字部分是 ;字母部分是 ;字母部分的指数的和是 。
下面各题的判断是否正确。
①-7xy 2的系数是7;( ) ②-x 2y 3与x 3没有系数;( ) ③-a b 3c 2的次数是0+3+2;( ) ④-a 3的系数是-1; ( ) ⑤-32x 2y 3的次数是7;( ) ⑥ πr 2h 的系数是π。
( )(1)单项式-5y 的系数是_____,次数是_____ (2)单项式a 3b 的系数是_____,次数是_____ (3)单项式 -5πR² 的系数是_____,次数是_____ 【四】 游戏规则:一个小组学生说出一个单项式,然后指定另一个小组的学生回答他的 系数和次数;然后交换,看两小组哪一组回答得快而准。
【五】运用拓展 1.(1)1223--m y x 是五次单项式,则m=__________; (2)若312z y x m +是五次单项式,则m=__________;【六】作业课本100页习题3.3第1题。
七年级数学上册 3 整式的加减复习导学案(无答案)(新版)华东师大版
第3章整式的加减1. 通过尝试学习的形式来对《整式的加减》这一章节进行系统的综合复习,以相应的练习来加强对有关概念和法则的理解;2. 通过合作交流来查漏补缺,培养良好的复习方法。
二.学习重点:结合知识要点进行基础训练三.自主复习(要求:先认真看书P82-P111,然后关上书回顾本章知识要点。
比一比,看谁掌握得更多,加油哦!)本章知识要点1.和统称为整式。
2.单项式中的叫做这个单项式的系数;单项式中所有字母的叫做这个单项式的次数。
单独一个或也是单项式。
3.多项式里,次数项的次数就是这个多项式的次数。
4.把一个多项式按某一个字母的从的顺序排列,叫做这个多项式按这一字母的升幂排列;相反,按某一个字母的从的顺序排列,叫做这个多项式按这一字母的降幂排列。
5.代数式的书写规则(1)代数式中出现的乘号,通常写作“”或者;(2)数字与字母相乘时,数字应写在的前面;带分数与字母相乘时,应先把带分数化成后与字母相乘;(3)除法运算写成形式,被除数作,除数作,“÷”号转化为 ;(4)数字与数字相乘时,一般仍用“×”号。
(5)代数式的最后一步是加减运算并且后面有单位时,要用()把代数式括起来。
6.同类项必须满足的两个条件(1)所含相同;(2)相同的也相同。
7.合并同类项的法则:把相加,字母和字母的保持不变。
8.去括号法则:(1)括号前面是“+”号,把括号和它前面的“+”去掉,括号里各项都正负号;(2)括号前面是“—”号,把括号和它前面的“—”去掉,括号里各项都正负号。
9.添括号法则:(1)所添括号前面是“+”号,括到括号里的各项都正负号;(2)所添括号前面是“—”号,括到括号里的各项都正负号。
10.整式的加减的步骤:(1)如果有括号,就先;(2)如果有同类项,再。
(注意:用多项式进行列式时,要用括号把它括起来,作为一个整体来使用。
)11.“求代数式的值”的注意事项:(1)若能化简,就先 ,再代入 ;(2)代入数字求值时,分数、负数的乘方要加括号。
初中数学华东师大七年级上册(2023年新编)第3章 整式的加减中考复习《整式的加减》导学案
中考复习--整式的加减学习目标1. 能分析简单问题的数量关系,并用代数式表示,会求代数式的值;能根据特定问题找到所需要的公式,并会代入具体的值进行计算.2. 了解整数指数幂的意义和基本性质;了解整式的概念和有关法则,会进行简单的整式加、减、乘、除运算.3. 会推导平方差公式和完全平方公式,会进行简单的计算;会用提公因式法、公式法进行因式分解. 考点1 代数式知识梳理(1)代数式:用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子,单独的一个数或一个字母也是代数式.(2)求代数式的值:用具体数值代替代数式中的字母,计算得出的结果,叫做求代数式的值. 难点突破1. 下列代数式中,整式为( )A .x +1B.1x +1C.x 2+1D.x +1x 方法总结考点2 整式 (单项式、多项式)知识梳理(1)单项式:表示数字与字母积的代数式,单独的一个数或一个字母也叫单项式.其中的数字因数叫做单项式的系数,所有字母的指数和叫做单项式的次数.(2)多项式:几个单项式的和.多项式中的每一项叫做多项式的项,次数最高的项的次数叫做多项式的次数.(3)整式:单项式和多项式统称为整式.(4)同类项:所含字母相同并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项. 难点突破1. 若单项式am -1b 2与12a 2b n 的和仍是单项式,则n m 的值是( ) A .3B .6C .8D .9 2. 如果2xa +1y 与x 2yb -1是同类项,那么a b 的值是( ) A.12B.32C .1D .3 方法总结(1)合并同类项法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.(2)去括号法则: 若括号外是“+”,则括号里的各项都不变号;若括号外是“-”,则括号里的各项都变号.(3)整式的加减运算法则:先去括号,再合并同类项.难点突破1. 若(x+3)(x+n)=x2+mx-15,则m等于( )A.-2 B.2 C.-5 D.52. 若2n+2n+2n+2n=2,则n=( )A.-1 B.-2 C.0 D.1 43.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:(1)求所捂的二次三项式;(2)若x=6+1,求所捂二次三项式的值.方法总结考点4:幂运算法则知识梳理(1)同底数幂的乘法:a m·a n=;(2)幂的乘方:(a m)n=;(3)积的乘方:(ab)n=;(4)同底数幂的除法:a m÷a n=(a≠0).难点突破1. 下列运算正确的是( )A.(-5)0=0 B.x2+x3=x5 C.(ab2)3=a2b5D.2a2·a-1=2a2. 下列各式中,计算结果为a8的是( )A.a4+a4B.a4·a-2 C.a10÷a2D.(-2a4)23.计算(a2)3-5a3·a3的结果是( )A.a5-5a6B.a6-5a9 C.-4a6D.4a6方法总结(1)单项式×单项式:①系数和同底数幂分别相乘;②只有一个字母的照抄.(2)单项式×多项式: m(a+b)= .(3)多项式×多项式: (m+n)(a+b)= .(4)单项式÷单项式:将系数、同底数幂分别相除.(5)多项式÷单项式:①多项式的每一项除以单项式;②商相加.(6)乘法公式:平方差公式:(a +b)(a -b)= .;完全平方公式:(a±b)2= .难点突破1. 下列计算正确的是( )A .a 4÷a 3=1B .a 4+a 3=a 7C .(2a 3)4=8a 12D .a 4·a 3=a 7 2. 已知多项式A =(x +1)2-(x 2-4y).(1)化简多项式A ;(2)若x +2y =1,求A 的值.3. 先化简,再求值:(a -2b)(a +2b)-(a -2b)2+8b 2,其中a =-2,b =12. 方法总结考点6:因式分解知识梳理(1)定义:把一个多项式化成几个整式的积的形式.(2)常用方法:①提公因式法:ma +mb +mc = .②公式法:a 2-b 2= ;a 2±2ab+b 2= .(3)一般步骤:①若有公因式,必先提公因式;②提公因式后,看是否能用公式法分解;③检查各因式能否继续分解.难点突破1. 分解因式:xy 2-2xy +x = .2. 若a +b =4,a -b =1,则(a +1)2-(b -1)2的值为 .方法总结随堂检测1. 下列运算正确的是( )A .a 8÷a 4=a 2B .(a 3)2=a 6C .a 2·a 3=a 6D .a 4+a 4=2a 82. 下列计算错误的是( )A.a2÷a0·a2=a4 B.a2÷(a0·a2)=1C.(-1.5)8÷(-1.5)7=-1.5 D.-1.58÷(-1.5)7=-1.53.(2023·枣庄中考)如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形,若拿掉边长为2b 的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )A.3a+2b B.3a+4bC.6a+2b D.6a+4b4.下列分解因式正确的是( )A.-x2+4x=-x(x+4) B.x2+xy+x=x(x+y)C.x(x-y)+y(y-x)=(x-y)2 D.x2-4x+4=(x+2)(x-2)5.若a+b=3,a2+b2=7,则ab等于( )A.2 B.1 C.-2 D.-16.分解因式:x2-9=.7.因式分解:x2y-4y3=.8.若3x2n y m与x4-n y n-1是同类项,则m+n=.9.先化简,再求值:(x+2)(x-2)+x(1-x),其中x=-1.通过本节课的学习在小组内谈一谈你的收获,并记录下来:我的收获_____________________________________________________________________________________________ _____________________________________________________________思考将全体正奇数排成一个三角形数阵:13 57 9 1113 15 17 1921 23 25 27 29…按照以上排列的规律,第25行第20个数是( )A.639 B.637 C.635 D.633。
七年级数学上册 第三章 整式的加减 3.4 整式的加减教案 (新版)华东师大版
3.4整式的加减教学目标:1.使学生掌握整式的加减运算,进一步巩固前面所学的去括号、合并同类项的方法;2.使学生进一步增强运算能力.教学重点:整式的加减运算.教学过程:做一做某中学合唱团出场时第一排站了n名同学,从第二排起每一排都比前一排多1人,一共站了四排,则该合唱团一共有名同学参加演唱.容易知道,第二、三、四排的人数分别为n+1,n+2,n+3.因而合唱团的总人数为n+(n+1)+(n+2)+(n+3).要把这个式子进一步化简,实际上是要进行整式的加减运算.概括不难发现,去括号和合并同类项是整式加减的基础.因此,整式加减的一般步骤可以总结为:(1)如果有括号,那么先去括号;(2)如果有同类项,再合并同类项.例1求整式x2-7x-2与-2x2+4x-1的差.解:x2-7x-2--2x2+4x-1=x2-7x-2+2x2-4x+1=3x2-11x-1例2计算:-2y3+(3xy2-x2y)-2(xy2-y3)解:-2y3+(3xy2-x2y)-2(xy2-y3)=-2y3+3xy2-x2y-2x y2+2y3=xy2-x2y例3化简求值:(2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3.解:(2 x 3-xyz)-2(x3-y3+xyz)+(xyz-2y3)=2x3-xyz-2x3+2y3-2x yz+xyz-2y3=-2x yz当x=1,y=2,z=-3时,原式=-2×1×2×(-3)=12.练习1.,其中.2.已知【答案】,求的值.1.-152.-102。
2022-2023学年华东师大版七年级数学上册《第3章整式的加减3.2代数式的值 》教案
2022-2023学年华东师大版七年级数学上册《第3章整式的加减3.2代数式的值》教案一. 教材分析本节课的内容是华东师大版七年级数学上册第3章整式的加减3.2代数式的值。
这部分内容是在学习了整式的加减法运算的基础上进行的,旨在让学生能够求出代数式的值。
教材通过具体的例题和练习题,帮助学生巩固整式加减法的运算规则,并能够灵活运用这些规则求解代数式的值。
二. 学情分析七年级的学生已经掌握了整式的加减法运算规则,但是对于代数式的值的理解还有一定的困难。
因此,在教学过程中,需要通过具体的例题和练习题,让学生逐步理解代数式的值的概念,并能够熟练地求解代数式的值。
三. 教学目标1.理解代数式的值的概念,能够求出简单代数式的值。
2.掌握整式加减法的运算规则,并能够灵活运用这些规则求解代数式的值。
3.培养学生的逻辑思维能力和解决问题的能力。
四. 教学重难点1.重点:求解代数式的值。
2.难点:灵活运用整式加减法的运算规则求解代数式的值。
五. 教学方法采用问题驱动的教学方法,通过具体的例题和练习题,引导学生逐步理解代数式的值的概念,并能够熟练地求解代数式的值。
同时,运用小组合作的学习方式,培养学生的团队协作能力和解决问题的能力。
六. 教学准备1.教材和教案。
2.投影仪和电脑。
3.练习题和答案。
七. 教学过程1.导入(5分钟)利用投影仪展示一些实际问题,例如:小明买了3本书和2支笔,每本书的价格是10元,每支笔的价格是2元,请问小明一共花了多少钱?让学生思考如何解决这个问题,从而引出代数式的值的概念。
2.呈现(10分钟)通过具体的例题,讲解如何求解代数式的值。
例如:求解代数式3x + 2y的值,其中x = 1,y = 2。
引导学生逐步理解代数式的值的概念,并能够熟练地求解代数式的值。
3.操练(10分钟)让学生独立完成一些类似的练习题,例如:求解代数式4a - 3b的值,其中a = 2,b = 1。
教师巡回指导,解答学生遇到的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习:整式的加减
【学习目标】 1.扎实掌握代数式、单项式、多项式、同类项的定义,会用合并同类项法则、去括号法则将整式化简. 2.提升运用数学知识解决实际问题的能力。
3.养成良好的学习学习习惯,超越自我。
【使用说明与学法指导】请同学们结合学习目标用10分钟时间复习课本P82-P114的内容,用35分钟时间认真独立完成学案,注意书写规范,保持卷面整洁。
知识梳理 一、构建知识树
导
学
案
装
订
线
二、我的疑惑
典型例题
探究点一:去括号、合并同类项
例1.先去括号,再合并同类项:
(
3)2(a
2
2
-
ab+
ab
-
4
+) 3(
)
a-
a
4)1(b
2
4)4(y
(3
x--)
-
x
b
(
)
-
)3(c
a
a-
探究点二:整式的加减运算
例2.先化简,再求值:
2222()3()4,1,1x y xy x y xy x y x y +---==-其中
【针对性练习】
1.下列去括号中错误的是( )
A.x 2-(x -2y+5z)=x 2
-x+2y -5z
B. d c b a a d c b a a 2332)23()3(222+---=----+
C. b x x b x x --=+-33)(3322
D. –22222)()2(y x y x y x y x -++-=+---
2、下列各组中,不是同类项的是( )
A 、 与
B 、y x 213 与224yx
C 、130与 21
D 、n n y x 23+- 与
22+n n x y
3.下列各式中与c b a --的值不相等的是 ( )。
A.)(c b a +-;
B.)(c b a --;
C.)()(c b a -+-;
D.)()(a b c ---
4、已知y x 625和y x m 25是同类项,m 的值为( )
A 、2
B 、3
C 、4
D 、2或3
5.先去括号,再合并同类项:
)54()106)(1(b a b a +-+- )75()53)(2(b a b a +--+-
)3(27)3(n m m -+
【拓展提升】
化简:
3()2()4()5()a b a b a b a b +-+-+++
【拓展小结】
1、知识方面:
2、数学思想方法:。
