自适应遗传算法
自适应遗传算法在相控阵雷达最优化调度中的应用

( De p a r t me n t O i E l e c t r i c De t e c t i o n,S h e n y a n g A ti r l l e r y Ac a d e my ,S h e n y a n g 1 l 0 8 6 7,C h i n a )
Ab s t r a c t : T h e a d p t i v e g e n e t i c a l g o r i t h m i s p r e s e n t e d f o r o p t i ma l s c h e d u l i n g o f p h a s e d a r r a y r a — d a r .T h e c o d i n g r u l e s ,f i t n e s s f u n c t i o n a n d g e n e t i c o p e r a t i o n f o r p h a s e d a ra y r a d a r s c h e d u l i n g b a s e d o n t h e r a d a r c o n s t r a i n t mo d e l a r e d e s i g n e d .T h e a d a p t i v e c r o s s o v e r p r o b a b i l i t y a n d a d a p — t i v e mu t a t i o n p r o b a b i l i t y a r e p r o p o s e d,w h i c h c o n s i d e r t h e i n l f u e n c e o f e v e r y g e n e r a t i o n t o a l g o — r i t h m a n d t h e e f f e c t i n d i v i d u a l f i t n e s s i n e v e r y g e n e r a t i o n .F i n a l l y,t h r o u g h a n a l y z i n g a n e x a m・ p i e ,t h i s a l g o r i t h m c a n a c c o mp l i s h s c h e d u l i n g r e a s o n a b l y a n d e n s u r e h i 【 g h s u c c e s s f u l s c h e d u l e d
一种基于方差的自适应遗传算法

维普资讯
维普资讯
・
8 0・
安庆师范学院学报( 自然科学版 )
2 0 年 06
实 算 时 , 种 算 法 都 采 用 二 进 制 编 码 , 群 规 模 为 1 0轮 盘 赌 选 择 方 法 , 术 交 又 , 匀 变 异 。S 四 种 0, 算 均 GA 交 叉 概 率 为 07. 异 概 率 为 001 . 变 . 。AGA 的 交 叉 率 和 变 异 率 由 白适 应 函 数 调 整 【。S AGA首 先 同定 算 法 2 E I
个 体 适 应 度 分 比较 集 中 , 此 时 应 该 自适 应 增 大 算 法 的 交 叉 率 和 变 异 率 , 以 增 强 算 法 的 搜 索 能 力 ; 反
收 稿 日期 : 0 6 0 — 2 2 0 — 4 1
作者简 介:江鹰( 99 )_ , 1 5 一 ,3 安徽黄L , , 人 池州 师范专科学校讲师 , 主要从事计算机基础理论教学 与研究工作。
= l
, 巾 P X= = ,, 是 的 分 布 率 。 其 [ x } ,=l … 2
我 们 将 种 群 中 各 个 体 的 适 应 度 看 作 是 离 散 型 的 随 机 变 , 用 式 () 种 群 个 体 的 适 应 度 计 算 适 应 运 1对
度 方 差 , 方 差 反 映 了 种 群 巾 个 体 适 应 度 的 分 砸 情 况 :如 果 种 群 适 应 度 方 差D ) , 明 种 群 的 大 部 分 此 小 说
一种自适应遗传算法的聚类分析及应用

c o s v rp b b l y a d mua in p b i t s o itd T e a g rtm s a p id t ma e cu tr g r s o e r a i t tt r a l y a s c ae . h o h o i n o o b i l i i p l o i g ls i , e e n h x e me tl s t e e p r na i l t n r s l h w t a ,c mp r d w t e k me n l se n g r h , t e i mu a o e u t s o t o a e i t - a s cu tr g a o t m h i s h h h i l i
0 引言
遗 传算法 ( 简称 G 作 为 一种 自适 应全 局优 化 A) 概率搜 索方法 , 最早 由美 国 Mi ia 它 c gn大学 的 H l h o—
l d教授 提 出。该算 法具 有很好 的鲁棒性 、 n a 随机 性 、 全局性 , 已被 人们 广泛 地 应用 于 以下 主要 应用 领 现
信息謦 — — — — — — —————
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
— — — — — — —
21年 4 0 第期 1
— — —
-= .
== = A
文章编号:0 9— 5 2 2 1 }4—09 0 10 2 5 (0 10 10— 3
Ab ta t Ac o dn et d t n lcu tr g ag r m n cu tr g p r t n p o l mssi xs n sr c : c r i g t t a i o a l se n l oi o h r i i h t i l s i a t i r be tl e it d en io l a t e p r t n e e t a i t s p o .B s d o t e v r l e o ma c d n u e t e GA a g r h h at i f c b l y i o r a e n h o e a p r r n e a e s r lo tm io i l f n h i
基于自适应遗传算法的入侵检测方法

第12卷第33期2012年11月1671—1815(2012)33-9075-04科学技术与工程Science Technology and EngineeringVol.12No.33Nov.2012 2012Sci.Tech.Engrg.基于自适应遗传算法的入侵检测方法鲁立刘颂(武汉软件工程职业学院,武汉430205)摘要提出了一种基于自适应遗传算法的入侵检测方法。
该方法采用自适应的适应度函数、交叉概率及变异概率取代固定的适应度函数、交叉概率及变异概率来改进遗传算法并用于入侵检测中。
实验结果证明算法显著提高了自身收敛性能,具有很强的自适应能力,用于入侵检测中在保证较高检测率的基础上,对不同类型的攻击检测具有良好的均衡性。
关键词遗传算法自适应入侵检测网络安全中图法分类号TP393.08;文献标志码A2012年7月31日收到第一作者简介:鲁立(1976—),男(汉族),湖北武汉人,武汉软件工程职业学院副教授,硕士,研究方向:计算机网络。
E-mail :yanger2011@ 。
入侵检测(Intrusion detection )是通过对系统数据的收集与分析,发现未经授权的攻击行为和网络访问,从而为网络安全提供有力的保障[1]。
目前入侵检测智能性研究成为热点,这主要是因为智能优化算法、神经网络、模式识别等技术的引入[2]。
例如刘永忠等[3]提出了一种基于模糊粗糙集的特征加权聚类算法(FRS-FCM ),该方法能有效提高入侵检测的检测准确率,降低误检率,并较大地提高低频攻击的检测率。
朱红萍等[4]提出一种基于遗传算法的入侵检测特征选择算法。
该算法在保证特征分类精度和确保入侵检测漏检率、误检率尽量小的前提下明显提高了入侵检测的效率。
胡明霞等[5]通过遗传算法找到BP 神经网络的最适合权值,解决直接使用BP 学习造成的训练样本数量过大而难以收敛的问题,与传统网络入侵检测算法相比,该算法的训练样本时间更短,具有较好的识别率和检测率。
交叉算子自适应遗传算法

交叉算子自适应遗传算法
自适应遗传算法(Adaptive Genetic Algorithm,AGA)是对基本遗传算法的一种改进,它通过对遗传参数的自适应调整,大大提高了遗传算法的收敛精度,加快了收敛速度。
适应度函数是评价个体适应环境的能力,在进行选择操作时经常用到,它的选取是否恰当直接影响到遗传算法的性能,所以就形成了很多计算适应度的函数,改进这些适应度函数是为了使适应度能更好的反映个体的优劣,使得适应度低的个体被淘汰,适应度高的个体被保留。
自适应的适应度函数可以随着种群代数的增加自适应的调整,在算法的开始阶段,适应度差别较大,为了防止一些适应度较差的个体在一开始就丢失,可以通过改变适应度函数使得它们得以保留下来,另外,当种群趋于收敛时,适应度差别很小,这时为了加快收敛的速度,应对适应度进行调整,使得个体适应度差别增大,从而更快的收敛到全局最优解。
常用的适应度变换方法有:线性变换、幂函数变换和指数变换。
另外,采用适应度结合了模拟退火的思想。
选择的作用是按某种方法从父代群体中选取一些将要进行交叉的个体,常用的选择方法很多,它们大多有一个共同的特点,就是都是基于适应度的选择,适应度大的个体被选中的概率就大,适应度小的个体被选中的概率就小。
常用的选择算法有适应度比例法、精英保留策略、联赛选择法等。
另外,也可以将这些选择算法混合使用,如今还出现了启发式的搜索选择策略,这种策略是用每个个体所带有的启发信息来确定它被选中的概率。
变异概率自适应调整的遗传算法GA程序
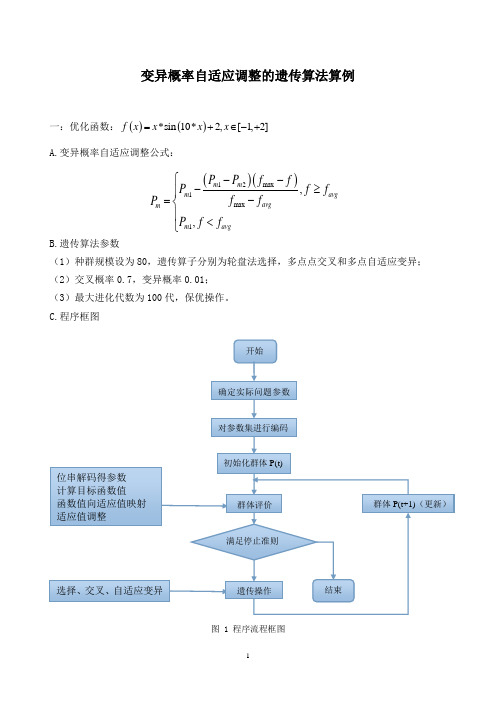
变异概率自适应调整的遗传算法算例一:优化函数:()()*sin 10*2,[1,2]f x x x x =+∈-+A.变异概率自适应调整公式:B.遗传算法参数 (1)种群规模设为80,遗传算子分别为轮盘法选择,多点点交叉和多点自适应变异;(2)交叉概率0.7,变异概率0.01;(3)最大进化代数为100代,保优操作。
C.程序框图图 1 程序流程框图()()12max 1max 1,,m m m avg avg m m avg P P f f P f f f f P P f f --⎧-≥⎪-=⎨⎪<⎩ 开始 确定实际问题参数对参数集进行编码 初始化群体P(t) 群体P(t+1)(更新) 位串解码得参数 计算目标函数值 函数值向适应值映射 适应值调整 选择、交叉、自适应变异群体评价 遗传操作 满足停止准则 结束二:程序及运行结果(1)%变异概率自适应调整的GA程序%优化函数为f=x*sin(10*x)+2,其中,-1=<x<=2%编码长度为12位%种群规模设为80,遗传算子分别为轮盘法选择,多点点交叉和多点自适应变异。
%交叉概率0.7,变异概率0.01%最大进化代数为100代,保优操作。
%**********************%主函数*****************************************function main()global chrom lchrom oldpop newpop varible fitness popsize sumfitness %定义全局变量global pcross pmutation temp bestfit maxfit gen bestgenglobal maxgen po pp mp nplchrom=12; %染色体长度popsize=80; %种群大小pcross=0.7; %交叉概率pmutation=0.01; %变异概率maxgen=100; %最大代数po=0.1; %淘汰概率pp=0.1; %保护概率mp=floor(pp*popsize); %保护的个数np=floor(po*popsize); %淘汰的个数initpop; % 初始化种群for gen=1:maxgenobjfun; %计算适应度值pp_po; %执行保优操作select; %选择操作selfmutation; %自变异操作crossover; %交叉操作endbestbestfit % 最佳个体适应度值输出bestgen % 最佳个体所在代数输出figuregen=1:maxgen;plot(gen,maxfit(1,gen)); % 进化曲线hold on;plot(bestgen,bestfit);xlabel('Generation');ylabel('Fitness');%********************** 产生初始种群 ************************************ function initpop()global lchrom oldpop popsize chromfor i=1:popsizechrom=rand(1,lchrom); % lchrom=12 染色体长度for j=1:lchromif chrom(1,j)<0.5chrom(1,j)=0;elsechrom(1,j)=1;endendoldpop(i,1:lchrom)=chrom;end%************************%计算适应度值************************************ function objfun()global lchrom oldpop fitness popsize chrom maxfit gen varible avgfiness savgfitness % a=0;b=3;a=0;b=10;for i=1:popsizechrom=oldpop(i,:);c=decimal(chrom);varible(1,i)=a+c*(b-a)/(2.^lchrom-1); %对应变量值fitness(1,i)=varible(1,i)*sin(10*varible(1,i))+2;avgfitness=sum(fitness)/popsize;lsort; % 个体排序maxfit(1,gen)=max(fitness); %求本代中的最大适应度值maxfit%************************二进制转十进制********************************** function c=decimal(chrom)global lchrom popsizec=0;for j=1:lchromc=c+chrom(1,j)*2.^(lchrom-j);end%************************* 个体从小到大排序 ************************ function lsort()global popsize fitness oldpopfor i=1:popsizej=i+1;while j<=popsizeif fitness(1,i)>fitness(1,j)tf=fitness(1,i); % 适应度值tc=oldpop(i,:); % 基因代码fitness(1,i)=fitness(1,j); % 适应度值互换oldpop(i,:)=oldpop(j,:); % 基因代码互换fitnescs(1,j)=tf;oldpop(j,:)=tc;endj=j+1;endend%*************************保优操作*****************************function pp_po()global popsize oldpop npi=np+1; % np=floor(po*popsize); %淘汰的个数npwhile i<=popsize %将(np+1)~popsize的个体放在toldpop中,共(popsize-np)个 toldpop(j,:)=oldpop(i,:);j=j+1;i=i+1;endfor i=1:(popsize-np) %从小到大顺序排列,将前面np个淘汰oldpop(i,:)=toldpop(i,:); % 适应度是否也要互换?end%*************************转轮法选择操作********************************** function select()global fitness popsize sumfitness oldpop temp mp npsumfitness=0; %个体适应度之和for i=1:(popsize-np-mp) % 仅计算(popsize-np-mp)个个体的选择概率sumfitness=sumfitness+fitness(1,i);endfor i=1:(popsize-mp-np) % 仅计算(popsize-np-mp)个个体的选择概率p(1,i)=fitness(1,i)/sumfitness; % 个体染色体的选择概率endq=cumsum(p); % 个体染色体的累积概率(内部函数),共(popsize-np-mp)个b=sort(rand(1,(popsize-mp))); % 产生(popsize-mp)个随机数,并按升序排列。
自适应遗传算法
自适应遗传算法
自适应遗传算法是一种改进的遗传算法,它是一种自适应机制,用于提高遗传算法的收敛速度和搜索能力。
它主要用于优化复杂的多目标函数、多约束条件和变分问题。
自适应遗传算法的核心思想是通过模拟生物进化的过程,模拟种群中个体的遗传进化,从而寻求最优解,最终实现目标函数的优化。
自适应遗传算法的基本过程是:首先,从初始种群中初始化一组可行解;其次,根据遗传算法的基本原理,依次执行变异、交叉和选择操作,从而生成新的种群;然后,根据变量的取值范围,采用自适应策略调整变量的值,使其符合约束条件;最后,根据适应度函数的值,选择出最优解,作为下一次迭代的初始种群,重复执行上述过程,直至收敛为止。
自适应遗传算法的优点在于:它可以在解的搜索过程中自动调整参数,使算法能够快速收敛,从而提高搜索效率;其次,它可以更好地处理多目标函数和多约束条件的问题;此外,它可以有效地控制变量的取值范围,避免出现取值范围过大的情况。
总而言之,自适应遗传算法是一种有效的优化算法,它可以提高搜索效率并有效地控制变量的取值范围,使得搜索过程更加高效、准确。
它已经被广泛应用于多目标优化、多约束优化和变分优化等领域。
基于实数编码的参数自适应遗传算法(matlab代码)
基于实数编码的参数⾃适应遗传算法(matlab代码)实数编码的遗传算法寻优:遗传算法的基本操作算⼦:(1)选择算⼦选择算⼦的作⽤主要是避免优良基因的丢失,使得性能⾼的个体能以更⼤的概率被选中,有机会作为⽗代繁殖下⼀代,从⽽提⾼遗传算法的全局收敛性及计算效率。
常见的选择算⼦包括轮盘赌选择法、随机遍历抽样法、局部选择法及锦标赛选择法等。
选择算⼦采⽤轮盘赌;(2)交叉算⼦在遗传算法中,交叉算⼦是区别于其它优化算法的本质特征,⽤于组合新的个体在解空间中快速有效地进⾏搜索,同时也降低了对有效模式的破坏程度,起到全局搜索寻优的效果。
交叉算⼦直接影响着遗传算法的最终搜索效果,⼀定程度上决定了其发展前景。
其中alpha为参数,0<alpha<1(3)变异算⼦群体基因的多样性是保证遗传算法寻找到全局最优解的前提条件,然⽽在进化过程中,遗传选择操作削弱了群体的多样性,上述交叉算⼦只有满⾜⼀定的条件才能保持群体的多样性,⽽变异操作则是保持群体多样性的有效算⼦,所以变异操作算⼦的选取也是必不可少的。
变异尺度⾃适应变化的变异算⼦在进化初期采⽤较⼤的变异尺度来保持群体的多样性,⽽在后期变异尺度将逐渐缩⼩以提⾼局部微调能⼒。
本⽂在此基础上做些改进,改进后的变异算⼦具有原有算⼦的优点,且操作上⽐原有算⼦简单⽅便,有效地加快遗传算法的收敛速度,具体如下:可以看出s(t) 决定了变异空间的⼤⼩,在迭代的初期,变异空间较⼤,在迭代的后期,变异空间缩⼩,算法的局部寻优能⼒变强。
变异算⼦参考⽂献: [1] 管⼩艳. 实数编码下遗传算法的改进及其应⽤[D].重庆⼤学,2012.参数⾃适应:交叉概率Pc和变异概率Pm是遗传算法的两个重要的参数,这两个参数决定了每个个体进⾏交叉或者变异操作的概率。
⾃适应算⼦参考⽂献:[2] M. Srinivas and L. M. Patnaik, "Adaptive probabilities of crossover and mutation in genetic algorithms," in IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 4, pp. 656-667, April 1994.doi: 10.1109/21.286385上述部分翻译⾃⽂献[2]按照论⽂描述,对算法的复现如下:% 测试函数图像% 测试函数图像% 改进的⾃适应遗传算法:% 参考⽂献:[7] M. Srinivas and L. M. Patnaik, "Adaptive probabilities of crossover and mutation in genetic algorithms,"% in IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 4, pp. 656-667, April 1994.% doi: 10.1109/21.286385clc;clear all;mode = 'Schaffer';% mode = 'self_define';if strcmp(mode, 'Schaffer')figure(1)x = -4:0.1:4;y = -4:0.1:4;[X,Y] = meshgrid(x,y);% Z = 3*cos(X.*Y)+X+Y.^2;Z = 0.5-((sin(sqrt(X.^2+Y.^2)).^2)-0.5)./(1+0.001.*(X.^2+Y.^2)).^2; surf(X,Y,Z);title('Schaffer Function');xlabel('X-轴');ylabel('Y-轴');zlabel('Z-轴');figure(2);contour(X, Y, Z, 8);title('Schaffer函数等⾼线');xlabel('X-轴');ylabel('Y-轴');endif strcmp(mode, 'self_define')figure(1);x = -4:0.1:4;y = -4:0.1:4;[X,Y] = meshgrid(x,y);% Z = 100.*(Y-X.^2).^2+(1-X).^2;Z = (cos(X.^2+Y.^2)-0.1)./(1+0.3*(X.^2+Y.^2).^2)+3;surf(X,Y,Z);%title('Rosen Brock valley Function');title('Self define Function');xlabel('X-轴');ylabel('Y-轴');zlabel('Z-轴');endclc;clearvars -except mode;r = 0.2;b = 3;NP=400;% Pc=0.65; % 将Pc,Pm参数改进为⾃适应参数% Pm=0.20;G=520; % 记得改D=2; % 变量个数k1 = 1;k3 = 1;k2 = 0.5;k4 = 0.5;X_min=-4;X_max=4;Y_min=-4;Y_max=4;% optimization_trace = []; % 三维数组, ⾏,列,叶for count_1=1:NP % 产⽣初始解temp1 = X_min+rand()*(X_max-X_min);temp2 = Y_min+rand()*(Y_max-Y_min);x(count_1,:) = [temp1,temp2];endsave_pic_cnt = 1;A = figure(3);for gen=1:G%pause(0.2);if rem(gen, 100)==1scatter(x(:,1), x(:, 2));axis([-4, 4, -4, 4]);title(['第', num2str(gen), '次迭代']);xlabel('变量X');ylabel('变量Y');base_path = 'C:\Users\18811\Desktop\graph\';cnt = num2str(save_pic_cnt);tail_path = '.jpg';frame = getframe(A);im=frame2im(frame);path_img = [base_path, cnt, tail_path];% imwrite(im, path_img);% save_x(:, :, save_pic_cnt) = x;save_pic_cnt = save_pic_cnt + 1;% scatter(0, 0, 'o', 'r');for count_2=1:NPfitness(count_2)=func(x(count_2,:), mode);end%[fitness_min,index0] = min(fitness);%fitness_max = max(fitness);[fitness_max,index0] = max(fitness);fitness_average = sum(fitness)/(length(fitness)); % 种群的平均值collect_fit_average(gen) = fitness_average; % 保存适应度的平均值collect_fitmax_subtract_fit_average(gen) = fitness_max - fitness_average; % 保存f_max-f_average ;fitness_min = min(fitness);best_indiv = x(index0,:); % 最优的个体% optimization_trace(gen,: , global_count) = best_indiv;% best_solution(gen) = fitness_min;best_solution(gen) = fitness_max;% 计算归⼀化的适应度值fitness = (fitness - fitness_min)/(fitness_max - fitness_min);fitness_sum = sum(fitness);fitness = fitness./fitness_sum;fitness = cumsum(fitness);% 选择算⼦:ms = sort(rand(NP,1));fiti = 1;newi = 1;while newi<=NPif ms(newi)<fitness(fiti)clone_x(newi,:) = x(newi,:);newi = newi + 1;elsefiti = fiti + 1;endendclone_x = clone_x(1:NP, :);% 进⾏交叉,变异操作% count=0;for count=1:2:NP% ⾃适应计算Pc.% 选区两个交叉的个体的较⼤的适应度值if fitness(count)>=fitness(count+1)fitness_selected = fitness(count);elsefitness_selected = fitness(count+1);end% 计算Pcif fitness_selected >= fitness_averagePc = k1*(fitness_max-fitness_selected)/(fitness_max-fitness_average);elsePc = k3;endcollect_Pc(gen, count) = Pc; % 保存Pc的值temp_cross = rand();if temp_cross < Pc% 交叉算⼦注:这种交叉算⼦效果更好temp_alpha = 0.6;cross_x(count,:) = temp_alpha*clone_x(count,:)+(1-temp_alpha)*clone_x(count+1,:);cross_x(count+1,:) = temp_alpha*clone_x(count+1,:)+(1-temp_alpha)*clone_x(count,:);% 改进的交叉算⼦参考⽂献:管⼩艳. 实数编码下遗传算法的改进及其应⽤[D].重庆⼤学,2012. 注:但这种交叉算⼦实际的效果不理想% temp_gama = rand();% temp_alpha = 0.98;% cross_x(count,:) = temp_alpha*clone_x(count,:)+(1-temp_alpha)*clone_x(count+1,:)+temp_gama*(clone_x(count,:)-clone_x(count+1,:)); % cross_x(count+1,:) = temp_alpha*clone_x(count+1,:)+(1-temp_alpha)*clone_x(count,:)+temp_gama*(clone_x(count,:)-clone_x(count+1,:)); elsecross_x(count,:)=clone_x(count,:);cross_x(count+1,:)=clone_x(count+1,:);end% 边界条件检查if cross_x(count,1)>X_max || cross_x(count,1)<X_min || cross_x(count,2)>Y_max || cross_x(count,2)<Y_mintemp1 = X_min+rand()*(X_max-X_min);temp2 = Y_min+rand()*(Y_max-Y_min);cross_x(count,:) = [temp1,temp2];endendcross_x = cross_x(1:NP,:);% cross_x为完成交叉的个体;% 变异操作for count=1:1:NP% 计算Pmif fitness(count)>=fitness_averagePm = k2*(fitness_max-fitness(count))/(fitness_max-fitness_average);elsePm = k4;collect_Pm(gen,count) = Pm; % 保存Pm的值temp_mutation=rand();if temp_mutation<Pm%mutation_x(count,:) = (1+0.01).*cross_x(count,:); %这种变异算⼦效果不理想% 变异算⼦参考⽂献:管⼩艳. 实数编码下遗传算法的改进及其应⽤[D].重庆⼤学,2012mutation_pos = randi(D);if mutation_pos==1low = X_min;high = X_max;elselow = Y_min;high = Y_max;ends_t(gen) = 1-r^((1-gen/G)^b);new_low = cross_x(count, mutation_pos)-s_t(gen)*(cross_x(count, mutation_pos)-low);new_high = cross_x(count, mutation_pos)+s_t(gen)*(high-cross_x(count, mutation_pos));mutation_x(count, :) = cross_x(count, :);mutation_x(count, mutation_pos) = new_low+rand()*(new_high-new_low);if mutation_x(count,1)>X_max || mutation_x(count,1)<X_min || mutation_x(count,2)>Y_max || mutation_x(count,2)<Y_min temp1 = X_min+rand()*(X_max-X_min);temp2 = Y_min+rand()*(Y_max-Y_min);mutation_x(count,:) = [temp1,temp2];endelsemutation_x(count,:) = cross_x(count,:);endend%边界条件处理x=mutation_x(1:NP, :);x(1,:)= best_indiv;end%% 作图figure(4)plot(best_solution);%hold on;xlabel('进化代数');ylabel('适应度值');title('适应度进化曲线');figure(5);plot(collect_fitmax_subtract_fit_average);title('f_{max}-f_{average}曲线');xlabel('进化代数');ylabel('f_{max}-f_{average}');% function f=func(buf)% f=0.5-((sin(sqrt(buf(1).^2+buf(2).^2)).^2)-0.5)./(1+0.001.*(buf(1).^2+buf(2).^2)).^2;% endfunction f=func(buf, md)if strcmp(md, 'Schaffer')f=0.5-((sin(sqrt(buf(1).^2+buf(2).^2)).^2)-0.5)./(1+0.001.*(buf(1).^2+buf(2).^2)).^2;endif strcmp(md,'self_define')% f = 100*(buf(2)-buf(1).^2).^2+(1-buf(1)).^2;f = (cos(buf(1).^2+buf(2).^2)-0.1)./(1+0.3*(buf(1).^2+buf(2).^2).^2)+3;endend测试函数:Schaffer函数:运⾏结果:种群的分布变化:-----------------------------------------------------分割线----------------------------------------------------2019/4/2 上⾯的代码有两个地⽅写错了,现在已经改正:1. ⽤于轮盘赌的fitness应该与⽤于计算⾃适应参数的fitness分开2.对轮盘赌选择算⼦进⾏修改修改后的代码:% 测试函数图像% 测试函数图像% 改进的⾃适应遗传算法:% 参考⽂献:[7] M. Srinivas and L. M. Patnaik, "Adaptive probabilities of crossover and mutation in genetic algorithms," % in IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 4, pp. 656-667, April 1994.% doi: 10.1109/21.286385clc;clear all;mode = 'Schaffer';% mode = 'self_define';if strcmp(mode, 'Schaffer')figure(1)x = -4:0.1:4;y = -4:0.1:4;[X,Y] = meshgrid(x,y);% Z = 3*cos(X.*Y)+X+Y.^2;Z = 0.5-((sin(sqrt(X.^2+Y.^2)).^2)-0.5)./(1+0.001.*(X.^2+Y.^2)).^2;surf(X,Y,Z);title('Schaffer Function');xlabel('X-轴');ylabel('Y-轴');zlabel('Z-轴');figure(2);contour(X, Y, Z, 8);title('Schaffer函数等⾼线');xlabel('X-轴');ylabel('Y-轴');endif strcmp(mode, 'self_define')figure(1);x = -4:0.1:4;y = -4:0.1:4;[X,Y] = meshgrid(x,y);% Z = 100.*(Y-X.^2).^2+(1-X).^2;Z = (cos(X.^2+Y.^2)-0.1)./(1+0.3*(X.^2+Y.^2).^2)+3;surf(X,Y,Z);%title('Rosen Brock valley Function');title('Self define Function');xlabel('X-轴');ylabel('Y-轴');zlabel('Z-轴');endclc;clearvars -except mode;r = 0.2;b = 3;NP=100;% Pc=0.65; % 将Pc,Pm参数改进为⾃适应参数% Pm=0.20;G=100; % 记得改D=2; % 变量个数k1 = 1;k3 = 1;k2 = 0.5;k4 = 0.5;X_min=-4;X_max=4;Y_min=-4;Y_max=4;% optimization_trace = []; % 三维数组, ⾏,列,叶for count_1=1:NP % 产⽣初始解temp1 = X_min+rand()*(X_max-X_min);temp2 = Y_min+rand()*(Y_max-Y_min);x(count_1,:) = [temp1,temp2];endsave_pic_cnt = 1;A = figure(3);for gen=1:Gpause(0.2);if rem(gen, 2)==1scatter(x(:,1), x(:, 2));axis([-4, 4, -4, 4]);title(['第', num2str(gen), '次迭代']);xlabel('变量X');ylabel('变量Y');base_path = 'C:\Users\18811\Desktop\graph\';cnt = num2str(save_pic_cnt);tail_path = '.jpg';frame = getframe(A);im=frame2im(frame);path_img = [base_path, cnt, tail_path];% imwrite(im, path_img);% save_x(:, :, save_pic_cnt) = x;save_pic_cnt = save_pic_cnt + 1;end% scatter(0, 0, 'o', 'r');for count_2=1:NPfitness(count_2)=func(x(count_2,:), mode);endfitness_ = fitness;%[fitness_min,index0] = min(fitness);%fitness_max = max(fitness);[fitness_max,index0] = max(fitness);fitness_average = sum(fitness)/(length(fitness)); % 种群的平均值collect_fit_average(gen) = fitness_average; % 保存适应度的平均值collect_fitmax_subtract_fit_average(gen) = fitness_max - fitness_average; % 保存f_max-f_average ; fitness_min = min(fitness);best_indiv = x(index0,:); % 最优的个体% optimization_trace(gen,: , global_count) = best_indiv;% best_solution(gen) = fitness_min;best_solution(gen) = fitness_max;% 计算归⼀化的适应度值fitness = (fitness - fitness_min)/(fitness_max - fitness_min);fitness_sum = sum(fitness);fitness = fitness./fitness_sum;fitness = cumsum(fitness);% 轮盘赌选择newi = 1;while newi<=NPrandom_num = rand(); % ⽣成随机数if random_num<fitness(1)clone_x(newi, :) = x(1, :);newi = newi+1;elsefor ct=1:NP-1if random_num>fitness(ct) && random_num<fitness(ct+1)clone_x(newi,:) = x(ct,:);newi = newi+1;break;endendendend% disp(clone_x - x);% 进⾏交叉,变异操作% count=0;for count=1:2:NP% ⾃适应计算Pc.% 选区两个交叉的个体的较⼤的适应度值if fitness_(count)>=fitness_(count+1)fitness_selected = fitness_(count);elsefitness_selected = fitness_(count+1);end% 计算Pcif fitness_selected >= fitness_averagePc = k1*(fitness_max-fitness_selected)/(fitness_max-fitness_average);elsePc = k3;endcollect_Pc(gen, count) = Pc; % 保存Pc的值temp_cross = rand();if temp_cross < Pc% 交叉算⼦注:这种交叉算⼦效果更好temp_alpha = 0.6;cross_x(count,:) = temp_alpha*clone_x(count,:)+(1-temp_alpha)*clone_x(count+1,:);cross_x(count+1,:) = temp_alpha*clone_x(count+1,:)+(1-temp_alpha)*clone_x(count,:);% 改进的交叉算⼦参考⽂献:管⼩艳. 实数编码下遗传算法的改进及其应⽤[D].重庆⼤学,2012. 注:但这种交叉算⼦实际的效果不理想% temp_gama = rand();% temp_alpha = 0.98;% cross_x(count,:) = temp_alpha*clone_x(count,:)+(1-temp_alpha)*clone_x(count+1,:)+temp_gama*(clone_x(count,:)-clone_x(count+1,:)); % cross_x(count+1,:) = temp_alpha*clone_x(count+1,:)+(1-temp_alpha)*clone_x(count,:)+temp_gama*(clone_x(count,:)-clone_x(count+1,:)); elsecross_x(count,:)=clone_x(count,:);cross_x(count+1,:)=clone_x(count+1,:);end% 边界条件检查if cross_x(count,1)>X_max || cross_x(count,1)<X_min || cross_x(count,2)>Y_max || cross_x(count,2)<Y_mintemp1 = X_min+rand()*(X_max-X_min);temp2 = Y_min+rand()*(Y_max-Y_min);cross_x(count,:) = [temp1,temp2];endendcross_x = cross_x(1:NP,:);% cross_x为完成交叉的个体;% 变异操作for count=1:1:NP% 计算Pmif fitness_(count)>=fitness_averagePm = k2*(fitness_max-fitness_(count))/(fitness_max-fitness_average);elsePm = k4;endcollect_Pm(gen,count) = Pm; % 保存Pm的值temp_mutation=rand();if temp_mutation<Pm%mutation_x(count,:) = (1+0.01).*cross_x(count,:); %这种变异算⼦效果不理想% 变异算⼦参考⽂献:管⼩艳. 实数编码下遗传算法的改进及其应⽤[D].重庆⼤学,2012mutation_pos = randi(D);if mutation_pos==1low = X_min;high = X_max;elselow = Y_min;high = Y_max;ends_t(gen) = 1-r^((1-gen/G)^b);new_low = cross_x(count, mutation_pos)-s_t(gen)*(cross_x(count, mutation_pos)-low);new_high = cross_x(count, mutation_pos)+s_t(gen)*(high-cross_x(count, mutation_pos));mutation_x(count, :) = cross_x(count, :);mutation_x(count, mutation_pos) = new_low+rand()*(new_high-new_low);if mutation_x(count,1)>X_max || mutation_x(count,1)<X_min || mutation_x(count,2)>Y_max || mutation_x(count,2)<Y_mintemp1 = X_min+rand()*(X_max-X_min);temp2 = Y_min+rand()*(Y_max-Y_min);mutation_x(count,:) = [temp1,temp2];endelsemutation_x(count,:) = cross_x(count,:);endend%边界条件处理x=mutation_x(1:NP, :);x(1,:)= best_indiv;end%% 作图figure(4)plot(best_solution);%hold on;xlabel('进化代数');ylabel('适应度值');title('适应度进化曲线');figure(5);plot(collect_fitmax_subtract_fit_average);title('f_{max}-f_{average}曲线');xlabel('进化代数');ylabel('f_{max}-f_{average}');% function f=func(buf)% f=0.5-((sin(sqrt(buf(1).^2+buf(2).^2)).^2)-0.5)./(1+0.001.*(buf(1).^2+buf(2).^2)).^2; % endfunction f=func(buf, md)if strcmp(md, 'Schaffer')f=0.5-((sin(sqrt(buf(1).^2+buf(2).^2)).^2)-0.5)./(1+0.001.*(buf(1).^2+buf(2).^2)).^2; endif strcmp(md,'self_define')% f = 100*(buf(2)-buf(1).^2).^2+(1-buf(1)).^2;f = (cos(buf(1).^2+buf(2).^2)-0.1)./(1+0.3*(buf(1).^2+buf(2).^2).^2)+3;endend修改后的算法寻优效果得到很⼤的提升,⾮常感谢指出代码中的错误:运⾏结果:。
遗传算法的改进
Pm
k3 ( fmax
fmax
f) ,
favg
k4 ,
f favg f favg
其中, fmax 群体中最大的适应度值 fmax 每代群体的平均适应度值 f 要交叉的两个个体重较大的适应度值
f 要变异个体的适应度值
从上式可以看出,当适应度度值越接近最大适应 度值时,交叉率和变异率就越小,当等于最大适 应度值时,交叉率和变异率为零,这种调整方法 对于群体处于进化后期比较合适,但对于进化初 期不利,因为进化初期群体中的较优个体几乎不 发生变化,容易使进化走向局部最优解的可能性 增大。为此,可以作进一步的改进,使群体中最 大适应度值的个体的交叉率和变异率分别为 Pc2 和 Pm2 。为了保证每一代的最优个体不被破坏, 采用精英选择策略,使他们直接复制到下一代中。
在生物学中, 小生境是指特定环境下的一种生存环境, 相同的生物 生活在同一个小生境中。借鉴此概念, 遗传算法将每一代个体划分为 若干类, 每个类中选出若干适应度较大的个体作为一个类的优秀代表 组成一个种群, 再在种群中以及不同种群之间通过杂交、变异产生新 一代个体群, 同时采用预选择机制或者排挤机制或共享机制完成选择 操作。这样可以更好的保持群体的多样性, 使其具有很高的全局寻优 能力和收敛速度。
1
Pk (i
j)
exp(
f
(i) t
f
(
j))
f (i) f ( j) f (i) f ( j)
背包问题 (knapsack problem)
这是一个典型的最优化问题。
基本背包问题:设n件物体的重量分别为s1 sn
使用价值分别为 p1
p
,一个背包能承受的总重量
n
为c, 如何装包使总价值最大。
自适应遗传算法(仅供参照)
自适应遗传算法一.主要流程:1. 参数的初始化。
设定遗传种群规模N ,阵元数M ,信源数P 等。
2. 编码。
采用十进制编码方法。
3. 初始种群的产生。
随机数生成。
4. 适应度函数的评价。
选取()()R P ΘA tr f = (1) 其中,H 1H )(A A A A P A -= (2)P A 是A 的投影矩阵,A 是阵列流型。
∑==Li L 1H 1XX R (3) R 是数据协方差矩阵的最大似然估计。
5. 选择。
比例选择方法与精英选择方法结合使用,在当代种群中选择优良个体遗传到下一代。
既保证了种群的多样性,也使最优个体得以保留。
1)比例选择方法(赌轮盘法):每个个体被选中的概率与它的适应度函数值大小成正比,即适应度函数越高的个体被选中的概率也就越高。
2)精英选择方法:让种群中适应度函数值最高的个体不进行配对交叉,直接复制到下一代中。
但是容易陷入局部最优解,全局搜索能力差。
6. 交叉。
按照概率P c 对种群中个体两两配对,进行交叉操作。
本文中选取算数交叉的方式。
算数交叉:是由两个个体的线性组合来产生新的个体,假设第t 代的两个个体为A (t)、B (t),则算数交叉后产生的新个体是()()()()t t t A B A αα-+=+11 (4)()()()()t t t B A B αα-+=+11 (5)其中,α选取(0,1)之间的随机数。
交叉概率:使交叉概率随着遗传代数的增长,逐渐减小,目的是进化前期注重交叉运算,全局搜索能力强。
2.02c o s *4.0+⎪⎭⎫ ⎝⎛*=πK T P c (6) 其中,T 是进化代数,K 是总进化次数。
7. 变异。
按照概率P m 对种群个体进行变异。
本文中选取均匀变异的方式。
均匀变异:如某基因座上的基因值为X k ,其取值范围为[Umin,Umax],对其进行变异后的值为)U -r(U +U =X min max min k (7)其中,r 选取[0,1]之间的随机数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自适应遗传算法一.主要流程:1. 参数的初始化。
设定遗传种群规模N ,阵元数M ,信源数P 等。
2. 编码。
采用十进制编码方法。
3. 初始种群的产生。
随机数生成。
4. 适应度函数的评价。
选取()()R P ΘAtr f = (1)其中,H 1H )(A A A A P A -= (2)P A 是A 的投影矩阵,A 是阵列流型。
∑==Li L 1H 1XX R (3)R是数据协方差矩阵的最大似然估计。
5. 选择。
比例选择方法与精英选择方法结合使用,在当代种群中选择优良个体遗传到下一代。
既保证了种群的多样性,也使最优个体得以保留。
1)比例选择方法(赌轮盘法):每个个体被选中的概率与它的适应度函数值大小成正比,即适应度函数越高的个体被选中的概率也就越高。
2)精英选择方法:让种群中适应度函数值最高的个体不进行配对交叉,直接复制到下一代中。
但是容易陷入局部最优解,全局搜索能力差。
6. 交叉。
按照概率P c 对种群中个体两两配对,进行交叉操作。
本文中选取算数交叉的方式。
算数交叉:是由两个个体的线性组合来产生新的个体,假设第t 代的两个个体为A (t)、B (t),则算数交叉后产生的新个体是()()()()t t t A B A αα-+=+11 (4)()()()()t t t B A B αα-+=+11 (5)其中,α选取(0,1)之间的随机数。
交叉概率:使交叉概率随着遗传代数的增长,逐渐减小,目的是进化前期注重交叉运算,全局搜索能力强。
2.02cos *4.0+⎪⎭⎫⎝⎛*=πK T P c (6)其中,T 是进化代数,K 是总进化次数。
7. 变异。
按照概率P m 对种群个体进行变异。
本文中选取均匀变异的方式。
均匀变异:如某基因座上的基因值为X k ,其取值范围为[Umin,Umax],对其进行变异后的值为)U -r(U +U =X min max min k (7)其中,r 选取[0,1]之间的随机数。
变异概率:使变异概率随着遗传代数的增长,逐渐增加,目的是进化后期注重变异运算,局部搜索能力强。
005.02sin *045.0+⎪⎭⎫⎝⎛*=πK T P m (8)其中,T 是进化代数,K 是总进化次数。
8. 终止条件判断。
若已达到设定的最大遗传代数,则迭代终止,输出最优解;若不满足终止条件,则返回第4步,进行迭代寻优过程。
图1 遗传算运算流程图二.仿真实验1.种群容量对角度均方根误差的影响实验条件:由8个阵元构成均匀线性阵列,阵元间距为半个波长,空间中有2个互不相关的窄带信号源,存在于该阵列的远场区域内。
两个信号源的波达方向分别为-20°和60°,快拍数取值128,信噪比取值20dB 。
种群容量范围[50,400],间隔50取值,循环代数200,交叉概率取值2.02cos *4.0+⎪⎭⎫ ⎝⎛*=πK T P c ,变异概率取值005.02sin *045.0+⎪⎭⎫⎝⎛*=πK T P m 。
蒙特卡洛实验次数200。
图2 种群容量对角度均方根误差的影响通过图2可知,当循环代数一定时,随着种群容量的增加,角度均方根误差逐渐减小。
2. 循环代数对角度均方根误差的影响实验条件:由8个阵元构成均匀线性阵列,阵元间距为半个波长,空间中有2个互不相关的窄带信号源,存在于该阵列的远场区域内。
两个信号源的波达方向分别为-20°和60°,快拍数取值128,信噪比取值20dB 。
种群容量200,循环代数范围[50,400],间隔50取值,交叉概率取值2.02cos *4.0+⎪⎭⎫ ⎝⎛*=πK T P c ,变异概率取值005.02sin *045.0+⎪⎭⎫⎝⎛*=πK T P m 。
蒙特卡洛实验次数200。
图3 循环代数对角度均方根误差的影响通过图3可知,当种群容量一定,随着循环代数的增加,角度均方根误差曲线平稳,角度测量准确度无改善。
3. 信噪比对角度均方根误差的影响实验条件:由8个阵元构成均匀线性阵列,阵元间距为半个波长,空间中有2个互不相关的窄带信号源,存在于该阵列的远场区域内。
两个信号源的波达方向分别为-20°和60°,快拍数取值128,信噪比取值[-10,20]dB,步进4dB 。
种群容量200,循环代数200,交叉概率取值2.02cos *4.0+⎪⎭⎫ ⎝⎛*=πK T P c ,变异概率取值005.02sin *045.0+⎪⎭⎫⎝⎛*=πK T P m 。
蒙特卡洛实验次数200。
图4 信噪比对角度均方根误差的影响通过图4可知,随着信噪比的增加,角度均方根误差逐渐减小,并趋于平稳,小于1°。
4. 小快拍数下角度差值对角度均方根误差的影响实验条件:由8个阵元构成均匀线性阵列,阵元间距为半个波长,空间中有2个互不相关的窄带信号源,存在于该阵列的远场区域内。
两个信号源的入射角相差[5,35]°,步进5°,快拍数取值20,信噪比取值20dB 。
种群容量200,循环代数200,交叉概率取值2.02cos *4.0+⎪⎭⎫ ⎝⎛*=πK T P c ,变异概率取值005.02sin *045.0+⎪⎭⎫⎝⎛*=πK T P m 。
蒙特卡洛实验次数100。
图5 小快拍条件下入射角度差值对均方根误差的影响通过图5可知,在相同条件下,随着入射角度之间差值增大,对角度测量的误差减小。
5. 低信噪比下快拍数对角度均方根误差的影响实验条件:由8个阵元构成均匀线性阵列,阵元间距为半个波长,空间中有2个互不相关的窄带信号源,存在于该阵列的远场区域内。
两个信号源的入射角分别为-20°、50°,快拍数取值[25,150],步进5,信噪比取值-10dB 。
种群容量200,循环代数200,交叉概率取值2.02cos *4.0+⎪⎭⎫ ⎝⎛*=πK T P c ,变异概率取值005.02sin *045.0+⎪⎭⎫⎝⎛*=πK T P m 。
蒙特卡洛实验次数100。
图6 低信噪比下快拍数对角度均方根误差的影响通过图6可知,低信噪比情况下,随着快拍数的增长,角度均方根误差的逐渐减小,但是角度估计的准确度低。
6. 高信噪比下快拍数对角度均方根误差的影响实验条件:由8个阵元构成均匀线性阵列,阵元间距为半个波长,空间中有2个互不相关的窄带信号源,存在于该阵列的远场区域内。
两个信号源的入射角分别为-20°、50°,快拍数取值[25,150],步进5,信噪比取值20dB 。
种群容量200,循环代数200,交叉概率取值2.02cos *4.0+⎪⎭⎫ ⎝⎛*=πK T P c ,变异概率取值005.02sin *045.0+⎪⎭⎫⎝⎛*=πK T P m 。
蒙特卡洛实验次数100。
图7 高信噪比下快拍数对角度均方根误差的影响通过图7可知,在信噪比较大的情况下,在不同的快拍数下,角度均方根误差变化趋于平稳,波动小。
三.仿真程序1.基于自适应遗传算法的最大似然估计 % 下面举例说明遗传算法 % % 求下列函数的最大值 %% 适应值函数:max{trace(PA*R)}, theta ∈[-90,90] % %十进制种群 均匀线阵 赌轮盘法 精英选择法 % 编程%----------------------------------------------- clear all clc tic M=8;doa=[-20 50];f=1000;%中心频率c=1500;%速度lambda=c/f;%波长d=lambda/2;%阵元间距%SNR=[-10:2:20];SNR=20;%信噪比N=128;%快拍数K=10;%试验次数%Iterations=[50:50:400];循环次数%popsize=[51:50:401];种群容量popsize=201;for g=1:length(SNR)%可以在这里修改循环条件%阵列流型Afor i=1:PA(:,i)=exp(-j*2*pi*d*[0:M-1]'/lambda*sin(doa(i)/180*pi));%均匀线性阵的阵列流型矢量。
end%信源模型建立S=zeros(P,N(g));for k=1:PS(k,:)=sqrt(10.^(SNR/10))*(randn(1,N(g))+j*randn(1,N(g)));%sqrt(10.^( snr/10))使信号符合该信噪比。
end%接收信号模型建立X=A*S+1/sqrt(2)*(randn(M,N(g))+j*randn(M,N(g)));%1/sqrt(2)使高斯白噪声的能量为1。
R=X*X'/N(g);[V,D]=eig(R);% [V,D]=eig(A):求矩阵R的全部特征值,构成对角阵D,并求A的特征向量构成V的列向量。
[Y,I]=sort(diag(D));%diag是将对角阵的对角元素提取成一个向量.如果A是向量,sort(A) 对A中元素按照升序排列。
% 如果A是矩阵sort(A) 对A按每一列元素按照升序排列。
Y为排列后矩阵,I是原矩阵中各元素位置所组成的新矩阵。
Un=V(:,I(1:M-P));%把原矩阵第1到M-P列中的数对应到V矩阵中的列数,建立新的矩阵赋值给Un。
Us=V(:,I(M-P+1:M));%信号子空间for k=1:K %试验次数%popsize=201; %群体大小chromlength=2; %字符串长度(个体长度)pop=initpop(popsize,chromlength);%随机产生初始群体for i=1: 200 %200为迭代次数pc=0.4*cos(i*pi/(2*200))+0.2; %交叉概率,进行自适应改变,随着代数增加,逐渐减小。
pm=0.045*sin(i*pi/(2*200))+0.05; %变异概率,随着代数增加,逐渐变大。
[objvalue]=calobjvalue(pop,M,d,lambda,R);%计算目标函数[newpop1]=selection(pop,objvalue);%复制[newpop2]=crossover(newpop1,pc); %交叉[newpop3]=mutation(newpop2,pm);%变异pop=newpop3;end[objvalue]=calobjvalue(newpop3,M,d,lambda,R);%计算目标函数[bestindividual,bestfit]=best(newpop3,objvalue); %求出群体中适应值最大的个体及其适应值y(k,:)=bestindividual;%最优个体y(k,:)=sort(y(k,:),2);%测得角度按顺序排列mistake(g,2*k-1:2*k)=y(k,:)-sort(doa);%每次实验的误差矩阵endRMSE(g,:)=sqrt(sum(mistake(g,:).^2,2)/2/K);%均方根误差endToc2.种群生成初始化(编码)% initpop.m函数的功能是实现群体的初始化,popsize表示群体的大小,chromlength表示染色体的长度.%遗传算法子程序%Name: initpop.m%初始化function pop=initpop(popsize,chromlength)pop=(rand(popsize,chromlength)-0.5*ones(popsize,chromlength))*180; %行数为popsize,列数为chromlength的矩阵,%这样产生的初始种群。
