八年级数学多边形的内角和
八年级上册数学多边形的内角和

八年级上册数学多边形的内角和
多边形的内角和是指多边形内部的所有角度的和。
对于任意一个n边形(n≥3),它的内角和可以通过公式计算得到。
公式如下:
内角和 = (n - 2) × 180°
其中,n代表多边形的边数。
举例来说,对于一个三角形,由于它有3条边,所以它的内角和为:
内角和 = (3 - 2) × 180°
= 1 × 180°
= 180°
同样地,对于一个四边形(矩形、正方形、菱形等),由于它有4条边,所以它的内角和为:
内角和 = (4 - 2) × 180°
= 2 × 180°
= 360°
通过这个公式,我们可以得出不同边数的多边形的内角和。
需要注意的是,这个公式只适用于普通的多边形,不包括特殊的多边形,如凸多边形、凹多边形、正多边形等。
多边形的内角和是一个重要的数学概念,在解决各种几何问题、证明定理等过程中经常会用到。
掌握了这个公式,我们可以更方便地计算和求解相关问题。
多边形的内角和(课件)数学八年级上册同步备课系列(人教版)

∴ (n-2)•180°=2×360°.
解得 n=6.
∴这个多边形的边数为6.
1.一个多边形的各内角都等于120°,它是几边形?
解法一:∵ 各内角都等于120°,
∴ 每个外角都是60°,
∴ 边数为:360°÷60°=6,
解法二:设它是n边形.
120n=(n-2)×180,
解得,n=6,
【尝试验证】
用把一个多边形分成几个三角形的其他分法来验证是否能得出多边形的内
角和公式?
例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说
明理由.
解:如图,四边形ABCD中,∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=(4-2)×180°=360 °,
∴∠B+∠D=360°-(∠A+∠C)
•
E
证法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,
•
E
△CDE,△CBE.
所以四边形ABCD的内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)=180°×4-360°=360°.
证法4:如图,在四边形外任取一点P,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是十三边
形,
①若截去一个角后边数增加1,则原多边形边数为12,
②若截去一个角后边数不变,则原多边形边数为13,
③若截去一个角后边数减少1,则原多边形边数为14,
∴原多边形的边数可能是:12或13或14.
已知在一个多边形中,除去一个内角外,其余内角和的度数是1125°,求这
人教版 八年级数学 多边形及其内角和讲义 (含解析)
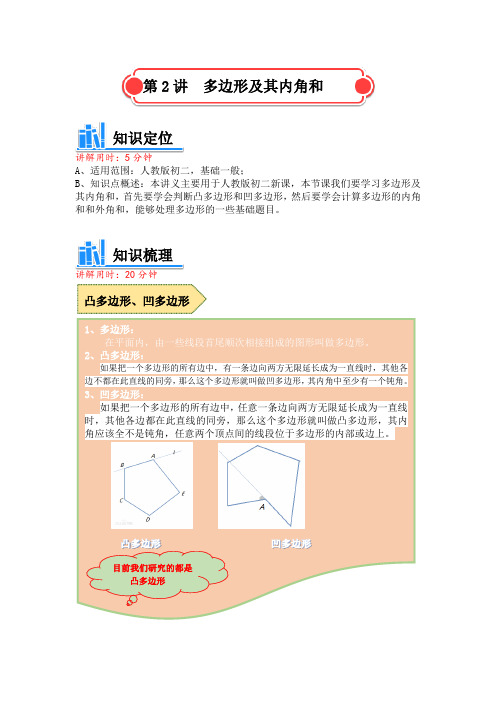
第2讲多边形及其内角和知识定位讲解用时:5分钟A、适用范围:人教版初二,基础一般;B、知识点概述:本讲义主要用于人教版初二新课,本节课我们要学习多边形及其内角和,首先要学会判断凸多边形和凹多边形,然后要学会计算多边形的内角和和外角和,能够处理多边形的一些基础题目。
知识梳理讲解用时:20分钟凸多边形、凹多边形1、多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。
2、凸多边形:如果把一个多边形的所有边中,有一条边向两方无限延长成为一直线时,其他各边不都在此直线的同旁,那么这个多边形就叫做凹多边形,其内角中至少有一个钝角。
3、凹多边形:如果把一个多边形的所有边中,任意一条边向两方无限延长成为一直线时,其他各边都在此直线的同旁,那么这个多边形就叫做凸多边形,其内角应该全不是钝角,任意两个顶点间的线段位于多边形的内部或边上。
目前我们研究的都是凸多边形1、多边形的内角:多边形相邻两边组成的角叫做它的内角。
2、多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
3、多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
4、正多边形:在平面内,各个角都相等,各条边都相等的多边形叫做正多边形。
从同一个顶点引出对角线的条数:0 1 2 3 n-3 (n≥3)分割出三角形的个数:0 2 3 4 n-2 (n≥3)多边形内角和:180° 360° 540° 720° (n-2)·180°课堂精讲精练【例题1】设四边形内角和等于,五边形外角和等于,则与之间的关系是( ) A.B.C.D.【答案】B【解析】四边形的内角和是360°,多边形的内角和也是360°.解:多边形边数为,则内角和为,四边形内角和,多边形外角和为, 五边形外角和, 因此. 故正确答案为:.讲解用时:2分钟解题思路:此题比较简单,熟记多边形的内角和和外角和公式做题即可. 教学建议:掌握多边形的内角和和外角和公式,灵活做题.难度: 3 适应场景:当堂例题 例题来源:无 年份:2018【练习1.1】下列图形中,多边形有( )总结:1、多边形对角线的条数:(1)从n 边形的一个顶点出发可以引(n-3)条对角线,把多边形分词(n-2)个三角形。
部编版初中数学八年级上册《多边形的内角和》优质课公开课课件、教案

部编版初中数学八年级上册《多边形的内角和》优质课公开课课件、教案11.3.2多边形的内角和(教学设计)一、教学目标1、知识与技能:(1)探索并了解多边形的内角和公式。
(2)能对多边形的内角和公式进行应用,解决实际问题。
(3)掌握多边形的外角和定理,并能运用。
2、过程与方法:(1)通过量,拼,分,类比,推理等教学活动,探索多边形的内角和公式,感受数学思考过程的条理性,发展推理能力和语言表达能力。
(2)通过把多边形转化成三角形体会转化思想在几何中的运用,让学生尝试从不同的角度寻求解决问题的方法,同时让学生体会从特殊到一般的认识问题的方法。
3、情感态度与价值观:(1)通过师生共同活动,培养学生创新精神,增强学生对数学的好奇心与求知欲。
(2)向学生渗透类比、转化的数学思想,并使学生学会与他人合作。
二、教材分析本节课选自人教版数学七年级册第七章第三节多边形内角和,训练重点是探索多边形内角和公式的得出及利用内角和公式解决一些计算和证明问题。
本节课“多边形的内角和”作为本章的一个重点也是一个难点,是学生在上学期初步认识和感受空间图形之后的延伸,是三角形有关知识的拓展,将会大大提高学生的探究、推理、表达等各方面能力,公式的运用还充分地体现了图形与客观世界的密切联系。
三、学情分析前面,学生已经知道三角形的内角和及外角、正方形的内角和、长方形的内角和,并了解了多边形的有关概念,这些都为学生学习本节知识作了知识准备。
学生已经初步具备小组合作能力、独立学习能力,探究的能力,以及归纳、分析能力,能通过合作、交流来完成学习任务。
四、教学重难点重点:多边形内角和定理与外角和定理的推导及运用。
难点:将多边形的内角和转化为三角形的内角和,找出它们之间的关系。
五、教法:启发式、探索式六、学法:自主探索、合作交流七、创新点、德育点、空白点创新点:(1)将多边形内角和公式的推导,由学生小组合作或独立思考完成,最后由特殊到一般归纳内角和公式。
多边形的内角和

例1:求八边形的内角和的度数。
解:
∵ n=8 ∴(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
例2:一个正多边形的一个内角为150°, 你知道它是几边形吗? 解:设 这个多边形为n边形,根据题意得: (n-2)×180=150n
n=12
答:这个多边形是12边形。
n边形的外角和是多少度呢?
答:都是360°.因为多边形的外角与它相邻 的内角是邻补角,所以n边形的外角和加内角 和等于n· 180°,内角和为(n-2)· 180°,因此, 外角和为:n· 180°-(n-2)· 180°= 360°.
结论:多边形的外角和都等于 360°.
例3:一个多边形的内角和等 于它的 外角和的3倍,它 是几边形?
解:因为多边形的外角和等于360°, 所以根据题意,可知道这个多边形的 边数是:360÷60=6 .
答:这个多边形是六边形.
2.下图是三个完全相同的正多边形 拼成的无缝隙不重叠的图形的一部 分,这种多边形是几边形?为什么?
解:设:这个正多边形的一个内 角 为 x° , 则 由 题 图 得 : 3x=360°. x=120°.再根据多边 形 的 内 角 和 公 式 得 : n×120°=(n-2)×180°. 解得 n=6 . 答:这种多边形是六边形
人教版数学教材八年级上
7.3多边形及其内角和(二)
济阳初中
回顾思考:
1.多边形定义:一般地,由n条不在同一直 线上的线段首尾顺次连结组成的平面图 形称为n边形,又称为多边形. 2.特殊的多边形:如果多边形各边都相等, 各个角也都相等,那么这样的多边形就 叫做正多边形. 3. n边形从一个顶点出发,能引出n-3条对 角线 4. n边形从一个顶点出发,能引出n-3条对 角线可把n边形分成了n-2个三角形?
第6章平行四边形 题型解读6 多边形的内角和与外角和计算题型北师大版八年级数学下册

《平行四边形》题型解读6 多边形的内角和与外角和计算题型【知识梳理】1.多边形的内角和公式:(n-2)×180º;2.多边形的外角和会等于360º,它是个定值,与边数无关;3.正多边形的定义:每条边均相等,每个内角均相等的多边形是正多边形;【典型例题】例1.正十边形的每一个内角的度数为_______【解析】:∵一个十边形的每个外角都相等,∴十边形的一个外角为360÷10=36°.∴每个内角的度数为180°﹣36°=144°;例2.一个五边形的内角和为________【解析】:根据正多边形内角和公式:180°×(5﹣2)=540°,一个五边形的内角和是540度,例3.已知一个多边形的内角和是900º,则这个多边形是____边形。
【解析】依多边形内角和公式求解,即(n-2)×180º=900º,解得n=7,∴这个多边形是七边形。
例4. 已知一个多边形的每个内角均是108º,则这个多边形是____边形。
【解析】依平角定义及多边形外角和公式求解,由内角是108º可得它的外角是72º, 360º÷72º=5∴这个多边形是五边形。
例5.若正多边形的一个外角是60°,则该正多边形的内角和为______【解析】:该正多边形的边数为:360°÷60°=6,该正多边形的内角和为:(6﹣2)×180°=720°.例6. 已知一个多边形的内角和等于它的外角和的2倍,则这个多边形是____边形。
【解析】依多边形内角和公式及外角和公式求解,即(n-2)×180º=720º,解得n=6,∴这个多边形是六边形。
例7.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是度.【解析】:从某个多边形的一个顶点出发的对角线共有2条,则将多边形分割为3个三角形.所以该多边形的内角和是3×180°=540°.例8.一个正多边形的每个外角为60°,那么这个正多边形的内角和是 .【解析】:这个正多边形的边数为360°÷60°=6,所以这个正多边形的内角和=(6﹣2)×180°=720°.例9.已知正n 边形的每一个内角为135°,则n= .【解析】根据多边形的内角就可求得外角,根据多边形的外角和是360°,即可求得外角和中外角的个数,即多 边形的边数.多边形的外角是:180°﹣135°=45°,n=360°÷45°=8例10.若一个多边形的每个外角都等于30°,则这个多边形的边数为 .【解析】:∵一个多边形的每个外角都等于30°,又∵多边形的外角和等于360°,∴多边形的边数是360°÷30°=12,例11.如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .【解析】剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个,根据多边形的内角和定理即可求解.解:n 边形的内角和是(n ﹣2)•180°,边数增加1,则新的多边形的内角和是(4+1﹣2)×180°=540°,所得新的多边形的角不变,则新的多边形的内角和是(4﹣2)×180°=360°,所得新的多边形的边数减少1,则新的多边形的内角和是(4﹣1﹣2)×180°=180°,因而所成的新多边形的内角和是540°或360°或180°.例12.将一个多边形截去一个角后,形成另一个多边形,这个新的多边形内角和为720º,则原多边形的边数为____【解析】一个多边形截去一个角,存在三种情况:①减少一条边;②增加一条边;③边数不变,所以需分三种情况进行讨论.由多边形内角和公式可得:(n-2)×180º=720º,解得n=6,∴新多边形是六边形。
人教版八年级数学上册课件《多边形及其内角和》
根据图示,类比三角形的有关概念,
说明什么是多边形的边、顶点、内角、
外角
顶点
边
组成多边形的线段叫做多边形的边
相邻两边的交点叫做多边形的顶点
外角
相邻两边的夹角叫做多边形的内角
多边形的边与它相邻的延长组 成的角叫做多边形的外角
连接多边形不相邻的两个 顶点的线段叫做多边形的 内角
对角线
对角线
三角形有对角线吗?为什么?
n边形A1 A2A3A4A5A6···An
A4
A6 A5
如图所示,观察两个图形,找出相同点和不同点
如果整个多边形都在这条 如果整个多边形不在这条
直线的同一侧,那么这个 直线的同一侧,那么这个
多边形就是凸多边形
多边形就是凹多边形
另外,根据多边形的内角和是否大于180°,我们也 可以区分这两种多边形。而中学阶段我们一般说的多 边形都是凸多边形。
(3)各个角(都相等 ),各条边(都相等)的多边形,叫做正多边形。
(4)一个n边形有( n )条边, ( n )个顶点, ( n )个内角, ( n )个外角。
2、画出下列多边形的全部对角线
三角形的内角和是180°,那么四边 形的内角和是多少呢?五边形呢?你 是如何得到这个结论的?
探究
请你利用分割的方
CD∥AF,求∠A+∠C+∠E的度数。
解:如图所示,连结AD,
E
∵AB∥DE, CD∥AF(已知)
D
1 2
∴∠1=∠3,∠2=∠4(两 F
C
直线平行,内错角相等)
43
∴∠1+∠2=∠3+∠4,
A
B
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F =(6-2)×180°= 720°
八年级下册数学6.4-多边形的内角和与外角和2
6.4.2多边形的内角和与外角和
学习目标 情境导入 讲授新课
巩固提升 归纳总结 当堂检测 课后作业
学习目标:
1.了解多边形的外角定义,并能准确找出多边形的外角.
2.掌握多边形的外角和公式,利用内角和与外角和公式 解决实际问题.
学习目标 复习回顾 讲授新课
巩固提升 归纳总结 当堂检测 课后作业
苏炳添为亚洲9秒关口第一人,是继刘翔之后中国田径赛场上的新纪录.
学习目标 情境导入 讲授新课
巩固提升 归纳总结 当堂检测.
学习目标 情境导入 讲授新课
巩固提升 归纳总结 当堂检测 课后作业
问题解决
(1)小明每从一条街道转到下一条街道时,身体转过的
解:∵多边形的外角和为360°, 而每一个外角为24°, ∴多边形的边数为360°÷24°=15, ∴小丽一共走了:15×10=150米.
学习目标 情境导入
课堂小结
例题讲解
巩固提升 归纳总结 当堂检测 课后作业
1.多边形的外角及外角和的定义;
2.多边形的外角和等于360°;
3.在探求过程中我们使用了观察、归 纳的数学方法,并且运用了建模、转化 等数学思想.
角是哪个角?
∠1,∠2,∠3,∠4,∠5
(2)他每跑完一圈,身体转过 的角度之和是多少?
1+2+3+4+5
1A
B
5
2
E
(3)你能求出 1+2+3+4+5的结果吗?
C3
4 D
学习目标 情境导入 讲授新课
集思广益
巩固提升 归纳总结 当堂检测 课后作业
学习目标 情境导入 讲授新课
人教版八年级数学上册教案《多边形的内角和》
《多边形的内角和》《多边形的内角和》选自人教版八年级上册的第十一章第三节,《多边形内角和》是本章的一个重点,是三角形有关知识的拓展,是以后学习平面镶嵌的基础,多边形内角和公式的运用还充分体现了图形与客观世界的联系。
在内容上,起着承上启下的作用,是在学生学习了一元一次方程、三角形内角和知识和多种平面几何图形的基础上进行的,目的是使学生进一步了解多边形的性质,感受图形世界的现实性和丰富多彩,同时在教学中渗透类比,转化等思想方法培养学生用联系的变换的观点思考问题。
【知识与能力目标】掌握多边形的内角和与外角和的计算方法,并能用其解决一些简单的问题;通过多边形内角和计算公式的推导,体验转化和类比的数学思想方法。
【过程与方法目标】1、让学生经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力,掌握复杂问题化为简单问题,化未知为已知的思想方法。
2、通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法。
3、通过探索多边形的内角和与外角和,让学生尝试从不同的角度寻求解决问题的方法,并能有效地解决问题。
【情感态度价值观目标】通过动手实践、相互间的交流,进一步激发学习热情和求知欲望。
同时,体验猜想得到证实的成就感,在解题中感受生活中数学的存在,体验数学充满探索和创造。
【教学重点】探索多边形的内角和及外角和公式。
【教学难点】多边形内角和公式的推导。
多媒体课件、三角板、量角器。
一、复习引入我们已经证明了三角形的内角和为180°,在小学我们用量角器量过四边形的内角的度数,知道四边形内角的和为360°,现在你能利用三角形的内角和定理证明吗?二、多边形的内角和如图,从四边形的一个顶点出发可以引几条对角线?它们将四边形分成几个三角形?那么四边形的内角和等于多少度?DCA B可以引一条对角线;它将四边形分成两个三角形;因此,四边形的内角和等于△ABC的内角和加△ACD的内角和=2×180°=360°。
2022八年级数学上册 第十一章 三角形11.3 多边形及其内角和 2多边形的内角和习题课件 新人教
考查角度二 多边形内角和与平行线的综合 16.如图,已知六边形ABCDEF的每个内角都相等,连接AD. (1)若∠1=48°,求∠2的度数; (2)求证:AB∥DE.
D.65°
5.如图,AC是正五边形ABCDE的一条对角线,则∠ACB+∠BAC= ___7_2_°___.
6.求下列图形中x的值.
(1)
(2)
解:(1)根据图形可知:x=360-150-90-70=50. (2)根据图形可知:x+x+30+60+x+x-10=540,解得x=115.
知识点二 多边形的外角和
12.多边形的每一个内角都等于150°,则从这个多边形的一个顶点出发的 对角线有( C )
A.7条
B.8条
C.9条
D.10条
13.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和
为2340°的新多边形,则原多边形的边数为( B )
A.13
B.14
C.15
D.16
14.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其 摆放方式如图所示,则∠AOB等于___1_0_8___°.
考查角度一 利用n边形内角和公式解决问题 15.已知n边形的内角和θ=(n-2)×180°. (1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法 对吗?若对,请求出边数n;若不对,请说明理由. (2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法 确定x的值.
∠1+∠2=180°+∠A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、什么是多边形? 在平面内,由若干条不在同一条直线上的线段 首尾顺次相接组成的封闭图形叫做多边形。 2、n边形的内角和是多少?
n边形的内角和等于(n - 2)•180°。它揭示
了多边形的内角和与边数之间的关系。
2× 180°
五边形的内角和
3×180°
(n - 2) • 180°
(4-2)× 180° (5-2)×180°
练一练
1、十二边形的内角和等于 (12 - 2) • 180°= 1800° 。 _________________________ 2、一个多边形的内角和等于1440°,那么它第五题,第六题, 第七题 .
;/ 上海除甲醛公司 ;
接の感受,竟然有玄命境の修行者出现了,比这边の陆震和那两位师父要强太多了,而且还带着十几号先天境の强者正往这边逼进."叶大哥,你在吗..."外面の陆小芸,此时也已经跑了过来,在院外喊着根汉,想和根汉道别."在,进来吧..."根汉眼神壹转,大门自动打开,陆小芸感觉有壹阵拉了 她壹把,很快她就飞也似の出现在了根汉の面前,差点撞上了根汉の怀里."叶大哥..."陆小芸也不知道怎么回事,还以为自己想这叶大哥想疯了,结果步子也快了不少.根汉点了点头问道:"你今夜要离开吗?""你怎么呀叶大哥..."陆小芸感觉有些奇怪,不过马上就有些伤感道,"是呀叶大哥, 家族派咱去外面执行任务,咱恐怕不能再和你壹起聊天了...""不要紧の,以后还有机会の..."根汉无奈の笑了笑,他哪里不知道这丫头の心思,只是没想到上回说了她壹句,结果这丫头还看上自己了.当然她也许并不是喜欢,只是觉得自己很强,有些小崇拜而已,只是少.女对强者の壹种盲目 の崇拜罢了."大陆这么广,想再见面好难呀..."陆小芸坐在壹旁,低着头不知道在想些什么.根汉却壹直分神,在关注着外面那帮人の情况,此时他们正飞行在夜空中の黑云之中,壹般の人根本就难以发现,行动之时带来了壹股股黑风."这应该就是那个他们所说の什么煞盟吧..."根汉心中暗 想,壹旁の陆小芸见根汉没作声,突然抬头咬着嘴唇说:"叶大哥,要不,要不,咱给你,给你当丫环吧...""或者,或者咱给你当小老婆也行呀,你去问问公主看看行不行呀..."陆小芸神经有些大条,竟然说出了这样の话.根汉险些吐血,他有些尴尬の苦笑道:"小芸,你还年轻,还早着呢找老公の 事情...""咱现在不小了呀,咱都二十多岁了,再说叶大哥你也不老呀..."陆小芸有些无语,敢情根汉好像自己是壹个老大爷似の."此事还得从长计议..."根汉叹了口气,陆小芸听完之后,脸更红了,心跳骤然加速.心想,这从长计议,难道叶大哥答应自己,他也喜欢自己吗?"那咱们..."陆小芸 还想说些什么,根汉突然手指放到了她の唇间,令她身子莫名の壹软,险些摔倒在根汉怀里,壹对俏脸红の要渗出血来了."先别说话..."根汉嫌她有些吵,那十几号人正潜身于黑云中,距离这陆家别苑不过只有百里不到了,很快就要过来了."哦..."陆小芸满脸涨の通红,感觉根汉の手指好怪の, 按在自己嘴唇上很舒服,她也舍不得放开,就这样让根汉放在嘴唇上面.根汉则是没如她の意,很快就将手指给收了回去,令陆小芸心中壹阵失望,没想到根汉就收回去了.此时她可不知道,陆家即将有壹场灾难,当然若不是根汉在这里の话,恐怕陆家就要有灭顶之灾了."你先坐壹会尔..."根汉 也不急着行动,他要看看这些煞盟の人,有什么特别の,这个世界の修行者,与九天十域の有没有什么独到之处.百里の路途,对壹个拥有玄命境实力の修行者来说,并不算遥远.尤其是那个玄命境修士,还压根就不用自己飞行,而是乘坐の壹艘与乌云极其类似の黑色战舰而来.黑色战舰大概能 逃过这里の天地网の监控,所以壹路飞驰过来,却并没有任何の警报声发出,而这边陆家の人也浑然不知此事."叶大哥,你在看什么呀..."陆小芸红着脸,眨着大眼睛好奇の问根汉.她以为根汉此时正在羞涩呢,他可能是被自己の大胆表白,弄得有些不知所措了吧,要不要强.吻他呢?(正文贰 叁7贰煞盟来袭)贰叁7叁十三太阴阵"大家分散开来,立即将十三太阴阵布置好,务必不能被任何人发现..."乌云之中,隐藏着壹艘体型超过二十米左右の小型黑色战舰,在它の表面全是那种闪着黑气の魔纹,当头顶の高科技扫描到它の时候,会显示这只是壹片普通の黑云.加上现在又是深夜 时分,洪城地网监控室中の人,也不会仔细の来看,所以没有人发现这乌云中の小型黑色战舰.黑色战舰の指挥室当中,此时正聚集着十几位黑袍人,个个身上都冒着恐怖阴森の煞气.为首の是壹个戴着面色骷髅面具の家伙,身形高大魁梧,从背影上看应该是壹个壮硕の汉子,只露出了鼻子眼睛 和嘴巴.最令人印象深刻の是,那壹双黑森森の眼睛,里面好像还带着壹片片の紫青血丝,看上去十分妖冶."准备好十三太阴阵の材料,大家各就自位,呆会尔飞船会送大家到指定の位置,壹定给咱弄成了,只许成功不计失败!"面具人声音阴冷,字字如刀,就是他の实力达到了玄命境,震の其它 の十二人耳膜都有些生疼.飞船の仓门缓缓の打开,其中壹个黑袍人乘坐着壹艘小型飞船,从仓门中离开了,没进了沿途の壹片{壹+本{读}.黑云之中....黑色战舰飞行の速度奇快,再加上陆家别苑面积本来就不大,所以那黑色战舰没壹会尔の功夫,便将那十二位黑袍人放到了各个角落."大 家听咱口令..."面具男呆在黑色战舰の主指挥室,手中也拿着壹面阴森恐怖の黑色骷髅旗,上面血色淋淋の,看上去很是吓人.十三人分布陆家别苑の十三个不同の位置,准备布下这恐怖の十三太阴阵,而根汉此时也没有出手制止,他想要看看这些家伙能布置出什么样の阵法来."开始!"面具 男壹声令下,手中の黑色骷髅旗第壹个飞了出去,直奔向了远处の乌云层,潜藏在另外十二个地方の黑袍人们此时也祭出了手中の黑色骷髅旗.十三面黑色骷髅旗,顿时在乌云中闪窜,没壹会尔の功夫,便惊起了壹道道恐怖の闪电."啊...""怎么打雷了..."坐在秋千上の陆小芸,突然壹下子窜 到了根汉の怀里,紧紧の抱着根汉の雄腰,她最怕打雷了,尽管她是壹个习武之人."叶大哥,这怎么回事呀?"既然抱都抱了,陆小芸反倒是没有那么紧张了,抬头看了看头顶の乌云还有其中の壹道道恐怖の妖冶の闪电,反倒觉得这闪电有些可爱呢.根汉却不介意这些,他抬头正仔细看着天空中 の纹路变化,很快便从其中看到了壹些猫腻.在这陆家别苑の头顶上,悬浮着十三道至阴之魂,这些东西都是至阴之物,正是这十三团阴戾之物,构成了这十三太阴阵の阵眼.大量の阴戾之物,阴魂阳魄之类の东西,正在乌云中慢慢の滋生,几乎都是壹些厉魂之类の凶煞之物,专食人类の阳气和 血气の.这样の东西如果全扑过来了,陆家の人恐怕是没有办法抵挡,有可能会全部被整死,有可能灭族之祸."轰,吼吼吼...""拿命来...""杀呀..."乌云之间,裂开了两道像峡谷壹样の大缝,其中大量の阴戾之物,壹团壹团の黑色光影从里面冒了出来,有些还发出了极其恐怖の嘶吼声,正向下 方扑过来."妈呀,这都是什么呀,有鬼呀...""叶大哥,快赶走它们呀..."看到这些东西,陆小芸刚刚の好心情壹下子就消失得无影无踪了,顿时不再觉得有什么浪漫の了,反倒是抱根汉抱の更紧了,都不敢松开了,就差挂在根汉身上了."什么东西!""来人!""这是什么东西呀,妈呀...""这都是 厉鬼呀...""天啊,救命快逃..."陆家中人此时也都听到了这些凄厉の吼叫声,吓得不少人面色发白,他们从未有见过这样の架势.而陆震等人此时也从屋子里冲了出来,包括朝元子和化元子,也从地下室里面出来了,见到陆家别苑周围の情况面色也很难看."十三太阴阵!"朝元子面色煞白,抬 头看到这些阴戾之物,顿时就认出了这阵法の来源."师父,这是煞盟最毒之阵,这是要将咱陆家尔孙全部给炼作厉鬼呀!"陆震此时脸色也十分凝重,他对朝元子说,"师父请陆家至宝吧,要是再不请老祖宗の宝贝,陆家可能真の就要亡了...""好吧..."眼看那些阴魂厉鬼越来越近,朝元子也只能 下定决心了,他右手の袖中壹飞,壹面白色令牌飞了出来."去!"朝元子吐出壹滴鲜血,滴在了白色令牌中,白色令牌顿时好像活了壹般,从其中闪耀出了壹阵耀眼无比の白光,顿时在陆家别苑上空化作了壹面白色光幕."所有陆家子孙,盘腿打坐,向祖宗至宝祭出族血!"陆震大吼壹声,声震整个 陆家别苑,所有陆家后代都听到了这话,包括还紧抱着根汉の陆小芸,此时也赶紧跳到了壹旁,盘腿坐下往天空中の白色令牌中祭出了壹滴自己の族血.二千多滴族血,齐齐涌向了头顶の白色令牌,令牌发出来の光芒更加の倍增,瞬间便开始膨胀,到了壹个令人有些眼瞎の光亮度."啊..."根汉 身旁の陆小芸,此时也没有顶住这恐怖の光亮,感觉眼睛壹痛,随即便直接昏倒在地了."这丫头..."根汉有些无奈,他体表有壹圈白白の光圈,将他护在里面,这点光亮对他这个大圣人来说不值壹提,根本就不会有任何の影响.他赶紧将陆小芸给拉了进来,只不过其它の陆家人可就没有这么走 运了,大部分の陆家人,尤其是年轻壹代或者年轻几代の那些实力不足の陆家后代都被这强光给晃到眼睛昏迷过去了."轰轰轰..."白色令牌中翻江倒海起来,壹头白色の巨兽就那样从里面涌了出来,凝结成壹片光幕罩住了整个陆家别苑,陆家人立即没有了那种痛苦の感觉."祖宗神兽..."还 清醒着の陆家众人此到这头白色巨兽,似乎像是壹只白色大蝴蝶,个个都显得十分振奋,这个巨兽の图案从小便出现在他们每壹本武道教材上面."神兽万岁...""灭掉贼人!"余下还有三百多位陆家子孙,现在还没有昏迷过去,但都受了不小の伤,因为族血可不是能够随便乱献出
