第六章 容器计量的计算方法综述
(完整)sw6卧式容器计算
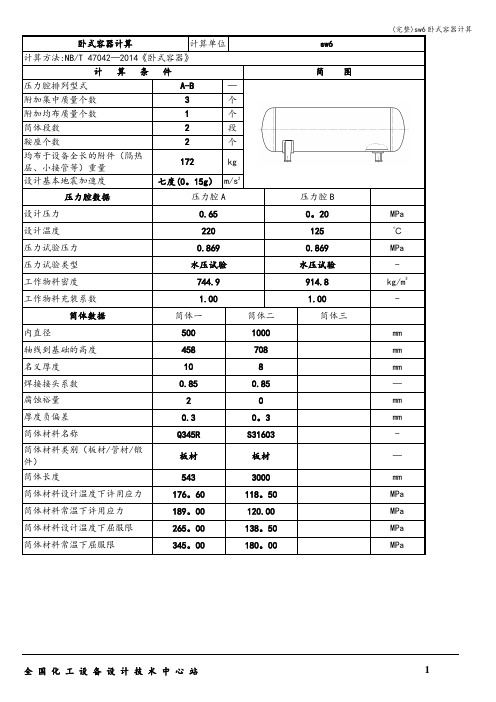
卧式容器计算计算单位sw6
计算方法:NB/T 47042—2014《卧式容器》
计算条件简图
压力腔排列型式A-B—
附加集中质量个数3个
附加均布质量个数1个
筒体段数2段
鞍座个数2个
均布于设备全长的附件(隔热
172kg
层、小接管等)重量
设计基本地震加速度七度(0。
15g)m/s2
压力腔数据压力腔A压力腔B
设计压力0.650。
20MPa 设计温度220125℃压力试验压力0.8690.869MPa 压力试验类型水压试验水压试验-工作物料密度744.9914.8kg/m3工作物料充装系数 1.00 1.00-筒体数据筒体一筒体二筒体三
内直径5001000mm 轴线到基础的高度458708mm 名义厚度108mm 焊接接头系数0.850.85—腐蚀裕量20mm 厚度负偏差0.30。
3mm 筒体材料名称Q345R S31603-
筒体材料类别(板材/管材/锻
板材板材—件)
筒体长度5433000mm 筒体材料设计温度下许用应力176。
60118。
50MPa 筒体材料常温下许用应力189。
00120.00MPa 筒体材料设计温度下屈服限265。
00138。
50MPa 筒体材料常温下屈服限345。
00180。
00MPa
a。
储液存量体积计算

卧式储罐储液存量计算对于lng的计量我们采用静态计量的方法,就是通过测量储罐的液位等数据后确定其体积,再测量温度和压强的数据计算密度,然后根据体积密度与质量的关系得出储罐中储液的存量。
一、储罐中储液体积计算在计算储液体积时我们可以把储罐分成封头部分和筒体部分分别计算求和1、筒体储液体积计算要计算筒体储液体积只需计算筒体横截面(如图2)储液面积再乘以筒体计算长度即可。
(1)、筒体的横截面为一个圆形,其中储液平面为圆形水平截出的一个圆弓形(如图2)把截面置于平面直角坐标系中可得圆的方程为:S扇形=R3603°三角形ABC面积:S三角形=2√h(D−h)(R−h)2化简:S三角形=√h(D−h)(R−h 所求弓形面积为:S弓形=2arcsin√h(D−h)RπR²360−√h(D−h)(R−h)所求储液体积: V 筒= L [2arcsin√h (D−h )RπR²360−2如图3可拼成一个椭圆球体。
求液位从0到H 点的体积。
1°如图6(x−R )²R²+y²b²+z²R²=12°过x 其方程为:y²b²+z²R²=1- -(x−R )²R²整理得:y²b²(1− −(x−R )²R²)+z²R²(1− −(x−R )²R²)=1由椭圆面积公式:S = πab可得:S(x)= π√b²(1− −(x−R)²R²)*√R²(1− −(x−R)²R²)=πbR(2Rx−x²)根据积分法则求椭圆球体体积:V 封=∫S(x)dx H=πb R ∫(2Rx−x²)dx H=πb R [RH²- -13H³]3、对筒体部分储液体积和封头部分储液体积求和得出储罐储液总体积:V 总=L[2arcsin√h(D−h)RπR²360−√h(D−h)(R−h)] + πbR[RH²- -13H³]二、储罐中储液密度计算。
sw6卧式容器计算

卧式容器计算计算单位sw6
计算方法:NB/T 47042-2014《卧式容器》
计算条件简图
压力腔排列型式A-B -
附加集中质量个数 3 个
附加均布质量个数1个
筒体段数2段
鞍座个数 2 个
均布于设备全长的附件(隔热层、小
172kg
接管等)重量
设计基本地震加速度七度(0.15g) m/s2
压力腔数据压力腔A压力腔B
设计压力0.65 0.20 MPa 设计温度220 125 ℃压力试验压力0.869 0.869 MPa 压力试验类型水压试验水压试验- 工作物料密度744.9 914.8 kg/m3工作物料充装系数 1.00 1.00 - 筒体数据筒体一筒体二筒体三
内直径500 1000 mm 轴线到基础的高度458 708 mm 名义厚度10 8 mm 焊接接头系数0.85 0.85 - 腐蚀裕量 2 0 mm 厚度负偏差0.3 0.3 mm 筒体材料名称Q345R S31603 - 筒体材料类别(板材/管材/锻件) 板材板材- 筒体长度543 3000 mm 筒体材料设计温度下许用应力176.60 118.50 MPa 筒体材料常温下许用应力189.00 120.00 MPa 筒体材料设计温度下屈服限265.00 138.50 MPa 筒体材料常温下屈服限345.00 180.00 MPa
注: 带#的材料数据是设计者给定的,下同。
a。
sw6卧式容器计算

卧式容器计算计算单位sw6
计算方法:NB/T 47042-2014《卧式容器》
计算条件简图
压力腔排列型式A-B -
附加集中质量个数 3 个
附加均布质量个数1个
筒体段数2段
鞍座个数 2 个
均布于设备全长的附件(隔热层、小
172kg
接管等)重量
设计基本地震加速度七度(0.15g) m/s2
压力腔数据压力腔A压力腔B
设计压力0.65 0.20 MPa 设计温度220 125 ℃压力试验压力0.869 0.869 MPa 压力试验类型水压试验水压试验- 工作物料密度744.9 914.8 kg/m3工作物料充装系数 1.00 1.00 - 筒体数据筒体一筒体二筒体三
内直径500 1000 mm 轴线到基础的高度458 708 mm 名义厚度10 8 mm 焊接接头系数0.85 0.85 - 腐蚀裕量 2 0 mm 厚度负偏差0.3 0.3 mm 筒体材料名称Q345R S31603 - 筒体材料类别(板材/管材/锻件) 板材板材- 筒体长度543 3000 mm 筒体材料设计温度下许用应力176.60 118.50 MPa 筒体材料常温下许用应力189.00 120.00 MPa 筒体材料设计温度下屈服限265.00 138.50 MPa 筒体材料常温下屈服限345.00 180.00 MPa
a。
容器设计的数学建模计算

容器设计的数学建模计算【摘要】本题目属于在一定条件下求最优解的问题。
具体到题目是求不同形状的容器在容积一定容器表面积最小的情况下,求容器的各项参数(圆锥台的高h,上下底面半径r, R, L;圆柱高H)之间的比值,并将解的精确度进行优化的问题。
求解的大体步骤为先建立简化模型,以便于计算且使结论具有一定普遍性。
使用Autocad2007绘图软件绘制图形。
建立容器各项参数与表面积、体积的正确的的函数关系式,并使容器表面积达到最小,求出此时各项参数间的比值。
解答过程中,因出现较为复杂的函数关系式,我们将借助数学软件LINGO9.0进行编程计算,调整输出数据的精确度的有效位数,得到最优解。
【关键词】优化最小值比值理想模型1、问题重述容器的设计问题:(1).要设计一个无盖的圆锥台形状的容器,上半径为R,下半径为r<R,高为h。
求容积在一个正常数的条件下,使该容器的表面积达到最小时的两个比值r/R , h/R的精确值(用整数的有限次四则运算及根式运算的最简形式表示)及它们精确到20位有效数字的近似值。
(2).要设计一个无盖的容器,是一个半径为R,高为H的圆柱面放在一个圆锥台上组成的。
圆锥台的半径为R,下半径为r<R,高为h.求容积在一个正常数的条件下,使该容器的表面积达到最小时的三个比值r/R, h/R, H/R的精确值(意义同(1))及它们精确到20位有效数字的近似值。
(3).要设计一个无上盖的容器,是一个高为H,上半径为L,下半径为R<L的圆锥台放在高为h,上半径为R,下半径为r<R的圆锥台组成的。
求容积为一整常数的条件下,使该容器的表面积达到最小时的四个比值h/L, H/L, r/L, R/L的精确到20位有效数字的值。
2、模型假设及符号说明这虽然是一道有关容器设计的实际应用问题,而在实际生产实践中,容器是具有一定的厚度的,而因种类、工艺、功能等原因,不同的容器对厚度的要求也不尽相同,例如从原始的陶器到现代的不锈钢容器,从生活中的碗到工业炼铁的高炉,它们的厚度都不尽相同,甚至同一容器在不同部位的厚度也有所差异(如啤酒瓶的侧壁薄而底厚)。
卧式容器计算

卧式容器计算1.卧式容器的强度计算 1.1支座反力按下式计算:2mgF =式中:F —每个支座的反力,N ;m —容器质量(包括容器自身质量、充满水或充满介质的质量、所有附件质量及隔热层等质量),Kg ;g —重力加速度,取g=9.812/s m 1.2圆筒轴向应力 1.2.1 圆筒轴向弯矩计算圆筒轴向最大弯矩位于圆筒中间截面或鞍座平面上。
圆筒中间横截面上的轴向弯矩,按下式计算:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-+=L A L h L h R FL M i i a 4341)(2142221式中:1M —圆筒中间处的轴向弯矩,mm N ⋅; F —每个支座的反力,N ; L —封头切线间的距离,mm ; a R —圆筒的平均半径,2/n i a R R δ+= i h —封头曲面深度,mm ;A —鞍座底板中心线至封头切线的距离,mm鞍座平面上的轴向弯矩,按下式计算:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+---=L h AL h R L A FA M ii a 341211222式中:2M —支座处圆筒的轴向弯矩,mm N ⋅; F —每个支座的反力,N ;A —鞍座底板中心线至封头切线的距离,mm ; L —封头切线间的距离,mm ;a R —圆筒的平均半径,2/n i a R R δ+= i h —封头曲面深度,mm ; 1.2.2圆筒轴向应力计算1.2.2.1圆筒中间横截面上,由压力及轴向弯矩引起的轴向应力,按下面两式计算: 1)最高点处:ea e a c R M R p δδσ21114.32-=式中:1σ—圆筒中间处横截面内最高点的轴向应力,MPa ; c p —计算压力,MPa ;a R —圆筒的平均半径,2/n i a R R δ+= e δ—圆筒有效厚度,mm ;A —鞍座底板中心线至封头切线的距离,mm ; 1M —圆筒中间处的轴向弯矩,mm N ⋅; 2)最低点处:ea e a c R M R p δδσ21214.32+=由上面可得: 1.2.2.2鞍座平面上,由压力及轴向弯矩引起的轴向应力,按下面两式计算: 1)当圆筒在鞍座平面上或靠近鞍座处有加强圈或被封头加强(即2/a R A ≤)时,轴向应力3σ位于横截面最高点处;当圆筒未被加强时,3σ位于靠近水平中心线处:ea e a c R K M R p δδσ212314.32-=式中:3σ—支座处圆筒横截面内最高点出的轴向应力,MPa ; c p —计算压力,MPa ;a R —圆筒的平均半径,2/n i a R R δ+= e δ—圆筒有效厚度,mm ;2M —支座处圆筒的轴向弯矩,mm N ⋅;1K —系数,由JB/T4731-2005钢制卧式容器表7-1查得:1K =1)在横截面最低点处的轴向应力4σ: ea e a c R K M R p δδσ212414.32+=由上面可得: 1.2.3圆筒轴向应力的校核 对于操作状态下应满足下条件:1)计算得到41~σσ,取出最大拉应力(最大正值): {}[]t σφσσσσ≤4321,,,m a x 式中:φ—焊缝接头系数,此处取φ=[]tσ—设计温度下壳体材料的许用应力,MPa ;2)计算得到41~σσ,取出最大压应力(最小负值):}[]tac σσσσσ≤4321,,,min式中:[]tac σ—设计温度下壳体材料的轴向许用压缩应力,取[]tσ、B 中较小 者,MPa ; 对于操作状态下应满足下条件:1) 充满水未加压时计算得到41~σσ,取出最大压应力(最小负值): {}[]ac T T T T σσσσσ≤4321,,,min式中:[]ac σ—常温下容器壳体材料的轴向许用压缩应力,取0.9)(2.0p el R R 、0B 中 较小者,MPa ;2) 加压状态下计算得到41~σσ,取出最大拉应力(最大正值): {})(9.0,,,m a x 2.04321P el T T T T R R φσσσσ≤ 式中:φ—焊缝接头系数,此处取φ=)(2.0p el R R —圆筒材料在试验温度下的屈服强度或0.2%规定非比例延伸强 度,MPa ; 1.3切向剪应力1.3.1圆筒切向剪应力计算在圆筒支座处横截面上的剪应力,按下面两式计算。
根据液体体积计算方法总结

根据液体体积计算方法总结
液体体积的计算是在很多实际情况中都需要进行的一项工作。
以下总结了一些常用的液体体积计算方法:
1.直接测量法
直接测量法是最简单的液体体积计算方法。
通过使用体积标尺、量杯或注射器等工具,直接测量液体的体积。
这种方法适用于较小
的液体容量。
具体步骤如下:
1.准备一个标有刻度的,如量杯。
2.将液体慢慢倒入中,使其达到所需的体积刻度。
3.读取液面高度并记录下来,即可获得液体的体积。
2.几何形状法
当液体存放在形状特殊的中时,直接测量法可能不容易实施。
这时可以利用的几何形状计算液体体积。
具体方法如下:
1.观察的形状,确定其几何特征,如圆柱体、圆锥体、矩形等。
2.根据的几何特征,使用相应的公式计算液体的体积。
3.根据的尺寸和液面高度,代入公式计算液体的体积。
3.等量代换法
等量代换法在一些特殊情况下适用,例如液体溢出或难以直接
测量的情况。
具体方法如下:
1.将中的液体全部倒入一个已知体积的中。
2.记录已知中的液体体积,设为V1.
3.将液体从已知倒回原,直到液面高度与原中的液面高度相同。
4.记录已知中剩余的液体体积,设为V2.
5.利用等量代换原理,计算原中的液体体积为V1 - V2.
以上是几种常用的液体体积计算方法。
在实际应用中,根据具
体情况选择合适的方法,并注意测量的准确性和精度。
圆柱与圆锥圆柱不规则容器容积的计算方法ppt

2023
圆柱与圆锥圆柱不规则容器容积的计算方法
CATALOGUE
目录
引言圆柱体的容积计算圆锥体的容积计算不规则容器的容积计算容器容积的计算应用研究成果与展望
01
引言
容积计算在实际生活中有着广泛的应用,如水利工程、化工、食品等行业。
对于一些不规则容器的容积计算,一般采用三维建模和数值计算等方法,但这些方法需要大量的人力和物力资源,因此研究圆柱与圆锥圆柱不规则容器的快速计算方法具有重要的实际意义。
根据圆柱体的体积公式,可以计算圆柱体的容积为:V=πr²h=3.14*(10/2)²*5=392.5立方厘米
圆柱体的容积计算实例
03
圆锥体的容积计算
$V = \frac{1}{3} \pi r^2 h$,其中r为底面半径,h为高。
圆锥体的体积公式为
$V = \frac{1}{3} \times \pi \times r^{2} \times h$。
圆柱形不规则容器
01
指底面为圆形,侧面为曲面或由直线和曲线构成的不规则圆柱体。
不规则容器的形状分类
圆锥形不规则容器
02
指底面为圆形或其它形状,侧面为曲面或由直线和曲线构成的不规则圆锥体。
其它不规则容器
03
指除圆柱形和圆锥形之外的不规则容器,如棱柱、棱锥、圆台、球台等。
圆柱形不规则容器的容积计算
圆锥形不规则容器的容积计算
圆锥体的体积也可以表示为
圆锥体的公式
圆锥体的直径D与半径r的关系为:$D = 2 \times r$。
圆锥体的高h与半径r的关系无直接计算公式,需要依据实际测量的数据锥体的底面半径为3厘米,高为4厘米,则其容积为
$V = \frac{1}{3} \times \pi \times 3^{2} \times 4 = 37.699111843077516$立方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二油品计算中空气浮力修正的方法 1空气浮力在油品计算中的影响
在日常生活和贸易中,人们习惯将质量称为 重量,而根据密度的定义,有质量
M=ρ20V20它指的是物质量的多少,它是惯性的
量度,是真空中的质量,与空气的浮力等外
界因素无关。这是物质质量的一种算法。
2.空气浮力修正系数Fa
Fa值的定义将石油在真空中的质量换算到空 气中重量修正系数. 下面用天平来说明: 质量为的油m1,质量为的砝码m 天平臂长均为a,油的密度为ρ1,砝码密度为ρ 空气密度为e.根据力矩平衡原理: ag(m1—m1/ρ1×e)=ag(m—m/ρ×e) 简化为:m=m1(1-e/ρ1)/(1-e/ρ)
得到:m=vρ1 (1-eρ1/+e/ρ) =v(ρ1-e+e×ρ1/ρ) =v〔ρ1-e(1-ρ1/ρ)〕 令B=e(1-ρ1/ρ)可得m=v(ρ1-B) 在标准温度下为m=v20(ρ20-B)
B=1.1kg/m3
m=v20(ρ20-1.1)
(ρ20-0.0011) V20 称0.0011为空气浮力修正值,这样可将真空中的质量换算 到空气中的质量(重量)。为了区别起见,习惯上把修正后的 质量也叫“商业质量”,有的也叫“重量”,这是贸易习 惯。国际上都是这样的。我国油品计量规定: m=VCF· Vt(ρ20-0.0011)=(ρ20-0.0011)V20
Vi--罐内附件体积 △VB---罐底不平度修正值 △VL---罐倾斜的修正值
2.立式金属罐容量表的编制
立式金属罐容量表包括
(1)主表:以间隔1cm高对应的容积.p262 (2)附表:又称小数表.1---9mm对应的有效容积.p262 (3)容积静压力修正表:在使用时应将相应的静压力容 器修正值乘以液体实际密度与4℃时水的密度比 值,得到修正值△VP.p273 (4)底量容积表
式中 Vt—油品在温度t下的体积,L;
V20—标准体积,L; ρ20—标准密度,kg/L,可由视密度换算表查得; 0.0011—空气浮力修正值,kg/L;(1.1kg/m3) VCF—石油体积修正系数由油品的ρ20,与计量温度t查 VCF表得到: M—石油的质量(商业质量),kg。
第二节:容量表的编制
第六章
容器计量的计算方法
第六章容器计量的计算方法
第一节:油量计算基础知识 一术语
(1)试验温度 (2)视密度:在试验温度下 (3)标准密度:标准温度下的密度 (4)标准温度(20 ℃) (5)计量温度 (6)标准体积:在20℃下,油品的体积,用V20表示,单位为m3、 dm3或L等
(7)石油体积修正系数 石油在20℃时的体积与它在t℃下的体积之比值,用VCF表示, 即VCF=V20 / Vt 所以有V20=VCF.Vt。 (8)原油含水率:所含水分的质量百分比 (9)石油在空气中的质量
4.立式金属罐容量的使用
1.必须将量油尺示值修正到20℃以下才可查 容量表. 修正公式为:H=H’ ×〔1+ α (t-20)〕 α---罐壁材质线胀系数,对于低碳钢 α=0.000012, 1/℃
二.卧式金属罐容积表 1.卧式金属罐容积表的编制
H1=H+△H H1---修正后的液位高度. H-----下尺点的液高. △H—液高修正值. 当计算卧式金属罐的毫米高度容量时,按线性 插值法近似计算.
立式金属罐容积表
立式金属罐容积表介绍
主表 立式油罐容积表 附表 静压力修正表
立式金属油罐容积表的使用: 容积=分米容积+厘米容积+毫米容积 +(静压容积×相对密度)
练习
(1).423#罐,测得液位高度为7.528m,求罐 内油品体积?
答案
解:7.52M高度的体积是:1237.023 m3 查小数表8mm的体积是:1.321 m3 静压力修正值为(7.5m)0.571 m3 油品体积=1237.023+1.321+0.571
一.立式金属罐容量表 1.立式金属罐容量表的编制依据 Vi=∏/4di2hi (i=1,2,3,----,n) di---第i圈板的内径 Hi---第i圈板的内高 若考虑罐底不平和罐内附件体积的修正值,及 液体静压力引起罐壁弹性变形的修正值,则总 容量为:
V=∑vi+△vP+△va+△vB+△VL
五、汽车罐车容积表
汽车罐车容积表的使用方法:
使用线性插值法计算
练习
练习题
(2).423号油罐检修后装水试验,经检测液位高 8.024m,试求罐内装水多少m3?
解:查附录表1的423号罐容积表: 8.02m高的容积 v1=1319.616kL 查小数表:4mm高的容积v2=0.661kL 8.00m高时水的容积静压力修正值 △VP=0.649kL 罐内装水量为:V=v1+v2+ △VP =1319.616+0.661+0.649 =1320.926m3
因为m1=vρ1, v是油体积.所以 m=vρ1 (1-e/ρ1)/(1-e/ρ) 令: Fa=(1-e/ρ1)/(1-e/ρ) 可得: m=V ρ1Fa 在标准温度下,则有:m=V20ρ20 Fa 根据油品的标准密度,可查得相应的Fa值. 标准附录表E(443页).
3.空气浮力修正值
m=vρ1 (1-e/ρ1)/(1-e/ρ) m=vρ1 (1-e/ρ1)(1+e/ρ) /(1-e/ρ) (1+e/ρ) m=vρ1 (1-e/ρ1)(1+e/ρ) /12-(e/ρ)2 空气密度与砝码密度的比值很小, (e/ρ)2更小 所以 m=vρ1 (1-e/ρ1)(1+e/ρ) m=vρ1 (1-e/ρ1+e/ρ-e2/ρ1ρ) 同样e2/ρ1ρ极小,可略去
练习
• 测得10号卧罐油水总高2436mm,水高 18mm,计算罐内油品体积。
答案
V1=48174+(48298-48174)/(244-243)× (243.6-243) =48248L=48.248 m3 V2=898+(988-898)/(2-1)×(1.8 - 1)=970L=0.970 m3 V =48248-970=47278L=47.278 m3
