一类时间随机环境中随机游动
随机游走的自相关系数

随机游走的自相关系数随机游走是一种常见的数学模型,常用于描述随机过程中的移动。
它可以用来研究许多领域,如金融市场、物理学、生物学等。
在随机游走中,自相关系数是一个重要的指标,用于衡量随机过程中的相关性。
让我们了解一下什么是随机游走。
随机游走是一种模型,描述了一个物体在每个时间步中随机移动的情况。
在一维情况下,物体可以向左或向右移动,每次移动的距离可以是固定的或服从某个特定的概率分布。
在二维或更高维的情况下,物体可以在各个方向上移动。
在随机游走中,自相关系数是一个重要的统计量。
它用来衡量随机过程中两个变量之间的相关性。
自相关系数的取值范围在-1到1之间,其中-1表示完全负相关,1表示完全正相关,0表示没有相关性。
自相关系数越接近于1或-1,表示两个变量之间的关联越强。
随机游走的自相关系数可以通过计算相邻步长之间的相关性得到。
例如,假设我们有一个随机游走模型,物体在每个时间步中向左或向右移动一个单位距离。
我们可以计算相邻步长之间的自相关系数,来衡量物体移动的趋势是否存在相关性。
随机游走的自相关系数在金融市场中有广泛的应用。
在股票市场中,投资者经常使用随机游走模型来预测股票价格的走势。
他们通过计算股票价格的自相关系数,来判断价格是否存在长期的趋势。
如果自相关系数接近于1,意味着价格存在明显的上涨或下跌趋势;如果自相关系数接近于0,意味着价格呈现随机波动。
除了金融市场,随机游走的自相关系数还可以应用于物理学和生物学领域。
在物理学中,随机游走模型可以用来描述分子在溶液中的扩散过程。
研究人员可以通过计算分子的自相关系数,来了解分子在溶液中的运动规律。
在生物学中,随机游走模型可以用来描述细胞的移动过程。
科学家可以通过计算细胞的自相关系数,来研究细胞的迁移行为和群体行为。
随机游走的自相关系数是一个重要的统计量,用于衡量随机过程中的相关性。
它在金融市场、物理学和生物学等领域都有广泛的应用。
通过计算自相关系数,我们可以了解随机游走模型中变量之间的关联程度,从而预测未来的趋势和行为。
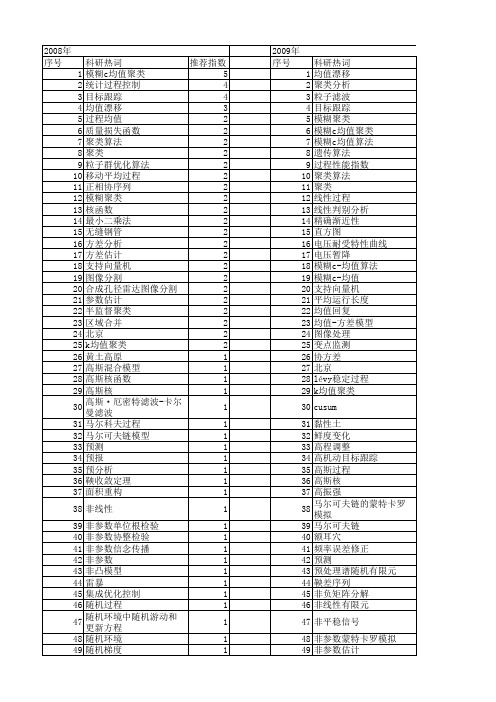
【国家自然科学基金】_过程均值_基金支持热词逐年推荐_【万方软件创新助手】_20140803
背景杂波 肺实质分割 肛门,畸形 聚集运算 聚类算法框架 聚类分析 联想存储 耦合扩张 羊卓雍错 维甲酸 统计 经验特征函数 织物染色 纹理图像分割 红外目标跟踪 红外测温仪 红外成像系统 絮凝粒径 累积和控制图 糠虾类 精确渐近性 粗差 粒子群 粒子滤波(pf) 粒子 管线 管理浮动汇率制 等离子熔射 符号截断特征 突触素 空间变化 空间分布 稳健设计 稳健性设计 稀疏数据过程 移动均值 积分方程 秘书问题 离散正交小波变换 离散时间排队 神经网络预测模型 神经网络预测 神经网络 神经细胞黏附分子 神经元集群 磷脂脂肪酸 矩阵几何解 知识转移 相关距离 相位恢复 相似查询 相似性测度 相似性匹配 相似度
科研热词 均值漂移 聚类分析 粒子滤波 目标跟踪 模糊聚类 模糊c均值聚类 模糊c均值算法 遗传算法 过程性能指数 聚类算法 聚类 线性过程 线性判别分析 精确渐近性 直方图 电压耐受特性曲线 电压暂降 模糊c-均值算法 模糊c-均值 支持向量机 平均运行长度 均值回复 均值-方差模型 图像处理 变点监测 协方差 北京 lévy稳定过程 k均值聚类 cusum 黏性土 鲜度变化 高程调整 高机动目标跟踪 高斯过程 高斯核 高振强 马尔可夫链的蒙特卡罗模拟 马尔可夫链 额耳穴 频率误差修正 预测 预处理谱随机有限元 鞅差序列 非负矩阵分解 非线性有限元 非平稳信号 非参数蒙特卡罗模拟 非参数估计 静脉识别 静脉注射 青藏高原
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
一类随机环境中的随机游动

粉 ∑
一
( 2)
这里 由过程的定义可知 当 z a时 , 辛 ( ) 0P () l当 z三 b , j z : l P z 一 , ・ z 一 ; 三 时 P = () ,
P t z) = 0 ]( .
l
返性准 则和 一些 极 限性 质 .
关键词 随 机 环境 ;随机 蝣 动 ;常 返性 ;首 中 时
中图分 类号
O 2 1 6 1.2
文 献 标识 码
A
X■
一
t
随 机 环 境 中 的 随 机 过 程 是 概 率 论 的 一 个 新 的 分 枝 , 机 环 境 中 的 随 机 游 动 ( 记 为 随 简
维普资讯
第 3 期
柳 向 东 等 : 类 随 机 环 境 中 的 随 机 游 动 一
・9 2 9・
( 若∑ 。 一 . 。且∑ ,… i ) ( 。 ) 一。, … 一 <。, i… X 一。 a . 。 。 则l a r . c . e () i 若∑二 ( … ) 一o, j . . 。 且∑二 一。, 一o 一l n—X < l 一 … 。则 。 i f ,. i m{I n
与 S l n一致 的 结果 . oo mo
定义 l 设 { , ,. , ∈ z) 为 概 率 空 间 ( , ( 。 )) , , 0, P) 卜的 一 列 随机 向 量 , 中 ( , 其 /) }
独 立 同分 布 , e一 { , ,. , ∈ z)定 义 在 z上 的 . 足 r 记 ( 。 )) , 满 列条 件 为 R I W RE:
(i i)如果 Eo a> 0 则 l … 。一 一 ∞ Ⅱ e i lg , i a r ..
随机游动中首达概率的研究与分析

随机游动中首达概率的研究与分析作者:李斯儒谭静来源:《现代信息科技》2021年第08期DOI:10.19850/ki.2096-4706.2021.08.004摘要:众所周知,随机游动作为一种特殊的马尔科夫链在诸多领域有着广泛的应用,而研究系统的阈值状态的首达概率则是重中之重。
文章首先对对称一维随机游动某状态的首达概率、首达时进行计算分析;然后采用了对递推公式求母函数的方法求解对称一维随机游动的首次返回概率,最后通过蒙特卡洛方法求其首次返回概率的模拟值与理论值对照,通过大样本容量的计算证实理论解的精确性。
关键词:随机游动;首达时间;首达概率;马尔科夫链中图分类号:O211.1 文献标识码:A 文章编号:2096-4706(2021)08-0013-04Research and Analysis on the First Arrival Probability in Random WalkLI Siru,TAN Jing(Nanhang Jincheng College,Nanjing 211156,China)Abstract:As we all know,the random walk is a special Markov chain that has wide applications in many fields,and the research on the first arrival probability of the threshold state of the system is the most important thing. First,the paper calculates and analyzes the first arrival probability and first arrival time of a certain state of a symmetric one-dimensional random walk;then uses the method of finding the generating function of the recurrence formula to solve the first return probability of the symmetric one-dimensional random walk,and finally uses Monte Carlo method compares the simulated value of the probability of its first return with the theoretical value,and confirms the accuracy of the theoretical solution through the calculation of a large sample volume.Keywords:random walk;first arrival time;first arrival probability;Markov chain0 引言在马尔科夫链中有一类非常特殊的随机过程被称为随机游走[1](Random Walk,RW)。
随机游走算法,转移概率-概述说明以及解释

随机游走算法,转移概率-概述说明以及解释1.引言1.1 概述:随机游走算法是一种基于概率的算法,用于模拟随机的行为和变化过程。
它可以描述在一个有限的状态空间中,通过按照一定的规则进行状态转移,从而模拟随机选择下的状态变化。
这一算法在许多领域中有着广泛的应用,包括计算机科学、物理学、生物学、金融等。
随机游走算法的核心思想是通过定义转移概率来描述状态之间的转移规则。
在一个随机游走过程中,每个状态都有一定的概率转移到其他状态,而这些概率可以根据实际情况进行确定。
通过迭代计算,随机游走算法可以模拟出状态的分布情况,进而提供对系统行为的理解和预测。
随机游走算法具有很多重要的特性和优点。
首先,它是一种非常灵活的模型,可以适用于各种不同的问题和场景。
其次,随机游走算法能够捕捉到系统中的随机变动和不确定性,从而可以更好地解释和预测实际情况。
此外,随机游走算法具有较快的收敛速度和较低的计算复杂度,使得它成为许多算法和模型的重要基础。
然而,随机游走算法也存在一些限制和缺点。
首先,它需要事先确定好状态空间和转移概率,这对于复杂系统可能是一个挑战。
其次,随机游走算法对初始状态的选择非常敏感,不同的初始状态可能会导致完全不同的结果。
此外,随机游走算法在处理长时间序列或具有周期性特征的问题时可能存在某些局限性。
综上所述,随机游走算法是一种重要且广泛应用的算法,能够在各个领域中提供对系统行为的建模和预测。
虽然它具有一些限制和缺点,但通过进一步研究和改进,随机游走算法有望在未来的发展中发挥更大的作用。
在接下来的章节中,我们将详细介绍随机游走算法的基本概念、应用领域以及优缺点,并对其重要性和未来发展进行总结和展望。
1.2 文章结构文章结构部分的内容可以包含以下内容:文章结构部分主要介绍了整篇文章的组织结构和各个部分的主要内容,将读者引导到整个文章的框架。
2. 文章结构本文分为引言、正文和结论三个主要部分。
2.1 引言部分引言部分主要对随机游走算法进行了概述,介绍了其基本概念以及本文的目的。
半直线上时间随机环境中随机游动的渐近性质

20 年 5月 0r 7
半 直 线 上 时 间 随机 环 境 中 随机 游 动 的渐 近性 质
胡 学 平
( 安庆师范学 院 数学 与计算科 学学 院 , 安徽省 安庆 2 6 1 ) 4 0 1
摘要 : 给出了半直线上时间随机环境下随机游动的模 型, 并利用马 氏链理论研 究 了该随机游 动 的常返 暂 留准则 和依 概 率 收敛 的大数定 律 ,得 到在 非 常返 情形 下 的 中心极 限定 理 . 关键词 : 随机环境 ; 随机游动; 常返 ; 大数定律;中心极限定理 中图分 类号 :0 1.2 2 16 文 献标识 码 : 文 章编 号 : 6 1 4 9 20 )30 3 - A 17 - 8 (0 7 0 -3 90 5 5
te r h n h g t i e,t e h td e b u e u l n e t n in e c tra a d l tt e r m y u i g s me r lt e i l h n t e su is a o tr c r c — a se c r e n i h o e b sn o e ai  ̄ r i i mi v h o i fMa k v c a n , t e r so r o h i s a d f al e trl t e rm f i a d m a k n te n n r c re c a e e n n l a c n e mi t oe o sr o w l si o — u r n e c s . i y i h h t n h e
As m p o i o e te o nd m a k n Ti e r n o y t tc Pr p r i s f r Ra o W l s i m - a d m En i o m e t n t e Ri htLi e vr n n s o h g n
随机游动练习题
随机游动练习题随机游动是一种在随机变化下进行的路径模拟,常用于模拟随机过程、金融市场走势等。
本文将通过练习题的方式,帮助读者更好地理解和应用随机游动。
练习题一:假设有一只蚂蚁在一条直线上移动,起始位置为原点,每次移动单位距离的概率相等,向左概率为0.3,向右概率为0.7,请问这只蚂蚁走了100步后,最有可能所处的位置在哪里?解答:从题目中可以得知,蚂蚁向左移动的概率为0.3,向右移动的概率为0.7。
根据随机游动的定义,蚂蚁在一条直线上移动时,每次的移动是相互独立的,且具有相同的概率。
因此,可以将蚂蚁的移动看作是一个随机过程,且满足二项分布。
对于每一步移动,蚂蚁向左的概率为0.3,向右的概率为0.7。
设蚂蚁向左移动的步数为X,向右移动的步数为Y,根据二项分布,可得出以下关系:X ~ B(100, 0.3)Y ~ B(100, 0.7)根据二项分布的特性,期望值E(X) = np,方差Var(X) = np(1-p),其中n为实验次数,p为成功概率。
同理,期望值E(Y) = np,方差Var(Y) = np(1-p)。
因此,蚂蚁所处位置的期望值E(X-Y) = E(X) - E(Y) = np - np = 0,方差Var(X-Y) = Var(X) + Var(Y) = np(1-p) + np(1-p) = 2np(1-p)。
代入题目给定的参数,可得到蚂蚁所处位置的期望值为0,方差为2*100*0.3*0.7 = 42。
练习题二:一只蚂蚁在一个无限大的二维网格上进行随机游动。
每次移动,蚂蚁以相等的概率向上、下、左、右四个方向移动一个单位距离。
假设蚂蚁从原点开始,连续移动1000步,请问蚂蚁最有可能到达的距离原点最远的位置是多远?解答:对于二维随机游动,蚂蚁在每个方向上的移动是相互独立的,且具有相同的概率。
因此,可以将蚂蚁的移动看作是一个二维随机过程。
设蚂蚁向上移动的步数为X,向下移动的步数为Y,向左移动的步数为Z,向右移动的步数为W。
随机环境中有界跳幅随机游动常返性暂留性的另一证明
能的跳幅,给出 ( , ) Q 上的一列随机变量 ( ) , P A 且满足 ∑ P w =1 -., ) , a. e 及椭圆条件
£>0 V , ∈A ≠0 (zp ) £ —.. , , P /R , a . e
收稿 日 期: 0 8 0 —5 修订 日 : 0 91 —9 2 0 —51 ; 期 2 0 22
让 7M , 是 M 关于 ( , T 的最大 的 La onv指数 .在 L中考 虑 L ( T) Q, , ) ip u o 范数 ,
即 l l C:{ 1 ∈R ,i ) LX >0 和它与球面的交集:
种 直觉来 自于 电网络 中 电压与 概率 的联 系. 我 们先 简要 的介绍 一下模型 , 文采用 B 6 n [ 中的记 号. 本 rmo t ] 。 给定 可逆 的 动力系统 ( , , Q ) 即概率 空 间 ( , 和可逆 变换 , , Q, ) 且 及其 逆都是 可 测的 ,且 保持测 度 , 假定 关 于 是遍 历 的.这 里 的 Q可看 为 随机环境 的空 间. 给 出两 个取 定的 整数 L 1和 R 1 引入整 数集 合 A= f , , , 们代表 游动 可 , —L … R} 它
数学物理学报
21,0 2: 9 26 008 A( 2 -9 )8 ht : atms i a. t / ca . p cG p/ w m. n
随机环境 中有界跳幅随机游动 常返性 暂 留性 的 另一 证 明
王 士东 洪文 明
( 北京师 范大学数学科 学学院数 学与复杂系统实验 室 北京 1 0 7 ) 0 8 5
20 9
数
学 物
理
学
报
V10 O3 l. A
时间随机环境中一维随机游动的极限性质
Ab ta t T eo e dme so a a d m l i a d m mee vrn nsi o s ed sr c h n — i n in l n o wakw t rn o t .n i me t Sc n i r .W h ne vrn n r h i o d e n i me . o
tl r c s s s t n r n r o i ,te mo e ai islw flr e n mb r a d c nr i tt e r m u d rc r a o e si t i ay a d e g d c h d ls t f a o g u e s n e t l o e n e e- p ao se a l a mi h
中心极 限定理.特别地 ,当环境独立 同分布时 , 可以得到更为具 体的结果 , 该结果类似于经典 的大数定律 和中心
极 限定理的相应结论.
关键词 随机环境中的随机游动 ; 大数定律 ; 中心极限定理 ; 时间随机环境 O 1 .2 2 16 文献标识码 A 文章编号 10 -57 20 )40 1-5 0023 {0 8 0 - 60 0 中图分类号
t —n i n e t i e vr m n me o
1 模型的建立
一
维空间随机环境 中随机游动的概念首先 由 K z v和 Sl e 提出, ol o o mn o 随后众多学者对此模型进行 了一
系列深入的研究[] C gu 1 . obr _ 3 n和李应求等发展了一类随机环境中马氏链的一般理论, 与前述空间随机环境
20 0 8年 1 2月
湖南师范大学 自然科学学报
J u n lo au a S in e o n n N r lU ie s y o r a fN tr l ce c fHu a o ma n v ri t
经济统计数据的随机游动模型与预测
经济统计数据的随机游动模型与预测随着经济的发展和全球化的加深,经济统计数据的重要性日益凸显。
政府、企业和个人都需要根据经济统计数据做出决策和预测。
然而,经济统计数据的变化往往是复杂而难以预测的,因此,建立准确的模型来预测经济统计数据变化成为了一个重要的课题。
一种常用的经济统计数据预测模型是随机游动模型。
随机游动模型假设经济统计数据是一个随机过程,即未来的数据取决于过去的数据,但没有任何趋势或规律可循。
这种模型的基本假设是,经济统计数据的变化是随机的,不受任何外部因素的影响。
随机游动模型可以用数学公式表示为:Y(t) = Y(t-1) + ε(t),其中Y(t)表示第t个时间点的经济统计数据,ε(t)表示随机误差项。
根据这个模型,我们可以通过观察过去的数据来预测未来的数据。
然而,由于随机游动模型没有考虑任何趋势或规律,它的预测能力通常较弱。
为了提高随机游动模型的预测能力,研究人员提出了许多改进的方法。
其中一种常用的方法是季节性调整。
经济统计数据往往存在季节性变化,例如,销售额在圣诞节期间通常会增加。
为了消除季节性的影响,我们可以对数据进行季节性调整,使得数据更加稳定和可预测。
另一种改进的方法是引入外部因素。
虽然随机游动模型假设经济统计数据的变化不受任何外部因素的影响,但实际上,经济统计数据往往受到许多因素的影响,例如政府政策、市场需求和自然灾害等。
因此,我们可以通过引入这些外部因素来改进模型的预测能力。
除了随机游动模型,还有许多其他的经济统计数据预测模型,例如ARIMA模型和GARCH模型等。
这些模型在考虑了更多的因素和规律后,通常具有更好的预测能力。
然而,这些模型也存在一些限制,例如需要大量的数据和计算资源,以及对参数的选择和调整等。
总的来说,经济统计数据的预测是一个复杂而困难的任务。
随机游动模型是一种常用的预测模型,但其预测能力有限。
为了提高预测能力,我们可以采用季节性调整和引入外部因素等方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证
一
n= 0 由 的定义知 = 0 故P( <。 ) 1 时, , 。 : .以下 只证 明礼> 0 时结论 成立.由
维 紧邻随机游 动 的性 质, 从0 出发 , 首达1 的步数一定为 奇数, 即孔 = 2 n+1礼= 0 1… . , ,, 记 从0 出发, n+ 1 第2 步首达 1 的一条路径 为 = (, lX , , 1, 2+ , 上述路径 的 0X , 2… 2 ,)E n 1 是 1
从而可得 , 1
1 是条件独立 同分布 的, 且有
( =2+ ) r n 1=U{o 0 1 1 1=2+ ,: n ( +) l X = , =一, , k 1 1 一2 1. X o =2 k )
即质 点必须先从0 点运动到一1 再经过2 , +1 步从一1 N达0 最后再经2 点, n一( 2 +1步首达1 1 点.
J + =j o , =X , , 一 =z ~ , = ;) F ) ( 1 l =0X1 l… 1 n 1 x e=
{ ( , f n扎 )) , 1(
一
【, 0
其中X , J ( ki ∈z 表示整数) =12… , , , k ,, 佗一10<w n <1 称{ , 0为z , () . n } 上的时间随机 环境e 中随机游 动(W R ) R E. 令Z +={,,, })=【 1 =x , 表示 上的B r 一 给定( ) 012… , ( 0] ,, o l 域. e , 上的一概率 测度Q 使得e ( 独立同分布的概率测度)则e 是一个随机环境. , ∈ 给定环境e f , 0 是z , 佗 } 上 的非时齐马 氏链.令X = Z 用 表示( ,) , 上的分布律, 它满足 ( o= x )= 1 .可定 义( ×Xz , × ) 十 上的概 率测度P : :Q , 它由下式扩 张:
高 校 应 用 数 学 学 报
第2 卷第 1 6 期
记 T = 0 =ifk>0: :n ( 0为{ , 0从0 o , n{ ) n≠ ) n ) 出发首次击中状态他 的时刻, 若{ > 0: = n , }= 则 = +。, 。 从而 为停时.令 = 一T — ,n> 0; n l( )类似 可定
=
1. o
+ l j
1
.
0 =mi nn>0 =- , =0 =m nn n>0X1 n , { , 1 ) i{ , , =- , + :0 . 1 1 )
表示对 = + 而言, 1 质点从一1 出发首次到达0 的时刻. 令
=
, 1 =m nn n>0 i{ , , =0 , :1. )
,
=
∑ Ⅱ ( z 一= = 一 )
vE E2n+ l 1 i 1 =
,
( J
=0 ( ) ) ( )1 1)1 2)・( 一 J ) 2 ( … t ( 一 l 2 )( 一 )・・1 ( ) 佗+1. ( )
n 表示从0 出发在2 n+1 时刻首次到达 1 的所有 可能的不同路径 的数 目, 显然n 0=a =1 1 .因为 随
而{ () 0 是独立同分布的, n 礼, n } 故{ ( +m) k } u 佗, k }J , n 一1与{ () n 一1D分布, 从而
P丁= ) E ( = { e= (+ . ( = e E + ( P = ) 1 ) )
高 校 应 用 数 学 学 报
第2 卷第 1 6 期
可见7与T , I n( l n>1是 同分布 的. ) 类似可得
P( = k, ,n = ) l… T =P( + = k,一, z = k) l・ + z .
即{ n 1是严格平稳的. , } 为证{ n 1是遍历的, , ) 只需证明{ , 1是强混合的. n ) 即证
(r l f 1 ∈A , r -
=
;m+ ∈B。l s J 7 。 " , )
() 9
( ∈A , r 尼 (m ∈B , s J 1 ) 『 + 1 )
对 1・ , , ,一 , 有 ,一 B1・ Bjc Z,
l i P ∈A , r m _( 1
” o 一十 。
:
; + ∈B l S J , )
() 7
P( ∈A , r 1
) ∈B 1 S J. P( , ) ) 丁 ∈B , s J. P(s 1 )
0
= 『 1
k= O
【
f) 3
比较()()
o 0
∑
0
n
设{ n 0生成的母函数为Sx = ∑ a X , 0 1 对() 0 , ) () n ( 0<X ) 4式两边同时乘 以 , . 再关
n= 0
一 一
于nn> 0求和可得 ( 1
机环境序 列是独立 同分布 的随机变量NREw n =P 对() () , 1式两边关于环境积分得
P T :2 +1= / ( =2 +1 ( ) ( 1 n ) n ) d Qe
2 n+ 1
=
∈ n + l 1 2 E
=
- / Ⅱ i
=
( = 五
一 1
¨ ) d) Q(e
高校应用数学学报
21 ,61: 73 01 2 () 2-2
一
类 时 间随机 环 境 中随机游 动
胡 学平
( 安庆师 范学 院 数学 与计算科学学院, 安徽安庆 2 6 3 ; 4 13 河海 大学 水利水电学院,江苏南京 2 0 9 ) 1 0 8
摘
要:利 用概率母 函数 方法, 通过对一 类时间随机 环境 中随机游动首 中时性质 的研
P F×G = /P () (e, , ) ( ) G Q d) F∈ G∈ . (
收稿 日期: 0 90 —9 2 0 .52 修 回 曰 : 0 01 —3 期 2 1。1 2 基金项 目: 安徽省教育厅 自 然科 学基金重点项 目( j00 3) K 2 1A24
厂
2 8
全 体 , ∈E2+ 1 且Xn 1 1X 0 即 1 , 2+ = ,{ , 12… ,佗 于是 由条件概 率及 马氏性知: = ,, 2.
.
=
2 n+1 = )
vEE2 + l1
,
( =0X1 o , =
2 n+ 1
一, 2 2, 2+ =1 X = X n 1 )
的常返性 和 中心极 限定理.本文首先给 出一个特殊 的时间随机环境 中随机游动模 型, 然后通 过 引进首 中时并利 用概率母 函数方法对 首 中时性质 的研 究, 得到 了时 间随机环 境 中随机游动 的常 返准则和一个 强大数定律 .
+
设e { () 0是取值于[ 1 = 佗, n ) 0】 , 的一列独立同分布的随机变量列, w n =P 考虑随机 E () , 游动( , 0, xn礼 } 如果满足: P X =0 =1 (o ) ;
k 0 =
佗一1
=
∑ q( 1= k 1 = 1 (I 2 一 一 ) 1 = ) P  ̄0 2+ I 一) T1 ( 1 l 0 T, P  ̄= 礼 +
k 0 =
n— l
0
0
=
∑ q( = k l o 0 ( 2 一 一 ) l o 0 P 1 2+ l = ) = ( k 1 l : ) T X P 凡 +X .
义 , ,n>0 . ( )
§ 的分布 及其 性质 2
定理 21 对 以上 随机游 动 .
(p去, < )1<时 (< ) , 0 i >时 ( 。=; 壶, 。= n ; ) P 。 p P 。 ( p三, <)1>时 ( <) , 0 i <时 ( ∞=; , ∞= 凡 ; i ) P p P
() 8
为证 () 先证: c (, 一 , 7式, 若B 0m ]则对m >k 有 , P(r 1Sr 7 ∈A , I ;m ∈B , s J = P(r 1 r q+ - 1 ) 1 ∈A , _
事实上, 对固定环境e { 凡 ) , , 关于 为马氏 故有 链,
§ 模 型及 记 号 1
随机环境 中随机游动是随机过程 中研究的一个重要分支 . 【2提 出的空 间随机 环境中随 文1] —
机游动的研究结果相当丰富, 研究方法也比 较多. 而文[ 4 3】 — 提出并研究了时间随机环境中马氏链 的有关理论, 得到 了常返 性, 遍历定理等结果. 【 研究 了右半直线上时 间随机环境 中随机游 动 文5 】
由于S() 为 的单增 函数, 故
x ) () =0 S ( 一s +1 . s :— _v - 4 () 1 / - l x
.
() 5 () 6
将( 式展开成幂级数有s = ∑ 6 ) ()
.
c , 而 得 从 可 口 =南 c .
n=U
PT< ) E T= 佗 1 ∑ 1 2 () ( ∞ = P  ̄ 2+) 1 ( = u p n 口 p
P <。= PT1 n 1 ( 。 E _ 1 ) ( 2+ )
Er < p q P>q J - l , ” ;
一
qq . () P
定理22 当 时, . p 随机变量序列{ 佗≥1为严格平稳遍历的, , ) 且有
【+ ∞,P q ・
证 由定理2 知当p . 1
1
… t z)
/ n ( )( )- ( (一 1 (一 2) (一 a t ・・ ) ) 1 )… 1 1 2 1 )
) (n ) (e ) 2 +1Qd)
=a ̄p ). n (q
为求n ( n>1. ) 利用概率母函数方法, 为此先对T n I 2 + 进行分解导 出0 的关系式. 令
