05 抽样误差 可信区间估计
概率与统计中的抽样误差与置信区间

概率与统计中的抽样误差与置信区间在概率与统计学中,抽样误差和置信区间是两个重要的概念。
抽样误差是指由于采样过程中的随机性所导致的估计值与真实值之间的差异。
而置信区间则是用于估计参数真值的一种统计区间。
一、抽样误差在统计学中,我们往往无法对总体所有个体进行观察和测量,而是通过从总体中抽取样本来进行研究。
抽样误差是由于所选样本的随机性而引起的估计误差。
当我们从总体中抽取不同的样本时,得到的样本统计量(如样本均值、样本比例)会有所不同,这种差异就是抽样误差。
抽样误差是概率性的,它会导致估计值偏离真实值。
为了评估估计值的精确性,我们需要考虑抽样误差的大小。
通常,抽样误差的大小与样本容量相关,样本容量越大,抽样误差越小,估计值越接近真实值。
二、置信区间抽样误差与置信区间密切相关。
在统计推断中,当我们根据样本统计量对总体参数(如总体均值、总体比例)进行估计时,往往需要给出一个估计值的范围,这个范围就是置信区间。
置信区间提供了一个估计值的范围,表示我们对真实参数值的信心程度。
一般来说,置信区间具有两个边界,下界和上界。
置信区间的计算需要考虑样本容量、抽样误差和置信水平等因素。
置信水平表示我们对估计值落在置信区间内的程度的信心。
常用的置信水平有95%和99%。
以估计总体均值为例,假设我们从总体中抽取了一个样本,计算得到样本均值为x,样本标准差为s,样本容量为n。
若假设总体服从正态分布或样本容量较大(满足中心极限定理),那么我们可以使用正态分布来计算置信区间。
根据置信水平和抽样误差,我们可以通过公式计算出置信区间的下界和上界。
三、示例假设我们想要估计某城市成年人的平均身高。
我们从该城市中随机抽取了100个成年人进行测量,得到样本均值为170cm,样本标准差为5cm。
我们希望以95%的置信水平估计该城市成年人的平均身高。
根据样本数据和公式,可以计算出置信区间的下界和上界:下界 = 样本均值 - 抽样误差上界 = 样本均值 + 抽样误差首先,计算抽样误差:抽样误差 = 1.96 * (样本标准差/ √样本容量)然后,代入样本数据计算下界和上界:下界 = 170 - 1.96 * (5 / √100)上界 = 170 + 1.96 * (5 / √100)计算结果为:下界≈ 168.04cm上界≈ 171.96cm因此,我们可以以95%的置信水平得出结论,该城市成年人的平均身高的置信区间为(168.04cm,171.96cm)。
抽样调查 区间估计

( x X )2 36 16 9 0.25 1 0 6.25 4 20.25 30.25 123
Xx
25
抽样平均误差
●计算抽样平均误差的间接计算公式
x N n n N 1
32 412 38 412 42 412 44 412 49 412
N N1 N 2 ....... N K n n1 n2 ...... nk
18
机械抽样(等距抽样)
(2)不等比例类型抽样
19
抽样与估计中的几个基本概念
★整群抽样
整群抽样在抽取调查单位时,不是从总体 中一个一个地抽选,而是整群整群地抽选,然 后,对选中的各群中的所有单位无一例外地全 部进行调查。
x X 43 41 2
该误差是实际误差
22
抽样平均误差
如果从总体中抽取另一个样本,其年龄分别为 (32,42),则平均年龄为37岁 实际误差 : 37-41=-4岁 实际误差是一个随机变量 ●抽样平均误差(标准误[S.E.mean]) 是把所有可能样本配合与总体指标的实际误 差,按照求标准差的方法求得平均值,称为抽 样平均误差。
5
抽样与估计中的几个基本概念
●全及总体和抽样总体(样本总体) ●全及指标和抽样指标 1、样本方差
s2
xi x 2
n 1
2、样本标准差
s
xi x 2
n 1
6
全及总体和抽样总体
●全及总体: 指所研究对象的全体。又 称为母体,简称为总体。例如:要了解 某种产品的质量,那么,全部该种产品 就构成了全及总体。 ●抽样总体:指从全及总体中,按照随机 原则抽取出的一部分单位所组成的总体。 如果样本单位数量 大于30个,称为大样 本,否则,称为小样本。
概率与统计中的抽样误差与置信区间

概率与统计中的抽样误差与置信区间概率与统计是一门研究数据分析和推断的学科,其中抽样误差和置信区间是两个重要的概念。
抽样误差是指由于从整体中选取样本而导致的估计值与真实值之间的差异,而置信区间则是用于表示估计值的不确定性范围。
本文将对概率与统计中的抽样误差和置信区间进行探讨。
一、抽样误差在概率与统计中,我们常常通过对样本进行研究来推断总体的特征。
然而,由于样本只代表了总体的一部分,因此样本统计量与总体参数之间存在差异。
这种差异即为抽样误差。
抽样误差是统计研究中不可避免的,但我们可以通过一些方法来控制和减小它。
1. 随机抽样:为了减小抽样误差,我们需要确保样本是随机选择的。
随机抽样可以使样本更好地代表总体,从而减小抽样误差。
2. 样本容量:样本容量是影响抽样误差的另一个重要因素。
通常情况下,样本容量越大,抽样误差越小。
因此,在实际研究中,我们应该尽可能选择较大的样本容量。
3. 抽样方法:不同的抽样方法对抽样误差的影响也不同。
常见的抽样方法包括简单随机抽样、系统抽样、分层抽样等。
在选择抽样方法时,需要根据具体情况进行合理选择,以减小抽样误差。
二、置信区间置信区间是用于表示估计值的不确定性范围。
在统计推断中,我们往往使用样本统计量来估计总体参数。
而置信区间则告诉我们一个范围,我们相信总体参数在这个范围内的可能性较大。
置信区间的计算通常涉及到抽样误差和置信水平两个概念。
置信水平是指在多次重复抽样中,置信区间包含总体参数的比例。
常见的置信水平包括95%和99%。
置信区间的计算方法根据总体参数的分布情况和样本容量的大小而不同。
对于大样本(样本容量大于30)且总体参数服从正态分布的情况,我们可以使用正态分布的性质进行计算。
而对于小样本,我们通常使用t分布来计算置信区间。
总之,置信区间提供了一种衡量估计值不确定性的方式。
通过置信区间,我们可以更准确地评估估计值的可靠性。
结论概率与统计中的抽样误差和置信区间是数据分析和推断过程中的关键概念。
概率与统计中的抽样误差与置信区间

概率与统计中的抽样误差与置信区间概率与统计是一门研究数据收集、分析和解释的学科,而在这一过程中,抽样误差与置信区间是非常重要的概念。
抽样误差是指通过抽取样本来估计总体参数时所引入的误差,而置信区间则是用于表示抽样误差的范围。
本文将深入探讨概率与统计中的抽样误差与置信区间的概念、计算方法以及其在实际问题中的应用。
一、抽样误差的概念抽样误差是指由于样本的有限性所引起的估计误差。
在概率与统计中,我们通常无法对整个总体进行调查,而是通过从总体中抽取一部分样本来对总体进行推断。
由于样本的有限性,样本所估计的参数值往往会与总体真值存在一定的差距,这种差距就是抽样误差。
二、置信区间的概念置信区间是用于表示样本所估计的参数值的范围。
在概率与统计中,我们通常会计算出一个置信区间,该区间给出了参数是落在其中的概率。
常用的置信水平有95%和99%等。
置信区间的计算是基于抽样误差的大小和样本统计量的分布情况来进行的。
三、抽样误差的计算方法抽样误差的计算方法主要有两种:标准误差和大样本抽样误差公式。
1. 标准误差:标准误差是指样本统计量的标准差。
对于均值来说,标准误差的计算公式如下:标准误差 = 样本标准差/ √n其中,n为样本的容量。
而对于比例来说,标准误差的计算公式如下:标准误差= √(比例估计值 * (1-比例估计值) / n)2. 大样本抽样误差公式:当样本容量足够大时,我们可以使用大样本抽样误差公式来计算抽样误差。
对于均值来说,大样本抽样误差公式如下:抽样误差 = 1.96 * (标准误差)其中,1.96是95%置信水平对应的z值。
而对于比例来说,大样本抽样误差公式如下:抽样误差= 1.96 * √(比例估计值 * (1-比例估计值) / n)四、置信区间的计算方法置信区间的计算方法主要有两种:Z分数法和t分数法。
Z分数法适用于样本容量较大(大于30)且总体标准差已知的情况,而t分数法适用于样本容量小于30或总体标准差未知的情况。
可信区间的估计方法

可信区间的估计方法一、引言在统计学中,可信区间是用于估计未知参数的一种方法。
它提供了一个范围,该范围内有一定概率包含真实的参数值。
可信区间的估计方法是统计学中一个重要的概念,它在实际问题中具有广泛的应用。
本文将介绍可信区间的估计方法及其在实际问题中的应用。
二、点估计与区间估计在统计学中,点估计是一种估计未知参数的方法,它给出一个具体的数值作为估计值。
然而,点估计只能提供一个数值,无法反映估计值的不确定性。
为了解决这个问题,统计学引入了可信区间的估计方法。
可信区间是用于估计未知参数的一种区间估计方法。
它提供了一个范围,该范围内有一定概率包含真实的参数值。
可信区间的估计方法主要有频率派方法和贝叶斯方法。
三、频率派方法频率派方法是一种基于频率统计理论的可信区间估计方法。
它假设参数是固定的但未知的,并利用样本信息对参数进行估计。
常用的频率派方法有置信度法和最大似然估计。
1. 置信度法置信度法是一种常用的可信区间估计方法。
它通过构造置信区间来估计未知参数。
置信区间是一个区间,它有一定的概率包含真实的参数值。
置信度是指在重复抽样的情况下,置信区间包含真实参数的概率。
构造置信区间的方法主要有正态分布法和t分布法。
正态分布法适用于大样本情况,t分布法适用于小样本情况。
2. 最大似然估计最大似然估计是一种常用的可信区间估计方法。
它通过寻找最大化似然函数的参数值来估计未知参数。
最大似然估计得到的估计值具有一定的不确定性,因此可以构造可信区间来表示估计值的不确定性。
四、贝叶斯方法贝叶斯方法是一种基于贝叶斯统计理论的可信区间估计方法。
它假设参数是随机的,并利用先验分布和样本信息来估计参数。
贝叶斯方法通过后验分布来表示参数的不确定性。
贝叶斯方法的核心是贝叶斯公式,它将先验分布和似然函数结合起来,得到后验分布。
通过后验分布可以得到参数的可信区间。
五、实际应用可信区间的估计方法在实际问题中具有广泛的应用。
例如,在市场调查中,我们可以利用可信区间的估计方法来估计产品的市场份额。
抽样误差与区间估计
ν =10的t分布图
f ( t)
t 界值表
(P406,附表2)
举例:
t
1.812
-2.228
2.228
① 10,单 =0.05,t , t0.05,10 1.812 ,则有
P(t 1.812) 0.05 或 P(t 1.812) 0.05
② 10,双 =0.05,t
标准误(standard error, SE)
即样本均数的标准差,可用于衡量抽样误差的大 小。
总体标准误
X
总体标准差
因通常σ 未知,计算标准误采用下式: 样本标准差 抽样误差的 S 估计:(抽 S X 样误) 通过增加样本 n
样误差。
n
含量n来降低抽
表4-1计算了100个样本的标准差S,由此可 计算每一样本的抽样误差大小。
6190 3556
0.20
0.42 11.54
30 ① 26 ① 410 ①
466 ①
②
814 24764 ①
②
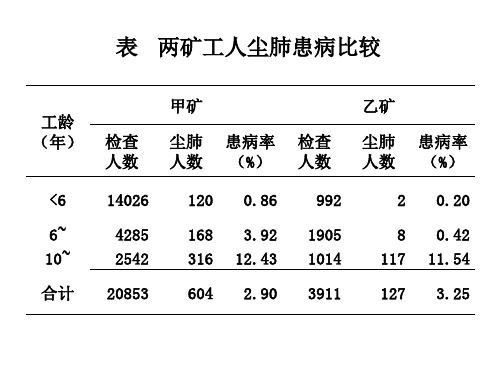
甲矿工人尘肺患病标准率=814/24764=3.29% 乙矿工人尘肺患病标准率=466/24764=1.88%
第四章 抽样误差与区间估计
第一节 均数的抽样误差与标准误
两个样本均数(或率)之间的差别有 两种可能: 一是由抽样误差引起的,即,两 个样本来自同一个总体,但是组成样本 的个体不同。由于个体差异引起样本均 数(或率)不同。 二是由处理因素引起的,即, 两个样本来自不同两个总体,由于处理 因素不同引起样本均数(或率)不同。
30 25 20
频数
15 10 5 0 4.2~ 4.3~ 4.4~ 4.5~ 4.6~ 4.7~ 4.8~ 4.9~ 5.0~ 5.1~ 5.2~ 红细胞数(×1012 /L)
数据统计中的抽样误差与置信区间

数据统计中的抽样误差与置信区间数据统计是一门研究通过收集、整理和分析数据来获取有关群体特征和趋势的学科。
在进行数据统计时,抽样是一个十分重要的步骤。
然而,由于取样过程的随机性和限制性,抽样误差是无法避免的。
为了对抽样误差做出准确的估计,统计学家们常常使用置信区间来量化结果的可靠性。
本文将详细探讨数据统计中的抽样误差与置信区间的概念和应用。
一、抽样误差的定义和影响因素抽样误差是指由于样本选取的随机性而导致的样本统计量与总体参数之间的差异。
当我们从总体中抽取一个样本并根据样本的统计量来推断总体的参数时,由于样本数量的限制以及样本抽取的随机性,样本统计量与总体参数之间的差异会产生抽样误差。
抽样误差的大小受到多种因素的影响。
首先,样本容量是影响抽样误差大小的重要因素。
样本容量越大,抽样误差越小,因为较大的样本容量能够更准确地代表总体的特征。
其次,总体的变异性也会影响抽样误差的大小。
当总体变异性较大时,即使样本容量很大,抽样误差仍可能较大。
另外,样本的抽取方式和样本的分布特征也会对抽样误差产生影响。
二、置信区间的定义和计算方法置信区间是用于估计总体参数的一种统计技术。
在数据统计中,我们通常无法获得整个总体的数据,因此需要通过样本推断总体参数的取值范围。
置信区间提供了一个参数估计的区间范围,表示我们对总体参数的估计值的不确定性。
置信区间由一个下限和一个上限组成,两个边界分别称为置信下限和置信上限。
在进行置信区间估计时,我们需要选择一个置信水平,通常常用的是95%或99%。
置信水平表示我们在重复抽样的情况下,有多大的可能性得到的置信区间包含了总体参数的真实值。
计算置信区间的方法根据不同的总体参数类型有所不同。
对于均值的置信区间估计,我们可以使用样本均值与样本标准差的组合来计算。
对于比例的置信区间估计,我们可以使用样本比例和二项分布的性质来计算。
三、置信区间的应用置信区间在数据统计中具有广泛的应用。
首先,置信区间可以用于估计总体参数的范围。
率的抽样误差及可信区间

二、两个独立样本率比较的u 检验
表5-1 两种疗法的心血管病病死率比较
疗法 盐酸苯乙双胍
安慰剂 合计
死亡
26 (X1) 2 (X2) 28
生存 178 62 240
合计 病死率(%)
204(n1) 64(n2) 268
12.75 (p1) 3.13 (p2) 10.45 (pc)
u 检验的条件:
n1p1 和n1(1- p1)与
1.正态近似法; (1)条件:a. n>100(50) b. np与 n(1-p)>5 (2)公式:1)总体率95%可信区间为:P±1.96SP.
2)总体率99%可信区间为:P±2.58SP 2.查表法:
适用于n≤50; P很接近0或100%时,可查百分率的可信 限表,求得百分率可信限
第二节 率的统计学推断
第三节 卡方检验
χ2检验(Chi-square test)是现代统计学的创始人 之一,英国人K . Pearson(1857-1936)于1900年提 出的一种具有广泛用途的统计方法,可用于两个或 多个率间的比较,计数资料的关联度分析,拟合优 度检验等等。
本章仅限于介绍两个和多个率或构成比比较的χ2 检验。
小结
1.样本率也有抽样误差,率的抽样误差的
大小用σp或Sp来衡量。
2.率的分布服从二项分布。
当n足够大,π和1-π均不太小, 有nπ≥5和n(1-π)≥5时,
近似正态分布。
3.总体率的可信区间是用样本率估计总体
率的可能范围。当p 分布近似正态分布
时,可用正态近似法估计率的可信区间
4.根据正态近似原理,可进行样本率与总
一、样本率与总体率比较u检验 二、两个样本率的比较u检验
u 检验的条件: n p 和n(1- p)均大于5时
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年6月18日4时58分
14
2、中心极限定理 central limit theorem
①即使从非正态总体中抽取样本,所得均数分布仍近似呈正态。 ②随着样本量的增大, 样本均数的变异范围也逐渐变窄。
2019年6月18日4时58分
15
t分布与可信区间
一、t分布
二、总体均数的估计 总体均数的点估计(point estimation)与区间 估计 总体均数的可信区间(confidence interval, CI) 大样本总体均数的可信区间
均数
450 400 350 300 250 200 150 100 50
0 3.71 3.92 4.12 4.33 4.54 4.74 4.95 5.15 5.36 5.57 5.77 5.98 6.19
均数
9
抽样实验小结
均数的均数围绕总体均数上下波动。
均数的标准差即标准误 X 与总体标准差 相差
宽
小(0.01)
30
区别点
总体均数可信区间
参考值范围
按预先给定的概率(可信度),确定的未知参数 的可能范围。 “正常人”的解剖,生理,
含 实际上一次抽样算得的可信区间要么包含了总体均数,要么 生化某项指标的波动范围。
不包含,二者必居其一,无概率可言;所谓 95%的可信度是
义 针对可信区间的构建方法而言。
标准正态分布
N(0,1)
标准正态分布
N(0,1)
Student t分布 自由度:n-1
17
t分布的概率密度函数
f (t) ( 1) 2 (1 t 2 / )( 1) 2
( 2)
式中 () 为伽玛函数; 圆周率(Excel函数为
PI( ))
为自由度(degree of freedom),是t分布
参数的估计
点估计:由样本统计量 X、S、p 直接估计 总体参数 、、
区间估计:按照预先给定的概率 (可信度),同时考虑抽样误差, 计算出一个区间,使它能够包含 未知的总体参数。
2019年6月18日4时58分
21
Confidence interval
可信度:事先给定的概率1-α称为可信度 一般,α取0.05 or 0.01,则1-α为0.95 or 0.99 可信区间(confidence interval,CI):计算得到的区 间称为可信区间。 可信限(confidence limit,CL):界定可信区间的两 个数值,上限和下限 总体均数估计的95%可信区间:表示该区间包括 总体均数μ的概率(可能性)为95%,即若作100 次抽样算的100个可信区间,则平均有95个可信区 间包括μ(估计正确),只有5个可信区间不包括μ (估计错误)。
通常未知,这时可以用其估计量S 代替,但 已不再服从标准正态分布,而是服从著
名的t 分布。
William Gosset
图6-1 不同自由度的 t 分布图
(二)σ未知且n较小时
t
X SX
X S
n
P(X
t0.052( )
S n
X
t0.052( )
S) n
0.95 0.025
①一簇单峰分布曲线,在
t=0 处最高,并以t=0为
中心左右对称
②与正态分布相比,曲线 最高处较矮,两尾部翘得 高(见绿线)
③ 随自由度增大,曲线逐 渐接近正态分布;分布的 2 3 4 极限为标准正态分布。
2019年6月18日4时58分
19
t分布曲线下面积(附表2)
2019年6月18日4时58分
双侧t0.05/2,9=2.262 =单侧t0.025,9
三、可信区间的解释
2019年6月18日4时58分
16
一、t分布(t distribution)
随机变量X N(,2)
u X
u变换
均数
X
N (, 2 n)
u X n
t变换
t X X , v n 1
S n SX
实际:s , sx x 或n较小时
的唯一参数;t为随机变量。 以t为横轴,f(t)为纵轴,可绘制t分布曲线。
2019年6月18日4时58分
18
t分布曲线
0.4 f( t) 0.4 0.3 0.3 0.2 0.2 0.1 0.1 0.0 -4 -3 -2 -1 0 1
t
t 分布有如下性质:
自由度为1的t分布 自由度为9的t分布 标准正态分布
包括:点估计与 区间估计
2. 假设检验(test of hypothesis)
2019年6月18日4时58分
2
一、均数的抽样误差
抽取部分观察单位
总体
样本
参数
统计推断
如:总体均数
总体标准差
总体率
统计量 如:样本均数 X
样本标准差S 样本率 P
抽样误差 (sampling error) :由于 抽样和变异引 起的样本统计 量与总体参数 间的差异或者 来自同一总体 的不同样本统 计量之间的差 异。
单侧t0.05,9=1.833 双侧t0.01/2,9=3.250
=单侧t0.005,9 单侧t0.01,9=2.821 双侧t0.05/2,∞=1.96
=单侧t0.025,∞ 单侧t0.05,∞ =1.64
20
二、总体均数的估计
1. 总体均数的点估计(point estimation)与 区间估计(interval estimation)
2019年6月18日4时58分
12
标准差与标准误的联系与区别
2. 随着样本量不断增大,样本标准差随机波 动的幅度越来越小,并且稳定在总体标准 差附近;随着样本量不断增大,样本均数 的标准误越来越小,并且趋向于0;
3. 样本含量n相同时,标准差越大,标准误相 对越大;标准差越小,标准误也相对越小。
2019年6月18日4时58分
0.025
Байду номын сангаас
t0.052( )
0 t分布曲线
t0.052( )
95%可信区间:(X
t0.052( )
S ,X n
t0.052( )
S) n
一
般
情
况
α/2
可信区间: (X
t 2( )
S ,X n
t 2( )
S) n
t 2( )
1-α
0 t分布曲线
α/2 t 2( )
括μ(估计正确),只有5个可信区间不包括 μ(估计错误)。
95%可信区间
公式 X
t 0.05 / 2,
S X
,
X t S 0.05 / 2, X
区间范围
窄
估计错误的概率 大(0.05)
2019年6月18日4时59分
99%可信区间
X
t0.01 / 2,
S X
,
X t S 0.01/ 2, X
13
标准差与标准误的区别与联系
标准差
标准误
1意义: 描述一组变量值之间的离散
区
程度(个体差异)
描述样本统计量间的离散 程度(抽样误差)
别
可用于估计某变量的正常值 估计总体参数所在的可信
2应用: 范围,n越大,标准差越趋于 区间,n越大,标准误越
稳定→σ
小→ 0
联 系
二者均是表示变异度大小的统计指标, n一定时,标准误与标准差成正比。
n=30 5.00 0.50 5.00
均数标准差
Sn
0.2212
0.1580
0.0920
n
0.2236 0.1581 0.0913
2019年6月18日4时58分
8
3个抽样实验结果图示
频数
450
400 350
n 5; S X 0.2212
300
250
200
150
100
50
0 3.71 3.92 4.12 4.33 4.54 4.74 4.95 5.15 5.36 5.57 5.77 5.98 6.19
总体均数的波动范围
计算
未知:
X
t ,
S X
*
公式 已知或未知但 n>100: X u X 或 X u SX **
用途 总体均数的区间估计
个体值的波动范围
正态分布: X u S **
偏态分布:PX~P100X
绝大多数(如 95%)观察对象
* t, 也可用 t /2, (对应于双尾概率时) ** u, 也可用 u /2, (对应于双尾概率时)
一个常数的倍数,即 / n X
实替,际得工到作标中准,误的未估知计时值,s可X用,样即本 标准差s代
s s/ n X
从正态总体N(μ,σ2)中抽取样本,获得均数的分 布仍近似呈正态分布N(μ,σ2/n) 。
2019年6月18日4时58分
10
标准误的应用
表示抽样误差大小:同质的资料标准误越小,表 明样本均数越接近于总体均数,抽样误差越小, 说明由样本均数推断总体均数的可靠性越大。反 之,标准误越大,表明样本均数远离总体均数, 抽样误差大,说明由样本均数推断总体均数的可 靠性小。医学文献中常以 x sx 表示资料的均 数及可靠程度。 确定总体均数的可信区间:结合样本均数对总体 均数做区间估计。 进行均数的t检验。
2019年6月18日4时59分
27
例 1 某市120名7岁男童的身高均数为 123.62cm,标准差为4.75cm,计算该市7岁 男童总体均数90%的可信区间
X 123.62, S 4.75, Sx 0.4336
