分振幅薄膜干涉(一)——等倾干涉知识讲解
合集下载
等倾干涉.ppt

所发出的光束对薄膜表面有不同的倾角,
正由于入射光的倾角改变而形成一组干
涉条纹。同一级条纹,对应着同一倾角, 不同级条纹,对应不同的倾角。即:由 于入射角相同的光经薄膜两表面反射形 成的反射光在相遇点有相同的光程差,也 就是说,凡入射角相同的光束就形成同一 级条纹,所以这些倾斜角度不同光束经 薄膜反射所形成的花样是一些明暗相间 的同心圆环,这种干涉称为等倾干涉。
等倾干涉 从点光源发出的锥面上光线的光路
等倾干涉 从点光源发出的锥面内光线的光路
1.6.2 单色面光源照明时的等倾干涉条纹
r环
oP
i1
f
··· 面光源 i1 n1
n2 > n1
d
n1
面光源上不同点而 相i1 同的入射光都将汇聚在同一个干涉 环上(非相干叠加),因而面光源照明比点光源照明条纹明
暗对比更鲜明。
1.6 分振幅薄膜干涉(一)——等倾干涉 ▲ 薄膜干涉是分振幅干涉。
▲ 日常中见到的薄膜干涉:肥皂泡上的彩色 、雨天 地上油膜的彩色、昆虫翅膀的彩色…。
▲ 膜为何要薄? ─ 光的相干长度所限。膜的薄、厚 是相对的,与光的单色性好坏有关。
▲ 普遍地讨论薄膜干涉是个极为复杂的问题。实际意 义最大的是厚度不均匀薄膜表面附近的等厚条纹和厚度 均匀薄膜在无穷远处的等倾条纹。
osi2
2
2h
n22
n22
s in 2
i2
2
2h
n22
n12
sin 2
i1
2
2n2h cosi2
2
2h
n22
n12
sin 2
i1
2
不论入射光的的入射角如何
满足n1<n2>n3(或n1 >n2 <n3)
正由于入射光的倾角改变而形成一组干
涉条纹。同一级条纹,对应着同一倾角, 不同级条纹,对应不同的倾角。即:由 于入射角相同的光经薄膜两表面反射形 成的反射光在相遇点有相同的光程差,也 就是说,凡入射角相同的光束就形成同一 级条纹,所以这些倾斜角度不同光束经 薄膜反射所形成的花样是一些明暗相间 的同心圆环,这种干涉称为等倾干涉。
等倾干涉 从点光源发出的锥面上光线的光路
等倾干涉 从点光源发出的锥面内光线的光路
1.6.2 单色面光源照明时的等倾干涉条纹
r环
oP
i1
f
··· 面光源 i1 n1
n2 > n1
d
n1
面光源上不同点而 相i1 同的入射光都将汇聚在同一个干涉 环上(非相干叠加),因而面光源照明比点光源照明条纹明
暗对比更鲜明。
1.6 分振幅薄膜干涉(一)——等倾干涉 ▲ 薄膜干涉是分振幅干涉。
▲ 日常中见到的薄膜干涉:肥皂泡上的彩色 、雨天 地上油膜的彩色、昆虫翅膀的彩色…。
▲ 膜为何要薄? ─ 光的相干长度所限。膜的薄、厚 是相对的,与光的单色性好坏有关。
▲ 普遍地讨论薄膜干涉是个极为复杂的问题。实际意 义最大的是厚度不均匀薄膜表面附近的等厚条纹和厚度 均匀薄膜在无穷远处的等倾条纹。
osi2
2
2h
n22
n22
s in 2
i2
2
2h
n22
n12
sin 2
i1
2
2n2h cosi2
2
2h
n22
n12
sin 2
i1
2
不论入射光的的入射角如何
满足n1<n2>n3(或n1 >n2 <n3)
光的干涉分振幅薄膜干涉等倾干涉

n2 n1 T |i1 0 0.96 反射率: |i1 0 n n 0.04 透射率为: 2 1 设入射光强度为100,则各反射相干光的相对光强为:
2
a1:4%×100=4 a2:100×96%×4%×96%=3.74 a3:100×96%×4%×4%×4% ×96% =5.9×10-3<<4
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
由于反射而引入的附加光程差2存在与否,可根据以下 条件判断 。 在不超过临界角的条件下,无论入射角的大小如 何,光在第一表面上反射和第二表面上反射并射出时: 若在薄膜上、下两个表面的两反射的物理性质不同,则两反 射相干光a1,a2(或b1,b2),或两透射光c1,c2(或d1,d2)之间将 有/2的附加光程差. 例如:如图
面甲等。为了增强反射能量,常在玻璃表面上镀一层高反射率
的透明薄膜,利用薄膜上、下表面的反射光的光程差满足干涉 相长条件,从而使反射光增强,这种薄膜叫增反膜。
在一光学元件的玻璃(折射率 n3 1.5 )表面上 镀一层厚度为e、折射率为 n2 1.38 的氟化镁薄膜, 为了使入射白光中对人眼最敏感的黄绿光 ( 5500 A) 反射最小,试求薄膜的厚度.
1
M1
2
i1
L 3
P
可见:波长一定、倾角i 相同的 入射光线,对应于同一级干涉 条纹—等倾条纹 .
n1
n2
A i 2
i2
i1
D C
d
M2
n1
B
4
E 5
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
2d n
明纹条件:
2 2
n sin i1 ( ) 2
2
a1:4%×100=4 a2:100×96%×4%×96%=3.74 a3:100×96%×4%×4%×4% ×96% =5.9×10-3<<4
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
由于反射而引入的附加光程差2存在与否,可根据以下 条件判断 。 在不超过临界角的条件下,无论入射角的大小如 何,光在第一表面上反射和第二表面上反射并射出时: 若在薄膜上、下两个表面的两反射的物理性质不同,则两反 射相干光a1,a2(或b1,b2),或两透射光c1,c2(或d1,d2)之间将 有/2的附加光程差. 例如:如图
面甲等。为了增强反射能量,常在玻璃表面上镀一层高反射率
的透明薄膜,利用薄膜上、下表面的反射光的光程差满足干涉 相长条件,从而使反射光增强,这种薄膜叫增反膜。
在一光学元件的玻璃(折射率 n3 1.5 )表面上 镀一层厚度为e、折射率为 n2 1.38 的氟化镁薄膜, 为了使入射白光中对人眼最敏感的黄绿光 ( 5500 A) 反射最小,试求薄膜的厚度.
1
M1
2
i1
L 3
P
可见:波长一定、倾角i 相同的 入射光线,对应于同一级干涉 条纹—等倾条纹 .
n1
n2
A i 2
i2
i1
D C
d
M2
n1
B
4
E 5
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
2d n
明纹条件:
2 2
n sin i1 ( ) 2
1.7 分振幅干涉——等倾干涉

波振面分割法:使一束 光分割为两束相干光。 不论点(或线)光源的 位相改变如何频繁,同 一波振面的这些光源的 位相差始终不变,故为 相干光。 振幅分割法: 振幅分割法:利用 物体两个表面对入 射光的反射或折射, 射光的反射或折射, 上表面 将入射光的振幅 其实是能量) (其实是能量)分 解为若干部分, 解为若干部分,这 些光波也互为相干 下表面 光。
衍射
S
S1 S2
相 遇 区
分束装置 分束 1 2 薄膜
相遇
常见的分振幅干涉现象
单色点光源引起的等倾干涉现象
装置简介
光源S发出的光线 光源 发出的光线 经过透镜L1后平行 经过透镜 后平行 入射到透明介质, 入射到透明介质,在 透明介质表面发生反 射和折射, 射和折射,从上表面 反射的光线和从下表 面反射回来的光线经 过透镜L2后成像与 过透镜 后成像与 L2的焦平面上的 。 的焦平面上的S’。 的焦平面上的
干涉条纹特点
等倾干涉条纹定域在无限远处。 等倾干涉条纹定域在无限远处。 具有相同入射角的光线对应同一干涉条纹。 具有相同入射角的光线对应同一干涉条纹。 h、λ一定,j值由i1决定,由知,i1愈小,j值愈大,内 一定, 值由i 决定,由知, 愈小, 值愈大, 部干涉条纹级次高。 部干涉条纹级次高。 条纹角间隔,对于相邻两明纹。 条纹角间隔,对于相邻两明纹。
1 − sin 2 i 2 λ λ λ ∴ δ = 2n 2 h / cos i 2 − 2n 2 h sin i 2 / cos i 2 − = 2n 2 h − = 2n 2 h cos i 2 − 2 cos i 2 2 2
2
2 n 2 cos i 2 = n 2 1 − sin 2 i 2 = n 2 − n 2 sin 2 i 2 = n 2 − n 1 sin 2 i1 2 2 2
1.6 分振幅薄膜干涉(一)——等倾干涉
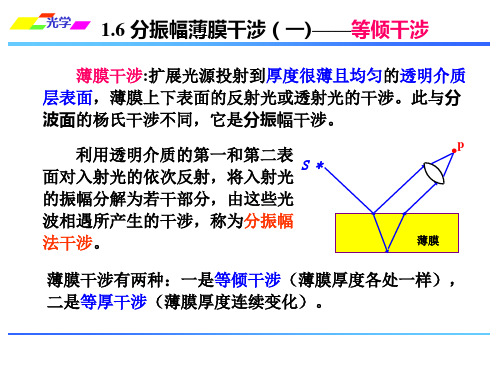
·
p
薄膜
薄膜干涉有两种:一是等倾干涉(薄膜厚度各处一样), 二是等厚干涉(薄膜厚度连续变化)。
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
分振幅法干涉是现代干涉仪和干涉计量技术的理论基础, 在日常生活中,这类干涉也很常见。例如: 1.水面上的油膜在阳光下呈现出彩色; 2.肥皂泡在阳光下也呈现出彩色; 3.有的照相机镜头,摄像机镜头镀有增透膜,常呈现出深蓝 色(反射光的颜色)。
s2
s '2 s '1
n1
n2
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
由平行介质膜干涉的光程差公式可知:
2e n
2 2
2 2 n1 sin i1 2 0
只要入射角相同,其光程差就相等,因而相同的 入射角形成的是同一级干涉条纹,称等倾干涉。
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
等倾条纹照片
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
2e n
2 2
三、等倾条纹讨论
n sin i1
2 1 2
2
2k
2
e一定,i1 ↓ ,则k ↑ ,即中心级数高,外围级数低 若中心处(i1=0)为明条纹,其级数为
k
2n2 e
2
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
两反射光2、3之间有附加光程差。 两透射光4、5之间无附加光程差。
若 n1 n2 n3 两反射光2、3之间无附加光程差。
两透射光4、5之间有附加光程差。
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
若有附加光程差,则
1-7 分振幅薄膜干涉(一)- -等倾干涉

A
a1 i1 C’
S’ C a2
B
d0
aa2 n1 SA n2 ( AB BC) n1 CS '
光aa1经分界面M1(疏-密或密-疏)反射,光aa2经分 界面M2(密-疏或疏-密),反射光a1与a2光振动反向, 有“额外光程”- -±/2产生; 光程差为: aa aa 2 1 2
1.7 分振幅薄膜干涉(一)-等倾干涉
分振幅是获得相干光源的方法之一。
制 作 人 周 杰
利用薄膜可实现分振幅干涉; 利用薄膜干涉可以制成增透膜(减小光能损 失)、干涉滤光片(可用来获得单色光)等,在 近代光学仪器上得到广泛应用。 下面分别讨论 1.7.1 单色点光源引起的干涉现象 1.7.2 单色发光平面引起的干涉现象 对“额外光程”的几点说明
若Iab=1,则Ia1b1=0.04,Ia2b2=0.037,Ia3b3=0.00006
返回 第1章 光的干涉
3/30/2013
1.7.2 单色发光平面引起的干涉现象
等倾干涉装置 等倾干涉及条纹特点 等倾干涉条纹定量分析* 薄膜厚度对条纹的影响 透射光的干涉情况
制 作 人 周 杰
3/30/2013
制 作 人 周 杰
返回
第1章 光的干涉
等倾干涉条纹(一)
条纹特点:
同心圆环:以L2的焦点为圆心的同心圆环; 中央疏而边缘密,干涉级次从中心向外递减(即中 心条纹干涉级j最大);
等倾干涉条纹出现在会聚镜的焦平面上,无透镜 时,产生的干涉条纹在无限远处--等倾干涉条 纹的定域为“无限远”,需通过透镜聚焦观察。
光学 等倾干涉

2nd 1co2si2 2 0 cois2
代入上式可得: 2n2d0cois22
2d0 n22n12sin2i1 2
n2d0 n2 2n1 2sin2i1/2
根据具体 情况而定
S
n1 n2 n1
L1
L2 S’ ➢ 透射光的光程差
b a A C′
a1 a2
C
c o si2 ' c o si2 i2 2 2 i2 2 '2i2 i2 ' i2 i2 ' /22 n 2 d 0
令 i2i2 ' i,i2i2 ' 2 i2 '
则有 i
2n2d0i2'
;
i 2 ' 远离 i ;i 2 ' 中 靠 心 近 i中
B
t 2d0 n22n12sin2i1
d0
注意:透射光和反 射光干涉具有互 补 性 , 符合能量守恒定律.
当光线垂直入射时 i 0
n1
当 n2 n1 时
n2
Δr 2dn2 2
n1
当 n3n2n1 时
n1
n2
Δr 2dn2
n3
由 2、干涉公式:
2 j
2
2 j 1
第一章
光的干涉
§1.6 薄膜干涉
(Interference from Thin Films)
一、透镜不引起附加的光程差
A F
o
B A
F'
B
焦平面
A
a
a
B
bFຫໍສະໝຸດ ··Sb·
C
c
c
A B C
·
光学1-7等倾干涉

n2 = 1.38
h
n3 =1.5
3λ 3× 550 ×10−9 h= = = 2.982 ×10−7 m 19 4n2 4 ×1.38
问:若反射光干涉相消的条件中取j=1,膜的厚度 为多少?此增透膜在可见光范围内有没有增反? 此膜对反射光干涉相长的条件:
2n2 h = jλ j =1 λ1 = 855nm j=2 λ2 = 412.5nm j =3 λ3 = 275nm
λ
2
= jc λ
15
从里到外级次为 jc、jc-1、jc-2、…
(3)条纹的分布为内疏外密 由 δ (i2 ) = 2 n2 d 0 cos i2 − λ = j λ 得 cos i2 =
i i4 cos 对入射角很小时, i ≈ 1 − 2! + 4! +
22
i2 ≈ 1− 2!
1 ⎛ λ⎞ jλ + ⎟ ⎜ 2n2 d 0 ⎝ 2⎠
2
21
题意: λ1=630nm处是干涉极大,λ2=525nm处出现干 涉极小,并且两者之间没有别的极值情况。由光程 λ 假设 差公式 δ = 2n2 d 0 − = k λ ,随着波长λ连续减小,k
2
连续增大,紧接着极大值级次k=j 出现的极小值级 次为k=j+1/2。则:
δ = 2n2 d 0 −
c1 c 2 c 3 d 1 d 2 d 3
δ1 = n2 ( AB + BC ) − n1 AC ′ −
d0 AB = BC = cos i2 n2 d 0 n2 ( AB + BC ) = cos i2
λ
2
补充
i1
A
a1
C′ C
a2 i1 n1 n2 d0
5.7 分振幅薄膜干涉(一) 等倾干涉

1 cosi2 2n 2 d 0
k 2
i2 i4 对入射角很小时, cosi 1 2! 4!
所以省略i 4以上各项,则
i2 cos i 1 2!
则相邻两明环或暗环间距为: i i2
2 2
n d
2
2
0
物理科学与信息工程学院
2
对于1=630nm的光产生的是极大值,设级次 为k。则 1 2n2 d 0 k1 (1) 2
物理科学与信息工程学院
设另一波长2也产生极大值,其级次为k+1, 则应有 2 2n2 d 0 (k 1)2 (2) 2 由(1)、(2)两式可得:
物理科学与信息工程学院
分振幅法干涉是现代干涉仪和干涉计量技术的理论基 础,在日常生活中,这类干涉也很常见。例如: 1.水面上的油膜在阳光下呈现出彩色
2.肥皂泡在阳光下也呈现出彩色;
3.有的照相机镜头,摄像机镜头镀有增透膜,常呈 现出深蓝色(反射光的颜色)。
一、单色点光源产生非定域干涉
设单色点光源S发出的光照在厚度均匀的平行薄膜上, 由于介质上下两表面的反射,在与S同侧的屏幕上,不 论屏幕的位置如何都可观察到干涉条纹。
物理科学与信息工程学院
0
为使问题简单化, 略去介质表面的折射, 则介质上下两表面的反 射光好像是从两个点光 源S1、S2发出的一样。
P
S
i n n > n n
S1
· i
·
1
在空间相遇的各点都 相干叠加。因此相遇空 间处处可见干涉条纹, 故称为非定域干涉。
S2
物理科学与信息工程学院
对于S同侧的空间中任一点P是 干涉相长还是干涉相消,决定于 S1和S2到P点的有效光程差。 包括由于几何路程不同而它 产生的光程差1和由于反射引起 的附加光程差2。 附加光程差若存在,则为/2,否则为0。
k 2
i2 i4 对入射角很小时, cosi 1 2! 4!
所以省略i 4以上各项,则
i2 cos i 1 2!
则相邻两明环或暗环间距为: i i2
2 2
n d
2
2
0
物理科学与信息工程学院
2
对于1=630nm的光产生的是极大值,设级次 为k。则 1 2n2 d 0 k1 (1) 2
物理科学与信息工程学院
设另一波长2也产生极大值,其级次为k+1, 则应有 2 2n2 d 0 (k 1)2 (2) 2 由(1)、(2)两式可得:
物理科学与信息工程学院
分振幅法干涉是现代干涉仪和干涉计量技术的理论基 础,在日常生活中,这类干涉也很常见。例如: 1.水面上的油膜在阳光下呈现出彩色
2.肥皂泡在阳光下也呈现出彩色;
3.有的照相机镜头,摄像机镜头镀有增透膜,常呈 现出深蓝色(反射光的颜色)。
一、单色点光源产生非定域干涉
设单色点光源S发出的光照在厚度均匀的平行薄膜上, 由于介质上下两表面的反射,在与S同侧的屏幕上,不 论屏幕的位置如何都可观察到干涉条纹。
物理科学与信息工程学院
0
为使问题简单化, 略去介质表面的折射, 则介质上下两表面的反 射光好像是从两个点光 源S1、S2发出的一样。
P
S
i n n > n n
S1
· i
·
1
在空间相遇的各点都 相干叠加。因此相遇空 间处处可见干涉条纹, 故称为非定域干涉。
S2
物理科学与信息工程学院
对于S同侧的空间中任一点P是 干涉相长还是干涉相消,决定于 S1和S2到P点的有效光程差。 包括由于几何路程不同而它 产生的光程差1和由于反射引起 的附加光程差2。 附加光程差若存在,则为/2,否则为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2n2d0 f
2 (2 j 1) 2n1d0
2n2d0
f
2n1
1
2d02
(2
j 1)
2n2
d0
4、条纹间距
1
2 (2 j 1)
2n2d0
令dj 1,则drj r rj rj1
r f
2n1
1
2d02
(2
j 1)
2n2
d0
d0 r
5、干涉图样中心是明条纹还是暗条纹?
干涉图样中 i1 心0
n1
n2
a1 a2
n1
0'2d0 n (2 22 d 0nn 21c2soii22n )si12 (2j(2 1 j))2 2
(相)长 (相)消
(j=0, 1, 2, …)
1.6.2 等倾干涉图样的讨论
1、干涉图样的形状
0'2d0 n22n12si2n i12 (2j(2 1 j))2
2
i1 i1
f
L
S i1 · i1
12
n2 n1
A··C·C r ·'
d0
n2
B
r环
o
P
i1 i1
rj f i1
f
f n 2 2 (2 j 1)
n1
2n2d0
L
等倾干涉条纹的半径
1
·S
2
i1 i1
d0 rj 条纹涌出
·
n2
· A
C'·C
d0 rj 条纹凹陷
n1
r·
d0
n2
B
drj f n 2 dj n1
额外光程差(半波损失) 用菲涅耳公式可以解释:光在垂直入射(i =0)或者掠入射 (i =90°)的情况下,如果光是从光疏媒质传向光密媒质, 在其分界面上反射时将发生半波损失。 折射波无半波损失。
n1 n1 >n2
n2
n1 n1< n2
n2
没有半波损 失
这里取负号,产生额外程差
'
2
有半波损失
★干涉相长、相消的条件
讨论
S
n1 n2 n1
L1
L2
S
’
a1
b a
a2
A C’
C
d0
B
★置于透镜L1焦平面的单色点光源S发出的光束 ab投射于介质薄膜AB时的干涉现象。
★分振幅
反射(a→A→a1) 折射(a→ A→B)→反射(B→C)→折射(C→a2)
相干光束a1、a2会聚于透镜L2的焦点S’处,
这一点究竟是亮还是暗的,这由a1、a2的光程 差来计算。
S
a n1 n2 n1
S′ a1
i1 c′
a2
C
A
d0
i2 B
C’
i1
A
i1
C
n1
i2
d0
n2
B
n1
C’
i1
A
i1
C
n1
i2
d0
n2
B
n1
0n2(ABBC )n1(AC')n2(cdo0i2scdo0i2s)n1(ACsini1)
(2cno2di2s0)n1(2d0tani2)(si1n)(2cno2di2s0)(2d0tani2)(n2sini2) 2d0n2coi2s2d0 n22n12sin2i1
2n2d0
2
j
4n2d0
(1)
2 j 1
400 nm 760 nm
400 nm 4 n 2 d 0 760 nm 2 j1
4 .32 j 8 .5 j取整数 j 5,6,7 ,8 代入 (1)式可得
654 .5 nm ,553 .8 nm ,480 nm ,423 .5 nm
若采用多色光入射,则在相同的入射角(即同 一级次条纹),有的波长是相干相长,有的是 相干相消
• 作业
1.7 1.8
光程差 2n2d0
2
明条纹:
j
2n2d0
2
jd0
(2j 1)
4n2
暗条纹:(2j
1)
2
2n2d0
2
(2j
1)
2
d0
j
2n2
1.6.3 单色面光源所引起的等倾干涉条纹
• 扩展光源的作用
光源上各发光点的同一级干涉条纹是重合的,光 源上每一点都给出一组等倾干涉圆环,它们彼此 准确重合,没有位移。因此将点光源换成扩展光 源,等倾干涉条纹的可见度不受影响,但强度大 大增加了,干涉花样更加明亮。
若采用多色光入射,则干涉图样是什么样的?
例题:波长是400nm~760nm的可见光,垂直照射到一厚度是1.2
微米,折射率是1.5的玻璃片上,试问从玻璃片的反射光中,可看
到哪些波长的光?
解:由题意知:入射角 i 0o
光程差
2n2d0
2
若要在反射光中看到某 一波长的光束,则该波 长的光
应是相干相长的,即: j
由折射定律:
n 1 sin i1 n 2 sin i 2
n 1i1 n 2 i2
i2
n1 n2
i1
( n1 n2
i1 ) 2
2
(2 j 1) 2n2d 0
i12
n
2 2
n
2 1
[2
(2 j 1) ]
2n2d 0
i1
n2 n1
2 (2 j 1) 2n2d 0
等倾干涉条纹的角半径
o r环 P
第一章 光的干涉
实验装置
1.6 分振幅薄膜干涉(一) ——等倾干涉
透明薄板、薄膜
S1 2
1P
2
S
1
21 P 2
反射空间任何区域都可以呈现干涉条纹—非定域
是否可以产生相干光束?
反射光干涉
1
i
2
薄膜
ne
透射光干涉
i 薄膜
ne 2
1
反射(透射)倾角相同--反射(透射)的光线对具有 恒定的相位差干涉
1.6.1 单色点光源引起的干涉现象
(相)长 (相)消
只要光线的入射方向相同,即有相同的入射角 i1各源点均在L 后焦面上相同点P产生相同的干涉级次(j相同)
每一条纹对应于同样的光线倾角—等倾干涉
i
屏幕
f
S
L
M
n2
等倾干涉的干涉图样是一组明暗相间的同心圆环
2、干涉条纹的级次
中央条纹的干涉级次高?还是边缘的干涉级次高?
2d0n2coi2s2j
★ d0一定,j↑ cosi2↑ i2↓ 干涉图样,中心级数高,外围级数低。
3、条纹半径
第j级明条纹
2d0n2coi2 s2(2j)2
c
ois2
1i22 i24 ...... 2! 4!
i 2 较小时
cos
i2
1
i
2 2
2!
2 d 0 n 2 (1
i
2 2
)
2!
2
j
i
2 2
2
(2 j 1) 2n2d 0
