推荐-数字信号处理课件 精品
合集下载
精品课程《数字信号处理》PPT课件第1章 离散时间信号与系统
n
(a) (a)
(b) (b)
第1章 离散时间信号与系统 3. 序列的和 z(n) x(n) y(n)
4. 序列的乘积
f (n) x(n) y(n)
5. 序列的标乘
f (n) cx(n)
两序列的和是指同序号 n 的序列值
逐项对应相加而构成的一个新序列
两序列相乘是指同序号 n
的序列值逐项对应相乘
k必为整数
第1章 离散时间信号与系统
分三种情况讨论正弦序列周期
N 2k = 2 k 0 0
2 1. 0
为正整数，只要 k =1，
N
2 0
为最小正整数，即序列周期；
第1章 离散时间信号与系统
1.
2 0
为正整数，只要
k
=1， N
2 0
为最小正整数，即周期
sinnω0
1
o1
5
10 n
1
第1章 离散时间信号与系统
x(n) sin(n0 )
sin(n0T
)
0
0T
数字域角频率 0：反映序列变化的速率 ，单位 ( rad/间隔 ) 模拟域角频率 0：反映信号变化的速率 ，单位 ( rad/s )
0 0T
0
0
fS
数字域角频率是模拟域角频率对采样频率的归一化
第1章 离散时间信号与系统 6. 复指数序列
x(n) Ae j0 n
x n
2 不是整数， 0
N k
（N，k为互素整数）N
k
2 0
已知：x n sin 4π n ，求其周期。
11
ω0
4π ， 则有：2π
11
ω0
2π
11 4π
高西全-丁玉美-数字信号处理课件
拉普拉斯变换：将信号从时 域变换到复频域，便于分析 信号的稳定性和收敛性
状态空间法：通过建立系统 的状态空间模型，分析系统 的动态特性和稳定性
信号流图法：通过绘制信号 流图，分析系统的信号流和 信号处理过程
信号通过非线性系统的分析方法
非线性系统的定义和分类
非线性系统的分析方法：如微分 方程、差分方程、傅里叶变换等
添加标题
添加标题
非线性系统的特性和特点
添加标题
添加标题
非线性系统的应用实例：如通信 系统、控制系统、图像处理等
03
离散时间信号与系统分析
离散时间信号的分类与表示
连续时间信号：在连 续时间上取值的信号
离散时间信号：在离 散时间上取值的信号
连续时间信号的表示： 通常用函数表示
离散时间信号的表示： 通常用序列表示
数字信号处理课件(第三版)
单击添加副标题
汇报人：
目录
01
课件概览
02
03
离散时间信号与系统分析
04
05 数 字 信 号 处 理 系 统 性 能 评 估 与 优 化
信号与系统基础 数字信号处理算法与实现
01
课件概览
作者介绍
作者：张辉
专业领域：数字 信号处理
教育背景：清华 大学电子工程系 博士
工作经历：清华 大学电子工程系 教授，从事数字 信号处理研究多 年
离散时间信号的分类： 周期信号和非周期信
号
周期信号：在离散时 间上重复出现的信号
非周期信号：在离散 时间上不重复出现的
信号
离散时间系统的分类与描述
线性系统：输入与输出之间 存在线性关系
添加标题
时不变系统：系统的特性不 随时间变化
数字信号处理ppt课件
23
三.自相关函数与 自协方差函数的性质
24
性质1 :相关函数与协方差函数的关系
Cxx m rxx m mx 2
Cxy m rxy m m*xmy
当 mx 0
Cxx m rxx m Cxy m rxy m
25
性质2：均方值、方差与相关函数和协方差函数
rxx
0
E
xn
2
Cxx 0 rxx 0 mx 2
五、功率谱密度
44
维纳——辛钦定理
1． 复频域
rxx
(m)
1
2
j
c Sxx (z)zm1dz,
Sxx
(z)
m
rxx
(m)z
m
C (Rx , Rx )
45
2. 频域
{ rxx(m)
1
2
Pxx (e j )e jm d
2
Pxx (e j ) rxx (m)e jm
m
46
3．性质
实平稳随机信号 rxx m rxx m
rxx m E x x n1 n1m
x1x2 p x1 , x2 ; m dx1dx2
18
自协方差函数
Cxx (m) E (xn1 mx )*(xn2 mx ) E (xn1 mx )*(xn1m mx )
rxx m mx 2
19
对于均值为零的随机过程 rxx m Cxx m
①偶函数
Pxx e j Pxx e j
②实函数
Pxx e j Pxx e j
③极点互为倒数出现
Sxx
z
Sxx
1 z
47
④功率谱在单位圆上的积分等于平均功率
E
x2
三.自相关函数与 自协方差函数的性质
24
性质1 :相关函数与协方差函数的关系
Cxx m rxx m mx 2
Cxy m rxy m m*xmy
当 mx 0
Cxx m rxx m Cxy m rxy m
25
性质2：均方值、方差与相关函数和协方差函数
rxx
0
E
xn
2
Cxx 0 rxx 0 mx 2
五、功率谱密度
44
维纳——辛钦定理
1． 复频域
rxx
(m)
1
2
j
c Sxx (z)zm1dz,
Sxx
(z)
m
rxx
(m)z
m
C (Rx , Rx )
45
2. 频域
{ rxx(m)
1
2
Pxx (e j )e jm d
2
Pxx (e j ) rxx (m)e jm
m
46
3．性质
实平稳随机信号 rxx m rxx m
rxx m E x x n1 n1m
x1x2 p x1 , x2 ; m dx1dx2
18
自协方差函数
Cxx (m) E (xn1 mx )*(xn2 mx ) E (xn1 mx )*(xn1m mx )
rxx m mx 2
19
对于均值为零的随机过程 rxx m Cxx m
①偶函数
Pxx e j Pxx e j
②实函数
Pxx e j Pxx e j
③极点互为倒数出现
Sxx
z
Sxx
1 z
47
④功率谱在单位圆上的积分等于平均功率
E
x2
《数字信号处理原理》课件
数字信号处理可用于医学图像处理、心电图 分析、脑电图分析等。
数字信号的采集与量化
数字信号处理的第一步是对连续信号进行采样和量化。采样将连续信号转换 为离散信号，而量化则将信号的幅值量化为离散数值。
数字信号处理傅里叶级数和傅里叶变换将 信号分解为频域成分，用于 频谱分析和滤波。
带阻滤波器阻止一定范围内的频率信号通过， 而允许其他频率信号通过。
FIR滤波器和IIR滤波器的区别
FIR滤波器（有限脉冲响应滤波器）和IIR滤波器（无限脉冲响应滤波器）是两 种常见的数字滤波器类型。它们在设计和性能上有所不同，适用于不同的应 用场景。
互相关和自相关分析
互相关和自相关分析是数字信号处理中常用的分析方法。互相关用于信号的 相似性比较，自相关用于信号的周期性分析。
卷积
卷积是数字信号处理中常见 的运算，可以用于信号滤波、 系统响应等方面。
离散时间系统
离散时间系统是数字信号处 理的基本模型，用于描述信 号处理系统的特性。
时域分析与频域分析
时域分析关注信号随时间的变化，频域分析关注信号在频率上的特征。通过 这两种分析方法，可以深入了解信号的属性和特性。
傅里叶变换及其应用
信号去噪
信号去噪是数字信号处理中的重要任务。通过滤波和降噪算法，可以有效地去除信号中的噪声，提升信号的质 量和可靠性。
信号增强
信号增强是数字信号处理的一项重要任务。通过滤波、增益调整等方法，可以增强信号的强度、清晰度和可感 知性。
信号压缩
信号压缩是数字信号处理中的重要技术。通过压缩算法和编码技术，可以减 少信号的存储空间和传输带宽，实现高效的信号处理和传输。
傅里叶变换是一种将信号从时域转换到频域的数学工具。它在数字信号处理 中广泛应用于频谱分析、滤波、压缩等领域，为信号处理提供了强大的工具。
数字信号的采集与量化
数字信号处理的第一步是对连续信号进行采样和量化。采样将连续信号转换 为离散信号，而量化则将信号的幅值量化为离散数值。
数字信号处理傅里叶级数和傅里叶变换将 信号分解为频域成分，用于 频谱分析和滤波。
带阻滤波器阻止一定范围内的频率信号通过， 而允许其他频率信号通过。
FIR滤波器和IIR滤波器的区别
FIR滤波器（有限脉冲响应滤波器）和IIR滤波器（无限脉冲响应滤波器）是两 种常见的数字滤波器类型。它们在设计和性能上有所不同，适用于不同的应 用场景。
互相关和自相关分析
互相关和自相关分析是数字信号处理中常用的分析方法。互相关用于信号的 相似性比较，自相关用于信号的周期性分析。
卷积
卷积是数字信号处理中常见 的运算，可以用于信号滤波、 系统响应等方面。
离散时间系统
离散时间系统是数字信号处 理的基本模型，用于描述信 号处理系统的特性。
时域分析与频域分析
时域分析关注信号随时间的变化，频域分析关注信号在频率上的特征。通过 这两种分析方法，可以深入了解信号的属性和特性。
傅里叶变换及其应用
信号去噪
信号去噪是数字信号处理中的重要任务。通过滤波和降噪算法，可以有效地去除信号中的噪声，提升信号的质 量和可靠性。
信号增强
信号增强是数字信号处理的一项重要任务。通过滤波、增益调整等方法，可以增强信号的强度、清晰度和可感 知性。
信号压缩
信号压缩是数字信号处理中的重要技术。通过压缩算法和编码技术，可以减 少信号的存储空间和传输带宽，实现高效的信号处理和传输。
傅里叶变换是一种将信号从时域转换到频域的数学工具。它在数字信号处理 中广泛应用于频谱分析、滤波、压缩等领域，为信号处理提供了强大的工具。
《数字信号处理原理》PPT课件
•Digital signal and image filtering
•Cochlear implants
•Seismic analysis
•Antilock brakes
•Text recognition
•Signal and image compression
•Speech recognition
•Encryption
•Satellite image analysis
•Motor control
•Digital mapping
•Remote medical monitoring
•Cellular telephones
•Smart appliances
•Digital cameras
•Home security
Upper Saddle River, New Jersey 07458
All rights reserved.
FIGURE 1-4 Four frames from high-speed video sequence. “ Vision Research, Inc., Wayne, NJ., USA.
Joyce Van de Vegte Fundamentals of Digital Signal Processing
ppt课件
11
Copyright ©2002 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Joyce Van de Vegte Fundamentals of Digital Signal Processing
精品课程数字信号处理PPT课件09
10 (k) (k) 4 (k)
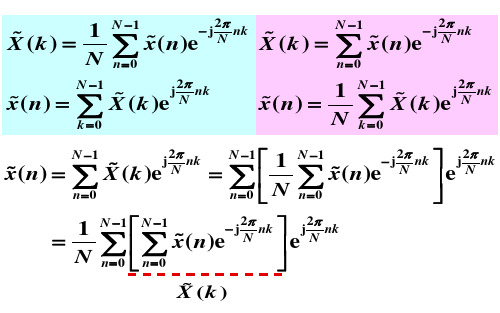
第3章 离散傅里叶变换
3.4.2 DFT与序列傅里叶变换、z变换的关系
若x(n)是一个有限长序列，长度为N
z变换 DFT
N 1
X ( z) x(n)zn
n0 N 1
X (z) zWNk x(n)WNnk X (k ) n0
X (k ) X (z) zWNk
第3章 离散傅里叶变换
3.4 有限长序列离散傅里变换（DFT）
周期序列只有个有限序列值有意义，和有限长序列有着本质联系。
周期序列的离散傅里叶级数 周期序列和有限长序列的关系
有限长序列的离散傅里叶变换（DFT）
第3章 离散傅里叶变换
x(n)为有限长序列，长度为N
x(n)
x(n)
0 n N 1
…
-10 -10 -10
(c)
(c)
-10
(c)
-10
-10
x (n) x (n) 1 x (n)
1 1
N=10 有限长序列
0
4
0 0
~~~xxx (((nnn)))
4 4
1
1 1
0
4
0
4
0 |X(k)| 4
|X(k)|
|X(k)|
… … …
10 10 10
n n
N=10 周期延拓
n n n
5
5 3.24
第3章 离散傅里叶变换
DTFT DFT
N 1
X (e j ) x(n)e jn
n0
X (e j ) 2 k
N 1
j2 kn
x(n)e N
X (k)
N
n0
X (k ) X (e j ) 2 k X (e jkN ) N
高西全_丁玉美_数字信号处理精品课件
若x1(n)* x2 (n) y(n) 则x1(n m1) * x2 (n m2 ) y(n m1 m2 )
典型信号的卷积
x(n)* (n) x(n)
n
x(n)*u(n) x(m) m
32
例6、设x(n)
n / 2
0
0
n 其他
3，h(n)
3
0
n
0n2 其他
求x(n) * h(n)
果性及稳定性的含义及判别方法。 掌握采样定理。
3
1.1 引 言
信号的定义： 载有信息的，随时间变化的物理量或
物理现象。 信号的分类：
➢ 时域连续信号 ➢ 模拟信号 ➢ 时域离散信号 ➢ 数字信号
4
系统定义： 系统分类： ➢ 时域连续系统 ➢ 模拟系统 ➢ 时域离散系统 ➢ 数字系统
5
一．单位阶跃信号
可加性：Tx1(n) x2 (n) y1(n) y2 (n) 齐次性：Tax1(n) ay1(n)
35
例7、判断y(n)=ax(n)+b(a和b是常数）所代表系统的 线性性质。
解：设输入x1(n)与x2 (n)所对应的输出分别为y1(n)与y2 (n) 设x3(n) m1x1(n) m2x2 (n)，则输出为 y3(n) ax3(n) b am1x1(n) am2 x2 (n) b m1 y1(n) m2 y2 (n) 故系统是非线性的。
| h(n) | | a |n 11| a |
n
n0
| a | 1 | a | 1
| a | 1时，系统稳定；| a | 1时，系统不稳定。
45
1.4 时域离散系统的输入输出描述 法——线性常系数差分方程
N阶线性常系数差分方程表示：
典型信号的卷积
x(n)* (n) x(n)
n
x(n)*u(n) x(m) m
32
例6、设x(n)
n / 2
0
0
n 其他
3，h(n)
3
0
n
0n2 其他
求x(n) * h(n)
果性及稳定性的含义及判别方法。 掌握采样定理。
3
1.1 引 言
信号的定义： 载有信息的，随时间变化的物理量或
物理现象。 信号的分类：
➢ 时域连续信号 ➢ 模拟信号 ➢ 时域离散信号 ➢ 数字信号
4
系统定义： 系统分类： ➢ 时域连续系统 ➢ 模拟系统 ➢ 时域离散系统 ➢ 数字系统
5
一．单位阶跃信号
可加性：Tx1(n) x2 (n) y1(n) y2 (n) 齐次性：Tax1(n) ay1(n)
35
例7、判断y(n)=ax(n)+b(a和b是常数）所代表系统的 线性性质。
解：设输入x1(n)与x2 (n)所对应的输出分别为y1(n)与y2 (n) 设x3(n) m1x1(n) m2x2 (n)，则输出为 y3(n) ax3(n) b am1x1(n) am2 x2 (n) b m1 y1(n) m2 y2 (n) 故系统是非线性的。
| h(n) | | a |n 11| a |
n
n0
| a | 1 | a | 1
| a | 1时，系统稳定；| a | 1时，系统不稳定。
45
1.4 时域离散系统的输入输出描述 法——线性常系数差分方程
N阶线性常系数差分方程表示：
《数字信号处理讲》课件
3
算法优化
FFTW等库提供了优化的FFT算法实现，提高了计算速度和效率。
频域分析方法
频谱分析
频谱分析是对信号的频域特性进行分析，可用于频率成分提取、噪声分析等。
滤波器设计
通过频域分析方法可以设计数字滤波器，实现信号的去噪、增强等处理。
频域采样
频域采样是一种通过对信号频谱的采样来实现快速分析和处理的方法。
噪声
噪声是信号处理中的随机干扰， 会影响信号质量和处理结果。
信噪比
信噪比是衡量信号与噪声强度之 间关系的指标，较高的信噪比表 示较好的信号质量。
噪声降低
噪声降低技术可用于减少噪声对 信号处理结果的影响，提高信号 质量。
数字信号处理应用
1 语音处理
通过数字信号处理技术可以实现语音合成、语音识别、语音增强等应用。
பைடு நூலகம்2 图像处理
数字信号处理在图像处理中可以进行图像增强、边缘检测、目标识别等。
3 音频处理
音频处理包括音频编码、音频特效处理、音频识别等多个方面的应用。
时域分析方法
1
时域信号表示
时域分析是对信号在时间上的变化进行分析，并用时域表示方法进行描述。
2
自相关函数
自相关函数衡量信号的相似性和周期性，可以用于信号的频率分析和滤波。
3
卷积
卷积是时域分析中常用的运算，可以用于信号的滤波、系统响应分析等。
离散傅里叶变换（DFT）
傅里叶变换
傅里叶变换将信号从时域变换到 频域，可用于频域分析和滤波。
离散傅里叶变换
离散傅里叶变换是有限长序列的 傅里叶变换，用于处理离散信号 的频谱分析。
DFT的应用
DFT广泛应用于图像处理、音频 编码、通信系统等领域。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
式中：A为常数，ci和di分别表示H(z)的零点和极点。由于H(z)的
分子和分母都是实系数多项式，而实系数多项式的根只有实根和
共轭复根两种情况。将每一对共轭零点（极点）合并起来构成一
个实系数的二阶因子，并把单个的实根因子看成是二次项系数等
于零的二阶因子，则可以把H(z)表示成多个实系数的二阶数字网
络Hj(z)的连乘积形式， 如式(5-5)
…
aN－ 1
aN
z－ 1 y(n－N)
从图上可以看出，直接Ⅰ型结构需要2N个延时器和
2N+1个乘法器。
5.2.2 直接Ⅱ型
直接Ⅱ型结构又称为正准型结构。由图5-2，直接Ⅰ型结构 的系统函数H(z)也可以看成是两个独立的系统函数的乘积。输 入信号x(n)先通过系统H1(z)，得到中间输出变量y1(n)，然后再 把y1(n)通过系统H2(z)得到输出信号y(n)。 即
H (z) H1(z)H2(z)
M
bi zi
i0 N
1 ai zi
i 1
式中,
M
H1(z) bi zi
i0
对应的差分方程为:
M
y1(n) bi x(n i)
i0
1 H2(z) N
1 ai zi
i 1
对应的差分方程为
N
y(n) ai y(n i) y1(n)
i 1
假设所讨论的IIR数字滤波器是线性非时变系统，显然交换 H1(z)和H2(z)的级联次序不会影响系统的传输效果，即
第5章 数字滤波器的基本结构
5.1 数字滤波器结构的表示方法 5.2 IIR滤波器的基本结构 5.3 FIR滤波器的基本结构
5.1 数字滤波器的结构特点与表示方法
数字滤波器是数字信号处理的一个重要组成 部分。数字滤波实际上是一种运算过程，其功能 是将一组输入的数字序列通过一定的运算后转变 为另一组输出的数字序列，因此它本身就是一台 数字式的处理设备。
:
K
H (z) A H j (z)
(5-5)
j 1
式中：
H j(z)
0 j 1 j z1 2 j z2 1 1 j z1 2 j z2
若每一个实系数的二阶数字网络的系统函数Hj(z)的网络结 构均采用前面介绍的直接Ⅱ型结构，则可以得到系统函数H(z) 的级联型结构，如图5-5所示。
x(n) A
x(n) x(n)
x1(n)
x(n－ 1) z－ 1
ax(n)
a x1(n)＋x2(n)
x(n)
z－ 1
x(n－ 1)
பைடு நூலகம்
x(n)
a
ax(n)
x1(n)
x1(n)＋x2(n)
x2(n)
x2(n)
图 5-1 三种基本运算的流图
5.2 IIR滤波器的结构
5.2.1 直接型（Ⅰ型） 一个N阶的IIR滤波器的输入输出关系可以用如式（5-1）
比较图5-2和图5-4可知: 直接Ⅱ型比直接Ⅰ型结构延时单元 少，用硬件实现可以节省寄存器，比直接Ⅰ型经济；若用软件实 现则可节省存储单元。但对于高阶系统直接型结构都存在调整零、 极点困难，对系数量化效应敏感度高等缺点。
x(n)
b0
y(n)
a1 z－ 1
b1
a2 z－ 1
b2
…
…
… …
…
aN－ 1 aN z－ 1
01
z－ 1
11
11
z－ 1
21
21
…
0K
z－ 1
…
1K
1K
z－ 1
2K
2K
y(n)
图 5-5 级联型结构
在级联型结构中，每一个一阶网络只关系到滤波器的一个 零点、一个极点；每个二阶网络只关系到滤波器的一对共轭零 点和一对共轭极点。调整系数β0j、β1j和β2j只会影响滤波器的第j 对零点，对其他零点并无影响；同样, 调整分母多项式的系数α1j 和α2j也只单独调整了第j对极点。因此，与直接型结构相比， 级 联型结构便于准确地实现滤波器零、极点的调整。此外，因为 在级联结构中，后面的网络的输出不会流到前面，所以其运算 误差也比直接型小。
bN－ 1 bN
图 5-4 直接Ⅱ型结构
5.2.3 级联型
若把式(5-2)描述的N阶IIR滤波器的系统函数H(z)的分子和
分母分别进行因式分解，得到多个因式连乘积的形式
M
M
bi zi
(1 ci z1)
H(z)
i0 N
A
i 1 N
1 ai zi
(1 di z1)
(5-4)
i 1
i 1
M
N
y(n) bi x(n i) ai y(n i)
i0
i 1
则其系统函数，即滤波器的传递函数为
M
bi zi
H(z)
i0 N
1 ai zi
i 1
(5-1) (5-2)
例如：
H (z)
1 1 3z1 2z2
2 1 2z1
1
1 z
1
1
1 2 z 1
1 1 z1
(5-3)
观察式(5-3)可知，对应于每一种不同的运算结构，我们都可 以用三种基本的运算单元：乘法器、加法器和单位延时器来 实现。这三种基本运算单元的常用流图表示方法如图4-1 所 示。
数字滤波器一般可以用两种方法实现：
一种是根据描述数字滤波器的数学模型或信号流 图，用数字硬件装配成一台专门的设备，构成专 用的信号处理机；
另一种方法就是直接利用通用计算机，将所需要 的运算编成程序让计算机来执行， 这也就是用软 件来实现数字滤波器。
数字滤波器是离散时间系统，所处理的信号是离散时间信号。 一般时域离散系统或网络可以用差分方程、单位脉冲响应以及系 统函数进行描述。如果系统输入、输出服从N阶差分方程
所 示的N阶的差分方程来描述。 把式（5-1）重写如下：
M
N
y(n) bi x(n 1) ai y(n i)
i0
i 1
… …
… … …
x(n)
b0
x(n－ 1) z－ 1 b1 x(n－ 2) z－ 1 b2
x(n－N)
bN－ 1 z－ 1 bN
y(n)
a1
z－ 1 y(n－ 1)
a2
z－ 1 y(n－ 2)
H (z) H1(z)H2(z) H2(z)H1(z)
若系统函数H(z)的分子阶数和分母阶数相等，即M=N时，其 结构如图5-3所示。
x(n)
y2(n)
b0
y(n)
a1 a2
z－ 1 z－ 1
y2(n－ )1 y2(n－ )2
z－ 1 b1 z－ 1 b2
…
…
… … … …
aN－ 1 aN z－ 1
y2(n－N)
bN－ 1 z－ 1 bN
图 5-3 直接Ⅰ型的变形结构
输入信号x(n)先经过反馈网络H2(z)，得到中间输出变量
N
y2 (n) ai y2(n i) x(n)
i 1
然后，将y2(n)通过系统H1(z)，得到系统的输出y(n)
M
y(n) bi y2(n i)
i0
结构图5-3中有两条完全相同的对中间变量y2(n)进行延迟的 延时链，我们可以合并这两条延时链，得到如图5-4所示的直接 Ⅱ型结构（图中取M=N）。