[常见几何体]转动惯量公式表
高数转动惯量

高数转动惯量
转动惯量(又称惯性矩)是描述物体绕某一轴旋转的惯性特性的物理量。
对于一个质量均匀分布的物体,其转动惯量可用以下公式计算:
I = ∫r^2 dm
其中,I为转动惯量,r为物体上每一点到旋转轴的距离,dm为物体上每一点的质量元素。
对于一些常见的物体,其转动惯量可以通过已知的几何形状和质量分布来计算。
以下是一些常见物体的转动惯量计算公式:
1. 细棒绕一端旋转:
I = (1/3) * m * L^2
其中,m为细棒的质量,L为细棒的长度。
2. 球体绕直径旋转:
I = (2/5) * m * R^2
其中,m为球体的质量,R为球体的半径。
3. 圆环绕直径旋转:
I = (1/2) * m * R^2
其中,m为圆环的质量,R为圆环的半径。
4. 薄圆盘绕垂直于平面轴旋转:
I = (1/2) * m * R^2
其中,m为圆盘的质量,R为圆盘的半径。
这些公式只是一些常见物体的转动惯量计算公式,对于其他形状的物体,通常需要根据具体几何形状来进行积分计算。
转动惯量公式表
常见几何体]转动惯量公式表对于细杆当回转轴过杆得中点并垂直于杆时;J=m(L^2)/12 其中m就是杆得质量,L就是杆得长度。
当回转轴过杆得端点并垂直于杆时:J=m(L^2)/3 其中m就是杆得质量,L就是杆得长度。
对于圆柱体当回转轴就是圆柱体轴线时;J=m(r^2)/2其中m就是圆柱体得质量,r就是圆柱体得半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1与R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳得切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体得中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体得切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量得计算方式而不能使用就是没有意义得。
下面给出一些(绕定轴转动时)得刚体动力学公式。
角加速度与合外力矩得关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以瞧出这个式子与牛顿第二定律就是对应得。
角动量:角动量刚体得定轴转动动能:转动动能注意这只就是刚体绕定轴得转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体得问题,就是因为其中不包含刚体得任何转动信息,里面得速度v只代表刚体得质心运动情况。
由这一公式,可以从能量得角度分析刚体动力学得问题。
转动惯量(Moment of Inertia)就是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止得特性)得量度,用字母I或J表示。
转动惯量计算公式高数

转动惯量计算公式高数
在高等数学中,转动惯量是描述刚体旋转惯性特性的物理量。
以下是常见的刚体转动惯量计算公式:
1. 点质量绕轴旋转:
转动惯量公式:I = m * r^2
其中,I 表示转动惯量,m 表示点质量,r 表示质点到旋转轴的距离。
2. 细长杆绕轴旋转:
转动惯量公式:I = (1/12) * m * L^2
其中,I 表示转动惯量,m 表示杆的质量,L 表示杆的长度。
3. 薄环绕轴旋转:
转动惯量公式:I = m * r^2
其中,I 表示转动惯量,m 表示环的质量,r 表示环的半径。
4. 薄球壳绕轴旋转:
转动惯量公式:I = (2/3) * m * r^2
其中,I 表示转动惯量,m 表示球壳的质量,r 表示球壳的半径。
5. 均匀圆盘绕轴旋转:
转动惯量公式:I = (1/4) * m * r^2
其中,I 表示转动惯量,m 表示圆盘的质量,r 表示圆盘的半径。
这些公式仅适用于特定形状的刚体,并假设刚体质量分布均匀。
在实际计算中,根据刚体的形状和质量分布,可能需要使用更复杂的积分计算或使用转动惯量表进行查询。
转动惯量手动计算公式

转动惯量1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2iJs J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量gw22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
[常见几何体]转动惯量公式表
![[常见几何体]转动惯量公式表](https://img.taocdn.com/s3/m/0a601c4f910ef12d2bf9e791.png)
[常见几何体]转动惯量公式表
R =严 H + r ?2) h = Iy =
[3 (ti 2 + r 22) + h 2
or when defining the normalized thickness ; fn = t/-r and letting r = 12,
then
h = mr 2 (1 —
打 + 折)
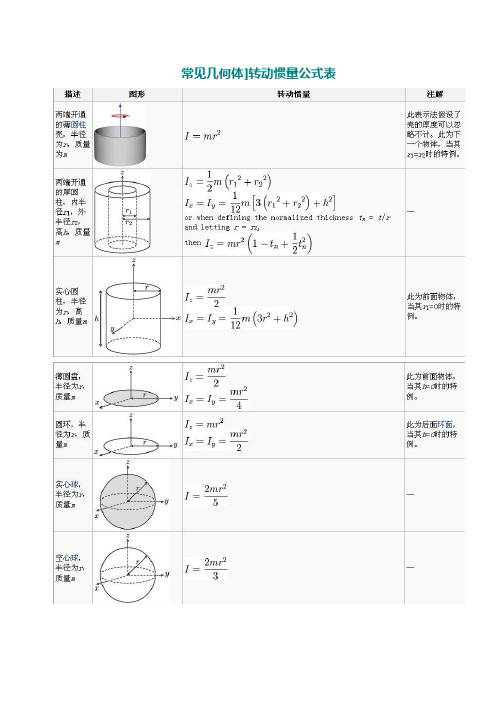
描述 转动惯量 注解
两端开通 的薄圆柱 壳,半径 为口质量 为烟
此表示法假设了
壳的厚度可味忍 略不计。
此为下 一节物体,当其 辺=22时的特例。
霽高
禺
此为前面物体, 当其巧=0时的特
薄圆盘, 半径为确 质量帀
■mr 2
2
此为前面物体,
当其H 朋寸的特 例耘
半成
环为衆 圆径量
此为后面环面费 当其H 邙寸的特 例。
实心球, 半径为邛 质量丹 空心球, 半径为邛 质量帀 2?nr 2
3
两端开通 的厚圆 柱,商半 径巧;外 咼打展量。
转动惯量公式表

常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时; J=m(L9)/12其中m 是杆的质量,L 是杆的长度。
当回转轴过杆的端点并垂直于杆时: J=m(L9)/3其中m 是杆的质量,L 是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时; J=m(r A 2)/2其中m 是圆柱体的质量,r 是圆柱体的半径。
对于细圆环当回转轴为球壳的切线时, R 为球壳半径。
对于实心球体当回转轴为球体的中心轴时, 当回转轴为球体的切线时, R 为球体半径对于立方体当回为其中心轴时, J= ( 1/6 ) mLA2 ; 当回转轴通过中心与环面垂直时, 当回转轴通过边缘与环面垂直时, R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时, 当回转轴通过边缘与盘面垂直时, R 为其半径对于空心圆柱当回转轴为对称轴时, J=( 1/2 R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时, J=( 2/3 J=mRA2 ;J=2mRA2 ;J= ( 1/2 ) mRA2 ;J= ( 3/2 ) mRA2 ;)m[ (R1 ) A2+ ( R2) A2];)mRA2 ;J= ( 5/3 ) mRA2 ;J= ( 2/5 ) mRA2 ;J= ( 7/5 ) mRA2 ;当回转轴为其棱边时,J= ( 2/3 ) mLA2 ;当回转轴为其体对角线时,J= ( 3/16 ) mLA2 ;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外,B为。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量冈M本的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E= (1/2 ) mv A2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
转动惯量公式表
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
转动惯量公式表
转动惯量公式表 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外,β为。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量计算公式
转动惯量计算公式转动惯量(也称为惯性矩或转动惯性)是物体抵抗转动的能力的度量,是物体转动时的一项重要物理性质。
在机械工程、物理学、航空航天等领域中,转动惯量的计算是解决相关问题的关键。
转动惯量可以通过各种形状的物体的质量分布来计算,例如直线、薄片、圆筒、球体等。
不同形状的物体转动惯量的计算公式也有所不同。
在本文中,我们将介绍几种常见形状的物体的转动惯量计算公式。
1. 直线的转动惯量计算公式当物体是一个直线时,其转动惯量可以用关于质量和长度的公式来计算。
以下是直线转动惯量的计算公式:•绕质心轴的转动惯量:$I = \\frac{1}{3} m l^2$•绕端点轴的转动惯量:$I = \\frac{1}{12} m l^2$其中,I是转动惯量,I是物体的质量,I是直线的长度。
2. 圆筒的转动惯量计算公式圆筒是一种常见的物体形状,例如水桶、轮胎等。
对于圆筒的转动惯量计算,有以下公式:•绕质心轴的转动惯量:$I = \\frac{1}{2} m r^2$•绕圆轴的转动惯量:I=II2其中,I是转动惯量,I是圆筒的质量,I是圆筒的半径。
3. 薄片的转动惯量计算公式薄片是一个平面形状的物体,例如纸片、金属片等。
对于薄片的转动惯量计算,有以下公式:•绕质心轴的转动惯量:$I = \\frac{1}{4} m a^2$•绕边缘轴的转动惯量:$I = \\frac{1}{3} m a^2$其中,I是转动惯量,I是薄片的质量,I是薄片的边长。
4. 球体的转动惯量计算公式球体是一个球形物体,例如篮球、乒乓球等。
对于球体的转动惯量计算,有以下公式:•绕质心轴的转动惯量:$I = \\frac{2}{5} m r^2$•绕直径轴的转动惯量:$I = \\frac{2}{3} m r^2$其中,I是转动惯量,I是球体的质量,I是球体的半径。
5. 其他形状的转动惯量计算公式除了上述常见形状的物体,其他形状的转动惯量计算公式也可以通过积分或者几何关系得到。
常用转动惯量公式
常用转动惯量公式
常用转动惯量表达式:I=mr2。
其中m是其质量,r是质点和转轴的垂直距离。
转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度。
扩展资料
转动惯量计算公式
1、对于细杆:
当回转轴过杆的中点(质心)并垂直于杆时I=mL2/I2;其中m是杆的'质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时I=mL2/3;其中m是杆的质量,L是杆的长度。
2、对于圆柱体:
当回转轴是圆柱体轴线时I=mr2/2;其中m是圆柱体的质量,r 是圆柱体的半径。
3、对于细圆环:
当回转轴通过环心且与环面垂直时,I=mR2;当回转轴通过环边缘且与环面垂直时,I=2mR2;I=mR2/2沿环的某一直径;R为其半径。
4、对于立方体:
当回转轴为其中心轴时,I=mL2/6;当回转轴为其棱边时I=2mL2/3;当回转轴为其体对角线时,I=3mL2/16;L为立方体边长。
5、对于实心球体:
当回转轴为球体的中心轴时,I=2mR2/5;当回转轴为球体的切线时,I=7mR2/5;R为球体半径。
向你推荐的相关文章
相关文章列表
微信扫码分享。
