第二讲流体静力学资料重点
流体力学2资料重点

第二章 流体静力学
第二章 流体静力学
§2-1 静止流体的应力特征 §2-2 流体平衡的微分方程及其积分 §2-3 重力作用下流体静压强的分布规律 §2-4 流体压强的量测
第二章 流体静力学
§2-5
液体的相对平衡
§2-6 静止液体作用在平面上的总压力
§2-7 静止液体作用在曲面上的总压力
不同液体,大截面杯的直径D=100mm,U形管的直径
Hale Waihona Puke d=10mm,测得h=30mm,计算两杯内的压强差为多少?
【解】 列1—2截面上的等压面方程
p1 1gh1 p2 1g(h2 h1 h) 2 gh
由于两边密度为ρ1的液体容量相等,所以D2h2=d2h,代入
上式得
p1
p2
2 g
1
d2 D2
当四面体的体积趋于零时,可证得px= py=pz=pn
即
p=p(x,y,z)
§2-2 流体的平衡微分方程及积分
一、流体的平衡微分方程
在平衡流体中取如图所示微小正交六面体。分析六面
体在x、y、z方向所受外力,列平衡方程,整理化简得
fx
1
p x
0
fy
1
p y
0
1 p
fz z 0
上式也可用矢量方程表示:
f
1
p
0
上式即为流体的平衡微分方程,亦称欧拉平衡微分方程。 对不可压缩和可压缩流体均适用。
二.流体平衡微分方程的积分
将欧拉平衡微分方程各分式分别乘以dx、dy、dz,然后相
加,得
p dx x
p dy y
p dz z
(
fxdx
f ydy
流体力学讲义 第二章 流体静力学资料

第二章流体静力学作用在流体上的力有面积力与质量力。
静止流体中,面积力只有压应力——压强。
流体静力学主要研究流体在静止状态下的力学规律:它以压强为中心,主要阐述流体静压强的特性,静压强的分布规律,欧拉平衡微分方程,等压面概念,作用在平面上或曲面上静水总压力的计算方法,以及应用流体静力学原理来解决潜体与浮体的稳定性问题等。
第一节作用于流体上的力一、分类1.按物理性质的不同分类:重力、摩擦力、惯性力、弹性力、表面张力等。
2.按作用方式分:质量力和面积力。
二、质量力1.质量力(mass force):是指作用于隔离体内每一流体质点上的力,它的大小与质量成正比。
对于均质流体(各点密度相同的流体),质量力与流体体积成正比,其质量力又称为体积力。
单位牛顿(N)。
2.单位质量力:单位质量流体所受到的质量力。
(2-1) 单位质量力的单位:m/s2 ,与加速度单位一致。
最常见的质量力有:重力、惯性力。
问题1:比较重力场(质量力只有重力)中,水和水银所受的单位质量力f水和f水银的大小?A. f水<f水银;B. f水=f水银;C. f水>f水银;D、不一定。
问题2:试问自由落体和加速度a向x方向运动状态下的液体所受的单位质量力大小(fX. fY. fZ)分别为多少?自由落体:X=Y=0,Z=0。
加速运动:X=-a,Y=0,Z=-g。
三、面积力1.面积力(surface force):又称表面力,是毗邻流体或其它物体作用在隔离体表面上的直接施加的接触力。
它的大小与作用面面积成正比。
表面力按作用方向可分为:压力:垂直于作用面。
切力:平行于作用面。
2.应力:单位面积上的表面力,单位:或图2-1压强(2-2)切应力(2-3) 考考你1.静止的流体受到哪几种力的作用?重力与压应力,无法承受剪切力。
2.理想流体受到哪几种力的作用?重力与压应力,因为无粘性,故无剪切力。
第二节流体静压强特性一、静止流体中任一点应力的特性1.静止流体表面应力只能是压应力或压强,且静水压强方向与作用面的内法线方向重合。
第02章流体静力学资料讲解
Py (pah)dAcos (pah)dAy
A
A
pa Ay hdAy paAyhcAy
A
若不计大气压作用 Py hc Ay
29
合压力在z方向的分量:
dPz=(pa+γh)dA cos(z,n)=(pa+γh) dAz
Pz (pah)dAcos (pah)dAz
解 各段的压力分布如图所示。 AB段:由平板受力公式得合力的大小及作用点
RAB ghc S
9.8103 0.512
4.9103N
25
2.6.1 例题
y ABcp
y ABc
I y ABc S
13 / 12 2
0.5
0.5 12
m 3
即作用线在距水面2/3处,垂直指向平板AB内侧。
BC段:由式(2.11)得合力的大小为
函数U=U(x,y,z),它满足:
X d x Y d y Z d z d U U d x U d y U d z x y z
比较dx、dy和dz前面的系数,可得:
X U x
Y U y
Z U z
(2-3)
U称为质量力函数 4
等压面: 压力相等的各点 等压面特性:
所组成的面 即在该面上,
即作用线在距O点1.96m处,垂直指向平板BC内侧。 26
2.6 例题 CD段:由式(2.11)得
R C D g c S h 9 . 8 1 3 ( 1 0 2 /2 ) 2 1 3 . 3 1 5 4 N 0
作用线在的中点且垂直向上。
27
§2-5 静止流体对曲面的作用力
1. 总压力的水平分量:
左 得右:两边分别同乘2-以1同欧dx上,拉d微y,分dz方,然程后相加,
第二章 流体静力学

h
h
一、解析法
如图所示,静止液体中有一倾斜放置的平面MN,试求作用 在该平面上的总压力。
1)粗线MN代表其侧视图,正面投影为绕其对称轴转90 度 2)平面MN的延伸面与自由液面的交角为;
3)坐标系:ox轴为平面MN的延伸面与自由液面的交线;
二、欧拉平衡微分方程的全微分形式
p X
x ×dx
p Y
y
×dy
p Z
z
×dz
p dx p dy p dz ( Xdx Ydy Zdz)
x y z
p p(x, y, z) dp p dx p dy p dz x y z
通常作用在流体上的单位 质量力是已知的,利用上 式便可求得流体静压强的 分布规律。
yD
sin Iox
P
sin Iox hc A
sin Iox yc sin A
I ox yc A
引入平行移轴公式 Iox Ic Ayc2
yD
I ox yc A
Ic yc2 A yc A
yc
Ic yc A
由此可知,压力中心D必位于受压面形心c之下。
说明:
工程中常见的受压平面多具有轴对称性(对称轴与
当流体存在真空时,工程习惯上用真空度(负压)表示。
真空
pv pabs pa
道 路
三者关系
当p>pa 时,绝对压强=表压强+当地大气压 当p<pa 时,绝对压强=当地大气压-真空度
p 表压强
p>pa 真空度
当地大气压 pa
绝对压强
p<pa
绝对真空 p=0
流体静力学专业知识讲座

EXIT
本章所得旳结论,对理想流体或实际流体都是合用旳。
作匀加速运动小车
第2章 流体静力学
【学习重点、难点】重点: 1.流体静压强及其特征,静止液体中旳压强计算。 2.流体作用在壁面上旳液体总压力。难点: 1、计算流体作用在曲面上总压力时虚压力体旳拟定。 2、两种以上不同液体对壁面总压力旳计算。
二、 流体静压强旳特征
流体静压强特征: (1)流体静压强旳方向必然重叠于受力面旳内法线方向。 反证法:
EXIT
第2章 流体静力学(hydrostatics)
2.1 流体静压强及其特征
(2)平衡流体中任意点旳静压强值只由该点旳坐标位置决定,而与该压强旳作用方向无关。 即: 第二特征证明留作参照题,详见书后参照文件3
Conclusions:平衡流体微团旳质量力与表面力不论在任何方向上都应保持平衡,即质量力与该方向上表面力旳合力应该大小相等,方向相反。
同理,沿
轴得
轴得
沿
知识沿拓
1.误差旳实质:近似替代。2.欧拉,L. ( Leonhard Euler 1707-1783)瑞士数学家、力学家。
function)。
例如,重力、惯性力等都是有势力。
对 式积分得
积分常数
流体平衡微分方程旳积分式。 已知 = f( ),可求任意点旳 。它表达了平衡流体中旳压强分布规律。
EXIT
三、等压面(equipressure surface)
在平衡流体中,压强相等旳各点所构成旳面称为等压面。
EXIT
对不可压缩流体,
为常量,上式右边括号内亦应是某一坐标函数旳
全微分。设此函数为
,则
பைடு நூலகம்对比能够看出
流体力学流体静力学
增大
流体力学
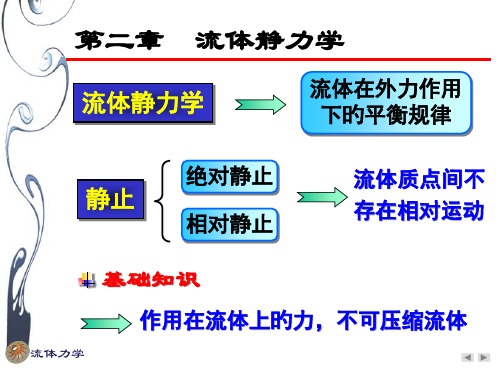
U型管测压计2
U型管测压计特点 测量范围较大 可测量气体压强
pAm 2 gh2 1gh1 2 gh2 可测量真空压强 指示液不能与被测液体掺混
流体力学
差压计
流体力学
pA pB 2 gh2 3 gh3 1gh1
倾斜式测压计(微压计)
一般用来测量气体压强
pAm 2 gl sin 1 gh1
倾斜管放大了测量距
离,提升了测量精
度
l h
1
sin
流体力学
等角速转动液体平衡
非惯性系,相对静止问题
流体相对于运动坐标系静止,质点间无 相对运动,流体与器壁间也无相对运
动 相对静止平衡微分方程
f
1
p
0
流体力学
相对静止平衡微分方程
g
a
1
p
0
取 z 轴垂直向上,其分量形式为
流体力学
ax ay
1
1
p x p y
0 0
g
az
1
p z
0
等角速转动液体旳平衡1
1 p
ax
x
0
ay
1
p y
0
g
az
1
p z
0
z
流体力学
x
θ
ay
ax y ar
等角速转动液体旳平衡2
dp 2 xdx 2 ydy gdz
等压面
z 2 r2 C
加旳力矩大小设水密
度 = 1000kg / m3,
壁面倾斜角为60º
流体力学
平面上旳流体静压力-例题1
解:1) 闸门所受总压力
第二章流体静力学yc课件

f F Fx i Fy j Fz k X i Y j Z k mm m m
设作用在流体上的质量 力只有重力,则:
X=0, Y=0, Z=-mg/m=-g
z p dz
o dy
x
p p d y y
dx y
如果容器内的液体是静
止的,一根测压管测得
的测压管水头也就是容
器内液体中任何一点的
pA /
测压管水头。如接上多
根测压管,则各测压管
中的液面都将位于同一
zA
水平面上。
O
pB /
zB
O
24
流体静力学基本方程的意义
• 敞口容器和封口容器接上测压管后的情况如图
25
流体静力学基本方程的意义
二、能量意义
z 位置势能,mgz
表 OBC 面
力 OAB
px
1 2
dydz
pz
1 2
dxdy
OAC ABC
p
y
1 2
dzdx
pn An
质量力
X 1 dxdydz
6
Y 1 dxdydz
6
Z 1 dxdydz
6
对于x轴,∑Fx=0,则
px
1 2
dydz
pn An
cos(n, x)
X
1 6
dxdydz
0
6
第二节 流体的静压力及其特性
三、 静压力的测量 1. 测压管
pA pa hA
N / m2
A点的压强
当地大气压
在该方程式中pA和pa应有相同的计量 基准,所以当pa =0时pA为相对压强。
水力学(工程流体力学)流体静力学要点总结

第二章 流体静力学•静水压强特性:(1)第一特性:静水压强的方向与作用面的内法线方向重合(2)第二特性:静止流体中某一点静水压强的大小与作用面的方位无关(只与深度位置有关)•流体平衡微分方程:⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂⋅-=∂∂⋅-=∂∂⋅-010101z p Z y p Y x p X ρρρ流体处于平衡状态时,作用于流体上的质量力与压强递增率间的关系 用途:质量力已知时,用该式求静止流体内的压强分布规律)(Zdz Ydy Xdx dp ++=ρ dz zW dy y W dx x W dW ∂∂+∂∂+∂∂= 势函数;有势的力zW Z y W Y x W X ∂∂=∂∂=∂∂=;; dW dp ρ= 积分得:p W C ρ=+ 当某点压强0p 、力的势函数0W 已知时(即边界条件已知)得 00()p p W W ρ=+-•静水压强分布规律:〖一〗 'pC z C γγ+== 或 1212p p z z γγ+=+z :单位重量流体具有的位能或位置水头;γp:单位重量流体具有的压能或压强水头; γp z +:单位重量流体具有的总势能或测压管水头(测压管液面相对于基准面的高度);C p z =+γ: 表明静止流体中单位重量流体具有的总势能守恒或测压管水头为常数物理意义:静止液体中各点单位重量液体具有的总势能相等几何意义:静止液体中各点的测压管水头相等,测压管水头线是水平线从能量意义上来说:静止流体中各点的位置水头与压强水头之和都相等,或者静止流体中各点的测压管水头线为一水平线。
〖二〗边界条件:0z z =时,0p p =则0p p h γ=+•22/10132533.107601m N O mH mmHg atm ===(标准大气压)22/98070107361m N O mH mmHg at ===(工程大气压)•压强表示方法:绝对压强:绝对真空状态做为压强起始计算零点,以abs p 表示;相对压强:一个大气压做为压强起始计算零点,以p 表示;•等压面及其性质:①等压面与质量力正交②水平面是等压面的条件:由于等压面与质量力正交,静止流体中等压面是水平面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fx 0
p x
fx
x
y
2-2 静止流体的平衡微分方程
同理可得
p x
fx
p y
fy
p z
fz
Euler presented in 1775.
欧拉平衡微分方程式
物理意义:
平衡流体中,某一 点的压强沿某一方 向的变化率与该方 向的单位体积上的 质量力相等。
2-2 静止流体的平衡微分方程
p x
fx
dx
提示:p(x,y,z) 为坐标的连续函数 ——多元函数的太勒级数
p( x x, y y, z z)
p( x,
y, z) ( p x
x
p y
y
p z) z
1( 2!
2 p x 2
x2
2 p y2
y2
2 p z 2
z2
2 p xy
xy
2 p yz
yz
2 p zx
zx
)
2-2 静止流体的平衡微分方程
p p0 h 重力作用下的液体平衡方程式
任意点的压强有两部分组成:
1)自由面(表面)上的气体压强 p0,它等值地 传到液体内部各点。
2)在液面下的深度与容重的乘积 γ h . 相当于 单位面积上,高度为 h 水柱重量。
2-3 重力作用下静水压强的基本公式
p p0 h
静水压强分布规律
1. 静水压强的分布是按直线分布的。
2-1 静水压强及其特性
1. 静水压力与静水压强
静水压力: 静止液体作用在与之接 触的表面上的水压力 P
静水压强: 当 A 0 时,
p lim P A0 A
2-1 静水压强及其特性
2. 静水压强的特性 特性一:
压强垂直作用面,且沿内法线方向. 或
静水压强的方向与受压面垂直,并 指向受压面
2-1 静水压强及其特性
g dz dz
z
两端积分
平衡微分方程式的积分形式
o
p z c
y
p0 x
2-3 重力作用下静水压强的基本公式
p z c
代入边界条件
z 0, p p0, c p0 z
任意一点
z h, p h p0
p p0 h
o yh
p0 x
2-3 重力作用下静水压强的基本公式
• 绝对静止状态
• 相对平衡状态
流体质点间不存在相对运动
流体力学
平衡流体相互之间没有相对运动,流体不呈现 粘性,作用在流体上的表面力只有法向的静压强。
本章主要任务:
➢ 流体静压强在空间的分布规律
本讲内容
2-1 静水压强及其特性 2-2 静止流体的平衡微分方程 2-3 重力作用下静水压强的基本公式 2-4 绝对压强与相对压强 2-5 压强的表示法,水头与测压管
z
在平衡液体中取一微小六面体,
各边分别与坐标轴平行,其边长
dy
为 dx, dy, dz .
dz A(x,y,z)
设六面体中心点为 A(x,y,z) y
该点压强为 p(x,y,z) x
考虑微团的平衡,建立平衡方程
2-2 静止流体的平衡微分方程
问题:微元体各面上的表面力大小?
思路:将表面点的压强用已知点 p(x,y,z) 的压强表示 how ?
dy
坐标为 A(x dx , y, z ) 2
dz A(x,y,z)
压强为 p" ( p p dx )
y
x 2 x
2-2 静止流体的平衡微分方程
在 x 方向上:
表面力
(
p
p x
dx )dydz 2
( p
p
dx )dydz
() ()
z
x 2
dz
质量力 dx dy dz f x
dy A(x,y,z)
在 x 方向上:
前平面中心点的坐标增量为:
z
x dx , y 0, z 0
dy
2
坐标为 A(x dx , y, z ) 2
dz A(x,y,z)
压强为 p ' ( p p dx )
y
x 2 x
2-2 静止流体的平衡微分方程
在 x 方向上:
后平面中心点的坐标增量为:
z
x dx , y 0, z 0 2
2. 静水中等压面是水平面。
思考:
➢ 船在水库中, 坝或堤的静水压强是否会增加 ? ➢ 水杯饮料加冰块,随冰块融化水杯的静水压强是否
变化?
2-4 绝对压强与相对压强
绝对压强
以设想没有大气压强存在的绝对真空状态作为零点
流体动力学仿真
电子科技大学 机械电子工程学院
第二讲 流体静力学
Lecture 2 Fluid Statics
流体力学
Fluid Dynamics 研究运动流体的机械运动规律
Fluid Kinematics 流体运动状态的描述
Fluid Statics
研究静止流体的受力平衡规律
粘滞力是否 起作用 ?
2. 静水压强的特性 特性二:
任一点静水压强的大小与受压面方向无关 或
作用与同一点上各方向静水压强大小相等 与作用面方向无关
2-1 静水压强及其特性
2. 静水压作用于静止流体上的力:
fx
质量力 fy
fz
表面力 平衡时
p0
0
关系 ?
2-2 静止流体的平衡微分方程
2-2 静止流体的平衡微分方程
等压面: 液体中压强相等的各点所组成的面。
由液体平衡微分方程:
dp ( f xdx f ydy fzdz)
在等压面上 p = const , dp = 0
( f xdx f ydy fzdz) 0
——等压面方程
2-2 静止流体的平衡微分方程
等压面: 液体中压强相等的各点所组成的面。
2)自由表面就是等压面。 3)不同流体的交界面一定是等压面。
2-3 重力作用下静水压强的基本公式
条件: 作用于液体的质量力——只有重力
单位质量力
fx 0 fy 0
G fz M g
z
o y
p0 x
2-3 重力作用下静水压强的基本公式
代入平衡微分方程式
dp ( f xdx f ydy fzdz)
性质1-
在平衡液体中等压面即为等势面。 (——作用于液体上的质量力必须是
有势力液体才能保持平衡)
性质2- 等压面与质量力正交。
2-2 静止流体的平衡微分方程
等压面: 液体中压强相等的各点所组成的面。
常见的等压面:
1)如果液体在重力场中处于静止状态,等压面 ? 局部范围而言:水平面。 大范围而言:处于与地心引力成正交的曲面。
p y
fy
dy
p z
fz
dz
p dx x
p dy p dz y z
( f xdx
f ydy
f z dz )
2-2 静止流体的平衡微分方程
p dx x
p dy y
p dz
z
(
f xdx
f ydy
f z dz )
左端是关于 p(x,y,z) 的全微分
dp ( fxdx f ydy fzdz)
