求解方程组的正交差分进化算法

合集下载

差分进化算法

差分进化算法简介差分进化算法是一种优化算法，源于遗传算法，通过模拟生物进化的过程来解决优化问题。

它不同于传统的遗传算法，是基于个体间的差异性来实现优化的。

差分进化算法的原理差分进化算法的基本原理是通过在候选解向量上进行简单算术运算来生成新的解向量，并通过比较这些解向量的适应度来更新种群。

差分进化算法包括三个关键步骤:1. 初始化种群: 初始种群是随机生成的一组解向量。

2. 变异操作: 通过选择多个解向量，并对它们进行简单算术运算来产生新的解向量。

3. 交叉和选择: 通过比较原解向量和新解向量的适应度来决定是否更新种群。

差分进化算法的优势1.不需要求导: 差分进化算法不需要求解目标函数的梯度，适用于解决非线性、非光滑和高维优化问题。

2.全局最优: 由于其能够维持种群的多样性，因此差分进化算法往往可以找到全局最优解。

3.较少参数设置: 差分进化算法相对于其他优化算法来说，参数配置相对较少，并且对初始参数不敏感。

差分进化算法的应用差分进化算法被广泛应用于各种领域，包括工程优化、机器学习、信号处理等。

1. 工程优化: 在电力系统、通信网络、管道设计等领域，差分进化算法被用来优化系统设计和参数。

2. 机器学习: 在神经网络训练、特征选择、模型调优等方面，差分进化算法常用于搜索最优解。

3. 信号处理: 在图像处理、语音识别、生物信息学等领域，差分进化算法被应用于信号处理和数据分析。

结论差分进化算法作为一种优化算法，通过模拟生物进化的过程，能够有效地解决各种优化问题。

其独特的优势使其在工程、机器学习、信号处理等领域广泛应用。

未来随着算法的不断改进和扩展，差分进化算法将发挥更大的作用，为解决复杂问题提供新的解决方案。

参考文献1.Storn, R., & Price, K. (1997). Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, 11(4), 341-359.2.Das, S., & Suganthan, P. N. (2011). Differential evolution: a survey of the state-of-the-art. IEEE Transactions on evolutionary computation, 15(1), 4-31.。

差分进化算法的几个公式

差分进化算法的几个公式差分进化算法（Differential Evolution, DE）是一种优化算法，通常用于解决函数优化问题。

以下是差分进化算法中的几个关键公式：1.生成新个体的公式：对于每个待优化的参数x_j，新个体u_i在第t+1代的值可以通过如下公式计算得到：u_{ij} = x_{r_1j} + F \cdot (x_{r_2j} - x_{r_3j})其中，u_{ij}表示新个体u_i的第j个参数的值，x_{r_1j}、x_{r_2j}、x_{r_3j}分别表示当前代第r_1、r_2、r_3个个体的第j个参数的值（r_1、r_2、r_3是不同的随机整数），F为控制变异程度的参数。

2.选择操作的公式：对于新个体u_i和原个体x_i，如果新个体的适应度函数值f(u_i)优于原个体的适应度函数值f(x_i)，则新个体u_i取代原个体x_i。

3.控制变异程度的公式：常见的控制变异程度的公式是：F_{t+1} = F_t \cdot (1 + rand(-1, 1))其中，F_{t+1}表示第t+1代的控制变异程度参数，F_t表示第t 代的控制变异程度参数，rand(-1, 1)表示在[-1, 1]之间均匀分布的随机数。

除了上述公式，差分进化算法还可以根据具体问题和设计需求进行一些拓展和改进。

例如，可以引入交叉操作，将生成的新个体与原个体进行交叉以产生子代。

常见的交叉操作包括二进制交叉、指数交叉等。

另外，还可以引入种群大小的变化机制，例如采用不同的选择策略，通过选择一些不适应的个体进行淘汰或保留最优的个体。

此外，差分进化算法还可以通过调整参数和策略来提高性能，如采用自适应调整参数的方法、引入多目标优化的技术等。

总体而言，差分进化算法具有很好的可拓展性，可以根据问题的特点和求解需求进行灵活的改进和扩展。

差分进化算法DE-DifferentialEvolution

差分进化算法DE-DifferentialEvolution差分进化算法 (Differential Evolution)Differential Evolution（DE）是由Storn等⼈于1995年提出的，和其它⼀样，DE是⼀种模拟⽣物进化的，通过反复，使得那些适应环境的个体被保存了下来。

但相⽐于进化算法，DE保留了基于种群的全局搜索策略，采⽤实数编码、基于差分的简单变异操作和⼀对⼀的竞争⽣存策略，降低了遗传操作的复杂性。

同时，DE特有的记忆能⼒使其可以动态跟踪当前的搜索情况，以调整其搜索策略，具有较强的全局收敛能⼒和，且不需要借助问题的特征信息，适于求解⼀些利⽤常规的数学规划⽅法所⽆法求解的复杂环境中的优化问题。

⽬前，DE已经在许多领域得到了应⽤，譬如⼈⼯⽹络、化⼯、电⼒、机械设计、机器⼈、信号处理、⽣物信息、经济学、现代农业、⾷品安全、环境保护和运筹学等。

DE算法-作者⽹站:维基百科资料库 :DE 算法主要⽤于求解的全局优化问题，其主要⼯作步骤与其他基本⼀致，主要包括变异(Mutation)、交叉(Crossover)、选择(Selection)三种操作。

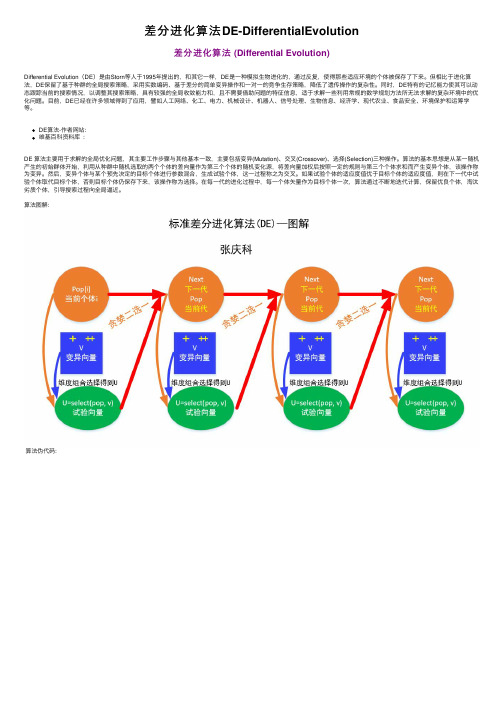
算法的基本思想是从某⼀随机产⽣的初始群体开始，利⽤从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源，将差向量加权后按照⼀定的规则与第三个个体求和⽽产⽣变异个体，该操作称为变异。

然后，变异个体与某个预先决定的⽬标个体进⾏参数混合，⽣成试验个体，这⼀过程称之为交叉。

如果试验个体的适应度值优于⽬标个体的适应度值，则在下⼀代中试验个体取代⽬标个体，否则⽬标个体仍保存下来，该操作称为选择。

在每⼀代的进化过程中，每⼀个体⽮量作为⽬标个体⼀次，算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，引导搜索过程向全局逼近。

算法图解:算法伪代码:算法C代码:1//********************************************************/2// DE/rand/1/bin --差分进化算法-(基本类型)3//********************************************************/456 #include <stdlib.h>7 #include <stdio.h>8 #include <time.h>9 #include <float.h>1011/* Function definitions */1213double func(double *);14int usage(char *);1516/* Random number generator defined by URAND should return17double-precision floating-point values uniformly distributed18over the interval [0.0, 1.0) */1920#define URAND ((double)rand()/((double)RAND_MAX + 1.0))2122/* Definition for random number generator initialization */2324#define INITRAND srand(time(0))2526/* Usage for the program */2728int usage(char *str)29 {30 fprintf(stderr, "Usage: %s [-h] [-u] [-s] [-N NP (20*D)] ", str);31 fprintf(stderr, "[-G Gmax (1000)]\n");32 fprintf(stderr, "\t[-C crossover constant, CR (0.9)]\n");33 fprintf(stderr, "\t[-F mutation scaling factor, F (0.9)]\n");34 fprintf(stderr, "\t[-o <outputfile>]\n\n");35 fprintf(stderr, "\t-s does not initialize random number generator\n");36 exit(-1);37 }383940int main(int argc, char **argv)41 {42 register int i, j, k, r1, r2, r3, jrand, numofFE = 0;43extern int D;44extern double Xl[], Xu[];4546int NP = 20 * D, Gmax = 1000, c, index = -1, s = 1;4748double **popul, **next, **ptr, *iptr, *U, CR = 0.9, F = 0.9,4950 min_value = DBL_MAX, totaltime = 0.0;5152char *ofile = NULL;5354 FILE *fid;55 clock_t starttime, endtime;565758/* Parse command line arguments given by user */5960for (i = 1; i < argc; i++)61 {62if (argv[i][0] != '-')63 usage(argv[0]);6465 c = argv[i][1];6667switch (c)68 {69case'N':70if (++i >= argc)71 usage(argv[0]);7273 NP = atoi(argv[i]);74break;75case'G':76if (++i >= argc)77 usage(argv[0]);7879 Gmax = atoi(argv[i]);80break;81case'C':82if (++i >= argc)83 usage(argv[0]);8485 CR = atof(argv[i]);86break;87case'F':88if (++i >= argc)89 usage(argv[0]);9091 F = atof(argv[i]);92break;93case'o':94if (++i >= argc)95 usage(argv[0]);9697 ofile = argv[i];98break;99case's': /* Flag for using same seeds for */100 s = 0; /* different runs */101break;102case'h':103case'u':104default:105 usage(argv[0]);106 }107 }108109if (s) INITRAND;110111/* Printing out information about optimization process for the user */ 112113 printf("Program parameters: ");114 printf("NP = %d, Gmax = %d, CR = %.2f, F = %.2f\n",115 NP, Gmax, CR, F);116117 printf("Dimension of the problem: %d\n", D);118119120/* Starting timer */121122 starttime = clock();123124125/* Allocating memory for current and next populations, intializing126 current population with uniformly distributed random values and127 calculating value for the objective function */128129130// NP:种群⼤⼩, Gmax:迭代次数, CR:交叉概率, F:扰动向量的缩放因⼦131132//当前种群133 popul = (double **)malloc(NP*sizeof(double *));134if (popul == NULL) perror("malloc");135136//下代种群137 next = (double **)malloc(NP*sizeof(double *));138if (next == NULL) perror("malloc");139140//当前种群popul[NP][D+1]141for (i = 0; i < NP; i++)142 {143//个体维度空间分配144 popul[i] = (double *)malloc((D + 1)*sizeof(double));145if (popul[i] == NULL) perror("malloc");146147//初始化维度值148for (j = 0; j < D; j++)149 popul[i][j] = Xl[j] + (Xu[j] - Xl[j])*URAND;150151//最后的元素内存放该个体的适应度值152 popul[i][D] = func(popul[i]);153154 numofFE++;//统计评估次数155156//下⼀代个体空间分配157 next[i] = (double *)malloc((D + 1)*sizeof(double));158if (next[i] == NULL) perror("malloc");159 }160161/* 为实验向量分配空间--Allocating memory for a trial vector U */ 162163 U = (double *)malloc((D + 1)*sizeof(double));164if (U == NULL) perror("malloc");165166167/* The main loop of the algorithm */168169for (k = 0; k < Gmax; k++)170 {171172for (i = 0; i < NP; i++) /* Going through whole population */173 {174175/* Selecting random indeces r1, r2, and r3 to individuls of176 the population such that i != r1 != r2 != r3 */177178//1.选择三个互不相同的随机个体r1,r2,r3179do180 {181 r1 = (int)(NP*URAND);182 } while (r1 == i);183184do185 {186 r2 = (int)(NP*URAND);187 } while (r2 == i || r2 == r1);188do189 {190 r3 = (int)(NP*URAND);191 } while (r3 == i || r3 == r1 || r3 == r2);192193 jrand = (int)(D*URAND);194195/* Mutation and crossover */196//2. 执⾏变异和交叉操作197for (j = 0; j < D; j++)198 {199//执⾏⼆项式交叉200if (URAND < CR || j == jrand)201 {202//试验向量部分来⾃变异后的向量203 U[j] = popul[r3][j] + F*(popul[r1][j] - popul[r2][j]);204 }205else206//试验向量部分来⾃个体i207 U[j] = popul[i][j];208 }209//3. 计算新⽣成向量的适应度值210 U[D] = func(U);211212 numofFE++;213214/* Comparing the trial vector 'U' and the old individual215 'next[i]' and selecting better one to continue in the216 next population.注意:空间的交替变换和使⽤ */217218//贪婪策略从试验向量U和当前个体i中选择⼀个好的放⼊到下⼀代个体中219if (U[D] <= popul[i][D])//新向量好220 {221222//试验向量U⽜逼, next指向当前的试验向量U,u指向next, ⽅法:指针交换223 iptr = U;224 U = next[i];225 next[i] = iptr;226 }227else//原始向量⽜逼, next指向个体i, ⽅法: 直接拷贝228 {229for (j = 0; j <= D; j++)230 next[i][j] = popul[i][j];231 }232233 } /* End of the going through whole population */234235236/* Pointers of old and new populations are swapped */237//指针交换,各指针指向的空间发⽣变化238 ptr = popul;239 popul = next;240 next = ptr;241242 } /* End of the main loop */243244245/* Stopping timer */246247 endtime = clock();248 totaltime = (double)(endtime - starttime);249250251/* If user has defined output file, the whole final population is252 saved to the file */253254if (ofile != NULL)255 {256if ((fid = (FILE *)fopen(ofile, "a")) == NULL)257 {258 fprintf(stderr, "Error in opening file %s\n\n", ofile);259 usage(argv[0]);260 }261262for (i = 0; i < NP; i++)263 {264for (j = 0; j <= D; j++)265 fprintf(fid, "%.15e ", popul[i][j]);266 fprintf(fid, "\n");267 }268 fclose(fid);269 }270271/* Finding best individual */272273for (i = 0; i < NP; i++)274 {275if (popul[i][D] < min_value)276 {277 min_value = popul[i][D];278 index = i;279 }280 }281282/* Printing out information about optimization process for the user */283284 printf("Execution time: %.3f s\n", totaltime / (double)CLOCKS_PER_SEC);285 printf("Number of objective function evaluations: %d\n", numofFE);286287 printf("Solution:\nValues of variables: ");288for (i = 0; i < D; i++)289 printf("%.15f ", popul[index][i]);290291 printf("\nObjective function value: ");292 printf("%.15f\n", popul[index][D]);293294295/* Freeing dynamically allocated memory */296297for (i = 0; i < NP; i++)298 {299free(popul[i]);300free(next[i]);301 }302free(popul);303free(next);304free(U);305306return(0);307 }经典⽂献:[1] Storn, R., "Designing Nonstandard Filters with Differential Evolution, IEEE Signal Processing Magazine, january 2005, pp. 103 - 106.[2] Storn, R., "Sytem Design by Constraint Adaptation and Differential Evolution", IEEE Trans. on Evolutionary Computation, 1999, Vol. 3, No. 1, pp. 22 - 34.[3] Storn, R. and Price, K., "Differential Evolution - a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces", Journal of Global Optimization, Kluwer Academic Publishers, 1997, Vol. 11, pp. 341 - 359.[4] Gitsels, M. and Storn, R., Internet-Videotelephonie nach dem H.323-Standard, ITG-Fachbericht 144, 7. Dortmunder Fernsehseminar, pp. 87 - 92.[5] Storn, R., , Technical Report TR-96-046, ICSI, November 1996, .[6] Storn, R., , Technical Report TR-96-039, ICSI, November 1996, .[7] Price, K. and Storn, R., "Differential Evolution: Numerical Optimization Made Easy", Dr. Dobb's Journal, April 97, pp. 18 - 24.[8] Storn, R., NAFIPS 1996, Berkeley, pp. 519 - 523.[9] Storn, R. and Price, K., IEEE Conference on Evolutionary Computation, Nagoya, 1996, pp. 842 - 844.[10] Storn, R., (IEEE Signal Processing Letters, Vol. 3, No. 8, August 1996, pp. 242 - 244), Technical Report TR-95-061, ICSI, September 1995, .[11] Storn, R., IEEE International Conference on Evolutionary Computation ICEC 96, pp. 268 - 273, Technical Report TR-95-026, ICSI, May 1995, .[12] Storn, R., , Technical Report TR-95-018, ICSI, May 1995, .[13] Storn, R. and Price, K., , Technical Report TR-95-012, ICSI, March 1995, . Anyone who is interested in trying Differential Evolution (DE) might access the .[14] Storn, R., "A Debug/Trace Tool for C SW Projects", Dr. Dobb's Journal, February 1997, pp. 22 - 26.[15] Storn, R., "Constrained Optimization", Dr. Dobb's Journal, May 1995, pp. 119 - 123.[16] Christ, J., Storn, R. and Lueder, E., " New Shortlength DFTs for the Prime Factor Implementation on DSP Architectures", Frequenz, 1995, Band 49, Issue 1-2, pp. 8 - 10.[17] Ballay, H. and Storn, R., "A Tool for Checking C Coding Conventions", C User's Journal, july 94, pp. 41 - 50..[18] Storn, R., "A Hashing Function Based on Algebraic Coding", submitted for publication in the I.E.E. Proceedings~E, Computers and Digital Techniques.[19] Storn, R., "A Radix-2 FFT-Pipeline Architecture With Reduced Noise to Signal Ratio", I.E.E. Proceedings~F, Radar and Signal Processing, 1994.[20] Storn, R. , "Datensicherung mit Prüfsummen", ST-Computer, 1994.[21] Storn, R., "Some Results in Fixed Point Error Analysis of the Bruun-FFT Algorithm, IEEE Trans. on Signal Processing, Vol. 41, No. 7, July 93, pp. 2371 - 2375.[22] Storn, R. , "Statistische Optimierung", ST-Computer, Issues 12/1992 and 1/1993.[23] Storn, R. , "On the Bruun Algorithm and its Inverse", Frequenz, Vol. 3-4, 1992, pp. 110 -116.[24] Storn, R. , "Logische Schaltungen und deren Vereinfachung nach Quine-McCluskey", ST-Computer, Issues 3, 4 and 5, 1990.[25] Storn, R. , "A novel Radix-2 Pipeline Architecture for the Computation of the DFT", IEEE Proc. of the ISCAS 1988, pp. 1899 -1902.[26] Storn, R. , "On the Reduction of Arithmetic Complexity in the Chirp-Transform", Proc. ECCTD, 1987, pp. 239 -244.[27] Storn, R. , "Ein Primfaktor-Algorithmus für die diskrete Hartley-Transformation", 9. DFG-Kolloquium über digitale Signalverarbeitung, 1986, pp. 79 -82.[28] Storn, R. , "Fast Algorithms for the Discrete Hartley Transform", AEÜ, Band 40, Heft 4, 1986, pp. 233 -240.[29] Storn, R. , "Dreieck-Quadratur-Oszillator. Nur ein zeitbestimmendes Glied erforderlich", Elektronik, Issue 5, 1982, p. 74.[30] Storn, R. , "Constant Current Adapter", Elektor, Issue 7/8, 1981.[31] Storn, R. , "De Luxe Transistor Tester", Elektor, Issue 7/8, 1979. (The corresponding circuit was among the winners of the european circuit design contest "EUROTRONIK").BOOKS[1] Price K., Storn R., Lampinen J., Differential Evolution - A Practical Approach to Global Optimization, Springer, Berlin, 2005.[2] Contributor for Babu, B.V., Onwubolu, G. (Editors), New Optimization Techniques in Engineering, Springer, Berlin, 2004.[3] Contributor for Corne, D., Dorigo., M, and Glover., F. (Editors), New Ideas in Optimization, McGraw-Hill, 1999.。

差分进化算法精品PPT课件

▪ 应用：在约束优化计算、聚类优化计算、非线性优化控制、神经网络优化、滤波器设计、阵列天线方向图综合及其它方面得到广泛应用。
引言
开始
根据实际问题进行编码设置参数
生成初始种群
计算个体适应值
是否满足进化终止条件
是
算法结束，输出最优个体
一般演化算法的过程
问题
遗传操作，生成新种群
否
1、遗传操作象 ✓ 种群中所有个体 ✓ 种群中部分个体 2、遗传操作顺序 ✓ 重叠 ✓ 非重叠 3、新种群重组方式
DE的改进方法
为了提高DE的寻优能力、加快收敛速度、克服启发式算法常见的早熟收敛现象，许多学者对DE算法进行改进:
▪ 控制参数的改进。 ▪ 差分策略的改进。 ▪ 选择策略的改进。 ▪ 种群重构 ▪ 混合算法。
DE的改进方法---多种扩展模式
DE算法的多种变形形式常用符号DE /x/y/ z 以示区分,其中:
开开开开开
基本原理
求解非线性函数f (x 1, x 2, ⋯, x n)的最小值问题, x i满足：
xi t xi,1 t , xi,2 t , , xi,n t
i 1, 2, , M ; t 1, 2, tmax.
令xi 是t 第t代的第i个染色体, 则
xiLj xij xiUj j 1, 2, n
行变异操作;
▪ ：一般在[ 0, 2 ]之间选择, 通常取0. 5;
▪ CR：一般在[ 0, 1 ]之间选择, 比较好的选择应在0. 3 左右,
CR 大些收敛速度会加快, 但易发生早熟现象。
差异演化算法的优缺点
和其它进化算法相比, 差异演化具有以下优点:
▪ 差异演化在求解非凸、多峰、非线性函数优化问题表现极强的稳健性。

差分进化算法介绍

1．差分进化算法背景差分进化(Differential Evolution，DE)是启发式优化算法的一种，它是基于群体差异的启发式随机搜索算法，该算法是Raincr Stom和Kenneth Price为求解切比雪夫多项式而提出的。

差分进化算法具有原理简单、受控参数少、鲁棒性强等特点。

近年来，DE在约束优化计算、聚类优化计算、非线性优化控制、神经网络优化、滤波器设计、阵列天线方向图综合及其它方面得到了广泛的应用。

差分算法的研究一直相当活跃，基于优胜劣汰自然选择的思想和简单的差分操作使差分算法在一定程度上具有自组织、自适应、自学习等特征。

它的全局寻优能力和易于实施使其在诸多应用中取得成功。

2.差分进化算法简介差分进化算法采用实数编码方式，其算法原理同遗传算法相似刚，主要包括变异、交叉和选择三个基本进化步骤。

DE算法中的选择策略通常为锦标赛选择，而交叉操作方式与遗传算法也大体相同，但在变异操作方面使用了差分策略，即：利用种群中个体间的差分向量对个体进行扰动，实现个体的变异。

与进化策略(Es)采用Gauss或Cauchy分布作为扰动向量的概率密度函数不同，DE使用的差分策略可根据种群内个体的分布自动调节差分向量(扰动向量)的大小，自适应好；DE 的变异方式，有效地利用了群体分布特性，提高了算法的搜索能力，避免了遗传算法中变异方式的不足。

3.差分进化算法适用情况差分进化算法是一种随机的并行直接搜索算法，最初的设想是用于解决切比雪夫多项式问题，后来发现差分进化算法也是解决复杂优化问题的有效技术。

它可以对非线性不可微连续空间的函数进行最小化。

目前，差分进化算法的应用和研究主要集中于连续、单目标、无约束的确定性优化问题，但是，差分进化算法在多目标、有约束、离散和噪声等复杂环境下的优化也得到了一些进展。

4.基本DE算法差分进化算法把种群中两个成员之间的加权差向量加到第三个成员上以产生新的参数向量，这一操作称为“变异”。

差分进化算法

ቤተ መጻሕፍቲ ባይዱ
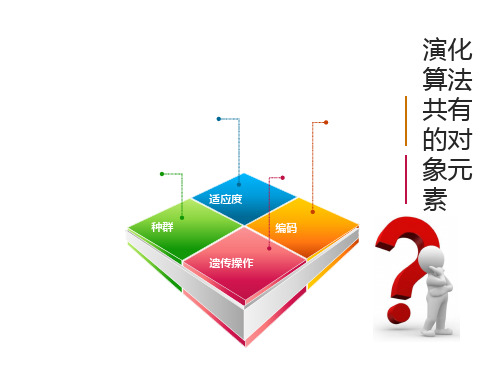
(x2
1)2
10(
1 5
x1
x13
x25)
e x12 x22
1 e(x11)2 x22 3
实验
差分进化算法
参数选取
差异演化算法主要涉及群体规模M 、缩放
因子以及交叉概率CR三个参数的设定。
• M：一般介于5×n 与10×n 之间, 但不能少于4, 否则无法进行
变异操作;
• ：一般在[ 0, 2 ]之间选择, 通常取0. 5;
现在，我们得到了第二代种群S2： s1=11001（25）, s2=01100（12）, s3=11011（27）, s4=10000（16）
表 1.3.2 第二代种群S2中各染色体的情况
染色体
s1=11001 s2=01100 s3=11011 s4=10000
适应度 625 144 729 256
• CR：一般在[ 0, 1 ]之间选择, 比较好的选择应在0. 3 左右, CR 大
些收敛速度会加快, 但易发生早熟现象。
差分进化算法优缺点
优点: 差异演化在求解非凸、多峰、非线性函数优化问题表现极强的稳健性。在同样的精度要求下, 差异演化算法收敛的速度快。差异演化算法尤其擅长求解多变量的函数优化问题。操作简单, 易编程实现。缺点：
▪ 控制参数的改进。 ▪ 差分策略的改进。 ▪ 选择策略的改进。 ▪ 种群重构 ▪ 混合算法。
开始
根据实际问题进行编码设置参数
生成初始种群
计算个体适应值
是否满足进化终止条件
是
算法结束，输出最优个体
一般演化算法的过程
问题
遗传操作，生成新种群
否
1、遗传操作象 ✓ 种群中所有个体 ✓ 种群中部分个体 2、遗传操作顺序 ✓ 重叠 ✓ 非重叠 3、新种群重组方式

差分进化算法综述

差分进化算法综述差分进化算法（Differential Evolution，DE）是一种基于种群演化的全局优化方法，通过模拟生物进化过程中的变异、交叉和选择操作，逐步寻找问题的最优解。

本文将对差分进化算法进行详细综述。

差分进化算法最早由R. Storn和K. Price于1996年提出，其设计初衷是为了解决连续优化问题。

与其他进化算法相比，差分进化算法具有简单易实现、少数参数、收敛性较好等优势，因此被广泛应用于各种实际问题的解决。

1.初始化种群：随机生成大小为N的初始种群，其中N为种群大小，每个个体包含D个维度的参数。

2.变异操作：对种群中的每个个体进行变异操作，通过选择随机的三个个体，计算他们的差分向量，并将其与当前个体进行相加，得到变异个体。

3.交叉操作：对变异个体和当前个体进行交叉操作，生成试验个体。

可以采用二项式交叉或指数交叉等方式。

4.选择操作：对比试验个体和当前个体的适应度，选择适应度更好的个体作为下一代个体。

5.终止条件判断：判断算法是否满足停止条件，如达到最大迭代次数，或适应度达到一定阈值等。

6.更新种群：将选择出的个体替代原来的个体，得到更新后的种群。

7.返回步骤2进行迭代，直到满足终止条件。

差分进化算法的性能与其参数设置密切相关，其中最重要的参数包括种群大小N、个体变异率F和交叉率CR。

种群大小决定了空间的覆盖程度，通常较大的种群大小可以提高算法的全局能力，但同时会增加计算复杂度。

个体变异率F控制了变异操作的程度，较大的F值可以增加种群的多样性，但在取值过大时可能会导致局部最优解的产生。

交叉率CR决定了交叉操作的概率，较高的CR值有助于全局，但过高的交叉率可能会导致个体解的退化。

近年来，差分进化算法得到了广泛的研究和应用，并出现了许多改进和变体算法。

例如，改进的差分进化算法（Improved Differential Evolution，IDE）采用自适应方法来调整算法的参数，在保证能力的同时降低了参数的设置难度。

差分进化算法

选择操作
ＤＥ的选择操作是一种基于贪婪的选择机制,若ui(t+1) 的适应度值好于xi(t)的适应度值,则保留到下一代种群的个体是ui(t+1),否则保留的将是xi(t).对于最小优化问题,则选择算子可由下式描述
其中f为目标函数.
ＤＥ的选择操作是在目标向量和其对应的试验向量两者中保留最优,使得子代个体的适应度值总是好于父代个体的适应度值,从而导致种群始终向最优解的位置进化并逐步聚焦到最优解位置或满意解位置．
标准差分进化算法原理
算法的基本思想是:从一个随机初始化的种群开始搜索，然后经过变异操作、交叉操作、选择操作产生下一时刻的种群，该过程重复进行，直到满足停止条件[2]。
群体初始化变异操作交叉操作选择操作
群体初始化
算法首先在问题的可行解空间随机产生第0代种群
NP为群体规模.
D 为优化问题的维数.
DE算法的搜索性能取决于算法全局探索和局部开发能力的平衡,而这在很大程度上依赖于算法的控制参数的选取,包括种群规模、缩放比例因子和交叉概率等.
差分优化算法优点
归纳起来, DE 算法具有如下优点: 1) 算法通用, 不依赖于问题信息; 2) 算法原理简单, 容易实现; 3) 群体搜索, 具有记忆个体最优解的能力; 4) 协同搜索, 具有利用个体局部信息和群体全局信息指导算法进一步搜索的能力; 5) 易于与其他算法混合, 构造出具有更优性能的算法.
[10]Kannan S, Slochanal S M R, Padhy N P. Application and comparison of metaheuristic techniques to gen ration expansion planning problem [J]. IEEE Trans on Power Systems. [11]宋立明, 李军, 丰镇平. 跨音速透平扭叶片的气动优化设计研究[J] . 西安交通大学学报, 2005, 39(11):1277-1281. [12]杨晓明, 邱清盈, 冯培恩, 等. 盘式制动器的全性能优化设计[J]. 中国机械工程, 2005, 16(7) : 630-633. [13]Doyle S, Corcoran D, Connell J. Automated mirror design using an evolution strategy [J]. Optical Engineering, 1999, 38(2):323-333. [14]张吴明, 钟约先.基于改进差分进化算法的相机标定研究[J]. 光学技术, 2004, 30(6):720-723

差分进化算法介绍

差分进化算法介绍差分进化算法（Differential Evolution, DE）是一种全局优化算法，适用于求解各种类型的优化问题。

该算法于1995年由Rainer Storn和Kenneth Price提出，并在之后的几十年中得到了广泛应用和研究。

算法流程：（1）初始化种群：首先随机生成初始的种群，个体的数目与问题的维度相关，每个个体由问题的解空间中的一个点表示。

（2）变异操作：对于每个个体，通过随机选择种群中的三个不同个体a、b和c，生成一个变异个体m。

具体的变异操作可以有多种实现方式，其中较为常见的是"rand/1"变异策略和"best/1"变异策略。

（3）交叉操作：对于每个个体，通过将变异个体m的一些基因与当前个体的对应基因进行交叉，进而得到一个试验个体u。

（4）选择操作：根据试验个体u的适应度值，决定是否将其纳入下一代种群。

如果u的适应度值优于当前个体，则将u替换当前个体；否则保留当前个体。

上述的（2）至（4）步骤迭代进行，直到满足终止条件（如达到最大迭代次数，或者找到满意的解）为止。

（1）全局优化能力强：差分进化算法基于种群的演化过程，能够较好地保持种群的多样性，从而有较高的全局能力。

（2）参数设置简单：相比于其他优化算法（如遗传算法、粒子群优化算法等），差分进化算法的参数设置较为简单，只需调整几个关键参数即可。

（3）对问题没有假设和限制：差分进化算法对问题没有特定的假设和限制，适用范围广，能够求解各种类型的优化问题。

（4）易于并行化：差分进化算法的计算过程中，各个个体之间是相互独立进行演化的，因此易于实现并行计算，提高求解效率。

总结来说，差分进化算法是一种全局优化算法，通过模拟自然界的演化过程来寻找最优解。

算法具有全局优化能力强、参数设置简单、适用范围广、易于并行化等特点和优势。

它在实际应用中取得了广泛成功，并且不断有新的改进和变种被提出。

差分进化算法pdf

差分进化算法pdf差分进化算法是一种基于群体智能的优化算法，其主要目的是在给定的问题中快速找到最优解。

相对于传统的进化算法，差分进化算法的主要优势在于其对于高维度问题的表现力更加出色。

以下是差分进化算法的具体步骤：1. 初始化种群在差分进化算法中，我们需要首先初始化一个种群，将其放在搜索空间中，以便进行进化。

每个个体都是由一个特定的向量组成，表示搜索空间中的一个点。

我们可以通过随机抽样的方式来初始化种群中每一个个体的向量值。

2. 差分算子差分运算符是差分进化算法的核心组成部分。

其主要功能是根据种群中已有的个体，构造并生成新的解向量。

在差分算子中，我们选取两个可行解x和y，然后通过差分算子构建新的解向量z。

具体地，z的构造方式如下：z = x + F(y-x)其中F是参数范围在[0,2]之间的可调整的参数，其作用是控制差分算子对y-x的影响程度。

3. 交叉运算符在差分进化算法中，交叉运算符主要用来融合一个个体的特征向量与由差分算子生成的新的特征向量。

具体来说，交叉运算符可以通过在两个向量矩阵中分别随机选取一些位置，并将这些位置标记为“父向量”和“子向量”来实现。

然后，我们可以根据随机选取的位置进行特征向量的融合。

4. 选择算子选择算子主要用来筛选种群中的优质解向量，并将其作为下一次进化的种子。

在差分进化算法中，我们可以根据优化的目标函数来度量一个解向量的质量。

具体来说，我们需要对整个种群中的解向量进行评估，并选取其中表现最优秀的个体作为下一次进化的种子。

总之，差分进化算法是一种非常高效的搜索算法，在很多领域中已经得到了广泛的应用。

相信通过学习差分进化算法的操作步骤以及其内在的优化机制，我们可以更好地理解并应用这个优秀的算法。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数。记向量空间ｐ－范数为 ‖ · ‖ｐ，于是非线性方程组转化为求解
ｎｘ∈Ｒ
ｍｉｎ‖Ｆ（ｘ） ‖ｐ
（）１
式中，令ｐ→ ∞ ，则问题转化为
ｎ１≤ ｉ ≤ｍｘ∈Ｒ
的一种随机直接搜索算法。该算法以易用性、稳健性和强大的全局寻优能力在多个领域取得成功，特别适合对不可微、非
３．２自适应正交交叉算子
（）５
（）４其中
…，， …，设ｘ为参与ｘｘｘｘｘｘｘ１＝（１１，１２，１ｎ）２＝（２１，２２，２ｎ），交叉操作的一对父个体，ｘｘｌｕ１，２确定的可行空间为［ｌｏｗ，ｕｐ］（，（， …，（］ｌｍｉｎｘｘｍｉｎｘｘｍｉｎｘｘｌｏｗ＝［１１，２１）１２，２２）１ｎ，２ｎ）（，（， …，（］ｕｍａｘｘｘｍａｘｘｘｍａｘｘｘｕ１１，２１）１２，２２）１ｎ，２ｎ）ｐ＝［（）６
方程组转化为光滑的优化函数，再利用智能算法求解，取得了很好的效果。但文献［指出凝聚态函数需要在一定的条件２］下才能收敛，并给出了一种修３］差分进化算法是Ｒ．于１Ｓｔｏｒｎ和Ｋ．Ｐｒｉｃｅ１９９５年提出
［１］ｎ命题１ｘ）ｘ）ｘ）对ｘ∈Ｒ， ≤Ｇ ≤ｆ（ｐ＞０成立，ｆ（ｐ（
｛
／＋ｌｎｍｐ。
［２］ｎ命题２随正数ｐ增加而增加，且ｆＧｘ）对ｘ∈Ｒ，ｐ（
（。ｘ）＝ｌｉｍＧｘ）ｐ（
ｐ→ ∞
ｘ１，ｘ２的第ｉ维相似度。／定义２令δ＝（称 δ 为ｘ１，ｎ，ｘ δ δ δ １＋２＋ … ＋ｎ）２的平
均相似度。 …，，记Ｂ＝｛称Ｂ为因素分割位置ｉｉ＝１，２，ｎ｝｜ δ α· δ，ｉ＞其中α 为常数。该集合用于调节满足相似度要求的位点集，，可根据实际情况调节）以防止相似度极高的基置点的个数（因作为因素分割位置点，导致种群多样性较差。 α 取值越大，集合Ｂ中的元素个数越少，能够选取作为因素分割的基因个分割越均匀，但随机性相对较差；反之分割均匀性较数越少，差，随机性较好。一般取值０．５５或０．１５。例如：设参与交叉操作的两个父代个体为ｘ２，４，１＝（），，和ｘ下限 Δ＝０．似度δ ３．３１，３，３．４）０５， δ δ １＝（１＝２＝１３＝显然均大于０．可能出现分割１，０５。不妨设因素个数为２，０．
１引言
在工程实践与理论研究中，很多问题都可以转换为方程因而求解方程组是数学与工程应用中的重要研究内容。组，近年来国内外专家学者对非线性方程组的求解问题做了大量提出了许多有效的算法，主要分为两类：一是经典算的工作，法，这些算法对初始点的选取和方程组具有较高的要求，一般是针对某一类型的方程组
，ＡｂｓｔｒａｃｔｉｒｓｔｎｏｎｌｉｎｅａｒｓｓｔｅｍｏｆｅｕａｔｉｏｎｓｗａｓｔｒａｎｓｆｏｒｍｅｄｉｎｔｏｕｎｃｏｎｓｔｒａｉｎｅｄｏｔｉｍｉｚａｔｉｏｎｒｏｂｌｅｍｂｕｓｉｎｔｈｅＦｙｑｐｐｙｇ，ｃｏｎｃｅｔｏｆｓｕｒｒｏａｔｅｃｏｎｓｔｒａｉｎｔｓａｎｄａｍｅｎｄｅｄｍａｘｉｍｕｍｅｎｔｒｏｆｕｎｃｔｉｏｎ．Ｔｈｅｎｔｈｅｃｏｎｃｅｔｏｆａｖｅｒａｅｓｉｍｉｌａｒｉｔｗａｓｐｇｐｙｐｇｙ，ｅｎｅｒａｔｅｏｕｌａｉｎｔｒｏｄｕｃｅｄｔｏｄｅｓｉｎａｄａｔｉｖｅｏｒｔｈｏｏｎａｌｃｒｏｓｓｏｖｅｒｏｅｒａｔｏｒａｎｄｏｒｔｈｏｏｎａｌｄｅｓｉｎｗａｓｕｓｅｄｔｏｉｎｉｔｉａｌ－ｇｐｐｇｐｇｐｇｇ，，ｔｉｏｎａｎｄｏｎｔｈｅｂａｓｉｓａｄａｔｉｖｅｏｒｔｈｏｏｎａｌｄｉｆｆｅｒｅｎｔｉａｌｅｖｏｌｕｔｉｏｎａｌｏｒｉｔｈｍｗａｓｒｏｏｓｅｄｆｏｒｓｏｌｖｉｎｔｈｅｍａｘｉｍｕｍｅｎｔｒｏ－ｐｇｇｐｐｇ，ｆｕｎｃｔｉｏｎ．Ｆｉｎａｌｌｕｓｉｎｅｕａｔｉｏｎｓｖｅｒｉｆｉｅｄｔｈｅａｌｏｒｉｔｈｍ．ｙｇｑｇｐｙ，，，ＫｅｗｏｒｄｓｒｔｈｏｏｎａｌｄｅｓｉｎＤｉｆｆｅｒｅｎｔｉａｌｅｖｏｌｕｔｉｏｎＭａｘｉｍｕｍｅｎｔｒｏＳｓｔｅｍｏｆｅｕａｔｉｏｎｓＯｇｇｐｙｙｑｙ凸、非光滑函数进行优化。一般差分进化算法的初始化是随随意性太强，在解空间中的取样不均匀，容易导致机初始化，早熟收敛、计算量大和局部搜索能力差等问题。因此，本文首先用 “ 极大值 ” 约束，将非线性方程组转化不然后利用代理约束概念和最大熵原理可微的无束优化问题，导出修正凝聚态光滑函数，以此逼近不可微极大值函数，从而将方程组等价地转化为可微的无约束优化函数；然后引入正交设计初始化差分进化算法的初始种群，并引入平均相似度概念，设计自适应正交交叉算子，提出了自适应正交差分进化用于求解修正凝聚态函数。算法，
第３９卷第５期２０１２年５月
计算机科学ＣｏｍｕｔｅｒｃｉｅｎｃｅＳｐ
Ｖｏｌ．３９Ｎｏ．５Ｍａ２０１２ｙ
求解方程组的正交差分进化算法
２１２２封全喜１，刘三阳唐国强林亮１２（））西安电子科技大学理学院西安７桂林理工大学理学院桂林５１００７１４１００４（
摘要首先利用代理约束概念和修正极大熵函数，将非线性方程组等价地转化为无约束优化函数；然后引入平均相似度概念，设计自适应正交交叉算子，利用正交设计产生初始种群，并在此基础上提出了自适应正交差分进化算法，用于求解修正极大熵函数；最后用方程组验证了算法的有效性。关键词正交设计，差分进化算法，极大熵，方程组中图法分类号ＴＰ２０２文献标识码Ａ
［６］ …，定义１其中ｉ称δ ｘｘ＝１，２，ｎ，令δ ｜｜，ｉ＝１ｉ－２ｉｉ为
式中，ｍ为约束个数。该函数又称为修正凝聚态函数，ｐ＞０，］是对文献［凝聚态函数的改进。当ｐ→ ∞ 时，在整个１Ｇｘ）ｐ（空间上一致逼近函数。
［１５］
；二是近年来兴起的智能算法，
］其广泛地应用于求解方程组，比如文献［将粒子群算法与拟４牛顿法结合构造求解非线性方程组的混合粒子群算法、文献［］引入经典算法和遗传算法相结合求解非线性方程组、文献７［］成功地将差分进化算法应用于求解方程组。这些算法初５始种群均是随机产生。
·１８７·
，则求解原非线性方程组问题转化为求解优化问题ｍｉｎｘ）ｆ（
ｎｘ∈Ｒ
其中函数ｆ（不可微。引入修正极大熵函数ｘ）
ｍｘ）１｛ｐｆ（／Ｇｘ）＝ｌｎ（ｅｉ）ｍ｝ ∑ ｐ（ｉ＝１ｐ
［２］
ＱＦ－１Ｍ≤ Ｑ－１
｝ｍｉｎｍａｘ｛ｘ）｜｜ｉ（ｆ
１≤ ｉ ≤ｍ
（）２）（３
记ｆ（ｘ）＝ｍａｘ｛ｆｘ）｝ｉ（
，到稿日期：广西区教育厅立项项目（２０１１０６２７２０１１０９３０本文受国家自然科学基金项目（６０９７４０８２，１１１０１１０１）２００８１１２－－返修日期：－－），）陕西省教育厅规划项目（和湖南省社科联课题（资助。ＬＸ８５１１ＪＫ１０５１１０１１０４４Ｂ），：，封全喜（男，博士生，讲师，主要研究方向为智能优化、鲁棒优化，刘三阳（男，博士，教授，主要研究１９８０－）Ｅ－ｍａｉｌｆｘ９９０４＠１６３．ｃｏｍ；１９５９－）ｑ，方向为最优化理论方法及其应用；唐国强（男，博士，副教授，主要研究方向为随机优化算法及其理论分析。１９７１－）