弹性力学第3章(徐芝纶第五版)
合集下载
（完整版）徐芝纶弹性力学主要内容及知识点
（完整版）徐芝纶弹性力学主要内容及知识点1.弹性力学是研究弹性体由于受到外力作用、边界约束或温度改变等原因而引起的应力、形变和位移。
2外力分为体积力和面积力。
体力是分布在物体体积内的力，重力和惯性力。
体积分量，以沿坐标轴正方向为正，沿坐标轴负方向为负。
面力是分布在物体表面上的力，面力分量以沿坐标轴正方向为正，沿坐标轴负方向为负。
3内力，即物体本身不同部分之间相互作用的力。
3弹性力学中的基本假定：连续性，完全弹性，均匀性，各向同性，小变形假定。
凡是符合连续性、完全弹性、均匀性、各向同性等假定的物体称之为理想弹性体。
连续性，假定整个物体的体积被组成这个物体的介质所填满，不留下任何空隙。
完全弹性，指的是物体能完全恢复原形而没有任何剩余形变。
均匀性，整个物体时统一材料组成。
各向同性，物体的弹性在所有各个方向都相同。
4求解弹性力学问题，即在边界条件上，根据平衡微分方程、几何方程、物理方程求解应力分量、形变分量和位移分量。
弹性力学、材料力学、结构力学的研究对象分别是弹性体，杆状构件和杆件系统。
解释在物体内同一点，不同截面上的应力是不同的。
应力的符号不同：在弹性力学和材料力学中，正应力规定一样，拉为正，压为负。
切应力：弹性力学中，正面沿坐标轴正方向为正，沿负方向为负。
负面上沿坐标轴负方向为正，沿正方向为负。
材料力学中，所在的研究对象上任一点弯矩转向顺时针为正，逆时针为负。
5.形变：所谓形变，就是形状的改变。
包括线应变（各各线段每单位长度的伸缩，即单位伸缩和相对伸缩，伸长时为正，收缩时为负）；切应变（各线段直接直角的改变，用弧度表示，以直角变小时为正，变大为负）6试述弹性力学平面应力问题与平面应变问题的主要特征及区别：平面应力问题：几何形状，等厚度薄板。
外力约束，平行于板面且不沿厚度变化。
平面应变问题：几何形状，横断面不沿长度变化，均匀分布。
外力约束，平行于横截面并不沿长度变化。
7.主应力：设经过P点的某一斜面上的切应力等于0，则该斜面上的正应力称为P点的一个主应力；应力主向：该斜面的法线方向称为该斜面的一个应力主向。
弹性力学简明教程简介与目录
徐芝纶教授（1911—1999），中国科学院资 深院士，著名的力学家和教育家。徐芝 纶编著的力学教材被我国工科院校广泛 采用，为培养科技人才起到了重要的作 用。徐芝纶在基础板梁的科研工作中作 出了许多重大成果，并为在我国引进、推广、研究有限单 元法作出了突出贡献。徐芝纶一生为人正直、品德高尚， 以“学无止境，教亦无止境”为座右铭，严谨治学、严格 教学，数十年如一日为国家培养建设人才贡献了毕生的精 力。
高等教育出版社
《弹性力学简明教程》 编著 徐芝纶教授
此教程是国内较广泛使用的一本工科院 校弹性力学教科书，是教育部“十五”国 家级规划教材。全书按照由浅入深的原 则，安排了平面问题的理论及解答、空间 问题的理论及解答和薄板弯曲理论，并着 重介绍了弹性力学的近似解法，即差分 法、变分法和有限元法。
作者简介
参考eory of elasticity》 Timoshenco S P, Goodier J N (有中译本) 三、《Applied Elasticity》 徐芝纶编
高等教育出版社
《弹性力学简明教程》 编著 徐芝纶教授
此教程是国内较广泛使用的一本工科院 校弹性力学教科书，是教育部“十五”国 家级规划教材。全书按照由浅入深的原 则，安排了平面问题的理论及解答、空间 问题的理论及解答和薄板弯曲理论，并着 重介绍了弹性力学的近似解法，即差分 法、变分法和有限元法。
作者简介
参考eory of elasticity》 Timoshenco S P, Goodier J N (有中译本) 三、《Applied Elasticity》 徐芝纶编
弹性力学__徐芝纶版第三章
4 f
y4
0
4 f 0
一、逆解法和半逆解法 （一）逆解法的基本步骤：
取满足相容方程的 f
求出应力分量 x , y , xy
根据边界条件求出面力
考察能解决什么问题
§3-1 逆解法与半逆解法 多项式解答
（二）半逆解法的基本步骤：
根据问题的特 点设出部分应 力分量
是 结束
否
求出应力函数 f
x
§3-3 位移分量的求出
0 u0 v0 0
y
z
u P x Eh
P x
v P y
Eh
习题
[1]写出边界条件。 解：
x x0,xb g( y h1)
0 xy x0,xb y y0 gh1, xy y0 0
y
P
hE
xy 0
u P x Eh
v P
y Eh
u v 0 y x
u
P Eh
x
f1y
v
P
Eh
y
f2 x
代入第三式得： df1 y df2 x 0
dy
dx
移项得： df1 y df2 x
u yh2 0
v yh2 0
hx1
g
b
h2
bb
y 22
FN gbh1
b
下边的等效应力边界条件： 0 y yh2 dx gbh1
b
0
xy
dx 0
y h2
b 0
y
y h2
弹性力学第03章精品PPT课件
在主要边界上： y h ,
2
s y 0,
t xy 0
因此，在y=±h/2的边界面上，无任何面力作用，即
fx 0, f y 0
在x=0,l的次要边界上：
x 0,
f x (s x ) x0 0,
fy
(t xy )
x0
3F 2h
(1 4
y2 h2
)
x l,
fx
(s x )
xl
12Fl h3
➢注意事项：由于全部基本方程和边界条件是由变形
前的坐标描述的，因此只有在小变形的条件下才可以 使用叠加原理。即变形对外力作用点位置的改变可以 忽略不计。
圣维南原理及应用
➢对于工程实际问题，构件表面面力或者位移很难满足
严格的边界条件。这使得弹性力学解的应用将受到极大 的限制。为了扩大弹性力学解的适用范围，放宽这种限 制，圣维南提出了局部影响原理。
➢圣维南原理主要内容：物体表面某一小面积上作用的
外力力系，如果被一个静力等效的力系所替带，那么物 体内部只能导致局部应力的改变。而在距离力的作用点 较远处，其影响可以忽略不计。
圣维南原理及应用
➢根据圣维南局部影响原理，假如我们用一静力等效力系取
代弹性体上作用的原外力，则其影响仅在力的作用区域附近。 离此区域较远处，几乎不受影响。
s
x
2f ( x,
y 2
y)
fx x,
s
y
2f ( x,
x 2
y)
fy y,
t xy
2f(x, y)
xy
逆解法与半逆解法
(3)在确定的坐标系下，考察具有确定的几何尺寸和 形状的弹性体，根据主要边界上的面力边界条件(2-15) 或次要边界上的积分边界条件, 分析这些应力分量对应 于边界上什么样的面力，从而得知所选取的应力函数可 以解决什么样的问题。（或者根据已知面力确定应力函 数或应力分量表达式中的待定系数）
河海大学弹性力学徐芝纶版 第三章PPT课件
( ) 0 . x yy h / 2
( b )
从式(a)可见，边界条件(b)均满足。 次要边界 x=0, l,
( xy)x0,l 0 ,
满足。
(c)
次要边界
主要边界
次要边界 x=0, l,
σ x 的边界条件无法 精确满足。
M
o l
h/2 M h/2
x
y
用两个积分的条件代替
h/2 h/2 ( σ ) y d y 1 M 。 x x 0, l h/2
次要边界
次要边界 x l ,
(x )xl 0
不满足
q
应用圣维南原理，列出三个积分条件，
h/2
h /2 h/2 h /2 h/2 h /2
思考题
如果区域内的平衡微分方程已经满足，且 除了最后一个小边界外，其余的应力边界条件 也都分别满足。则我们可以推论出，最后一个 小边界上的三个积分的应力边界条件（即主矢 量、主矩的条件）必然是满足的，因此可以不 必进行校核。试对此结论加以说明。
问题提出
§3-3 位移分量的求出
在按应力求解中，若已得出应力，如何求 出位移？
半逆解法
解出:
3 2 f1 Ey Fy Gy, 5 4 3 2 A B f 2 y y Hy Ky . 10 6 f Ay3 By2 cy D,
(b)
式(b)中已略去对于Φ 的一次式。 将式(b)代入式(a)，即得 Φ 。
半逆解法
⑷由 Φ 求应力。 在无体力下，应力公式如书中式( f ), (g),(h)所示。 对称性条件─由于结构和荷载对称于 y 轴，故 Φ , σ应为 为 x x , σ y 的偶函数，
弹性力学-第二章 平面问题基本理论 (徐芝纶第五版)
基本方程是二维的。
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束，仅平行于 板面作用，沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力，有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 （一）本章学习要求及重点
本章系统地介绍了平面问题的基本理论： 基本方程和边界条件，及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此，学好平面问题的基本理论，就可以方 便地学习其他各章。为此，我们要求学生深 入地理解本章的内容，掌握好以下几点：
)
f
y
0.
68
（2）用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
（在s 上ss）
69
（3）位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题（平面应力问题），
应力分量 σ x , σ y ,t x必y 须满足下列全部条件：
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束，仅平行于 板面作用，沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力，有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 （一）本章学习要求及重点
本章系统地介绍了平面问题的基本理论： 基本方程和边界条件，及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此，学好平面问题的基本理论，就可以方 便地学习其他各章。为此，我们要求学生深 入地理解本章的内容，掌握好以下几点：
)
f
y
0.
68
（2）用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
（在s 上ss）
69
（3）位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题（平面应力问题），
应力分量 σ x , σ y ,t x必y 须满足下列全部条件：
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
弹性力学-绪论(徐芝纶第五版)
15
弹力基本假定，确定了弹力的研究范围:
理想弹性体的小变形问题。
16
弹性力学未知量
已知——几何参数和载荷； 坐标——x、y、z； 6个应力分量 6个应变分量 3个位移分量
——15个未知量
基本方程是三维的。
x3 33
x1
e2
11
e3
31 13
3223
22
12 21 x2
e1
A BC
.
A: (x, y, z)
1
教材及参考书
教材：
-《弹性力学》(上)，徐芝纶编，高等教育出版社。
参考书：
-《弹性理论》，王龙甫，科学出版社。
习题册：
-《弹性力学学习方法解题指导》，王俊民，同济大 学出版社
2
弹性力学第一章、绪论
一、力学相关课程简介 二、力学的研究方法 三、弹性力学基本概念 四、弹性力学的一些普遍原理
3
弃材力中大部分假定。
7
弹性力学研究方法
弹力研究方法：
在区域V内严格考虑静力学、几何学和物 理学三方面条件，建立三套方程; 在边界s上考虑受力或约束条件，并在边 界条件下求解上述方程，得出较精确的 解答。
8
二、力学的研究方法
z x y
σx σy
ρ gy, 2
( ρ g cot 1
α
2ρ 2
g
小变形假定。
4、弹性力学问题的研究方法
已知：物体的边界形状，材料性质，体力,
边界上的面力或约束。
求解：应力、形变和位移。
19
解法：在弹性体区域V 内，
根据微分体上力的平衡条件，建立平衡 微分方程；根据微分线段上应变和位移的 几何条件，建立几何方程；根据应力和应 变之间的物理条件，建立物理方程。
弹力基本假定，确定了弹力的研究范围:
理想弹性体的小变形问题。
16
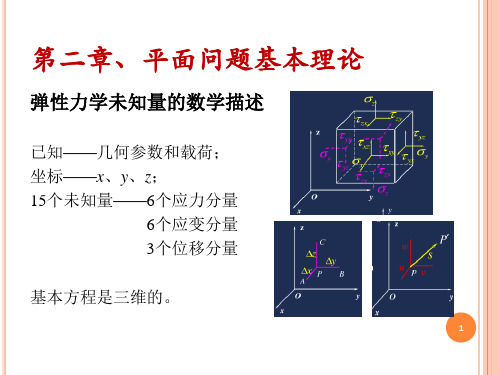
弹性力学未知量
已知——几何参数和载荷； 坐标——x、y、z； 6个应力分量 6个应变分量 3个位移分量
——15个未知量
基本方程是三维的。
x3 33
x1
e2
11
e3
31 13
3223
22
12 21 x2
e1
A BC
.
A: (x, y, z)
1
教材及参考书
教材：
-《弹性力学》(上)，徐芝纶编，高等教育出版社。
参考书：
-《弹性理论》，王龙甫，科学出版社。
习题册：
-《弹性力学学习方法解题指导》，王俊民，同济大 学出版社
2
弹性力学第一章、绪论
一、力学相关课程简介 二、力学的研究方法 三、弹性力学基本概念 四、弹性力学的一些普遍原理
3
弃材力中大部分假定。
7
弹性力学研究方法
弹力研究方法：
在区域V内严格考虑静力学、几何学和物 理学三方面条件，建立三套方程; 在边界s上考虑受力或约束条件，并在边 界条件下求解上述方程，得出较精确的 解答。
8
二、力学的研究方法
z x y
σx σy
ρ gy, 2
( ρ g cot 1
α
2ρ 2
g
小变形假定。
4、弹性力学问题的研究方法
已知：物体的边界形状，材料性质，体力,
边界上的面力或约束。
求解：应力、形变和位移。
19
解法：在弹性体区域V 内，
根据微分体上力的平衡条件，建立平衡 微分方程；根据微分线段上应变和位移的 几何条件，建立几何方程；根据应力和应 变之间的物理条件，建立物理方程。
弹性力学徐芝纶课后习题及答案
弹性力学徐芝纶课后习题及答案弹性力学是固体力学的重要分支，对于工程技术领域有着广泛的应用。
徐芝纶先生所著的弹性力学教材备受推崇，其中的课后习题更是帮助学习者巩固知识、深化理解的重要途径。
接下来，让我们一起深入探讨一下其中的一些典型习题及答案。
首先，我们来看一道关于平面应力问题的习题。
题目给出了一个矩形薄板，在其边界上受到特定的载荷分布，要求求解板内的应力分布。
对于这类问题，我们首先需要根据已知条件，确定边界条件。
在这个例子中，矩形板的四条边上可能分别有均布力、集中力或者固定约束等。
然后，我们运用弹性力学中的平衡方程、几何方程和物理方程来建立求解方程。
平衡方程描述了物体内部的力的平衡关系；几何方程则将位移与应变联系起来；物理方程则反映了应力与应变之间的关系。
通过联立这些方程，并结合边界条件，我们可以使用数学方法（如傅里叶级数展开、分离变量法等）进行求解。
经过一系列的计算和推导，我们得到板内的应力表达式。
需要注意的是，在计算过程中，要仔细处理各项的系数和积分，确保计算的准确性。
再来看一道关于应变能的习题。
已知物体的应力状态，要求计算其应变能密度。
应变能密度的计算需要先根据应力求出应变，然后利用应力应变的关系计算应变能密度。
这道题主要考察对基本概念和公式的熟练掌握程度。
在求解过程中，要清晰地记住各种应力和应变的分量关系，以及它们在不同坐标系下的转换。
同时，对于复杂的应力状态，要善于运用矩阵运算来简化计算。
还有一道关于厚壁圆筒的习题。
题目给出了圆筒的内外半径、材料属性和承受的内压外压，要求求解圆筒内的应力分布。
对于这种轴对称问题，我们可以利用拉梅方程来求解。
首先确定圆筒的边界条件，即内表面和外表面的压力。
然后代入拉梅方程进行求解。
在计算中，要注意公式中各项的物理意义和单位的统一。
并且要理解厚壁圆筒在不同半径处应力的变化规律。
下面我们来探讨一下答案的重要性以及如何正确使用答案。
答案是对习题的一种验证和参考，但不能完全依赖答案。
弹性力学徐芝纶课后习题答案
C 0
3、边界条件定常数： ( xy ) x 0 0
( xy ) x b q
q A 2 (3 Ab2 2 Bb) q b b q 上端面 0 ( xy ) dx 0 Ab3 Bb2 0 即Ab B 0 y 0 B b
U 2 Fxy 3 3Fxy h3 2h
(1)
U
qx 2 4
4 y 3 3 y qy 2 2 y 3 y 1 3 3 (2) h h h 10 h
应力分 量
x xy
12 Fxy , y 0 h3 2 6 Fy 3F 3 h 2h
2 2 f x 0 x y 2 y 2 f ( x) y 4 0 x 2 y 2 yf ( x ) f1 ( x ) 4 0 y 4
4 d 4 f ( x ) d 4 f1 ( x ) y x 4 dx 4 dx 4
4 0 即 y
d 4 f ( x) 0 dx 4 d 4 f1 ( x ) 0 dx 4
d 4 f ( x ) d 4 f1 ( x ) 0 对 y 的任意值均成立则有： dx 4 dx 4
f ( x ) Ax 3 Bx 2 Cx (略去了与应力无关的常数项 ) f1 ( x ) Ex 3 Fx 2 (略去了与应力无关的常数项及次项 )
0 ( y ) y 0 dy 0 0 ( y ) y 0 xdx 0
则 x 0 y
b
b
3Eb 2 F 0 E F 0 2 Eb F 0
习
题
2-1 如果某一问题中， z zx xy 0 ，只存在平面应力分量 x ， y ， xy ，且它们不沿 z 方向变化，仅为 x，y 的函数，试考虑此问题是否就是平面应力 问题？(是) 2-2 如果某一问题中， z zx zy 0 ，只存在平面应变分量 x ， y ， xy ，且它们不沿 z 方向变化，仅为 x，y 的函数，试考虑此问题是否就是平面应变问题？ (是) 2-3 试分析说明，在不受任何面力作用的空间体表面附近的薄层中，图 2-11，其应力状态接 近于平面应力的情况。(自由表面薄层中： z 0 yz xz 0 x y xy 0 近于平面应力问 题)
3、边界条件定常数： ( xy ) x 0 0
( xy ) x b q
q A 2 (3 Ab2 2 Bb) q b b q 上端面 0 ( xy ) dx 0 Ab3 Bb2 0 即Ab B 0 y 0 B b
U 2 Fxy 3 3Fxy h3 2h
(1)
U
qx 2 4
4 y 3 3 y qy 2 2 y 3 y 1 3 3 (2) h h h 10 h
应力分 量
x xy
12 Fxy , y 0 h3 2 6 Fy 3F 3 h 2h
2 2 f x 0 x y 2 y 2 f ( x) y 4 0 x 2 y 2 yf ( x ) f1 ( x ) 4 0 y 4
4 d 4 f ( x ) d 4 f1 ( x ) y x 4 dx 4 dx 4
4 0 即 y
d 4 f ( x) 0 dx 4 d 4 f1 ( x ) 0 dx 4
d 4 f ( x ) d 4 f1 ( x ) 0 对 y 的任意值均成立则有： dx 4 dx 4
f ( x ) Ax 3 Bx 2 Cx (略去了与应力无关的常数项 ) f1 ( x ) Ex 3 Fx 2 (略去了与应力无关的常数项及次项 )
0 ( y ) y 0 dy 0 0 ( y ) y 0 xdx 0
则 x 0 y
b
b
3Eb 2 F 0 E F 0 2 Eb F 0
习
题
2-1 如果某一问题中， z zx xy 0 ，只存在平面应力分量 x ， y ， xy ，且它们不沿 z 方向变化，仅为 x，y 的函数，试考虑此问题是否就是平面应力 问题？(是) 2-2 如果某一问题中， z zx zy 0 ，只存在平面应变分量 x ， y ， xy ，且它们不沿 z 方向变化，仅为 x，y 的函数，试考虑此问题是否就是平面应变问题？ (是) 2-3 试分析说明，在不受任何面力作用的空间体表面附近的薄层中，图 2-11，其应力状态接 近于平面应力的情况。(自由表面薄层中： z 0 yz xz 0 x y xy 0 近于平面应力问 题)
弹性力学讲义(徐芝纶版)-PPT
换，
E
1
E
2
,
。 1
边界条件
边界条件--应用极坐标时，弹性体的 边界面通常均为坐标面，即：
常数，或 常数,
故边界条件形式简单。
平面应力问题在极坐标下的基本方程
1
f
0
1
2
f
0
4 1
u
,
1
u
u
,
u
1
u
u
。
1 E
(
),
1 E
(
),
x ρ x φ x
Φ y
Φ ρ
ρ y
Φ φ
φy .
一阶导数
而
cos,
x
sin , x
sin;
y
y
cos 。
代入，即得一阶导数的变换公式,
Φ cosφ Φ sin Φ (cosφ sinφ )Φ
x
ρ ρ φ
ρ ρ φ
，
(e)
Φ sinφ Φ cos Φ (sinφ cosφ )Φ。
σ x σ ρ cos2 φσφsin2 φ2τ ρφ cosφsinφ,
而
σ
x
2Φ y 2
2Φ ρ2
sin
2
φ(
1 ρ
Φ ρ
1 ρ2
2Φ ρ2
)cos2
φ
2[ ( 1 Φ )]cosφsinφ, ρ ρ
比较两式的 cos2 φ,sin2 φ,cosφsinφ 的系数，便 得出 σ ρ,σφ,τ ρφ 的公式。
2(1 E
)
。
4 2
物理方程
物理方程
对于平面应变问题，只须将物理方程作如下 的变换即可。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
最主要量级q( l )2 h
,和次要量级 q l h
, 在材力
中均已反映,且与弹力相同。
最小量级 ~ q, 在材力中没有:
当lh
时,
仅占主项
M I
y
的1/15
( 6 %) ,
当 l 时h , 量级q 的值很小,可以不计。
弹力与材力的解法比较:
应力比较
弹力严格考虑并满足了A内的平衡微分 方程 ,几何方程和微分方程,以及S上的所有 边界条件(在小边界上尽管应用了圣维南 原理,但只影响小边界附近的局部区域)。
4 楔形体受重力和液体压力 问题
设有楔形体， 左面垂直，顶角为α， 下端无限长，受重 力及齐顶液体压力,
fx 0, f y 1g.
o
α 2g
y
x
n
α
2
1g
用半逆解法求解。
（1）用量纲分析法假设应力: （2）由应力~Φ关系式，Φ应为x,y的三次式，
（3）Φ 满足相容方程 4Φ 0.
（4）由 Φ求应力， （5）考察边界条件——本题只有两个大边 界，均应严格满足应力边界条件:
o
M
y
h/2
h/2
x
M
l
( l >>h)
半逆解法
3.半逆解法 步骤：
⑴ 假设应力的函数形式 （根据受力情况， 边界条件等）；
⑵ 由应力(d)式，推测 的Φ 函数形式；
⑶ 代入 4Φ，解0 出 ； Φ
半逆解法
⑷ 由式（d），求出应力；
⑸ 校核全部应力边界条件（对于多连体， 还须满足位移单值条件）. 如能满足，则为正确解答；否则修改假 设，重新求解。
为b,如图,水的密
度为 2 ，试求
应力分量。
y
o
bb 22
2g
1g
x
第三章 重点归纳
本章学习重点及要求
本章是按应力求解平面问题的实际 应用。其中采用应力函数Φ 作为基本未 知数进行求解，并以直角坐标来表示问 题的解答。在学习本章时，应重点掌握：
1. 按应力函数 Φ求 解时，Φ 必须满足的条件。
2. 逆解法和半逆解法。
⑶ 多连体中的位移单值条件。 (c)
对于单连体，(c)通常是自然满足的。 只须满足(a),(b)。
由 Φ求应力的公式是
σ
x
2Φ y 2
f
x
x,
σ
y
2Φ x2
f
y
y,
(d)
τ
xy
2Φ xy
.
逆解法
2 .逆解法 ── 先满足(a),再满足(b)。 步骤:
⑴ 先找出满足 4Φ的解0 Φ;
⑵ 代入(d), 求出 σ x , σ y , xy;
x的奇函数，故 E F 。G 0
⑸ 考察边界条件。
主要边界 y h / 2,
次要边界 x=l 上,
主要边界
应力
最后应力解答为：
σx
6q h3
(l 2
x2)y
q
y h
(4
y2 h2
3) 5
M I
y
q
y h
(
4
y h
2 2
3 5
),
xy
6q h3
x(
h2 4
y
2
)
FS S bI
,
σ
y
q 2
(1
2
函数 Φ Ax3 Bx2 , 求解图示问题的应力及
位移，设在A点的位移和转角均为零。
F
Fb/2
O
x
bb h
A y (h b, 1)
例题4
图中矩形截面的简支梁上，作用有三 角形分布荷载。试用下列应力函数
Φ Ax3 y3 Bxy5 Cx3 y Dxy3 Ex3 Fxy,
求解应力分量。
3. 由应力求位移的方法。
4. 从简支梁受均布荷载的问题中，比较弹力 学和材料力学解法的异同。
在早期应用逆解法和半逆解法，曾经 得出许多平面问题的解答。但是对于有复 杂荷载和边界条件的工程实际问题，是
难以用这些方法找出函数式解答的。我们 可以采用弹性力学的近似解法来求解工程 实际问题。因此，我们不要求读者去求解 新的问题的解答，而是要求读者了解弹性 力学问题是如何求解的，如何满足有关的 方程和边界条件的。从而使读者能阅读和 理解弹性力学已有的解答，并应用到工程 实践中去。
例题2
设单位厚度的悬臂梁在左端受到集中力 和力矩的作用，体力可以不计，l h 如图，
试用应力函数 Φ Axy By2 Cy3 Dxy3求解
应力分量。
Fs
M
o
FN
σ xτ xy
y dy
y
Φ Axy By2 Cy3 Dxy3
h/2
h/2
x
图l 3-5
(l h, 1)
例题3
图中所示的矩形截面柱体，在顶部受有 集中力F 和力矩 M Fb 的作用，试用应力
的应力和边
xo
b
x
o
x
b
y b 2c y 2c
逆解法
例3
设图中所示的矩形长梁，l >>h，试考
察应力函数 Φ
F 2h3
xy(3h2
4y2 )能解决什么
样的受力问题？
o
h/2
h/2
x
l y
( l >>h)
xy
(b)
F
(c)
x
F
M＝Fl
例4
问题提出
梁l×h×1，无体力，只受M作用（力矩/ 单宽，与力的量纲相同）。本题属于纯弯曲 问题。
第三章 平面问题的直角坐标解答
多项式解答 位移分量的求出 简支梁受均布荷载 楔形体受重力和液体压力
1 多项式解答
按Φ 求解
1. 当体力为常量，按应力函数Φ求解平面应 力问题时， 应Φ满足
⑴ A内相容方程 4Φ 0.
(a)
⑵ S = S上应力边界条件,
l x m yx s f x , m y l xy s f y . (b)
材力在许多方面都作了近似处理,所以 得出的是近似解答。
例如：在材力中
几何条件中引用平截面假定 u, ε, σ x
沿 y为直线分布；
平衡条件中，略去 σ y作用，没有考虑微分 体的平衡，只考虑 h d x b 的内力平衡；
边界条件也没有严格考虑； 材力解往往不满足相容条件。
对于杆件，材力解法及解答具有足够 的精度; 对于非杆件，不能用材力解法求 解，应采用弹力解法求解。
⑶ 在给定边界形状S下，由式(b)反推出 各边界上的面力，
f x (lσ x mτ xy )s,
(e)
f y (mσ y lτ xy )s.
逆解法
从而得出，在面力(e)作用下的解答，
就是上述 和应Φ力。
逆解法没有针对性，但可以积累基本 解答。
逆解法
例1 一次式 Φ=ax+by+c,对应于无体力， 无面力，无应力状态。 故应力函数中加减一次式，不影响应力。 例2 二次式 Φ ax2 b，xy分c别y2表示常量
1. 弯应力 σ x与材力相同。
2. 铅直线的转角 u M x 故在任一
y EI 截面x 处，平面截面假设成立。
3.纵向纤维的曲率
1
2v x 2
(常 E曲MI 率)，
同材力。
故在纯弯曲情况下，弹力解与材力解相同。
思考题
弹性力学中关于纯弯曲梁的解答，与材 料力学的解答在应力、形变等方面完全 一致。由此是否可以说在纯弯曲情况下 材料力学中的平截面假设成立？
水平截面上的应力分布如图所示。 σx σy
yx
楔形体解答的应用: 作为重力坝的参考解答, 分缝重力坝接近于平面应力问题， 在坝体中部的应力，接近于楔形体的解答。 重力坝规范规定的解法
——材料力学解法（重力法）。 重力坝的精确分析，可按有限单元法进行。
例题1 已知
(a) Φ Ay 2 (a2 x2 ) BxyC(x2 y2 ); (b) Φ Ax 4 Bx3 yCx2 y2 Dxy2 Ey4 , 试问它们能否作为平面问题的应力函数？
3 简支梁受均布荷载
问题
简支梁 2l h 1 ，受均布荷载q 及两端
。 支撑反力 ql 。
q
ql
o
h/2
x
h/2 ql
l yl
半逆解法
按半逆解法求解。 ⑴ 假设应力分量。 ⑵ 由应力分量推出应力函数的形式。
⑶ 将 Φ代入相容方程，求解 :Φ ⑷ 由 Φ求应力。
对称性条件─由于结构和荷载对称于
y轴，∴ Φ, σ应x ,为σ y 的偶x函数， 为 xy
2 位移分量的求出
问题提出
在按应力求解中，若已得出应力，如何求 出位移？
以纯弯曲问题为例，已知
σ
x
M I
y,
σ y xy 0,
试求解其位移。
归纳：从应力求位移的步骤： 1. 由物理方程求出形变；
2.代入几何方程，积分求 u, v；
3.由边界约束条件确定确定刚体位移分量
u0 , v0 , 。
纯弯曲问题的讨论：
ql
6o
y
qx l
ql
h/2
3
h/2
x
l
(h l, 1)
例题5
矩形截面的柱体受到 顶部的集中力 2F 和 力矩M的作用，不计 体力，试用应力函数
M
2F
45
y
o
b/2 b/2
hq
q
Φ Ay 2 Bxy Cxy3 Dy3
求解其应力分量。
(h b, 1) x
例题6
挡水墙的密
度为 1 ，厚度