第七章-平面直角坐标系基础练习题
人教版七年下数学第七章平面直角坐标系测试题(最新整理)

考点1:点的坐标与象限的关系各个象限的点的坐标符号特征如下:(特别注意的是,坐标轴上的点不属于任何象限.)1、在平面直角坐标中,点M(-2,3)在()A.第一象限B.第二象限C.第三象限D.第四象限2、在平面直角坐标系中,点P(-2,-2x-1)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限3、若点P(a,b)在第四象限,则点M(b-a,a-b)在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4、点M(a,-a-1)不可能在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限5、如果b-a<0,且ab<0,那么点(a,b)在( )A.第一象限B.第二象限C.第三象限, D.第四象限.6、若点P(2,k-1)在第一象限,则k的取值范围是__________7、如果点A(x,y)在第三象限,则点B(-x,y-1)在考点2:点在坐标轴上的特点x轴上的点纵坐标为0, y轴上的点横坐标为0. 坐标原点(0,0)1、若点P(x ,y)的坐标满足xy=0,则点P在()A.原点上 B.x轴上 C.y轴上 D.坐标轴2、点P(m+3,m+1)在x轴上,则P点坐标为()A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)3、已知点P(m,2m-1)在y轴上,则P点的坐标是4、点P(a-1,a 2-9)在x轴负半轴上,则P点坐标是 _______考点3:点到直线的距离点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|,1、点M(-6,5)到x轴的距离是_____,到y轴的距离是______.2、已知点P(x,y)在第四象限,且│x│=3,│y│=5,则点P的坐标是()A.(-3,5) B.(5,-3) C.(3,-5) D.(-5,3)x y3、点P(x,y)位于x轴下方,y轴左侧,且=2 ,=4,点P的坐标是()A.(4,2) B.(-2,-4) C.(-4,-2) D.(2,4)4、若点P 到x 轴的距离为3,到y 轴的距离为5,则点P 的坐标是 ____ ____5、若点P 坐标为(2-a ,3a +6),且点P 到两坐标轴距离相等,则点P 的坐标是 _ _考点4:对称点的坐标关于x 轴对称: A (a ,b )关于x 轴对称的点的坐标为(a ,-b )。
安徽省安庆一中七年级数学下册第七章【平面直角坐标系】基础卷

1.在直角坐标系中,ABC 的顶点()1,5A -,()3,2B ,()0,1C ,将ABC 平移得到A B C ''',点A 、B 、C 分别对应A '、B '、C ',若点()1,4A ',则点'C 的坐标( ) A .()2,0- B .()2,2- C .()2,0 D .()5,12.已知点32,)6(M a a -+.若点M 到两坐标轴的距离相等,则a 的值为( ) A .4 B .6- C .1-或4 D .6-或23 3.如果点A (a ,b )在第二象限,那么a 、b 的符号是( )A .0>a ,0>bB .0<a ,0>bC .0>a ,0<bD .0<a ,0<b 4.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A ()2,1-和B ()2,3--,那么第一架炸机C 的平面坐标是( )A .()2,1B .()3,1-C .()2,1-D .()3,15.在平面直角坐标系中,点A 的坐标为(21a +,3-),则点A 在( )A .第一象限B .第二象限C .第三象限D .第四象限 6.点(,)M x y 在第二象限,且230,40x y -=-=,则点M 的坐标是( )A .(3,2)-B .(3,2)-C .(2,3)-D .(2,3)- 7.在平面直角坐标系中,对于点P (x ,y ),我们把点P ′(-y +1,x +1)叫做点P 的幸运点.已知点A 1的幸运点为A 2,点A 2的幸运点为A 3,点A 3的幸运点为A 4,……,这样依次得到点A 1,A 2,A 3,…,A n .若点A 1的坐标为(3,1),则点A 2020的坐标为( )A .(-3,1)B .(0,-2)C .(3,1)D .(0,4)800412个数为4个,那么a 的取值范围为( )A .﹣1<a ≤0B .0<a ≤1C .1≤a <2D .﹣1≤a ≤1 9.如图,线段OA ,OB 分别从与x 轴和y 轴重合的位置出发,绕着原点O 顺时针转动,已知OA 每秒转动45︒,OB 的转动速度是每秒转动30,则第2020秒时,OA 与OB 之间的夹角的度数为( )A .90︒B .145︒C .150︒D .165︒10.若把点A (-5m ,2m -1)向上平移3个单位后得到的点在x 轴上,则点A 在( ) A .x 轴上 B .第三象限 C .y 轴上 D .第四象限 11.已知点M (12,﹣5)、N (﹣7,﹣5),则直线MN 与x 轴、y 轴的位置关系分别为( ) A .相交、相交 B .平行、平行 C .垂直相交、平行 D .平行、垂直相交二、填空题12.如图,一只甲虫在55⨯的方格(每小格边长为1)上沿着网格线运动.它从A 处出发去看望B .C .D 处的其它甲虫,规定:向上向右走为正,向下向左走为负、如果从A 到B 记为:(1,4)A B →++,从B 到A 记为:(1,4)B A →--,其中第一个数表示左右方向,第二个数表示上下方向.(1)图中A C →(______,______),B C →(______,______),C →______(1+,______);(2)若图中另有两个格点M .N ,且M A →(3,4)a b --,M N →(5,2)a b --,则N A →应记为______.131231114.若点p(a+13,2a+23)在第二,四象限角平分线上,则a=_____.15.点P先向左平移4个单位,再向上平移1个单位,得到点Q(2,-3),则点P坐标为__ 16.在平面直角坐标系中,有点A(a﹣2,a),过点A作AB⊥x轴,交x轴于点B,且AB =2,则点A的坐标是___.17.若P(2-a,2a+3)到两坐标轴的距离相等,则点P的坐标是____________________.18.已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a﹣c|+8b-=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为_____.19.如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为_____.20.在平面直角坐标系中,点A(2,0)B(0,4),作△BOC,使△BOC和△ABO全等,则点C坐标为________21.若点A(-2,n)在x轴上,则点B(n-2,n+1)在第_____象限.三、解答题22.某部队在大西北戈壁滩上进行军事演习,部队司令部把部队分为“蓝军”、“黄军”两方.蓝军的指挥所在A地,黄军的指挥所地B地,A地在B地的正西边(如图).部队司令部在C 地.C在A的北偏东60︒方向上、在B的北偏东30方向上.(1)BAC∠=______°;(2)请在图中确定(画出)C的位置,标出字母C;(3)演习前,司令部要蓝军、黄军派人到C地汇报各自的准备情况.黄军一辆吉普车从B 地出发、蓝军一部越野车在吉普车出发3分钟后从A地出发,它们同时到达C地.已知吉普车行驶了18分钟.A到C的距离是B到C的距离的1.7倍.越野车速度比吉普车速度的2倍多4千米.求越野车、吉普车的速度及B地到C地的距离(速度单位用:千米/时).23.如图,己知()(),2,53,3A C -,将三角形ABC 向右平移3个的单位长度,再向下平移4个单位长度,得到对应的三角形111A B C .(1)画出三角形111A B C ;(2)直接写出点111A B C 的坐标;(3)求三角形111A B C 的面积.24.如图,四边形ABCD 所在的网格图中,每个小正方形的边长均为1个单位长度. (1)建立以点B 为原点,AB 边所在直线为x 轴的直角坐标系;(2)写出点A 、B 、C 、D 的坐标;(3)求出四边形ABCD 的面积.25.已知点P (2x ﹣6,3x +1),求下列情形下点P 的坐标.(1)点P 在y 轴上;23241.正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 2C 3C 2,…按如图所示的方式放置,点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y =x +1和x 轴上,已知点B 1(1,1),B 2(3,2),则B n 的坐标是( )A .(2n ﹣1,2n ﹣1)B .(2n ﹣1,2n ﹣1)C .(2n ﹣1,2n ﹣1)D .(2n ﹣1,2n ﹣1) 2.已知P(a ,b )满足ab=0,则点P 在( )A .坐标原点B .X 轴上C .Y 轴上D .坐标轴上 3.在平面直角坐标系中,与点P 关于原点对称的点Q 为()1,3-,则点P 的坐标是( ) A .()1,3 B .()1,3-- C .()1,3- D .()1,3- 4.点M 在第二象限,距离x 轴5个单位长度,距离y 轴3个单位长度,则M 点的坐标为( )A .(-3,5)B .(5,- 3)C .(-5,3)D .(3,5)5.若点P(3a+5,-6a-2)在第四象限,且到两坐标轴的距离相等,则a 的值为( ) A .-1 B .79- C .1 D .26.已知点A 坐标为()2,3-,点A 关于x 轴的对称点为A ',则A '关于y 轴对称点的坐标为( )A .()2,3--B .()2,3C .()2,3-D .以上都不对7.已知点(224)P m m +,﹣在x 轴上,则点P 的坐标是( ) A .(40), B .(0)4, C .40)(-, D .(0,4)-8.在平面直角坐标系xOy 中,对于点P (x ,y ),我们把点P ′(﹣y +1,x +1)叫做点P 的伴随点.已知点A 1的伴随点为A 2,点A 2的伴随点为A 3,点A 3的伴随点为A 4…,这样依次得到点A 1,A 2,A 3,…,A n ,若点A 1的坐标为(3,1),则点A 2019的坐标为( ) A .(0,﹣2) B .(0,4) C .(3,1) D .(﹣3,1)9210.在平面直角坐标系中,将点A (﹣2,﹣2)先向右平移6个单位长度再向上平移5个单位长度得到点A ',则点A '的坐标是( )A .(4,5)B .(4,3)C .(6,3)D .(﹣8,﹣7) 11.已知点M (12,﹣5)、N (﹣7,﹣5),则直线MN 与x 轴、y 轴的位置关系分别为( ) A .相交、相交 B .平行、平行 C .垂直相交、平行 D .平行、垂直相交二、填空题12.某人从A 点沿北偏东60︒的方向走了100米到达点B ,再从点B 沿南偏西10︒的方向走了100米到达点C ,那么点C 在点A 的南偏东__度的方向上.13.点(1,1)P -向左平移2个单位,向上平移3个单位得1P ,则点1P 的坐标是________. 14.在平面直角坐标系中,与点A (5,﹣1)关于y 轴对称的点的坐标是_____. 15.若点M (5,a )关于y 轴的对称点是点N (b ,4),则(a+b )2020= __16.已知点P (a ,a +1)在平面直角坐标系的第二象限内,则a 的取值范围___. 17.如图,点A 的坐标(-2,3)点B 的坐标是(3,-2),则图中点C 的坐标是______.18.如图,一个机器人从0点出发,向正东方向走3米到达1A 点,记为()3,0;再向正北方向走6米到达2A 点,记为()3,6:再向正西方向走9米到达3A 点,记为()6,6-;再向正南方向走12米到达4A 点,再向正东方向走15米到达5A 点,按如此规律走下去,当机器人走到99A 点时,则99A 的坐标为________.19.三角形A′B′C′是由三角形ABC 平移得到的,点A(-1,4)的对应点为A′(1,-1),若点C′的坐标为(0,0),则点C′的对应点C 的坐标为______.20140021.如果点P (a ﹣1,a +2)在x 轴上,则a 的值为_____.三、解答题22.如图所示,若()34A ,,按要求回答下列问题:(1)在图中建立正确的平面直角坐标系.(2)将ABC 向右平移3个单位,再向下平移2个单位得111A B C ,在图中画出111A B C ,并写出1B 点坐标.(3)求ABC 的面积.23.如图1,长方形OABC 的边OA 在数轴上,O 为原点,长方形OABC 的面积为12,OC 边长为3(1)数轴上点A 表示的数为______.(2)将长方形OABC 沿数轴水平移动,移动后的长方形记为O A B C '''',移动后的长方形O A B C ''''与原长方形OABC 重叠部分(如图2中阴影部分)的面积记为S①设点A 的移动距离AA x '=.当4S =时,x =______.②当S 恰好等于原长方形OABC 面积的一半时,求数轴上点A '表示的数为多少. 24.已知点P(m +2,3),Q(−5,n−1),根据以下条件确定m 、n 的值12325.如图,将△ABC向右平移4个单位长度,再向下平移2个单位长度,得到△A′B′C′.(1)请画出平移后的图形△A′B′C′.(2)写出△A′B'C'各顶点的坐标.(3)求出△A′B′C′的面积.1.已知点32,)6(M a a -+.若点M 到两坐标轴的距离相等,则a 的值为( ) A .4 B .6- C .1-或4 D .6-或23 2.如果点A (a ,b )在第二象限,那么a 、b 的符号是( )A .0>a ,0>bB .0<a ,0>bC .0>a ,0<bD .0<a ,0<b 3.如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O 旋转180︒到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A 在丙位置中的对应点A '的坐标为( )A .()3,1-B .()1,3C .()3,1D .()3,1- 4.在平面直角坐标系中,点()2,1-关于x 轴对称的点的坐标是( )A .()2,1B .()2,1-C .()2,1--D .()2,1- 5.点()1,3P --向右平移3个单位,再向上平移5个单位,则所得到的点的坐标为( ) A .()4,2- B .()2,2 C .()4,8-- D .()2,8- 6.点M 在第二象限,距离x 轴5个单位长度,距离y 轴3个单位长度,则M 点的坐标为( )A .(-3,5)B .(5,- 3)C .(-5,3)D .(3,5) 7.在平面直角坐标系中,点P 在第二象限,且点P 到x 轴的距离为3个单位长度,到y 轴的距离为4个单位长度,则点P 的坐标是( )A .()3,4B .()3,4--C .()4,3-D .()3,4- 8.如图,在棋盘上建立平面直角坐标系,若使“将”位于点(-1,-2),“象”位于点(4,-1),则“炮”位于点( )A .(2,-1)B .(-1,2)C .(-2,1)D .(-2,2) 9.如图,在ABC ∆中,90ACB ∠=︒,AC BC =,点C 的坐标为()2,0-,点B 的坐标为()1,4,则点A 的坐标为( )A .()6,3-B .()3,6-C .()4,3-D .()3,4- 10.在平面直角坐标系xOy 中,对于点P (x ,y ),我们把点P ′(﹣y +1,x +1)叫做点P 的伴随点.已知点A 1的伴随点为A 2,点A 2的伴随点为A 3,点A 3的伴随点为A 4…,这样依次得到点A 1,A 2,A 3,…,A n ,若点A 1的坐标为(3,1),则点A 2019的坐标为( ) A .(0,﹣2) B .(0,4) C .(3,1) D .(﹣3,1) 11.若点P (﹣m ,﹣3)在第四象限,则m 满足( )A .m >3B .0<m≤3C .m <0D .m <0或m >3二、填空题12.小华在小明南偏西75°方向,则小明在小华______方向.(填写方位角) 13.若点P 位于x 轴上方,y 轴左侧,距离x 轴4个单位长度,距离y 轴2个单位长度,则点P 的坐标是_____________.14.点P 先向左平移4个单位,再向上平移1个单位,得到点Q(2,-3),则点P 坐标为__ 15.如图,点A 的坐标(-2,3)点B 的坐标是(3,-2),则图中点C 的坐标是______.161111217.在平面直角坐标系中,将点A (5,﹣8)向左平移得到点B (x +3,x ﹣2),则点B 的坐标为_____.18.如图点 A 、B 的坐标分别为(1,2)、(3,0),将△AOB 沿 x 轴向右平移,得到△CDE . 已知点 D 在的点 B 左侧,且 DB =1,则点 C 的坐标为 ____ .19.如图,已知1(1,0)A ,2(1,1)A ,3(1,1)A -,4(1,1)A --,5(2,1)A -,则2020A 的坐标为_______.20.点A (m ,﹣3),点B (2,n ),AB //x 轴,则n=_____.21.若点()35,62P a a +--到 两坐标轴的距离相等,则a 的值为____________三、解答题22.已知△ABC 在平面直角坐标系中的位置如图所示.将△ABC 向右平移6个单位长度,再向下平移4个单位长度得到△A 1B 1C 1.(图中每个小方格边长均为1个单位长度)(1)在图中画出平移后的△A 1B 1C 1;(2)直接写出△A 1B 1C 1各顶点的坐标;(3)求△ABC 的面积.23.在如图的直角坐标系中,将三角形ABC 平移后得到三角形111A B C ,他们的对应点坐标如下表所示:ABC(,0)A a (3,0)B (5,5)C 111A B C △ 1(4,2)A 1(7,)B b1(,)C c d (1)观察表中各对应点坐标变化,写出平移规律:________.(2)在坐标系中画出两个三角形.(3)求出111A B C △面积.24.在平面直角坐标系中,点P(2﹣m ,3m +6).(1)若点P 与x 轴的距离为9,求m 的值;(2)若点P 在过点A(2,﹣3)且与y 轴平行的直线上,求点P 的坐标.25.如图,平面直角坐标系中,已知点A (-3,3),B (-5,1),C (-2,0),P ( )是△ABC 的边AC 上任意一点,△ABC 经过平移后得到△A 1B 1C 1,点P 的对应点为 P 1 ( a +6,b+2 )1111 2111(3)求△ABC的面积.。
人教版七年级数学下册第七章 平面直角坐标系练习(含答案)

第七章 平面直角坐标系一、单选题1.下列数据不能确定物体位置的是( ) A .电影票5排8号 B .北偏东30°C .希望路25号D .东经118︒,北纬40︒2.点P 的横坐标是一3,且到x 轴的距离为5,则点P 的坐标是( ) A .()3,5-B .()3,5--C .()5,3-或()3,5-D .()3,5-或()3,5--3.若点A (2,﹣2),B (﹣1,﹣2),则直线AB 与x 轴和y 轴的位置关系分别是( ) A .相交,相交 B .平行,平行 C .平行,垂直相交 D .垂直相交,平行4.点P(2,3)到y 轴的距离是( ) A .3B .2C .1D .05.点A 到x 轴的距离是3,到y 轴的距离是6,且点A 在第二象限,则点A 的坐标是( ) A .(-3,6)B .(-6,3)C .(3,-6)D .(6,-3)6.如果()5,y 在第四象限,则y 的取值范围是( ) A .0y >B .0y <C .0y ≥D .0y ≤7.如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),则“炮”位于点( )A.(1,3)B.(﹣2,1)C.(﹣1,2)D.(﹣2,2)8.如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )A.(2,3),(3,2)B.(3,2),(2,3)C.(2,3),(-3,2)D.(3,2),(-2,3) 9.如图,在边长为1的正方形网格中,两个三角形的顶点都在格点(网线的交点)上,下列方案中不能把△ABC平移至△DEF位置的是()A.先把△ABC沿水平方向向右平移4个单位长度,再向上平移3个单位长度B.先把△ABC向上平移3个单位长度,再沿水平方向向右平移4个单位长度C.把△ABC沿BE方向移动5个单位长度D.把△ABC沿BE方向移动6个单位长度10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2019次运动后,动点P的坐标是()A.(2018,0)B.(2017,1)C.(2019,1)D.(2019,2)二、填空题11.如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2020次变换后,等边△ABC的顶点C 的坐标为___________.P-先向右平移2个单位,再向下平移3个单位,得到点P',则点P'的坐标12.将点(2,3)为__________.13.若点P(3a﹣2,2a+7)在第二、四象限的角平分线上,则点P的坐标是_____.14.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动一个单位,依次得到点P1(0,1);P2(1,1);P3(1,0);P4(1,﹣1);P5(2,﹣1);P6(2,0)……,则点P2019的坐标是_____.三、解答题15.如图所示,△BCO是△BAO经过折叠得到的.(1)图中A与C的坐标之间的关系是什么?(2)如果△AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?16.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.(1)写出汽车站和消防站的坐标;(2)某星期日早晨,小英同学从家里出发,沿(3,2)→(3,−1)→(0,−1)→(−1,−2)→(−3,−1)的路线转了一下,又回到家里,写出路上她经过的地方.17.已知,点P(2m﹣6,m+2).(1)若点P在y轴上,P点的坐标为;(2)若点P和点Q都在过A(2,3)点且与x轴平行的直线上,AQ=3,求Q点的坐标.18.已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.(1)分别写出B、B'的坐标:B______;B′______;(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为______;(3)求△ABC的面积答案2.D3.C4.B5.B6.B7.B8.D9.D10.D11(-1)12.(0,0)13.(﹣5,5).14.(673,0)15.解:(1)△A(5,3),C(5,-3)△点A与点C的横坐标相同,纵坐标互为相反数;(2)△△BCO和△BAO中对应点坐标,横坐标相同,纵坐标互为相反数,△△AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是:N(x,-y)16.(1)汽车站(1,1),消防站(2,﹣2);(2)(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.17.解:(1)△点P在y轴上△2m-6=0△m+2=3+2=5△P(0,5)(2)根据题意可得PQ△x轴,且过A(2,3)点,△m+2=3△m=1△2m-6=-4△P(-4,3)△PQ=3△Q点横坐标为-4+3=-1,或-4-3=-7△Q点坐标为(-1,3)或(-7,3)18.解:(1)由图知点B′的坐标为(2,0)、点B坐标为(-2,-2),故答案为:(2,0)、(-2,-2);(2)由图知△ABC向左平移4个单位,再向下平移2个单位可得到△A'B'C′,则平移后△A'B'C内的对应点P′的坐标为(a-4,b-2),故答案为:(a-4,b-2);(3)△ABC的面积为2×3-12×1×3-12×1×1-12×2×2=2。
2024年第七章平面直角坐标系课堂练习题及答案7.1.2 平面直角坐标系

基础通关
能力突破
素养达标
(2)已知点C(m,2),若点B和点C的k系和点为点D,且点D的横坐标等于纵
坐标.
①求m的值;
解:∵点D为B(2,0)和C(m,2)的k系和点,
∴设点D的坐标为(x,y),则x=2k+mk,y=2k,即D(2k+mk,2k).
∵点D的横坐标等于纵坐标,∴2k+mk=2k.∴mk=0.
平面直角坐标系
能力突破
素养达标
能力突破
10.如果点M(m,-n)在第二象限,则点N(m-2,n-2)在 ( C )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
11.[2023·廊坊霸州市部分学校期中]已知点P的坐标是(m+2,2m-4),若点
P在y轴上,则m=
-2
;若点P到x轴的距离是6,则m=
A.(3,1)
B.(2,0)
C.(0,4)
D.(-2,-3)
7.已知点P在第四象限,且到x轴的距离为2,到y轴的距离为4,则点P的坐
标为 ( A )
A.(4,-2)
B.(-4,2)
C.(-2,4)
D.(2,-4)
(2,0)或(0,-2) .
8.若点P(m+3,m+1)在坐标轴上,则点P的坐标为
1
2
3
4Hale Waihona Puke 5678
9
7.1.2
基础通关
平面直角坐标系
能力突破
素养达标
各象限内,坐标轴上点的坐标特点
5.在平面直角坐标系中,点A(6,-7)位于 ( D )
A.第一象限
B.第二象限
C.第三象限
第七章平面直角坐标系基础训练2022-2023学年七年级数学下册人教版
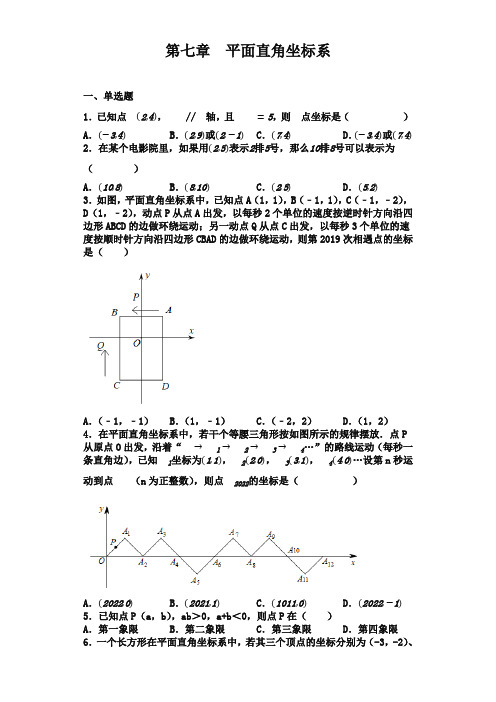
第七章平面直角坐标系一、单选题1.已知点A(2,4),AA//A轴,且AA=5,则A点坐标是()A.(−3,4)B.(2,9)或(2,−1)C.(7,4)D.(−3,4)或(7,4) 2.在某个电影院里,如果用(2,5)表示2排5号,那么10排8号可以表示为()A.(10,8)B.(8,10)C.(2,5)D.(5,2)3.如图,平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2019次相遇点的坐标是()A.(﹣1,﹣1)B.(1,﹣1)C.(﹣2,2)D.(1,2)4.在平面直角坐标系中,若干个等腰三角形按如图所示的规律摆放.点P 从原点O出发,沿着“A→A1→A2→A3→A4…”的路线运动(每秒一条直角边),已知A1坐标为(1,1),A2(2,0),A3(3,1),A4(4,0)…设第n秒运动到点A A(n为正整数),则点A2022的坐标是()A.(2022,0)B.(2021,1)C.(1011,0)D.(2022,−1) 5.已知点P(a,b),ab>0,a+b<0,则点P在()A.第一象限B.第二象限C.第三象限D.第四象限6.一个长方形在平面直角坐标系中,若其三个顶点的坐标分别为(-3,-2)、(2,-2)、(2,1),则第四个顶点坐标为()A.(2,-5)B.(2,2)C.(3,1)D.(-3,1)7.若点A在第二象限,且点A到A轴的距离为1,到A轴的距离为2,则点A的坐标为()A.(2,−1)B.(1,−2)C.(−2,1)D.(−1,2) 8.如图,已知A:(1,0).A2(1,-1),A3(-1,-l).A4 (-1, 1), A5 (2, 1),...则点A2020的坐标是()A.(506,505) B.(-505,-505) C.(505,-505) D.(-505,505) 9.如图所示,在平面直角坐标系中,已知A(0,0),A(2,0),△AA1A是等腰直角三角形,且∠A1=90°,把△AA1A绕点A顺时针旋转180°,得到△AA2A;把△AA2A绕点A顺时针旋转180°,得到△AA3A,……,依此类推,则旋转2017次后得到的等腰直角三角形的直角顶点A2018的坐标为()A.(4034,1)B.(4033,−1)C.(4036,1)D.(4035,−1) 10.如图所示的象棋盘上,若“帅”位于点(﹣1,﹣2)上,“相”位于点(1,﹣2)上,则“炮”位于点()A.(﹣2,﹣2)B.(﹣2,1)C.(﹣4,1)D.(4,﹣1)二、填空题11.若点P(a-2,a)在第二象限,则a的取值范围是__________.12.已知点P的坐标是(a+2,3),且点P到两坐标轴的距离相等,则点P 的坐标是__________13.已知点A(A−2,A+1)在y轴上,则A点坐标为 ________.14.如图,这一部分棋盘是两个五子棋爱好者的对弈图,以O当原点建立坐标系,若黑子A坐标与(7,5)和白子B的位置如图所示,为了不让白方获胜,此时黑方应该下在坐标为_______的位置处.15.观察中国象棋的棋盘,以红“帅”(红方“5”的位置)为坐标原点建立平面直角坐标系后,发现红方“马”的位置可以用一个数对(2,4)来表示,则红“马”到达A点后,A点的位置可以用数对表示为__________.三、解答题16.已知三角形AAA与三角形A′A′A′在平面直角坐标系中的位置如图(1)分别写出点A、A′的坐标:A______,A′______;(2)若点A(A,A)是三角形AAA内部一点,则平移后三角形A′A′A′内的对应点A的坐标为______;(3)求三角形AAA的面积.17.如图,在边长为1个单位长的正方形网格图中,将三角形ABC经过平移后得到三角形A1B1C1的图形,点A,B,C均在格点上,其中B(1,﹣3),B1(5,0).(1)在网格图中画出平面直角坐标系xOy及三角形A1B1C1;(2)写出点A,C和点A1的坐标.18.如图,已知△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(﹣1,﹣4),C(2,﹣3).(1)将△ABC先向右平移4个单位,再向上平移6个单位,得到△A1B1C1,作出△A1B1C1,线段AC在平移过程中扫的面积为;(2)作出△A1B1C1关于y轴对称的图形△A2B2C2,则坐标C2为;(3)若△ABD与△ABC全等,则点D的坐标为(点C与点D不重合)19.如图,在平面直角坐标系中,△ABC 的三个顶点的坐标分别为:A(-1,2),B(-2,-1), C(2,0).(1)作图:将△ABC先向右平移3个单位,再向上平移 4个单位,则得到△A1B1C1,作出△A1B1C1;(2)写出下列点的坐标:A1;B1;C1;(3)△ABC的面积为.20.如图是由边长为1个单位长度的小正方形组成的网格,△ABC的顶点都在格点上.(1)画出△ABC关于y轴对称的△A1A1A1;(2)把△A1A1A1向下平移3个单位,再向左平移1个单位得到△A2A2A2,请你画出△A2A2A2;(3)若点A(A,A)在△A1A1A1上,与△A2A2A2上的点Q是对应点,写出点Q的坐标.21.三角形ABC三点的坐标为A(-2,1),B(1,2),C(k,h)(1)在直角坐标系上画出点A,B.(2)若点C(-2,-1)时,求三角形ABC的面积.(3)若点C在y轴上,当三角形ABC的面积为6时,求点C的坐标.。
人教版七年级数学下册第七章 平面直角坐标系练习(含答案)

第七章 平面直角坐标系一、单选题1.兰州是古丝绸之路上的重镇,以下准确表示兰州市的地理位置的是( )A .北纬3403︒'B .在中国的西北方向C .甘肃省中部D .北纬3403︒',东经10349︒' 2.若x 轴上的点P 到y 轴的距离为3,则点P 的坐标为( )A .(3,0)B .(3,0)或(–3,0)C .(0,3)D .(0,3)或(0,–3)3.在平面直角坐标系中,点P 的坐标是(2,3),则点P 到y 轴的距离是( ) A .2 B .3 C .13 D .44.下列各点中,位于平面直角坐标系第四象限的点是( )A .(1,2)B .(﹣1,2)C .(1,﹣2)D .(﹣1,﹣2)5.点(3)P m ,是坐标平面内的一点,则这点在( )A .第一象限B .第四象限C .第一象限或第四象限D .第一象限或第四象限或x 轴上6.甲、乙两名同学下棋,甲执圆子,乙执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示,甲将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,甲放的位置是( )A .(-2,1)B .(-1,1)C .(-1,0)D .(-1,2) 7.在平面直角坐标系中,已知A (﹣2,3),B (2,1),将线段AB 平移后,A 点的坐标变为(﹣3,2),则点B 的坐标变为( )A .(﹣1,2)B .(1,0)C .(﹣1,0)D .(1,2) 8.如图,//,//AB CD AD BC 且平行于x 轴,下列说法正确的是( )A .A 和D 关于y 轴对称B .A 和B 关于x 轴对称C .B 和C 的纵坐标相同D .C 和D 的横坐标相同9.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )A .(﹣3,3)B .(3,2)C .(1,3)D .(0,3) 10.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点()1,1,第2次接着运动到点()2,0,第3次接着运动到点()3,2,···,按这样的运动规律,经过第2020次运动后,动点P 的坐标是( )A .()2020,1B .()2020,0C .()2020,2D .()2019,0二、填空题 11.如果用(7,8)表示七年级八班,那么八年级七班可表示成______.12.已知点M (a ﹣1,2a +3)关于原点对称的点在第四象限,则a 的取值范围是_____. 13.点B 在y 轴上且到点A (0,4)的线段长度是5,点B 的坐标是____14.在平面直角坐标系中,一个点从原点O 出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点1A ,第二次移动到点2A ……第n 次移动到点n A ,则点2019A 的坐标是__________.三、解答题15.已知点P 的坐标为()2,36a a -+.(1)若点P 在y 轴上,求P 点坐标.(2)若点P 到两坐标轴的距离相等,求点P 的坐标.16.在平面直角坐标系中,已知点()1,3M a +-,()3,21N a +.(1)若点M 在y 轴上,求点N 的坐标;(2)若MN x P 轴,求a 的值.17.如图是某校的平面示意图,已知图书馆、行政楼的坐标分别为()()3,2,2,3.-完成下列问题:()1请根据题意在图上建立直角坐标系,并写出图上信息楼综合楼的坐标;()2在图中用点P 表示体育馆()1,3--的位置18.(1)如图,要把小河里的水引到田地A 处,就作AB ⊥l(垂足为B),沿AB 挖水沟,水沟最短.理由是___________.(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式._____________________________ .(3)比较大小:3718-______ 13- . (4)已知22-2m x y -与423m n x y +是同类项,则m -3n 的平方根是___.(5)已知点P 的坐标为(3a+6,2﹣a ),且点P 到两坐标轴的距离相等,则点P 的坐标是______.(6) 如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P 的坐标是______________答案1.D2.B3.A4.C5.D6.B7.B8.C9.C10.B11.(8,7)12.﹣32<a <1 13.(0,9)和(0,-1).14.()1009,015.(1)由题意得:2-a=0,解得:a=2,3a+6=12,所以点P 的坐标为(0,12);(2)根据题意得|2-a|=|3a+6|,所以2-a=3a+6或2-a=-(3a+6),解得a=-1或a=-4,当a=-1时,2-a=3,3a+6=3,所以点P 坐标为(3,3);当a=-4时,2-a=6,3a+6=-6,所以点P 坐标为(6,-6),综上点P 的坐标为(3,3)或(6,-6).16.解:(1)∵M 在y 轴上∴10a +=即1a =-∴()3,1N -(2)∵MN ∥x 轴∴213a +=-即2a =-.17.解:(1)直角坐标系如图所示.∴信息楼的坐标为:(1,-2),综合楼的坐标为:(-5,-3);(2)点P 的位置如图所示.18.(1)∵AB ⊥直线l ,∴AB 最短,理由是:垂线段最短,故答案为:垂线段最短;(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式是如果两条直线都和第三条直线平行,那么这两条直线也互相平行,故答案为:如果两条直线都和第三条直线平行,那么这两条直线也互相平行;(3)3718-12-,且12-<13-, 3718-<13-, 故答案为:<;(4)∵22-2m x y -与423m n x y +是同类项,∴m-2=4,2m+n=2,∴m=6,n=-10,∴m-3n=6+30=36,∴m -3n 的平方根是6±,故答案为:6±;(5)∵点P 的坐标为(3a+6,2﹣a ),且点P 到两坐标轴的距离相等,∴36(2)a a +=±-,∴362a a +=-或36(2)a a +=--,∴a=-1或a=-4;当a=-1时,点P 的坐标是(3,3),当a=-4时,点P 的坐标是(-6,6),故答案为:(3,3)或(-6,6);(6)第1次运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),第4次运动到点(4,0),第5次运动到点(5,1),第6次运动到点(6,0),第7次运动到点(7,2)第8次运动到点(8,0),L ,由此得到规律:图形每4次变化一次,且点的横坐标与点运动的次数相同,纵坐标依次是1、0、2、0循环变化,∵201845042÷=L ,∴经过第2018次运动后,动点P 的坐标是(2018,0),故答案为:(2018,0)6) (2018,0)。
七年级数学(下)第七章《平面直角坐标系》练习题含答案
七年级数学(下)第七章《平面直角坐标系》练习题一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.点P(3,–2)在平面直角坐标系中所在的象限是A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】由点的坐标特征可得点P(3,–2)在第四象限,故选D.2.已知点P位于x轴上方,到x轴的距离为2,到y轴的距离为5,则点P坐标为A.(2,5)B.(5,2)C.(2,5)或(–2,5)D.(5,2)或(–5,2)【答案】D【解析】由题意得P(5,2)或(–5,2).故选D.3.在平面直角坐标系中,点P在x轴的下方,y轴右侧,且到x轴的距离为5,到y轴距离为1,则点P的坐标为A.(1,–5) B.(5,1)C.(–1,5) D.(5,–1)【答案】A故选A.4.如图,小手盖住的点的坐标可能为A.(5,2) B.(–6,3)C.(–4,–6) D.(3,–4)【答案】C【解析】根据图示,小手盖住的点在第三象限,第三象限的点坐标特点是:横负纵负;分析选项可得只有C符合.故选C.5.在平面直角坐标系中,将点P(–1,–3)向右平移2个单位后得到的点位于A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】先确定移动后的点,再根据各象限符号特征进行判断.由题意得移动后的点为(1,–3),再由1>0和–3<0可知移动后的该点位于第四象限.故选D.二、填空题:请将答案填在题中横线上.6.点A的坐标(–3,4),它到y轴的距离为__________.【答案】3【解析】点A的坐标(–3,4),它到y轴的距离为|–3|=3,故答案为:3.7.直线a平行于x轴,且过点(–2,3)和(5,y),则y=__________.【答案】3∴y=3.故填3.8.在平面直角坐标系中,若点A坐标为(–1,3),AB∥y轴,线段AB=5,则B点坐标为__________.【答案】(–1,8)或(–1,–2)【解析】∵AB与y轴平行,∴A、B两点的横坐标相同,又AB=5,∴A点纵坐标为:3+5=8,或3−5=−2,∴A点的坐标为:(−1,8)或(−1,−2).故答案为:(−1,8)或(−1,−2).9.在平面直角坐标系中,已知点A的坐标为(a–2,7–2a),若点A到两坐标轴的距离相等,则a的值为__________.【答案】3或5【解析】∵点A(a–2,7–2a)到两坐标轴的距离相等,∴|a–2|=|7–2a|,∴a–2=7–2a或a–2=–(7–2a),解得a=3或a=5.故答案为:3或5.10.将点A(–2,–3)先向右平移3个单位长度再向上平移4个单位长度得到点B,则点B所在象限是第__________象限.【答案】一【解析】将点A(–2,–3)先向右平移3个单位长度再向上平移4个单位长度得到点B(–2+3,–3+4),即(1,1),在第一象限.故答案为:一.三、解答题:解答应写出文字说明、证明过程或演算步骤.11.在如图所示的平面直角坐标系中,用有序数对表示出A,B,C,D各点的位置.【解析】A(1,2),B(2,1),C(–2,1),D(–1,–2).12.在直角坐标系中,标出下列各点的位置,并写出各点的坐标.(1)点A在x轴上,位于原点的左侧,距离坐标原点4个单位长度;(2)点B在y轴上,位于原点的上侧,距离坐标原点4个单位长度;(3)点C在y轴的左侧,在x轴的上侧,距离每个坐标轴都是4个单位长度.【解析】(1)如图所示:A(-4,0);(2)如图所示:B(0,4);(3)如图所示:C(-4,4).。
七年级数学上册-第七章《平面直角坐标系》解析版
第七章《平面直角坐标系》同步单元基础与培优高分必刷卷一:选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.根据下列表述,能够确定具体位置的是()A .北偏东25°方向B .距学校800米处C .国家大剧院音乐厅4排D .东经116°20″北纬39°56″【答案】D【分析】根据确定一个点的具体位置的方法判断即得.确定一个点的具体位置的方法是确定点所在的方向和距离,或用有序数对.【详解】A.北偏东25°方向不能确定一个点的具体位置,缺少距离,故此选项错误;B.距学校800米处不能确定一个点的具体位置,缺少方向,故此选项错误;C.国家大剧院音乐厅4排不能确定一个点的具体位置,应具体到8排几号,故此选项错误;D.东经116°20″北纬39°56″可以确定一个点的具体位置,故此选项正确.故选:D .【点睛】本题考查确定位置的方法,熟练掌握确定一个点的具体位置是解题的关键.2.象棋起源于中国,中国象棋文化历史悠久.如图,是中国象棋棋盘的一部分,若“帅”位于点()1,1-,“炮”位于点()2,1上,则“兵”位于点()上A .()0,2B .()2,3-C .()3,0-D .()1,2-【答案】D【分析】本题考查了根据点的位置求点的坐标,根据纵坐标在上用加法,横坐标在左用减法,即可求出“兵”的坐标,解题的关键是找到点所对应的横坐标和纵坐标,再写出点的坐标.【详解】解: “兵”在“炮”的上面一行,∴“兵“的纵坐标是112+=,“兵”在“帅”的左面第二格上,∴“兵”的横坐标是121-=-,∴“兵”的坐标是()1,2-,故选:D .3.平面直角坐标系中,已知(,3)A a ,(3,)B b 位置如图所示,则下列关系一定成立的是()A .3a <B .3b >C .a b >D .a b<A 、3a <,故A 符合题意;B 、3b <,故B 不符合题意;C 、a 与b 的大小关系不能确定,故D 、a 与b 的大小关系不能确定,故故选:A .4.如图,在直角坐标系中,已知点()3,1A --,点()2,1B -,平移线段AB ,使点A 落在()10,1A -,点B 落在点1B ,则点1B 的坐标为()A .()0,2B .()1,3C .()2,2D .()1,1故选:D .5.直角坐标系中,点()2,3A 向右平移2个单位得到点1A ,则1A 点的坐标是()A .()4,3B .()-2,1C .()0,3D .()4,3-【答案】A【分析】本题考查了坐标与图形的变化——平移,根据点向右平移,横坐标加,纵坐标不变,即可解答.【详解】∵点()2,3A 向右平移2个单位得到点1A ,∴点1A 的横坐标为:224+=,纵坐标为3,∴点1A 的坐标为()4,3.故选:A6.已知点(),P a b 在第二象限,且3a =,8b =,则点P 的坐标为()A .()3,8B .()3,8--C .()3,8-D .()3,8-7.如图,在平面直角坐标系中,点A 的坐标是()3,0-,点B 的坐标是()0,2-,将线段AB 平移,使其一个端点到点()2,2C ,则平移后另一个端点的坐标是()A .()5,0B .()1,4-C .()5,0或()1,5-D .()5,0或()1,4-【答案】D【分析】分两种情况进行讨论求解即可.【详解】解:①当,A C 为对应点时,∵()30A -,,()2,2C ∴平移规则为:先向右平移5个单位长度,再向上平移2个单位长度,∴点B 的对应点为:()05,22+-+,即为:()5,0;②当,B C 为对应点时,∵()0,2B -,()2,2C ∴平移规则为:先向右平移2个单位长度,再向上平移4个单位长度,∴点A 的对应点为:()32,04-++,即为:()1,4-;综上:平移后另一个端点的坐标是()5,0或()1,4-;故选D .【点睛】本题考查坐标轴下的平移.解题的关键是确定平移规则.8.如图,在平面直角坐标系中,等腰直角三角形OA 1A 2的直角边OA 1在y 轴的正半轴上,且OA 1=A 1A 2=1,以OA 2为直角边作第二个等腰直角三角形OA₂A 3,以OA 3为直角边作第三个等腰直角三角OA 3A 4,…,依此规律,得到等腰直角三角形OA 2017A 2018,则点A 2017的坐标为()A .(0,21008)B .(21008,0)C .(0,21007)D .(21007,0)9.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点()1,1,第2次接着运动到点()2,0,第3次接着运动到点()3,2,⋯,按这样的运动规律,经过第25次运动后,动点P 的坐标是()A .()26,0B .()25,0C .()25,1D .()25,2【详解】解:由题可知:每次运动后点的横坐标都增加1,所以第25次运动后点的横坐标为25;点P 的纵坐标按1,0,2,0,1,0,2,0,……,重复出现,每4个数为一个循环,25461÷= ,∴经过第25次运动后,动点P 的坐标是()25,1.故选C .10.数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算1234100+++++ 时,用到了一种方法,将首尾两个数相加,进而得到100(1100)12341002⨯++++++= .人们借助于这样的方法,得到(1)12342n n n ++++++=(n 是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点(),i i i A x y ,其中1,2,3,,,i n = ,且,i i x y 是整数.记n n n a x y =+,如1(0,0)A ,即120,(1,0)a A =,即231,(1,1)a A =-,即30,a = ,以此类推.则下列结论正确的是()A .202340a =B .202443a =C .2(21)26n a n -=-D .2(21)24n a n -=-二:填空题(本大题共7小题,每小题4分,共28分)11.已知点(),P x y 在第二象限,且3x =,5y =,则点P 的坐标是.12.下图是贵州省部分城市在地图中的位置,若贵阳的位置坐标为()13,,安顺的位置坐标为()01,,请在图中建立适当的直角坐标系,写出遵义的坐标为.【答案】()4,5【分析】本题主要考查了实际问题中用坐标表示位置,根据贵阳和安顺的坐标确定出坐标轴和原点的位置,然后画出坐标系即可得到答案.【详解】解:根据题意可得如下坐标系,∴遵义的坐标为()4,5,故答案为:()4,5.13.若把点523a a -+(,)向上平移3个单位长度后,该点正好落在x 轴上,则a 的值为.【答案】3-【分析】本题主要考查坐标与图形变化—平移,解题的关键是掌握平移的规律:横坐标,右移加,左移减;纵坐标,上移加,下移减.根据平移坐标的变化规律列方程求解即可.【详解】解:∵点523a a -+(,)向上平移3个单位长度后为526a a -+(,),平移后正好落在x 轴上,∴260a +=,解得3a =-.故答案为:3-14.在直角坐标系中,把点A 先向右平移1个单位,再向下平移3个单位得到点B .若点B 的横坐标和纵坐标互为相反数,则点A 的横坐标和纵坐标的和是.【详解】解:设(),A x y ,∵把点A 先向右平移1个单位,再向下平移3个单位得到点B ∴()1,3B x y +-,∵点B 的横坐标和纵坐标互为相反数,∴130x y ++-=,∴312x y +=-=,故答案为:2.15.对于平面直角坐标系中任意两点()11,A x y ,()22,B x y 定义一种新运算“※”;()()()11221221,,,A B x y x y x y x y ==※※,根据这个规则计算:()(),2,335=-※.【答案】(10,9)-;【分析】本题考查新运算,平面直角坐标系;根据()()()11221221,,,A B x y x y x y x y ==※※代入求解即可得到答案;【详解】解:由题意可得,()()2,33,5(25,33)(10,9)-=-⨯⨯=-※,故答案为:(10,9)-.16.如图,一个机器人从点O 出发,向正西方向走2m 到达点1A ;再向正北方向走4m 到达点2A ,再向正东方向走6m 到达点3A ,再向正南方向走8m 到达点4A ,再向正西方向走10m 到达点5A ,…按如此规律走下去,当机器人走到点2021A 时,点2021A 的坐标为.17.如图,在平面直角坐标系中,已知点()()()111112(1)2A B C D ----,,,,,,,,点P ,点Q 分别从点A ,点C 同时出发,沿长方形ABCD 的边作环绕运动,点P 按逆时针方向以每秒2个单位长度的速度匀速运动,点Q按顺时针方向以每秒3个单位长度的速度匀速运动,则第2023秒P,Q两点相遇地点的坐标是.【点睛】本题考查了点坐标的规律探究.解题的关键在于根据题意正确的推导一般性规律.三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤)18.在平面直角坐标系中,已知点()21,3M m m ++,点()2,1N .(1)若点M 在第一象限,且点M 到x 轴的距离与到y 轴的距离相等,求m 的值;(2)若线段MN ∥x 轴,求线段MN 的长度.【答案】(1)2m =;(2)5.【分析】(1)根据第一象限内点的坐标符号特征及点M 到x 轴的距离与到y 轴的距离相等可得321m m +=+,解之即可求解;(2)根据线段//MN x 轴,得到点M N ,的纵坐标相等,即31m +=,解之即可求解;本题考查了点到坐标轴的距离,平行于坐标轴的直线上点的坐标特征,解题的关键是掌握点到x 轴距离等于纵坐标的绝对值,到y 轴距离等于横坐标的绝对值;平行于x 轴的直线上的点纵坐标相等,平行于y 轴的直线上的点横坐标相等.【详解】(1)解:∵M 在第一象限,点M 到x 轴的距离与到y 轴的距离相等,∴321m m +=+,解得2m =;(2)解:∵线段MN ∥x 轴,∴点M N ,的纵坐标相等,即31m +=,解得2m =-,∴()3,1M -,∴线段MN 的长度为()235--=.19.中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图①中“马”所在的位置可以直接走到点A 、B 处.(1)如果“帅”位于点(0,0),“相”位于点(4,2),则“马”所在的点的坐标为,点C的坐标为,点D的坐标为.(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,并用坐标表示.三个顶点的坐标分别为20.如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,ABC()()()----,,,.A B C23,42,10(1)将ABC 先向右平移4个单位长度,再向下平移3个单位长度,得到A B C ''' (点A 、B 、C 的对应点分别为A B C '''、、),请在图中作出A B C ''' ′;(2)在(1)的条件下,连接AA C C ''、,求四边形AA C C ''的面积.(2)四边形AA C C ''的面积为A AC S ' 21.如图,在平面直角坐标系中,点A ,B 坐标分别为(),0a ,(),a b ,点C 在y 轴上,且BC x ∥轴,a ,b 满足340a b -+-=.一动点P 从原点出发,以每秒2个单位长度的速度沿着O A B C O ----的路线运动(点P 首次回到点O 时停止),运动时间为t 秒()0t ≠.(1)直接写出点A ,B 的坐标;(2)点P 在运动过程中,是否存在点P 到x 轴的距离为12t 个单位长度的情况,若存在,求出点P 的坐标,若不存在,请说明理由.22.在平面直角坐标系中,对于点()A x y ,,若点B 的坐标为()x ay ax y ++,,其中a 为常数,则称点B 是点A 的“a 倍相关点”.例如,点()1,2A 的“3倍相关点”B 的横坐标为:1327+⨯=,纵坐标为:3125⨯+=,所以点A 的“3倍相关点”B 的坐标为()75,.(1)已知点()46M -,的“12倍相关点”是点()N s t ,,求2s t +的值;(2)已知点()12P m ,的“2-倍相关点”是点Q ,且点Q 在y 轴上,求点Q 到x 轴的距离.23.如图1:在平面直角坐标系内,O 为坐标原点,线段AB 两端点在坐标轴上且点()4,0A -,点()0,3B ,将AB 向右平移4个单位长度至OC 的位置.(1)直接写出点C 的坐标______;(2)如图2,过点C 作CD x ⊥轴于点D ,在x 轴正半轴有一点()1,0E ,过点E 作x 轴的垂线,在垂线上有一动点P ,求三角形PCD 的面积;(3)如图3,在(2)的条件下,连接AC ,当ACP △的面积为332时,求点P 的坐标.CD x ⊥轴,4D C x x ∴==,413DE ∴=-=,∵3CD =,PE x ⊥轴,12PCD S CD DE ∴=⋅ 1332=⨯⨯92=;故三角形PCD 的面积为(3)解:①当P 在AC 如图,将PAC △补成直角梯形设()1,P m ,AG DF m ∴==,GP AE ==∴PAC AGP ACFG S S S S =-- 梯形()1122FG CF AG AG GP =⋅+-⋅12PAC S AD CD =⋅ 1832=⨯⨯33122=<,∴此种情况不存在;③当P 在x 的下方时,如图,将PAC △补成直角梯形设()1,P m ,AN DM m ∴==-,NP AE =∴PAC ANP ACMN S S S S =-- 梯形24.如图,已知长方形ABCO 中,8,4AB BC ==,以点O 为原点,,OA OC 所在直线为x 轴和轴建立平面直角坐标系.(1)写出,,A B C 三点的坐标;(2)若点P 从点C 出发,以2个单位长度/秒的速度向CO 方向移动(不超过点O ),点Q 从原点O 出发,以1个单位长度/秒的速度向OA 方向移动(不超过点A ).设,P Q 两点同时出发,在它们移动的过程中,四边形OPBQ 的面积是否发生变化?若不变,求其值;若变化,请说明理由.【答案】(1)A 的坐标为()0,4,点B 的坐标为()8,4,点C 的坐标为()8,0(2)面积不发生变化,为16【详解】(1) 四边形ABCO 是长方形,,,8,4AB OC BC OA AB OC OA BC ∴====∥∥,∴点A 的坐标为()0,4,点B 的坐标为()8,4,点C 的坐标为()8,0.(2)在它们移动的过程中,四边形OPBQ 的面积不发生变化.设运动时间为s t ,则,2OQ t PC t ==,4AQ t ∴=-,25.在平面直角坐标系中,有点(,0),(0,)A a B b ,且a ,b |2|0b +=,将线段AB 向上平移k 个单位得到线段CD .(1)求出点A 、B 的坐标;(2)如图1,若5k =,过点C 作直线l x ∥轴,点M 为直线l 上一点,若MAB △的面积为8,求点M 的坐标;(3)如图2,点E 为线段CD 上任意一点,点F 为线段AB 上任意一点,120EOF ∠=︒.点G 为线段AB 与线段CD 之间一点,连接GE ,GF ,且13DEG DEO ∠=∠,80EGF ∠=︒.试写出AFG ∠与GFO ∠之间的数量关系,并证明你的结论;5k = ,5BC ∴=,(0,2)B - ,2OB ∴=,52OC BC OB ∴=-=-(4,0)A ,4∴=OA ,MAB ABC ACM S S S =+- MAB 的面积为8,108CM ∴-=,2CM ∴=,∴点(2,3)M ,②当点M 在点C 右侧,且在直线⨯MAB ABC BCM ACM S S S S =+- MAB 的面积为8,108CM ∴+=,2CM ∴=-(不合题意舍去)综上所述:点M 的坐标为(3)12AFG GFO ∠=∠,理由如下:延长FG 、CD 交于点N。
最新人教版七年级数学下册第七章 平面直角坐标系 7.1.2 平面直角坐标系 基础训练题(含答案)
最新人教版七年级数学下册第七章平面直角坐标系基础训练题(含答案)7.1.2 平面直角坐标系1.下列说法错误的是()A.平面内两条互相垂直的数轴就构成了平面直角坐标系B.平面直角坐标系中两条坐标轴是相互垂直的C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限D.坐标轴上的点不属于任何象限2.在平面直角坐标系中,点(1,5)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限3.如图,下列各点在阴影区域内的是()A.(3,2) B.(-3,2) C.(3,-2) D.(-3,-2)4.如图,点A(-2,1)到y轴的距离为()A.-2 B.1 C.2 D.55.点P在第三象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为()A.(-4,3) B.(-3,-4) C.(-3,4) D.(3,-4)6.已知点A(1,2),AC⊥x轴于C,则点C的坐标为()A.(2,0) B.(1,0) C.(0,2) D.(0,1)7.在平面直角坐标系中,点(0,-10)在()A.x轴的正半轴上B.x轴的负半轴上C.y轴的正半轴上D.y轴的负半轴上8.写出一个平面直角坐标系中第三象限内的点的坐标:_______________________.9.点P(4,-3)到x轴的距离是________个单位长度,到y轴的距离是________个单位长度.10.平面直角坐标系内有一点P(x,y),若点P在横轴上,则____________;若点P在纵轴上,则____________;若P为坐标原点,则____________。
11.写出图中A,B,C,D,E,F,O各点的坐标.12.在平面直角坐标系中,点P(2,x2)在()A.第一象限B.第四象限C.第一或者第四象限D.以上说法都不对13.如果点P(m+3,m+1)在直角坐标系的x轴上,那么P点坐标为()A.(0,2) B.(2,0) C.(4,0) D.(0,-4)14.已知坐标平面内点M(a,b)在第三象限,那么点N(b,-a)在()A.第一象限B.第二象限C.第三象限D.第四象限15.点P(a,b)满足ab>0,则点P在第____________象限;点P(a,b)满足ab<0,则点P在第____________象限;点P(a,b)满足ab=0,则点P在____________.16.已知点M到x轴的距离为3,到y轴的距离为4.(1)若M点位于第一象限,则其坐标为____________;(2)若M点位于x轴的上方,则其坐标为________________________;(3)若M点位于y轴的右侧,则其坐标为________________________.17.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是____________.18.请写出点A,B,C,D的坐标.并指出它们的横坐标和纵坐标.参考答案:1.A2.A3.A4.C5.B6.B7.D8.答案不唯一,如:(-3,-6)9.3 410.y=0 x=0 x=y=011.解:观察图,得A(2,3),B(3,2),C(-2,1),D(-1,-2),E(2.5,0),F(0,-2),O(0,0).12.D13.B14.B15.一、三二、四坐标轴上16.(4,3) (4,3)或(-4,3) (4,3)或(4,-3)17.(-3,5)18.解:A(3,2),横坐标是3,纵坐标是2;B(-3,4),横坐标是-3,纵坐标是4;C(-4,-3),横坐标是-4,纵坐标是-3;D(3,-3),横坐标是3,纵坐标是-3.。
第七章 平面直角坐标系 全章知识点归纳及典型题目练习(含答案)
第七章 平面直角坐标系1. 把有顺序的两个数 a 与b 组成的数对,叫做_____________,记作_______ . 利用________,可以很准确地表示出一个位置.2. 数轴上的点可以用____个数来表示,这个数叫做这个点的_______.反之,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.3. 平面直角坐标系⑴平面直角坐标系 在平面内画两条互相____、原点重合的数轴,组成____________.水平的数轴称为____________,习惯上取______为正方向;竖直的数轴称为____________,取______为正方向;两坐标轴的交点为平面直角坐标系的_____. ⑵点的坐标 平面内点的坐标是有序数对,其顺序是________在前,______在后,中间用“,”分开.⑶象限的概念 建立了平面直角坐标系的平面是坐标平面,坐标平面被两条坐标轴分成四个部分,分别叫做第一、二、三、四象限. 坐标轴上的点不属于_____.4. 特殊位置的点的坐标特征⑴ x 轴将坐标平面分为两部分,x 轴上方的点的纵坐标为正数,x 轴下方的点的纵坐标为______;y 轴把坐标平面分为两部分,y 轴左侧的点的横坐标为_____,y 轴右侧的点的横坐标为_____.⑵规定原点坐标是_____.⑶坐标平面内的点的坐标有如下特征:点(),P x y 在第一象限:0,0.x y >>点(),P x y 在第二象限:_________.点(),P x y 在第三象限:_________.点(),P x y 在第四象限:_________.⑷x 轴上的点可以记为(),0x ,y 轴上的点可记为()0,y ,也就是说x 轴(横轴)上的点的纵坐标为____,y 轴(纵轴)上的点的横坐标为_____ .⑸点(),P a b 关于x 轴对称的点的坐标是__________;关于y 轴对称的点的坐标是_______;关于原点对称的点的坐标是___________.5. 利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程.(1)建立坐标系,选择一个____________为原点,确定x 轴、y 轴的___方向;(2)根据具体问题确定______________,在坐标轴上标出__________;(3)在坐标平面内画出这些点,写出各点的_______和各个地点的名称.6. 利用坐标表示平移的规律:⑴在平面直角坐标系中,将点(x ,y )向右(或左)平移a (a 是正数)个单位长度,可以得到对应点(x +a ,y )(或( , ));将点(x ,y )向上(或下)平移b (b 是正数)个单位长度,可以得到对应点(x ,y +b )(或( , )). ⑵在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a ,相应的新图形就是把原图形向___(或向____)平移___个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a ,相应的新图形就是把原图形向___(或向 __) 平移___个单位长度.熟悉以下各题:7. 已知A (-4,2),B (1,2),则A ,B 两点的距离是( )A .3个单位长度B .4个单位长度C .5个单位长度D .6个单位长度8. 点P (m +3,m +1)在直角坐标系的x 轴上,则点P 的坐标是( )A .(2,0)B .(0,-2)C .(4,0)D .(0,-4)9. 点A (-2,3)在第____象限,它到x 轴的距离是____.10. 点B (-5,0)在_____轴上;若点C (a +2,a -1)在y 轴上,则a =____.11. 点A (2,-5)关于x 轴的对称点的坐标是_________,关于y 轴的对称点的坐标是_________.12. 若点A (a ,2)与B (-3,b )关于x 轴对称,则a =____,b =_____.13. 如图,△ABC 中任意一点P (00,x y )经平移后对应点为100(5,3)P x y ++.将△ABC作同样的平移得到△A 1B 1C 1.求:⑴111,,A B C 坐标;⑵△A 1B 1C 1的面积.参考答案1.有序数对 (a ,b ) 有序数对2. 一 坐标3.⑴垂直 平面直角坐标系 横轴( x 轴) 向右 纵轴(y 轴) 向上 原点 ⑵横坐标 纵坐标 ⑶任何象限4.⑴负数 负数 正数 ⑵(0,0)⑶0,0;0,0;0,0.x y x y x y <><<><⑷0,0.⑸(a ,-b )(-a ,b ) (-a ,-b )5.适当的参照点 正 单位长度 单位长度 坐标6.,x a y - ,x y b - 右 (左) a 上 (下)a.7.C8.A9.二 3 10.x -2 11.()2,5()2,5--12. -3 -2 13.()()()3,61,27,3 11平方单位.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 平面直角坐标系基础练习题一、选择题1. 下列各点中,在第二象限的点是( )A. (2,3)B. (2,-3)C. (-2,-3)D. (-2,3)2. 将点A (-4,2)向上平移3个单位长度得到的点B 的坐标是( )A. (-1,2)B. (-1,5)C. (-4,-1)D. (-4,5)3.在平面直角坐标系中,点()1,12+-m 一定在( )A .第一象限B .第二象限C .第三象限D .第四象限4. 点A (m +3,m +1)在x 轴上,则A 点的坐标为( )A (0,-2)B 、(2,0)C 、(4,0)D 、(0,-4)5. 点P 的横坐标是-3,且到x 轴的距离为5,则P 点的坐标是( )A. (5,-3)或(-5,-3)B. (-3,5)或(-3,-5)C. (-3,5)D. (-3,-5)6. 若点P (a ,b )在第四象限,则点M (b-a ,a-b )在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限7.若点P (a ,b )到x 轴的距离是2,到y 轴的距离是3,则这样的点P 有 ( )A.1个 B.2个 C.3个 D.4个8.点P 在第二象限内,点P 到x 轴的距离是2,到y 轴的距离是3,那么点P 的坐标为( ).A.(-2,3)B.(-3,-2)C.(-3,2)D.(3,-2)9.将点P ()3,4-先向左平移2个单位,再向下平移2个单位得点P ′,则点P ′的坐标为( )A .()5,2-B .()1,6-C .()5,6-D .()1,2-10.如果点P (m -,3)与点P 1(5-,n )关于y 轴对称,则m ,n 的值分别为 ( )A .3,5=-=n mB .3,5==n mC .3,5-=-=n mD .5,3=-=n m11.已知点A ()2,2-,如果点A 关于x 轴的对称点是B ,点B 关于原点的对称点是C ,那么C 点的坐标是( )A .()2,2B .()2,2-C .()1,1--D .()2,2--12.在平面直角坐标系中,将点A (1,2)的横坐标乘以-1,纵坐标不变,得到点A ´,则点A 与点A ´的关系是( ). A 、关于x 轴对称 B 、关于y 轴对称C 、关于原点对称D 、将点A 向x 轴负方向平移一个单位得点A ´13.已知正方形ABCD 的三个顶点坐标为A (2,1),B (5,1),D(2,4),现将该正方形向下平移3个单位长度,再向左平移4个单位长度,得到正方形A'B'C'D',则C’点的坐标为( )A. (5,4)B. (5,1)C. (1,1)D. (-1,-1)14.已知点A 的坐标是(a ,b),若a +b <0、ab >0.则点A 在( ).A .第一象限B .第二象限C .第三象限D .第四象限15.若点M 在第一、三象限的角平分线上,且点M 到x 轴的距离为2,则点M 的坐标是( )A .(2,2)B .(-2,-2)C .(2,2)或(-2,-2)D .(2,-2)或(-2,2)16.已知点P 的坐标为()63,-2+a a ,且点P 到两坐标轴的距离相等,则点P 的坐标是( )A.(3,3)B.(3,-3)C. (6,-6)D.(3,3)或(6,-6)17.如果点()3,2+x x 在x 轴上方,y 轴右侧,且该点到x 轴和y 轴的距离相等,则x 的值为( )A.1B.-1C.3D.-318. 已知M (1,-2),N(-3,-2)则直线MN 与x 轴,y 轴的位置关系分别为( )A.相交,相交B.平行,平行C.垂直,平行D.平行,垂直19.已知点A ()b a 2,3在x 轴上方,y 轴的左边,则点A 到x 轴.y 轴的距离分别为( )A .b a 2,3-B .b a 2,3-C .a b 3,2-D .a b 3,2-20.如果点M ()y x ,的坐标满足0=yx ,那么点M 的可能位置是( ) A.x 轴上的点的全体 B. 除去原点后x 轴上的点的全体C.y 轴上的点的全体D. 除去原点后y 轴上的点的全体21.若三角形ABC 中经平移后任意一点P ()00,y x 的对应点为()3,5001-+y x P ,则点A (-1,4)的对应点1A 的坐标是( ) A.(4,1) B.(9,-4) C.(-6,7) D.(-1,2)22. 到x 轴的距离等于2的点组成的图形是( )A. 过点(0,2)且与x 轴平行的直线B. 过点(2,0)且与y 轴平行的直线C. 过点(0,-2且与x 轴平行的直线D. 分别过(0,2)和(0,-2)且与x 轴平行的两条直线二、填空题1. 在奥运游泳馆“水魔方”一侧的座位席上,5排2号记为(5,2),则3排5号记为 .2. 如果点A ()b a ,在x 轴上,且在原点右侧,那么a ,b3. 如果点()1,-a a M 在x 轴下方,y 轴的右侧,那么a 的取值范围是4. 点A(3,-4)到y 轴的距离为_______,到x 轴的距离为_____.5. 若点P(2,k-1)在第一象限,则k 的取值范围是_______.6.已知点M (m ,m -1)在第二象限,则m 的取值范围是 .7.已知点M ()a a -+4,3在y 轴上,则点M 的坐标为_____.8. 已知点P(0,a)在y 轴的负半轴上,则点Q(-2a -1,-a+1)在第 象限.9.如果点M ()ab b a ,+在第二象限,那么点N ()b a ,在第___象限.10. 第二象限内的点()P x y ,满足||9x =,24y =,则点P 的坐标是 .11.已知点P 的坐标是(m ,1-),且点P 关于x 轴对称的点的坐标是(3-,n 2),则_________,==n m . 12.若 ),()与,(13-m n N m M 关于原点对称,则 __________,==n m .13.已知点P ()3,3b a +与点Q ()b a 2,5+-关于x 轴对称,则___________==b a .14.点 A 在第二象限 ,它到 x 轴 、y 轴的距离分别是 3 、2,则A 点的坐标是 .15. 已知点M(2m+1,3m-5)到x 轴的距离是它到y 轴距离的2倍,则m=16. 已知△ABC 三顶点坐标分别是A (-7,0)、B (1,0)、C (-5,4),那么△ABC 的面积等于______.17. 直线a ∥x 轴,且过点(-2,3)和(5,y ),则y=18. 已知两点A ()m ,3-,B ()4,-n ,若AB ∥y 轴,则n = , m 的取值范围是 .19. 已知AB∥x 轴,点A 的坐标为(3,2),并且AB =5,则点B 的坐标为 .20. 过点A (-2,5)作x 轴的垂线L ,则直线L 上的点的坐标特点是_________.21. 线段CD 是由线段AB 平移得到的,点(14)A -,的对应点为(47)C ,,则点(41)B --,的对应点D 的坐标是 .22. 将点P (-3,y )向下平移3个单位,向右平移2个单位后得到点Q (x ,-1),则xy =________.23.点K ()n m ,在坐标平面内,若0>mn ,则点K 位于___象限;若0<mn ,则点K 不在___象限.24.已知0=mn ,则点(m ,n )在 .25. △ABC 上有一点P (0,2),将∆ABC 先沿x 轴负方向平移2个单位长度,再沿y 轴正方向平移3个单位长度,得到的新三角形上与点P 相对应的点的坐标是 .26. 李明的座位在第5排第4列,简记为(5,4),张扬的座位在第3排第2列,简记为(3,2),若周伟的座位在李明的后面相距2排,同时在他的左边相距3列,则周伟的座位可简记为 .27. 如果点M (3a-9,1-a )是第三象限的整数点(即横、纵坐标均为整数),则M 的坐标为 ;28. 在平面直角坐标系中,点A 的坐标为(11),,点B 的坐标为(111),,点C 到直线AB 的距离为4,且ABC △是直角三角形,则满足条件的点C 有 个.三、解答题1.如图,这是某市部分简图,请以火车站为坐标原点建立平面直角坐标系,并分别写出各地的坐标.2. 如图,△ABC 中任意一点P (x 0,y 0)经平移后对应点为P 1(x 0+5,y 0+3),将△ABC 作同样的平移得到△A 1B 1C 1.画出△A 1B 1C 1,并求A 1,B 1,C 1的坐标.3. 在平面直角坐标系中, △ABC的三个顶点的位置如图所示, 点A'的坐标是(-2,2), 现将△ABC平移,使点A 变换为点A', 点B′、C′分别是B 、C 的对应点. (1)请画出平移后的像△A'B'C'(不写画法) , 并直接写出点B′、C′的坐标:B′ ,C′ ;(2)若△ABC 内部一点P 的坐标为(a,b ),则点P 的对应点P ′的坐标是 .4. 如图,△ABC 三个顶点A 、B 、C 的坐标分别为A (1,2)、B (4,3)、C (3,1).(1)把△A 1B 1C 1向右平移2个单位,再向上平移3个单位,恰好得到△ABC ,试画出△A 1B 1C 1并写出△A 1B 1C 1三个顶点的坐标;(2)求出△ A 1B 1C 1的面积。
5.如图,在平面直角坐标系中,点A ,B 的坐标分别为A (a ,0),B (b ,0),且a 、b 满足a=b -3+3-b -1,现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1) 求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形(2) 在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.6.如图,在下面直角坐标系中,已知A (0,a ),B (b ,0),C (b ,c )三点,其中a 、b 、c 满足关系式:()0322=-+-b a ,()24-c ≤0. (1)求a 、b 、c 的值;(2)如果在第二象限内有一点P (m ,21),请用含m 的式子表示四边形ABOP 的面积; (3)在(2)的条件下,是否存在点P ,使四边形ABOP 的面积与△ABC的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.。
